Substructure-Based Topology Optimization for Symmetric Hierarchical Lattice Structures
Abstract
1. Introduction
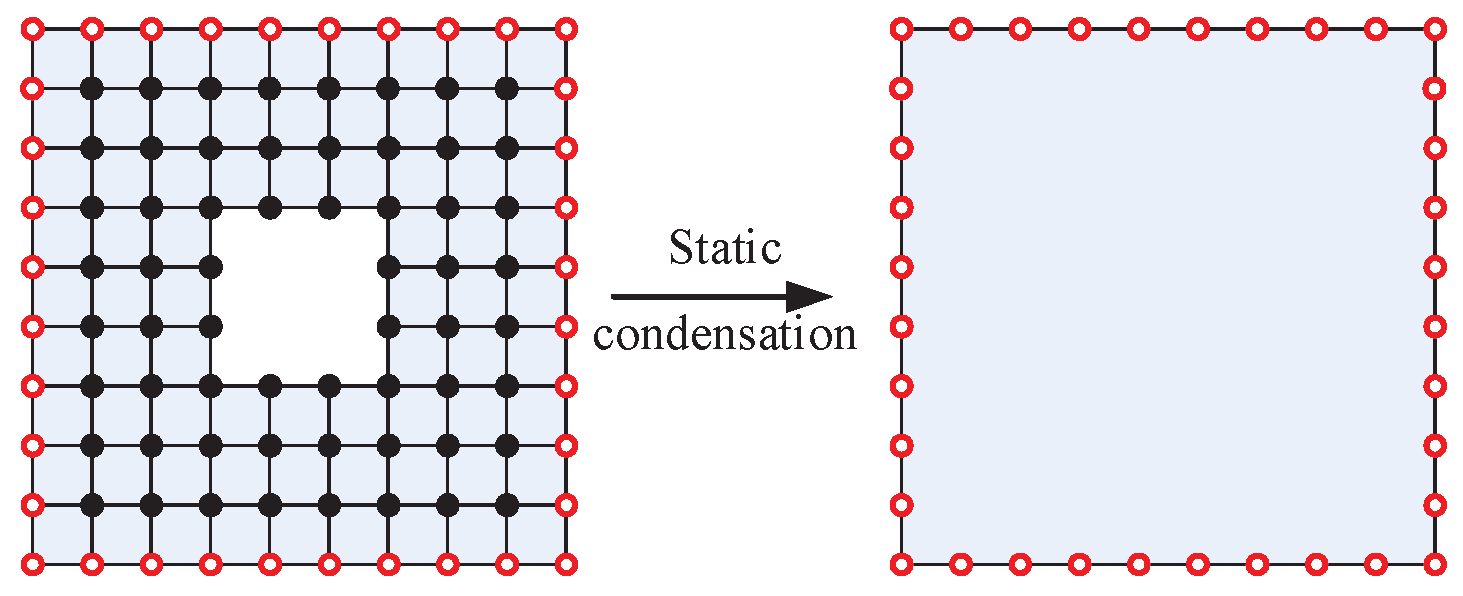
2. The Static Condensation of Substructure
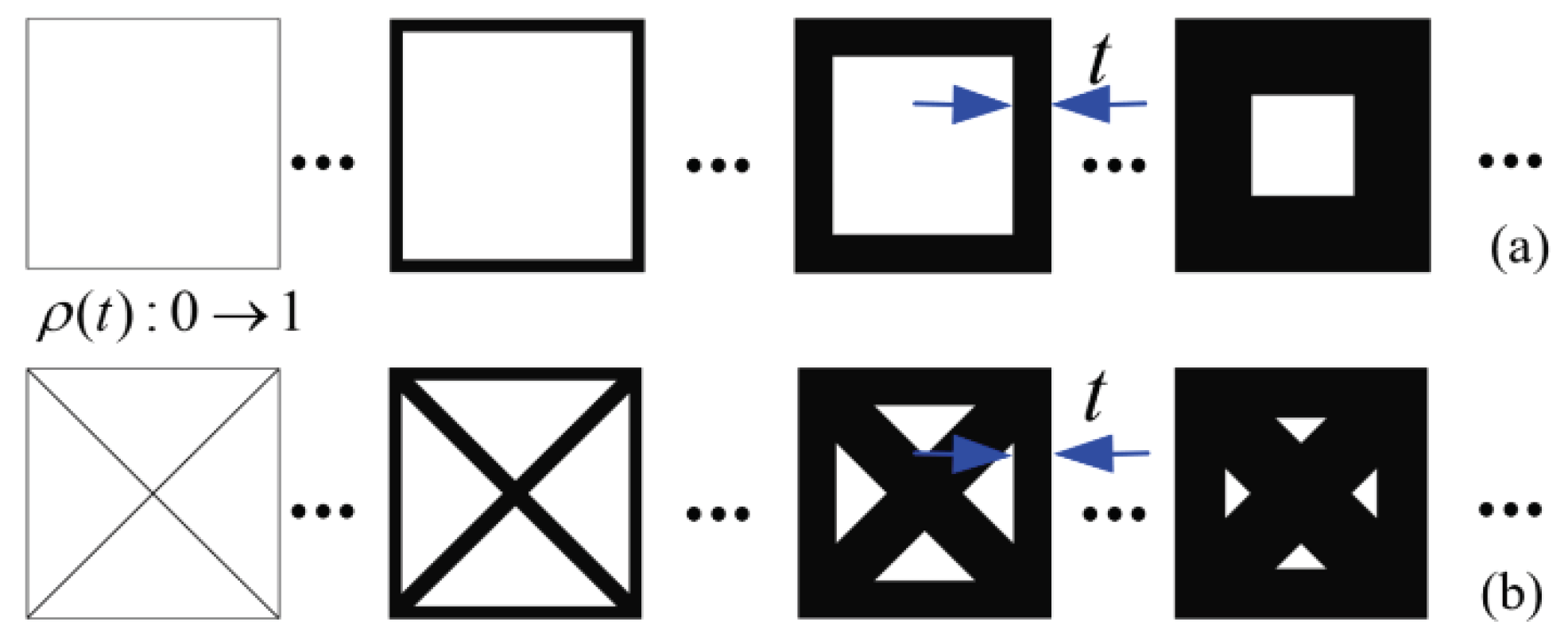
3. Substructure-Based Symmetric Microstructure Model
4. Symmetric Structures Design Method
4.1. The Topology Optimization Model
4.2. Sensitivity Analysis
5. Numerical Example
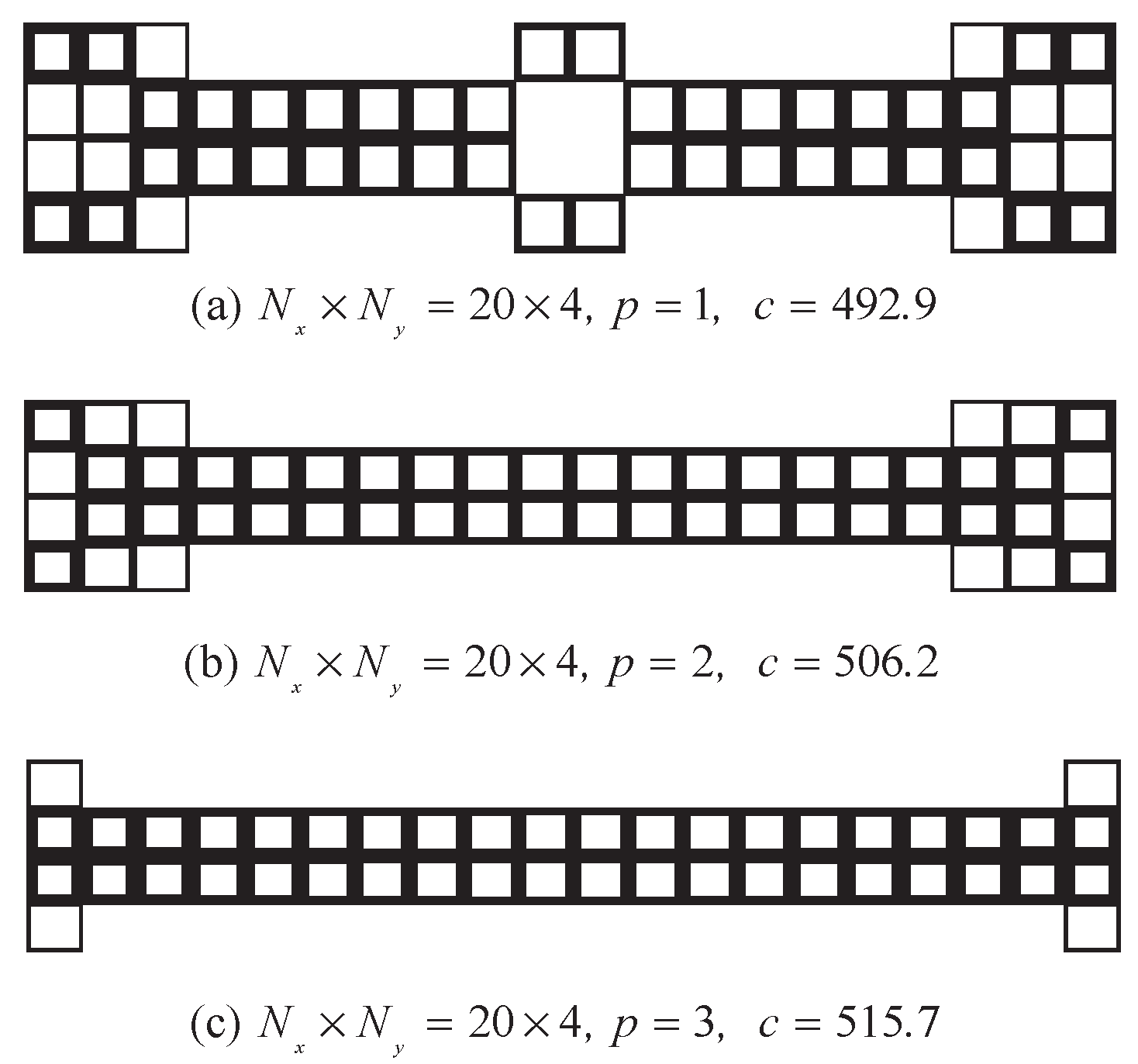
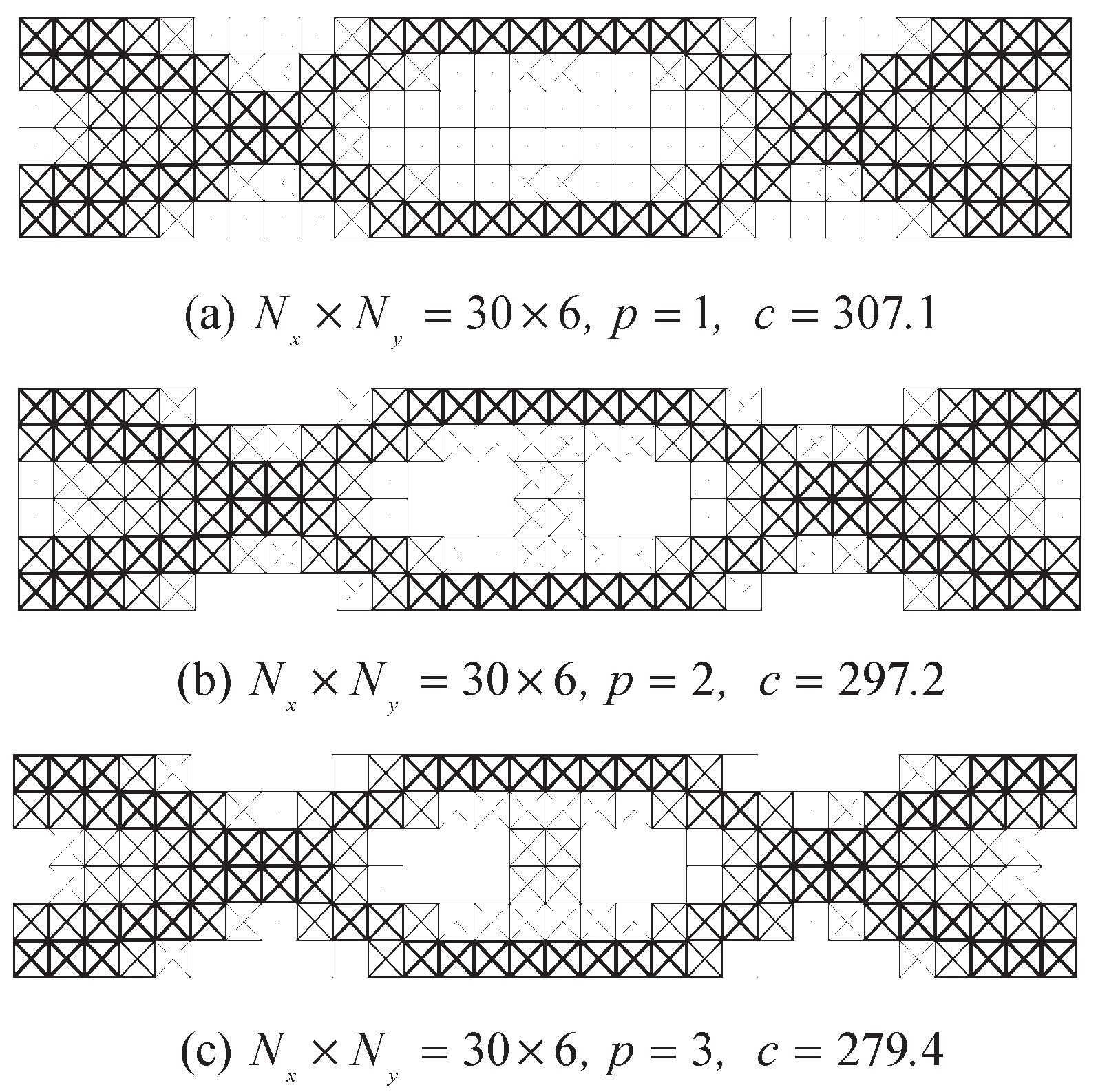
5.1. Clamped Ends Beam
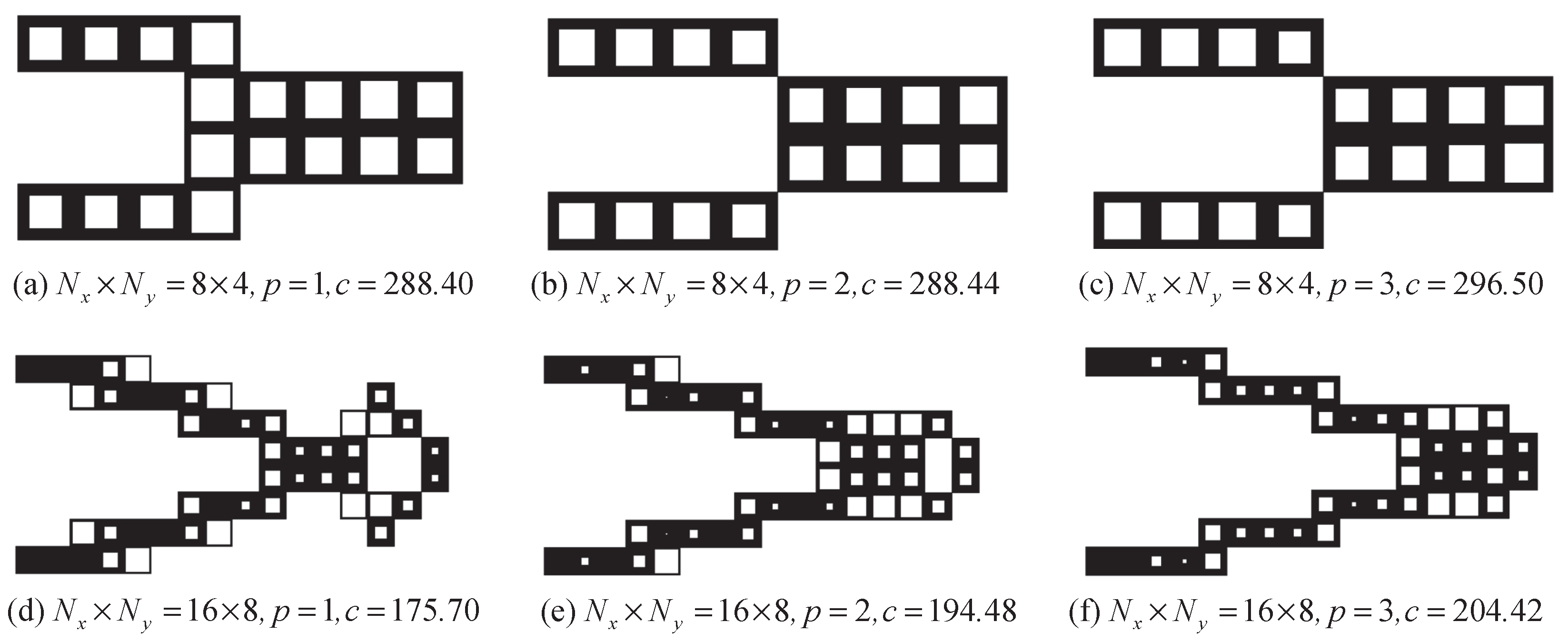
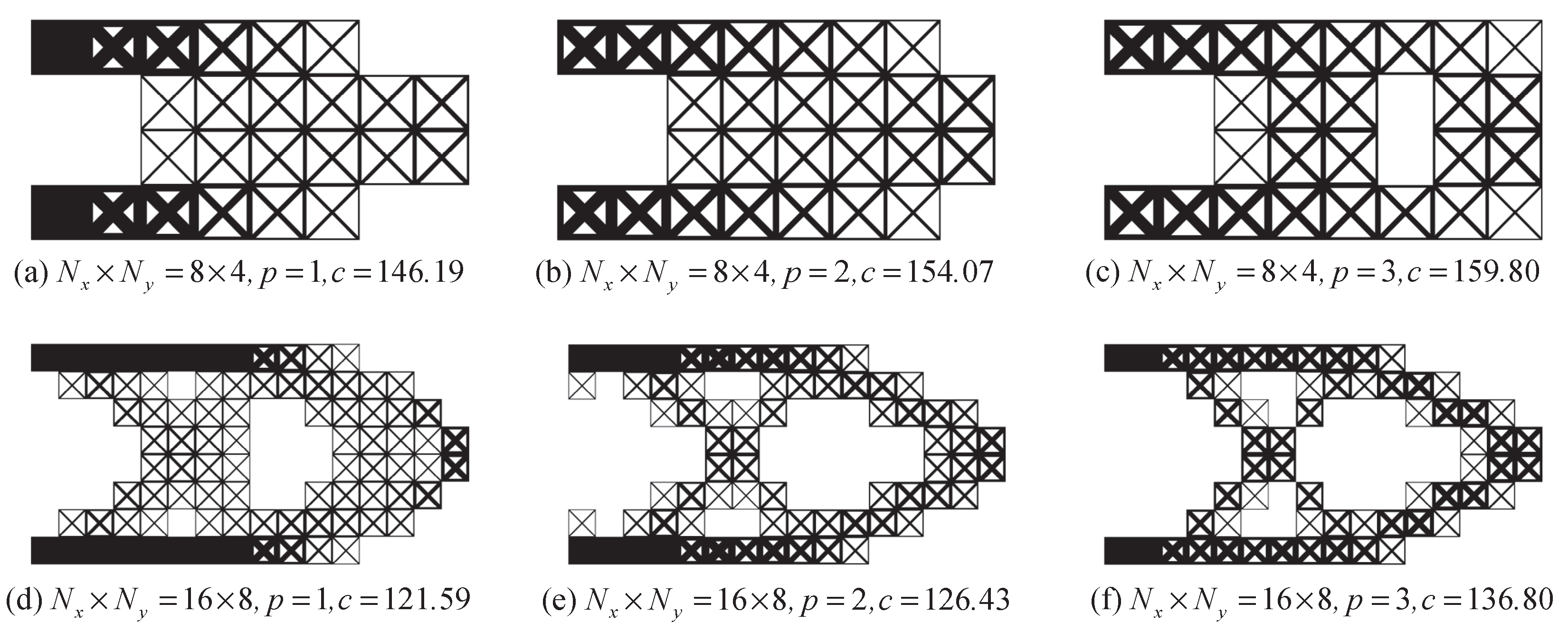
5.2. The Cantilever Design
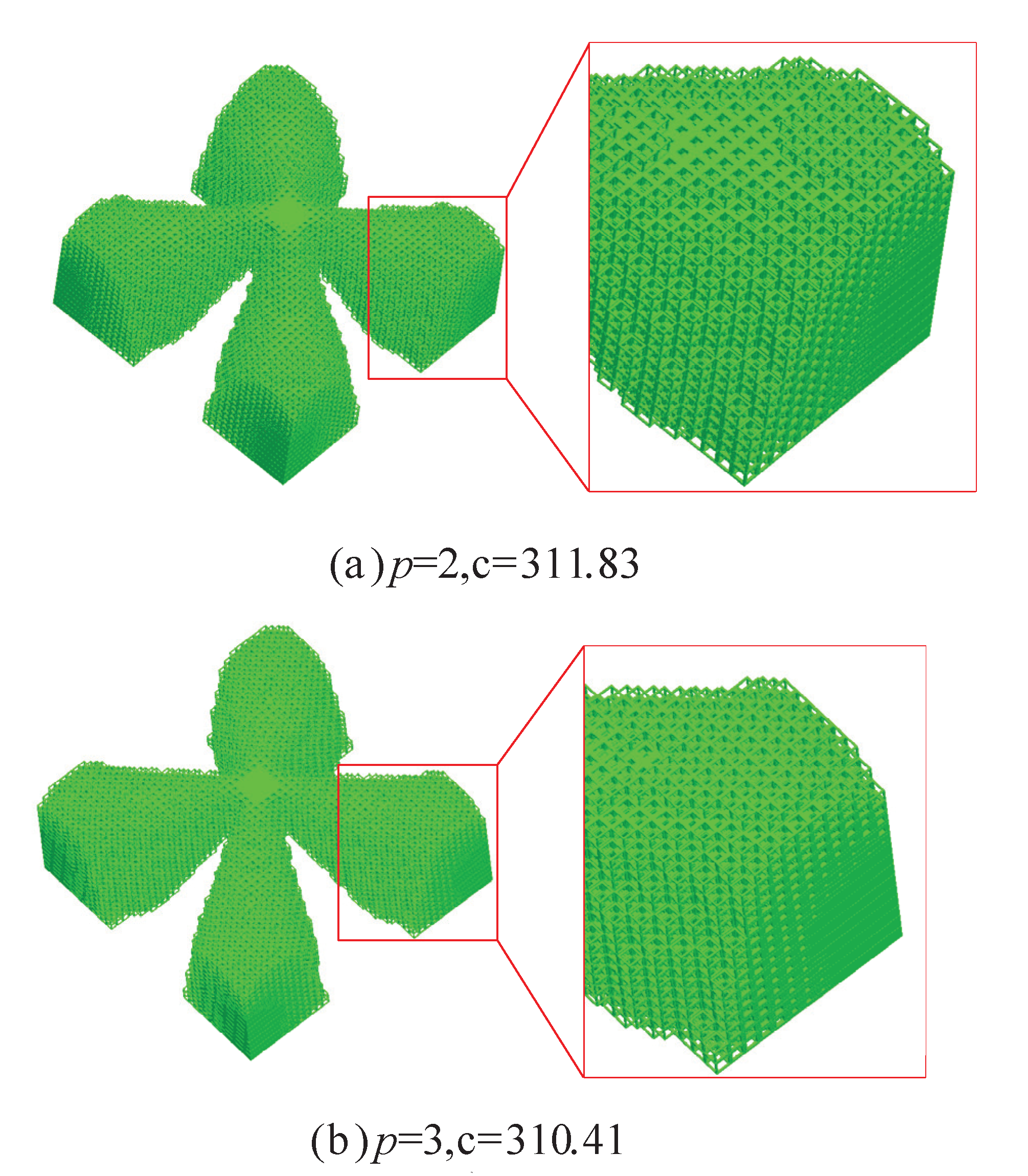
5.3. D Simply Supported Cube Design
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| SIMP | Solid isotropic material with penalization |
| BESO | Bi-directional evolutionary structural optimization |
| MOR | Model Order Reduction |
| FEA | Finite element analysis |
References
- Xia, L.; Breitkopf, P. Concurrent topology optimization design of material and structure within FE2 nonlinear multiscale analysis framework. Comput. Methods Appl. Mech. Eng. 2014, 278, 524–542. [Google Scholar] [CrossRef]
- Sigmund, O.; Søndergaard Jensen, J. Systematic design of phononic band–gap materials and structures by topology optimization. Philos. Trans. R. Soc. Lond. Ser. A: Math. Phys. Eng. Sci. 2003, 361, 1001–1019. [Google Scholar] [CrossRef]
- Park, J.H.; Yang, S.H.; Lee, H.R.; Yu, C.B.; Pak, S.Y.; Oh, C.S.; Kang, Y.J.; Youn, J.R. Optimization of low frequency sound absorption by cell size control and multiscale poroacoustics modeling. J. Sound Vib. 2017, 397, 17–30. [Google Scholar] [CrossRef]
- Cheng, L.; Liu, J.; Liang, X.; To, A.C. Coupling lattice structure topology optimization with design-dependent feature evolution for additive manufactured heat conduction design. Comput. Methods Appl. Mech. Eng. 2018, 332, 408–439. [Google Scholar] [CrossRef]
- Wang, Y.; Arabnejad, S.; Tanzer, M.; Pasini, D. Hip implant design with three-dimensional porous architecture of optimized graded density. J. Mech. Des. 2018, 140, 111406. [Google Scholar] [CrossRef]
- Bendsøe, M.P.; Kikuchi, N. Generating optimal topologies in structural design using a homogenization method. Comput. Methods Appl. Mech. Eng. 1988, 71, 197–224. [Google Scholar] [CrossRef]
- Da, D.; Yvonnet, J.; Xia, L.; Le, M.V.; Li, G. Topology optimization of periodic lattice structures taking into account strain gradient. Comput. Struct. 2018, 210, 28–40. [Google Scholar] [CrossRef]
- Xia, L.; Breitkopf, P. Multiscale structural topology optimization with an approximate constitutive model for local material microstructure. Comput. Methods Appl. Mech. Eng. 2015, 286, 147–167. [Google Scholar] [CrossRef]
- Liu, S.; Li, Q.; Chen, W.; Tong, L.; Cheng, G. An identification method for enclosed voids restriction in manufacturability design for additive manufacturing structures. Front. Mech. Eng. 2015, 10, 126–137. [Google Scholar] [CrossRef]
- Geers MG, D.; Yvonnet, J. Multiscale modeling of microstructure–property relations. Mrs Bull. 2016, 41, 610–616. [Google Scholar] [CrossRef]
- Langelaar, M. Topology optimization of 3D self-supporting structures for additive manufacturing. Addit. Manuf. 2016, 12, 60–70. [Google Scholar] [CrossRef]
- Langelaar, M. An additive manufacturing filter for topology optimization of print-ready designs. Struct. Multidiscip. Optim. 2017, 55, 871–883. [Google Scholar] [CrossRef]
- Zhang, K.; Cheng, G.; Xu, L. Topology optimization considering overhang constraint in additive manufacturing. Comput. Struct. 2019, 212, 86–100. [Google Scholar] [CrossRef]
- Osanov, M.; Guest, J.K. Topology optimization for architected materials design. Annu. Rev. Mater. Res. 2016, 46, 211–233. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, L.; Daynes, S.; Zhang, H.; Feih, S.; Wang, M.Y. Design of graded lattice structure with optimized mesostructures for additive manufacturing. Mater. Des. 2018, 142, 114–123. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, H.; Pasini, D. Multiscale isogeometric topology optimization for lattice materials. Comput. Methods Appl. Mech. Eng. 2017, 316, 568–585. [Google Scholar] [CrossRef]
- Cramer, A.; Challis, V.; Roberts, A. Microstructure interpolation for macroscopic design. Struct. Multidiscip. Optim. 2016, 53, 489–500. [Google Scholar] [CrossRef]
- Du, Z.; Kim, H. Multiscale design considering microstructure connectivity. In Proceedings of the 2018 AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar]
- Wang, Y.; Chen, F.; Wang, M. Concurrent design with connectable graded microstructures. Comput. Methods Appl. Mech. Eng. 2017, 317, 84–101. [Google Scholar] [CrossRef]
- Groen, J.; Sigmund, O. Homogenization-based topology optimization for high-resolution manufacturable microstructures. Int. J. Numer. Methods Eng. 2018, 113, 1148–1163. [Google Scholar] [CrossRef]
- Arabnejad, S.; Pasini, D. Mechanical properties of lattice materials via asymptotic homogenization and comparison with alternative homogenization methods. Int. J. Mech. Sci. 2013, 77, 249–262. [Google Scholar] [CrossRef]
- Li, Q.; Xu, R.; Liu, J.; Liu, S.; Zhang, S. Topology optimization design of multi-scale structures with alterable microstructural length-width ratios. Compos. Struct. 2019, 230, 111454. [Google Scholar] [CrossRef]
- Radman, A.; Huang, X.; Xie, Y.M. Topology optimization of functionally graded cellular materials. J. Mater. Sci. 2013, 48, 1503–1510. [Google Scholar] [CrossRef]
- Guyan, R.J. Reduction of Stiffness and Mass Matrices. AIAA J. 1965, 3, 380. [Google Scholar] [CrossRef]
- Groen, J.P.; Langelaar, M.; Sigmund, O.; Ruess, M. Higher-Order Multi-Resolution Topology Optimization Using the Finite Cell Method. Int. J. Numer. Methods Eng. 2017, 110, 903–920. [Google Scholar] [CrossRef]
- Borrvall, T.; Petersson, J. Large-Scale Topology Optimization in 3d Using Parallel Computing. Comput. Methods Appl. Mech. Eng. 2001, 190, 6201–6229. [Google Scholar] [CrossRef]
- Wu, Z.; Xia, L.; Wang, S.; Shi, T. Topology optimization of hierarchical lattice structures with substructuring. Comput. Methods Appl. Mech. Eng. 2019, 345, 602–617. [Google Scholar] [CrossRef]
- Fu, J.; Xia, L.; Gao, L.; Xiao, M.; Li, H. Topology optimization of periodic structures with substructuring. J. Mech. Des. 2019, 141, 071403. [Google Scholar] [CrossRef]
- Valero-Lara, P.; Jansson, J. A Non-uniform Staggered Cartesian Grid Approach for Lattice-boltzmann Method. Procedia Comput. Sci. 2015, 51, 296–305. [Google Scholar] [CrossRef]
- Valero-Lara, P.; Jansson, J. Multi-domain Grid Refinement for Lattice-Boltzmann Simulations on Heterogeneous Platforms. In Proceedings of the IEEE International Conference on Computational Science & Engineering, Porto, Portugal, 23–23 October 2015. [Google Scholar]


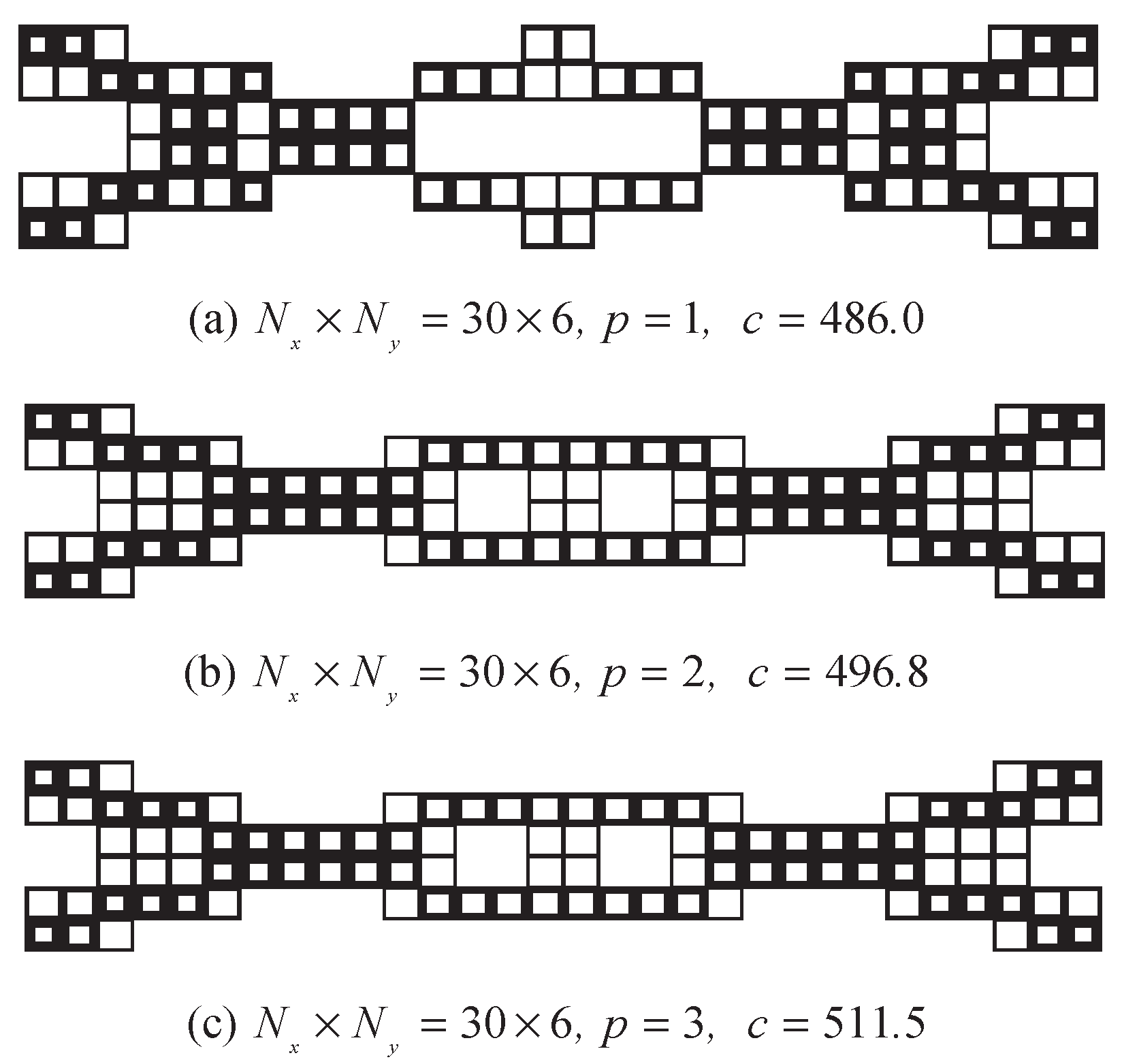





© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.; Xiao, R. Substructure-Based Topology Optimization for Symmetric Hierarchical Lattice Structures. Symmetry 2020, 12, 678. https://doi.org/10.3390/sym12040678
Wu Z, Xiao R. Substructure-Based Topology Optimization for Symmetric Hierarchical Lattice Structures. Symmetry. 2020; 12(4):678. https://doi.org/10.3390/sym12040678
Chicago/Turabian StyleWu, Zijun, and Renbin Xiao. 2020. "Substructure-Based Topology Optimization for Symmetric Hierarchical Lattice Structures" Symmetry 12, no. 4: 678. https://doi.org/10.3390/sym12040678
APA StyleWu, Z., & Xiao, R. (2020). Substructure-Based Topology Optimization for Symmetric Hierarchical Lattice Structures. Symmetry, 12(4), 678. https://doi.org/10.3390/sym12040678



