Symmetry Classes and Matrix Representations of the 2D Flexoelectric Law

Abstract

We determine the different symmetry classes of bi-dimensional flexoelectric tensors. Using the harmonic decomposition method, we show that there are six symmetry classes. We also provide the matrix representations of the flexoelectric tensor and of the complete flexoelectric law, for each symmetry class.

1. Introduction

In recent years, the study of electromechanical effects has attracted the attention of many researchers. The best known of these electromechanical effects are piezoelectricity [1,2,3] and flexoelectricity [4,5]. Piezoelectricity is the appearance of a polarization in a dielectric material when it is subjected to an uniform mechanical strain, while flexoelectricity is the linear response of a polarization to a non-uniform strain or a strain-gradient. Flexoelectricity is a non classical electromechanical coupling and it can be viewed as a higher-order electromechanical effect with respect to piezoelectricity [5].

This higher-order electromechanical coupling has attracted a lot of interest in recent years as it allows electromechanical couplings in materials for which the piezoelectric tensor is zero [6,7]. For instance, this flexoelectricity coupling has been identified in polymers [8], biological membranes [9], and, recently its role in the bone remodeling process has been evidenced [10,11]. The design of mesostructure producing this effect is a new trend in topological optimization [12] since the mastery of this effect makes it possible to consider the development of new sensors, energy harvesting devices, and even the development of polymer actuators. This last application arouses a strong interest in the field of soft robotics, where the optimization of this coupling would allow the control of the geometry of polymers via an electric field [13]. Recently, the flexoelectricity phenomenon is highlighted in 2D materials like 2D crystalline membranes or graphene sheets, and also in thin films [14,15].

Our work is part of a project in line with this perspective of optimal design of higher-order electromechanical mesostructures. Following the approach opened in elasticity to work with tensor invariants [16], we aim at developing an invariant-based topological optimization algorithm. But before considering algorithmic questions related to topological optimization, the first step is to fully characterize the different tensors that contribute to the considered constitutive law. The present contribution will solely concern this aspect of the project. Furthermore, this task has to be undertaken by considering the final application, hence by trying to give a physical content to invariants.

Piezoelectric and flexoelectric effects can be introduced via the following constitutive equation [1,5]:

$$\underline{\mathrm{p}}={\underset{\simeq }{\mathrm{P}}}^{\top }:\underset{\sim }{\mathsf{\epsilon }}+{\underset{\approx }{\mathrm{F}}}^{\top }⋮\underset{\simeq }{\mathsf{\eta }}+\underset{\sim }{\mathrm{S}}·\underline{\mathrm{q}},$$

(1)

where $\underline{\mathrm{p}}$ is the polarization, $\underline{\mathrm{q}}$ the electric field, $\underset{\sim }{\mathsf{\epsilon }}$ the strain tensor, and $\underset{\simeq }{\mathsf{\eta }}$ the strain-gradient tensor. The second-order tensor $\underset{\sim }{\mathrm{S}}$, the third-order tensor ${\underset{\simeq }{\mathrm{P}}}^{\top }$, and the fourth-order tensor ${\underset{\approx }{\mathrm{F}}}^{\top }$ describe the dielectric effect, the direct piezoelectric and flexoelectric effects [5], respectively. It is important to note that in centrosymmetric materials, the third-order tensor ${\underset{\simeq }{\mathrm{P}}}^{\top }$ vanishes. This means that piezoelectricity exists only in non-centrosymmetric materials.

The vector space of flexoelectric tensors is denoted by $\mathbb{F}\mathrm{lex}$. For the optimal design of flexoelectric structures, the understanding of the algebraic structure of $\mathbb{F}\mathrm{lex}$ is mandatory. Important issues concerning $\mathbb{F}\mathrm{lex}$ include the following questions:

• What types of anisotropies can flexoelectric tensors model?
• How does one characterize flexoelectric materials independently of their spatial orientation?
• How does one parametrize the different characteristics (anisotropy, coupling, etc.) of flexoelectric materials in an intrinsic way?

In mathematical terms, these questions consist of studying the linear representation of the d-dimensional orthogonal group $\mathrm{O}\left(d\right)$ on $\mathbb{F}\mathrm{lex}$ ($d=2$ in 2D and $d=3$ in 3D) and characterizing the geometry of the orbit space $\mathbb{F}\mathrm{lex}/\mathrm{O}\left(d\right)$. Answering these questions in the 3D setting is a rather difficult task. For instance, for the well-known situation of the elasticity tensor, the invariant basis comprises 294 invariants in 3D, for only 5 invariants in 2D. Hence, to develop a mesostructural optimization algorithm, we aim to first formulate the problem in a 2D setting. In addition to the desire to reduce the complexity of the problem, the 2D case has an intrinsic interest for the study of 2D materials or structures with flexoelectric effects.

The objective of the present study is more modest since only the 2D situation is considered. Furthermore, only the first of the three questions will be considered in this article. Our goal is to set the framework to answer two other questions in future work.

The problem of classifying flexoelectric materials by determining the number and types of symmetry classes of flexoelectric tensors has been solved in 3D [17]. In this work, we will solve the same problem in the two-dimensional context by using a completely different approach than the one used in [17]. Compared to the article [17], and in order to move towards the study of invariant algebras, the present contribution states in a more detailed way the structure of the space $\mathbb{F}\mathrm{lex}$. Furthermore, we introduce a harmonic decomposition obtained by the Clebsch–Gordan algorithm, which differs from the one of [17] obtained by the Spencer algorithm [18]. Another significant difference is that our decomposition is orthogonal and based on the physics of strain-gradient elasticity while the one of [17] has no clear physical interpretation. The physical content of our decomposition is detailed in the present contribution. As such, the present paper is not a reduced version of the reference [17] but a complete study on its own.

From the above presentation, it can be seen that the flexoelectricity theory is closely related to the strain-gradient elasticity theory [19,20]. Some studies [21,22] provide the complete description of bi-dimensional anisotropic strain-gradient elasticity by determining the different symmetry classes of the constitutive tensors and their associated matrix forms. We will complete these studies in the case where strain-gradient effects are coupled with flexoelectric ones.

Unlike elasticity tensors, it is not always possible to use for the flexoelectric tensors the Voigt notation as pointed out by Yudin et al. in [5]. Therefore, to provide the matrix representation of the complete flexoelectric law we need to construct appropriate orthonormal bases in order to express the different constitutive tensors in a matrix form.

This article is organized as follows. In Section 2, we introduce the notation used throughout the text. Section 3 is devoted to the description of the flexoelectricity law. We present the constitutive equations for a flexoelectric material. Then we describe how we can decompose the space of flexoelectric tensors into a direct sum of irreducible spaces. Finally, we determine the different symmetry classes of the flexoelectric tensor and of the complete flexoelectricity law. In Section 4, we provide the matrix representations of the flexoelectric tensor and of the complete flexoelectricity law. In Section 5, we give the explicit harmonic decomposition of the flexoelectric tensor. We rewrite the matrix representations of the flexoelectric tensor obtained in Section 4 in terms of the components of the harmonic decomposition and discuss the degenerated situations. We wish to emphasize that the explicit harmonic decomposition provided in Section 5 is a new result of practical importance for the computation of physically-based invariants of the flexoelectricity tensor.

2. Notation

In this section we provide some notation and conventions that will be used throughout the article. Let ${\mathbb{R}}^m$ be the m-dimensional real Euclidean space. We equip this space with a rectangular Cartesian coordinate system with origin O and an orthonormal basis $\mathcal{P}=\{{\underline{\mathrm{e}}}_1,\dots ,{\underline{\mathrm{e}}}_m\}$. We associate with each point in ${\mathbb{R}}^m$ a unique m-tuple of real numbers $(x_1,\dots ,x_m)$. We can then view ${\mathbb{R}}^m$ as a m-dimensional vector space with elements $\underline{\mathrm{x}}=(x_1,\dots ,x_m)=x_1{\underline{\mathrm{e}}}_1+\cdots +x_m{\underline{\mathrm{e}}}_m=x_i{\underline{\mathrm{e}}}_i$, where Einstein summation convention is used, i.e., when an index appears twice in an expression, it implies the summation of that term over all the values of the index.

Below are provided some specific notations and conventions used in this article.

Groups:

The following matrix groups are considered in this article:

• $\mathrm{GL}\left(2\right)$ the group of invertible $2\times 2$ matrices over $\mathbb{R}$;
• $\mathrm{O}\left(2\right)$ the group of $2\times 2$ matrices $\mathrm{Q}$ satisfying $\mathrm{Q}\in \mathrm{GL}\left(2\right)$ and ${\mathrm{Q}}^{-1}={\mathrm{Q}}^T$, where ${\mathrm{Q}}^{-1}$ and ${\mathrm{Q}}^T$ stand for the inverse and the transpose of the matrix $\mathrm{Q}$. This group is called the orthogonal group;
• $\mathrm{SO}\left(2\right)$ the subgroup of $\mathrm{O}\left(2\right)$ of matrices $\mathrm{Q}$ of determinant 1, called the special orthogonal group.

As a matrix group, $\mathrm{O}\left(2\right)$ is generated by:

$$\mathrm{R}\left(\theta \right)=\left(\begin{array}{cc}cos\theta & -sin\theta \\ sin\theta & cos\theta \end{array}\right)\mathrm{with}0\le \theta <2\pi \mathrm{and}\mathrm{P}\left({\underline{\mathrm{e}}}_2\right)=\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right),$$

where $\mathrm{R}\left(\theta \right)$ is a rotation by an angle $\theta$ and $\mathrm{P}\left(\underline{\mathrm{n}}\right)$ is the reflection across the line normal to $\underline{\mathrm{n}}$. $\mathrm{SO}\left(2\right)$ corresponds to the group of plane rotations generated by $\mathrm{R}\left(\theta \right)$. The following finite subgroups of $\mathrm{O}\left(2\right)$ will be used:

• $\mathbb{1}$ the identity group;
• ${\mathrm{Z}}_k(k\ge 2)$ the cyclic group with k elements, generated by $\mathrm{R}(2\pi /k)$. For $k=1$, we have ${\mathrm{Z}}_k=\mathbb{1}$;
• ${\mathrm{D}}_k^{\underline{\mathrm{n}}}(k\ge 2)$ the dihedral group with $2k$ elements, generated by $\mathrm{R}(2\pi /k)$ and $\mathrm{P}\left(\underline{\mathrm{n}}\right)$. For $k=1$, the group ${\mathrm{D}}_1^{\underline{\mathrm{n}}}$ will be denoted by ${\mathrm{Z}}_2^{\underline{\mathrm{n}},\pi }$.

It has to be noted that, up to conjugacy by an element of $\mathrm{SO}\left(2\right)$, any ${\mathrm{D}}_k^{\underline{\mathrm{n}}}$ is conjugate to ${\mathrm{D}}_k^{{\underline{\mathrm{e}}}_2}$, will simply be denoted by ${\mathrm{D}}_k$.

Subgroups of $\mathrm{O}\left(2\right)$ can be divided into four subsets according to the nature of their generators. A group will be said to be:

• Centrosymmetric (denoted by $\mathcal{I}$) if its contains the inversion $\mathrm{R}\left(\pi \right)$, and non-centrosymmetric ($\overline{\mathcal{I}}$) otherwise;
• Chiral (denoted by $\mathcal{C}$) if its does not contain reflection or mirror $\pi :=\mathrm{P}\left(\underline{\mathrm{n}}\right)$, and achiral ($\overline{\mathcal{C}}$) otherwise.

The different situations are reported in Table 1.

Table 1. Classification of $\mathrm{O}\left(2\right)$ subsets according to their chirality and centro-invariance.

	$\mathcal{I}$	$\overline{\mathcal{I}}$
$\overline{\mathcal{C}}$	${\mathrm{D}}_{2k}$	${\mathrm{D}}_{2k+1}$
$\mathcal{C}$	${\mathrm{Z}}_{2k}$	${\mathrm{Z}}_{2k+1}$

Tensor products:

• ⊗ denotes the usual tensor product of two tensors or vector spaces;
• ${\otimes }^n$ denotes the n-th power of the tensor product, e.g., ${\otimes }^{n}V:=V\otimes \cdots \otimes V$ (n copies);
• ${\otimes }^s$ denotes the symmetrized tensor product;
• $\underline{\overline{\otimes }}$ indicates the twisted tensor product defined by:

  $${\left(\underset{\sim }{\mathrm{a}}\underline{\overline{\otimes }}\underset{\sim }{\mathrm{b}}\right)}_{ijkl}=\frac{1}{2}(a_{ik}{b}_{jl}+a_{il}{b}_{jk}).$$

Tensor spaces:

• ${\mathbb{T}}^n:={\otimes }^n{\mathbb{R}}^2$ is the space of n-th order tensors with no index symmetry on ${\mathbb{R}}^2$;
• ${\mathbb{S}}^n:=S^n\left({\mathbb{R}}^2\right)$ is the space of completely symmetric (by completely symmetric we mean symmetric with respect to all permutations of indices) n-th order tensors on ${\mathbb{R}}^2$;
• ${\mathbb{K}}^n$ is the space of n-th order harmonic tensors (i.e., completely symmetric and traceless tensors), with

  $$dim\left({\mathbb{K}}^n\right)=\left\{\begin{array}{cc}2\hfill & \mathrm{if}n>0,\hfill \\ 1\hfill & \mathrm{if}n=0,-1;\hfill \end{array}\right.$$
• ${\mathbb{K}}^0$ is the space of scalars;
• ${\mathbb{K}}^{-1}$ is the space of pseudo-scalars (i.e., scalars which change sign under improper transformations).

We will use tensors which are of different orders. Tensors of order $-1$, 0, 1, 2, 3, 4, 5, and 6 are denoted by $\beta$, $\alpha$, $\underline{\mathrm{v}}$, and $\underset{\sim }{\mathrm{a}}$ or $\underset{\sim }{\mathrm{A}}$, $\underset{\simeq }{\mathrm{B}}$, $\underset{\approx }{\mathrm{C}}$, $\underset{\approxeq }{\mathrm{D}}$, and $\underset{≋}{\mathrm{E}}$, respectively. The simple, double, triple, and fourth-order contractions are written ·, :, ⋮, and $::$, respectively. In components with respect to $\mathcal{P}$, for general tensors $\mathrm{A}$ and $\mathrm{B}$, these notations correspond to:

$${(\mathrm{A}·\mathrm{B})}_{i_1\dots i_n}=A_{i_1\dots i_{p}j}{B}_{j{i}_{p+1}\dots i_n},{(\mathrm{A}:\mathrm{B})}_{i_1\dots i_n}=A_{i_1\dots i_{p}jk}{B}_{jk{i}_{p+1}\dots i_n},$$

$${(\mathrm{A}⋮\mathrm{B})}_{i_1\dots i_n}=A_{i_1\dots i_{p}jkl}{B}_{jkl{i}_{p+1}\dots i_n},{(\mathrm{A}::\mathrm{B})}_{i_1\dots i_n}=A_{i_1\dots i_{p}jklm}{B}_{jklm{i}_{p+1}\dots i_n}.$$

When needed, index symmetries of both spaces and their elements are expressed as follows: $(..)$ indicates invariance under permutations of the indices in parentheses and $\underline{..}\underline{..}$ indicates symmetry with respect to permutations of the underlined blocks. For example, $\underset{\sim }{\mathrm{a}}\in {\mathbb{T}}_{\left(ij\right)}$ means that $a_{ij}=a_{ji}$.

Special tensors:

• $\underset{\sim }{1}$ is the second-order identity tensor with components ${\delta }_{ij}$, where ${\delta }_{ij}$ is the Kronecker delta;
• $\underset{\approx }{\mathrm{I}}=\underset{\sim }{1}\underline{\overline{\otimes }}\underset{\sim }{1}$ is the fourth-order identity tensor on ${\mathbb{S}}^2$;
• $\underset{\sim }{\mathsf{ϵ}}$ denotes the 2D Levi–Civita tensor defined by:

  $${\mathsf{ϵ}}_{ij}=\left\{\begin{array}{cc}1\hfill & \mathrm{if}ij=12,\hfill \\ -1\hfill & \mathrm{if}ij=21,\hfill \\ 0\hfill & \mathrm{if}i=j.\hfill \end{array}\right.$$

Matrix spaces:

• ${\mathcal{M}}_n$ is the space of $n\times n$ dimensional square matrices;
• ${\mathcal{M}}_n^s$ is the space of $n\times n$ dimensional symmetric square matrices;
• ${\mathcal{M}}_{p,q}$ is the space of $p\times q$ rectangular matrices.

Miscellaneous notation:

• ⊕ direct sum;
• ≃ denotes hereafter an isomorphism.

3. Flexoelectricity Law

In this section we describe the flexoelectric law in the static regime. In [6,23] the flexoelectric effect was introduced via an energy density function. Here, we introduce this effect via constitutive equations.

3.1. Constitutive Equations

We begin by introducing the constitutive equations of the strain-gradient elasticity theory [19,20]. These constitutive equations define the stress tensor $\underset{\sim }{\mathsf{\sigma }}$ and the hyperstress tensor $\underset{\simeq }{\mathsf{\tau }}$ as linear functions of the strain tensor $\underset{\sim }{\mathsf{\epsilon }}:=\frac{1}{2}(\underline{\mathrm{u}}\otimes \underline{\nabla }+\underline{\nabla }\otimes \underline{\mathrm{u}})$ and the strain-gradient tensor $\underset{\simeq }{\mathsf{\eta }}:=\underset{\sim }{\mathsf{\epsilon }}\otimes \underline{\nabla }$, where $\underline{\mathrm{u}}$ is the displacement field and $\underline{\nabla }$ denotes the nabla differential operator. They are given by:

$$\left\{\begin{array}{cc}\underset{\sim }{\mathsf{\sigma }}\hfill & =\underset{\approx }{\mathrm{C}}:\underset{\sim }{\mathsf{\epsilon }}+\underset{\approxeq }{\mathrm{M}}⋮\underset{\simeq }{\mathsf{\eta }}\hfill \\ \underset{\simeq }{\mathsf{\tau }}\hfill & ={\underset{\approxeq }{\mathrm{M}}}^{\top }:\underset{\sim }{\mathsf{\epsilon }}+\underset{\approx }{\mathrm{A}}⋮\underset{\simeq }{\mathsf{\eta }}\hfill \end{array}\right.$$

(2)

where

• $\underset{\approx }{\mathrm{C}}\in \mathbb{E}{\mathrm{la}}_4:=\left\{\underset{\approx }{\mathrm{T}}\in {\otimes }^4{\mathbb{R}}^2\mid \underset{\approx }{\mathrm{T}}\in {\mathbb{T}}_{\underline{\left(ij\right)}\underline{\left(kl\right)}}\right\}$ is a fourth-order elasticity tensor;
• $\underset{\approxeq }{\mathrm{M}}\in \mathbb{E}{\mathrm{la}}_5:=\left\{\underset{\approxeq }{\mathrm{T}}\in {\otimes }^5{\mathbb{R}}^2\mid \underset{\approxeq }{\mathrm{T}}\in {\mathbb{T}}_{\left(ij\right)\left(kl\right)m}\right\}$ is a fifth-order elasticity tensor;
• ${\underset{\approxeq }{\mathrm{M}}}^{\top }\in \mathbb{E}{\mathrm{la}}_5^{\top }:=\left\{\underset{\approxeq }{\mathrm{T}}\in {\otimes }^5{\mathbb{R}}^2\mid \underset{\approxeq }{\mathrm{T}}\in {\mathbb{T}}_{\left(ij\right)k\left(lm\right)}\right\}$ is the fifth-order elasticity tensor defined as the transpose of $\underset{\approxeq }{\mathrm{M}}$ in the following sense ${\left({\underset{\approxeq }{\mathrm{M}}}^{\top }\right)}_{ijklm}=M_{lmijk}$;
• $\underset{≋}{\mathrm{A}}\in \mathbb{E}{\mathrm{la}}_6:=\left\{\underset{≋}{\mathrm{T}}\in {\otimes }^6{\mathbb{R}}^2\mid \underset{≋}{\mathrm{T}}\in {\mathbb{T}}_{\underline{\left(ij\right)k}\underline{\left(lm\right)n}}\right\}$ is the sixth-order elasticity tensor.

For a linear flexoelectric material, the constitutive equations define the stress tensor $\underset{\sim }{\mathsf{\sigma }}$, the hyperstress tensor $\underset{\simeq }{\mathsf{\tau }}$, and the polarization $\underline{\mathrm{p}}$ as linear functions of the strain tensor $\underset{\sim }{\mathsf{\epsilon }}$, the strain-gradient tensor $\underset{\simeq }{\mathsf{\eta }}$, and the electric field $\underline{\mathrm{q}}$. These constitutive equations are given by:

$$\left\{\begin{array}{cc}\underset{\sim }{\mathsf{\sigma }}=\underset{\approx }{\mathrm{C}}:\underset{\sim }{\mathsf{\epsilon }}+\underset{\approxeq }{\mathrm{M}}⋮\underset{\simeq }{\mathsf{\eta }}-\underset{\simeq }{\mathrm{P}}·\underline{\mathrm{q}}\hfill & \mathrm{(3)}\\ \underset{\simeq }{\mathsf{\tau }}={\underset{\approxeq }{\mathrm{M}}}^{\top }:\underset{\sim }{\mathsf{\epsilon }}+\underset{≋}{\mathrm{A}}⋮\underset{\simeq }{\mathsf{\eta }}+\underset{\approx }{\mathrm{F}}·\underline{\mathrm{q}}\hfill & \mathrm{(4)}\\ \underline{\mathrm{p}}={\underset{\simeq }{\mathrm{P}}}^{\top }:\underset{\sim }{\mathsf{\epsilon }}-{\underset{\approx }{\mathrm{F}}}^{\top }⋮\underset{\simeq }{\mathsf{\eta }}+\underset{\sim }{\mathrm{S}}·\underline{\mathrm{q}}\hfill & \mathrm{(5)}\end{array}\right.$$

where

• $\underset{\sim }{\mathrm{S}}\in \mathbb{C}\mathrm{on}:=\left\{\underset{\sim }{\mathrm{T}}\in {\otimes }^2{\mathbb{R}}^2\mid \underset{\sim }{\mathrm{T}}\in {\mathbb{T}}_{\left(ij\right)}\right\}$ is the dielectric susceptibility tensor;
• $\underset{\simeq }{\mathrm{P}}\in \mathbb{P}\mathrm{iez}:=\left\{\underset{\simeq }{\mathrm{T}}\in {\otimes }^3{\mathbb{R}}^2\mid \underset{\simeq }{\mathrm{T}}\in {\mathbb{T}}_{\left(ij\right)k}\right\}$ is the piezoelectric tensor;
• ${\underset{\simeq }{\mathrm{P}}}^{\top }\in \mathbb{P}{\mathrm{iez}}^{\top }:=\left\{\underset{\simeq }{\mathrm{T}}\in {\otimes }^3{\mathbb{R}}^2\mid \underset{\simeq }{\mathrm{T}}\in {\mathbb{T}}_{i\left(jk\right)}\right\}$ is the transpose of the piezoelectric tensor $\underset{\simeq }{\mathrm{P}}$. The transposition is defined as ${\left({\underset{\simeq }{\mathrm{P}}}^{\top }\right)}_{ijk}=P_{jki}$;
• $\underset{\approx }{\mathrm{F}}\in \mathbb{F}\mathrm{lex}:=\left\{\underset{\approx }{\mathrm{T}}\in {\otimes }^4{\mathbb{R}}^2\mid \underset{\approx }{\mathrm{T}}\in {\mathbb{T}}_{\left(ij\right)kl}\right\}$ is the flexoelectric tensor;
• ${\underset{\approx }{\mathrm{F}}}^{\top }\in \mathbb{F}{\mathrm{lex}}^{\top }:=\left\{\underset{\approx }{\mathrm{T}}\in {\otimes }^4{\mathbb{R}}^2\mid \underset{\approx }{\mathrm{T}}\in {\mathbb{T}}_{i\left(jk\right)l}\right\}$ is the transpose of the flexoelectric tensor $\underset{\approx }{\mathrm{F}}$. The transposition is defined as ${\left({\underset{\approx }{\mathrm{F}}}^{\top }\right)}_{ijkl}=F_{jkli}$.

The first two right-hand side terms in Equation (5) describe the direct piezoelectric and flexoelectric effects (we use the convention to represent the direct piezoelectric and flexoelectric effects by the transposed tensors ${\underset{\simeq }{\mathrm{P}}}^{\top }$ and ${\underset{\approx }{\mathrm{F}}}^{\top }$, respectively). Expressing constitutive law, we distinguish two types of tensors:

• State tensors: $\underset{\sim }{\mathsf{\sigma }}$, $\underset{\sim }{\mathsf{\epsilon }}$, $\underset{\simeq }{\mathsf{\tau }}$, $\underset{\simeq }{\mathsf{\eta }}$, $\underline{\mathrm{q}}$, and $\underline{\mathrm{p}}$;
• Constitutive tensors: $\underset{\sim }{\mathrm{S}}$, $\underset{\simeq }{\mathrm{P}}$, $\underset{\approx }{\mathrm{F}}$, $\underset{\approx }{\mathrm{C}}$, $\underset{\approxeq }{\mathrm{M}}$, and $\underset{≋}{\mathrm{A}}$.

State tensors describe point-wisely the different physical fields (primal and dual) considered in the model. Constitutive tensors model the influence of the matter on these state tensor fields, more precisely they describe how primal and dual fields are connected by the matter. The behaviour of a linear flexoelectric material is described by the constitutive tensors. In what follows, we will denote by $\mathcal{F}$ the sextuplet $\left(\underset{\sim }{\mathrm{S}},\underset{\simeq }{\mathrm{P}},\underset{\approx }{\mathrm{F}},\underset{\approx }{\mathrm{C}},\underset{\approxeq }{\mathrm{M}},\underset{≋}{\mathrm{A}}\right)$ and by $\mathcal{F}\mathrm{lex}$ the complete space of the flexoelectricity law, i.e.,

$$\mathcal{F}:=\left(\underset{\sim }{\mathrm{S}},\underset{\simeq }{\mathrm{P}},\underset{\approx }{\mathrm{F}},\underset{\approx }{\mathrm{C}},\underset{\approxeq }{\mathrm{M}},\underset{≋}{\mathrm{A}}\right)\in \mathcal{F}\mathrm{lex}$$

with

$$\mathcal{F}\mathrm{lex}=\mathbb{C}\mathrm{on}\times \mathbb{P}\mathrm{iez}\times \mathbb{F}\mathrm{lex}\times \mathbb{E}{\mathrm{la}}_4\times \mathbb{E}{\mathrm{la}}_5\times \mathbb{E}{\mathrm{la}}_6.$$

(6)

Our goal is to classify flexoelectric materials with respect to their spatial symmetry properties. To do this, we need to introduce the notion of symmetry class.

3.2. Notions of Symmetry Group and Symmetry Class

We give here some abstract definitions which contain all the information we need to classify flexoelectric materials. We begin by defining the action of the orthogonal group $\mathrm{O}\left(2\right)$ on the space ${\mathbb{T}}^n$. The group $\mathrm{O}\left(2\right)$ acts on the space ${\mathbb{T}}^n$ by the Rayleigh product defined, with respect to a basis, by

$${\left(\underset{\sim }{\mathrm{Q}}\star \mathrm{T}\right)}_{i_1\cdots i_n}:=Q_{i_1{j}_1}\dots Q_{i_n{j}_n}{T}_{j_1\cdots j_n},\mathrm{for}\mathrm{all}\underset{\sim }{\mathrm{Q}}\in \mathrm{O}\left(2\right)\mathrm{and}\mathrm{T}\in {\mathbb{T}}^n.$$

(7)

Here and throughout the rest of the article, we use the convention to treat elements of $\mathrm{O}\left(2\right)$ as orthogonal second-order tensors, this justifies the notation $\underset{\sim }{\mathrm{Q}}$.

We will say that a given tensor $\mathrm{T}\in {\mathbb{T}}^n$ is fixed under an orthogonal transformation $\underset{\sim }{\mathrm{Q}}\in \mathrm{O}\left(2\right)$ if $\underset{\sim }{\mathrm{Q}}\star \mathrm{T}=\mathrm{T}$. We define the symmetry group of $\mathrm{T}$, denoted $G_{\mathrm{T}}$, as the set of all orthogonal transformations that leave $\mathrm{T}$ fixed:

$$G_{\mathrm{T}}:=\left\{\underset{\sim }{\mathrm{Q}}\in \mathrm{O}\left(2\right)\mid \underset{\sim }{\mathrm{Q}}\star \mathrm{T}=\mathrm{T}\right\}.$$

It is known [24,25] that each symmetry group is a closed subgroup of $\mathrm{O}\left(2\right)$. We say that two subgroups $H_1$ and $H_2$ of $\mathrm{O}\left(2\right)$ are conjugate if there exists $\underset{\sim }{\mathrm{Q}}\in \mathrm{O}\left(2\right)$ such that $H_2=\underset{\sim }{\mathrm{Q}}{H}_1{\underset{\sim }{\mathrm{Q}}}^T$. It is proved [24] that every closed subgroup of $\mathrm{O}\left(2\right)$ is conjugate to exactly one element of the following collection:

$$\mathcal{S}:={\left\{\mathbb{1},{\mathrm{Z}}_2^{\pi },{\mathrm{Z}}_n,{\mathrm{D}}_n,\mathrm{SO}\left(2\right),\mathrm{O}\left(2\right)\right\}}_{n\ge 2}.$$

We will say that two tensors ${\mathrm{T}}_1$ and ${\mathrm{T}}_2$ are symmetrically equivalent (we write ${\mathrm{T}}_1\sim {\mathrm{T}}_2$) if their symmetry groups $G_{{\mathrm{T}}_1}$ and $G_{{\mathrm{T}}_2}$ are conjugate. We define the symmetry class of a tensor $\mathrm{T}$ as the set $\left[G_{\mathrm{T}}\right]$ of all subgroups of $\mathrm{O}\left(2\right)$ conjugate to $G_{\mathrm{T}}$, i.e.,

$$\left[G_{\mathrm{T}}\right]:=\left\{\mathcal{G}\subseteq \mathrm{O}\left(2\right)\mid \mathcal{G}=\underset{\sim }{\mathrm{Q}}{G}_{\mathrm{T}}{\underset{\sim }{\mathrm{Q}}}^T,\underset{\sim }{\mathrm{Q}}\in \mathrm{O}\left(2\right)\right\}.$$

In other words, two tensors are symmetrically equivalent if and only if their symmetry groups belong to the same symmetry class. One can show [26] that the relation ∼ is an equivalence relation on ${\mathbb{T}}^n$. An equivalence class for this equivalence relation is called a stratum [27]. For each element $H\in \mathcal{S}$, we distinguish two types of strata: The open stratum denoted ${\mathrm{\Sigma }}_{\left[H\right]}$ which is the stratum of tensors whose symmetry class is exactly $\left[H\right]$ and the closed stratum denoted ${\overline{\mathrm{\Sigma }}}_{\left[H\right]}$ which is the stratum of tensors whose symmetry class is at least $\left[H\right]$ (in the set of all symmetry classes we introduce a partial ordering relation ⪯ as follows: $\left[H_1\right]⪯\left[H_2\right]$ if there exists $\underset{\sim }{\mathrm{Q}}\in \mathrm{O}\left(2\right)$ such that $\underset{\sim }{\mathrm{Q}}{H}_1{\underset{\sim }{\mathrm{Q}}}^T\subseteq H_2$).

3.3. Symmetry Classes of the Complete Flexoelectric Law

We now apply the previous notions to the complete space $\mathcal{F}\mathrm{lex}$ defined in Equation (6). The action of $\mathrm{O}\left(2\right)$ on the space $\mathcal{F}\mathrm{lex}$ is given by:

$$\underset{\sim }{\mathrm{Q}}\star \mathcal{F}=\left(\underset{\sim }{\mathrm{Q}}\star \underset{\sim }{\mathrm{S}},\underset{\sim }{\mathrm{Q}}\star \underset{\simeq }{\mathrm{P}},\underset{\sim }{\mathrm{Q}}\star \underset{\approx }{\mathrm{F}},\underset{\sim }{\mathrm{Q}}\star \underset{\approx }{\mathrm{C}},\underset{\sim }{\mathrm{Q}}\star \underset{\approxeq }{\mathrm{M}},\underset{\sim }{\mathrm{Q}}\star \underset{≋}{\mathrm{A}}\right)$$

where ⋆ is the action defined in Equation (7). The symmetry group of $\mathcal{F}$ is defined as the intersection of the symmetry groups of the constitutive tensors, i.e.,

$$G_{\mathcal{F}}=G_{\underset{\sim }{\mathrm{S}}}\cap G_{\underset{\simeq }{\mathrm{P}}}\cap G_{\underset{\approx }{\mathrm{F}}}\cap G_{\underset{\approx }{\mathrm{C}}}\cap G_{\underset{\approxeq }{\mathrm{M}}}\cap G_{\underset{≋}{\mathrm{A}}}$$

and its symmetry class is defined as:

$$\left[G_{\mathcal{F}}\right]=\left\{\mathcal{G}\subseteq \mathrm{O}\left(2\right)\mid \mathcal{G}=\underset{\sim }{\mathrm{Q}}{G}_{\mathcal{F}}{\underset{\sim }{\mathrm{Q}}}^T,\underset{\sim }{\mathrm{Q}}\in \mathrm{O}\left(2\right)\right\}.$$

In 2D, the number and types of symmetry classes of each tensor space in Equation (6) are present in the literature except for $\mathbb{F}\mathrm{lex}$ up to authors best knowledge. The calculations of the types of symmetry classes and their number are based on the technique of harmonic decomposition [26,28]. The theorems leading to the results summed-up in the following tables can be found in [28]. In the following tables, $\#\mathrm{indep}\left(\mathrm{T}\right)$ indicates the number of independent components of the tensor $\mathrm{T}$ in each symmetry class and the in-parenthesis number indicates the minimal number of components in an appropriate basis. It is important to note that for tensors belonging to a stratum of type ${\mathrm{\Sigma }}_{\left[{\mathrm{Z}}_k\right]}$, and conversely to elements of ${\mathrm{\Sigma }}_{\left[{\mathrm{D}}_k\right]}$, bases adapted to symmetry elements are determined up to a rotation angle. This free rotation parameter can hence be used to decrease the number of minimal parameters in these optimized bases. In general, this rotation is not uniquely defined.

• $\mathbb{C}\mathrm{on}$:

  Name	Orthotropic	Isotropic
  $\left[G_{\underset{\sim }{\mathrm{S}}}\right]$	$\left[{\mathrm{D}}_2\right]$	$\left[\mathrm{O}\right(2\left)\right]$
  $\#\mathrm{indep}\left(\underset{\sim }{\mathrm{S}}\right)$	2	1

• $\mathbb{P}\mathrm{iez}$ [29,30]:

  Name	Oblique	Rectangular	Trigonal	Isotropic
  $\left[G_{\underset{\simeq }{\mathrm{P}}}\right]$	$\left[\mathbb{1}\right]$	$\left[{\mathrm{Z}}_2^{\pi }\right]$	$\left[{\mathrm{D}}_3\right]$	$\left[\mathrm{O}\right(2\left)\right]$
  $\#\mathrm{indep}\left(\underset{\simeq }{\mathrm{P}}\right)$	$6\left(5\right)$	3	1	0

• $\mathbb{E}{\mathrm{la}}_4$ [26,31]:

  Name	Digonal	Orthotropic	Tetragonal	Isotropic
  $\left[G_{\underset{\approx }{\mathrm{C}}}\right]$	$\left[{\mathrm{Z}}_2\right]$	$\left[{\mathrm{D}}_2\right]$	$\left[{\mathrm{D}}_4\right]$	$\left[\mathrm{O}\right(2\left)\right]$
  $\#\mathrm{indep}\left(\underset{\approx }{\mathrm{C}}\right)$	$6\left(5\right)$	4	3	2

• $\mathbb{E}{\mathrm{la}}_5$ [21]:

  Name	Oblique	Rectangular	Trichiral	Trigonal	Pentachiral	Pentagonal	Isotropic
  $\left[G_{\underset{\approxeq }{\mathrm{M}}}\right]$	$\left[\mathbb{1}\right]$	$\left[{\mathrm{Z}}_2^{\pi }\right]$	$\left[{\mathrm{Z}}_3\right]$	$\left[{\mathrm{D}}_3\right]$	$\left[{\mathrm{Z}}_5\right]$	$\left[{\mathrm{D}}_5\right]$	$\left[\mathrm{O}\right(2\left)\right]$
  $\#\mathrm{indep}\left(\underset{\approxeq }{\mathrm{M}}\right)$	$18\left(17\right)$	9	$6\left(5\right)$	3	$2\left(1\right)$	1	0

• $\mathbb{E}{\mathrm{la}}_6$ [21]:

  Name	Digonal	Orthotropic	Tetrachiral	Tetragonal	Hexachiral	Hexagonal	Hemitropic	Isotropic
  $\left[G_{\underset{≋}{\mathrm{A}}}\right]$	$\left[{\mathrm{Z}}_2\right]$	$\left[{\mathrm{D}}_2\right]$	$\left[{\mathrm{Z}}_4\right]$	$\left[{\mathrm{D}}_4\right]$	$\left[{\mathrm{Z}}_6\right]$	$\left[{\mathrm{D}}_6\right]$	$\left[\mathrm{SO}\right(2\left)\right]$	$\left[\mathrm{O}\right(2\left)\right]$
  $\#\mathrm{indep}\left(\underset{≋}{\mathrm{A}}\right)$	21	12	$9\left(8\right)$	6	$7\left(6\right)$	5	5	4

To complete the picture, it remains to determine the symmetry classes of flexoelectric tensors. The tool we use to do this is the isotypic decomposition, which consists in decomposing a finite-dimensional vector space into a direct sum of $\mathrm{O}\left(2\right)$-irreducible subspaces. A subspace $\mathbb{K}$ of ${\mathbb{T}}^n$ is called $\mathrm{O}\left(2\right)$-irreducible if it is $\mathrm{O}\left(2\right)$-invariant (i.e., $\underset{\sim }{\mathrm{Q}}\star \mathrm{T}\in \mathbb{K}$ for all $\underset{\sim }{\mathrm{Q}}\in \mathrm{O}\left(2\right)$ and $\mathrm{T}\in \mathbb{K}$) and its only invariant subspaces are itself and the null space. It is known that each $\mathrm{O}\left(2\right)$-irreducible space is isomorphic to a direct sum of spaces of harmonic tensors ${\mathbb{K}}^n$ [28,32]. Such a decomposition is interesting since the $\mathrm{O}\left(2\right)$-action on ${\mathbb{K}}^n$ is elementary and given by ${\rho }_n$ [33], with for $n\ge 1$:

$${\rho }_n\left(\mathrm{R}\left(\theta \right)\right):=\left(\begin{array}{cc}cosn\theta & -sinn\theta \\ sinn\theta & cosn\theta \end{array}\right),{\rho }_n\left(\mathrm{P}\left({\underline{\mathrm{e}}}_2\right)\right):=\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right).$$

(8)

The $\mathrm{O}\left(2\right)$-action on ${\mathbb{K}}^0$ is the identity and the $\mathrm{O}\left(2\right)$-action on ${\mathbb{K}}^{-1}$ is given by the determinant of the transformation.

We will now determine the isotypic decomposition of the space $\mathbb{F}\mathrm{lex}$.

3.4. Isotypic Decomposition of the Space of Flexoelectric Tensors

Due to the linear relation $\underset{\simeq }{\mathsf{\tau }}=\underset{\approx }{\mathrm{F}}·\underline{\mathrm{q}}$, we can identify $\underset{\approx }{\mathrm{F}}$ with a linear map from ${\mathbb{T}}_l$ into ${\mathbb{T}}_{\left(ij\right)k}$. Therefore, we have $\mathbb{F}\mathrm{lex}\simeq {\mathbb{T}}_{\left(ij\right)k}\otimes {\mathbb{T}}_l$. To determine the isotypic decomposition of $\mathbb{F}\mathrm{lex}$, we use the Clebsch–Gordan formula which allows us to decompose a tensor product of two irreducible spaces into a direct sum of irreducible spaces. For more details, we refer to [28]. We remark that ${\mathbb{T}}_l$ is nothing but ${\mathbb{K}}^1$. It then remains to determine the isotypic decomposition of the space ${\mathbb{T}}_{\left(ij\right)k}$. For this, we use the following result, the proof of which is found in [28].

Lemma 1.

For every integers $p>0$ and $q>0$, we have the following isotypic decompositions, where the meaningless products are indicated by ×:

⊗	${\mathbb{K}}^q$	${\mathbb{K}}^0$	${\mathbb{K}}^{-1}$
${\mathbb{K}}^p$	$\left\{\begin{array}{cc}{\mathbb{K}}^{p+q}\oplus {\mathbb{K}}^{|p-q|},\hfill & p\ne q\hfill \\ {\mathbb{K}}^{2p}\oplus {\mathbb{K}}^0\oplus {\mathbb{K}}^{-1},\hfill & p=q\hfill \end{array}\right.$	${\mathbb{K}}^p$	${\mathbb{K}}^p$
${\mathbb{K}}^0$	${\mathbb{K}}^q$	${\mathbb{K}}^0$	${\mathbb{K}}^{-1}$
${\mathbb{K}}^{-1}$	${\mathbb{K}}^q$	${\mathbb{K}}^{-1}$	${\mathbb{K}}^0$

${\otimes }^s$	${\mathbb{K}}^p$	${\mathbb{K}}^0$	${\mathbb{K}}^{-1}$
${\mathbb{K}}^p$	${\mathbb{K}}^{2p}\oplus {\mathbb{K}}^0$	×	×
${\mathbb{K}}^0$	×	${\mathbb{K}}^0$	×
${\mathbb{K}}^{-1}$	×	×	${\mathbb{K}}^0$

Proposition 1.

The space $\mathbb{F}\mathrm{lex}$ admits the following isotypic decomposition:

$$\mathbb{F}\mathrm{lex}\simeq {\mathbb{K}}^4\oplus 3{\mathbb{K}}^2\oplus 2{\mathbb{K}}^0\oplus 2{\mathbb{K}}^{-1}$$

(9)

where the notation $m_k{\mathbb{K}}^k:={⨁}_{l=1}^{m_k}{\mathbb{K}}^k$ is used ($m_k$ is called the multiplicity of ${\mathbb{K}}^k$).

Proof. 

We have $\mathbb{F}\mathrm{lex}\simeq {\mathbb{T}}_{\left(ij\right)k}\otimes {\mathbb{T}}_l$. Let us decompose the space ${\mathbb{T}}_{\left(ij\right)k}$:

$${\mathbb{T}}_{\left(ij\right)k}\simeq {\mathbb{T}}_{\left(ij\right)}\otimes {\mathbb{T}}_k\simeq \left({\mathbb{K}}^1{\otimes }^s{\mathbb{K}}^1\right)\otimes {\mathbb{K}}^1.$$

From Lemma 1 we get ${\mathbb{K}}^1{\otimes }^s{\mathbb{K}}^1\simeq {\mathbb{K}}^2\oplus {\mathbb{K}}^0$, then

$${\mathbb{T}}_{\left(ij\right)k}\simeq ({\mathbb{K}}^2\oplus {\mathbb{K}}^0)\otimes {\mathbb{K}}^1\simeq ({\mathbb{K}}^2\otimes {\mathbb{K}}^1)\oplus ({\mathbb{K}}^0\otimes {\mathbb{K}}^1)\simeq ({\mathbb{K}}^3\oplus {\mathbb{K}}^1)\oplus {\mathbb{K}}^1\simeq {\mathbb{K}}^3\oplus 2{\mathbb{K}}^1.$$

(10)

Using again Lemma 1, we deduce that:

$$\begin{array}{cc}\hfill \mathbb{F}\mathrm{lex}\simeq ({\mathbb{T}}_{\left(ij\right)}\otimes {\mathbb{T}}_k)\otimes {\mathbb{T}}_l& \simeq ({\mathbb{K}}^3\oplus {\mathbb{K}}^1\oplus {\mathbb{K}}^1)\otimes {\mathbb{K}}^1\hfill \\ \hfill & \simeq ({\mathbb{K}}^3\otimes {\mathbb{K}}^1)\oplus ({\mathbb{K}}^1\otimes {\mathbb{K}}^1)\oplus ({\mathbb{K}}^1\otimes {\mathbb{K}}^1)\hfill \\ \hfill & \simeq ({\mathbb{K}}^4\oplus {\mathbb{K}}^2)\oplus ({\mathbb{K}}^2\oplus {\mathbb{K}}^0\oplus {\mathbb{K}}^{-1})\oplus ({\mathbb{K}}^2\oplus {\mathbb{K}}^0\oplus {\mathbb{K}}^{-1}).\hfill \end{array}$$

We obtain the decomposition of Equation (9) by grouping spaces of the same order. □

To determine the symmetry classes of the flexoelectric tensor, we will use the following result.

Lemma 2

(Proposition 4.10 of [28]). Let ${\mathbb{T}}^{2p}(p>0)$ be a space of even-order tensors. If ${\mathbb{T}}^{2p}$ contains the irreducible space ${\mathbb{K}}^{-1}$ in its isotypic decomposition, then

$$\mathfrak{I}\left({\mathbb{T}}^{2p}\right)={\{\left[{\mathrm{Z}}_{2k}\right],\left[{\mathrm{D}}_{2k}\right]\}}_{1\le k\le p}\cup \{\left[\mathrm{SO}\left(2\right)\right],\left[\mathrm{O}\left(2\right)\right]\},$$

where $\mathfrak{I}\left({\mathbb{T}}^{2p}\right)$ denotes the set of symmetry classes of the elements of ${\mathbb{T}}^{2p}$.

We remark that the case of the space $\mathbb{F}\mathrm{lex}$ is an immediate corollary of this result. Indeed, $\mathbb{F}\mathrm{lex}$ is a space of fourth-order tensors containing the irreducible space ${\mathbb{K}}^{-1}$ in its isotypic decomposition of Equation (9). Thus, the symmetry classes of $\mathbb{F}\mathrm{lex}$ are:

$$\mathfrak{I}\left(\mathbb{F}\mathrm{lex}\right)=\{\left[{\mathrm{Z}}_2\right],\left[{\mathrm{D}}_2\right],\left[{\mathrm{Z}}_4\right],\left[{\mathrm{D}}_4\right],\left[\mathrm{SO}\left(2\right)\right],\left[\mathrm{O}\left(2\right)\right]\}.$$

(11)

The space $\mathbb{F}\mathrm{lex}$ is hence divided into 6 strata:

$$\mathbb{F}\mathrm{lex}={\mathrm{\Sigma }}_{\left[{\mathrm{Z}}_2\right]}\cup {\mathrm{\Sigma }}_{\left[{\mathrm{D}}_2\right]}\cup {\mathrm{\Sigma }}_{\left[{\mathrm{Z}}_4\right]}\cup {\mathrm{\Sigma }}_{\left[{\mathrm{D}}_4\right]}\cup {\mathrm{\Sigma }}_{\left[\mathrm{SO}\right(2\left)\right]}\cup {\mathrm{\Sigma }}_{\left[\mathrm{O}\right(2\left)\right]}.$$

(12)

The partition of Equation (12) is called the stratification of $\mathbb{F}\mathrm{lex}$.

It remains to calculate the dimension of each symmetry class in Equation (11). There are formulas in [28] to do this. We recall these formulas in the following lemma.

Lemma 3

(see Lemma 3.10 of [28]). Let ${\mathbb{T}}^n$ a space of n-th order tensors having the isotypic decomposition:

$${\mathbb{T}}^n\simeq \underset{k}{⨁}{m}_k{\mathbb{K}}^k.$$

Then,

$$\begin{array}{cc}\hfill dim\left({\left({\mathbb{T}}^n\right)}^{{\mathrm{Z}}_p}\right)=m_{-1}+m_0+2\sum _{\underset{p|k}{k\ge 1}}{m}_k& ;dim\left({\left({\mathbb{T}}^n\right)}^{{\mathrm{D}}_p}\right)=m_0+\sum _{\underset{p|k}{k\ge 1}}{m}_k;\hfill \\ \hfill dim\left({\left({\mathbb{T}}^n\right)}^{\mathrm{SO}\left(2\right)}\right)=m_{-1}+m_0& ;dim\left({\left({\mathbb{T}}^n\right)}^{\mathrm{O}\left(2\right)}\right)=m_0,\hfill \end{array}$$

where the notation $p|k$ means p divides k and ${\left({\mathbb{T}}^n\right)}^H$ is the fixed-point space associated to $H\subset \mathrm{O}\left(2\right)$ defined as:

$${\left({\mathbb{T}}^n\right)}^H:=\left\{T\in {\mathbb{T}}^n\mid \underset{\sim }{\mathrm{Q}}\star \mathrm{T}=\mathrm{T},\forall \underset{\sim }{\mathrm{Q}}\in H\right\}.$$

Now applying these formulas to the space $\mathbb{F}\mathrm{lex}$, remembering that:

$$\mathbb{F}\mathrm{lex}\simeq {\mathbb{K}}^4\oplus 3{\mathbb{K}}^2\oplus 2{\mathbb{K}}^0\oplus 2{\mathbb{K}}^{-1},$$

we obtain:

$$\begin{array}{cc}\hfill & dim\left({\left(\mathbb{F}\mathrm{lex}\right)}^{{\mathrm{Z}}_2}\right)=12;dim\left({\left(\mathbb{F}\mathrm{lex}\right)}^{{\mathrm{Z}}_4}\right)=6;dim\left({\left(\mathbb{F}\mathrm{lex}\right)}^{{\mathrm{D}}_2}\right)=6;dim\left({\left(\mathbb{F}\mathrm{lex}\right)}^{{\mathrm{D}}_4}\right)=3;\hfill \\ \hfill & dim\left({\left(\mathbb{F}\mathrm{lex}\right)}^{\mathrm{SO}\left(2\right)}\right)=4;dim\left({\left(\mathbb{F}\mathrm{lex}\right)}^{\mathrm{O}\left(2\right)}\right)=2.\hfill \end{array}$$

We can summarize the previous results in Table 2.

Table 2. The names, the set of subgroups, and number of independent components for the symmetry classes of $\underset{\approx }{\mathrm{F}}$.

Name	Digonal	Orthotropic	Tetrachiral	Tetragonal	Hemitropic	Isotropic
$\left[G_{\underset{\approx }{\mathrm{F}}}\right]$	$\left[{\mathrm{Z}}_2\right]$	$\left[{\mathrm{D}}_2\right]$	$\left[{\mathrm{Z}}_4\right]$	$\left[{\mathrm{D}}_4\right]$	$\left[\mathrm{SO}\right(2\left)\right]$	$\left[\mathrm{O}\right(2\left)\right]$
#indep ($\underset{\approx }{\mathrm{F}}$)	$12\left(11\right)$	6	$6\left(5\right)$	3	4	2

Remark 1.

Notice that the use of these formulas does not allow the determination of the stratification of the space [28].

The associated closed strata satisfy the following inclusion relations:

$$\left\{\begin{array}{cc}{\overline{\mathrm{\Sigma }}}_{\left[{\mathrm{Z}}_n\right]}\supset {\overline{\mathrm{\Sigma }}}_{\left[{\mathrm{D}}_n\right]}\supset {\overline{\mathrm{\Sigma }}}_{\left[\mathrm{O}\right(2\left)\right]}\hfill & \left(n\ge 2\right);\hfill \\ {\overline{\mathrm{\Sigma }}}_{\left[{\mathrm{Z}}_m\right]}\supset {\overline{\mathrm{\Sigma }}}_{\left[{\mathrm{Z}}_n\right]}\mathrm{and}{\overline{\mathrm{\Sigma }}}_{\left[{\mathrm{D}}_m\right]}\supset {\overline{\mathrm{\Sigma }}}_{\left[{\mathrm{D}}_n\right]}\hfill & \mathrm{if}m\mathrm{divides}n;\hfill \\ {\overline{\mathrm{\Sigma }}}_{\left[{\mathrm{Z}}_n\right]}\supset {\overline{\mathrm{\Sigma }}}_{\left[\mathrm{SO}\right(2\left)\right]}\supset {\overline{\mathrm{\Sigma }}}_{\left[\mathrm{O}\right(2\left)\right]}\hfill & \left(n\ge 2\right).\hfill \end{array}\right.$$

(13)

The connection between these closed strata is provided by the diagram given in Figure 1, where an arrow from ${\overline{\mathrm{\Sigma }}}_{\left[H_1\right]}$ to ${\overline{\mathrm{\Sigma }}}_{\left[H_2\right]}$ means that ${\overline{\mathrm{\Sigma }}}_{\left[H_1\right]}\supset {\overline{\mathrm{\Sigma }}}_{\left[H_2\right]}$.

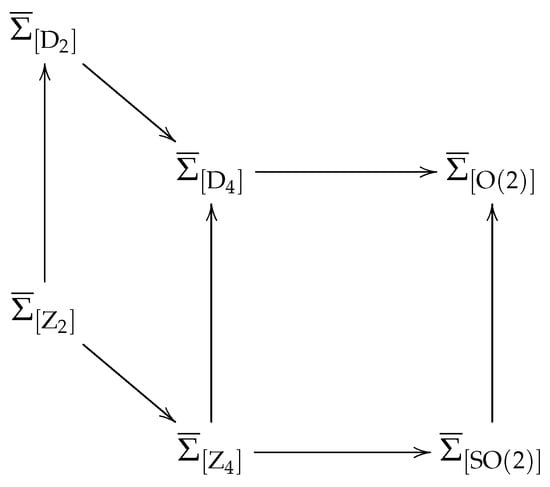
Figure 1. Bifurcation diagram of $\mathbb{F}\mathrm{lex}$.

Remark 2.

Although the elasticity tensors and the flexoelectric ones are both fourth-order tensors, the structure of flexoelectric tensors is richer than that of the elasticity tensors. Indeed, it has been shown [26,31] that the space of bi-dimensional elasticity tensors $\mathbb{E}{\mathrm{la}}_4$ is divided into four strata which are ${\mathrm{\Sigma }}_{\left[{\mathrm{Z}}_2\right]}$, ${\mathrm{\Sigma }}_{\left[{\mathrm{D}}_2\right]}$, ${\mathrm{\Sigma }}_{\left[{\mathrm{D}}_4\right]}$, and ${\mathrm{\Sigma }}_{\left[\mathrm{O}\right(2\left)\right]}$. As a consequence of relations in Equation (13), the bifurcation diagram of $\mathbb{E}{\mathrm{la}}_4$ is linear. However, in the case of $\mathbb{F}\mathrm{lex}$, the diagram is no longer linear and we remark the presence of two new strata ${\mathrm{\Sigma }}_{\left[{\mathrm{Z}}_4\right]}$ and ${\mathrm{\Sigma }}_{\left[\mathrm{SO}\right(2\left)\right]}$ corresponding to the tetrachiral class $\left[{\mathrm{Z}}_4\right]$ and the hemitropic class $\left[\mathrm{SO}\right(2\left)\right]$. These classes characterize the so-called chiral-sensitivity.

Now by collecting the results given in the literature and those we obtained for $\mathbb{F}\mathrm{lex}$, we get all the symmetry classes of the complete space $\mathcal{F}\mathrm{lex}$:

$$\mathfrak{I}\left(\mathcal{F}\mathrm{lex}\right)={\{\left[\mathbb{1}\right],\left[{\mathrm{Z}}_2^{\pi }\right],\left[{\mathrm{Z}}_k\right],\left[{\mathrm{D}}_k\right],\left[\mathrm{SO}\left(2\right)\right],\left[\mathrm{O}\left(2\right)\right]\}}_{2\le k\le 6}$$

(14)

and then $\mathcal{F}\mathrm{lex}$ is divided into 14 strata.

Our goal in the following section is to determine the matrix representations of the complete flexoelectricity law, for each symmetry class.

4. Matrix Representations

It is common practice in continuum mechanics [34] to rewrite a constitutive tensorial law in matrix form for being able to implement it in a FEM code. This procedure requires the construction of appropriate bases which allows us to express state tensors as vectors and constitutive tensors as matrices. The matrix representations associated to tensors $\underset{\sim }{\mathrm{S}}$, $\underset{\simeq }{\mathrm{P}}$, $\underset{\approx }{\mathrm{C}}$, $\underset{\approxeq }{\mathrm{M}}$, and $\underset{≋}{\mathrm{A}}$ are given in the literature [22]. We will now determine the matrix representations associated to the tensor $\underset{\approx }{\mathrm{F}}$.

4.1. Matrix Representations of the Flexoelectric Tensor

Since $\underset{\approx }{\mathrm{F}}$ is a fourth-order tensor in ${\mathbb{R}}^2$, it possesses generally $2^4=16$ components. However, the symmetry relation $F_{ijkl}=F_{jikl}$ reduces the number of independent components from 16 to 12. To rewrite the tensorial relation $\underset{\simeq }{\mathsf{\tau }}=\underset{\approx }{\mathrm{F}}·\underline{\mathrm{q}}$ into a matrix form, we need to construct appropriate orthonormal bases for the vector spaces ${\mathbb{T}}_{\left(ij\right)k}$ and ${\mathbb{T}}_{\left(ij\right)kl}$. Let ${\mathcal{B}}_i$ be a basis for the space of i-th order tensors constructed from the canonical basis $\mathcal{B}:=\{{\underline{\mathrm{e}}}_1,{\underline{\mathrm{e}}}_2\}$ of ${\mathbb{R}}^2$. For ${\mathbb{T}}_{\left(ij\right)}$ we chose:

$${\mathcal{B}}_2=\left\{\underset{\sim }{{\tilde{\mathrm{e}}}_1}:={\underline{\mathrm{e}}}_1\otimes {\underline{\mathrm{e}}}_1,\underset{\sim }{{\tilde{\mathrm{e}}}_2}:={\underline{\mathrm{e}}}_2\otimes {\underline{\mathrm{e}}}_2,\underset{\sim }{{\tilde{\mathrm{e}}}_3}:=\frac{\sqrt{2}}{2}({\underline{\mathrm{e}}}_1\otimes {\underline{\mathrm{e}}}_2+{\underline{\mathrm{e}}}_2\otimes {\underline{\mathrm{e}}}_1)\right\}.$$

In this basis, the stress tensor $\underset{\sim }{\mathsf{\sigma }}$ and the strain tensors $\underset{\sim }{\mathsf{\epsilon }}$ are represented by vectors $\left[\underline{\widehat{\mathsf{\sigma }}}\right]\in {\mathcal{M}}_{3,1}$ and $\left[\underline{\widehat{\mathsf{\epsilon }}}\right]\in {\mathcal{M}}_{3,1}$:

$$\left[\underline{\widehat{\mathsf{\sigma }}}\right]={\left(\begin{array}{c}{\sigma }_{11}\\ {\sigma }_{22}\\ \sqrt{2}{\sigma }_{12}\end{array}\right)}_{{\mathcal{B}}_2},\left[\underline{\widehat{\mathsf{\epsilon }}}\right]={\left(\begin{array}{c}{\epsilon }_{11}\\ {\epsilon }_{22}\\ \sqrt{2}{\epsilon }_{12}\end{array}\right)}_{{\mathcal{B}}_2}.$$

For ${\mathbb{T}}_{\left(ij\right)k}$, we chose:

$${\mathcal{B}}_3=\left\{\underset{\simeq }{{\widehat{\mathrm{e}}}_1}:=\underset{\sim }{{\tilde{\mathrm{e}}}_1}\otimes {\underline{\mathrm{e}}}_1,\underset{\simeq }{{\widehat{\mathrm{e}}}_2}:=\underset{\sim }{{\tilde{\mathrm{e}}}_2}\otimes {\underline{\mathrm{e}}}_1,\underset{\simeq }{{\widehat{\mathrm{e}}}_3}:=\underset{\sim }{{\tilde{\mathrm{e}}}_3}\otimes {\underline{\mathrm{e}}}_2,\underset{\simeq }{{\widehat{\mathrm{e}}}_4}:=\underset{\sim }{{\tilde{\mathrm{e}}}_2}\otimes {\underline{\mathrm{e}}}_2,\underset{\simeq }{{\widehat{\mathrm{e}}}_5}:=\underset{\sim }{{\tilde{\mathrm{e}}}_1}\otimes {\underline{\mathrm{e}}}_2,\underset{\simeq }{{\widehat{\mathrm{e}}}_6}:=\underset{\sim }{{\tilde{\mathrm{e}}}_3}\otimes {\underline{\mathrm{e}}}_1\right\}.$$

The ordering for basis elements in ${\mathcal{B}}_3$ is chosen so that the matrix forms of $\underset{≋}{\mathrm{A}}$ are block diagonals for the dihedral classes [21]. Since this ordering is the one considered in the references [21,22], the results from these different papers can directly be combined.

In the basis ${\mathcal{B}}_3$, the hyperstress tensor $\underset{\simeq }{\mathsf{\tau }}$ and the strain-gradient tensor $\underset{\simeq }{\mathsf{\eta }}$ are represented by vectors $\left[\underline{\widehat{\mathsf{\tau }}}\right]\in {\mathcal{M}}_{6,1}$ and $\left[\underline{\widehat{\mathsf{\eta }}}\right]\in {\mathcal{M}}_{6,1}$:

$$\left[\underline{\widehat{\mathsf{\tau }}}\right]={\left(\begin{array}{c}{\tau }_{111}\\ {\tau }_{221}\\ \sqrt{2}{\tau }_{122}\\ {\tau }_{222}\\ {\tau }_{112}\\ \sqrt{2}{\tau }_{121}\end{array}\right)}_{{\mathcal{B}}_3},\left[\underline{\widehat{\mathsf{\eta }}}\right]={\left(\begin{array}{c}{\eta }_{111}\\ {\eta }_{221}\\ \sqrt{2}{\eta }_{122}\\ {\eta }_{222}\\ {\eta }_{112}\\ \sqrt{2}{\eta }_{121}\end{array}\right)}_{{\mathcal{B}}_3}.$$

For ${\mathbb{T}}_{\left(ij\right)kl}$ we chose:

$${\mathcal{B}}_4=\left\{\underset{\simeq }{{\widehat{\mathrm{e}}}_{\mathrm{I}}}\otimes {\underline{\mathrm{e}}}_{\alpha },1\le I\le 6,1\le \alpha \le 2\right\}.$$

In the basis ${\mathcal{B}}_4$, the flexoelectric tensor $\underset{\approx }{\mathrm{F}}$ is represented by a matrix $\left[\underset{\sim }{\widehat{\mathrm{F}}}\right]\in {\mathcal{M}}_{6,2}$:

$$\left[\widehat{\underset{\sim }{\mathrm{F}}}\right]={\left(\begin{array}{cc}{F}_{1111}& F_{1112}\\ F_{2211}& F_{2212}\\ \sqrt{2}{F}_{1221}& \sqrt{2}{F}_{1222}\\ F_{2221}& F_{2222}\\ F_{1121}& F_{1122}\\ \sqrt{2}{F}_{1211}& \sqrt{2}{F}_{1212}\end{array}\right)}_{{\mathcal{B}}_4}.$$

We will now determine the matrix forms of the flexoelectric tensor in each stratum.

4.1.1. ${\mathrm{Z}}_2$-Class

The generator of the group ${\mathrm{Z}}_2$ is $\mathrm{R}\left(\pi \right)$. The condition that ${(\underset{\sim }{\mathrm{Q}}\star \underset{\approx }{\mathrm{F}})}_{ijkl}=F_{ijkl}$ is trivially satisfied because the minimal symmetry class of an even-order tensor is ${\mathrm{Z}}_2$. Indeed, the orthogonal transformation in the ${\mathrm{Z}}_2$ situation is $\mathrm{R}\left(\pi \right)=-\mathrm{I}$. Moreover, in the transformation of an even-order tensor (cf. Equation (7)), the orthogonal transformation acts an even number of times. As a consequence $\mathrm{R}\left(\pi \right)$ is in the symmetry group of any even-order tensor or, said differently, any even-order tensor is centrosymmetric. We have 12 independent coefficients, as indicated below:

$${\left[\widehat{\underset{\sim }{\mathrm{F}}}\right]}_{{\mathrm{Z}}_2}={\left(\begin{array}{cc}{F}_{1111}& F_{1112}\\ F_{2211}& F_{2212}\\ \sqrt{2}{F}_{1221}& \sqrt{2}{F}_{1222}\\ F_{2221}& F_{2222}\\ F_{1121}& F_{1122}\\ \sqrt{2}{F}_{1211}& \sqrt{2}{F}_{1212}\end{array}\right)}_{{\mathcal{B}}_4}.$$

4.1.2. ${\mathrm{Z}}_4$-Class

The generator of the group ${\mathrm{Z}}_4$ is $\mathrm{R}(\pi /2)$. The condition ${\left(\underset{\sim }{\mathrm{Q}}\star \underset{\approx }{\mathrm{F}}\right)}_{ijkl}=F_{ijkl}$ yields:

$$\begin{array}{cccc}\hfill & F_{2221}={\left(\underset{\sim }{\mathrm{Q}}\star \underset{\approx }{\mathrm{F}}\right)}_{2221}=-F_{1112},\hfill & \hfill & F_{1121}={\left(\underset{\sim }{\mathrm{Q}}\star \underset{\approx }{\mathrm{F}}\right)}_{1121}=-F_{2212},\hfill \\ \hfill & F_{1211}={\left(\underset{\sim }{\mathrm{Q}}\star \underset{\approx }{\mathrm{F}}\right)}_{1211}=-F_{1222},\hfill & \hfill & F_{2222}={\left(\underset{\sim }{\mathrm{Q}}\star \underset{\approx }{\mathrm{F}}\right)}_{2222}=F_{1111},\hfill \\ \hfill & F_{1122}={\left(\underset{\sim }{\mathrm{Q}}\star \underset{\approx }{\mathrm{F}}\right)}_{1122}=F_{2211},\hfill & \hfill & F_{1212}={\left(\underset{\sim }{\mathrm{Q}}\star \underset{\approx }{\mathrm{F}}\right)}_{1212}=F_{1221}.\hfill \end{array}$$

(15)

Thus, we have 6 independent coefficients, as indicated below:

$${\left[\widehat{\underset{\sim }{\mathrm{F}}}\right]}_{{\mathrm{Z}}_4}={\left(\begin{array}{cc}{F}_{1111}& F_{1112}\\ F_{2211}& F_{2212}\\ \sqrt{2}{F}_{1221}& \sqrt{2}{F}_{1222}\\ -F_{1112}& F_{1111}\\ -F_{2212}& F_{2211}\\ -\sqrt{2}{F}_{1222}& \sqrt{2}{F}_{1221}\end{array}\right)}_{{\mathcal{B}}_4}.$$

4.1.3. $\mathrm{SO}\left(2\right)$-Class

Consider a rotation of order n. For $n>4$ the order of the rotation exceed the order of the tensor $\underset{\approx }{\mathrm{F}}$. And, according to the Hermann’s theorem if ${\mathrm{Z}}_{n>4}$ is contained in the symmetry group of $\underset{\approx }{\mathrm{F}}$, the symmetry group is conjugate to either $\mathrm{SO}\left(2\right)$ or $\mathrm{O}\left(2\right)$ [35]. Exploiting this theorem, $\mathrm{SO}\left(2\right)$-invariant tensors are here generated by imposing $\mathrm{R}(\pi /4)$-invariance ($n=8$) to $\underset{\approx }{\mathrm{F}}$. The condition ${\left(\underset{\sim }{\mathrm{Q}}\star \underset{\approx }{\mathrm{F}}\right)}_{ijkl}=F_{ijkl}$ adds to Equation (15) the new conditions:

$$F_{1221}=\frac{1}{2}(F_{1111}-F_{2211}),F_{1222}=\frac{1}{2}(F_{1112}-F_{2212}).$$

(16)

Thus, we have 4 independent coefficients, as indicated below:

$${\left[\widehat{\underset{\sim }{\mathrm{F}}}\right]}_{\mathrm{SO}\left(2\right)}={\left(\begin{array}{cc}{F}_{1111}& F_{1112}\\ F_{2211}& F_{2212}\\ \frac{\sqrt{2}}{2}(F_{1111}-F_{2211})& \frac{\sqrt{2}}{2}(F_{1112}-F_{2212})\\ -F_{1112}& F_{1111}\\ -F_{2212}& F_{2211}\\ -\frac{\sqrt{2}}{2}(F_{1112}-F_{2212})& \frac{\sqrt{2}}{2}(F_{1111}-F_{2211})\end{array}\right)}_{{\mathcal{B}}_4}.$$

Remark 3.

As in [22], one can show that there exist rotations which allow us to reduce the number of parameters of ${\left[\widehat{\underset{\sim }{\mathrm{F}}}\right]}_{{\mathrm{Z}}_4}$ and ${\left[\widehat{\underset{\sim }{\mathrm{F}}}\right]}_{\mathrm{SO}\left(2\right)}$ from 6 to 5 and from 4 to 3, respectively.

4.1.4. ${\mathrm{D}}_2$-Class

The generators of the group ${\mathrm{D}}_2$ are $\mathrm{R}\left(\pi \right)$ and $\mathrm{P}\left({\underline{\mathrm{e}}}_2\right)$. The condition ${(\underset{\sim }{\mathrm{Q}}\star \underset{\approx }{\mathrm{F}})}_{ijkl}=F_{ijkl}$ yields:

$$F_{2221}=F_{1121}=F_{1211}=F_{1112}=F_{2212}=F_{1222}=0.$$

(17)

We have 6 independent coefficients, as indicated below:

$${\left[\widehat{\underset{\sim }{\mathrm{F}}}\right]}_{{\mathrm{D}}_2}={\left(\begin{array}{cc}{F}_{1111}& 0\\ F_{2211}& 0\\ \sqrt{2}{F}_{1221}& 0\\ 0& F_{2222}\\ 0& F_{1122}\\ 0& \sqrt{2}{F}_{1212}\end{array}\right)}_{{\mathcal{B}}_4}$$

4.1.5. ${\mathrm{D}}_4$-Class

The generators of the group ${\mathrm{D}}_4$ are $\mathrm{R}(\pi /2)$ and $\mathrm{P}\left({\underline{\mathrm{e}}}_2\right)$. The condition ${\left(\underset{\sim }{\mathrm{Q}}\star \underset{\approx }{\mathrm{F}}\right)}_{ijkl}=F_{ijkl}$ adds to Equation (15) the new conditions:

$$F_{2222}=F_{1111},F_{1122}=F_{2211},F_{1212}=F_{1221}.$$

(18)

We have 3 independent coefficients, as indicated below:

$${\left[\widehat{\underset{\sim }{\mathrm{F}}}\right]}_{{\mathrm{D}}_4}={\left(\begin{array}{cc}{F}_{1111}& 0\\ F_{2211}& 0\\ \sqrt{2}{F}_{1221}& 0\\ 0& F_{1111}\\ 0& F_{2211}\\ 0& \sqrt{2}{F}_{1221}\end{array}\right)}_{{\mathcal{B}}_4}$$

4.1.6. $\mathrm{O}\left(2\right)$-Class

Exploiting again the Hermann’s theorem, $\mathrm{O}\left(2\right)$-invariant tensors are obtained by imposing ${\mathrm{D}}_8$-invariance, with generators $\mathrm{R}(\pi /4)$ and $\mathrm{P}\left({\underline{\mathrm{e}}}_2\right)$, to $\underset{\approx }{\mathrm{F}}$. The condition ${(\underset{\sim }{\mathrm{Q}}\star \underset{\approx }{\mathrm{F}})}_{ijkl}=F_{ijkl}$ adds to Equation (16) the new conditions:

$$F_{1112}=F_{2212}=0.$$

We have 2 independent coefficients, as indicated below:

$${\left[\widehat{\underset{\sim }{\mathrm{F}}}\right]}_{\mathrm{O}\left(2\right)}={\left(\begin{array}{cc}{F}_{1111}& 0\\ F_{2211}& 0\\ \frac{\sqrt{2}}{2}(F_{1111}-F_{2211})& 0\\ 0& F_{1111}\\ 0& F_{2211}\\ 0& \frac{\sqrt{2}}{2}(F_{1111}-F_{2211})\end{array}\right)}_{{\mathcal{B}}_4}.$$

We recover the number of independent components for each symmetry class of $\underset{\approx }{\mathrm{F}}$ given in Table 2.

4.2. Matrix Representations of the Complete Flexoelectric Law

The determination of the matrix representations of the complete flexoelectric law is done in two stages: First to express the sate tensors as vectors and the constitutive tensors as matrices in appropriate orthonormal bases and then to assemble these matrices. The orthonormal bases associated to the state tensors and the constitutive tensors $\underset{\sim }{\mathrm{S}}$, $\underset{\simeq }{\mathrm{P}}$, and $\underset{\approx }{\mathrm{F}}$ are given in Section 4.1. The matrix representations of the tensors $\underset{\approx }{\mathrm{C}}$, $\underset{\approxeq }{\mathrm{M}}$, and $\underset{≋}{\mathrm{A}}$ and the associated orthonormal bases are given in Section 3, Appendices A and B of [21], so we do not describe them here. By assembly of all the submatrices, we obtain the matrix form of the complete flexoelectricity law of Equations (3)–(5):

$$\left(\begin{array}{c}\left[\underline{\widehat{\mathsf{\sigma }}}\right]\\ [\underline{\widehat{\mathsf{\tau }}}]\\ [\underline{\mathrm{p}}]\end{array}\right)=\left(\begin{array}{ccc}\left[\underset{\sim }{\widehat{\mathrm{C}}}\right]& \left[\underset{\sim }{\widehat{\mathrm{M}}}\right]& \left[\underset{\sim }{\widehat{\mathrm{P}}}\right]\\ [\underset{\sim }{\widehat{\mathrm{M}}}{]}^T& \left[\underset{\sim }{\widehat{\mathrm{A}}}\right]& \left[\underset{\sim }{\widehat{\mathrm{F}}}\right]\\ [\underset{\sim }{\widehat{\mathrm{P}}}{]}^T& {\left[\underset{\sim }{\widehat{\mathrm{F}}}\right]}^T& \left[\underset{\sim }{\mathrm{S}}\right]\end{array}\right)\left(\begin{array}{c}\left[\underline{\widehat{\mathsf{\epsilon }}}\right]\\ [\underline{\widehat{\mathsf{\eta }}}]\\ [\underline{\mathrm{q}}]\end{array}\right)$$

where $\left[\underset{\sim }{\widehat{\mathrm{C}}}\right]\in {\mathcal{M}}_3^s$, $\left[\underset{\sim }{\widehat{\mathrm{M}}}\right]\in {\mathcal{M}}_{3,6}$, $\left[\underset{\sim }{\widehat{\mathrm{P}}}\right]\in {\mathcal{M}}_{3,2}$, $\left[\underset{\sim }{\widehat{\mathrm{A}}}\right]\in {\mathcal{M}}_6^s$, and $\left[\underset{\sim }{\widehat{\mathrm{F}}}\right]\in {\mathcal{M}}_{6,2}$.

For each symmetry class, the assembly of the sub-matrices is done taking into account two rules:

• Any odd-order tensor vanishes for the centrosymmetric symmetry classes: $\left[{\mathrm{Z}}_{2k}\right]$, $\left[{\mathrm{D}}_{2k}\right]$;
• An even-order tensor can not see an odd-order material invariance (in 2D), the invariance seen will be twice the order of the former (see [36] (Theorem 5)).

Using the above rules, we obtain the following matrix representations of the complete flexoelectricity law in each stratum:

$${\left[\mathcal{F}\right]}_{\mathbb{1}}=\left(\begin{array}{ccc}{\left[\underset{\sim }{\widehat{\mathrm{C}}}\right]}_{{\mathrm{Z}}_2}& {\left[\underset{\sim }{\widehat{\mathrm{M}}}\right]}_{\mathbb{1}}& {\left[\underset{\sim }{\widehat{\mathrm{P}}}\right]}_{\mathbb{1}}\\ {\left[\underset{\sim }{\widehat{\mathrm{M}}}\right]}_{\mathbb{1}}^T& {\left[\underset{\sim }{\widehat{\mathrm{A}}}\right]}_{{\mathrm{Z}}_2}& {\left[\underset{\sim }{\widehat{\mathrm{F}}}\right]}_{{\mathrm{Z}}_2}\\ {\left[\underset{\sim }{\widehat{\mathrm{P}}}\right]}_{\mathbb{1}}^T& {\left[\underset{\sim }{\widehat{\mathrm{F}}}\right]}_{{\mathrm{Z}}_2}^T& {\left[\underset{\sim }{\mathrm{S}}\right]}_{{\mathrm{D}}_2}\end{array}\right);{\left[\mathcal{F}\right]}_{{\mathrm{Z}}_2^{\pi }}=\left(\begin{array}{ccc}{\left[\underset{\sim }{\widehat{\mathrm{C}}}\right]}_{{\mathrm{D}}_2}& {\left[\underset{\sim }{\widehat{\mathrm{M}}}\right]}_{{\mathrm{Z}}_2^{\pi }}& {\left[\underset{\sim }{\widehat{\mathrm{P}}}\right]}_{{\mathrm{Z}}_2^{\pi }}\\ {\left[\underset{\sim }{\widehat{\mathrm{M}}}\right]}_{{\mathrm{Z}}_2^{\pi }}^T& {\left[\underset{\sim }{\widehat{\mathrm{A}}}\right]}_{{\mathrm{D}}_2}& {\left[\underset{\sim }{\widehat{\mathrm{F}}}\right]}_{{\mathrm{D}}_2}\\ {\left[\underset{\sim }{\widehat{\mathrm{P}}}\right]}_{{\mathrm{Z}}_2^{\pi }}^T& {\left[\underset{\sim }{\widehat{\mathrm{F}}}\right]}_{{\mathrm{D}}_2}^T& {\left[\underset{\sim }{\mathrm{S}}\right]}_{{\mathrm{D}}_2}\end{array}\right)$$

$${\left[\mathcal{F}\right]}_{{\mathrm{Z}}_2}=\left(\begin{array}{ccc}{\left[\underset{\sim }{\widehat{\mathrm{C}}}\right]}_{{\mathrm{Z}}_2}& 0& 0\\ 0& {\left[\underset{\sim }{\widehat{\mathrm{A}}}\right]}_{{\mathrm{Z}}_2}& {\left[\underset{\sim }{\widehat{\mathrm{F}}}\right]}_{{\mathrm{Z}}_2}\\ 0& {\left[\underset{\sim }{\widehat{\mathrm{F}}}\right]}_{{\mathrm{Z}}_2}^T& {\left[\underset{\sim }{\mathrm{S}}\right]}_{{\mathrm{D}}_2}\end{array}\right);{\left[\mathcal{F}\right]}_{{\mathrm{D}}_2}=\left(\begin{array}{ccc}{\left[\underset{\sim }{\widehat{\mathrm{C}}}\right]}_{{\mathrm{D}}_2}& 0& 0\\ 0& {\left[\underset{\sim }{\widehat{\mathrm{A}}}\right]}_{{\mathrm{D}}_2}& {\left[\underset{\sim }{\widehat{\mathrm{F}}}\right]}_{{\mathrm{D}}_2}\\ 0& {\left[\underset{\sim }{\widehat{\mathrm{F}}}\right]}_{{\mathrm{D}}_2}^T& {\left[\underset{\sim }{\mathrm{S}}\right]}_{{\mathrm{D}}_2}\end{array}\right)$$

$${\left[\mathcal{F}\right]}_{{\mathrm{Z}}_3}=\left(\begin{array}{ccc}{\left[\underset{\sim }{\widehat{\mathrm{C}}}\right]}_{\mathrm{O}\left(2\right)}& {\left[\underset{\sim }{\widehat{\mathrm{M}}}\right]}_{{\mathrm{Z}}_3}& {\left[\underset{\sim }{\widehat{\mathrm{P}}}\right]}_{{\mathrm{D}}_3}\\ {\left[\underset{\sim }{\widehat{\mathrm{M}}}\right]}_{{\mathrm{Z}}_3}^T& {\left[\underset{\sim }{\widehat{\mathrm{A}}}\right]}_{{\mathrm{Z}}_6}& {\left[\underset{\sim }{\widehat{\mathrm{F}}}\right]}_{\mathrm{SO}\left(2\right)}\\ {\left[\underset{\sim }{\widehat{\mathrm{P}}}\right]}_{{\mathrm{D}}_3}^T& {\left[\underset{\sim }{\widehat{\mathrm{F}}}\right]}_{\mathrm{SO}\left(2\right)}^T& {\left[\underset{\sim }{\mathrm{S}}\right]}_{\mathrm{O}\left(2\right)}\end{array}\right);{\left[\mathcal{F}\right]}_{{\mathrm{D}}_3}=\left(\begin{array}{ccc}{\left[\underset{\sim }{\widehat{\mathrm{C}}}\right]}_{\mathrm{O}\left(2\right)}& {\left[\underset{\sim }{\widehat{\mathrm{M}}}\right]}_{{\mathrm{D}}_3}& {\left[\underset{\sim }{\widehat{\mathrm{P}}}\right]}_{{\mathrm{D}}_3}\\ {\left[\underset{\sim }{\widehat{\mathrm{M}}}\right]}_{{\mathrm{D}}_3}^T& {\left[\underset{\sim }{\widehat{\mathrm{A}}}\right]}_{{\mathrm{D}}_6}& {\left[\underset{\sim }{\widehat{\mathrm{F}}}\right]}_{\mathrm{O}\left(2\right)}\\ {\left[\underset{\sim }{\widehat{\mathrm{P}}}\right]}_{{\mathrm{D}}_3}^T& {\left[{\underset{\sim }{\widehat{\mathrm{F}}}}^T\right]}_{\mathrm{O}\left(2\right)}& {\left[\underset{\sim }{\mathrm{S}}\right]}_{\mathrm{O}\left(2\right)}\end{array}\right)$$

$${\left[\mathcal{F}\right]}_{{\mathrm{Z}}_4}=\left(\begin{array}{ccc}{\left[\underset{\sim }{\widehat{\mathrm{C}}}\right]}_{{\mathrm{D}}_4}& 0& 0\\ 0& {\left[\underset{\sim }{\widehat{\mathrm{A}}}\right]}_{{\mathrm{Z}}_4}& {\left[\underset{\sim }{\widehat{\mathrm{F}}}\right]}_{{\mathrm{Z}}_4}\\ 0& {\left[\underset{\sim }{\widehat{\mathrm{F}}}\right]}_{{\mathrm{Z}}_4}^T& {\left[\underset{\sim }{\mathrm{S}}\right]}_{\mathrm{O}\left(2\right)}\end{array}\right);{\left[\mathcal{F}\right]}_{{\mathrm{D}}_4}=\left(\begin{array}{ccc}{\left[\underset{\sim }{\widehat{\mathrm{C}}}\right]}_{{\mathrm{D}}_4}& 0& 0\\ 0& {\left[\underset{\sim }{\widehat{\mathrm{A}}}\right]}_{{\mathrm{D}}_4}& {\left[\underset{\sim }{\widehat{\mathrm{F}}}\right]}_{{\mathrm{D}}_4}\\ 0& {\left[\underset{\sim }{\widehat{\mathrm{F}}}\right]}_{{\mathrm{D}}_4}^T& {\left[\underset{\sim }{\mathrm{S}}\right]}_{\mathrm{O}\left(2\right)}\end{array}\right)$$

$${\left[\mathcal{F}\right]}_{{\mathrm{Z}}_5}=\left(\begin{array}{ccc}{\left[\underset{\sim }{\widehat{\mathrm{C}}}\right]}_{\mathrm{O}\left(2\right)}& {\left[\underset{\sim }{\widehat{\mathrm{M}}}\right]}_{{\mathrm{D}}_5}& 0\\ {\left[\underset{\sim }{\widehat{\mathrm{M}}}\right]}_{{\mathrm{D}}_5}^T& {\left[\underset{\sim }{\widehat{\mathrm{A}}}\right]}_{\mathrm{SO}\left(2\right)}& {\left[\underset{\sim }{\widehat{\mathrm{F}}}\right]}_{\mathrm{SO}\left(2\right)}\\ 0& {\left[\underset{\sim }{\widehat{\mathrm{F}}}\right]}_{\mathrm{SO}\left(2\right)}^T& {\left[\underset{\sim }{\mathrm{S}}\right]}_{\mathrm{O}\left(2\right)}\end{array}\right);{\left[\mathcal{F}\right]}_{{\mathrm{D}}_5}=\left(\begin{array}{ccc}{\left[\underset{\sim }{\widehat{\mathrm{C}}}\right]}_{\mathrm{O}\left(2\right)}& {\left[\underset{\sim }{\widehat{\mathrm{M}}}\right]}_{{\mathrm{D}}_5}& 0\\ {\left[\underset{\sim }{\widehat{\mathrm{M}}}\right]}_{{\mathrm{D}}_5}^T& {\left[\underset{\sim }{\widehat{\mathrm{A}}}\right]}_{\mathrm{O}\left(2\right)}& {\left[\underset{\sim }{\widehat{\mathrm{F}}}\right]}_{\mathrm{O}\left(2\right)}\\ 0& {\left[\underset{\sim }{\widehat{\mathrm{F}}}\right]}_{\mathrm{O}\left(2\right)}^T& {\left[\underset{\sim }{\mathrm{S}}\right]}_{\mathrm{O}\left(2\right)}\end{array}\right)$$

$${\left[\mathcal{F}\right]}_{{\mathrm{Z}}_6}=\left(\begin{array}{ccc}{\left[\underset{\sim }{\widehat{\mathrm{C}}}\right]}_{\mathrm{O}\left(2\right)}& 0& 0\\ 0& {\left[\underset{\sim }{\widehat{\mathrm{A}}}\right]}_{{\mathrm{Z}}_6}& {\left[\underset{\sim }{\widehat{\mathrm{F}}}\right]}_{\mathrm{SO}\left(2\right)}\\ 0& {\left[\underset{\sim }{\widehat{\mathrm{F}}}\right]}_{\mathrm{SO}\left(2\right)}^T& {\left[\underset{\sim }{\mathrm{S}}\right]}_{\mathrm{O}\left(2\right)}\end{array}\right);{\left[\mathcal{F}\right]}_{{\mathrm{D}}_6}=\left(\begin{array}{ccc}{\left[\underset{\sim }{\widehat{\mathrm{C}}}\right]}_{\mathrm{O}\left(2\right)}& 0& 0\\ 0& {\left[\underset{\sim }{\widehat{\mathrm{A}}}\right]}_{{\mathrm{D}}_6}& {\left[\underset{\sim }{\widehat{\mathrm{F}}}\right]}_{\mathrm{O}\left(2\right)}\\ 0& {\left[\underset{\sim }{\widehat{\mathrm{F}}}\right]}_{\mathrm{O}\left(2\right)}^T& {\left[\underset{\sim }{\mathrm{S}}\right]}_{\mathrm{O}\left(2\right)}\end{array}\right)$$

$${\left[\mathcal{F}\right]}_{\mathrm{SO}\left(2\right)}=\left(\begin{array}{ccc}{\left[\underset{\sim }{\widehat{\mathrm{C}}}\right]}_{\mathrm{O}\left(2\right)}& 0& 0\\ 0& {\left[\underset{\sim }{\widehat{\mathrm{A}}}\right]}_{\mathrm{SO}\left(2\right)}& {\left[\underset{\sim }{\widehat{\mathrm{F}}}\right]}_{\mathrm{SO}\left(2\right)}\\ 0& {\left[\underset{\sim }{\widehat{\mathrm{F}}}\right]}_{\mathrm{SO}\left(2\right)}^T& {\left[\underset{\sim }{\mathrm{S}}\right]}_{\mathrm{O}\left(2\right)}\end{array}\right);{\left[\mathcal{F}\right]}_{\mathrm{O}\left(2\right)}=\left(\begin{array}{ccc}{\left[\underset{\sim }{\widehat{\mathrm{C}}}\right]}_{\mathrm{O}\left(2\right)}& 0& 0\\ 0& {\left[\underset{\sim }{\widehat{\mathrm{A}}}\right]}_{\mathrm{O}\left(2\right)}& {\left[\underset{\sim }{\widehat{\mathrm{F}}}\right]}_{\mathrm{O}\left(2\right)}\\ 0& {\left[\underset{\sim }{\widehat{\mathrm{F}}}\right]}_{\mathrm{O}\left(2\right)}^T& {\left[\underset{\sim }{\mathrm{S}}\right]}_{\mathrm{O}\left(2\right)}\end{array}\right)$$

It is important to notice that the matrix representations of the complete flexoelectricity law as given above do not provide a clear picture of their physical content (symmetry, coupling, etc.). For example, if we only focus on the relation $\underline{\mathrm{p}}={\underset{\approx }{\mathrm{F}}}^{\top }⋮\underset{\simeq }{\mathsf{\eta }}$ describing the direct flexoelectric effect, we can not predict the coupling between the different mechanisms: Stretch-gradient and rotation-gradient, that occur in strain-gradient elasticity [19]. The tool that will allow us to analyse such couplings is the harmonic decomposition, i.e., the decomposition of a tensor into a sum of harmonic tensors, via an explicit isomorphism [26]. We will rewrite the matrix representations of $\underset{\approx }{\mathrm{F}}$ in terms of the components of the harmonic tensors of the harmonic decomposition. This procedure will be called the harmonic parametrization of the flexoelectric tensor.

5. Harmonic Parametrization of the Flexoelectric Tensor

In Section 3.4, we have shown that the space $\mathbb{F}\mathrm{lex}$ has the isotypic decomposition:

$$\mathbb{F}\mathrm{lex}\simeq {\mathbb{K}}^4\oplus 3{\mathbb{K}}^2\oplus 2{\mathbb{K}}^0\oplus 2{\mathbb{K}}^{-1}.$$

In this subsection, we give an explicit isomorphism that realizes this decomposition. This decomposition, as provided here, is not the restriction of the one proposed in [17] to the 2D situation, but another, albeit isomorphic, decomposition. This harmonic decomposition is referred to as the Clebsch–Gordan harmonic decomposition, and aims at giving a precise meaning to its elements. This procedure will be detailed in a forthcoming paper [37]. We just provide here the main results.

Due to the multiplicities of the spaces ${\mathbb{K}}^2$, ${\mathbb{K}}^0$, and ${\mathbb{K}}^{-1}$ in the isotypic decomposition, the isomorphism that realizes this decomposition is not uniquely defined [28]. Among the different possibilities, some decompositions have more physical content than others. The decomposition we consider for the constitutive tensor is chosen in order to be compatible with the explicit harmonic decomposition of the state tensor space ${\mathbb{T}}_{\left(ij\right)k}$ as proposed in the following subsection.

5.1. Decomposition of the State Tensor Space ${\mathbb{T}}_{\left(ij\right)k}$

We recall that $\mathbb{F}\mathrm{lex}$ is isomorphic to ${\mathbb{T}}_{\left(ij\right)k}\otimes {\mathbb{T}}_l$. The decomposition we choose here consists first of decomposing the state space ${\mathbb{T}}_{\left(ij\right)k}$ into a sum of $\mathrm{O}\left(2\right)$-irreducible spaces. We recall from Section 3.4 that the space ${\mathbb{T}}_{\left(ij\right)k}$ has the following isotypic decomposition:

$${\mathbb{T}}_{\left(ij\right)k}\simeq {\mathbb{K}}^3\oplus 2{\mathbb{K}}^1.$$

An explicit decomposition is carried out as follows. We split any tensor $\underset{\simeq }{\mathrm{T}}\in {\mathbb{T}}_{\left(ij\right)k}$ into a complete symmetric tensor $\underset{\simeq }{\mathrm{S}}\in {\mathbb{T}}_{\left(ijk\right)}$ and a remainder ${\underset{\simeq }{\mathrm{V}}}^r$ as:

$$\underset{\simeq }{\mathrm{T}}=\underset{\simeq }{\mathrm{S}}+{\underset{\simeq }{\mathrm{V}}}^r$$

(19)

with

$$S_{ijk}=\frac{1}{3}(T_{ijk}+T_{ikj}+T_{jki})\mathrm{and}{V}_{ijk}^r=\frac{1}{3}(2T_{ijk}-T_{ikj}-T_{jki}).$$

(20)

When applied to the strain-gradient tensor $\underset{\simeq }{\mathsf{\eta }}$, the decomposition of Equation (19) has a well-known mechanical interpretation in the strain-gradient elasticity theory [19,20]: The tensor $\underset{\simeq }{\mathrm{S}}$ is the stretch-gradient tensor and the tensor ${\underset{\simeq }{\mathrm{V}}}^r$ is the rotation-gradient tensor.

It is easy to check that the tensor ${\underset{\simeq }{\mathrm{V}}}^r$ belongs to the space:

$${\mathbb{H}}^{r(3,1)}:=\left\{\underset{\simeq }{\mathrm{T}}\in {\mathbb{T}}_{\left(ij\right)k}\mid T_{ijk}+T_{ikj}+T_{jki}=0\right\}$$

(21)

and that the two subspaces ${\mathbb{T}}_{\left(ijk\right)}$ and ${\mathbb{H}}^{r(3,1)}$ are in direct sum. Since $dim\left({\mathbb{H}}^{(3,1)}\right)=2=dim\left({\mathbb{K}}^1\right)$, we can associate a vector ${\underline{\mathrm{v}}}^r\in {\mathbb{K}}^1$ to the tensor ${\underset{\simeq }{\mathrm{V}}}^r$ via an embedding ${\underset{\approx }{\mathrm{\Phi }}}^{r(3,1)}:{\mathbb{K}}^1\hookrightarrow {\mathbb{H}}^{r(3,1)}$. This embedding is given by:

$$V_{ijk}^r=\frac{1}{3}(2{\delta }_{ij}{v}_k^r-{\delta }_{ik}{v}_j^r-{\delta }_{jk}{v}_i^r)$$

which can be rewritten in an intrinsic form as

$${\underset{\simeq }{\mathrm{V}}}^r={\underset{\approx }{\mathrm{\Phi }}}^{r(3,1)}·{\underline{\mathrm{v}}}^r\mathrm{with}{\underset{\approx }{\mathrm{\Phi }}}^{r(3,1)}=\frac{1}{3}\left(2\underset{\approx }{{\mathrm{i}}_1}-\underset{\approx }{{\mathrm{i}}_2}-\underset{\approx }{{\mathrm{i}}_3}\right)\in \mathbb{F}\mathrm{lex}$$

(22)

where $\underset{\approx }{{\mathrm{i}}_1}$, $\underset{\approx }{{\mathrm{i}}_2}$, and $\underset{\approx }{{\mathrm{i}}_3}$ are the fourth-order isotropic tensors with components:

$${\left(\underset{\approx }{{\mathrm{i}}_1}\right)}_{ijkl}:={\delta }_{ij}{\delta }_{kl},{\left(\underset{\approx }{{\mathrm{i}}_2}\right)}_{ijkl}:={\delta }_{ik}{\delta }_{jl}\mathrm{and}{\left(\underset{\approx }{{\mathrm{i}}_3}\right)}_{ijkl}:={\delta }_{il}{\delta }_{jk}.$$

(23)

In order to construct an $\mathrm{O}\left(2\right)$-irreducible decomposition of the tensor $\underset{\simeq }{\mathrm{T}}$, we decompose the tensor $\underset{\simeq }{\mathrm{S}}$ into the sum of a harmonic tensor $\underset{\simeq }{\mathrm{K}}\in {\mathbb{K}}^3$ and an element ${\underset{\simeq }{\mathrm{V}}}^s$ belonging to the subspace:

$${\mathbb{H}}^{s(3,1)}:=\left\{\underset{\simeq }{\mathrm{T}}\in {\mathbb{T}}_{\left(ijk\right)}\mid {\underset{≋}{\mathrm{P}}}^{{\mathbb{K}}^3}⋮\underset{\simeq }{\mathrm{T}}=0\right\},$$

(24)

where ${\underset{≋}{\mathrm{P}}}^{{\mathbb{K}}^3}$ is the projector from ${\mathbb{T}}_{\left(ijk\right)}$ onto ${\mathbb{K}}^3$ defined by:

$${\underset{≋}{\mathrm{P}}}^{{\mathbb{K}}^3}={\underset{≋}{\mathrm{I}}}^{{\mathbb{S}}^3}-\frac{1}{4}\left(\underset{\approx }{{\mathrm{i}}_1}+\underset{\approx }{{\mathrm{i}}_2}+\underset{\approx }{{\mathrm{i}}_3}\right)\otimes \underset{\sim }{1}$$

with ${\underset{≋}{\mathrm{I}}}^{{\mathbb{S}}^3}$ the identity tensor on ${\mathbb{T}}_{\left(ijk\right)}$ with components:

$${\left({\underset{≋}{\mathrm{I}}}^{{\mathbb{S}}^3}\right)}_{ijklmn}:=\frac{1}{6}({\delta }_{il}{\delta }_{jm}{\delta }_{kn}+{\delta }_{im}{\delta }_{jn}{\delta }_{kl}+{\delta }_{in}{\delta }_{jl}{\delta }_{km}+{\delta }_{im}{\delta }_{jl}{\delta }_{kn}+{\delta }_{il}{\delta }_{jn}{\delta }_{km}+{\delta }_{in}{\delta }_{jm}{\delta }_{kl}).$$

Since $dim\left({\mathbb{T}}_{\left(ijk\right)}\right)=4$ and $dim\left({\mathbb{K}}^3\right)=2$, we deduce that $dim\left({\mathbb{H}}^{s(3,1)}\right)=2$. As a consequence, we can associate a vector ${\underline{\mathrm{v}}}^s$ to the tensor ${\underset{\simeq }{\mathrm{V}}}^s$ via an embedding ${\underset{\approx }{\mathrm{\Phi }}}^{s(3,1)}:{\mathbb{K}}^1\hookrightarrow {\mathbb{H}}^{s(3,1)}$, given by:

$${\underset{\simeq }{\mathrm{V}}}^s={\underset{\approx }{\mathrm{\Phi }}}^{s(3,1)}·{\underline{\mathrm{v}}}^s\mathrm{with}{\underset{\approx }{\mathrm{\Phi }}}^{s(3,1)}=\frac{1}{4}\left(\underset{\approx }{{\mathrm{i}}_1}+\underset{\approx }{{\mathrm{i}}_2}+\underset{\approx }{{\mathrm{i}}_3}\right)\in {\mathbb{T}}_{\left(ijkl\right)}.$$

(25)

Finally, an explicit $\mathrm{O}\left(2\right)$-irreducible decomposition of the tensor $\underset{\simeq }{\mathrm{T}}\in {\mathbb{T}}_{\left(ij\right)k}$ is given by:

$$\underset{\simeq }{\mathrm{T}}=\underset{\simeq }{\mathrm{K}}+{\underset{\approx }{\mathrm{\Phi }}}^{s(3,1)}·{\underline{\mathrm{v}}}^s+{\underset{\approx }{\mathrm{\Phi }}}^{r(3,1)}·{\underline{\mathrm{v}}}^r.$$

(26)

When applied to the strain-gradient tensor $\underset{\simeq }{\mathsf{\eta }}$, this decomposition has a clear interpretation: The vectors ${\underline{\mathrm{v}}}^s$ and ${\underline{\mathrm{v}}}^r$ represent the vector parts of the stretch-gradient tensor $\underset{\simeq }{\mathrm{S}}$ and the rotation-gradient tensor ${\underset{\simeq }{\mathrm{V}}}^r$, respectively.

5.2. The Harmonic Basis

With those results at hands, the harmonic parametrization of an element of ${\mathbb{T}}_{\left(ij\right)k}$ can be obtained. Since $dim\left({\mathbb{K}}^{n>0}\right)=2$ in 2D, each of the harmonic tensors $\underset{\simeq }{\mathrm{K}}$, ${\underline{\mathrm{v}}}^{1s}$ and ${\underline{\mathrm{v}}}^{1r}$ has two independent components. Therefore, we can represent them as vectors in appropriate orthonormal bases for ${\mathbb{K}}^3$ and ${\mathbb{K}}^1$. Let us denote by $(K_1,K_2)$, $(v_1^{1s},v_2^{1s})$, and $(v_1^{1r},v_2^{1r})$ the independent components of the tensors $\underset{\simeq }{\mathrm{H}}$, ${\underline{\mathrm{v}}}^{1s}$, ${\underline{\mathrm{v}}}^{1r}$ in ${\mathbb{K}}^3$ and ${\mathbb{K}}^1$, respectively. Since the space ${\mathbb{K}}^1$ coincides with ${\mathbb{R}}^2$, elements ${\underline{\mathrm{v}}}^{1s}$ and ${\underline{\mathrm{v}}}^{1r}$ are standard vectors:

$${\underline{\mathrm{v}}}^{1s}={\left(\begin{array}{c}{v}_1^{1s}\\ v_2^{1s}\end{array}\right)}_{\mathcal{B}}\mathrm{and}{\underline{\mathrm{v}}}^{1r}={\left(\begin{array}{c}{v}_1^{1r}\\ v_2^{1r}\end{array}\right)}_{\mathcal{B}}.$$

For the space ${\mathbb{K}}^3$, we consider the basis ${\mathcal{K}}_3:=\left\{\underset{\simeq }{{\tilde{\mathrm{E}}}_1},\underset{\simeq }{{\tilde{\mathrm{E}}}_2}\right\}$ with:

$$\begin{array}{cc}\hfill \underset{\simeq }{{\tilde{\mathrm{E}}}_1}& =\frac{1}{2}({\underline{\mathrm{e}}}_1\otimes {\underline{\mathrm{e}}}_1\otimes {\underline{\mathrm{e}}}_1-{\underline{\mathrm{e}}}_2\otimes {\underline{\mathrm{e}}}_2\otimes {\underline{\mathrm{e}}}_1-{\underline{\mathrm{e}}}_2\otimes {\underline{\mathrm{e}}}_1\otimes {\underline{\mathrm{e}}}_2-{\underline{\mathrm{e}}}_1\otimes {\underline{\mathrm{e}}}_2\otimes {\underline{\mathrm{e}}}_2),\hfill \\ \hfill \underset{\simeq }{{\tilde{\mathrm{E}}}_2}& =-\frac{1}{2}({\underline{\mathrm{e}}}_2\otimes {\underline{\mathrm{e}}}_2\otimes {\underline{\mathrm{e}}}_2-{\underline{\mathrm{e}}}_1\otimes {\underline{\mathrm{e}}}_1\otimes {\underline{\mathrm{e}}}_2-{\underline{\mathrm{e}}}_1\otimes {\underline{\mathrm{e}}}_2\otimes {\underline{\mathrm{e}}}_1-{\underline{\mathrm{e}}}_2\otimes {\underline{\mathrm{e}}}_1\otimes {\underline{\mathrm{e}}}_1).\hfill \end{array}$$

In this basis, each tensor $\underset{\simeq }{\mathrm{K}}\in {\mathbb{K}}^3$ is represented as a vector:

$$\underline{\mathrm{K}}={\left(\begin{array}{c}2K_1\\ 2K_2\end{array}\right)}_{{\mathcal{K}}_3}.$$

Using the relations given in Section 5.1 and a formal calculation software, we obtain:

$$\begin{array}{cc}\hfill K_1& =\frac{1}{2}\underset{\simeq }{\mathrm{K}}⋮\underset{\simeq }{{\tilde{\mathrm{E}}}_1}=\frac{1}{4}(T_{111}-2T_{122}-T_{221}),\hfill \\ \hfill K_2& =\frac{1}{2}\underset{\simeq }{\mathrm{K}}⋮\underset{\simeq }{{\tilde{\mathrm{E}}}_2}=\frac{1}{4}(T_{112}+2T_{121}-T_{222}),\hfill \\ \hfill v_1^{1s}& ={\underline{\mathrm{v}}}^{1s}·{\underline{\mathrm{e}}}_1=\frac{1}{3}(3T_{111}+2T_{122}+T_{221}),\hfill \\ \hfill v_2^{1s}& ={\underline{\mathrm{v}}}^{1s}·{\underline{\mathrm{e}}}_2=\frac{1}{3}(3T_{222}+2T_{121}+T_{112}),\hfill \\ \hfill v_1^{1r}& ={\underline{\mathrm{v}}}^{1r}·{\underline{\mathrm{e}}}_1=T_{221}-T_{122},\hfill \\ \hfill v_2^{1r}& ={\underline{\mathrm{v}}}^{1r}·{\underline{\mathrm{e}}}_2=T_{112}-T_{121}.\hfill \end{array}$$

Using this parameterization, any element $\underset{\simeq }{\mathrm{T}}\in {\mathbb{T}}_{\left(ij\right)k}$ can be expressed in the basis ${\mathcal{B}}_3$ under the following form:

$$\left[\underline{\widehat{\mathrm{T}}}\right]={\left(\begin{array}{c}\frac{1}{4}(4K_1+3v_1^{1s})\\ \frac{1}{12}(-12K_1+3v_1^{1s}+8v_1^{1r})\\ \frac{\sqrt{2}}{12}(-12K_1+3v_1^{1s}-4v_1^{1r})\\ \frac{1}{4}(-4K_2+3v_2^{1s})\\ \frac{1}{12}(12K_2+3v_2^{1s}+8v_2^{1r})\\ \frac{\sqrt{2}}{12}(12K_2+3v_2^{1s}-4v_2^{1r})\end{array}\right)}_{{\mathcal{B}}_3}.$$

For the case of the strain-gradient tensor $\underset{\simeq }{\mathsf{\eta }}$, the splitting between the stretch-gradient and rotation-gradient contributions is not apparent when the stretch-gradient tensor $\underset{\simeq }{\mathrm{S}}$ and the rotation-gradient tensor ${\underset{\simeq }{\mathrm{V}}}^r$ are expressed in the basis ${\mathcal{B}}_3$. To have a better insight, we have to define an appropriate orthonormal basis ${\mathcal{H}}_3$, called the harmonic basis associated to the basis ${\mathcal{B}}_3$. This harmonic basis ${\mathcal{H}}_3$ is constructed from the explicit harmonic decomposition of ${\mathbb{T}}_{\left(ij\right)k}$. By applying the projectors defined by Equations (28) to the basis vectors $\underset{\simeq }{{\widehat{\mathrm{e}}}_{\mathrm{i}}}$ of ${\mathcal{B}}_3$, we obtain the orthonormal harmonic basis ${\mathcal{H}}_3=\left\{\underset{\simeq }{{\widehat{\mathrm{f}}}_{31}},\underset{\simeq }{{\widehat{\mathrm{f}}}_{32}},\underset{\simeq }{{\widehat{\mathrm{f}}}_{11}^{\mathrm{s}}},\underset{\simeq }{{\widehat{\mathrm{f}}}_{12}^{\mathrm{s}}},\underset{\simeq }{{\widehat{\mathrm{f}}}_{11}^{\mathrm{r}}},\underset{\simeq }{{\widehat{\mathrm{f}}}_{12}^{\mathrm{r}}}\right\}$ with

$$\left\{\begin{array}{cc}\underset{\simeq }{{\widehat{\mathrm{f}}}_{31}}\hfill & =\frac{1}{2}(\underset{\simeq }{{\widehat{\mathrm{e}}}_1}-\underset{\simeq }{{\widehat{\mathrm{e}}}_2}-\sqrt{2}\underset{\simeq }{{\widehat{\mathrm{e}}}_3})\hfill \\ \underset{\simeq }{{\widehat{\mathrm{f}}}_{32}}\hfill & =\frac{1}{2}(-\underset{\simeq }{{\widehat{\mathrm{e}}}_4}+\underset{\simeq }{{\widehat{\mathrm{e}}}_5}+\sqrt{2}\underset{\simeq }{{\widehat{\mathrm{e}}}_6})\hfill \\ \underset{\simeq }{{\widehat{\mathrm{f}}}_{11}^{\mathrm{s}}}\hfill & =\frac{\sqrt{3}}{6}(3\underset{\simeq }{{\widehat{\mathrm{e}}}_1}+\underset{\simeq }{{\widehat{\mathrm{e}}}_2}+\sqrt{2}\underset{\simeq }{{\widehat{\mathrm{e}}}_3})\hfill \\ \underset{\simeq }{{\widehat{\mathrm{f}}}_{12}^{\mathrm{s}}}\hfill & =\frac{\sqrt{3}}{6}(3\underset{\simeq }{{\widehat{\mathrm{e}}}_4}+\underset{\simeq }{{\widehat{\mathrm{e}}}_5}+\sqrt{2}\underset{\simeq }{{\widehat{\mathrm{e}}}_6})\hfill \\ \underset{\simeq }{{\widehat{\mathrm{f}}}_{11}^{\mathrm{r}}}\hfill & =\frac{\sqrt{3}}{3}(\sqrt{2}\underset{\simeq }{{\widehat{\mathrm{e}}}_2}-\underset{\simeq }{{\widehat{\mathrm{e}}}_3})\hfill \\ \underset{\simeq }{{\widehat{\mathrm{f}}}_{12}^{\mathrm{r}}}\hfill & =\frac{\sqrt{3}}{3}(\sqrt{2}\underset{\simeq }{{\widehat{\mathrm{e}}}_5}-\underset{\simeq }{{\widehat{\mathrm{e}}}_6}).\hfill \end{array}\right.$$

(27)

In this new basis, any tensor $\underset{\simeq }{\mathrm{T}}\in {\mathbb{T}}_{\left(ij\right)k}$ has the following representation:

$$\left[\underline{\widehat{\mathrm{T}}}\right]={\left(\begin{array}{c}2K_1\\ 2K_2\\ \frac{\sqrt{3}}{2}{v}_1^{1s}\\ \frac{\sqrt{3}}{2}{v}_2^{1s}\\ \frac{\sqrt{6}}{3}{v}_1^{1r}\\ \frac{\sqrt{6}}{3}{v}_2^{1r}\end{array}\right)}_{{\mathcal{H}}_3}.$$

In the above representation, for the strain-gradient tensor $\underset{\simeq }{\mathsf{\eta }}$, the first four components are associated with the stretch-gradient part of the strain-gradient while the last two components are associated with the rotation-gradient part of the strain gradient. Hence elementary mechanisms that work in the strain-gradient tensor appear clearly separated once expressed in ${\mathcal{H}}_3$.

Now let us go to the decomposition of the constitutive tensor $\underset{\approx }{\mathrm{F}}$.

5.3. Explicit Harmonic Decomposition of the Flexoelectric Tensor

From the tensors ${\underset{\approx }{\mathrm{\Phi }}}^{s(3,1)}$ and ${\underset{\approx }{\mathrm{\Phi }}}^{r(3,1)}$ defined in Equations (25) and (22), we construct a family of orthogonal projectors $\left({\underset{≋}{\mathrm{P}}}^{1s},{\underset{≋}{\mathrm{P}}}^{1r},{\underset{≋}{\mathrm{P}}}^3\right)$ on ${\mathbb{H}}^{s(3,1)}$, ${\mathbb{H}}^{r(3,1)}$, and ${\mathbb{K}}^3$, respectively, as follows:

$$\left\{\begin{array}{c}{\underset{≋}{\mathrm{P}}}^{1s}:=\frac{4}{3}{\underset{\approx }{\mathrm{\Phi }}}^{s(3,1)}·{\underset{\approx }{\mathrm{\Phi }}}^{s(1,3)},\hfill \\ {\underset{≋}{\mathrm{P}}}^{1r}:=\frac{3}{2}{\underset{\approx }{\mathrm{\Phi }}}^{r(3,1)}·{\underset{\approx }{\mathrm{\Phi }}}^{r(1,3)},\hfill \\ {\underset{≋}{\mathrm{P}}}^3:=\underset{≋}{\mathrm{I}}-{\underset{≋}{\mathrm{P}}}^{1s}-{\underset{≋}{\mathrm{P}}}^{1r}\hfill \end{array}\right.$$

(28)

where ${\underset{≋}{\mathrm{I}}}^{\mathbb{P}\mathrm{iez}}$ is the identity tensor on ${\mathbb{T}}_{\left(ij\right)k}$ with components:

$${\left({\underset{≋}{\mathrm{I}}}^{\mathbb{P}\mathrm{iez}}\right)}_{ijklmn}:=\frac{1}{2}({\delta }_{il}{\delta }_{jm}+{\delta }_{im}{\delta }_{jl}){\delta }_{kn},$$

${\underset{\approx }{\mathrm{\Phi }}}^{s(1,3)}$ and ${\underset{\approx }{\mathrm{\Phi }}}^{r(1,3)}$ are the transposes of ${\underset{\approx }{\mathrm{\Phi }}}^{s(3,1)}$ and ${\underset{\approx }{\mathrm{\Phi }}}^{r(3,1)}$ defined by:

$${\left({\underset{\approx }{\mathrm{\Phi }}}^{s(1,3)}\right)}_{ijkl}={\left({\underset{\approx }{\mathrm{\Phi }}}^{s(3,1)}\right)}_{jkli}\mathrm{and}{\left({\underset{\approx }{\mathrm{\Phi }}}^{r(1,3)}\right)}_{ijkl}={\left({\underset{\approx }{\mathrm{\Phi }}}^{r(3,1)}\right)}_{jkli}.$$

An explicit harmonic decomposition of the flexoelectric tensor is given in the following result. The proof of this result will be given in [37].

Proposition 2.

A tensor $\underset{\approx }{\mathrm{F}}\in \mathbb{F}\mathrm{lex}$ admits the uniquely defined Clebsch–Gordan decomposition associated to the family of projectors $\left({\underset{≋}{\mathrm{P}}}^3,{\underset{≋}{\mathrm{P}}}^{1s},{\underset{≋}{\mathrm{P}}}^{1r}\right)$:

$$\begin{array}{cc}\hfill \underset{\approx }{\mathrm{F}}=\underset{\approx }{\mathrm{H}}& +{\underset{≋}{\mathrm{\Phi }}}^{(4,2)}:{\underset{\sim }{\mathrm{h}}}^3+\frac{4}{3}{\underset{\approx }{\mathrm{\Phi }}}^{s(3,1)}·{\underset{\sim }{\mathrm{h}}}^{1s}+\frac{3}{2}{\underset{\approx }{\mathrm{\Phi }}}^{r(3,1)}·{\underset{\sim }{\mathrm{h}}}^{1r}\hfill \\ \hfill & +\frac{2}{3}{\alpha }^{1s}{\underset{\approx }{\mathrm{\Phi }}}^{s(3,1)}+\frac{3}{4}{\alpha }^{1r}{\underset{\approx }{\mathrm{\Phi }}}^{r(3,1)}+\frac{2}{3}{\beta }^{1s}{\underset{\approx }{\mathrm{\Phi }}}^{s(3,1)}·\underset{\sim }{\mathsf{ϵ}}+\frac{3}{4}{\beta }^{1r}{\underset{\approx }{\mathrm{\Phi }}}^{r(3,1)}·\underset{\sim }{\mathsf{ϵ}}\hfill \end{array}$$

(29)

where $\underset{\approx }{\mathrm{H}}\in {\mathbb{K}}^4$, $\left({\underset{\sim }{\mathrm{h}}}^3,{\underset{\sim }{\mathrm{h}}}^{1s},{\underset{\sim }{\mathrm{h}}}^{1r}\right)\in {\mathbb{K}}^2\times {\mathbb{K}}^2\times {\mathbb{K}}^2$, $({\alpha }^{1s},{\alpha }^{1r})\in {\mathbb{K}}^0\times {\mathbb{K}}^0$ and $({\beta }^{1s},{\beta }^{1r})\in {\mathbb{K}}^{-1}\times {\mathbb{K}}^{-1}$, with

$${\left({\underset{≋}{\mathrm{\Phi }}}^{(4,2)}:{\underset{\sim }{\mathrm{h}}}^3\right)}_{ijkl}:=\frac{1}{2}(h_{ij}^3{\delta }_{kl}+h_{ik}^3{\delta }_{jl}-h_{il}^3{\delta }_{jk}).$$

Those elements are determined from $\underset{\approx }{\mathrm{F}}$ as follows:

${\mathbb{K}}^{-1}$	${\mathbb{K}}^0$	${\mathbb{K}}^2$	${\mathbb{K}}^4$
${\beta }^{1s}=\left({\underset{\approx }{\mathrm{\Phi }}}^{s(1,3)}⋮\underset{\approx }{\mathrm{F}}\right):\underset{\sim }{\mathsf{ϵ}}$	${\alpha }^{1s}=\left({\underset{\approx }{\mathrm{\Phi }}}^{s(1,3)}⋮\underset{\approx }{\mathrm{F}}\right):\underset{\sim }{1}$	${\underset{\sim }{\mathrm{h}}}^{1s}=\left({\underset{\approx }{\mathrm{\Phi }}}^{s(1,3)}⋮\underset{\approx }{\mathrm{F}}\right):{\overline{\underset{\approx }{\mathrm{P}}}}^2$
${\beta }^{1r}=\left({\underset{\approx }{\mathrm{\Phi }}}^{r(1,3)}⋮\underset{\approx }{\mathrm{F}}\right):\underset{\sim }{\mathsf{ϵ}}$	${\alpha }^{1r}=\left({\underset{\approx }{\mathrm{\Phi }}}^{r(1,3)}⋮\underset{\approx }{\mathrm{F}}\right):\underset{\sim }{1}$	${\underset{\sim }{\mathrm{h}}}^{1r}=\left({\underset{\approx }{\mathrm{\Phi }}}^{r(1,3)}⋮\underset{\approx }{\mathrm{F}}\right):{\overline{\underset{\approx }{\mathrm{P}}}}^2$
		${\underset{\sim }{\mathrm{h}}}^3={tr}_{14}\left({\underset{≋}{\mathrm{P}}}^3⋮\underset{\approx }{\mathrm{F}}\right)$	$\underset{\approx }{\mathrm{H}}={\underset{≋}{\mathrm{P}}}^3⋮\underset{\approx }{\mathrm{F}}-{\underset{≋}{\mathrm{\Phi }}}^{(4,2)}:{\underset{\sim }{\mathrm{h}}}^3$

Above, ${\overline{\underset{\approx }{\mathrm{P}}}}^2$ is the tensor defined by ${\overline{\underset{\approx }{\mathrm{P}}}}^2:=\frac{1}{2}\left(2\underset{\approx }{{\mathrm{i}}_2}-\underset{\approx }{{\mathrm{i}}_1}-\underset{\sim }{\mathsf{ϵ}}\otimes \underset{\sim }{\mathsf{ϵ}}\right)$ and ${tr}_{pq}\left(\mathrm{T}\right)$ stands for the tensor obtained by the contraction of the tensor $\mathrm{T}$ over its indices p and q.

To denote explicitly the components of $\underset{\approx }{\mathrm{F}}\in \mathbb{F}\mathrm{lex}$ in the harmonic decomposition in Equation (29), we use the compact notation:

$$\underset{\approx }{\mathrm{F}}=\left(\underset{\approx }{\mathrm{H}},{\underset{\sim }{\mathrm{h}}}^3,{\underset{\sim }{\mathrm{h}}}^{1s},{\underset{\sim }{\mathrm{h}}}^{1r},{\beta }^{1s},{\beta }^{1r},{\alpha }^{1s},{\alpha }^{1r}\right).$$

In this case, we define the $\mathrm{O}\left(2\right)$-action of $\underset{\approx }{\mathrm{F}}$ as:

$$\underset{\sim }{\mathrm{Q}}\star \underset{\approx }{\mathrm{F}}=\left(\underset{\sim }{\mathrm{Q}}\star \underset{\approx }{\mathrm{H}},\underset{\sim }{\mathrm{Q}}\star {\underset{\sim }{\mathrm{h}}}^3,\underset{\sim }{\mathrm{Q}}\star {\underset{\sim }{\mathrm{h}}}^{1s},\underset{\sim }{\mathrm{Q}}\star {\underset{\sim }{\mathrm{h}}}^{1r},det\left(\underset{\sim }{\mathrm{Q}}\right){\beta }^{1s},det\left(\underset{\sim }{\mathrm{Q}}\right){\beta }^{1r},{\alpha }^{1s},{\alpha }^{1r}\right).$$

5.4. Associated Matrix Representations

Since $dim\left({\mathbb{K}}^{n>0}\right)=2$ in 2D, each of the harmonic tensors $\underset{\approx }{\mathrm{H}}$, ${\underset{\sim }{\mathrm{h}}}^3$, ${\underset{\sim }{\mathrm{h}}}^{1s}$ and ${\underset{\sim }{\mathrm{h}}}^{1r}$ has two independent components. Therefore, we can represent them as vectors in appropriate orthonormal bases for ${\mathbb{K}}^2$ and ${\mathbb{K}}^4$. As in [38,39], for ${\mathbb{K}}^2$ we choose the basis ${\mathcal{K}}_2:=\{\underset{\sim }{{\mathrm{E}}_1},\underset{\sim }{{\mathrm{E}}_2}\}$ with:

$$\underset{\sim }{{\mathrm{E}}_1}=\frac{\sqrt{2}}{2}({\underline{\mathrm{e}}}_1\otimes {\underline{\mathrm{e}}}_1-{\underline{\mathrm{e}}}_2\otimes {\underline{\mathrm{e}}}_2),\underset{\sim }{{\mathrm{E}}_2}=\frac{\sqrt{2}}{2}({\underline{\mathrm{e}}}_1\otimes {\underline{\mathrm{e}}}_2+{\underline{\mathrm{e}}}_2\otimes {\underline{\mathrm{e}}}_1),$$

and for ${\mathbb{K}}^4$ we choose the basis ${\mathcal{K}}_4:=\{\underset{\approx }{{\widehat{\mathrm{E}}}_1},\underset{\approx }{{\widehat{\mathrm{E}}}_2}\}$ with

$$\underset{\approx }{{\widehat{\mathrm{E}}}_1}=\frac{\sqrt{2}}{2}(\underset{\sim }{{\mathrm{E}}_1}\otimes \underset{\sim }{{\mathrm{E}}_1}-\underset{\sim }{{\mathrm{E}}_2}\otimes \underset{\sim }{{\mathrm{E}}_2}),\underset{\approx }{{\widehat{\mathrm{E}}}_2}=\frac{\sqrt{2}}{2}(\underset{\sim }{{\mathrm{E}}_1}\otimes \underset{\sim }{{\mathrm{E}}_2}+\underset{\sim }{{\mathrm{E}}_2}\otimes \underset{\sim }{{\mathrm{E}}_1}).$$

Let us denote $(H_1,H_2)$, $(h_1^3,h_2^3)$, $(h_1^{1s},h_2^{1s})$, and $(h_1^{1r},h_2^{1r})$ the independent components of the tensors $\underset{\approx }{\mathrm{H}}$, ${\underset{\sim }{\mathrm{h}}}^3$, ${\underset{\sim }{\mathrm{h}}}^{1s}$, ${\underset{\sim }{\mathrm{h}}}^{1r}$, respectively. In the basis ${\mathcal{H}}_4$, each tensor $\underset{\approx }{\mathrm{H}}\in {\mathbb{K}}^4$ is represented as a vector:

$$\underline{\mathrm{H}}={\left(\begin{array}{c}\sqrt{8}{H}_1\\ \sqrt{8}{H}_2\end{array}\right)}_{{\mathcal{K}}_4}$$

and in the basis ${\mathcal{K}}_2$, each tensor $\underset{\sim }{\mathrm{h}}\in {\mathbb{K}}^2$ is represented as a vector:

$$\underline{\mathrm{h}}={\left(\begin{array}{c}\sqrt{2}{h}_1\\ \sqrt{2}{h}_2\end{array}\right)}_{{\mathcal{K}}_2}.$$

As the tensors $\underset{\approx }{\mathrm{H}}$, ${\underset{\sim }{\mathrm{h}}}^3$, ${\underset{\sim }{\mathrm{h}}}^{1s}$, ${\underset{\sim }{\mathrm{h}}}^{1r}$ are defined from $\underset{\approx }{\mathrm{F}}$ (see Proposition 2), the matrices introduced in Section 4.1 can be parametrized in terms of the independent components of the tensors $\underset{\approx }{\mathrm{H}}$, ${\underset{\sim }{\mathrm{h}}}^3$, ${\underset{\sim }{\mathrm{h}}}^{1s}$, ${\underset{\sim }{\mathrm{h}}}^{1r}$, the scalars ${\alpha }^{1s}$, ${\alpha }^{1r}$, and the pseudo-scalars ${\beta }^{1s}$, ${\beta }^{1r}$. Using the relations given in Proposition 2 and a formal calculation software, we obtain:

$$\begin{array}{cc}\hfill H_1& =\frac{\sqrt{8}}{8}\underset{\approx }{\mathrm{H}}::\underset{\approx }{{\widehat{\mathrm{E}}}_1}=\frac{1}{8}(F_{1111}-F_{1122}-2F_{1212}-2F_{1221}-F_{2211}+F_{2222}),\hfill \\ \hfill H_2& =\frac{\sqrt{8}}{8}\underset{\sim }{\mathrm{H}}::\underset{\approx }{{\widehat{\mathrm{E}}}_2}=\frac{1}{8}(F_{1112}+F_{1121}+2F_{1211}-2F_{1122}-F_{2212}-F_{2221}),\hfill \\ \hfill h_1^3& =\frac{\sqrt{2}}{2}{\underset{\sim }{\mathrm{h}}}^3:\underset{\sim }{{\mathrm{E}}_1}=\frac{1}{4}(F_{1111}+F_{1122}+2F_{1212}-2F_{1221}-F_{2211}-F_{2222}),\hfill \\ \hfill h_2^3& =\frac{\sqrt{2}}{2}{\underset{\sim }{\mathrm{h}}}^3:\underset{\sim }{{\mathrm{E}}_2}=\frac{1}{4}(-F_{1112}+F_{1121}+2F_{1211}+2F_{1222}+F_{2212}-F_{2221}),\hfill \\ \hfill h_1^{1s}& =\frac{\sqrt{2}}{2}{\underset{\sim }{\mathrm{h}}}^{1s}:\underset{\sim }{{\mathrm{E}}_1}=\frac{1}{8}(3F_{1111}-F_{1122}-2F_{1212}+2F_{1221}+F_{2211}-3F_{2222}),\hfill \\ \hfill h_2^{1s}& =\frac{\sqrt{2}}{2}{\underset{\sim }{\mathrm{h}}}^{1s}:\underset{\sim }{{\mathrm{E}}_2}=\frac{1}{8}(3F_{1112}+F_{1121}+2F_{1211}+2F_{1122}+F_{2212}+3F_{2221}),\hfill \\ \hfill h_1^{1r}& =\frac{\sqrt{2}}{2}{\underset{\sim }{\mathrm{h}}}^{1r}:\underset{\sim }{{\mathrm{E}}_1}=\frac{1}{3}(-F_{1122}+F_{1212}-F_{1221}+F_{2211}),\hfill \\ \hfill h_2^{1r}& =\frac{\sqrt{2}}{2}{\underset{\sim }{\mathrm{h}}}^{1r}:\underset{\sim }{{\mathrm{E}}_2}=\frac{1}{3}(F_{1121}-F_{1211}-F_{1222}+F_{2212}),\hfill \\ \hfill {\alpha }^{1s}& =\frac{1}{4}(3F_{1111}+F_{1122}+2F_{1212}+2F_{1221}+F_{2211}+3F_{2222}),\hfill \\ \hfill {\alpha }^{1r}& =\frac{2}{3}(F_{1122}-F_{1212}-F_{1221}+F_{2211}),\hfill \\ \hfill {\beta }^{1s}& =\frac{1}{4}(3F_{1112}-F_{1121}-2F_{1211}+2F_{1222}+F_{2212}-3F_{2221}),\hfill \\ \hfill {\beta }^{1r}& =\frac{2}{3}(-F_{1121}+F_{1211}-F_{1222}+F_{2212}).\hfill \end{array}$$

By resolving the above system with respect to the components of the tensor $\underset{\approx }{\mathrm{F}}$, we obtain the following matrix:

$$\begin{array}{cc}\hfill {\left[\underset{\sim }{\widehat{\mathrm{F}}}\right]}_{{\mathrm{Z}}_2}& ={\left(\begin{array}{cc}\frac{1}{2}(2H_1+h_1^3+2h_1^{1s}+{\alpha }^{1s})& \frac{1}{2}(2H_2-h_2^3+2h_2^{1s}+{\beta }^{1s})\\ \frac{1}{6}(-6H_1-3h_1^3+2h_1^{1s}+6h_1^{1r}+{\alpha }^{1s}+3{\alpha }^{1r})& \frac{1}{6}(-6H_2+3h_2^3+2h_2^{1s}+6h_2^{1r}+{\beta }^{1s}+3{\beta }^{1r})\\ \frac{\sqrt{2}}{12}(-12H_1-6h_1^3+4h_1^{1s}-6h_1^{1r}+2{\alpha }^{1s}-3{\alpha }^{1r})& \frac{\sqrt{2}}{12}(-12H_2+6h_2^3+4h_2^{1s}-6h_2^{1r}+2{\beta }^{1s}-3{\beta }^{1r})\\ \frac{1}{2}(-2H_2-h_2^3+2h_2^{1s}-{\beta }^{1s})& \frac{1}{2}(2H_1-h_1^3-2h_1^{1s}+{\alpha }^{1s})\\ \frac{1}{6}(6H_2+3h_2^3+2h_2^{1s}+6h_2^{1r}-{\beta }^{1s}-3{\beta }^{1r})& \frac{1}{6}(-6H_1+3h_1^3-2h_1^{1s}-6h_1^{1r}+{\alpha }^{1s}+3{\alpha }^{1r})\\ \frac{\sqrt{2}}{12}(12H_2+6h_2^3+4h_2^{1s}-6h_2^{1r}-2{\beta }^{1s}+3{\beta }^{1r})& \frac{\sqrt{2}}{12}(-12H_1+6h_1^3-4h_1^{1s}+6h_1^{1r}+2{\alpha }^{1s}-3{\alpha }^{1r})\end{array}\right)}_{{\mathcal{B}}_4}.\hfill \end{array}$$

According to the mechanical interpretations given in Section 5.1 and following the procedure introduced in Section 5.2, it would be interesting to highlight the coupling encoded by the flexoelectric tensor between the stretch-gradient and the rotation-gradient tensors. When the matrix representations of the flexoelectric tensor are expressed in ${\mathcal{B}}_4$, these couplings are not apparent. As in Section 5.2, to clear things up we have to define an appropriate orthonormal basis ${\mathcal{H}}_4$, called the harmonic basis associated to the basis ${\mathcal{B}}_4$. The vectors of the basis ${\mathcal{H}}_4$ are constructed from the vectors of ${\mathcal{H}}_3$ and $\mathcal{B}$ as:

$${\mathcal{H}}_4=\left\{\underset{\simeq }{{\widehat{\mathrm{f}}}_{\mathrm{I}}}\otimes {\underline{\mathrm{e}}}_{\alpha },1\le I\le 6,1\le \alpha \le 2\right\}$$

where we used the slight abuse of notation to label the vectors of the basis ${\mathcal{H}}_3$ by the subscript I according to the order given in Equation (27). In the basis ${\mathcal{H}}_4$, the matrix of the flexoelectric tensor is written:

$$\begin{array}{cc}\hfill {\left[\underset{\sim }{\widehat{\mathrm{F}}}\right]}_{{\mathrm{Z}}_2}& ={\left(\begin{array}{cc}2H_1+h_1^3& 2H_2-h_2^3\\ 2H_2+h_2^3& -2H_1+h_1^3\\ \frac{\sqrt{3}}{3}\left(2h_1^{1s}+{\alpha }^{1s}\right)& \frac{\sqrt{3}}{3}\left(2h_2^{1s}+{\beta }^{1s}\right)\\ \frac{\sqrt{3}}{3}\left(2h_2^{1s}-{\beta }^{1s}\right)& \frac{\sqrt{3}}{3}\left(-2h_1^{1s}+{\alpha }^{1s}\right)\\ \frac{\sqrt{6}}{4}\left(2h_1^{1r}+{\alpha }^{1r}\right)& \frac{\sqrt{6}}{4}\left(2h_2^{1r}+{\beta }^{1r}\right)\\ \frac{\sqrt{6}}{4}\left(2h_2^{1r}-{\beta }^{1r}\right)& \frac{\sqrt{6}}{4}\left(-2h_1^{1r}+{\alpha }^{1r}\right)\end{array}\right)}_{{\mathcal{H}}_4}.\hfill \end{array}$$

Now using the above matrix, we can see clearly the couplings encoded by the flexoelectric tensor. Indeed, the structure of the former matrix is as follows:

$${\left[\underset{\sim }{\widehat{\mathrm{F}}}\right]}_{{\mathrm{Z}}_2}=\left(\begin{array}{c}[{\mathbb{K}}^3\otimes {\mathbb{K}}^1]\\ {\mathbb{K}}^1\otimes {\mathbb{K}}^1]\\ {\mathbb{K}}^1\otimes {\mathbb{K}}^1]\end{array}\right)=\left(\begin{array}{c}[{\mathbb{K}}^4\oplus {\mathbb{K}}^2]\\ {\mathbb{K}}^2\oplus {\mathbb{K}}^0\oplus {\mathbb{K}}^{-1}]\\ {\mathbb{K}}^2\oplus {\mathbb{K}}^0\oplus {\mathbb{K}}^{-1}]\end{array}\right),$$

Returning to the partition of a third-order tensor (Equation (19)), the first two blocks correspond to the coupling between $\underline{\mathrm{q}}$ and $\underset{\simeq }{\mathrm{S}}$ while the third block corresponds to the coupling between $\underline{\mathrm{q}}$ and ${\underset{\simeq }{\mathrm{V}}}^r$. In more physical terms, the basis ${\mathcal{H}}_4$ makes apparent the fact that the matrix of the flexoelectric tensor can be split into two parts:

• The first part $\left[{\underset{\sim }{\widehat{\mathrm{F}}}}^S\right]$ relates the generation of double-forces [19,40] to the electric field. And, on its side, its transpose describes how the stretch-gradient generates an electric polarization;
• The second part $\left[{\underset{\sim }{\widehat{\mathrm{F}}}}^R\right]$ relates the generation of a couple-stress [41,42] to the electric field. And, on its side, its transpose describes how the rotation-gradient generates an electric polarization.

In a formula, we have:

$$\left[\underset{\sim }{\widehat{\mathrm{F}}}\right]=\left[{\underset{\sim }{\widehat{\mathrm{F}}}}^S\right]+\left[{\underset{\sim }{\widehat{\mathrm{F}}}}^R\right]$$

with

$$\left[{\underset{\sim }{\widehat{\mathrm{F}}}}^S\right]={\left(\begin{array}{cc}2H_1+h_1^3& 2H_2-h_2^3\\ 2H_2+h_2^3& -2H_1+h_1^3\\ \frac{\sqrt{3}}{3}\left(2h_1^{1s}+{\alpha }^{1s}\right)& \frac{\sqrt{3}}{3}\left(2h_2^{1s}+{\beta }^{1s}\right)\\ \frac{\sqrt{3}}{3}\left(2h_2^{1s}-{\beta }^{1s}\right)& \frac{\sqrt{3}}{3}\left(-2h_1^{1s}+{\alpha }^{1s}\right)\\ 0& 0\\ 0& 0\end{array}\right)}_{{\mathcal{H}}_4},\left[{\underset{\sim }{\widehat{\mathrm{F}}}}^R\right]={\left(\begin{array}{cc}0& 0\\ 0& 0\\ 0& 0\\ 0& 0\\ \frac{\sqrt{6}}{4}\left(2h_1^{1r}+{\alpha }^{1r}\right)& \frac{\sqrt{6}}{4}\left(2h_2^{1r}+{\beta }^{1r}\right)\\ \frac{\sqrt{6}}{4}\left(2h_2^{1r}-{\beta }^{1r}\right)& \frac{\sqrt{6}}{4}\left(-2h_1^{1r}+{\alpha }^{1r}\right)\end{array}\right)}_{{\mathcal{H}}_4}.$$

For a Koiter continuum, also known as a constrained couple-stress continuum, the flexoelectric tensor reduces to the sole contribution of ${\underset{\approx }{\mathrm{F}}}^R$ [43]. As a consequence, and conversely to a complete strain-gradient continuum, the flexoelectric tensor behaves like a second-order one with respect to orthogonal transformations. At the other end, a continuum for which the contribution of higher-order effects to the mechanical energy is restricted to the symmetric part of the strain-gradient tensor is given by the sole contribution of ${\underset{\approx }{\mathrm{F}}}^S$. With this interpretation in mind, let us consider the flexoelectric matrices for the different symmetry classes:

$${\left[\underset{\sim }{\widehat{\mathrm{F}}}\right]}_{{\mathrm{Z}}_4}={\left(\begin{array}{cc}2H_1& 2H_2\\ 2H_2& -2H_1\\ \frac{\sqrt{3}}{3}{\alpha }^{1s}& \frac{\sqrt{3}}{3}{\beta }^{1s}\\ \frac{\sqrt{3}}{3}{\beta }^{1s}& \frac{\sqrt{3}}{3}{\alpha }^{1s}\\ \frac{\sqrt{6}}{4}{\alpha }^{1r}& \frac{\sqrt{6}}{4}{\beta }^{1r}\\ \frac{\sqrt{6}}{4}{\beta }^{1r}& \frac{\sqrt{6}}{4}{\alpha }^{1r}\end{array}\right)}_{{\mathcal{H}}_4};{\left[\underset{\sim }{\widehat{\mathrm{F}}}\right]}_{\mathrm{SO}\left(2\right)}={\left(\begin{array}{cc}0& 0\\ 0& 0\\ \frac{\sqrt{3}}{3}{\alpha }^{1s}& \frac{\sqrt{3}}{3}{\beta }^{1s}\\ \frac{\sqrt{3}}{3}{\beta }^{1s}& \frac{\sqrt{3}}{3}{\alpha }^{1s}\\ \frac{\sqrt{6}}{4}{\alpha }^{1r}& \frac{\sqrt{6}}{4}{\beta }^{1r}\\ \frac{\sqrt{6}}{4}{\beta }^{1r}& \frac{\sqrt{6}}{4}{\alpha }^{1r}\end{array}\right)}_{{\mathcal{H}}_4};$$

$$\begin{array}{cccc}\hfill {\left[\underset{\sim }{\widehat{\mathrm{F}}}\right]}_{{\mathrm{D}}_2}& ={\left(\begin{array}{cc}2H_1+h_1^3& 0\\ 0& -2H_1+h_1^3\\ \frac{\sqrt{3}}{3}\left(2h_1^{1s}+{\alpha }^{1s}\right)& 0\\ 0& \frac{\sqrt{3}}{3}\left(-2h_1^{1s}+{\alpha }^{1s}\right)\\ \frac{\sqrt{6}}{4}\left(2h_1^{1r}+{\alpha }^{1r}\right)& 0\\ 0& \frac{\sqrt{6}}{4}\left(-2h_1^{1r}+{\alpha }^{1r}\right)\end{array}\right)}_{{\mathcal{H}}_4};{\left[\underset{\sim }{\widehat{\mathrm{F}}}\right]}_{{\mathrm{D}}_4}\hfill & \hfill ={\left(\begin{array}{cc}2H_1& 0\\ 0& -2H_1\\ \frac{\sqrt{3}}{3}{\alpha }^{1s}& 0\\ 0& \frac{\sqrt{3}}{3}{\alpha }^{1s}\\ \frac{\sqrt{6}}{4}{\alpha }^{1r}& 0\\ 0& \frac{\sqrt{6}}{4}{\alpha }^{1r}\end{array}\right)}_{{\mathcal{H}}_4};{\left[\underset{\sim }{\widehat{\mathrm{F}}}\right]}_{\mathrm{O}\left(2\right)}& ={\left(\begin{array}{cc}0& 0\\ 0& 0\\ \frac{\sqrt{3}}{3}{\alpha }^{1s}& 0\\ 0& \frac{\sqrt{3}}{3}{\alpha }^{1s}\\ \frac{\sqrt{6}}{4}{\alpha }^{1r}& 0\\ 0& \frac{\sqrt{6}}{4}{\alpha }^{1r}\end{array}\right)}_{{\mathcal{H}}_4}.\hfill \end{array}$$

Using this decomposition, it can be observed, for instance, that the restriction of a strain-gradient model to a Koiter continuum, can not describe the tetragonal anisotropy.

A second interesting point is that the explicit harmonic decomposition allows us to construct a graphical representation of a flexoelectric tensor in ${\mathbb{R}}^2$ by identifying its harmonic tensors with their associated vectors, as illustrated in Figure 2.

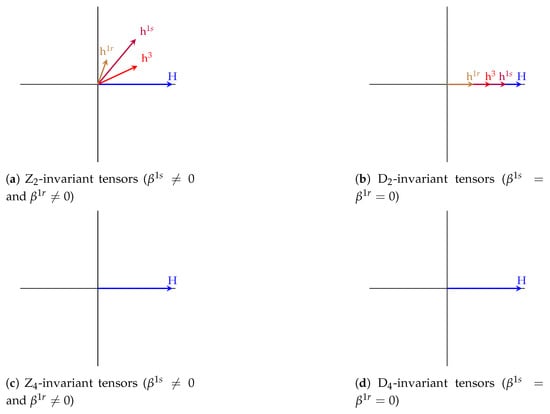
Figure 2. Representation of flexoelectric tensors using harmonic tensors (the hemitropic and isotropic coefficients are not represented here).

In this graphical representation, the vectors associated with the different harmonic components are transformed by an orthogonal transformation according to the irreducible space ${\mathbb{K}}^n$ they belong to (cf. Equation (8)).

6. Discussion

In this work we solved the problem of the determination of the number and types of symmetry classes of the complete flexoelectricity law. Our work completed previous ones [21,22] where attention focused only on the determination of the number and types of symmetry classes of the strain-gradient elasticity law.

Furthermore, we introduced an explicit harmonic decomposition of the flexoelectric tensor.

This decomposition helps to understand the nature of the different electromechanical couplings that took place in a flexoelectric material, such as the contribution of the stretch-gradient or the couple-stress to the electric polarization. This decomposition will be of prime importance for the determination of an explicit basis of polynomial invariants for the flexoelectric tensor.

Using the introduced parametrization, the next step, object of a future contribution will consist in the construction of a finite set of such invariants. This set of invariants will then be used to formulate objective functions for the optimization algorithm.