Entropy Generation and Consequences of MHD in Darcy–Forchheimer Nanofluid Flow Bounded by Non-Linearly Stretching Surface
Abstract
1. Introduction
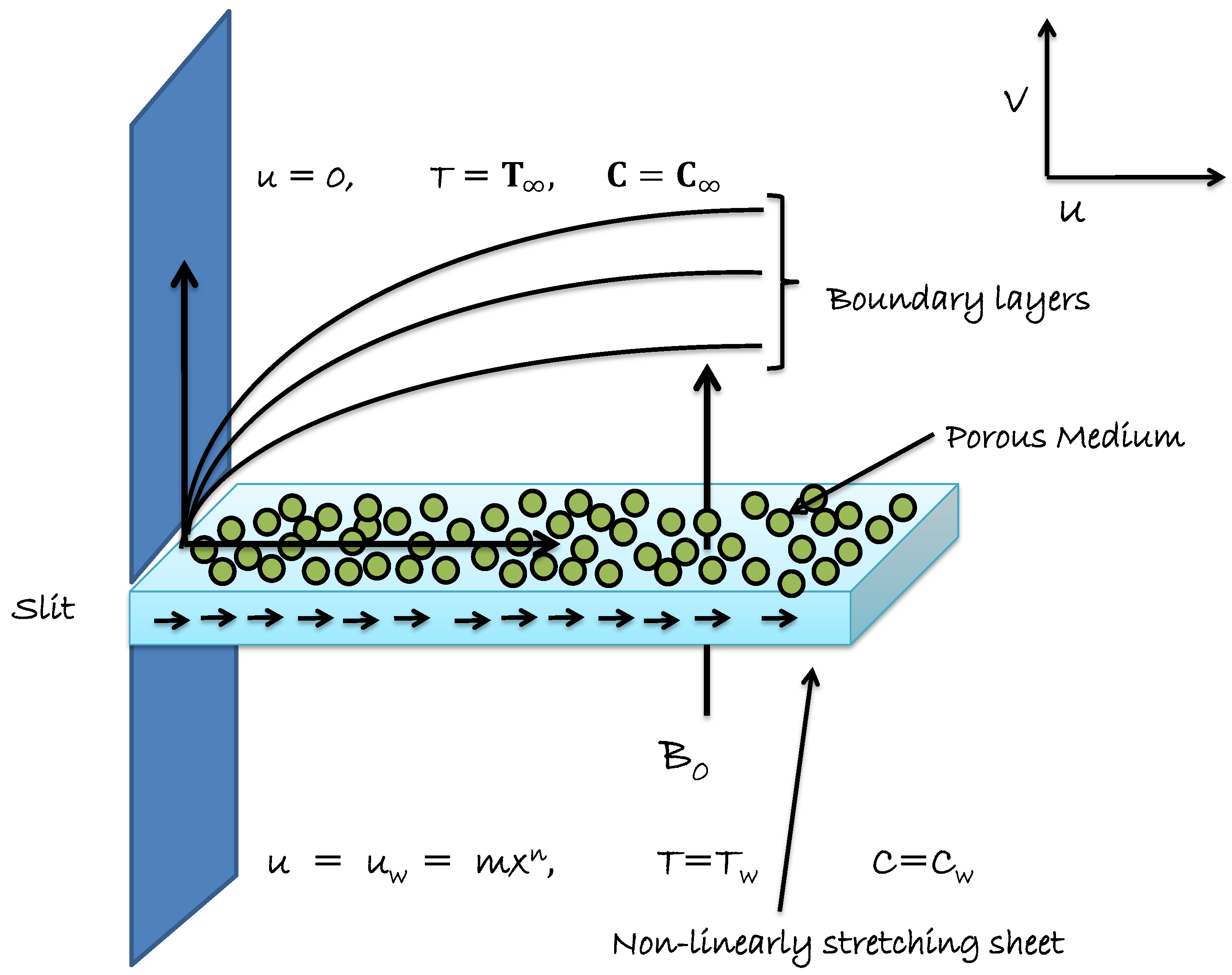
2. Mathematical Modeling
Entropy Generation Modeling
3. Solution Methodology
4. Analysis
5. Conclusions
- Entropy optimization, heat and mass transport in Darcy–Forchheimer and MHD type nanofluid flow surrounded by a non-linear stretching surface is analyzed.
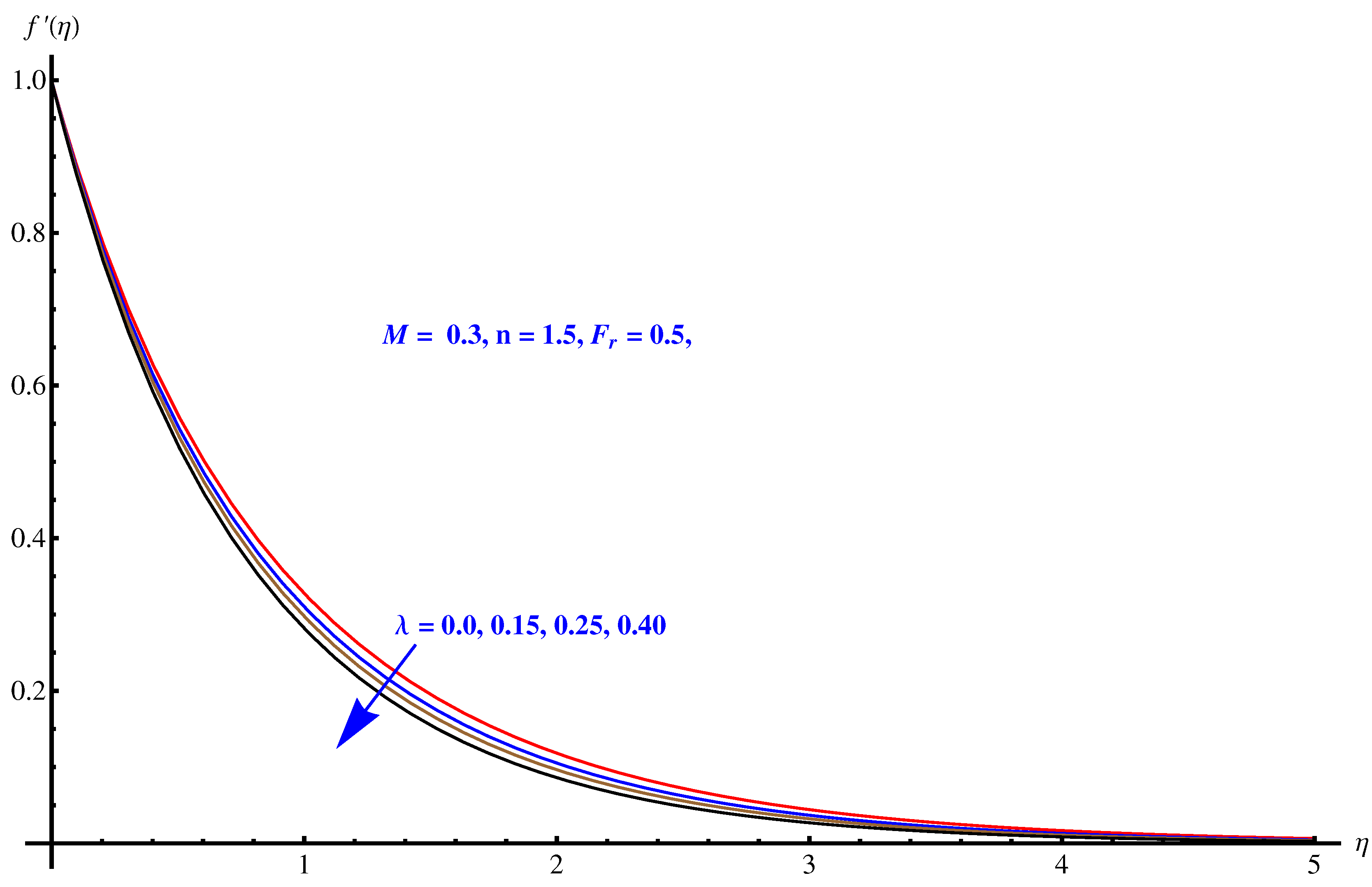
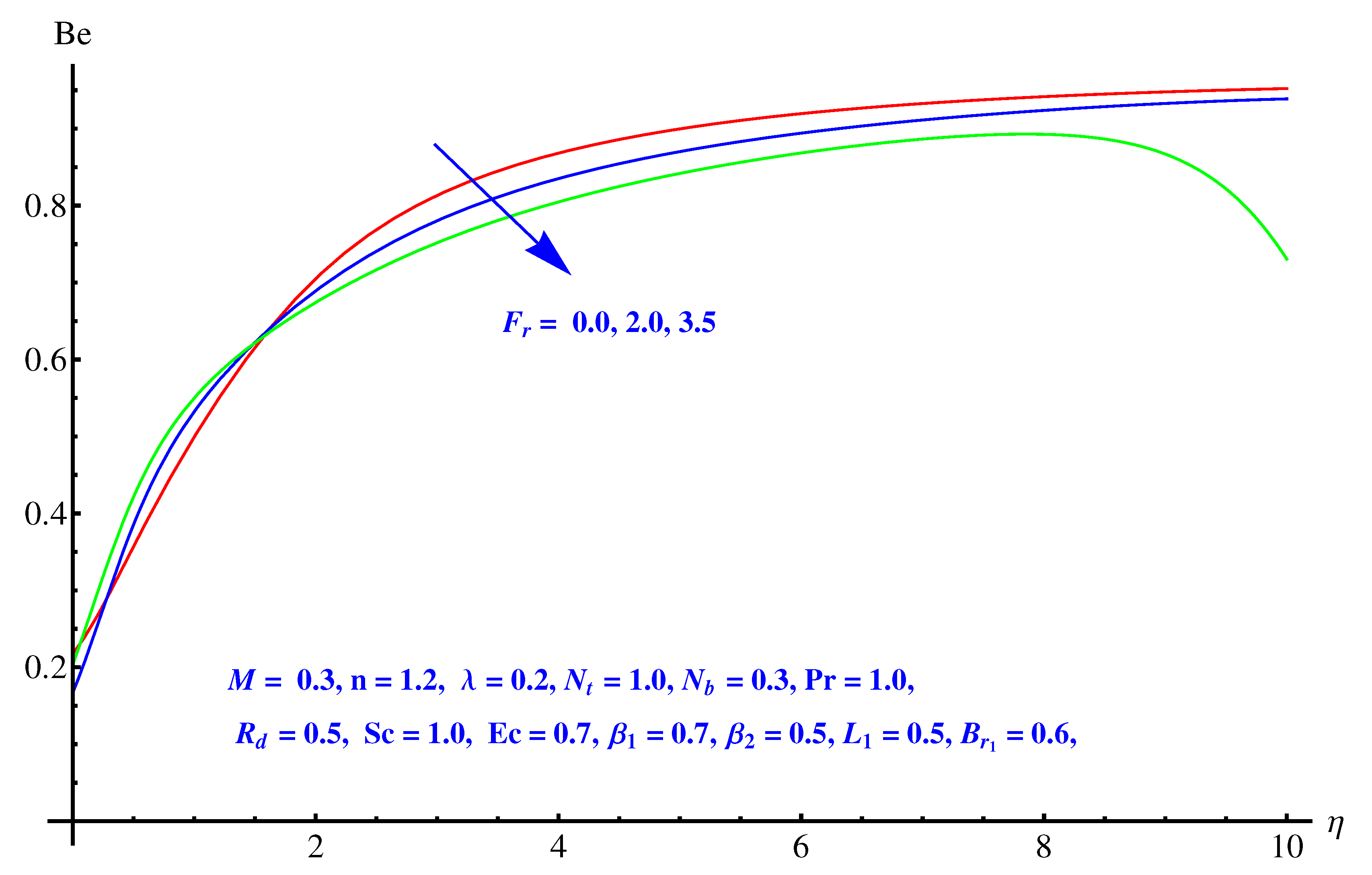
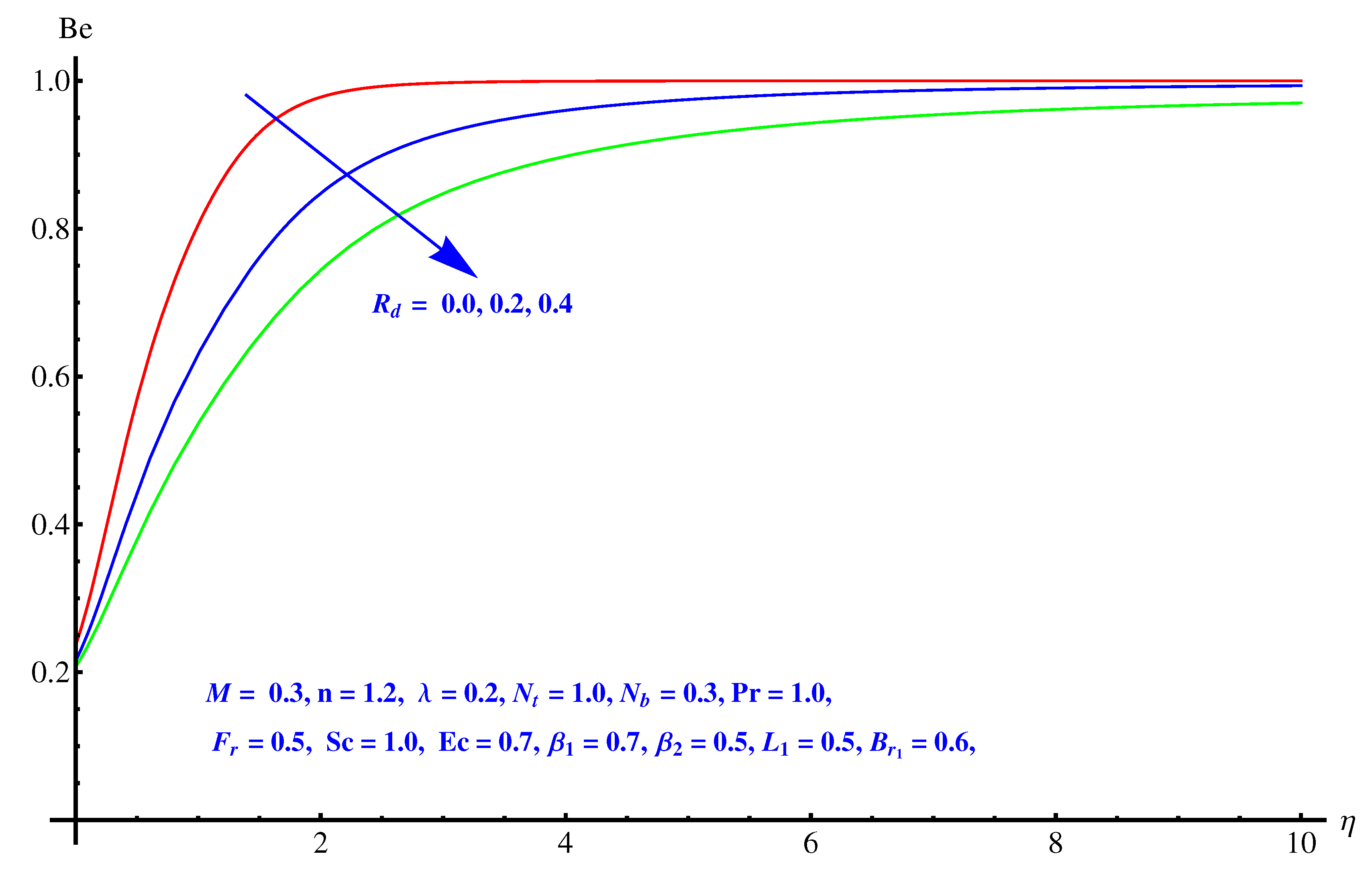
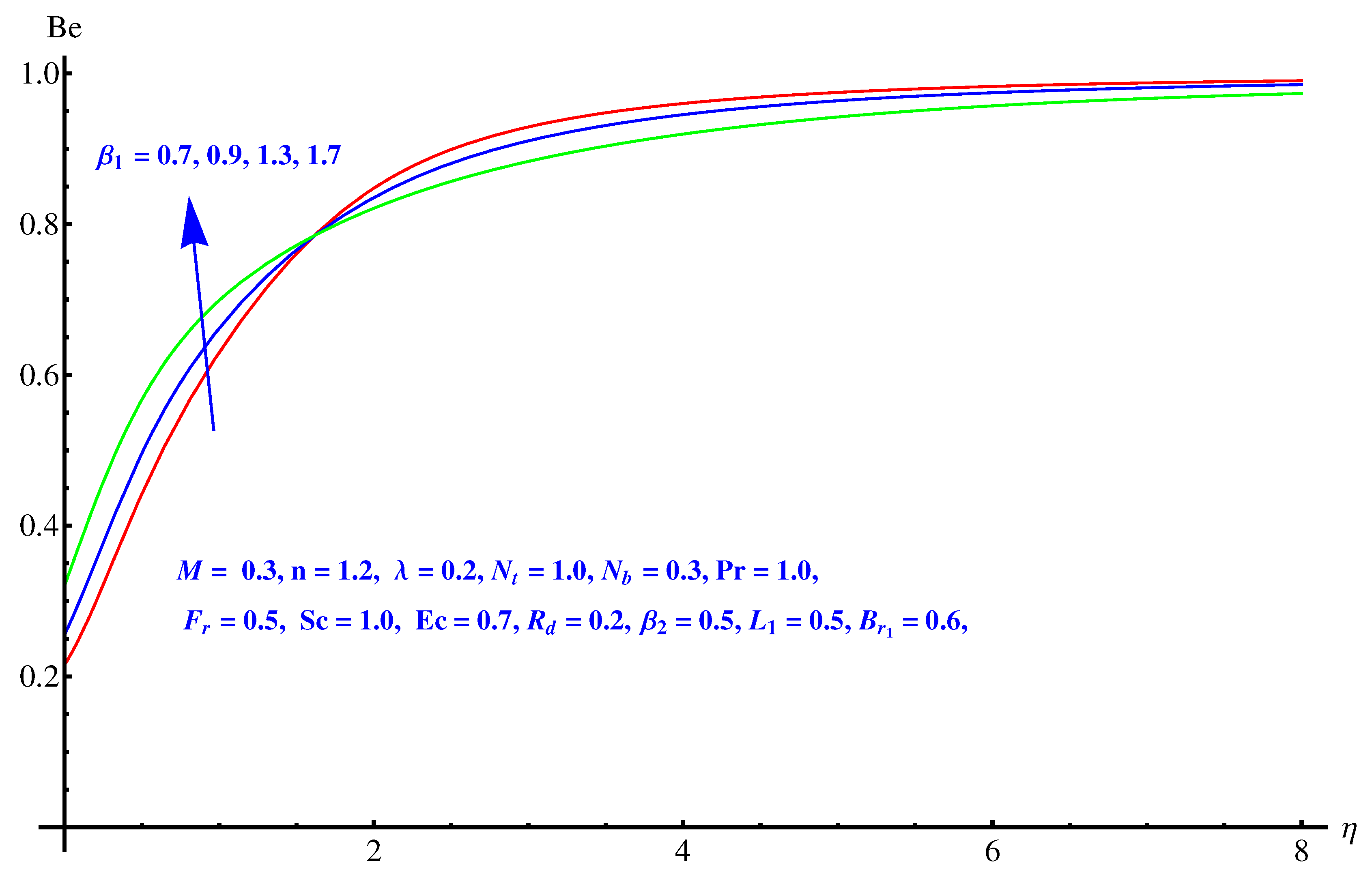
- Rate of Bejan number shows mixed behavior for elevated values of temperature difference parameter. An enhancement is noted for larger values.
- Skin friction enhances for all the parameters involved in momentum equation.
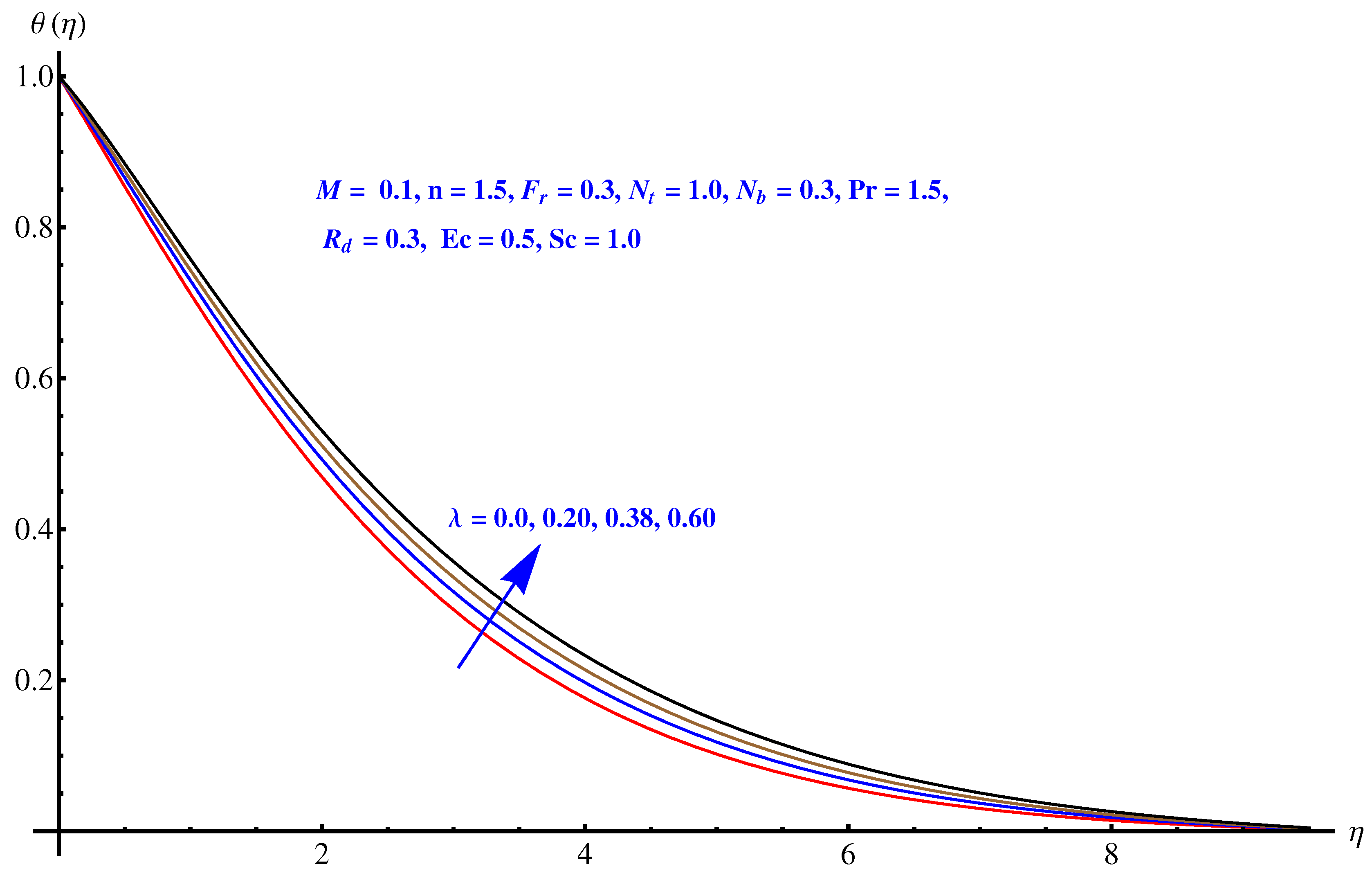
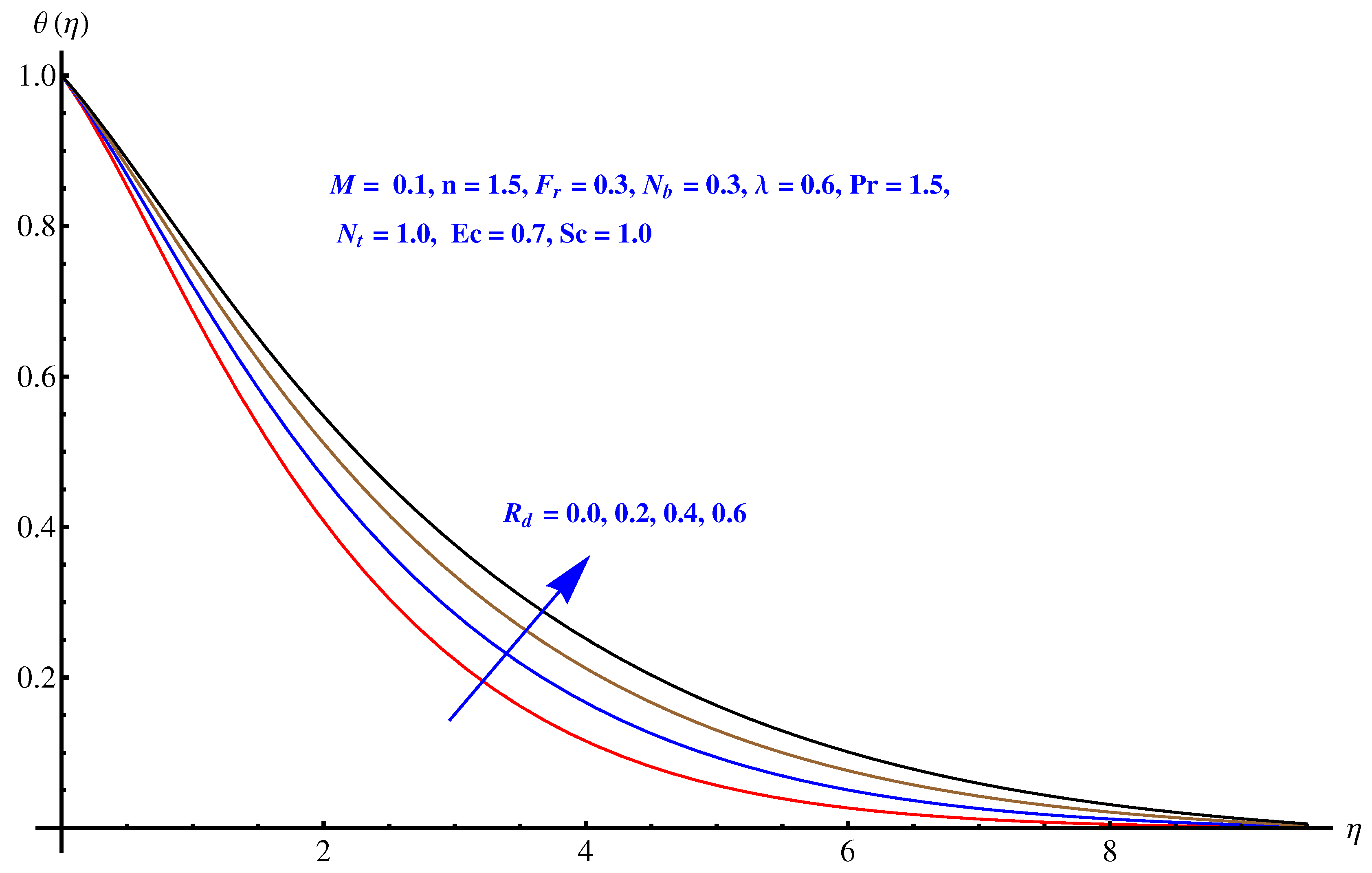
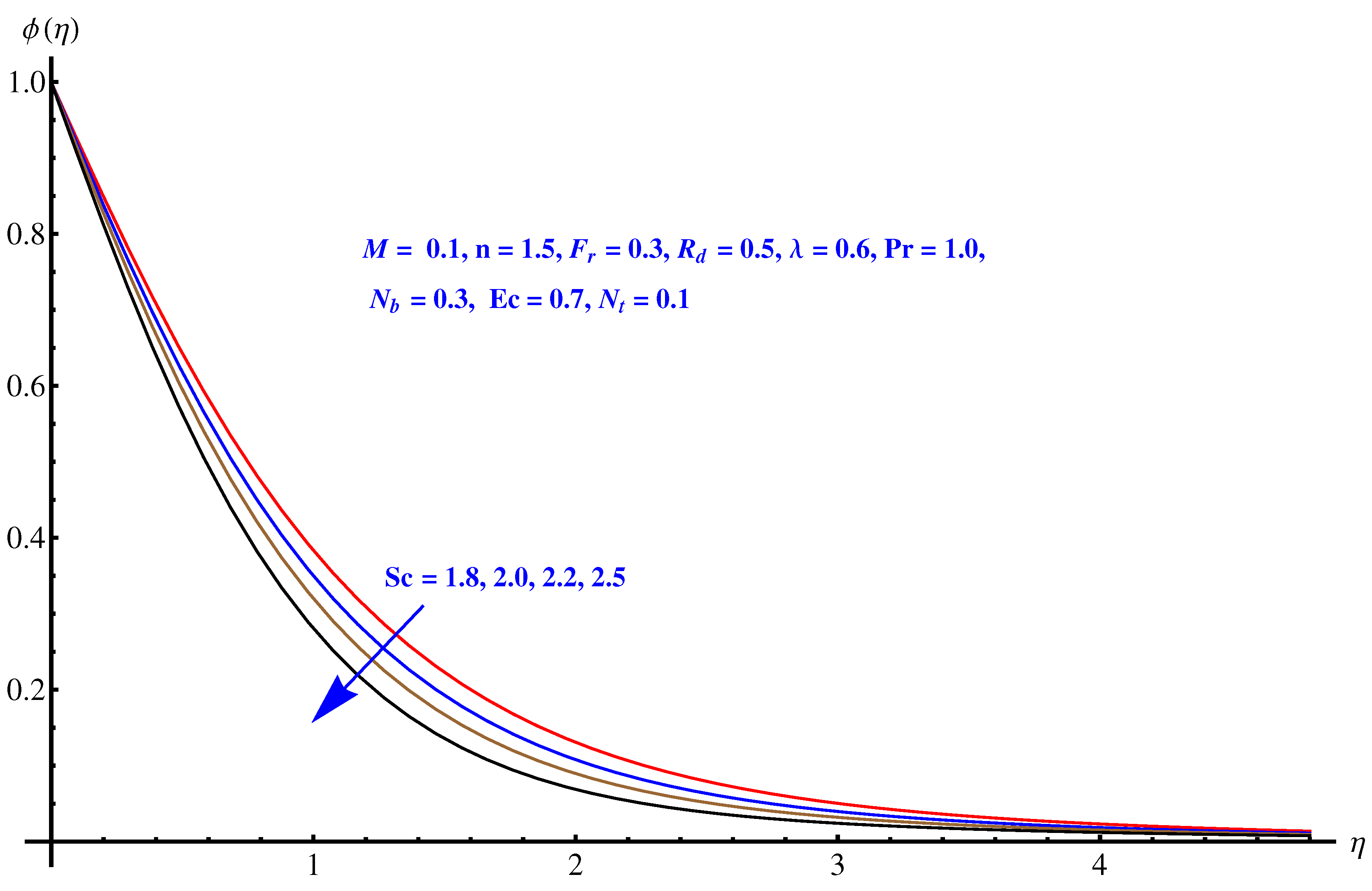
- Heat transfer rate declines while mass transfer intensifies for elevated numbers of thermal radiation parameters.
- Resistive force due to inertia and enhanced friction are the source of enhancement in heat convection.
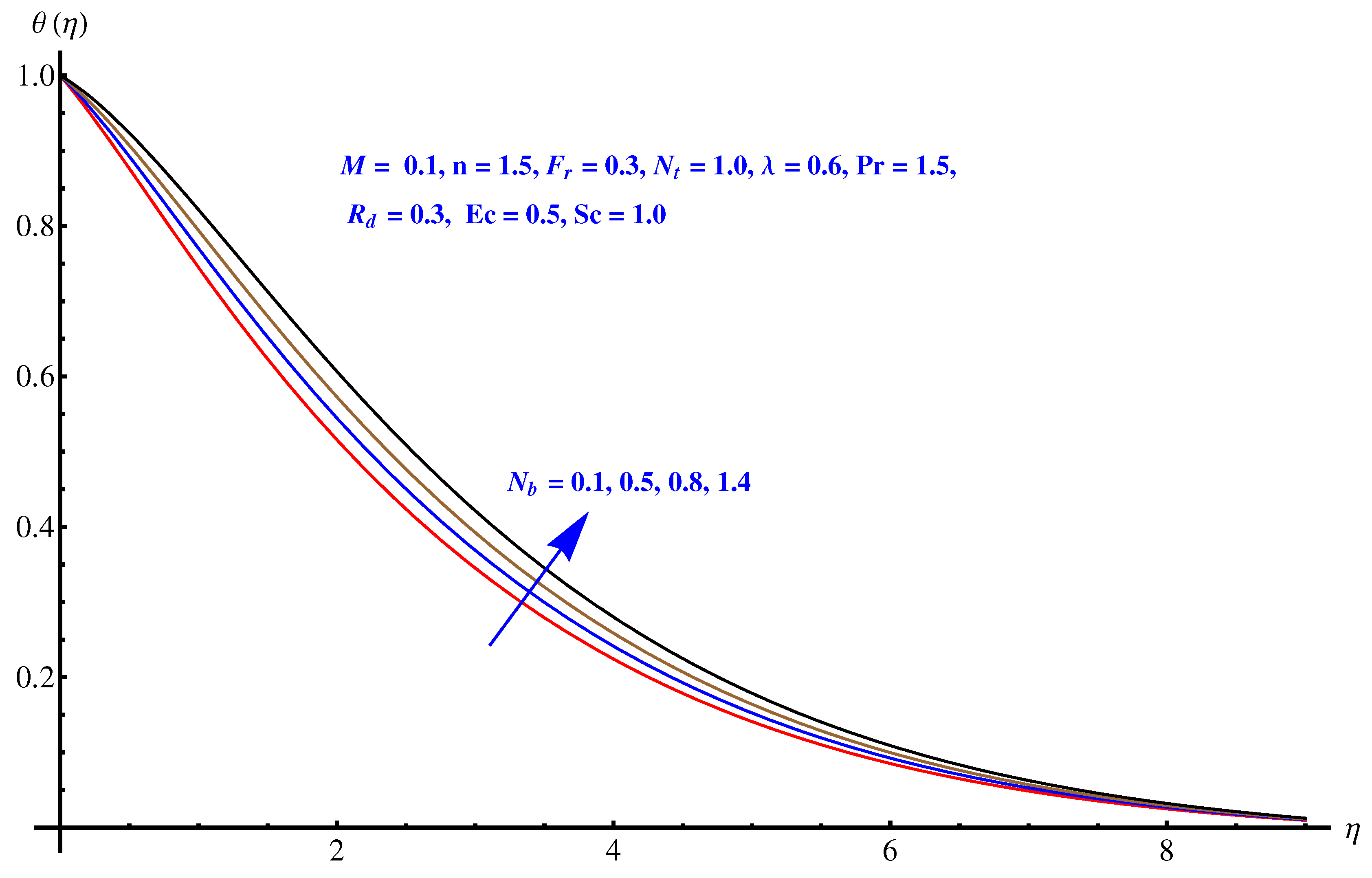
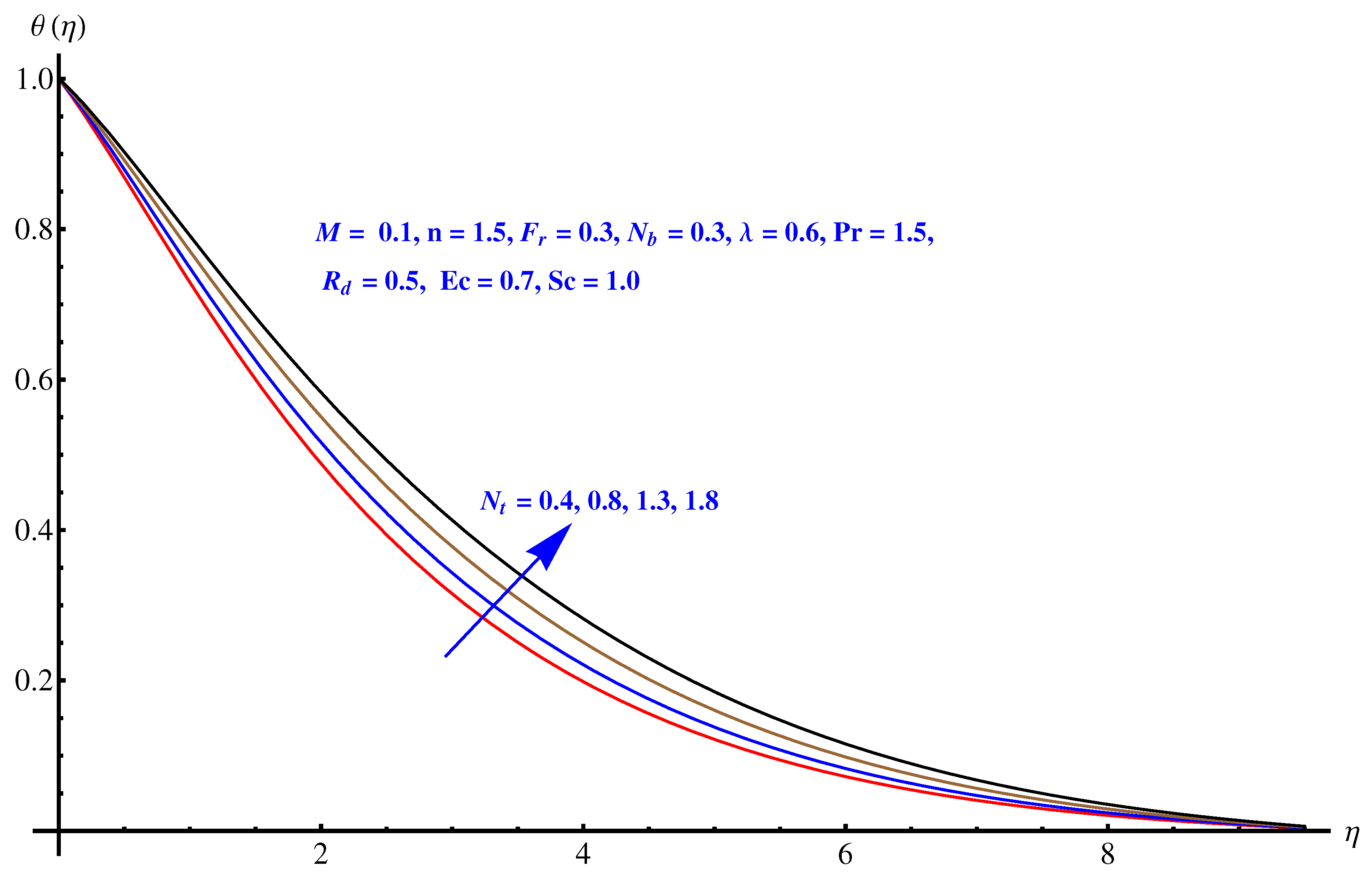
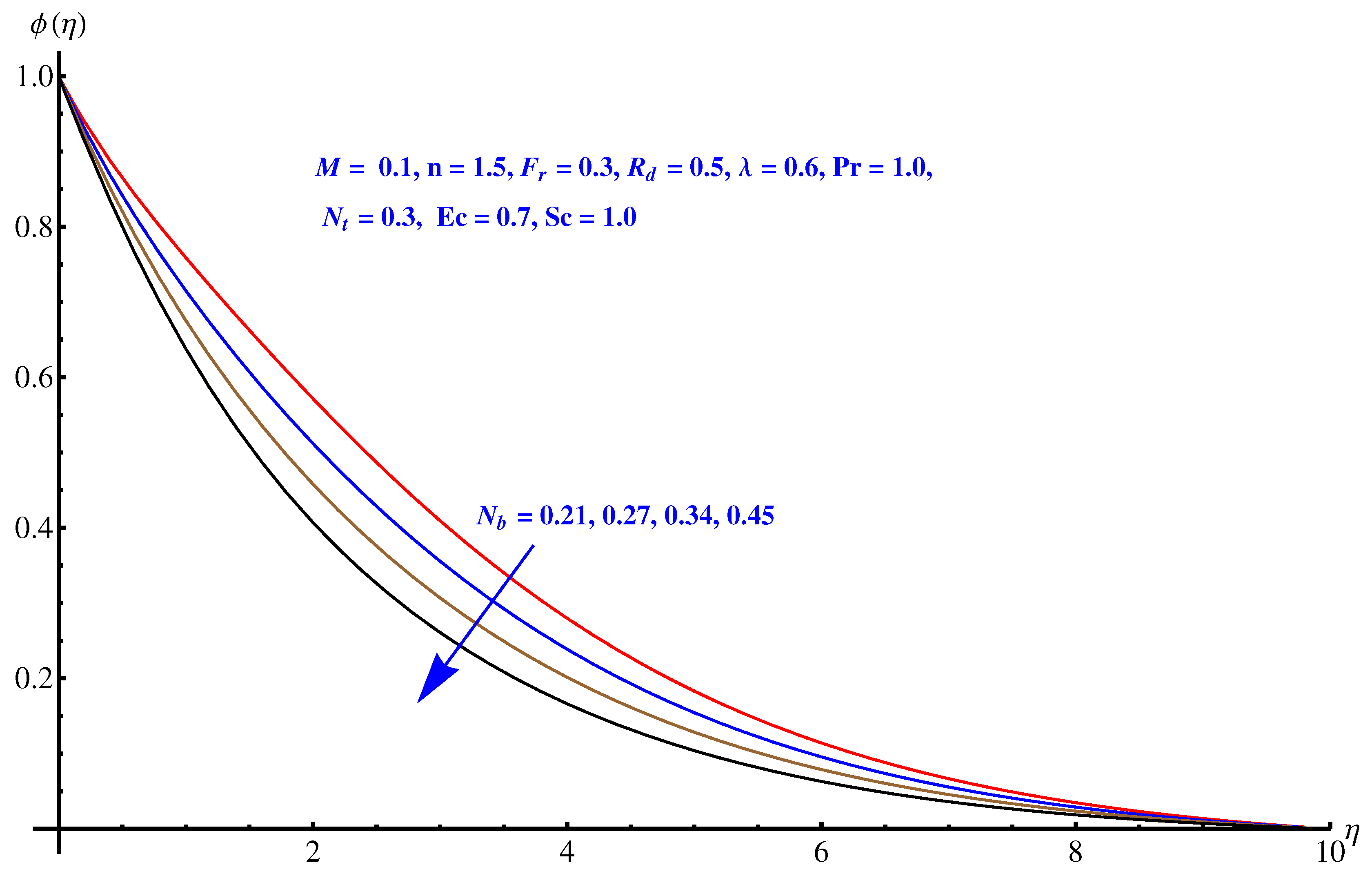
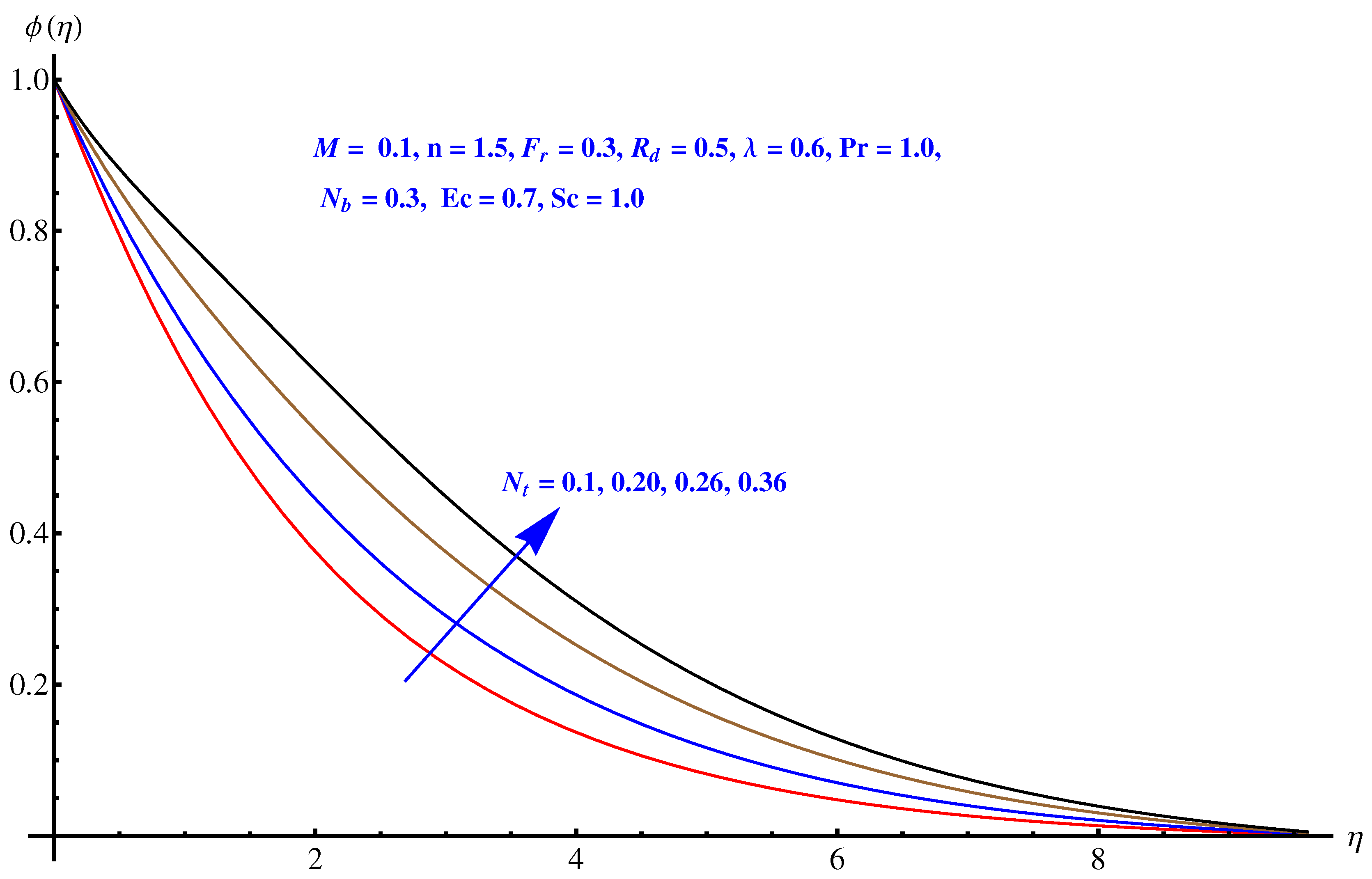
- The concentration of nanoparticles reduces near the surface, whereas an enhancement is noted in the case of thermophoresis due to stronger thermophoretic force.
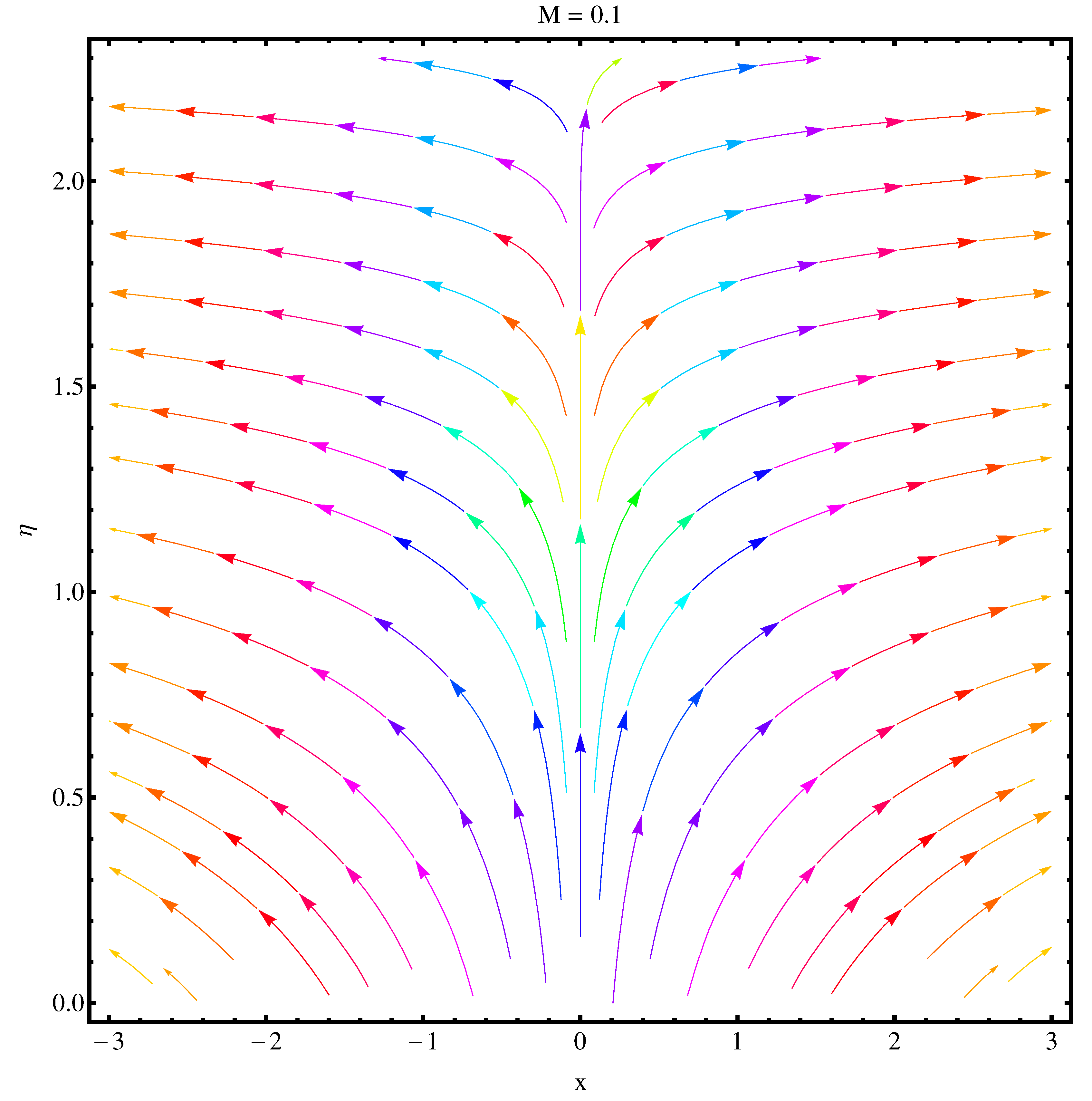
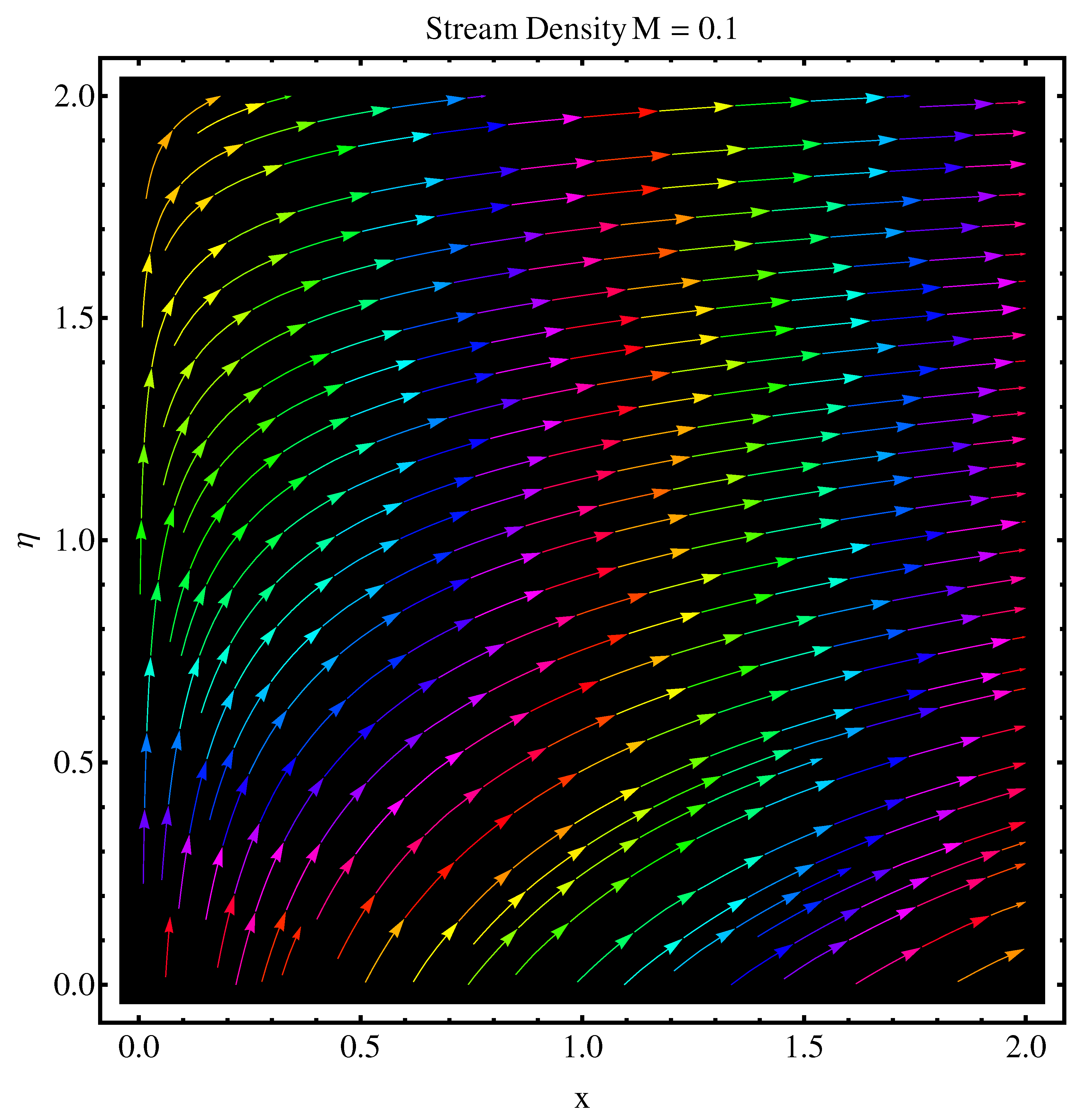
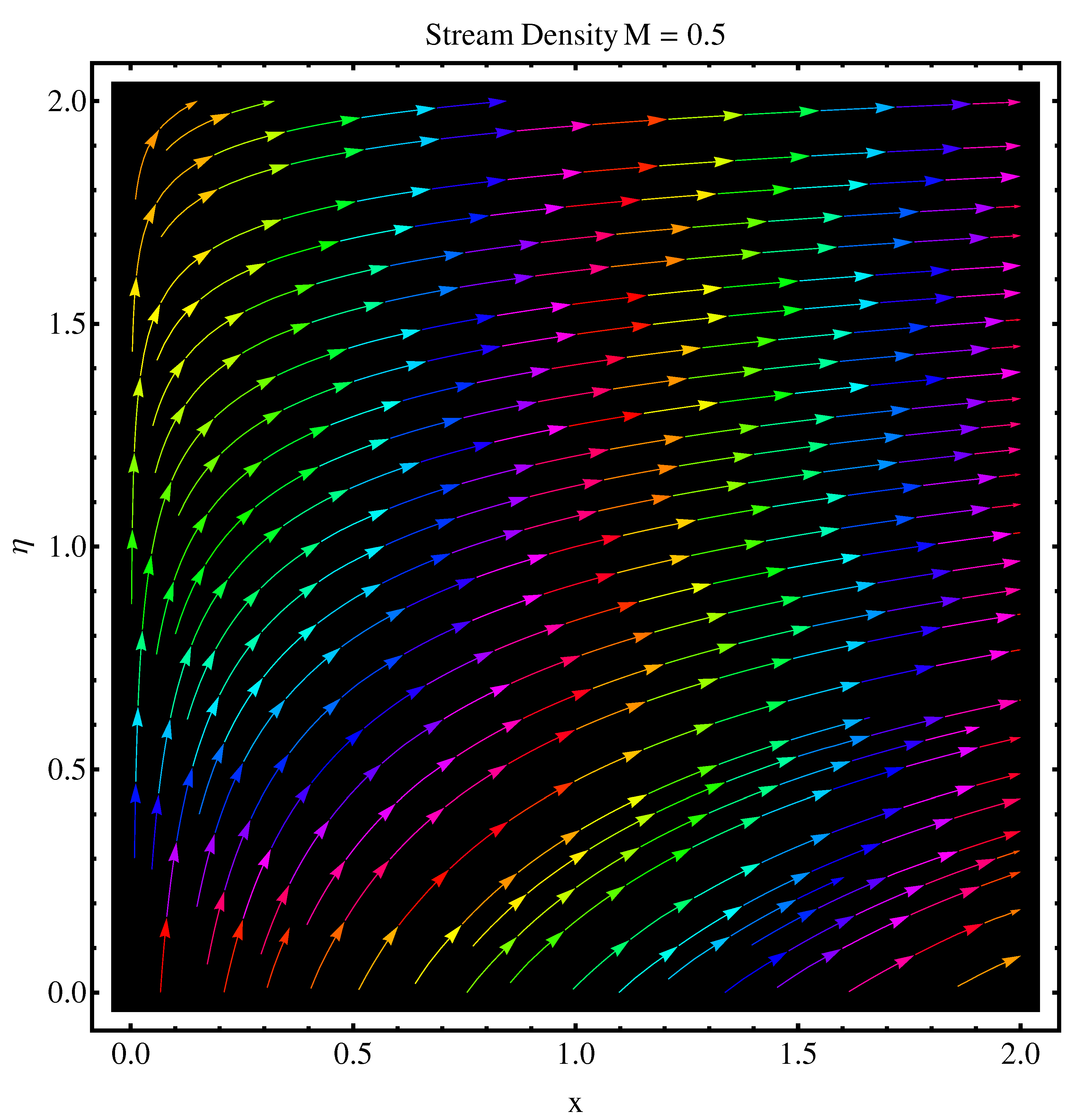
- An enhanced variation in stream lines is noted at distance far away from the origin. Near to the origin, this variation is very narrow.
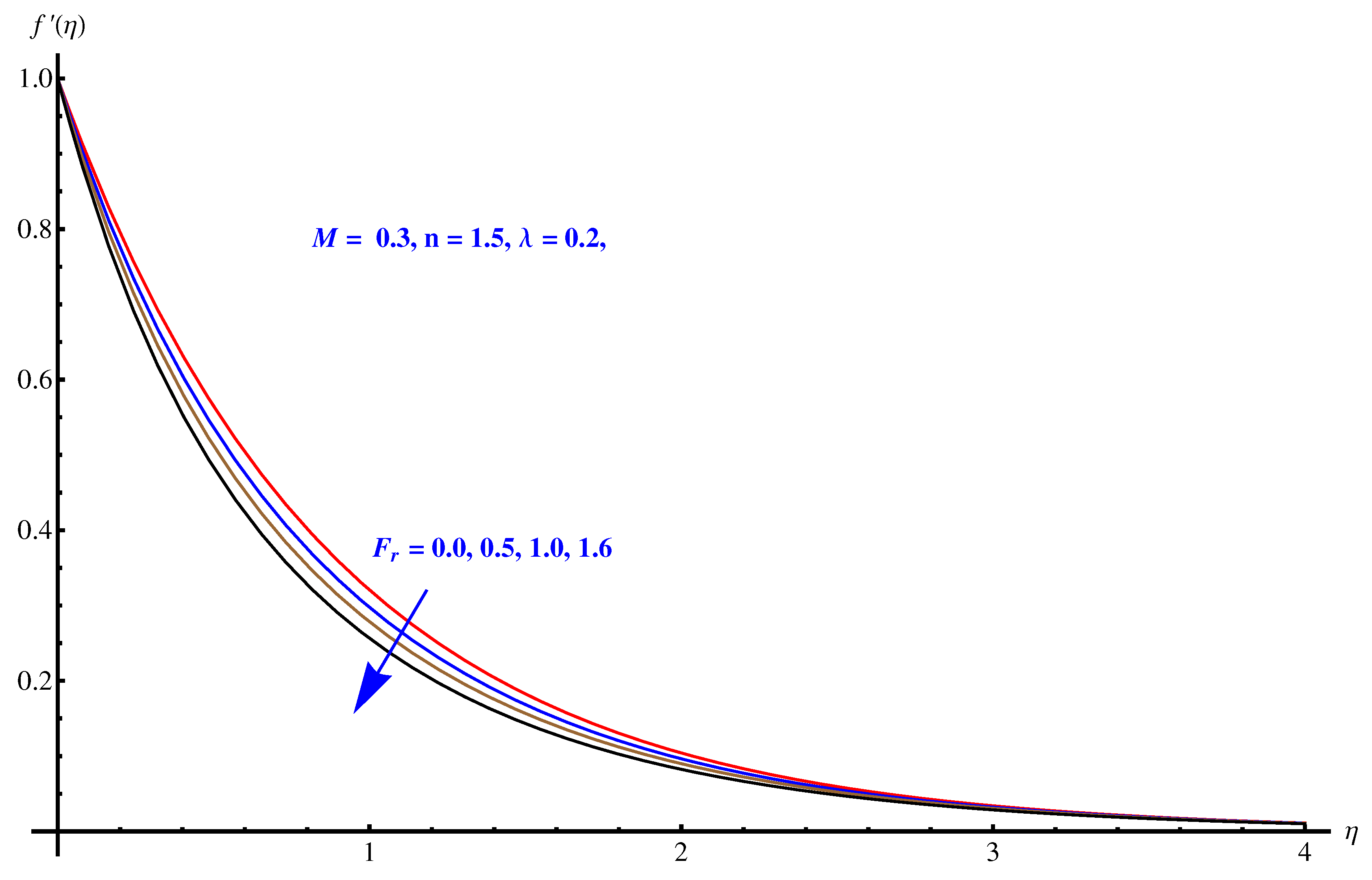
- We observed that a more porous medium offers more retardational force (friction), which continuously diminishes the velocity of the fluid.
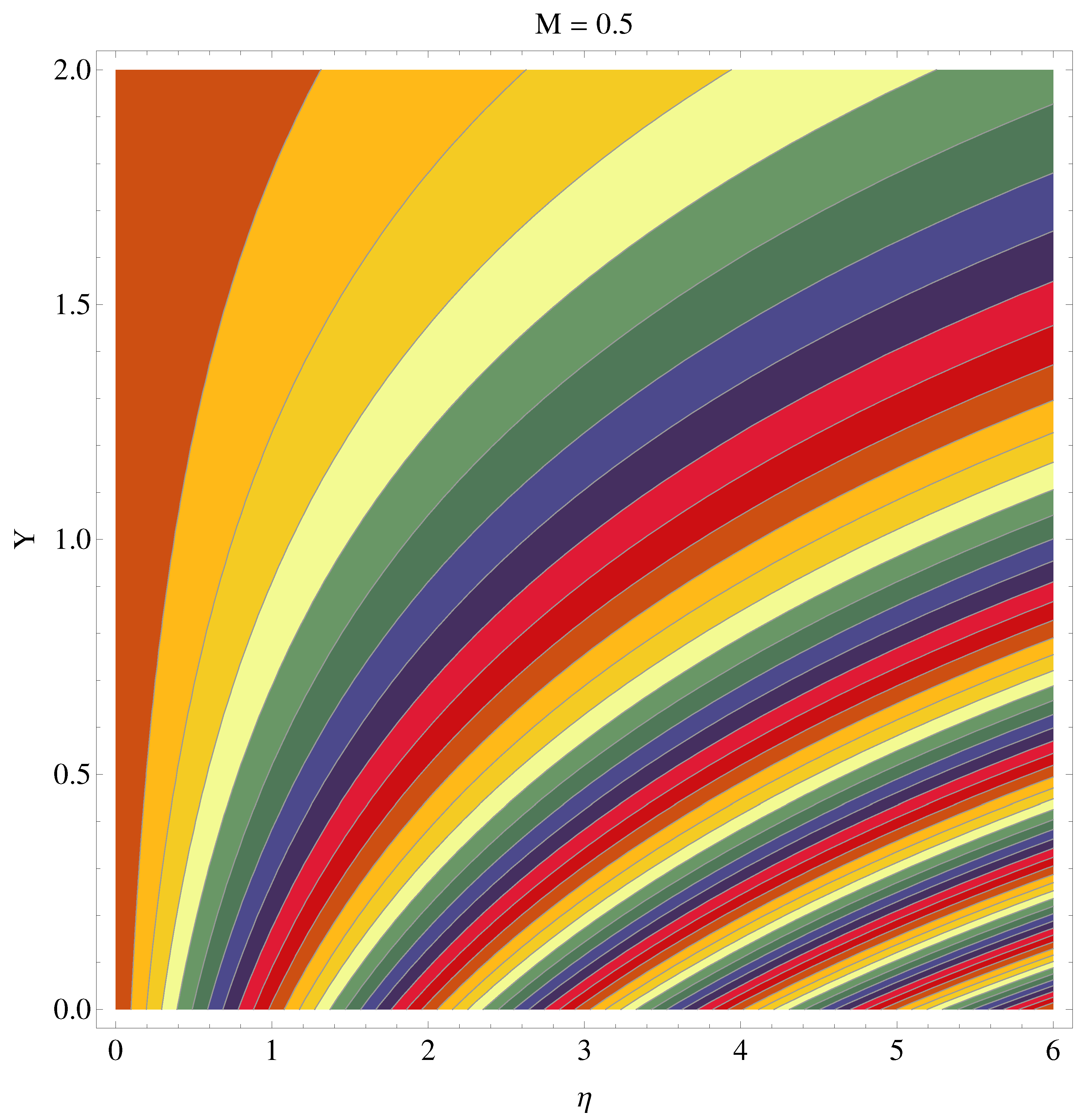
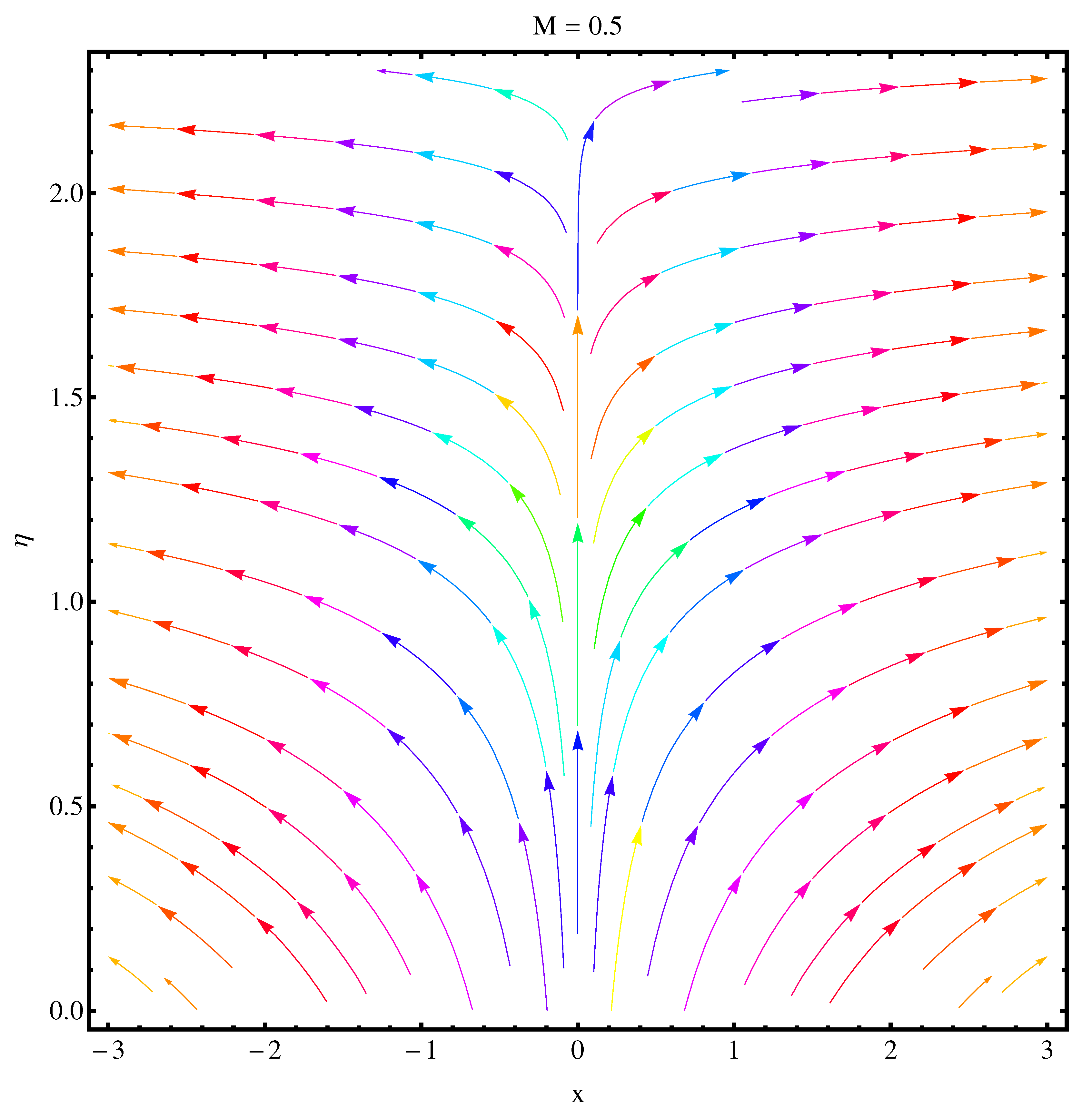
- Contour graphs given at and show an enhanced variation at distance sufficiently away from origin. Near to the origin, the variation is very narrow.
- Stream function graphs at and show a very narrow variation in the stream lines. At curves are not spread much as compared to case . Stronger magnetic effect boosts the opposing Lorentz forces which occur in the way of fluid motion and stream lines get affected.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Runge-Kutta 45 Method | |
| MHD | Magnetohydrodynamics |
| PDE | Partial Differential Equation |
| ODE | Ordinary Differential Equation |
| Cartesian velocity coordinates/m·s | |
| Cartesian distance coordinates/m | |
| Velocity (stretching)/m·s | |
| m | Stretching rate/s |
| Dynamic viscosity/Pa·s | |
| Magnetic impact/intensity/A·m | |
| Kinematic viscosity/ms | |
| Density/kg·m | |
| Brownian diffusion | |
| thermophoresis | |
| T | Temperature distributions /K |
| C | Concentration distributions/kg·m |
| Electric conductivity of the base fluid/( m) | |
| Nanoparticles’ heat capacity/J·mk | |
| Fluid’s heat capacity/J·mk | |
| Drag force coefficient | |
| K | Permeability |
| Ratio of heat capacity of fluid and nanoparticles | |
| Radiative heat flux | |
| Stephen boltzmann constant | |
| Mean absorption constant | |
| Thermal diffusivity/m | |
| k | Thermal conductivity/ |
| Dimensionless Parameters | |
| M | Magnetic parameter |
| Prandtl number | |
| Schmidt number | |
| Brownian diffusion | |
| thermophoresis | |
| Sherwood factor | |
| Nusselt factor | |
| Entropy generation rate in two dimensions | |
| Difference ratio | |
| Entropy generation rate | |
| Temperature difference | |
| Brinkman number | |
| Diffusive parameter | |
| Forchheimer number | |
| Porosity | |
| Radiation parameter | |
| Eckert number | |
| Viscosity at initial position | |
| Variable | |
| Concentration distribution (dimensionless) | |
| Temperature distribution (dimensionless) | |
| Velocity (dimensionless) | |
References
- Choi, S.U.S.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids With Nanoparticles; ASME International Mechanical Engineering Congress & Exposisition, American Society of Mechanical Engineers: San Francisco, CA, USA, 1995; Volume 66, pp. 99–105. [Google Scholar]
- Chamkha, A.J.; Khaled, A.-A. Similarity Solutions for Hydromagnetic Mixed Convection Heat and Mass Transfer for Hiemenz Flow Through Porous Media. Int. J. Numer. Methods Heat Fluid Flow 2000, 10, 94–115. [Google Scholar] [CrossRef]
- Parvin, S.; Chamkha, A.J. An Analysis on Free Convection Flow, Heat Transfer and Entropy Generation in an Odd-Shaped Cavity Filled with Nanofluid. Int. Commun. Heat Mass Transf. 2014, 54, 8–17. [Google Scholar] [CrossRef]
- Zaraki, A.; Ghalambaz, M.; Chamkha, A.J.; Ghalambaz, M.; Rossi, D.D. Theoretical Analysis of Natural Convection Boundary Layer Heat and Mass Transfer of Nanofluids: Effects of Size, Shape and Type of Nanoparticles, Type of Base Fluid and Working Temperature. Adv. Powder Technol. 2015, 26, 935–946. [Google Scholar] [CrossRef]
- Reddy, S.; Chamkha, A.J. Soret and Dufour Effects on MHD Convective Flow of Al2O3-Water and TiO2-Water Nanofluids Past a Stretching Sheet in Porous Media with Heat Generation/Absorption. Adv. Powder Technol. 2016, 27, 1207–1218. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Ismael, M.; Kasaeipoor, A.; Armaghani, T. Entropy Generation and Natural Convection of CuO-Water Nanofluid in C-Shaped Cavity under Magnetic Field. Entropy 2016, 18, 50. [Google Scholar] [CrossRef]
- Rasool, G.; Shafiq, A.; Khalique, C.M.; Zhang, T. Magnetohydrodynamic Darcy Forchheimer nanofluid flow over nonlinear stretching sheet. Phys. Scr. 2019, 94, 105221. [Google Scholar] [CrossRef]
- Ismael, M.; Armaghani, T.; Chamkha, A.J. Conjugate Heat Transfer and Entropy Generation in a Cavity Filled with a Nanofluid-Saturated Porous Media and Heated by a Triangular Solid. J. Taiwan Inst. Chem. Eng. 2016, 59, 138–151. [Google Scholar] [CrossRef]
- Sheikh, M.; Abass, Z. Effects of thermophoresis and heat generation/absorption on MHD flow due to an oscillatory stretching sheet with chemically reactive species. J. Mag. Mag. Mater. 2015, 396, 204–213. [Google Scholar] [CrossRef]
- Rasool, G.; Zhang, T.; Shafiq, A. Second grade nanofluidic flow past a convectively heated vertical Riga plate. Phys. Scr. 2019, 94, 125212. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, I.; Raza, J.; Bakouri, M.; Tlili, I. Stability analysis of Darcy-Forchheimer flow of Casson type Nanofluid over an exponential sheet: Investigation of critical points. Symmetry 2019, 11, 412. [Google Scholar] [CrossRef]
- Rasool, G.; Zhang, T. Darcy-Forchheimer nanofluidic flow manifested with Cattaneo-Christov theory of heat and mass flux over non-linearly stretching surface. PLoS ONE 2019, 14, e0221302. [Google Scholar] [CrossRef] [PubMed]
- Lund, L.A.; Omar, Z.; Khan, I.; Dero, S. Multiple solutions of Cu–C6H9NaO7 and Ag–C6H9NaO7 nanofluids flow over nonlinear shrinking surface. J. Cent. South Univ. 2019, 26, 1283–1293. [Google Scholar] [CrossRef]
- Rasool, G.; Shafiq, A.; Tlili, I. Marangoni convective nano-fluid flow over an electromagnetic actuator in the presence of first order chemical reaction. Heat Transf. Res. 2019, 49, 274–289. [Google Scholar] [CrossRef]
- Rasool, G.; Shafiq, A.; Durur, H. Darcy-Forchheimer relation in Magnetohydrodynamic Jeffrey nanofluid flow over stretching surface. Discr. Continu. Dynam. Syst.-Ser. S 2019. accepted. [Google Scholar]
- Rasool, G.; Shafiq, A.; Khalique, C.M. Marangoni forced convective Casson type nanofluid flow in the presence of Lorentz force generated by Riga plate. Discr. Continu. Dynam. Syst.-Ser. S 2019. accepted. [Google Scholar]
- Sohail, M.; Naz, R.; Abdelsalam, S.I. On the onset of entropy generation for a nanofluid with thermal radiation and gyrotactic microorganisms through 3D flows. Phys. Scr. 2019. accepted. [Google Scholar] [CrossRef]
- Sohail, M.; Naz, R. Modified heat and mass transmission models in the magnetohydrodynamic flow of Sutterby nanofluid in stretching cylinder. Phys. Stat. Mech. Its Appl. 2020, 124088. [Google Scholar] [CrossRef]
- Rasool, G.; Zhang, T.; Chamkha, A.J.; Shafiq, A.; Tlili, I.; Shahzadi, G. Entropy Generation and Consequences of Binary Chemical Reaction on MHD Darcy–Forchheimer Williamson Nanofluid Flow Over Non-Linearly Stretching Surface. Entropy 2020, 22, 18. [Google Scholar] [CrossRef]
- Tlili, I. Tawfeeq Abdullah Alkanhal, Nanotechnology for water purification: Electrospun nanofibrous membrane in water and wastewater treatment. J. Water Reuse Desalin. 2019, 24. [Google Scholar] [CrossRef]
- Tlili, I.; Khan, W.A.; Ramadan, K. MHD flow of Nanofluid flow across horizontal circular cylinder: Steady forced convection. J. Nanofluids 2019, 8, 179–186. [Google Scholar] [CrossRef]
- Wakif, A.; Boulahia, Z.; Ali, F.; Eid, M.R.; Sehaqui, R. Numerical Analysis of the Unsteady Natural Convection MHD Couette Nanofluid Flow in the Presence of Thermal Radiation Using Single and Two-Phase Nanofluid Models for Cu–Water Nanofluids. Int. J. Appl. Comput. Math. 2018, 4, 81. [Google Scholar] [CrossRef]
- Wakif, A.; Boulahia, Z.; Sehaqui, R. A semi-analytical analysis of electro-thermo-hydrodynamic stability in dielectric nanofluids using Buongiorno’s mathematical model together with more realistic boundary conditions. Results Phys. 2018, 9, 1438–1454. [Google Scholar] [CrossRef]
- Cortell, R. Fluid flow and radiative nonlinear heat transfer over stretching sheet. J. King Saud Univ. Sci. 2013, 26, 161–167. [Google Scholar] [CrossRef]
- Shehzad, S.A.; Hayat, T.; Alsaedi, A.; Obid, M.A. Nonlinear thermal radiation in three-dimensional flow of Jeffrey nanofluid: A model for solar energy. Appl. Math. Comput. 2014, 248, 273–286. [Google Scholar] [CrossRef]
- Shafiq, A.; Rasool, G.; Masood, C.M. Significance of thermal slip and convective boundary conditions on three dimensional rotating Darcy-Forchheimer nanofluid flow. Symmetry 2020. accepted. [Google Scholar]
- Animasaun, I.L.; Raju, C.S.K.; Sandeep, N. Unequal diffusivities case of homogeneous heterogeneous reactions within viscoelastic fluid flow in the presence of induced magnetic-field and nonlinear thermal radiation. Alex. Eng. J. 2016, 55, 1595–1606. [Google Scholar] [CrossRef]
- Hayat, T.; Imtiaz, M.; Alsaedi, A.; Kutbi, M.A. MHD three-dimensional flow of nanofluid with velocity slip and nonlinear thermal radiation. J. Mag. Mag. Mater. 2015, 396, 31–37. [Google Scholar] [CrossRef]
- Bejan, A. A study of entropy generation in fundamentsl convective heat transfer. J. Heat Trans. 1979, 101, 718–725. [Google Scholar] [CrossRef]
- Bejan, A. Method of entropy generation minimization, or modeling and optimization based on combined heat transfer and thermodynamics. Rev. Therm. 1996, 35, 637–646. [Google Scholar] [CrossRef]
- Liu, W.; Shahsavar, A.; Barzinjy, A.A.; Rashed, A.; Afrand, M. Natural convection and entropy generation of a nanofluid in two connected inclined triangular enclosures under magnetic field effects. Int. Commun. Heat Mass Trans. 2019, 108, 104309. [Google Scholar] [CrossRef]
- Hosseinzadeha, K.; Asadi, A.; Mogharrebi, A.R.; Khalesi, J.; Mousavisani, S.; Ganji, D.D. Entropy generation analysis of (CH2OH)2 containing CNTs nanofluid flow under effect of MHD and thermal radiation. Case Stud. Ther. Eng. 2019, 14, 100482. [Google Scholar] [CrossRef]
- Khan, M.I.; Hayat, T.; Khan, M.I.; Waqas, M.; Alsaedi, A. Numerical simulation of hydromagnetic mixed convective radiative slip flow with variable fluid properties: A mathematical model for entropy generation. J. Phy. Chem. Solid. 2019, 125, 153–164. [Google Scholar] [CrossRef]
- Hu, Z.; Lu, W.; Thouless, M.D. Slip and wear at a corner with coulomb friction and an inter-facial strength. Wear 2015, 338, 242–251. [Google Scholar] [CrossRef]
- Hu, Z.; Lu, W.; Thouless, M.D.; Barber, J.R. Effect of plastic deformation on the evolution of wear and local stress fields in fretting. Int. J. Solids Struct. 2016, 82, 1–8. [Google Scholar] [CrossRef]
- Crane, L.J. Flow past a stretching plate. J. Appl. Math. Phys. 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Sajid, M.; Ali, N.; Javed, T.; Abbas, Z. Stretching a curved surface in a viscous fluid. Chin. Phys. Lett. 2010, 27, 0247-03. [Google Scholar] [CrossRef]
- Rosca, N.C.; Pop, I. Unsteady boundary layer flow over a permeable curved stretching/shrinking surface. Eur. J. Mech. B. Fluids 2015, 51, 61–67. [Google Scholar] [CrossRef]
- Naveed, M.; Abbas, Z.; Sajid, M. MHD flow of a microploar fluid due to curved stretching surface with thermal radiation. J. Appl. Fluid Mech. 2016, 9, 131–138. [Google Scholar]
- Abbas, Z.; Naveed, M.; Sajid, M. Hydromagnetic slip flow of nanofluid over a curved stretching surface with heat generation and thermal radiation. J. Mol. Liq. 2016, 215, 756–762. [Google Scholar] [CrossRef]



| M | |||
|---|---|---|---|
| M | Pr | Nusselt | Sherwood | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.330523 | 0.5403 | |||||||||
| 0.294335 | 0.539539 | |||||||||
| 0.146822 | 0.196834 | |||||||||
| 0.298447 | 0.550958 | |||||||||
| 0.294335 | 0.539539 | |||||||||
| 0.29052 | 0.529184 | |||||||||
| 0.386878 | 0.542202 | |||||||||
| 0.294335 | 0.539539 | |||||||||
| 0.157756 | 0.222705 | |||||||||
| 0.397385 | 0.501379 | |||||||||
| 0.294335 | 0.539539 | |||||||||
| 0.24219 | 0.561276 | |||||||||
| 0.294335 | 0.539539 | |||||||||
| 0.374306 | 0.509569 | |||||||||
| 0.43873 | 0.487011 | |||||||||
| 0.294335 | 0.539539 | |||||||||
| 0.271793 | 0.309337 | |||||||||
| 0.244013 | 0.081471 | |||||||||
| 0.294335 | 0.539539 | |||||||||
| 0.26720 | 0.589734 | |||||||||
| 0.241696 | 0.606221 | |||||||||
| 0.39101 | 0.495559 | |||||||||
| 0.321959 | 0.526972 | |||||||||
| 0.252895 | 0.55839 | |||||||||
| 0.294335 | 0.539539 | |||||||||
| 0.290366 | 0.76239 | |||||||||
| 0.288085 | 0.952778 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rasool, G.; Shafiq, A.; Khan, I.; Baleanu, D.; Sooppy Nisar, K.; Shahzadi, G. Entropy Generation and Consequences of MHD in Darcy–Forchheimer Nanofluid Flow Bounded by Non-Linearly Stretching Surface. Symmetry 2020, 12, 652. https://doi.org/10.3390/sym12040652
Rasool G, Shafiq A, Khan I, Baleanu D, Sooppy Nisar K, Shahzadi G. Entropy Generation and Consequences of MHD in Darcy–Forchheimer Nanofluid Flow Bounded by Non-Linearly Stretching Surface. Symmetry. 2020; 12(4):652. https://doi.org/10.3390/sym12040652
Chicago/Turabian StyleRasool, Ghulam, Anum Shafiq, Ilyas Khan, Dumitru Baleanu, Kottakkaran Sooppy Nisar, and Gullnaz Shahzadi. 2020. "Entropy Generation and Consequences of MHD in Darcy–Forchheimer Nanofluid Flow Bounded by Non-Linearly Stretching Surface" Symmetry 12, no. 4: 652. https://doi.org/10.3390/sym12040652
APA StyleRasool, G., Shafiq, A., Khan, I., Baleanu, D., Sooppy Nisar, K., & Shahzadi, G. (2020). Entropy Generation and Consequences of MHD in Darcy–Forchheimer Nanofluid Flow Bounded by Non-Linearly Stretching Surface. Symmetry, 12(4), 652. https://doi.org/10.3390/sym12040652










