Abstract
Present communication aims to inspect the entropy optimization, heat and mass transport in Darcy-Forchheimer nanofluid flow surrounded by a non-linearly stretching surface. Navier-Stokes model based governing equations for non-Newtonian nanofluids having symmetric components in various terms are considered. Non-linear stretching is assumed to be the driving force whereas influence of thermal radiation, Brownian diffusion, dissipation and thermophoresis is considered. Importantly, entropy optimization is performed using second law of thermodynamics. Governing problems are converted into nonlinear ordinary problems (ODEs) using suitably adjusted transformations. RK-45 based built-in shooting mechanism is used to solve the problems. Final outcomes are plotted graphically. In addition to velocity, temperature, concentration and Bejan number, the stream lines, contour graphs and density graphs have been prepared. For their industrial and engineering importance, results for wall-drag force, heat flux (Nusselt) rate and mass flux (Sherwood) rate are also given in tabular data form. Outputs indicate that velocity reduces for Forchheimer number as well as for the porosity factor. However, a rise is noted in temperature distribution for elevated values of thermal radiation. Entropy optimization shows enhancement for larger values of temperature difference ratio. Skin-friction enhances for all relevant parameters involved in momentum equation.
1. Introduction
Tiny particles having diameter between 1–100 nm are termed nanoparticles. These particles belong to any suitable class of metals with significant thermo-physical properties. Conventional base materials/liquids are treated through these particles. Though tiny particles are suspended in base liquid for a shorter period of time, the achieved results are more effective than using a simple base fluid. This formulated mixture is known as nanofluid. These mixtures have enormous applications in engineering, industry and advanced nanotechnology. The manufacturing procedures at micro-level industries, nuclear reactors and power engines are directly related to these formulations. Petroleum industry, chemical industry, geothermal industry, and other related fields are important in this context. The pioneer study on this formulation has been reported by Choi [1]. The process of heat transport had shown much improvement after involvement of nanofluids. In particular, the dramatic effect is noted in power engines, refrigerators, nuclear reactors, fuel cells, thermal management, etc. For example, Chamkha and Khaled [2] reported some similarity solutions of mixed convection and heat transfer in Darcy medium. Parvin and Chamkha [3] disclosed features of odd-shaped cavity filled with nanofluid. They also performed entropy optimization in this study. Zaraki et al. [4] analyzed natural convection and boundary layer phenomena in nanofluid flow. Reddy and Chamkha [5] discussed properties of and -Water type nanofluid flow bounded by stretching surface. Chamkha et al. [6] discussed entropy optimization in and water nanofluid flow subject to C-shaped cavity. Rasool et al. [7] reported Darcy relation in MHD nanofluid flow bounded by non-linear stretching surface. Ismael et al. [8] discussed heat flux and entropy optimization in nanofluid flow subject to porous medium. Sheikh and Abbas [9] analyzed consequences of heat generation and thermophoresis in MHD nanofluid flow subject to oscillatory stretched surface. Rasool et al. [10] discussed the properties and heat transfer attributes of second grade nanofluid flow subject to a convective and vertical Riga pattern. Lund et al. [11] reported a study on Darcy type Casson nanofluid flow using exponential sheet. Rasool et al. [12] implemented the famous Cattaneo–Christove model to analyze the Darcy relation in MHD nanofluid flow past a non-linearly stretching flat surface. In another study, Lund et al. [13] modeled nanofluid flow using and type nanoparticles for enhancement of thermophysical properties of the base liquid. Rasool et al. [14] involved an electromagnetic actuator to study the Marangoni convection in nanofluid flow. In another study, Rasool et al. [15] reported Darcy type nanofluid flow subject to Jeffrey model. Involvement of Riga plate and Marangoni convection together in one study is reported by Rasool et al. [16]. Sohail et al. [17,18] disclosed the features of Entropy and MHD in nanofluid flow, respectively. Entropy optimization has been discussed by Rasool et al. [19] in their study based on Darcy model. Tlili et al. [20,21] reported some good results about enhancement of thermophysical properties of base fluids when saturated with nanoparticles. Wakif et al. [22] analyzed unsteady natural convection in Coette nanofluid flow subject to MHD and thermal radiation. In another study, Wakif et al. [23] reported electro-thermohydrodynamic stability of nanofluids using Buongiorno model.
Involvement of thermal radiation in nanofluids flow has been extensively used in previous literature especially in case of non-Newtonian and incompressible fluids. Design of heat ex-changers and other such equipment, propulsion devices, nuclear power plants, gas turbines, space devices and vehicles and satellites, etc. are typical examples of the applications of thermal radiation. Cortell [24], for the first time, involved thermal radiation parameter in his study on heat and mass transport mechanism using stretching surface. Shehzad et al. [25] reported Jeffrey nanofluid using non-linear thermal radiation effect. Shafiq et al. [26] reported properties of convective conditions and thermal slip effects in MHD three dimensional Darcy-Forchheimer rotating nanofluid flow. Animasaun et al. [27] reported homogeneous and heterogeneous reactions involving thermal radiation and MHD in nanofluids flow. Hayat et al. [28] reported slip effects in MHD three dimensional flow of nanofluid under the influence of thermal radiation.
Recently, the concept of entropy optimization has received utmost attention from research community for various reasons. Thermo-dynamical irreversibility in any flow system is directly measured by the system irreversibility. The second law of thermodynamics is helpful in this context because it has more significance as compared to the first law of thermodynamics. In particular, heat produced during any irreversible process in a heat transport mechanism is known as entropy generation. It might occur for different reasons such as kinetic energy, spin movement, internal movement of molecules and internal molecular vibrations, etc. In such cases, heat loss is noted which ultimately varies entropy systems. Numerous systems such as refrigeration, energy storage systems, solar energy systems, etc. are important areas that involve minimization of entropy generation. Numerous research articles are available in literature wherein, researchers have tried to compute the entropy to see its influence on whole heat transport mechanism. Bejan [29,30] reported a pioneer study on entropy optimization in heat and mass transport mechanisms. Later on, this concept of entropy optimization has been greatly reflected in studies such as Liu et al. [31] reported some good results for natural convection and entropy optimization in nanofluid flow bounded by triangular enclosures. Hosseinzadeha et al. [32] reported entropy optimization in type CNTs based nanofluid flow subject to MHD and thermal radiation. Khan et al. [33] analyzed numerical findings in MHD mixed convective flow targeting entropy optimization.
Flow analysis and boundary layers behavior involving a stretching sheet is known as one of the important fluid models to analyze three main profiles in any kind of heat and mass transport mechanism. It is connected with numerous industrial and engineering applications such as paper production, plastic sheet production and extrusion, metallic plates cooling process and similar other procedures (see for example Hu et al. [34,35]). The concept was build by Crane [36] in the pioneer study on stretching surfaces involved in fluid flow analysis. This study was reported on the variations in fluid movement instigated by a stretching velocity (via stretching surface). Sajid et al. [37] reported a fluid stream inspired by a curvy extended stretching surface. Rosca and Pop [38] further observed the properties of stretching surfaces in fluid flow phenomena using various fluid models. Naveed et al. [39] reported another good article on magnetohydrodynamic micropolar nanofluid flow due to extended sheet. They accounted for the effect of thermal radiation as well. Abbas et al. [40] reported a radiative flow analysis instigated by stretching surface.
This study is inspired by the novelty in various aspects. The concept of entropy optimization in fluid flow through Darcy channel together with non-linearly stretching surface has not been reported in the literature yet. Since, non-linear stretching has been of utmost importance in fluid flow analysis, therefore the present model comprising the Darcy channel, non-linear stretching sheet and MHD is directly affected by irreversible heat loss phenomena and entropy optimization. Overall, the study is organized as follows. Firstly, an incompressible MHD involved nanofluid flow is assumed surrounded by a non-linearly stretched surface flowing through a Darcy (porous medium) channel. Importantly, Brownian diffusion, viscous dissipation and thermophoresis are considered. In addition, thermal radiation is also considered in the present model. Secondly, the problem is solved by the numerical RK45 scheme using shooting technique. Thirdly, a graphical representation of results is given with a comprehensive discussion on each graph. Finally, the main findings are listed in a precise and conclusive manner, especially data tables on Nusselt and Sherwood numbers and skin-friction, which is very helpful in industrial and many other applications of nanofluids.
2. Mathematical Modeling
Here we adopted an incompressible, viscous, Darcy–Forchheimer MHD nanofluid convection surrounded by a non-linear stretching surface. Entropy optimization, heat and mass transport in Darcy–Forchheimer type nanofluid flow is analyzed. Non-linear stretching is assumed to be the driving force whereas effects of radiation, Brownian diffusion, dissipation and thermophoresis are accounted for. Importantly, entropy optimization is performed using second law of thermodynamics. The model is purely taken in two dimension having axis along the fluid flow while axis spreads surface normal to flow direction. A schematic diagram is sketched in Figure 1.
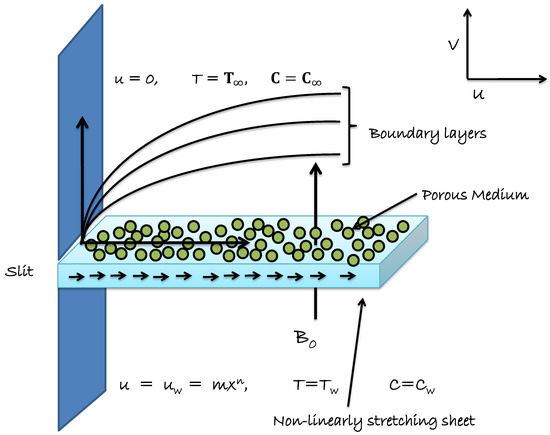
Figure 1.
Flow Chart.
Let and be the velocity components, T be the temperature distribution and C be the concentration of nanoparticles. Therefore, the governing equations for mass, momentum, energy and concentration distribution are as follows:
subject to the following boundary conditions,
Here, is dynamic viscosity, is magnetic impact/intensity, is used for kinematic viscosity, is the density, is used for Brownian diffusion, is used for thermophoresis. is electric conductivity of base fluid, is called nanoparticles’ heat capacity, is called fluid’s heat capacity. is used as drag force coefficient and K permeability. and are Stephen Boltzmann constant and mean absorption constant, respectively. is called radiative heat-flux. By virtue of Rosseland’s approximation subjected to Taylor expansion and neglecting higher order terms,
Define the following similarity transformations,
Using (6) and (7a)–(7e) in (1)–(5), we have the following governing equations in one dimensional form:
Here, M is given for MHD, , is used for inertia (Forchheimer number), Pr is Prandtl parameter, is Brownian factor, is Thermophoretic factor and is Schmidt factor, is the given radiation, is the given Eckert number and is used for thermal radiation. Mathematically,
Entropy Generation Modeling
For the viscous flow, following is the governing equation for entropy phenomenon,
Above equation comprises of four major irreversible parts, (i) thermal radiation, (ii) Joule heating, (iii) porous/Darcy relation and (iv) Concentration distribution. Using the transformations, Equation (13) reduces to following one dimensional form:
where is the given entropy generation, is the given temperature difference term, is the Brinkman number and is known as the diffusive variable. Mathematically,
3. Solution Methodology
Numerical scheme RK45 with shooting technique is applied on final governing Ordinary differential equations to plot the results. The below mentioned procedure has been adopted:
Subject to
A careful choice for initial guess of the core functions is adopted for solving initial value problems using RK45. Based on previous iterations, a suitable convergence criteria is adopted. Iterations are repeated unless a difference upto or a less than is obtained. This numerical scheme has various advantages and accuracy as compared to previous and classical methods of solutions such as HAM, OHAM, etc. Results are more efficient and speedy convergence is achieved. Similar procedure is adopted for Entropy optimization.
4. Analysis
Here we adopted an incompressible, viscous, MHD and Darcy–Forchheimer nanofluid convection surrounded by a non-linear stretching surface. Importantly, entropy optimization, heat and mass transport is analyzed. Non-linear stretching is assumed to be the driving force whereas effects of radiation, Brownian diffusion, dissipation and thermophoresis are accounted for. We have incorporated the RK45 built-in system with shooting technique to plot the numerical outcomes of non-linear system of equations. Properties of velocity field, temperature and concentration distributions, stream functions, Bejan number are disclosed in this section.
In Figure 2, Figure 3 and Figure 4, we have evaluated physical behavior of velocity field for variation in different parameters involved in momentum equation. In particular, Forchheimer number (), porosity factor (), magnetic (MHD) field effect on fluid flow is analyzed graphically. Figure 2 illustrates impact of Forchheimer number on velocity field and corresponding boundary layer. Continuous enhancement in resistance offered to fluid motion by inertial factor results in smooth decay in velocity profile. In Figure 3 we see the plot of impact of porosity factor imparted on fluid flow (velocity field) and corresponding boundary layer formulation. We observe that porous medium offers more retardational force (friction) which continuously diminishes the velocity of liquid. Boundary layer becomes thinner. Impact of Lorentz forces generated by applied magnetic (MHD) field on fluid flow and corresponding boundary layer thickness is plotted in Figure 4. Effective magnetic (MHD) field to the surface normal along vertical axis creates sudden bumps and hurdles in the way of fluid movement that causes a declination in the fluid motion. The stronger the impact of MHD, the lesser the fluid movement along the horizon.
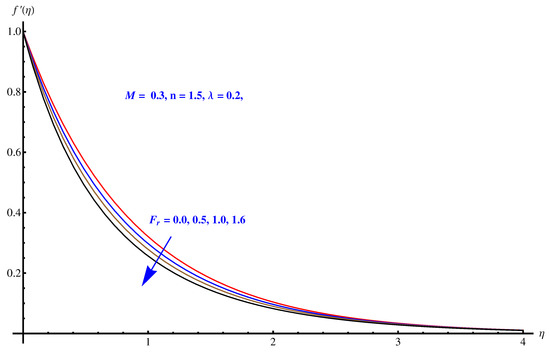
Figure 2.
Impact of Forchheimer number on .
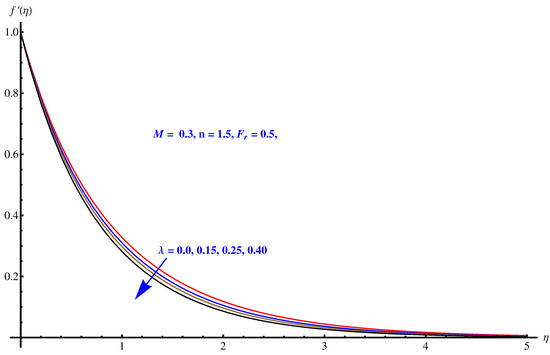
Figure 3.
Impact of porosity factor on .
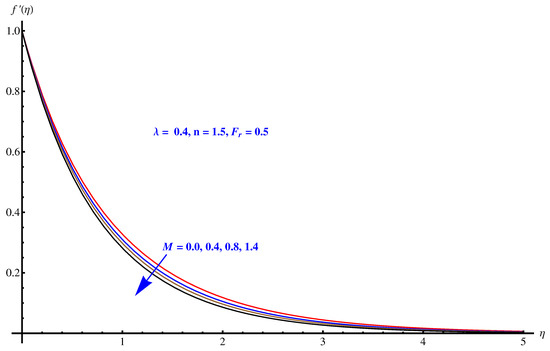
Figure 4.
Impact of magnetic parameter on .
Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9 are graphical results related to the parameters involved in momentum and energy equations to see variations in given domain. Since the article mainly emphasis on Darcy relation, therefore, Forchheimer number and porosity factors are two important parameters that vary the temperature distribution. Furthermore, thermal radiation is another important factor. Besides these, the impact of Brownian diffusion and thermophoresis influence on thermal state (distribution) are also noted herein. In particular, Figure 5 and Figure 6 display the consequences of inertia and porosity factors on thermal distribution, respectively. The resistive force due to inertia and enhanced friction are the source of enhancement in heat convection. Temperature distribution rises for rising values of both the factors whereas, opposite behavior is observed for anti-augmented numerical values. Impact of Brownian diffusion and thermophoresis is given in Figure 7 and Figure 8, respectively. An intensive thermophoretic force gives rise to the in-predictive motion of the nanoparticles that rises the field temperature and corresponding boundary layer shows more thickness. Influence of thermal radiation factor () is plotted in Figure 9. A certain rise in thermal state (distribution) is noted for elevated numerical values of thermal radiation factor.
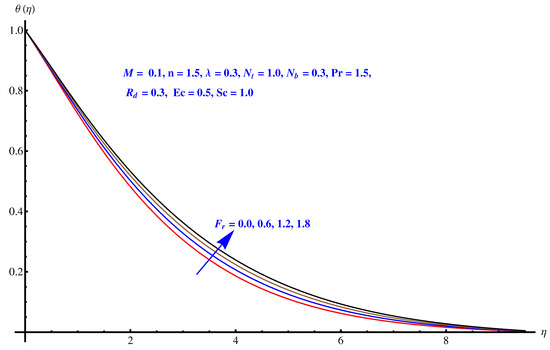
Figure 5.
Impact of Forchheimer number on .
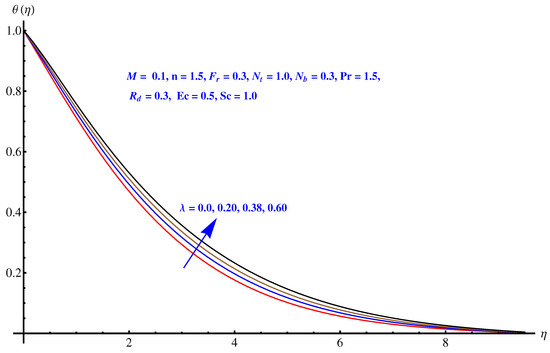
Figure 6.
Impact of porosity factor on .
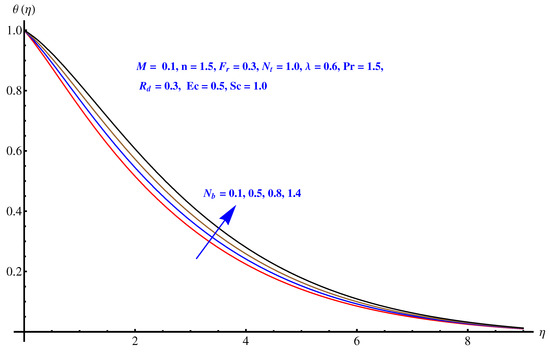
Figure 7.
Impact of Brownian diffusion on .
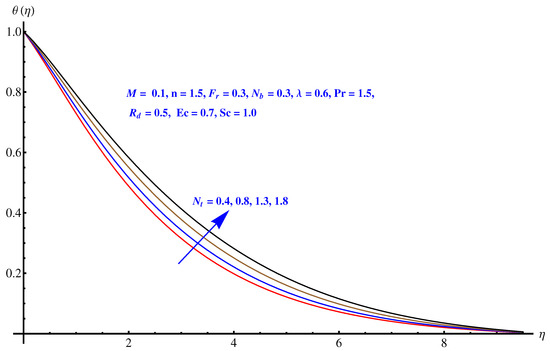
Figure 8.
Impact of thermophoresis on .
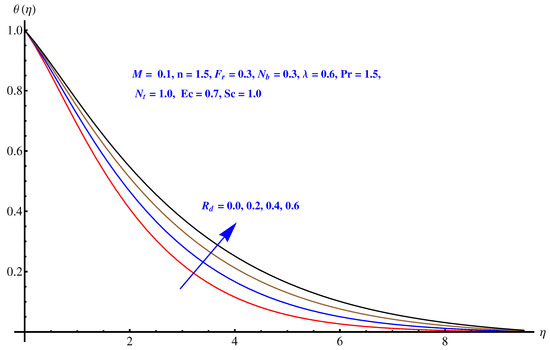
Figure 9.
Impact of thermal radiation on .
Figure 10, Figure 11 and Figure 12 are plotted to see the impact of Brownian diffusion, thermophoresis and Schmidt number on concentration of nanoparticles. In particular, Figure 10 is a plot of variations recorded in concentration distribution for rising values associated with Brownian diffusion. The concentration of the nanoparticles reduces near to surface. An enhancement is noted in case of thermophoresis due to the stronger thermophoretic force, which effectively produces more in-predictive movements as shown in Figure 11. Variation noted in concentration field for rising numerical values of Schmidt number is plotted in Figure 12. A decline is observed in the respective field. Physically, the inverse relation of Brownian diffusion and kinematic viscosity gives rise to this behavior in concentration profile.
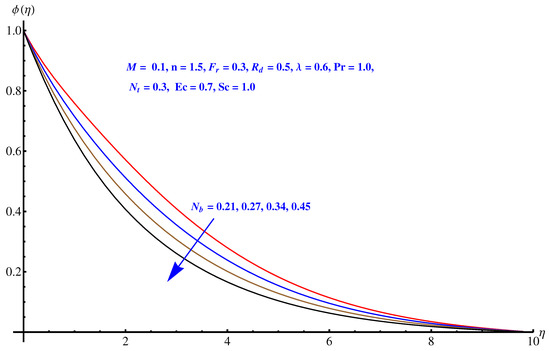
Figure 10.
Impact of Brownian diffusion on .
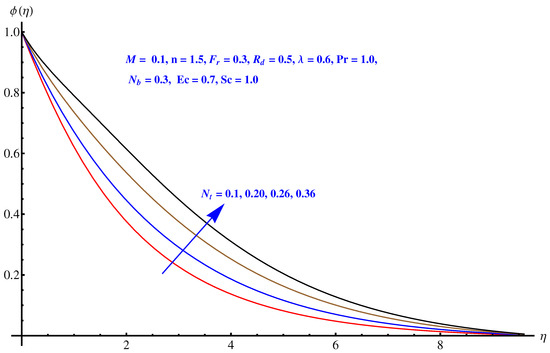
Figure 11.
Impact of thermophoresis on .
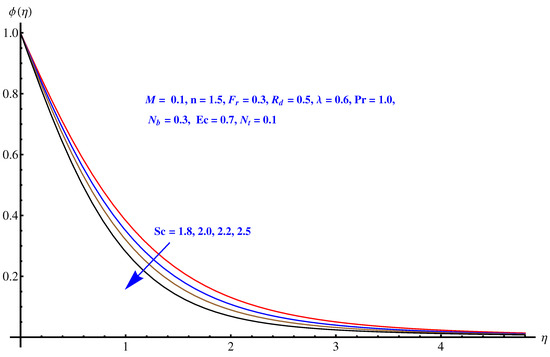
Figure 12.
Impact of Schmidt number on .
We have sketched stream functions as well as contour graphs at different numerical values of magnetic parameter M given in Figure 13, Figure 14, Figure 15 and Figure 16, respectively. In particular, Figure 13 and Figure 14 are the contour graphs given at and . An enhanced variation can be seen at the distance much away from origin. Near the origin, this variation is very narrow. Figure 15 and Figure 16 are stream functions graphs at and , respectively. A very narrow variation is noticed between two pictures. On a closer look, one can see that at the curves are not spread much as compared to the case . Physically, the stronger magnetic effect boosts the opposing Lorentz forces which occur in the way of fluid motion and stream lines get affected, whereas Figure 17 and Figure 18 present the stream density at and , respectively.
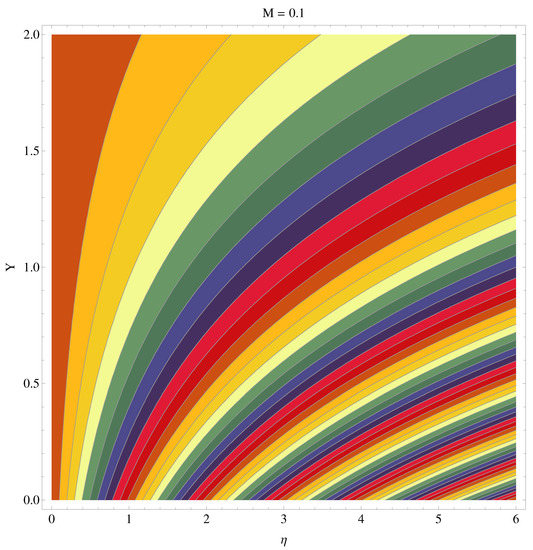
Figure 13.
Contour graph at .
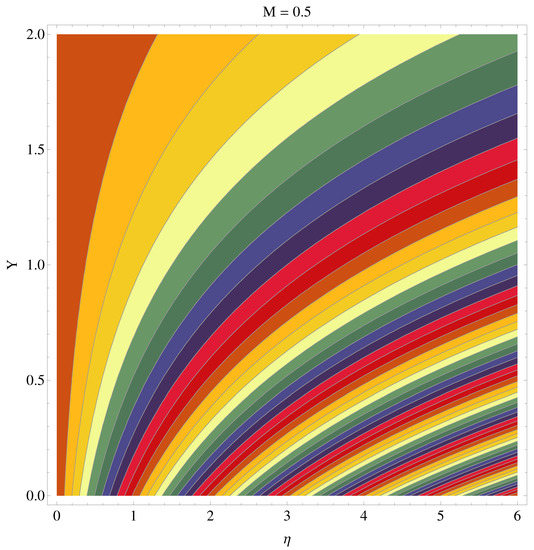
Figure 14.
Contour graph at .
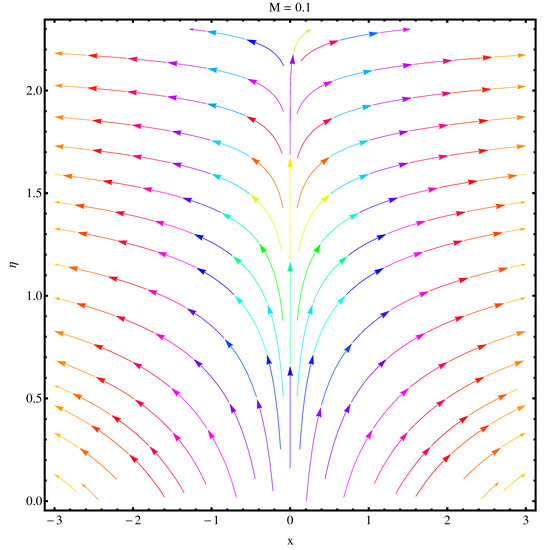
Figure 15.
Streamlines at .
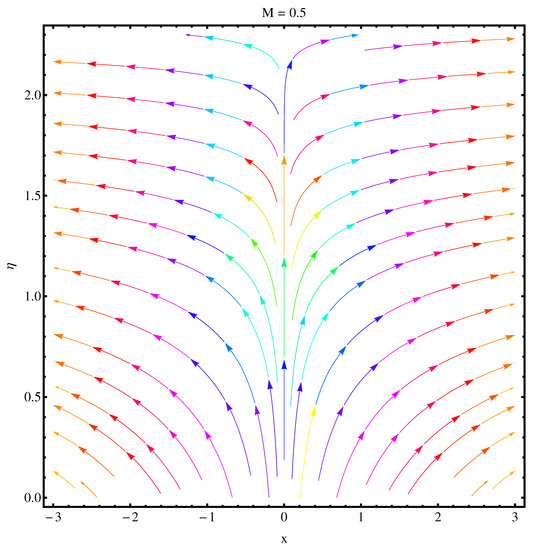
Figure 16.
Streamlines at .
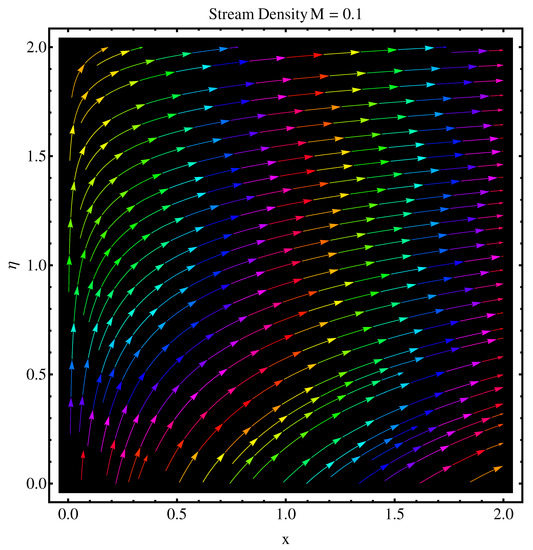
Figure 17.
Stream density at .
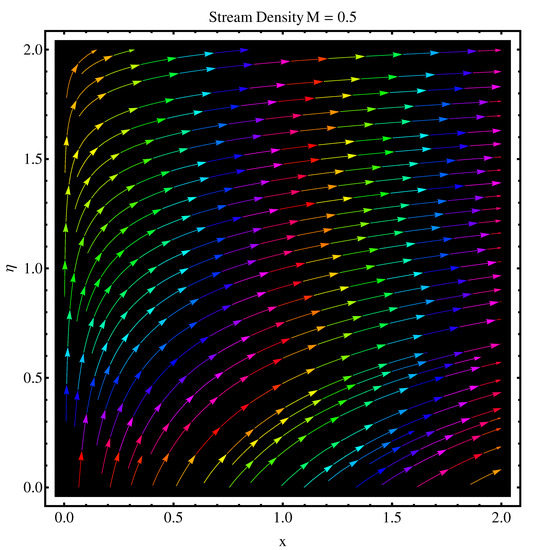
Figure 18.
Stream density at .
Figure 19, Figure 20 and Figure 21 are given on variations noted in Bejan number for various values of inertia factor, thermal radiation and temperature difference ratio parameter. In particular, Figure 19 shows the behavior of Bejan number with respect to the elevated values of Inertia factor. The effect is narrowed near the surface, however a comprehensive change is noted away from surface. Physically, irreversibility enhances due to friction offered by porous media to fluid and nanoparticles. A certain decrease is noted in Bejan number for elevated values of thermal radiation shown in Figure 20. Physically, larger emission rate of radiation impacts on Bejan number which shows reduction. A mixed behavior of Bejan number is noted for temperature difference ratio parameter. After a certain value, rising nature switches back to the declining trend as shown in Figure 21.
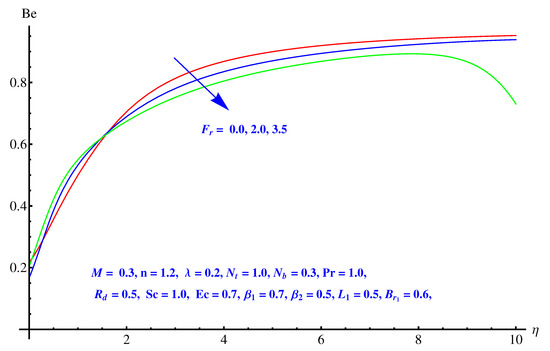
Figure 19.
Impact of Forchheimer number on Bejan number.
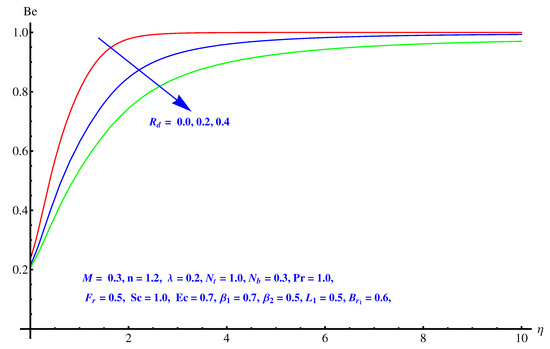
Figure 20.
Impact of thermal radiation on Bejan number.
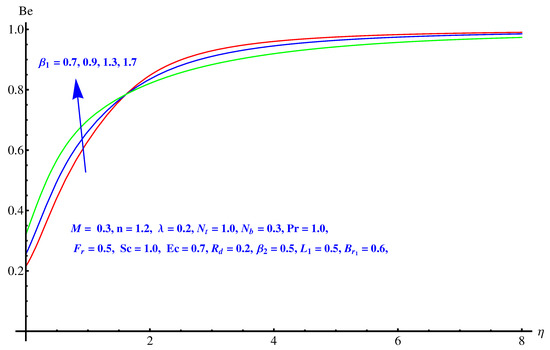
Figure 21.
Impact of temperature difference parameter on Bejan number.
Outcomes obtained numerically in lieu of skin friction, heat flux (Nusselt) rate and also mass flux (Sherwood) rate, respectively are given in Table 1 and Table 2. In particular, Table 1 gives the results of skin-frictional force for various values of magnetic parameter, inertia factor and porosity factor. A rising trend is noticed for all the variations. In Table 2, the results are given for heat flux (Nusselt) rate and also, mass transfer (Sherwood) rate, respectively. Inside out thermal (radiation) behaves as a continuous heat source. Specifically, thermal radiation shows reduction in heat transport phenomena (Nusselt) and enhancement in mass flux (Sherwood) rate. A reducing trend in both heat transport rate (Nusselt) and also mass transport rate (Sherwood) is noticed for elevated values of porosity factor. Strong retardation offered by porous media is the reason behind this decline in both physical quantities.

Table 1.
Numerical outcomes of skin-friction given at while values of other parameters are varied one by one.

Table 2.
Numerical outcomes of heat transfer (Nusselt) rate and mass transfer (Sherwood) rate given at while values of other parameters are varied one by one.
5. Conclusions
Here we have analyzed entropy optimization, heat and mass transport in Darcy–Forchheimer MHD nanofluid flow surrounded by a non-linearly stretching surface. Non-linear stretching is assumed to be the driving force whereas effects of radiation, Brownian diffusion, dissipation and thermophoresis are also considered. Here, we have incorporated RK45 built-in system with shooting technique to plot the numerical outcomes of a non-linear system of equations. Properties of velocity field, thermal and solute distributions, stream functions and Bejan number are disclosed in this article. Salient findings of this study are listed below:
- Entropy optimization, heat and mass transport in Darcy–Forchheimer and MHD type nanofluid flow surrounded by a non-linear stretching surface is analyzed.
- Rate of Bejan number shows mixed behavior for elevated values of temperature difference parameter. An enhancement is noted for larger values.
- Skin friction enhances for all the parameters involved in momentum equation.
- Heat transfer rate declines while mass transfer intensifies for elevated numbers of thermal radiation parameters.
- Resistive force due to inertia and enhanced friction are the source of enhancement in heat convection.
- The concentration of nanoparticles reduces near the surface, whereas an enhancement is noted in the case of thermophoresis due to stronger thermophoretic force.
- An enhanced variation in stream lines is noted at distance far away from the origin. Near to the origin, this variation is very narrow.
- We observed that a more porous medium offers more retardational force (friction), which continuously diminishes the velocity of the fluid.
- Contour graphs given at and show an enhanced variation at distance sufficiently away from origin. Near to the origin, the variation is very narrow.
- Stream function graphs at and show a very narrow variation in the stream lines. At curves are not spread much as compared to case . Stronger magnetic effect boosts the opposing Lorentz forces which occur in the way of fluid motion and stream lines get affected.
Author Contributions
G.R. formulated the problem, derived the equations, generated the results, wrote the analysis & discussion and concluded the paper. A.S. generated the results and validated the model. I.K. checked the model and proofread the whole manuscript. D.B. and K.S.N. helped in revision and provided funding. G.S. checked the whole manuscript, helped in revision and proofread the final version. Finally, All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Deanship of Scientific Research at Prince Sattam Bin Abdulaziz University under the research project No. 2020/01/16436.
Acknowledgments
The authors are highly obliged and thankful to unanimous reviewers for their valuable comments and suggestions on the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Runge-Kutta 45 Method | |
| MHD | Magnetohydrodynamics |
| PDE | Partial Differential Equation |
| ODE | Ordinary Differential Equation |
| Cartesian velocity coordinates/m·s | |
| Cartesian distance coordinates/m | |
| Velocity (stretching)/m·s | |
| m | Stretching rate/s |
| Dynamic viscosity/Pa·s | |
| Magnetic impact/intensity/A·m | |
| Kinematic viscosity/ms | |
| Density/kg·m | |
| Brownian diffusion | |
| thermophoresis | |
| T | Temperature distributions /K |
| C | Concentration distributions/kg·m |
| Electric conductivity of the base fluid/( m) | |
| Nanoparticles’ heat capacity/J·mk | |
| Fluid’s heat capacity/J·mk | |
| Drag force coefficient | |
| K | Permeability |
| Ratio of heat capacity of fluid and nanoparticles | |
| Radiative heat flux | |
| Stephen boltzmann constant | |
| Mean absorption constant | |
| Thermal diffusivity/m | |
| k | Thermal conductivity/ |
| Dimensionless Parameters | |
| M | Magnetic parameter |
| Prandtl number | |
| Schmidt number | |
| Brownian diffusion | |
| thermophoresis | |
| Sherwood factor | |
| Nusselt factor | |
| Entropy generation rate in two dimensions | |
| Difference ratio | |
| Entropy generation rate | |
| Temperature difference | |
| Brinkman number | |
| Diffusive parameter | |
| Forchheimer number | |
| Porosity | |
| Radiation parameter | |
| Eckert number | |
| Viscosity at initial position | |
| Variable | |
| Concentration distribution (dimensionless) | |
| Temperature distribution (dimensionless) | |
| Velocity (dimensionless) | |
References
- Choi, S.U.S.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids With Nanoparticles; ASME International Mechanical Engineering Congress & Exposisition, American Society of Mechanical Engineers: San Francisco, CA, USA, 1995; Volume 66, pp. 99–105. [Google Scholar]
- Chamkha, A.J.; Khaled, A.-A. Similarity Solutions for Hydromagnetic Mixed Convection Heat and Mass Transfer for Hiemenz Flow Through Porous Media. Int. J. Numer. Methods Heat Fluid Flow 2000, 10, 94–115. [Google Scholar] [CrossRef]
- Parvin, S.; Chamkha, A.J. An Analysis on Free Convection Flow, Heat Transfer and Entropy Generation in an Odd-Shaped Cavity Filled with Nanofluid. Int. Commun. Heat Mass Transf. 2014, 54, 8–17. [Google Scholar] [CrossRef]
- Zaraki, A.; Ghalambaz, M.; Chamkha, A.J.; Ghalambaz, M.; Rossi, D.D. Theoretical Analysis of Natural Convection Boundary Layer Heat and Mass Transfer of Nanofluids: Effects of Size, Shape and Type of Nanoparticles, Type of Base Fluid and Working Temperature. Adv. Powder Technol. 2015, 26, 935–946. [Google Scholar] [CrossRef]
- Reddy, S.; Chamkha, A.J. Soret and Dufour Effects on MHD Convective Flow of Al2O3-Water and TiO2-Water Nanofluids Past a Stretching Sheet in Porous Media with Heat Generation/Absorption. Adv. Powder Technol. 2016, 27, 1207–1218. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Ismael, M.; Kasaeipoor, A.; Armaghani, T. Entropy Generation and Natural Convection of CuO-Water Nanofluid in C-Shaped Cavity under Magnetic Field. Entropy 2016, 18, 50. [Google Scholar] [CrossRef]
- Rasool, G.; Shafiq, A.; Khalique, C.M.; Zhang, T. Magnetohydrodynamic Darcy Forchheimer nanofluid flow over nonlinear stretching sheet. Phys. Scr. 2019, 94, 105221. [Google Scholar] [CrossRef]
- Ismael, M.; Armaghani, T.; Chamkha, A.J. Conjugate Heat Transfer and Entropy Generation in a Cavity Filled with a Nanofluid-Saturated Porous Media and Heated by a Triangular Solid. J. Taiwan Inst. Chem. Eng. 2016, 59, 138–151. [Google Scholar] [CrossRef]
- Sheikh, M.; Abass, Z. Effects of thermophoresis and heat generation/absorption on MHD flow due to an oscillatory stretching sheet with chemically reactive species. J. Mag. Mag. Mater. 2015, 396, 204–213. [Google Scholar] [CrossRef]
- Rasool, G.; Zhang, T.; Shafiq, A. Second grade nanofluidic flow past a convectively heated vertical Riga plate. Phys. Scr. 2019, 94, 125212. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, I.; Raza, J.; Bakouri, M.; Tlili, I. Stability analysis of Darcy-Forchheimer flow of Casson type Nanofluid over an exponential sheet: Investigation of critical points. Symmetry 2019, 11, 412. [Google Scholar] [CrossRef]
- Rasool, G.; Zhang, T. Darcy-Forchheimer nanofluidic flow manifested with Cattaneo-Christov theory of heat and mass flux over non-linearly stretching surface. PLoS ONE 2019, 14, e0221302. [Google Scholar] [CrossRef] [PubMed]
- Lund, L.A.; Omar, Z.; Khan, I.; Dero, S. Multiple solutions of Cu–C6H9NaO7 and Ag–C6H9NaO7 nanofluids flow over nonlinear shrinking surface. J. Cent. South Univ. 2019, 26, 1283–1293. [Google Scholar] [CrossRef]
- Rasool, G.; Shafiq, A.; Tlili, I. Marangoni convective nano-fluid flow over an electromagnetic actuator in the presence of first order chemical reaction. Heat Transf. Res. 2019, 49, 274–289. [Google Scholar] [CrossRef]
- Rasool, G.; Shafiq, A.; Durur, H. Darcy-Forchheimer relation in Magnetohydrodynamic Jeffrey nanofluid flow over stretching surface. Discr. Continu. Dynam. Syst.-Ser. S 2019. accepted. [Google Scholar]
- Rasool, G.; Shafiq, A.; Khalique, C.M. Marangoni forced convective Casson type nanofluid flow in the presence of Lorentz force generated by Riga plate. Discr. Continu. Dynam. Syst.-Ser. S 2019. accepted. [Google Scholar]
- Sohail, M.; Naz, R.; Abdelsalam, S.I. On the onset of entropy generation for a nanofluid with thermal radiation and gyrotactic microorganisms through 3D flows. Phys. Scr. 2019. accepted. [Google Scholar] [CrossRef]
- Sohail, M.; Naz, R. Modified heat and mass transmission models in the magnetohydrodynamic flow of Sutterby nanofluid in stretching cylinder. Phys. Stat. Mech. Its Appl. 2020, 124088. [Google Scholar] [CrossRef]
- Rasool, G.; Zhang, T.; Chamkha, A.J.; Shafiq, A.; Tlili, I.; Shahzadi, G. Entropy Generation and Consequences of Binary Chemical Reaction on MHD Darcy–Forchheimer Williamson Nanofluid Flow Over Non-Linearly Stretching Surface. Entropy 2020, 22, 18. [Google Scholar] [CrossRef]
- Tlili, I. Tawfeeq Abdullah Alkanhal, Nanotechnology for water purification: Electrospun nanofibrous membrane in water and wastewater treatment. J. Water Reuse Desalin. 2019, 24. [Google Scholar] [CrossRef]
- Tlili, I.; Khan, W.A.; Ramadan, K. MHD flow of Nanofluid flow across horizontal circular cylinder: Steady forced convection. J. Nanofluids 2019, 8, 179–186. [Google Scholar] [CrossRef]
- Wakif, A.; Boulahia, Z.; Ali, F.; Eid, M.R.; Sehaqui, R. Numerical Analysis of the Unsteady Natural Convection MHD Couette Nanofluid Flow in the Presence of Thermal Radiation Using Single and Two-Phase Nanofluid Models for Cu–Water Nanofluids. Int. J. Appl. Comput. Math. 2018, 4, 81. [Google Scholar] [CrossRef]
- Wakif, A.; Boulahia, Z.; Sehaqui, R. A semi-analytical analysis of electro-thermo-hydrodynamic stability in dielectric nanofluids using Buongiorno’s mathematical model together with more realistic boundary conditions. Results Phys. 2018, 9, 1438–1454. [Google Scholar] [CrossRef]
- Cortell, R. Fluid flow and radiative nonlinear heat transfer over stretching sheet. J. King Saud Univ. Sci. 2013, 26, 161–167. [Google Scholar] [CrossRef]
- Shehzad, S.A.; Hayat, T.; Alsaedi, A.; Obid, M.A. Nonlinear thermal radiation in three-dimensional flow of Jeffrey nanofluid: A model for solar energy. Appl. Math. Comput. 2014, 248, 273–286. [Google Scholar] [CrossRef]
- Shafiq, A.; Rasool, G.; Masood, C.M. Significance of thermal slip and convective boundary conditions on three dimensional rotating Darcy-Forchheimer nanofluid flow. Symmetry 2020. accepted. [Google Scholar]
- Animasaun, I.L.; Raju, C.S.K.; Sandeep, N. Unequal diffusivities case of homogeneous heterogeneous reactions within viscoelastic fluid flow in the presence of induced magnetic-field and nonlinear thermal radiation. Alex. Eng. J. 2016, 55, 1595–1606. [Google Scholar] [CrossRef]
- Hayat, T.; Imtiaz, M.; Alsaedi, A.; Kutbi, M.A. MHD three-dimensional flow of nanofluid with velocity slip and nonlinear thermal radiation. J. Mag. Mag. Mater. 2015, 396, 31–37. [Google Scholar] [CrossRef]
- Bejan, A. A study of entropy generation in fundamentsl convective heat transfer. J. Heat Trans. 1979, 101, 718–725. [Google Scholar] [CrossRef]
- Bejan, A. Method of entropy generation minimization, or modeling and optimization based on combined heat transfer and thermodynamics. Rev. Therm. 1996, 35, 637–646. [Google Scholar] [CrossRef]
- Liu, W.; Shahsavar, A.; Barzinjy, A.A.; Rashed, A.; Afrand, M. Natural convection and entropy generation of a nanofluid in two connected inclined triangular enclosures under magnetic field effects. Int. Commun. Heat Mass Trans. 2019, 108, 104309. [Google Scholar] [CrossRef]
- Hosseinzadeha, K.; Asadi, A.; Mogharrebi, A.R.; Khalesi, J.; Mousavisani, S.; Ganji, D.D. Entropy generation analysis of (CH2OH)2 containing CNTs nanofluid flow under effect of MHD and thermal radiation. Case Stud. Ther. Eng. 2019, 14, 100482. [Google Scholar] [CrossRef]
- Khan, M.I.; Hayat, T.; Khan, M.I.; Waqas, M.; Alsaedi, A. Numerical simulation of hydromagnetic mixed convective radiative slip flow with variable fluid properties: A mathematical model for entropy generation. J. Phy. Chem. Solid. 2019, 125, 153–164. [Google Scholar] [CrossRef]
- Hu, Z.; Lu, W.; Thouless, M.D. Slip and wear at a corner with coulomb friction and an inter-facial strength. Wear 2015, 338, 242–251. [Google Scholar] [CrossRef]
- Hu, Z.; Lu, W.; Thouless, M.D.; Barber, J.R. Effect of plastic deformation on the evolution of wear and local stress fields in fretting. Int. J. Solids Struct. 2016, 82, 1–8. [Google Scholar] [CrossRef]
- Crane, L.J. Flow past a stretching plate. J. Appl. Math. Phys. 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Sajid, M.; Ali, N.; Javed, T.; Abbas, Z. Stretching a curved surface in a viscous fluid. Chin. Phys. Lett. 2010, 27, 0247-03. [Google Scholar] [CrossRef]
- Rosca, N.C.; Pop, I. Unsteady boundary layer flow over a permeable curved stretching/shrinking surface. Eur. J. Mech. B. Fluids 2015, 51, 61–67. [Google Scholar] [CrossRef]
- Naveed, M.; Abbas, Z.; Sajid, M. MHD flow of a microploar fluid due to curved stretching surface with thermal radiation. J. Appl. Fluid Mech. 2016, 9, 131–138. [Google Scholar]
- Abbas, Z.; Naveed, M.; Sajid, M. Hydromagnetic slip flow of nanofluid over a curved stretching surface with heat generation and thermal radiation. J. Mol. Liq. 2016, 215, 756–762. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).