Microstructure Instance Segmentation from Aluminum Alloy Metallographic Image Using Different Loss Functions
Abstract
1. Introduction
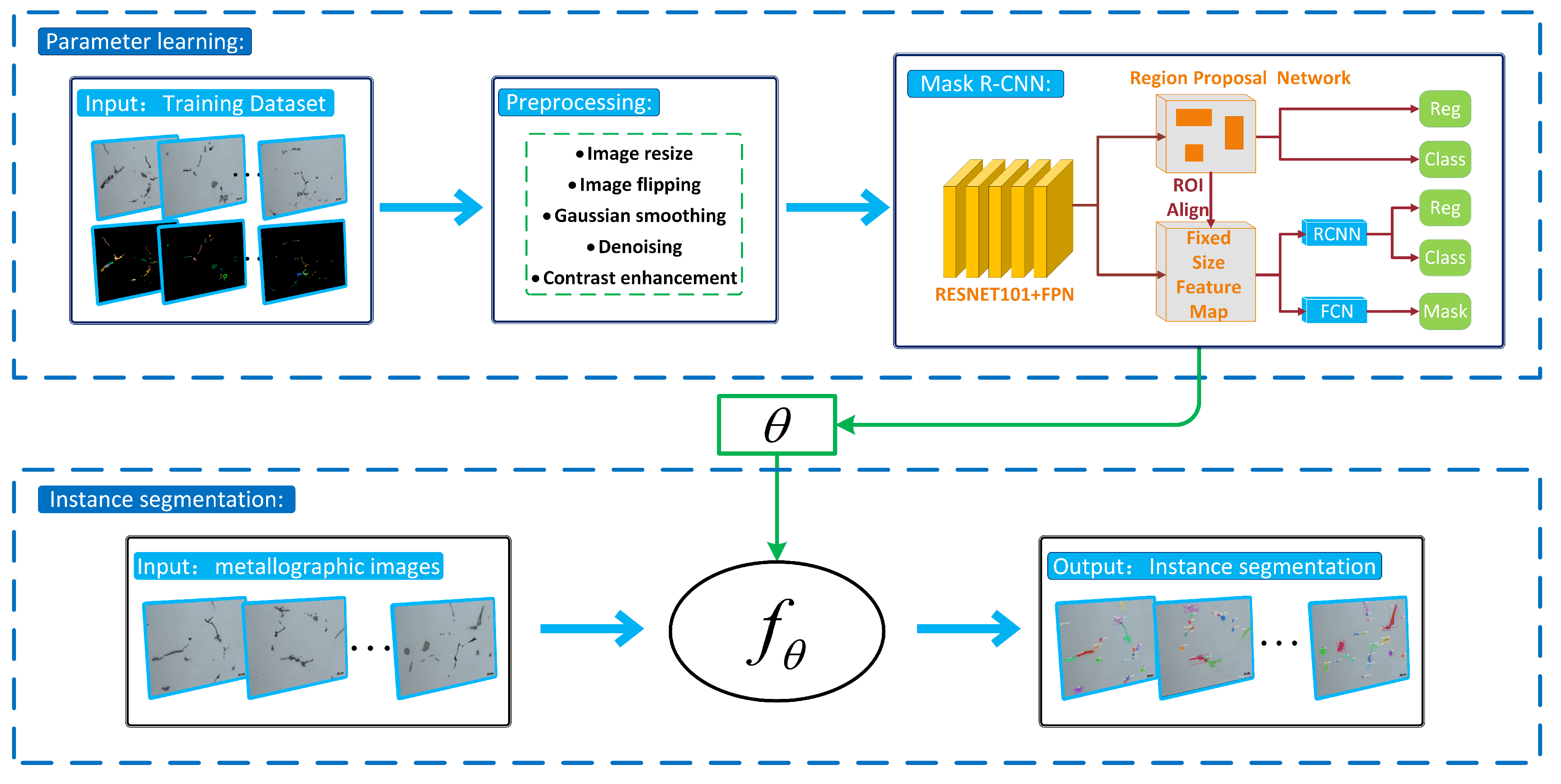
2. Proposed Method
2.1. Overview
2.2. Parameter Learning
2.3. Instance Segmentation
| Algorithm 1 Microstructure instance segmentation method. |
| Input: Training dataset , new aluminum alloy metallographic image ; Output: The instance segmentation image ; Step 1: Initializations:
Step 2: Optimize by using D:
Step 3: Compute by using Equation (6). |
2.4. Loss Functions
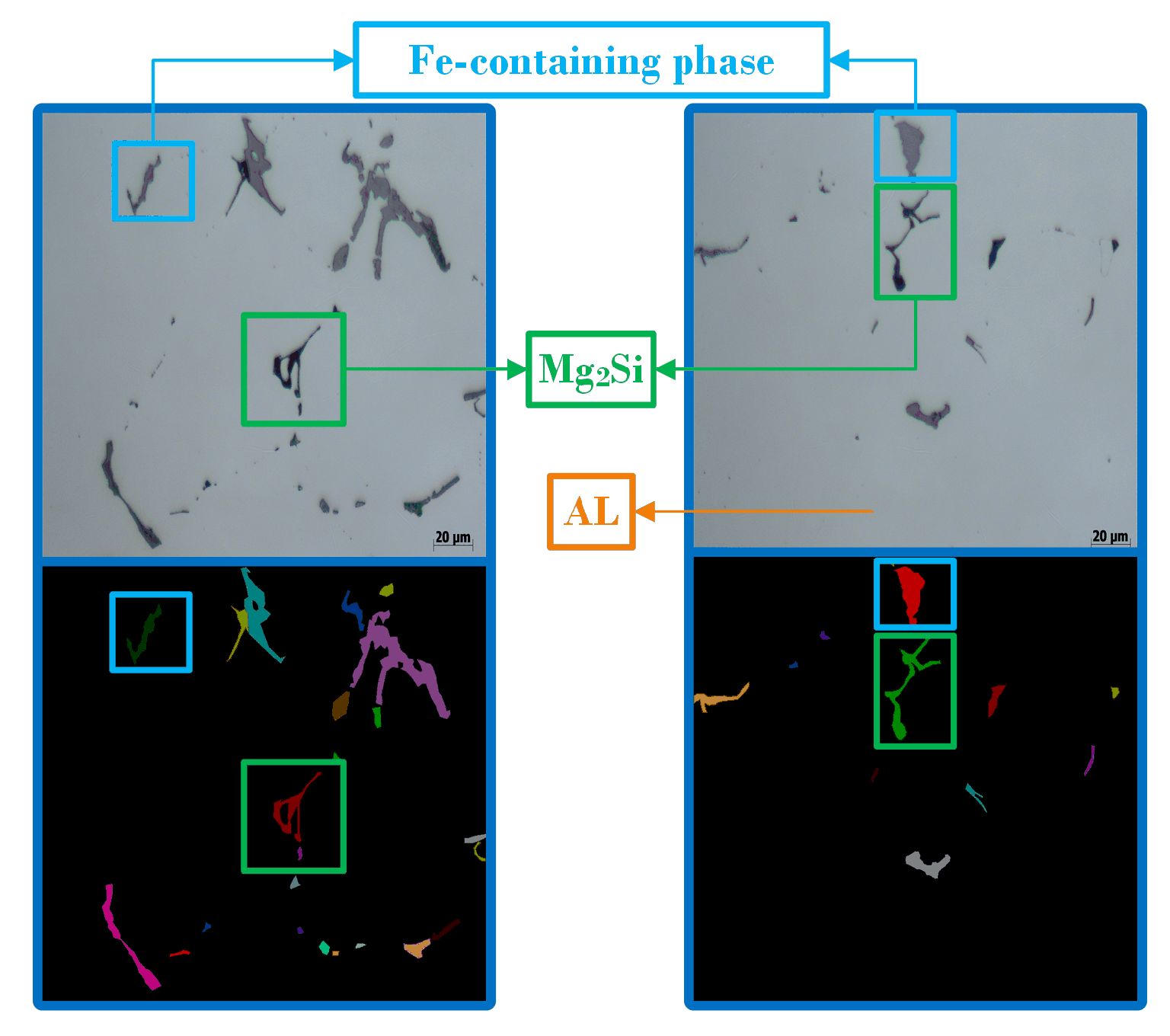
3. Experimental Results
3.1. Experimental Setup
3.2. Evaluation Metrics
3.3. Performance Comparison
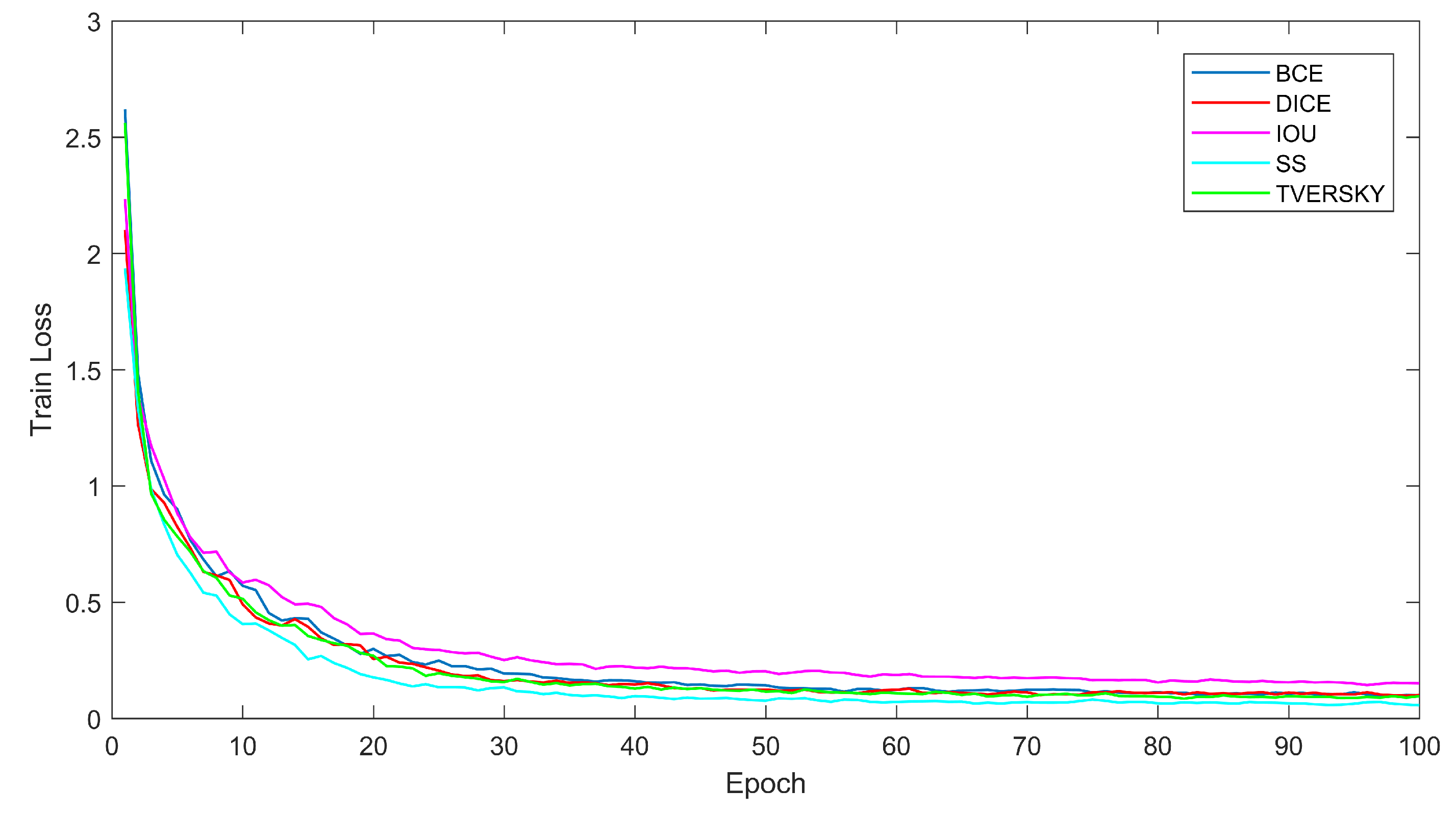
3.4. Convergence Analysis
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Heinz, A.; Haszler, A.; Keidel, C.; Moldenhauer, S.; Benedictus, R.; Miller, W. Recent development in aluminium alloys for aerospace applications. Mater. Sci. Eng. A 2000, 280, 102–107. [Google Scholar] [CrossRef]
- Hirsch, J.; Al-Samman, T. Superior light metals by texture engineering: Optimized aluminum and magnesium alloys for automotive applications. Acta Mater. 2013, 61, 818–843. [Google Scholar] [CrossRef]
- Martin, J.H.; Yahata, B.D.; Hundley, J.M.; Mayer, J.A.; Schaedler, T.A.; Pollock, T.M. 3D printing of high-strength aluminium alloys. Nature 2017, 549, 365. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Song, B.; Wei, Q.; Bourell, D.; Shi, Y. A review of selective laser melting of aluminum alloys: Processing, microstructure, property and developing trends. J. Mater. Sci. Technol. 2019, 35, 270–284. [Google Scholar] [CrossRef]
- Roy, N.; Samuel, A.; Samuel, F. Porosity formation in AI-9 Wt pct Si-3 Wt pct Cu alloy systems: Metallographic observations. Metall. Mater. Trans. A 1996, 27, 415–429. [Google Scholar] [CrossRef]
- Rajasekhar, K.; Harendranath, C.; Raman, R.; Kulkarni, S. Microstructural evolution during solidification of austenitic stainless steel weld metals: A color metallographic and electron microprobe analysis study. Mater. Charact. 1997, 38, 53–65. [Google Scholar] [CrossRef]
- Girault, E.; Jacques, P.; Harlet, P.; Mols, K.; Van Humbeeck, J.; Aernoudt, E.; Delannay, F. Metallographic methods for revealing the multiphase microstructure of TRIP-assisted steels. Mater. Charact. 1998, 40, 111–118. [Google Scholar] [CrossRef]
- Rohatgi, A.; Vecchio, K.; Gray Iii, G. A metallographic and quantitative analysis of the influence of stacking fault energy on shock-hardening in Cu and Cu–Al alloys. Acta Mater. 2001, 49, 427–438. [Google Scholar] [CrossRef]
- Moreira, F.; Xavier, F.; Gomes, S.; Santos, J.; Freitas, F.; Freitas, R. New analysis method application in metallographic images through the construction of mosaics via speeded up robust features and scale invariant feature transform. Materials 2015, 8, 3864–3882. [Google Scholar]
- Povstyanoi, O.Y.; Sychuk, V.; McMillan, A.; Zabolotnyi, O. Metallographic analysis and microstructural image processing of sandblasting nozzles produced by powder metallurgy methods. Powder Metall. Metal Ceram. 2015, 54, 234–240. [Google Scholar] [CrossRef]
- Chowdhury, A.; Kautz, E.; Yener, B.; Lewis, D. Image driven machine learning methods for microstructure recognition. Comput. Mater. Sci. 2016, 123, 176–187. [Google Scholar] [CrossRef]
- Campbell, A.; Murray, P.; Yakushina, E.; Marshall, S.; Ion, W. New methods for automatic quantification of microstructural features using digital image processing. Mater. Design 2018, 141, 395–406. [Google Scholar] [CrossRef]
- Zhenying, X.; Jiandong, Z.; Qi, Z.; Yamba, P. Algorithm based on regional separation for automatic grain boundary extraction using improved mean shift method. Surf. Topogr. Metrol. Prop. 2018, 6, 025001. [Google Scholar] [CrossRef]
- Journaux, S.; Gouton, P.; Paindavoine, M.; Thauvin, G. Evaluating creep in metals by grain boundary extraction using directional wavelets and mathematical morphology. Revue de Métall. Int. J. Metall. 2001, 98, 485–499. [Google Scholar] [CrossRef]
- Sun, Q.D.; Gao, S.F.; Huang, J.W.; Chen, W. Metallographical Image Segmentation and Compression. In Applied Mechanics and Materials; Trans Tech Publications Ltd.: Bäch SZ, Switzerland, 2012; Volume 152, pp. 276–280. [Google Scholar]
- Simmons, J.; Przybyla, C.; Bricker, S.; Kim, D.W.; Comer, M. Physics of MRF regularization for segmentation of materials microstructure images. In Proceedings of the 2014 IEEE International Conference on Image Processing (ICIP), Paris, France, 27–30 October 2014; pp. 4882–4886. [Google Scholar]
- Cheng, H.C.; Cardone, A.; Varshney, A. Interactive exploration of microstructural features in gigapixel microscopy images. In Proceedings of the 2017 IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 335–339. [Google Scholar]
- Chen, L.; Han, Y.; Cui, B.; Guan, Y.; Luo, Y. Two-dimensional fuzzy clustering algorithm (2DFCM) for metallographic image segmentation based on spatial information. In Proceedings of the 2015 2nd International Conference on Information Science and Control Engineering, Shanghai, China, 24–26 April 2015; pp. 519–521. [Google Scholar]
- De Albuquerque, V.H.C.; de Alexandria, A.R.; Cortez, P.C.; Tavares, J.M.R. Evaluation of multilayer perceptron and self-organizing map neural network topologies applied on microstructure segmentation from metallographic images. NDT E Int. 2009, 42, 644–651. [Google Scholar] [CrossRef]
- Bulgarevich, D.S.; Tsukamoto, S.; Kasuya, T.; Demura, M.; Watanabe, M. Pattern recognition with machine learning on optical microscopy images of typical metallurgical microstructures. Sci. Rep. 2018, 8, 2078. [Google Scholar] [CrossRef] [PubMed]
- Papa, J.P.; Nakamura, R.Y.; De Albuquerque, V.H.C.; Falcão, A.X.; Tavares, J.M.R. Computer techniques towards the automatic characterization of graphite particles in metallographic images of industrial materials. Expert Syst. Appl. 2013, 40, 590–597. [Google Scholar] [CrossRef]
- De Albuquerque, V.H.C.; Silva, C.C.; Menezes, T.I.D.S.; Farias, J.P.; Tavares, J.M.R. Automatic evaluation of nickel alloy secondary phases from SEM images. Microsc. Res. Tech. 2011, 74, 36–46. [Google Scholar] [CrossRef]
- DeCost, B.L.; Holm, E.A. A computer vision approach for automated analysis and classification of microstructural image data. Comput. Mater. Sci. 2015, 110, 126–133. [Google Scholar] [CrossRef]
- Gola, J.; Britz, D.; Staudt, T.; Winter, M.; Schneider, A.S.; Ludovici, M.; Mücklich, F. Advanced microstructure classification by data mining methods. Comput. Mater. Sci. 2018, 148, 324–335. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Sanchez-Lengeling, B.; Aspuru-Guzik, A. Inverse molecular design using machine learning: Generative models for matter engineering. Science 2018, 361, 360–365. [Google Scholar] [CrossRef] [PubMed]
- Azimi, S.M.; Britz, D.; Engstler, M.; Fritz, M.; Mücklich, F. Advanced steel microstructural classification by deep learning methods. Sci. Rep. 2018, 8, 2128. [Google Scholar] [CrossRef] [PubMed]
- Ma, B.; Ban, X.; Huang, H.; Chen, Y.; Liu, W.; Zhi, Y. Deep learning-based image segmentation for al-la alloy microscopic images. Symmetry 2018, 10, 107. [Google Scholar] [CrossRef]
- Chen, H.; Qi, X.; Yu, L.; Dou, Q.; Qin, J.; Heng, P.A. DCAN: Deep contour-aware networks for object instance segmentation from histology images. Med. Image Anal. 2017, 36, 135–146. [Google Scholar] [CrossRef] [PubMed]
- Yi, J.; Wu, P.; Jiang, M.; Huang, Q.; Hoeppner, D.J.; Metaxas, D.N. Attentive neural cell instance segmentation. Med. Image Anal. 2019, 55, 228–240. [Google Scholar] [CrossRef]
- De Bel, T.; Hermsen, M.; Litjens, G.; van der Laak, J. Structure Instance Segmentation in Renal Tissue: A Case Study on Tubular Immune Cell Detection. In Computational Pathology and Ophthalmic Medical Image Analysis; Springer: Berlin, Germany, 2018; pp. 112–119. [Google Scholar]
- Guerrero-Pena, F.A.; Fernandez, P.D.M.; Ren, T.I.; Yui, M.; Rothenberg, E.; Cunha, A. Multiclass weighted loss for instance segmentation of cluttered cells. In Proceedings of the 2018 25th IEEE International Conference on Image Processing (ICIP), Athens, Greece, 7–10 October 2018; pp. 2451–2455. [Google Scholar]
- Mou, L.; Zhu, X.X. Vehicle instance segmentation from aerial image and video using a multitask learning residual fully convolutional network. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6699–6711. [Google Scholar] [CrossRef]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2961–2969. [Google Scholar]
- Milletari, F.; Navab, N.; Ahmadi, S.A. V-net: Fully convolutional neural networks for volumetric medical image segmentation. In Proceedings of the 2016 Fourth International Conference on 3D Vision (3DV), Stanford, CA, USA, 25–28 October 2016; pp. 565–571. [Google Scholar]
- Rahman, M.A.; Wang, Y. Optimizing intersection-over-union in deep neural networks for image segmentation. In Proceedings of the International Symposium on Visual Computing, Las Vegas, NV, USA, 12–14 December 2016; pp. 234–244. [Google Scholar]
- Salehi, S.S.M.; Erdogmus, D.; Gholipour, A. Tversky loss function for image segmentation using 3D fully convolutional deep networks. In Proceedings of the International Workshop on Machine Learning in Medical Imaging, Quebec, QC, Canada, 10 September 2017; pp. 379–387. [Google Scholar]
- Brosch, T.; Yoo, Y.; Tang, L.Y.; Li, D.K.; Traboulsee, A.; Tam, R. Deep convolutional encoder networks for multiple sclerosis lesion segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; pp. 3–11. [Google Scholar]
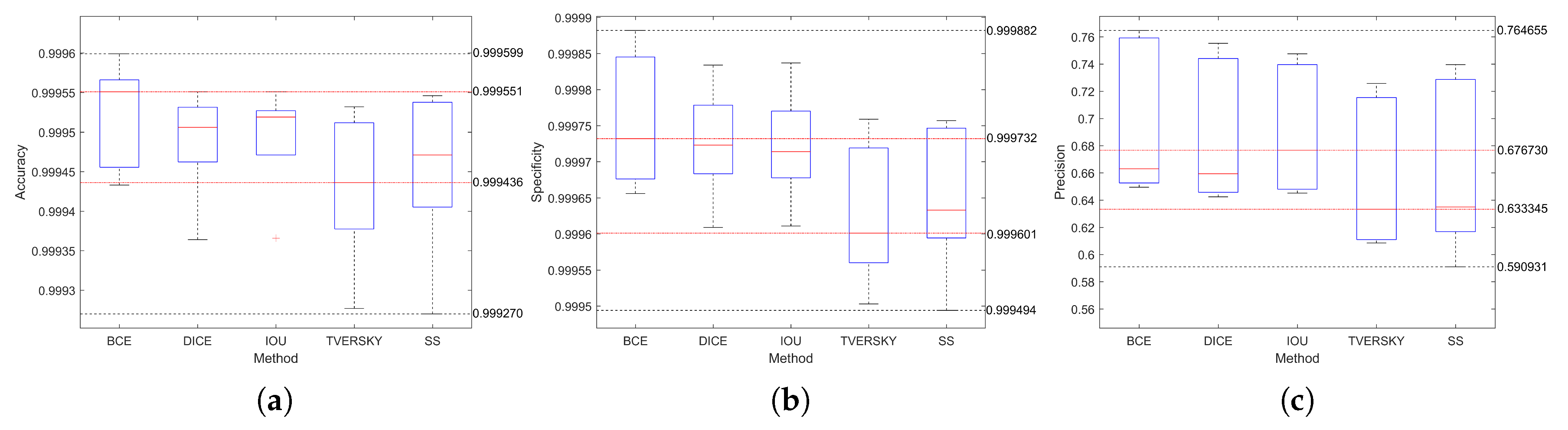



| Acc | 1 | 2 | 3 | 4 | 5 | Median |
|---|---|---|---|---|---|---|
| 0.999555 | 0.999433 | 0.999463 | 0.999551 | 0.999599 | 0.999551 | |
| 0.999551 | 0.999364 | 0.999495 | 0.999506 | 0.999525 | 0.999506 | |
| 0.999519 | 0.999366 | 0.999506 | 0.999551 | 0.999519 | 0.999519 | |
| 0.999436 | 0.999277 | 0.999411 | 0.999532 | 0.999505 | 0.999436 | |
| 0.999471 | 0.999270 | 0.999450 | 0.999535 | 0.999546 | 0.999471 |
| SP | 1 | 2 | 3 | 4 | 5 | Median |
|---|---|---|---|---|---|---|
| 0.999732 | 0.999683 | 0.999656 | 0.999882 | 0.999833 | 0.999732 | |
| 0.999723 | 0.999609 | 0.999708 | 0.999834 | 0.999760 | 0.999723 | |
| 0.999700 | 0.999611 | 0.999714 | 0.999837 | 0.999748 | 0.999714 | |
| 0.999601 | 0.999503 | 0.999579 | 0.999759 | 0.999706 | 0.999601 | |
| 0.999628 | 0.999494 | 0.999633 | 0.999757 | 0.999743 | 0.999633 |
| Precision | 1 | 2 | 3 | 4 | 5 | Median |
|---|---|---|---|---|---|---|
| 0.649482 | 0.653678 | 0.663011 | 0.757276 | 0.764655 | 0.663011 | |
| 0.646859 | 0.642432 | 0.659344 | 0.740331 | 0.755242 | 0.659344 | |
| 0.645198 | 0.648885 | 0.676730 | 0.747458 | 0.736909 | 0.676730 | |
| 0.608518 | 0.611837 | 0.633345 | 0.725710 | 0.711829 | 0.633345 | |
| 0.625438 | 0.590931 | 0.634894 | 0.739520 | 0.725018 | 0.634894 |
| SN | 1 | 2 | 3 | 4 | 5 | Median |
|---|---|---|---|---|---|---|
| 0.630825 | 0.639066 | 0.677610 | 0.669518 | 0.711701 | 0.669518 | |
| 0.637324 | 0.633961 | 0.685101 | 0.677832 | 0.696087 | 0.677832 | |
| 0.624957 | 0.631685 | 0.658808 | 0.689806 | 0.695827 | 0.658808 | |
| 0.641941 | 0.661190 | 0.690875 | 0.748032 | 0.733668 | 0.690875 | |
| 0.667652 | 0.641828 | 0.670456 | 0.746207 | 0.756356 | 0.670456 |
| IOU | 1 | 2 | 3 | 4 | 5 | Median |
|---|---|---|---|---|---|---|
| 0.562809 | 0.564019 | 0.590477 | 0.618716 | 0.648613 | 0.590477 | |
| 0.564172 | 0.557246 | 0.588999 | 0.618948 | 0.632580 | 0.588999 | |
| 0.556383 | 0.559084 | 0.584960 | 0.628808 | 0.627891 | 0.584960 | |
| 0.549827 | 0.554891 | 0.579945 | 0.646644 | 0.636055 | 0.579945 | |
| 0.567711 | 0.537472 | 0.572862 | 0.651192 | 0.653169 | 0.572862 |
| F1 | 1 | 2 | 3 | 4 | 5 | Median |
|---|---|---|---|---|---|---|
| 0.636120 | 0.641956 | 0.666217 | 0.705793 | 0.733540 | 0.666217 | |
| 0.638624 | 0.633869 | 0.667450 | 0.702997 | 0.720067 | 0.667450 | |
| 0.631062 | 0.635787 | 0.663737 | 0.712935 | 0.711942 | 0.663737 | |
| 0.621341 | 0.631540 | 0.657220 | 0.731635 | 0.718488 | 0.657220 | |
| 0.642051 | 0.611533 | 0.648007 | 0.737506 | 0.736652 | 0.648007 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, D.; Guo, D.; Liu, S.; Liu, F. Microstructure Instance Segmentation from Aluminum Alloy Metallographic Image Using Different Loss Functions. Symmetry 2020, 12, 639. https://doi.org/10.3390/sym12040639
Chen D, Guo D, Liu S, Liu F. Microstructure Instance Segmentation from Aluminum Alloy Metallographic Image Using Different Loss Functions. Symmetry. 2020; 12(4):639. https://doi.org/10.3390/sym12040639
Chicago/Turabian StyleChen, Dali, Dinghao Guo, Shixin Liu, and Fang Liu. 2020. "Microstructure Instance Segmentation from Aluminum Alloy Metallographic Image Using Different Loss Functions" Symmetry 12, no. 4: 639. https://doi.org/10.3390/sym12040639
APA StyleChen, D., Guo, D., Liu, S., & Liu, F. (2020). Microstructure Instance Segmentation from Aluminum Alloy Metallographic Image Using Different Loss Functions. Symmetry, 12(4), 639. https://doi.org/10.3390/sym12040639




