Abstract
In this paper, deep reinforcement learning (DRL) and knowledge transfer are used to achieve the effective control of the learning agent for the confrontation in the multi-agent systems. Firstly, a multi-agent Deep Deterministic Policy Gradient (DDPG) algorithm with parameter sharing is proposed to achieve confrontation decision-making of multi-agent. In the process of training, the information of other agents is introduced to the critic network to improve the strategy of confrontation. The parameter sharing mechanism can reduce the loss of experience storage. In the DDPG algorithm, we use four neural networks to generate real-time action and Q-value function respectively and use a momentum mechanism to optimize the training process to accelerate the convergence rate for the neural network. Secondly, this paper introduces an auxiliary controller using a policy-based reinforcement learning (RL) method to achieve the assistant decision-making for the game agent. In addition, an effective reward function is used to help agents balance losses of enemies and our side. Furthermore, this paper also uses the knowledge transfer method to extend the learning model to more complex scenes and improve the generalization of the proposed confrontation model. Two confrontation decision-making experiments are designed to verify the effectiveness of the proposed method. In a small-scale task scenario, the trained agent can successfully learn to fight with the competitors and achieve a good winning rate. For large-scale confrontation scenarios, the knowledge transfer method can gradually improve the decision-making level of the learning agent.
1. Introduction
1.1. Reinforcement Learning
Reinforcement learning uses a trial and error method to train agents, which is inspired by behaviorist psychology [1]. Reinforcement learning is a type of machine learning method for robot learning [2]. After performing an action, the learning agent receives a reward from the environment. Through continuous interaction with the environment, a learning agent can finally achieve the goal. The concept of reinforcement learning has been proposed as early as the last century [3]. Reinforcement learning is mainly applied to many interactive behaviors and decision-making problems—such as video games, robot control systems, human-computer dialogue, etc, which cannot be well dealt with by the well-known supervised learning and unsupervised learning methods [4,5,6,7].
1.2. Multi-Agent Confrontation in the Real-Time Strategy Game
In the last decades, Artificial Intelligence (AI) technology has made remarkable progress. As an excellent test platform for AI research, video games have provided strong support for the development of AI technology, such as the traditional Atari video games, imperfect information games, and so on [8]. However, classical methods only consider video games in smaller scenes and researchers only need to control a single agent in these game environments. In addition, a large number of game scenarios include complex confrontation tasks and complex game rules, which is difficult for current AI research.
Real-time strategy (RTs) games usually have a time-varying scene, which is different from board games [9]. In many traditional RTs games, StarCraft has a large number of players and a large number of competitions, which requires different countermeasures, tactics and even control techniques, so it has attracted the attention of international scholars [10]. StarCraft provides a relatively ideal environment for AI research in video games and it can achieve confrontation decision-making via a computer program. Figure 1 shows the confrontation task in a large-scale StarCraft scenario. Recently, with the rise of StarCraft AI competitions and the emergence of the brood war application program interface (BWAPI), the research on AI for StarCraft has made remarkable progress.

Figure 1.
Large-scale task scenes in StarCraft task.
Researchers have developed some auxiliary platforms, such as Torchcraft and pysc2, to help develop AI programs for StarCraft. Recent research works have focused more on some problems such as multi-agent confrontation, opponent modeling, situation assessment, and behavior planning and so on [11]. However, it is still very difficult to develop an effective behavior decision-making method using machine learning algorithms for StarCraft competition. It is a key step in the research of RTs game AI to achieve effective confrontation decision-making. Previous works have developed some methods to achieve the confrontation decision-making in a multi-agent system, such as the Bayesian method for incompleteness and uncertainty, the neural network model for controlling individuals, and the potential fields for obstacle avoidance.
1.3. Confrontation Decision-Making with Reinforcement Learning for Multi-Agent System
A multi-agent system contains many autonomous agents. In the same work space, each agent will receive different environmental information and perform different actions. The critical problem of the research on the multi-agent confrontation is to develop an effective confrontation mechanism so that multiple agents with different roles can finish complex target tasks or solve complex problems by performing different actions. Compared with the classical reinforcement learning methods for a single agent, multi-agent reinforcement learning is more suitable to solve complex multi-agent confrontation problems for the dynamic task. Multi-agent RL methods face some new challenges, such as the relationship between individual reward and team reward, the relationship between Exploration and Exploitation, the curse of dimensionality and so on.
As a type of machine learning method, reinforcement learning has been proved to have excellent performance in continuous decision-making tasks. Previous works have developed many advanced applications for StarCraft using a reinforcement learning algorithm. Reference [12] developed a SARSA learning method using a reward function with short-term memory to control the movement for the learning agent. However, this method needs expert experience, and the number of input layer nodes increases sharply with the number of agents. Reference [13] developed several reinforcement learning methods to finish the confrontation task, including an improved Q-learning. They use this learning method to train a mind agent to fight several agents that do not cooperate with each other.
Classical methods have some difficulties in handling complex state representation and mastering confrontation strategies to achieve a more intelligent game AI agent for the multi-agent systems. Furthermore, they are often helpless for task scenes with continuous action. Recent methods use the computational power of deep learning to achieve deeper feature extraction [14]. It usually takes a lot of time to train a smart learning agent using the RL method, especially in large-scale task scenes. Therefore, how to develop a suitable reinforcement learning algorithm to achieve more effective confrontation decision-making has become a hot topic. Meanwhile, the developed learning model needs to be suitable for more complex scenarios.
1.4. Deep Reinforcement Learning
The latest development of deep learning models makes it possible to achieve the high-level features representation using the perceptual data, which provides an opportunity for the RL algorithm to expand the learning model to the confrontation tasks of infinite state space. The deep reinforcement learning (DRL) is developed to learn a mapping in an end-to-end method and DRL methods apply the computational power of deep learning model to relaxing the curse of dimensionality in complex tasks [15]. A Deep Deterministic Policy Gradient (DDPG) is a practical RL algorithm and it learns a Q-value function and a policy [16]. The Bellman equation and the off-policy sample data are used to learn the Q-value function and the Q-value is used to train an agent to get a policy. In this work, we use the DDPG algorithm to achieve behavioral decision-making for different agents.
1.5. Knowledge Transfer
Generally speaking, the reinforcement learning algorithms need sufficient training samples to get the optimal strategy. When task scenarios change, new learning experiences need to be acquired again. For the classical reinforcement learning methods, it is difficult to get a reasonable strategy for more complex tasks if the state space is larger [17]. Especially, in the StarCraft game, there are a large number of task scenes and different roles, which need to train agents from scratch. For a new task, it is very time-consuming to train a strategy from scratch. Previous works are trying to transfer the learning experience from the trained task to the new tasks to improve the learning performance [18]. Transfer learning may be a solution. Transfer learning can transfer prior knowledge from the source task to the target task.
If there is a large gap between the initial task and the target task, an intermediate task is set to achieve higher performance. The learning experience from the source task and the intermediate task is regarded as prior experience to finish the target task. The developed knowledge transfer method is used to train the strategy for agents in more complex tasks and the difficulty of these intermediate tasks is gradually increasing.
1.6. Contributions in This Work
This paper proposed a multi-agent DDPG method with parameter sharing to achieve the multi-agent confrontation. Four deep neural networks are used to achieve the action selection and value function approximation respectively. In the game, each agent shares the parameters of the neural network to reduce the loss of experience storage. Meanwhile, each robot not only considers its own information but also uses the information of other robots to update the network parameters, which can improve the performance of the collaborative decision-making for the agent. For each agent, a policy-based RL method is used as an auxiliary controller and it can achieve continuous motion control for the separated action space, which is more suitable for real-time decision-making of the RTS game. This method can effectively provide more effective decision support. In addition, the momentum mechanism is added to the back-propagation process to accelerate the convergence rate for the neural network. In the reinforcement learning model, a reward function is proposed to balance the losses of enemies and our side. Furthermore, a knowledge transfer method is used to extend the learning model to adapt to various task situations. Compared with the method of learning from scratch, the proposed method can improve the learning performance for the RL model in a new task. In the large-scale task scene, a group of agents is trained by the proposed method with the knowledge transfer method. As far as the winning rate is concerned, the performance of the proposed method in the target scenario is better than that of the baseline methods.
There are three main contributions in this work. Firstly, a multi-agent DDPG method with parameter sharing is proposed to train the confrontation strategy for multi-agents. Meanwhile, a momentum mechanism is introduced into the training process to improve the performance of the neural networks. This method can accelerate the convergence rate of the neural network model. Secondly, a policy-based RL model for learning agents is introduced to the auxiliary control and it can achieve continues action selection in real-time decision-making. Finally, the proposed method integrates knowledge transfer and it can be extended to larger task scenarios.
1.7. Paper Structure
This paper is organized as follows: Section 2 describes the background knowledge for the proposed method, such as neural network, reinforcement learning. Section 3 describes a continuous control problem in the semi-Markov decision-making process (SMDP) and the actor–critic algorithm. Section 4 shows a multi-agent DDPG method with parameter sharing and this method uses a multi-agent DDPG algorithm integrating a neural network model with a momentum mechanism. The structure of the proposed DDPG method and an auxiliary controller are also shown in this section. The parameters of the neural network are shared by multi-agents. Section 5 introduces a knowledge transfer method to improve the generalization of the proposed method. Experimental results are detailed in the next sections, to show that the proposed method has good performance. Conclusions are drawn in the last section.
2. Background
2.1. Reinforcement Learning
Reinforcement learning is a learning process in which the agent constantly interacts with the environment to gain learning experience, which has the characteristics of active learning and adaptive learning. In computer games, the reinforcement learning frame for the non-player character (NPC) is shown in Figure 2. The RL model for NPC consists of three modules: the sensing model, the reward model, policy model. The sensing model to map the state to the action of NPC, and reward model will give reward r to the NPC according to the transition of states. The policy model allows NPC to choose an action using an action policy.
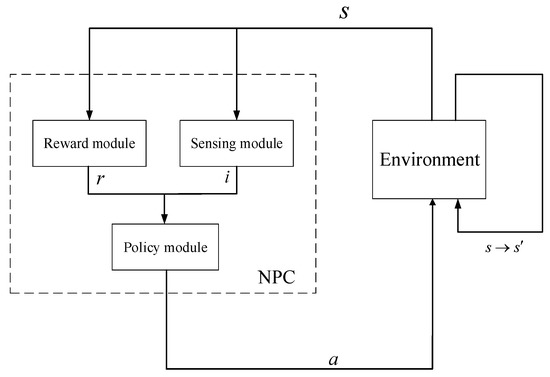
Figure 2.
Reinforcement learning framework for NPC.
Q-learning algorithm is a classical reinforcement learning algorithm, and it is an off-policy learning algorithm [19]. Q Learning is easy to use and fast convergence. The definition for the Q-value function is given by,
In the Q-learning systems, the Time Difference (TD) method is used to estimate the Q value function, which is given by,
where is the learning rate, and its range is (0, 1). is the discount factor. The learning rate reflects the efficiency of the learning process. is the current state and is the next state. is the current action and is the next action. When the NPC arrives at the target state, an episode ends. When an episode is over, the NPC returns to its initial state, and the next episode begins until the entire learning process is achieved, and policy is obtained.
2.2. Neural Network
In this work, we use a multilayer feed-forward network model for the DRL method and the neural network model has three components, which are an input layer, a hidden layer, and an output layer [20]. Each component contains multiple neural layers, each layer contains one or more neurons. The back propagation algorithm is used to update the connection weight for neural networks and this algorithm has two processes: the forward transmission of the input information and the back propagation of errors [21].
In the process of the forward transmission, the input signal is input from the input layer, and then processed layer by layer through the hidden layer until it reaches the output layer, and finally, the output result is calculated in the output layer. If there is a gap between the current results and the desired results, the output values are transmitted back to the neural network via the back propagation algorithm. The weight of the neural network is updated by the back propagation algorithm. Previous research results show that the neural network model can approach any nonlinear function. The basic structure for the neural network is shown in Figure 3. The research of deep neural network is initially inspired by the artificial neural network. Recently, deep neural networks use multiple hidden layers to achieve more advanced feature extraction, which has been widely used to develop an effective application for the robot controller.
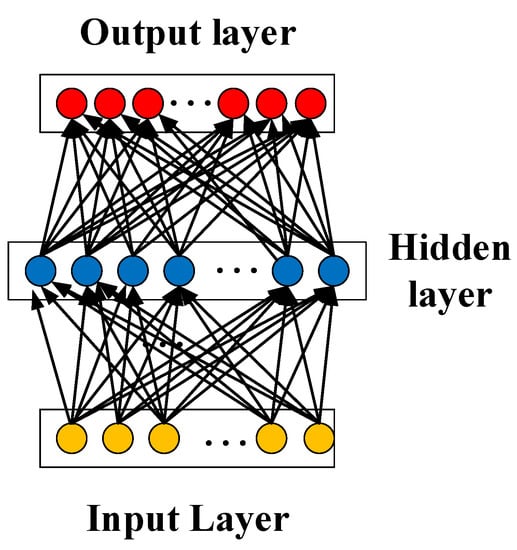
Figure 3.
Structure for the neural network.
3. Description of Continuous Control Problem and a Classical Method
3.1. Optimal Control Problem Using Value Function in SMDPs Process
In the game scene, the process of decision-making for multi-agent systems is regarded as an SMDPs process [9]. Figure 4 shows the SMDPs process. Sojourn time is the time cost for the RL agent to move from one state to the next state. In an SMDPs process, the agent can take a series of the same actions before entering the next state. In Figure 4, after the agent takes the same action times, its state changes from to . The sojourn time is in Figure 4.
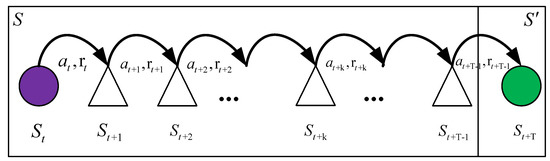
Figure 4.
SMDPs process.
For a game agent, the game environment needs a continuous movement, so it can be regarded as a continuous decision-making system. The continuous decision-making system using a set of state equations is given by,
where S is the state space, and U is the utility function, and t is the current time, and is the initial state. The cost function for the continuous decision-making system can be described by,
where is a discount factor, the value range is , and is the current time, is the utility function, which represents the immediate cost of the system in the previous K time period. is the cost function associated with the initial state. If is the start time and is the end time of the episode, the process of solving optimal control is to gain the control sequence , which minimizes the cost function. According to the principle of Berman optimality, the optimal cost function is given by,
The optimal control problem is described by a value function, which is given by,
The optimal control problem under the SMDPs process is to search the optimal policy . When the agent adopts the optimal policy, a set of action sequences can be obtained. Through this action sequence, the expectation of the cumulative reward obtained by the agent is the maximum, and the performance index function is the smallest. We define the state function using the expected cumulative reward at state , which is given by,
where is the initial state, and is the discount factor, and the value range is , and is the immediate reward for the agent at time t + k + 1. represents the expected cumulative reward obtained from the initial state using the learned policy .
3.2. Classical Method for Optimal Control Using Actor–Critic
The actor–critic algorithm is a very common method to achieve continuous control, which is often used to develop an AI agent in real-time strategy games. In this paper, as a baseline method, this method is compared in this experiment. The framework for the actor–critic algorithm is given in Figure 5. The actor–critic algorithm is one of the methods of reinforcement learning [22]. In the actor–critic algorithm, the advantages of actor-only and critic-only methods are combined. The critic learns a Q-value function using an architecture of approximation and then uses this architecture to modify the parameters for the actor.
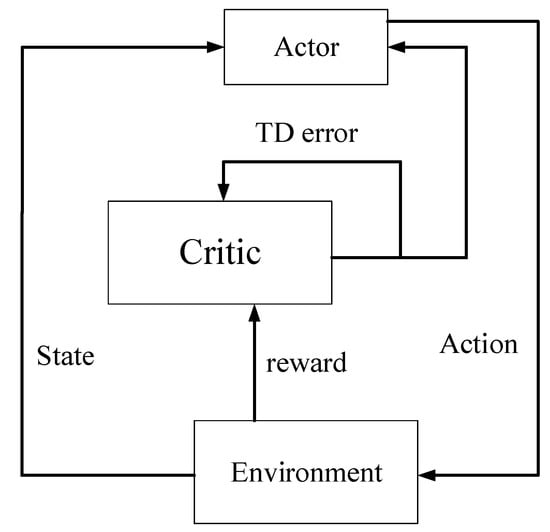
Figure 5.
Framework for the actor–critic algorithm.
In Figure 4, the actor is updated by a policy gradient method. The actor outputs an action, which is evaluated by the critic. The critic is updated using the TD-error. The actor uses the random gradient descent method to update the parameter of the random strategy and uses the estimated Q-value function obtained by the critic to replace the unknown real Q-value function . The action output by the actor is input into critic with the state . The critic uses a policy evaluation algorithm such as TD learning method to estimate Q-value function ≈ . The basic procedure for the actor–critic algorithm is shown in Algorithm 1.
| Algorithm 1: Basic Procedure for Actor–Critic Algorithm |
|
4. Multi-Agent DDPG Algorithm with an Auxiliary Controller for Confrontation Decision-Making
4.1. Back Propagation Algorithm with a Momentum Mechanism
This paper uses a multi-agent DDPG algorithm to train each learning agent. In the StarCraft confrontation scenario, each agent needs to make real-time decisions, and the agent may produce continuous actions. Therefore, this paper uses a DDPG algorithm to make the agent produce continuous action. There are four neural networks in the DDPG algorithm to achieve confrontation decision-making. The traditional neural network model is inefficient. The neural network with the momentum mechanism is more suitable for real-time decision-making tasks. Therefore, in this work, the momentum optimization mechanism [23] is used to accelerate the neural network.
In the training process of the neural networks, the conventional method is the back propagation algorithm using gradient descent. In this method, the weight of the neural network is updated in the opposite direction of the derivative of the error function, which is minimized in the training process, as shown in Equation (8).
Compared with the classical neural network, the deep neural network is more complex. is the current weight and is the weight of the previous time. In the training process, the convergence rate of the classical gradient descent method is slow. Therefore, the momentum mechanism can effectively accelerate the training process of the neural network. The weight update method using the momentum mechanism is shown in Equations (9) and (10).
where γ is a constant, and it is set to 0.9. is the mean square error for the output value. In this paper, Adam algorithm is used to optimize the back propagation algorithm, and the updating process of network weight is shown in below.
where and are constants, and their values are all 0.9. The basic procedure of the back propagation algorithm with Adam momentum algorithm is shown in Algorithm 2.
| Algorithm 2: Procedure for the Back-Propagation Algorithm with Momentum |
|
4.2. Multi-Agent DDPG Algorithm with Parameter Sharing
DDPG algorithm is a combination of the actor–critic algorithm and the DQN algorithm. DDPG algorithm is similar to the actor–critic algorithm in two parts, one is an actor network, and the other is the critic network. Meanwhile, the DDPG algorithm also employs a dual network structure of the DQN algorithm, that is, the actor and critic networks have a target network and current network respectively. In the simulator, each agent can usually obtain information about other agents using a built-in communication channel. Therefore, in order to improve decision-making performance, we allow agents to use extra information to ease training, but not in the test phase. The input of the critic network includes the actions of all agents except the current state information. Actor network outputs actions, including target network and current network. Similarly, critic networks are the Q-value function evaluation network, including the target network and current network respectively. Critic updates network parameters using the TD error, as shown in Equation (16).
where is obtained by the Q-value function evaluation network for agents. is the current action produced by the current actor network. is the Q value produced by the target critic network. is produced by the target actor network. The current critic network uses the TD error to update its parameters. For the actor network, the parameters of the current network are updated by Equation (17).
where is the parameters for the critic network and is the parameters for the actor network. is the probability of the joint action is taken at the state when the parameter is .
When the DDPG algorithm updates the parameters in the target network at each step. The soft parameter update method in the DDPG algorithm improves the stability of exploration for an agent in an unknown environment. The momentum mechanism is used in the back propagation process of the neural network to accelerate the convergence rate. DDPG algorithm addresses the dilemma of exploration–exploitation using an Ornstein Uhlenbeck method [24]. The training method using the DDPG algorithm with momentum is shown in Algorithm 3.
| Algorithm 3: Multi-Agent DDPG Algorithm with Parameter Sharing |
| Initialization: |
| Initialize the current network for the critic , using ; Initializes the current network for actor using . |
| Initialize the target networks for the critic and actor: , |
| Initialize the sampling pool For each agent =1, K do |
| For episode = 1, do |
| Initialize a random noise ; |
| Get the current state |
| For , do |
| , Perform action and observe the next state. , ; |
| Randomly select samples from the sampling pool ; |
| Update the parameters of the current network with momentum mechanism for critic using the Loss function: ; |
| Update the parameters of the current network with momentum mechanism for actor using : |
| Update target networks for the actor and the critic separately: , ; |
| End for End for |
| End for |
4.3. Neural Network Structure for the DDPG Algorithm
The basic neural network structure for the proposed method is shown in Figure 6. The structure of neural networks is symmetrical. For the DDPG agent, the actor and critic neural networks consist of feed-forward neural networks [25] with an input layer, the output layer and three hidden layers of 93, 110, and 9 units. The number of neurons depends on the specific task. The activation function uses the linear rectification function (RELU) [26]. Compared with other saturated nonlinear activation functions such as Sigmoid or tanh, the RELU function is non-linear, and its training speed for gradient descent is faster. While running the reinforcement learning model, we should pay attention to the continuity of action. Because RTs game is a real-time game, agents can no longer take action at every frame. One of its solutions is to use frame skipping technology [27], that is, to perform a training process every fixed number of frames. Referring to the previous research work, this paper sets the number of frame skipping to 10, that is, every 10 frames to perform an action [25].
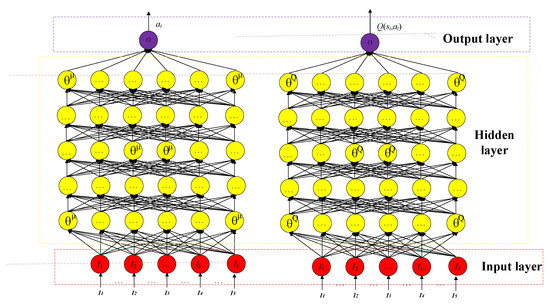
Figure 6.
Structure for the DDPG agent.
In the learning process of the neural network, multiple robots will share the same neural network parameters. The way of neural network parameter sharing can not only accelerate the convergence rate of the deep neural network but also save the storage space of learning experience. Therefore, multiple agents are set to share the weight parameters of the DDPG neural network at the same time. Each agent will use its own learning experience to update the weight parameters.
4.4. An Auxiliary Controller Using a Policy-Based RL Method
In the game, the action space of the game agent may be multidimensional. For example, an action space contains a direction of movement and a move distance. We separate the action space. The DDPG method can achieve real-time continuous decision-making on the move distance. We use the policy-based method as an auxiliary controller. The policy-based method can achieve the real-time decision-making of the moving direction.
The initial state of the agent is . After some same actions agent took, its state is converted to and the environment generates reward . The policy-based RL model is to parameterize the policy which is expressed as , and obtain the maximum expectation of cumulative reward by calculating the optimal parameter .
For a set of state-action sequence , the reward is after the agent takes the state-action sequence. This paper sets the probability that indicates the occurrence of action-sequence , and the expected cumulative reward is given by,
If makes , then is the optimal parameter, and it can get the maximum cumulative reward. So, this paper transforms the policy search problem into the optimal parameter problem and uses the policy gradient [11] to compute the optimal parameter. In this paper, we set the updating law of parameter as , and the Equation (8) can be obtained from the derivative of Equation (19).
After using the current policy to try group state-action sequences, we can get the expression of the policy gradient as shown in the Equation (20) by using the average empirical approximation of the n group sequence to approximate the policy gradient.
In real-time tasks, agents can produce continuous actions using this policy-based RL method.
5. Knowledge Transfer Method
Knowledge Transfer for Different Tasks
The proposed method has three parts: the multi-agent DDPG algorithm with parameter sharing, the auxiliary controller and a knowledge transfer method. For different task scenarios, agents need a large number of learning samples to learn the optimal strategy of the model-free RL algorithm. Agents waste a lot of time if it starts from scratch. If there is a big gap between the source task and the target task, the training method is obviously inefficient. Previous works focused on how to use prior knowledge of similar tasks to improve the efficiency of current tasks. Transfer learning extends the learning experience of source tasks to current tasks to improve training efficiency. This paper uses a direct knowledge transfer method to transfer the learning experience from similar tasks to more complex task scenarios [28]. For a confrontation decision-making task, we use a mapping to adapt the target task and the current task. In this work, each scene has the same state space and action space , which is shown in Equation (21).
For this knowledge transfer method, an intermediate task is set, if there is a big difference between the current task and the target task. Agents can gain more prior experience by learning intermediate tasks. The knowledge transfer method with an intermediate task for confrontation decision-making is shown in Figure 7.
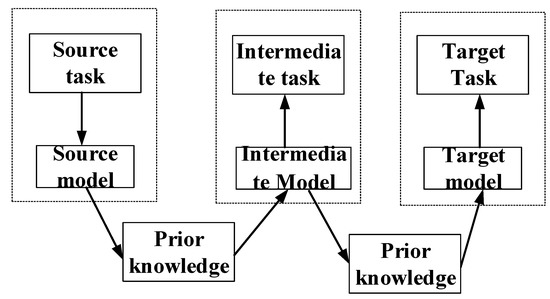
Figure 7.
Knowledge transfer method.
6. Effect Test for the Proposed Policy-Based RL Method
In order to verify the effectiveness of the proposed policy-based RL method, we performed an experiment on the inverted pendulum system. Figure 8 shows the inverted pendulum system used in this experiment, in which the inverted pendulum model can move freely to the left or right in orbit, and the inverted pendulum is balanced by exerting the force left or right. The balance control of the inverted pendulum model can be regarded as the optimal control problem, so the policy-based RL method can be used to solve it. The reinforcement learning model for the optimal control problem of the inverted pendulum is defined as follows:
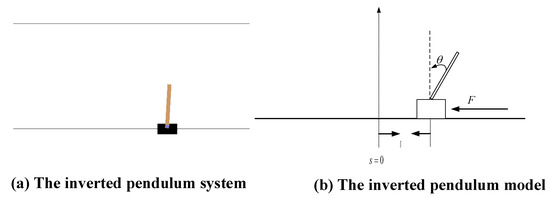
Figure 8.
Experiment on the inverted pendulum.
State space: The state space of the inverted pendulum system is composed of four components, as shown below. The distance of the inverted pendulum deviating from the center of the orbit , the angle of the inverted pendulum offsetting the vertical direction , the motion velocity of the inverted pendulum on the orbit , and the angular velocity of the inverted pendulum swinging . The state space is given by,
Action space and reward function: The action space for the inverted pendulum system consists of two kinds of actions: pushing to the left and pushing to the right, and the size of the two thrusts is the same. The reward function is .
This paper sets the upper limit of the inverted pendulum balance time is 1000 time step. If the balance time exceeds 1000 time steps, this round is terminated. Figure 9 shows the curve of the balance time for the inverted pendulum system. The experiment of the inverted pendulum is performed for 150 rounds, and the balance time of inverted pendulum is recorded in each round. The condition for the end of a round is that the inverted pendulum falls or the balance time is more than 1000 time step. Therefore, the balance time is recorded as 1000 time steps, when the balance time reaches the upper limit.
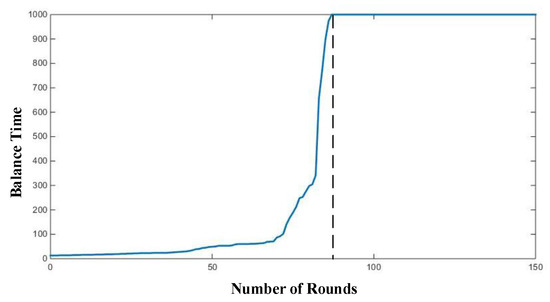
Figure 9.
The curve of balance time for the inverted pendulum.
The experimental results show that the balance time of the inverted pendulum increases gradually with the increase of rounds. When the training times reach 87 rounds, the balance time of the inverted pendulum reaches 1000 time steps. After 87 rounds, the balance time of the inverted pendulum keeps convergence, which further shows that the proposed method is convergent. The proposed method can achieve continuous action and can be convergent. Then, this paper performs the experiments for confrontation decision-making.
7. Experiment on StarCraft Task
7.1. Reinforcement Learning Model for StarCraft Task
State space: State representation in StarCraft is a challenge and there is no unified solution. In [25], a very excellent state representation method is introduced, and the dimension of the state representation method is less than 100. This representation method is proved to be effective and will not be affected by the number of agents. Inspired by this work, we use a state representation using the task characteristics and the input of the game engine of StarCraft. The state representation method consists of three parts: the current state information, the final state information, and the final action.
The current state information includes the cooling time of the equipped weapon, Health points, distance, enemy distance, and terrain distance. The representation of the final state information is the same as the former. According to the test, the state representation method has good generality and it can be used in other RTS games. The map is divided into eight sectors and the distance of each area is calculated. The distance of the agent includes the following: the total distance of each area, the maximum distance of each area, the total distance of each area’s enemies and the maximum distance of each area’s enemies. If the agent exceeds the visible range of the central agent, the distance value of the agent will be set to 0.05. In addition, the distance is linearly related to the distance from the central agent. For terrain distance, if the obstacle is outside the visible range of the central agent, the value is set to 0. The terrain distance is linearly related to the distance from the obstacle to the central agent.
Action space: In the scene of the StarCraft game, the original action space is very large. It allows agents to move any distance in any direction in any time step. When the agent chooses to attack, it can fire at any enemy within its fire range. In order to simplify the action space, inspired by [25], we selected eight moving directions with flexible moving distance and attacked the weakest enemy in the firing range. When moving direction is selected, our agent can move a flexible distance in eight directions: up, down, left, right, left up, right up, left down, right down. The moving distance is determined by a DDPG algorithm. When an enemy is selected, the agent will stay in place and attack the enemy. At present, we give priority to the enemy with the lowest health points in the firing range.
Reward function: In the task scene, if the robot is hit by the enemy, its own health points will change. In this paper, a reward function is proposed to balance the loss of the enemy and our side. The reward function is given by,
where the current health points of our side is and the last health points is . The current health points of the enemy is and is the last health points of the enemy. The proportion of changes in absolute health points on both sides will encourage our agents to do more harm to our opponents in the war. If we lose fewer health points than our enemies, we will get a positive reward.
7.2. Experimental Configuration
In the small-scale scenario, we take the first scenario as the initial task for the training agent. In other scenarios, the transfer learning method is introduced to extend the model to large-scale scenarios. The goal of the confrontation game is to defeat all enemies and improve the winning rate in these scenes. Therefore, this paper takes the winning rate as the performance metrics. This paper sets up several StarCraft game scenarios using different agents: Goliaths vs. Zealots, Goliaths vs. Zerglings, Marines vs. Zerglings, as shown in Figure 10, Figure 11 and Figure 12. In the first scenario, we control four Goliaths to fight three Zealots. In the second scenario, there are 10 Zerglings enemies, with more enemies and shorter cooling times. Our three Goliaths are superior in health, attack power, and fire range. In the third scenario, we control 23 Marines to fight 35 Zerglings. The enemy is superior in speed and combat capability, while our side is superior in firepower range and attack power.

Figure 10.
Task 1: Goliaths vs. Zealots.

Figure 11.
Task 2: Goliaths vs. Zerglings.

Figure 12.
Task 3: Marines vs. Zerglings.
These scenarios are divided into two categories. The first and second scenes are small-scale confrontation tasks, and the last scene is large-scale confrontation tasks. In these tasks, all agents of the enemy are controlled by the AI built in the game. When either side is destroyed, this round ends. In the experiment, the reinforcement learning agent learns to use the advantages and avoid the disadvantages to win the battles in the above scenarios through continuous training.
In the reinforcement learning system, the learning agent makes more use of previous experience with a higher learning rate and a larger discount factor enables a learning agent to consider more long-term rewards. The setting of the initial value of the parameter is inspired by the previous work [25]. A certain effort was made to tune the parameters for the learning system. During the training process, in all scenarios, the mini-batch size for the DDPG algorithm is 64. The Soft target update for the DDPG agent is 0.001. The maximum number of time steps in each round is 1000. In order to speed up a learning process, the game sets the game speed to 25 via BWAPI. The parameters for these experiments are shown in Table 1.

Table 1.
Experimental parameters for the StarCraft experiment
In the small-scale confrontation task, Goliaths are trained under different enemy numbers and types. In the second scenario, the transfer learning method is integrated to train Goliaths using the training results of the first scenario. Both scenes trained more than 5000 rounds. In addition to the rewards generated by basic actions, inspired by previous work, we used an additional reward (AR) as internal assistance to speed up the training progress [25]. When an agent is destroyed, a negative reward value is given, which is set to - 10 in the experiment. In addition, we hope to punish behaviors that cause our agents to be hurt and have negative effects on game results.
In order to promote team cooperation among agents, this paper also introduces a reward mechanism to generate more reward depending on the agent’s movement: if there is no team member or enemy in the direction of movement, a small negative reward will be obtained, which is set as - 0.5 in the experiment. The experimental results using the additional reward mechanism are shown in Figure 13. The experimental results show that the additional reward mechanism has a positive effect on the training process. After 4000 rounds, the additional reward mechanism makes the winning rate of the learning agent close to 1, while the winning rate of the conventional method is still around 0.8. The additional reward is to keep the agents in line and attack the enemy together.
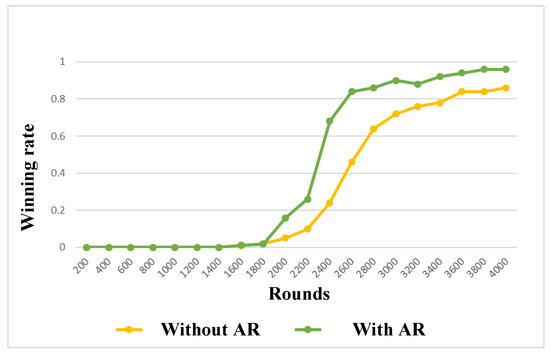
Figure 13.
Experimental results of additional reward.
7.3. Confrontation Task-Goliaths vs. Zealots
In this scenario, we train all Goliath from scratch and analyze the results. First, the performance of the proposed training method using reinforcement learning with additional rewards will be tested. We set the number of battles to 200, and each battle includes 200 rounds. The experimental results are shown in Figure 14. It can be seen from the experimental results that Goliaths cannot defeat any battle before 1500 rounds. With continuous training, the winning rate of agents has improved significantly after 2400 rounds. Finally, after 3400 rounds of training, the trained agents achieved a winning rate of about 90%. After 1800 rounds, the AR method won more than the method without AR. Deep reinforcement learning allows our agents to gain more and more learning experience to learn more effective countermeasures. Meanwhile, an additional incentive mechanism will further improve learning efficiency. Our robots have learned to form more effective countermeasures and defensive formations to defeat the enemy.
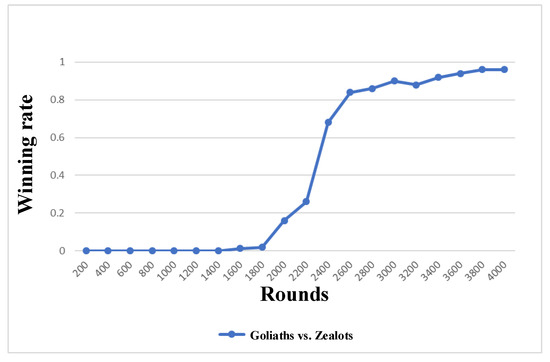
Figure 14.
Experimental results of Goliaths vs. Zealots.
7.4. Confrontation Task-Goliaths vs. Zerglings
In this scenario, an enemy is a group of Zerglings, and we use the training results in the first scenario as a prior experience for the second scenario. Figure 15 shows the experimental results. If we start from scratch, the training speed is relatively slow, and we will not win until after 1900 rounds. If we do not use knowledge transfer (KT), the winning rate is still less than 60% after 4000 rounds. When the learning process uses the prior experience in the first scenario, the training speed will be greatly improved. Even at the beginning of a process, we won fewer times, and the final winning rate is about 90%. The transfer learning method can make the agent use the previous learning experience to improve the performance of the current task. At the beginning of the task, the agent using transfer learning gets a higher winning rate than the competitor. With the increase in the number of learning rounds, the winning rate of the two methods is increasing, but the transfer learning method makes the winning rate of the agent increase faster. Finally, the winning rate of the agents using a transfer learning is close to 1, while that of the competitor is less than 0.6.
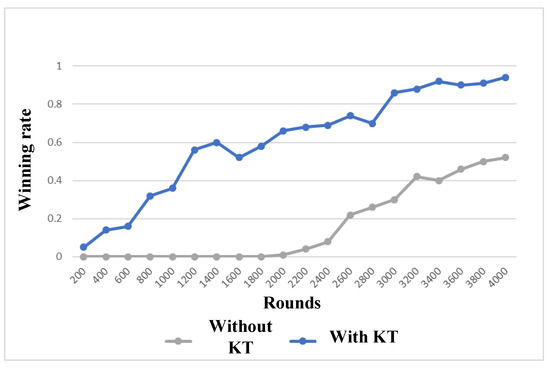
Figure 15.
Experimental results of Goliaths vs. Zerglings.
7.5. Large Scale Confrontation Scenario
We prepared three intermediate tasks to train the agent, as shown in Table 2. After the training, the model was tested in two target scenarios: 13 Marines vs. 15 Zerglings; 23 Marines vs. 35 Zerglings.

Table 2.
Three intermediate tasks for Task 3
The training process of each intermediate task and the target task is shown in Figure 16 and Figure 17. It can be seen from the experimental results that the transfer learning method can effectively improve the learning efficiency and performance in the large-scale task scene. Transfer learning can make agents gradually use prior experience to get higher scores in the current task. If the current task is quite different from the source task, multiple intermediate tasks can allow agents to gain more experience in handling the complex target task. The results in Figure 16 and Figure 17 show that by using the learning experience of the previous intermediate task, the agent can achieve better confrontation performance in the current task. Intermediate tasks provide a step for solving the complex target task.
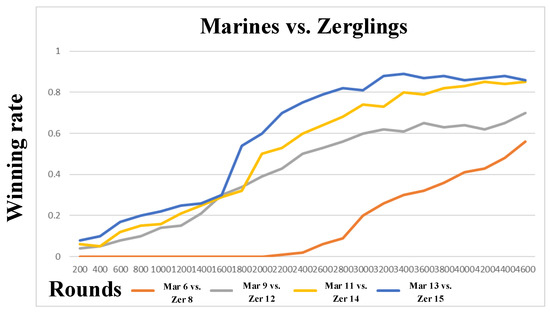
Figure 16.
Experimental results of Marines vs. Zerglings for Task 1.
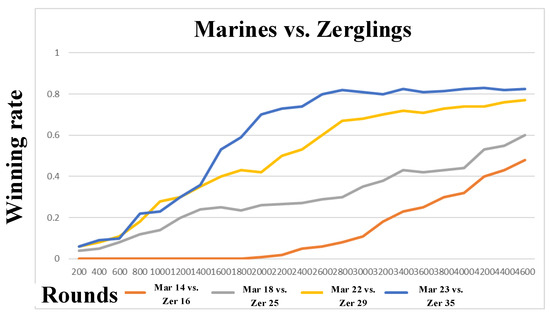
Figure 17.
Experimental results of Marines vs. Zerglings for Task 2.
Through the DDPG algorithm and transfer learning, agents can obtain a more effective confrontation strategy. In the confrontation task, our agents can acquire the policy mapping from state to action through reinforcement learning. In the process of confrontation, we can gradually learn to disperse and destroy the enemy one by one and keep a certain distance from the enemy in the process of fighting to reduce their losses. At the same time, additional rewards can encourage agents to move in the same direction and keep the formation consistent, which enables multi-agents to take action to the same goal. Finally, for Task 1 and Task 2, the proposed method has achieved a winning rate of more than 0.8 after 4600 rounds.
8. Experiment on Tank War Task
8.1. Experimental Configuration for Tank War Task
The Tank war experiment was performed on the Robocode platform [6,9], where two or more tank robots fought to win. Robocode is a 1000 × 800 pixel two-dimensional simulator, and the size of the tank itself is 36 × 45 pixels. On this platform, there is a built-in AI robot, which is named Fire, and the movement rule of the tank fire is as follows: Keep the random movement and shoot at the opponent after the opponent is found. Three methods are compared, the classical actor–critic algorithm (AC-learning) [21], the classical DDPG algorithm (DDPG-learning) [29], and the proposed multi-agent DDPG algorithm with parameter sharing (MDDPG-learning). First of all, we set up a group of robots as an opponent, which consists of 10 built-in AI robots. We train a group of robots with three methods: AC-learning, DDPG-learning, and MDDPG-learning. Each group contains five robots. Then, we use these three groups of RL robots to fight against the group of built-in AI robots. The number of rounds is 500. We record the score every ten rounds. Every 10 rounds are called a session. Both sides have 100 health points (HPs) at the beginning of a round. If the health points of one tank are 0, a round is over.
State space: The state space is formed by the combination of the absolute orientation angle, the relative direction angle, the distance between the tank agent, whether the tank collides to the wall and whether the tank is hit by a bullet. The absolute direction angle range is , which is discretized into four states, similarly, and the relative direction angle is also discretized into four kinds of states. The distance between the tank agent is defined as the distance between the center point of the tank agent, which is divided into 20 discrete values. The number 0 means the tank did not hit the wall, and the number 1 means the tank hit the wall. The number 0 means that the tank is not hit by bullets, and the number 1 means the tank is hit by a bullet.
Action space: The movement of the tank consists of two basic movements: movement and rotation. This paper sets up the action space includes: forward, backward, front left turn, front right turn, back left turn, and back right turn six kinds of different movements.
Reward function: In this task, the reward function is the same as for the StarCraft game.
8.2. Experimental Results and Analysis
In this paper, the experimental parameters are set up. The learning rate for the RL method is , discount rate . The Mini-batch size for the DDPG algorithm is 32. The soft target update is 0.01. The parameters for the Tank War are shown in Table 3. The average score of the tank in each training process was recorded as total score/100. Figure 18 shows the curve for the average scores of the RL tank group trained by three different methods and the built-in AI group respectively, where the horizontal axis represents the number of sessions and the vertical axis represents the score. As we can see from Figure 18, the total score of the proposed MDDPG-learning method is higher than the other three methods, especially after 33 sessions, which shows that the control performance of the proposed method is better than the classical AC-learning algorithm and the DDPG-learning algorithm.

Table 3.
Experimental parameters for the Tank War experiment
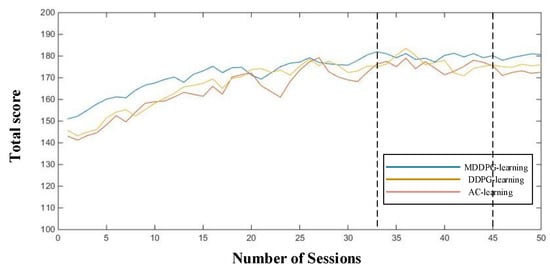
Figure 18.
The curve for the total score.
Figure 19 shows the curve for the attack score of three methods. Because we need to compare the final control performance of the agent in the game, we need to train the agent in advance. Our experimental results show the results after the training. In order to further compare the performance of the three methods, the attack score and the defense score are recorded. In Figure 19 and Figure 20, the horizontal axis represents the number of sessions, and the longitudinal axis represents the defensive score or the attack score for each session. From Figure 19 and Figure 20, we can see that the attack score curve and the defensive curve of the AC-learning algorithm and the DDPG-learning algorithm are more volatile and less stable, and the proposed MDDPG-learning method is relatively stable. For the proposed method, the momentum mechanism can improve the control performance of the algorithm and the parameter sharing mechanism and the additional reward will encourage the agents to maintain cooperation. The proposed algorithm makes the agent learn a better countermeasure strategy to effectively hurt the enemy. At the same time, the auxiliary controller can improve the countermeasure performance and make detailed decision-making in the separated action space. Additional rewards can help our robots form a better formation, which helps improve their defense performance. Higher attack and defense scores lead to higher total scores. Finally, the total scores of the proposed MDDPG-learning method, DDPG-learning method, and AC-learning algorithm are about 180, 175, and 170 respectively.
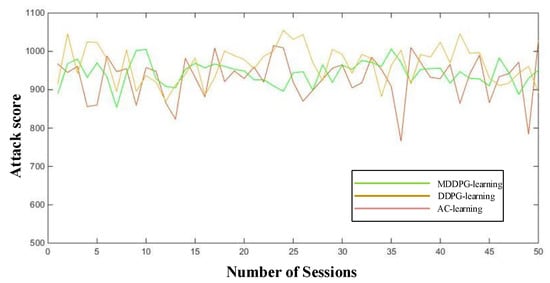
Figure 19.
Curve for the attack score.
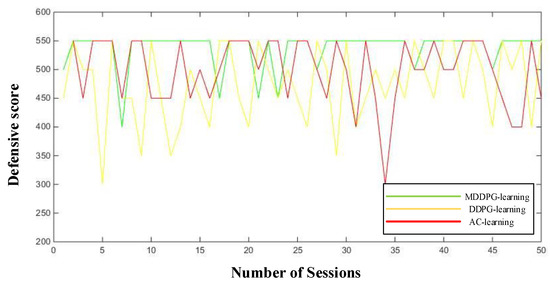
Figure 20.
Curve for the deference score.
In order to test the performance of the proposed method integrating the knowledge transfer method, this paper designed a target task with 15 built-in AI enemies. The learning method with knowledge transfer (with KT) is compared with the learning method without knowledge transfer (without KT). Two groups fight 500 rounds, and every 10 rounds have recorded a session. Figure 21 shows the score ratio of the two methods, and the score ratio is calculated by calculating the value of our score/total scores. As shown in Figure 21, the score ratio of the method with KT is higher than the method without KT. Some effort has been made to tune the parameters to suit the new task. The score rate of the proposed method with KT is about 0.7. However, the score rate of the comparison method is about 0.35. Figure 22 shows the attack score for the two methods. Figure 22 shows that the attack score of the KT method is also higher than without the KT method in each session, which shows that the learning agent with the knowledge transfer has better performance. The attack score of the proposed method with KT is about 700, while that of the proposed method without KT is about 300. The previous experience is helpful to improve the performance of the reinforcement learning algorithm.
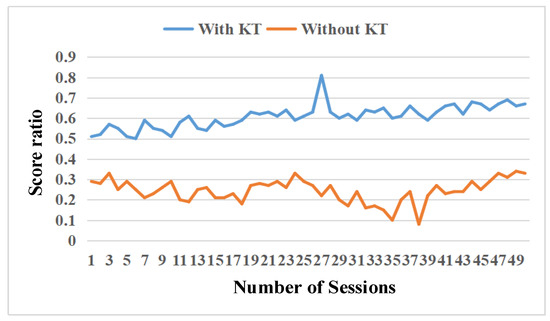
Figure 21.
Curve of the score ratio.
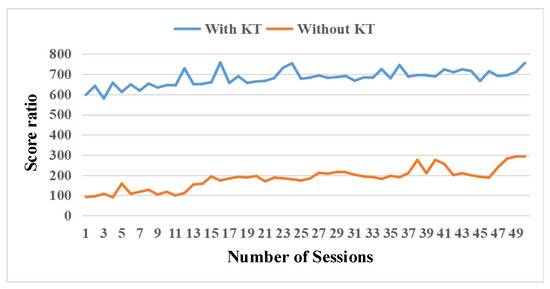
Figure 22.
The curve of the attack score.
9. Conclusions
This paper mainly investigates the decision-making method of real-time confrontation for multi-agent systems using reinforcement learning in the RTs game task. A multi-agent DDPG algorithm is mainly used to train each agent. Each agent can reduce the storage loss through parameter sharing. At the same time, multiple learners can accelerate the efficiency of the weight update for the deep neural network. Each agent will consider the information and actions of other agents when updating the network weight, which will improve the decision-making performance. In order to accelerate the learning speed of the neural network, momentum is added in the back propagation process of the deep neural networks, and the learning efficiency of the deep neural network is improved by momentum mechanism. The auxiliary controller with a policy-based method can achieve continuous control for the separated action space. The additional reward will further encourage the cooperative behavior of agents. Finally, knowledge transfer learning is used to extend the model to different scenarios. There are three experiments. The experiment of the inverted pendulum system verifies the effectiveness of the policy-based RL method. In this paper, for the experiment of confrontation decision-making, we test the effectiveness of the proposed method in small and large scale scenarios. Two confrontation experiments are the StarCraft task and the Tank War task. The experimental results show that the proposed method can effectively train agents to learn appropriate strategies, and can defeat the competitors in some different scenes.
There are still some works to be solved in the future. First, for the knowledge transfer method, if there is a large gap between the current task and the target task, how to transfer the learning experience from the previous task to the current task is a problem worthy of investigation. Secondly, because the reward in the task scenario is sparse, how to solve the problem of sparse reward is a problem worthy of investigation [30,31]. A curiosity driven reinforcement learning (RL) method may be a solution. At the same time, how to improve the intrinsic reward function also needs further work [32,33].
Author Contributions
Methodology, C.H.; software, C.H.; investigation, C.H.; writing—original draft preparation, C.H.; writing—review and editing, C.H. The author has read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Natural Science Foundation of Hubei Province under grant 2013CFC026, and in part by the International Science and Technology Cooperation Program of Hubei Province under grant 2017AHB060.
Conflicts of Interest
The author declares no conflict of interest.
References
- Emary, E.; Hossam; Zawbaa, M.; Grosan, C. Experienced Gray Wolf Optimization Through Reinforcement Learning and Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 681–694. [Google Scholar] [CrossRef]
- Kiumarsi, B.; Kyriakos; Vamvoudakis, G.; Modares, H.; Lewis, F.L. Optimal and Autonomous Control Using Reinforcement Learning: A Survey. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 2042–2062. [Google Scholar] [CrossRef]
- Pradeep, D.J.; Noel, M.M.; Arun, N. Nonlinear control of a boost converter using a robust regression based reinforcement learning algorithm. Eng. Appl. Artif. Intell. 2016, 52, 1–9. [Google Scholar] [CrossRef]
- Hu, C.; Xu, M. Adaptive Exploration Strategy With Multi-Attribute Decision-Making for Reinforcement Learning. IEEE Access 2020, 8, 32353–32364. [Google Scholar] [CrossRef]
- Tan, X.; Chng, C.B.; Su, Y.; Lim, K.B.; Chui, C.K. Robot-assisted training in laparoscopy using deep reinforcement learning. IEEE Robot. Autom. Lett. 2019, 4, 485–492. [Google Scholar] [CrossRef]
- Li, Z.; Liu, J.; Huang, Z.; Peng, Y.; Pu, H.; Ding, L. Adaptive impedance control of human–robot cooperation using reinforcement learning. IEEE Trans. Ind. Electron. 2017, 64, 8013–8022. [Google Scholar] [CrossRef]
- Yuan, Y.; Li, Z.; Zhao, T.; Gan, D. DMP-based Motion Generation for a Walking Exoskeleton Robot Using Reinforcement Learning. IEEE Trans. Ind. Electron. 2019, 67, 3830–3839. [Google Scholar] [CrossRef]
- Balducci, F.; Grana, C.; Cucchiara, R. Affective level design for a role-playing videogame evaluated by a brain-computer interface and machine learning methods. Vis. Comput. 2016, 33, 1–15. [Google Scholar] [CrossRef]
- Hu, C.; Xu, M. Fuzzy Reinforcement Learning and Curriculum Transfer Learning for Micromanagement in Multi-Robot Confrontation. Information 2019, 10, 341. [Google Scholar] [CrossRef]
- Othman, N.; Decraene, J.; Cai, W.; Hu, N.; Gouaillard, A. Simulation-based optimization of StarCraft tactical AI through evolutionary computation. J. Yunnan Agric. Univ. 2012, 3, 639–643. [Google Scholar]
- Ontanon, S.; Synnaeve, G.; Uriarte, A.; Richoux, F. A Survey of Real-Time Strategy Game AI Research and Competition in StarCraft. IEEE Trans. Comput. Intell. AI Games 2013, 5, 293–311. [Google Scholar] [CrossRef]
- Shantia, A.; Begue, E.; Wiering, M. Connectionist reinforcement learning for intelligent unit micro management in StarCraft. In Proceedings of the International Joint Conference on Neural Networks, San Jose, CA, USA, 31 July–5 August 2011; pp. 1794–1801. [Google Scholar]
- Wender, S.; Watson, I. Applying reinforcement learning to small scale combat in the real-time strategy game StarCraft: Broodwar. In Proceedings of the IEEE Conference on Computational Intelligence and Games, Granada, Spain, 11–14 September 2012; pp. 402–408. [Google Scholar]
- Mansoor, A.; Juan; Cerrolaza, J.; Idrees, R.; Biggs, E.; Alsharid, M.A.; Avery, R.A.; Linguraru, M.G. Deep Learning Guided Partitioned Shape Model for Anterior Visual Pathway Segmentation. IEEE Trans. Med Imaging 2016, 35, 1856–1865. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Tang, L.; Tong, S.; Chen, C.L.; Li, D.J. Reinforcement Learning Design-Based Adaptive Tracking Control With Less Learning Parameters for Nonlinear Discrete-Time MIMO Systems. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 165–176. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Hou, Z.; Wang, W.; Xu, B.; Zhang, K.; Chen, K. Feedback deep deterministic policy gradient with fuzzy reward for robotic multiple peg-in-hole assembly tasks. IEEE Trans. Ind. Inform. 2018, 15, 1658–1667. [Google Scholar] [CrossRef]
- Machado, M.C.; Bellemare, M.G.; Bowling, M. A laplacian framework for option discovery in reinforcement learning. In Proceedings of the 34th International Conference on Machine Learning-Volume 70. JMLR. org, Sydney, Australia, 6–11 August 2017; pp. 2295–2304. [Google Scholar]
- Jialin, P.S.; Qiang, Y. A Survey on Transfer Learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar]
- Wei, Q.; Lewis, F.L.; Sun, Q.; Yan, P.; Song, R. Discrete-time deterministic Q-learning: A novel convergence analysis. IEEE Trans. Cybern. 2016, 47, 1224–1237. [Google Scholar] [CrossRef]
- Luo, B.; Liu, D.; Huang, T.; Wang, D. Model-free optimal tracking control via critic-only Q-learning. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 2134–2144. [Google Scholar] [CrossRef]
- Vamvoudakis, K.G.; Lewis, F.L. Online actor–critic algorithm to solve the continuous-time infinite horizon optimal control problem. Automatica 2010, 46, 878–888. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, R.; Yu, F.R.; Fu, F.; Yan, Q. QoS Aware Transcoding for Live Streaming in Edge-Clouds Aided HetNets: An Enhanced Actor-Critic Approach. IEEE Trans. Veh. Technol. 2019, 68, 11295–11308. [Google Scholar] [CrossRef]
- Wang, Z.; Dedo, M.I.; Guo, K.; Zhou, K.; Shen, F.; Sun, Y.; Guo, Z. Efficient recognition of the propagated orbital angular momentum modes in turbulences with the convolutional neural network. IEEE Photonics J. 2019, 11, 1–14. [Google Scholar] [CrossRef]
- Schurz, H. Preservation of probabilistic laws through Euler methods for Ornstein-Uhlenbeck process. Stoch. Anal. Appl. 1999, 17, 463–486. [Google Scholar] [CrossRef]
- Shao, K.; Zhu, Y.; Zhao, D. Starcraft micromanagement with reinforcement learning and curriculum transfer learning. IEEE Trans. Emerg. Top. Comput. Intell. 2018, 3, 73–84. [Google Scholar] [CrossRef]
- Garten, F.; Vrijmoeth, J.; Schlatmann, A.R.; Gill, R.E.; Klapwijk, T.M.; Hadziioannou, G. Light-emitting diodes based on polythiophene: Influence of the metal work function on rectification properties. Synth. Met. 1996, 76, 85–89. [Google Scholar] [CrossRef]
- Miao, Y.; Li, J.; Wang, Y.; Zhang, S.; Gong, Y. Simplifying long short-term memory acoustic models for fast training and decoding. In Proceedings of the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016; pp. 2284–2288. [Google Scholar]
- Wang, H.; Gao, Y.; Chen, X.G. Transfer of Reinforcement Learning: The State of the Art. Acta Electron. Sin. 2008, 36, 39–43. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.M.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. In Proceedings of the International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. abs/1509.02971. [Google Scholar]
- Nair, A.; McGrew, B.; Andrychowicz, M.; Zaremba, W.; Abbeel, P. Overcoming exploration in reinforcement learning with demonstrations. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–26 May 2018; pp. 6292–6299. [Google Scholar]
- De Hauwere, Y.; Devlin, S.; Kudenko, D.; Nowé, A. Context-sensitive reward shaping for sparse interaction multi-agent systems. Knowl. Eng. Rev. 2016, 31, 59–76. [Google Scholar] [CrossRef]
- Kompella, V.R.; Stollenga, M.; Luciw, M.; Schmidhuber, J. Continual curiosity-driven skill acquisition from high-dimensional video inputs for humanoid robots. Artif. Intell. 2017, 247, 313–333. [Google Scholar] [CrossRef]
- Mikhail, F.; Jürgen, L.; Marijn, S.; Alexander, F.; Jürgen, S. Curiosity driven reinforcement learning for motion planning on humanoids. Front. Neurorobotics 2014, 7, 1–15. [Google Scholar]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).