Abstract
Due to the rapid prominence and popularity of social media, social broadcasting networks with voluntary information sharing have become one of the most powerful ways to spread word-of-mouth opinions, and thus, have influence on consumers’ preferences toward products. Therefore, sentiment analysis data from social media have become more important in forecasting product sales. For the movie industry, the opinions expressed on social media have increasing impacts on movie sales. In addition, some databases, such as the Box Office Mojo and Internet Movie Database (IMDb), contain structured data for predicting movie sales. Thus, three categories of data—data of movie databases, data of tweets, and hybrid data including movies databases and tweets—are employed symmetrically in this study. The aim of this study is to employ the least squares support vector regression (LSSVR) to forecast movie sales worldwide according to these three forms of data. In addition, three other forecasting techniques—namely, the back propagation neural network (BPNN), the generalized regression neural network (GRNN), and the multivariate linear regression (MLR) model—were used to forecast movie sales with the three types of data. The empirical results show that the LSSVR model with hybrid data can obtain more accurate results than the other forecasting models with all data types. Thus, forecasting movie sales using the LSSSVR model with data containing movie databases and tweets is a feasible and prospective method to forecast movie sales.
1. Introduction
Due to the booming popularity of the Internet, people have become accustomed to expressing opinions through social media, which has subsequently become a crucial communication channel among consumers. Therefore, social media data is one of the most essential tools in learning consumers’ preferences, and data gathered from social media have become very important in terms of data sources. Text is one of the major data forms appearing on social media, such as Twitter and Facebook, and thus, sentiment analysis is an effective way to obtain some insight from text on social media. Pai and Liu [1] used the sentiment analysis of tweets and stock market values to predict vehicle sales, and the numerical results indicated that the use of hybrid data can result in a satisfying forecasting performance. Kang et al. [2] employed tweets and semantic analysis to investigate vaccine opinions, which were divided into positive, negative, and neutral, and the results showed that the use of semantic analysis is an effective method to learn vaccine willingness. Giatsoglou et al. [3] used four review datasets to forecast the emotions of comments on websites in Greek and English, where an in-house Greek dictionary and an English emotional dictionary from the Word–Emotion Association Lexicon were used as basic databases to analyze emotion words and sentences in Greek and English. Xu et al. [4] developed a self-learning convolutional neural network framework for clustering short texts and optimal clusters, which can be obtained by K-means approaches. The experimental results revealed that the proposed framework is an effective and flexible method to cluster short text datasets. Tran and Kavuluru [5] utilized short textual descriptions of symptoms from historical psychotic patients to predict a set of common mental conditions, where two deep neural networks, namely, convolutional neural networks and recurrent neural networks with hierarchical attention, were employed in the investigation. The numerical results showed that the proposed methods provide feasible and effective ways of analyzing the short textual history of symptoms for psychiatric evaluation. Oliveira et al. [6] employed Sina microblog sentiment data to forecast stock market indices, including return on investment, stock volatility, and trading volume, and the numerical results indicated that microblogging data is able to predict stock market behaviors. Leitch and Sherif [7] used sentiment Twitter scores to study the relationship between the successions of chief executive officers and stock returns in both the U.K. and U.S.A, and the results of that investigation illustrated a positive and highly significant relationship between CEO age at announcement and stock returns. Li et al. [8] analyzed sentimental texts from Chinese microblogging systems to predict the emotions of emergency disaster-related events, where the emotional lexicon was collected from COAE2014 (6th China Opinion Analysis and evaluation). Experimental results revealed that the developed model was feasible and effective for these two real-world datasets. Poria et al. [9] designed a deep convolutional neural network with linguistic patterns to analyze customers’ opinions of products or services by aspect extraction, and the experimental outcomes indicated that the proposed model could obtain more accurate results than the other state-of-the-art techniques. Corea [10] employed English tweets to predict the emotions of the stock investors of three companies, namely, Apple, Facebook, and Google, and the results showed that the posting volume of tweets is an essential factor in increasing the accuracy of forecasting. Huberty [11] designed a naive Bayes classifier, and used tweets to predict the election results in the United States, Germany, and other democratic countries. The numerical results revealed that the proposed model can achieve very satisfactory forecasting accuracy, and thus, is a feasible way to predict election results. Li and Wu [12] integrated support vector machines and K-means to analyze the emotion of comments from the Sina sports forum, and obtained the emotional polarities of the texts. The experimental results revealed that the forecasting accuracy generated by the developed model is satisfactory.
The literature of forecasting movie sales is sequentially addressed as follows: Ma et al. studied the influences of movie reviews on movie sales, and reported that advertising reviews have more impact on the movie opening time; however, the influence decreases within two weeks after the release of the movie. Ru et al. [13] employed LSTM networks to forecast daily box office performance with both dynamic data and static data, and the numerical results indicated that LSTM networks outperformed the multilayer perceptron neural networks and support vector regression models in terms of forecasting accuracy. Baek et al. [14] studied the impacts of four social media sites on box office revenues in the early and later stages of movie opening periods, and the findings revealed that Twitter has more of an influence on box office revenue in the early stage of movie opening periods, while Yahoo! Movies has a greater impact in the late stage of a movie’s opening. In addition, this study showed that there are no impact differences between blogs and YouTube on box office revenues in both the initial and the later periods. Lee et al. [15] investigated the impact of emotional entropy on the relationship between word-of-mouth and movie box office sales, and found that the strength of entropy obtained from reviews positively influences the relationship between word-of-mouth and movie box office sales. Ding et al. [16] studied the impact of “likes” provided by Facebook on box office sales. The “likes” were collected in five different time intervals before movies were released, and the results indicated that “likes” have a highly positive impact on box office performance. Hur et al. [17] integrated machine learning approaches with the independent subspace method to forecast box office performance by using the sentiments of movie reviews. They found that the proposed models were able to obtain accurate and robust forecasting results for different forecasting periods. Kim et al. [18] employed machine learning-based techniques with social network service data to predict box office performance, where genetic algorithms were applied for selecting the essential input variables for the proposed models. The empirical results revealed that the designed box office performance forecasting framework has achieved obvious improvements in terms of forecasting accuracy. Gopinath et al. [19] investigated the influences of pre-and post-release blog volume, blog valence, and advertising on opening day box office performance one month later in various geographic markets. Multivariate regression models were employed to analyze the collected data, and the numerical results revealed that the number of blogs and advertisements are critical for box offices in the pre-release periods, while the blog valence and user ratings are important for box offices in the post-release periods. Rui et al. [20] used the dynamic panel data model, support vector machines, naive Bayesian methods, and tweets to predict the impact of word-of-mouth on movie sales, and found that its influence was proportional to the number of followers. Karniouchina [21] analyzed the impact of buzz on movie distribution and box office income, and the results showed that it helps movie fans to anticipate the film before its release. Chakravarty et al. [22] investigated the influence of online users’ comments on the box office of forthcoming movies, and three hypotheses were tested. This study concluded that positive reviews may be drowned out by negative reviews, and thus, negative reviews are crucial and should receive greater attention. Mishne and Glance [23] employed correlation analysis with blogger sentiment to predict movie sales, and the results indicated that sentiment could be an effective variable in forming a model for predicting movie sales. Liu [24] studied the influence of word-of-mouth on movie box office revenues, and the numerical results revealed that the impact of word-of-mouth is relatively essential in the movie’s prerelease week and the first opening week. In the previous literature review, the positive influences of social media data on forecasting tasks was predominantly examined. However, influences of social media data, structured data and hybrid data on movie sales predictions were rarely investigated. In addition, the least square support vector regression [25] has been a prevailing technique in dealing with multivariate regression problems [26]. Thus, the aim of this study is to employ the least square support vector regression to predict movie sales by using different data types symmetrically. Three other forecasting models were employed to deal with the same data sets to compare and analyze the results. The rest of this study is organized as follows: Section 2 introduces the least square support vector regression method and the architecture of forecasting movie sales. The numerical results are demonstrated in Section 3, and Section 4 elucidates conclusions.
2. The Developed Movie Sales Forecasting Architecture
2.1. The Least Square Support Vector Regression
To reduce computation complexity, the least square support vector regression presented an improvement from the support vector regression by solving a linear problem, instead of dealing with the convex quadratic programming problem. The support vector regression [27,28,29] originates in support vector machines [30,31], which are designed to solve binary classification problems, and then, extended to regression functions. While the LSSVR has been applied in dealing with regression forecasting problems [26], it has received little attention for forecasting movie sales in the multivariate form. The LSSVR is briefly explained as follows: for a training data set TD, including m data points,
where and represent the input data and output data, respectively. The least square support vector regression can be transformed into an optimization model for representation, which is expressed as follows [25]:
subject to
where is the weighted vector or the norm of the hyperplane, is a regularization factor that trades the minimization of the estimation error off against the function smoothness, is the error variable, is the mapping function, mapping from the original space into a high dimension feature space, and b represents a bias parameter. By using the Lagrange multiplier method, the optimization problem can be reformulated to find solutions of w and µ, as follows:
where indicate Lagrange multipliers.
By partially differentiating L with respect to variables , b, µ, and λ, s, and setting all partial derivatives equal to zero, the solution of the problem can be obtained according to the Karush–Kuhn–Tucker conditions [32,33,34]. Thus, Equations (4)–(7) are derived.
Sequentially, solving Equations (4)‒(7) by the least squares method, the solution of the LSSVR can be generated in the following form:
where is the kernel function satisfying the Mercer’s condition [35]. Some options, such as the Gaussian kernel function, the polynomial kernel function, and the sigmoid kernel function, are candidates for kernel functions. The Gaussian kernel function, as represented by Equation (9), was used as the kernel function for this study.
2.2. The Proposed Architecture for Forecasting Movie Sales
Figure 1 illustrates the proposed architecture for forecasting movie sales. Both structured data and unstructured data were collected in this study. The structured data include data from Box Office Mojo and the Internet Movie Database, and the unstructured data were gathered from tweets related to the investigated movies. From the Box Office Mojo website (http://www.boxofficemojo.com), ranks, titles, release dates, worldwide box office, distributors, genres, MPAA (Motion Picture Association of America) ratings were collected, while two data, runtime and budgets, were collected from the IMDB (http://www.imdb.com/) website. As some values of runtime and budget cannot be obtained from Box Office Mojo during the study period, these two data sets were generated from IMDB. The ranks of movie sales were used to select the top 150 movies in terms of worldwide movie sales from 2010 to 2017. Moreover, this study collected movies released on Fridays in U.S. time, and a total of 128 movie data were gathered. In addition, movie titles and release dates were employed for collecting tweets. The worldwide box office was treated as the dependent variable. The other five data sets, namely, distributors, genres, MPAA ratings, runtime, and budget, served as a set of independent variables. Movies titles were used as keywords to collect tweets three days before the films’ release dates. Figure 2 shows the time period of tweets collection. The sentiment scores of tweets, as calculated by SentiStrength [36,37], were the other set of independent variables. Before conducting SentiStrength, the data preprocessing procedure of tweets was performed. Only comments in tweets were collected, thus, texts with the same contents as advertising texts were deleted. The noisy data of dates, user names, forwarding numbers, websites, single quotation marks, semicolons, and symbols were filtered out. The cleaned tweets were employed by SentiStrength, and sentiment scores were calculated. SentiStrength provides positive sentiment scores from 1 to 5 and negative sentiment scores from −1 to −5 to indicate the various positive and negative sentiment strengths of the texts, and assigned scores. The score of 0 does not exist, thus, the scores 1 and −1 represent neutral sentiments. Table 1 shows the statements of the variables used in this study, where three types of data, namely, data of movie databases, data of tweets, and hybrid data, were employed to predict movie sales. The hybrid data consists of the data of movie databases and the data of tweets.
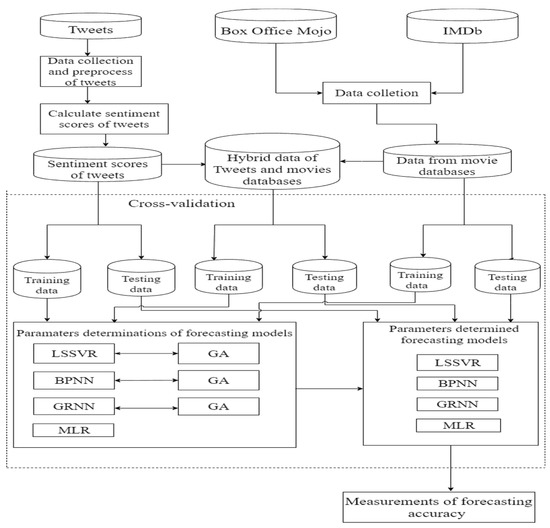
Figure 1.
The developed movie sales forecasting architecture.
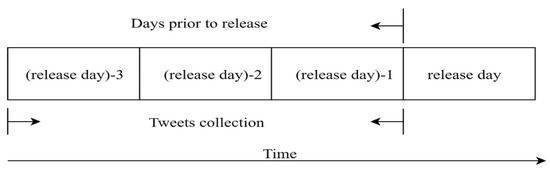
Figure 2.
The time period of tweets collection.

Table 1.
Statements of variables.
Furthermore, a 10-fold cross-validation procedure was conducted in this study to investigate the forecasting performances of forecasting models. The data number is 13 for the eight data subsets and 12 for the two data subsets. Three other forecasting models, namely, the back propagation neural network [38], the generalized regression neural network [39], and the multivariate linear regression method, were used to deal with the same data sets in this study. In this study, the architecture of the back propagation neural network is one hidden layer with ten hidden nodes. The genetic algorithms [40] were employed to determine the parameters of the least squares support vector regression, the back propagation neural networks, and the generalized regression neural networks, by using training forecasting errors as the fitness function. The parameters selected by the genetic algorithms of the three forecasting models were the regularization factor and the width parameter of the Gaussian kernel function of the LSSVR models, the learning rate and the momentum of the BPNN models, and the smoothing parameter of the GRNN models. In this study, the parameters are represented by a chromosome including 40 genes in the form of binary numbers, the population size is 10, and the crossover and mutation rates are 0.5 and 0.7, respectively.
3. Numerical Results
The results of the predicted movie sales are presented in this section. The average absolute percentage error (MAPE) and the root mean square error (RMSE), illustrated as Equations (10) and (11), respectively, were used to investigate the forecasting performances of the forecasting models. Figure 3 and Figure 4 illustrate the average MAPE and RMSE values of the 10-fold cross-validation, as provided by the four forecasting models. Table 2 indicates the averages of the MAPE and RMSE of the four forecasting models.
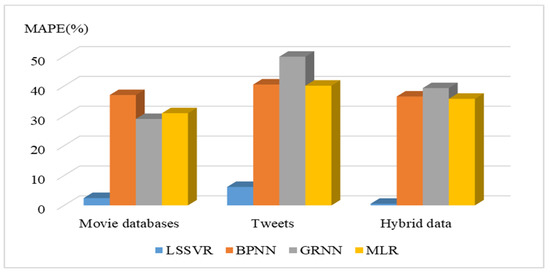
Figure 3.
Average absolute percentage error (MAPE(%)) values obtained by four forecasting models with three data sources.
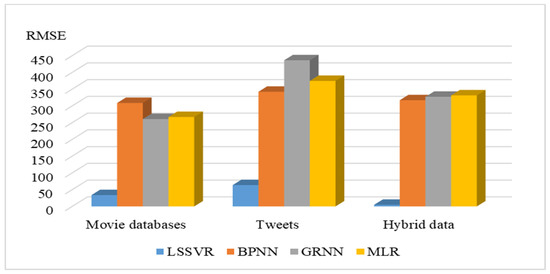
Figure 4.
Average root mean square error (RMSE) values obtained by four forecasting models with three data sources.

Table 2.
Average forecasting accuracy measurements generated by four models with three data types and 10-folds cross-validation.
4. Conclusions
This study proposed a framework using data from Twitter and movie databases to predict movie sales with several forecasting models. Genetic algorithms were employed to determine the parameters of the least squares support vector regression, the back propagation neural network, and the generalized regression neural networks. Two single data types, collected from movie databases and tweets, and one hybrid data type, including movie databases and tweets, were used to examine the influences of various data types on different forecasting models. The numerical results indicated that using the LSSVR with GA to forecast movie sales can result in the best forecasting performance in terms of prediction accuracy for the three data types with the four forecasting models. The superior prediction performance of using the LSSVR with GA in forecasting movie sales is most likely due to the use of hybrid data and the forecasting capability of LSSVR models. Thus, using the least squares support vector regression model to forecast movie sales by data from Twitter and movie databases is a feasible and promising alternative in predicting box office performance. The superior performance of LSSVR with GA in predicting movie sales in this study can be concluded as follows: First, the LSSVR is able to capture the nonlinearity of multivariate regression in forecasting box office performance. Secondly, the addition of tweets and sentiment analyses [41,42] does improve the forecasting performance of LSSVR models. In this study, using only movies databases can result in better forecasting performances than using only data from Twitter for the four forecasting models. Moreover, using only movie databases can generate more accurate forecasting results than using the hybrid data with the GRNN and MLR models. Thus, this finding indicates that the traditional structured data, such as movie databases, cannot be underestimated for some models in forecasting movie sales. However, limitations of this finding arise from methods used in this study. Only four models were employed to analyze the forecasting movie sales by different data types. Possibly a more general conclusion could be reached by applying more forecasting models to cope with the same data sets.
For future work, the expansion of data collection in both structured and unstructured data to improve forecasting performance may be a possible direction. For structured data, in addition to movie databases, some global economic indicators could be included. In the unstructured data aspect, other social media, such as Instagram, Facebook, and the comments of movie trailers on YouTube, could be gathered to forecast box office performance. In addition, the effectiveness of social media data on the forecasting accuracy improvement for different problems is crucial. Thus, another possible direction for future study could be to analyze influences of social media data, structured data and hybrid data on forecasting accuracy for various problem domains.
Author Contributions
Conceptualization, P.-F.P.; Data curation, Y.-T.H.; Formal analysis, P.-F.P.ai and Y.-T.H.; Funding acquisition, P.-F.P.; Methodology, P.-F.P. and Y.-T.H.; Software, Y.-T.H.; Visualization, P.-F.P.; Writing—original draft, P.-F.P. and Y.-T.H.; Writing—review and editing, P.-F.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Ministry of Science and Technology, Taiwan under Contract Numbers MOST105-2410-H-260-017-MY2 and MOST107-2410-H-260-012.
Acknowledgments
The authors would like to thank Wei-Cheng Lo and Sheng-Hong Dai who assisted with data collection and analysis.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pai, P.-F.; Liu, C.-H. Predicting vehicle sales by sentiment analysis of Twitter data and stock market values. IEEE Access 2018, 6, 57655–57662. [Google Scholar] [CrossRef]
- Kang, G.J.; Ewing-Nelson, S.R.; Mackey, L.; Schlitt, J.T.; Marathe, A.; Abbas, K.M.; Swarup, S. Semantic network analysis of vaccine sentiment in online social media. Vaccine 2017, 35, 3621–3638. [Google Scholar] [CrossRef] [PubMed]
- Giatsoglou, M.; Vozalis, M.G.; Diamantaras, K.; Vakali, A.; Sarigiannidis, G.; Chatzisavvas, K.C. Sentiment analysis leveraging emotions and word embeddings. Expert Syst. Appl. 2017, 69, 214–224. [Google Scholar] [CrossRef]
- Xu, J.; Xu, B.; Wang, P.; Zheng, S.; Tian, G.; Zhao, J. Self-taught convolutional neural networks for short text clustering. Neural Netw. 2017, 88, 22–31. [Google Scholar] [CrossRef] [PubMed]
- Tran, T.; Kavuluru, R. Predicting mental conditions based on “history of present illness” in psychiatric notes with deep neural networks. J. Biomed. Inform. 2017, 75, S138–S148. [Google Scholar] [CrossRef]
- Oliveira, N.; Cortez, P.; Areal, N. The impact of microblogging data for stock market prediction: Using Twitter to predict returns, volatility, trading volume and survey sentiment indices. Expert Syst. Appl. 2017, 73, 125–144. [Google Scholar] [CrossRef]
- Leitch, D.; Sherif, M. Twitter mood, CEO succession announcements and stock returns. J. Comput. Sci-Neth. 2017, 21, 1–10. [Google Scholar] [CrossRef]
- Li, Q.; Jin, Z.; Wang, C.; Zeng, D.D. Mining opinion summarizations using convolutional neural networks in Chinese microblogging systems. Knowl-Based. Syst. 2016, 107, 289–300. [Google Scholar] [CrossRef]
- Poria, S.; Cambria, E.; Gelbukh, A. Aspect extraction for opinion mining with a deep convolutional neural network. Knowl-Based. Syst. 2016, 108, 42–49. [Google Scholar] [CrossRef]
- Corea, F. Can twitter proxy the investors’ sentiment? The case for the technology sector. Big Data Research 2016, 4, 70–74. [Google Scholar] [CrossRef]
- Huberty, M. Can we vote with our tweet? On the perennial difficulty of election forecasting with social media. Int. J. Forecast. 2015, 31, 992–1007. [Google Scholar] [CrossRef]
- Li, N.; Wu, D.D. Using text mining and sentiment analysis for online forums hotspot detection and forecast. Decis. Support Syst. 2010, 48, 354–368. [Google Scholar] [CrossRef]
- Ru, Y.; Li, B.; Liu, J.; Chai, J. An effective daily box office prediction model based on deep neural networks. Cogn. Syst. Res. 2018, 52, 182–191. [Google Scholar] [CrossRef]
- Baek, H.; Oh, S.; Yang, H.-D.; Ahn, J. Electronic word-of-mouth, box office revenue and social media. Electron. Commer. R. A. 2017, 22, 13–23. [Google Scholar] [CrossRef]
- Lee, J.H.; Jung, S.H.; Park, J. The role of entropy of review text sentiments on online WOM and movie box office sales. Electron. Commer. R. A. 2017, 22, 42–52. [Google Scholar] [CrossRef]
- Ding, C.; Cheng, H.K.; Duan, Y.; Jin, Y. The power of the “like” button: The impact of social media on box office. Decis. Support Syst. 2017, 94, 77–84. [Google Scholar] [CrossRef]
- Hur, M.; Kang, P.; Cho, S. Box-office forecasting based on sentiments of movie reviews and Independent subspace method. Inform. Sci. 2016, 372, 608–624. [Google Scholar] [CrossRef]
- Kim, T.; Hong, J.; Kang, P. Box office forecasting using machine learning algorithms based on SNS data. Int. J. Forecast. 2015, 31, 364–390. [Google Scholar] [CrossRef]
- Gopinath, S.; Chintagunta, P.K.; Venkataraman, S. Blogs, advertising, and local-market movie box office performance. Manag. Sci. 2013, 59, 2635–2654. [Google Scholar] [CrossRef]
- Rui, H.; Liu, Y.; Whinston, A. Whose and what chatter matters? The effect of tweets on movie sales. Decis. Support Syst. 2013, 55, 863–870. [Google Scholar] [CrossRef]
- Karniouchina, E.V. Impact of star and movie buzz on motion picture distribution and box office revenue. Int. J. Res. Mark. 2011, 28, 62–74. [Google Scholar] [CrossRef]
- Chakravarty, A.; Liu, Y.; Mazumdar, T. The differential effects of online word-of-mouth and critics’ reviews on pre-release movie evaluation. J. Interact. Mark. 2010, 24, 185–197. [Google Scholar] [CrossRef]
- Mishne, G.; Glance, N.S. Predicting movie sales from blogger sentiment. In Proceedings of the AAAI Spring Symposium: Computational Approaches to Analyzing Weblogs, Stanford, CA, USA, 27–29 March 2006; pp. 155–158. [Google Scholar]
- Liu, Y. Word of mouth for movies: Its dynamics and impact on box office revenue. J. Mark. 2006, 70, 74–89. [Google Scholar] [CrossRef]
- Suykens, J.A.; Vandewalle, J. Least squares support vector machine classifiers. Neural Process Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Pai, P.-F.; Hong, L.-C.; Lin, K.-P. Using internet search trends and historical trading data for predicting stock markets by the least squares support vector regression model. Comput. Intel. Neuros. 2018, 2018, 6305246. [Google Scholar] [CrossRef]
- Mukherjee, S.; Osuna, E.; Girosi, F. Nonlinear prediction of chaotic time series using support vector machines. In Proceedings of the Neural Networks for Signal Processing VII, Amelia Island, FL, USA, 24–26 September 1997; pp. 511–520. [Google Scholar]
- Müller, K.-R.; Smola, A.J.; Rätsch, G.; Schölkopf, B.; Kohlmorgen, J.; Vapnik, V. Predicting time series with support vector machines. In Proceedings of the International Conference on Artificial Neural Networks, Munich, Germany, 17–19 September 2019; pp. 999–1004. [Google Scholar]
- Vapnik, V.; Golowich, S.E.; Smola, A.J. Support vector method for function approximation, regression estimation and signal processing. In Proceedings of the Advances Neural Information Processing System, Denver, CO, USA, 2‒6 December 1997; pp. 281–287. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. MLear 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Fletcher, R. Practical Methods of Optimization; Wiley: Hoboken, NJ, USA, 1987; pp. 80–94. [Google Scholar]
- Karush, W. Minima of Functions of Several Variables with Inequalities As Side Conditions. Master’s Thesis, University of Chicago, Chicago, IL, USA, 1939. [Google Scholar]
- Kuhn, H.W.; Tucker, A.W. Nonlinear programming. In Proceedings of the 2nd Berkeley Symposium on Mathematical Statistics and Probabilities, Berkeley, CA, USA, 31 July–12 August 1951; pp. 481–492. [Google Scholar]
- Mercer, J. Functions of Positive and Negative Type and Their Connection with the Theory of Integral Equations. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 1909, 209, 415–446. [Google Scholar]
- Thelwall, M.; Buckley, K.; Paltoglou, G.; Cai, D.; Kappas, A. Sentiment strength detection in short informal text. JASIS 2010, 61, 2544–2558. [Google Scholar] [CrossRef]
- Thelwall, M.; Buckley, K.; Paltoglou, G. Sentiment strength detection for the social web. JASIS 2012, 63, 163–173. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Specht, D.F. A general regression neural network. IEEE Trans. Neural Netw. 1991, 2, 568–576. [Google Scholar] [CrossRef] [PubMed]
- Holland, J. Adaptation in Natural and Arti_cial Systems: An Introductory Analysis with Applications to Biology, Control, and Artifcial Intelligence; University of Michigan Press: Ann Arbor, MI, USA, 1975; pp. 439–444. [Google Scholar]
- Arias, M.; Arratia, A.; Xuriguera, R. Forecasting with Twitter data. ACM Trans. Intell. Syst. 2013, 5, 1–24. [Google Scholar] [CrossRef]
- Maqsood, H.; Mehmood, I.; Maqsood, M.; Yasir, M.; Afzal, S.; Aadil, F.; Selim, M.M.; Muhammad, K. A local and global event sentiment based efficient stock exchange forecasting using deep learning. Int. J. Inf. Manag. 2020, 50, 432–451. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).