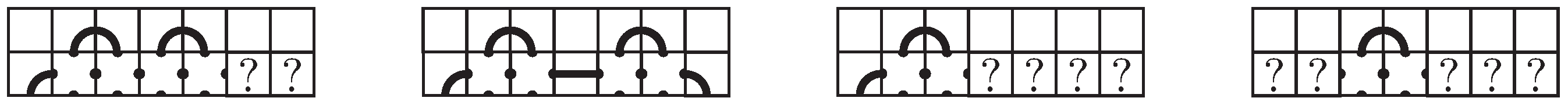In this section, we will prove Theorem 1. As we progress toward this goal, we first provide some useful terms and observations that we will make use of as we attempt to create space-efficient mosaics and count the number of non-blank tiles needed to create them.
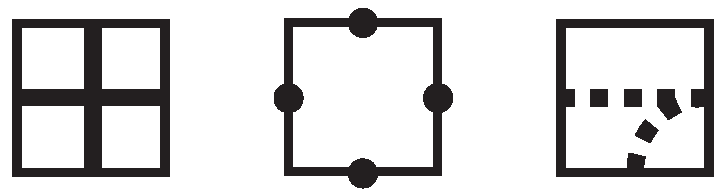
Suppose there are two adjacent single arc tiles,
,
,
, or
, that share a connection point, and the other connection points enter the same adjacent row or column. The four options are shown in
Figure 10, and we will refer to these collectively as
caps and individually as
top caps,
right caps,
bottom caps, and
left caps, respectively. We will encounter mosaics that have pieces that are similar to caps but with line segment tiles,
or
, between the arc tiles or pieces that can be easily changed to these via planar isotopy moves. We will call these
reducible caps and define them to be a collection of suitably connected tiles with no crossing tiles that are, or can be changed via planar isotopy moves to, two single arc tiles that are connected by line segment tiles and whose other connection points enter the same adjacent row or column. Essentially, a reducible cap can meander around but can easily be reduced to a reducible cap that does not meander, such as the last example in
Figure 10, which could be simplified to the fifth example.
This first observation tells us that we can create all of our space-efficient knot mosaics without using the corner tile locations, the first and last tiles in the first row and last row of the mosaic. Because the outer rows and columns need not be occupied, we may assume that the first tile and the last tile in the first occupied row and column is a blank tile, and similarly for the last occupied row and column.
As we have previously noted, the use of the horizontal and vertical segment tiles, and , are not necessary for create space-efficient mosaics. Once we show this fact, proving Theorem 1 is simple. Observation 3 tells us that and tiles are not needed in the first and last occupied rows and columns. Next, we show that they are not needed in the second and penultimate occupied rows and columns.
The proof of this lemma is quite simple but long because of the accompanying figures that depict the various cases. However, knowing that we do not need to use horizontal and vertical segment tiles in the first two and last two rows and columns greatly reduces the possibilities for the layouts of a space-efficient 7-mosaic.
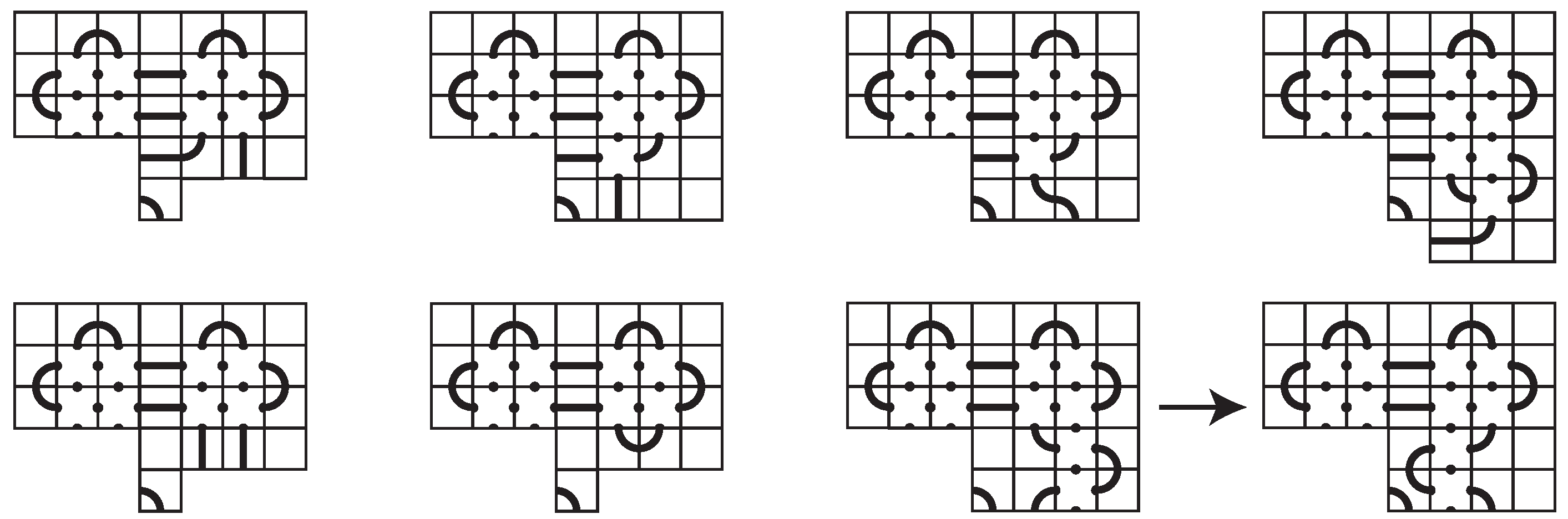
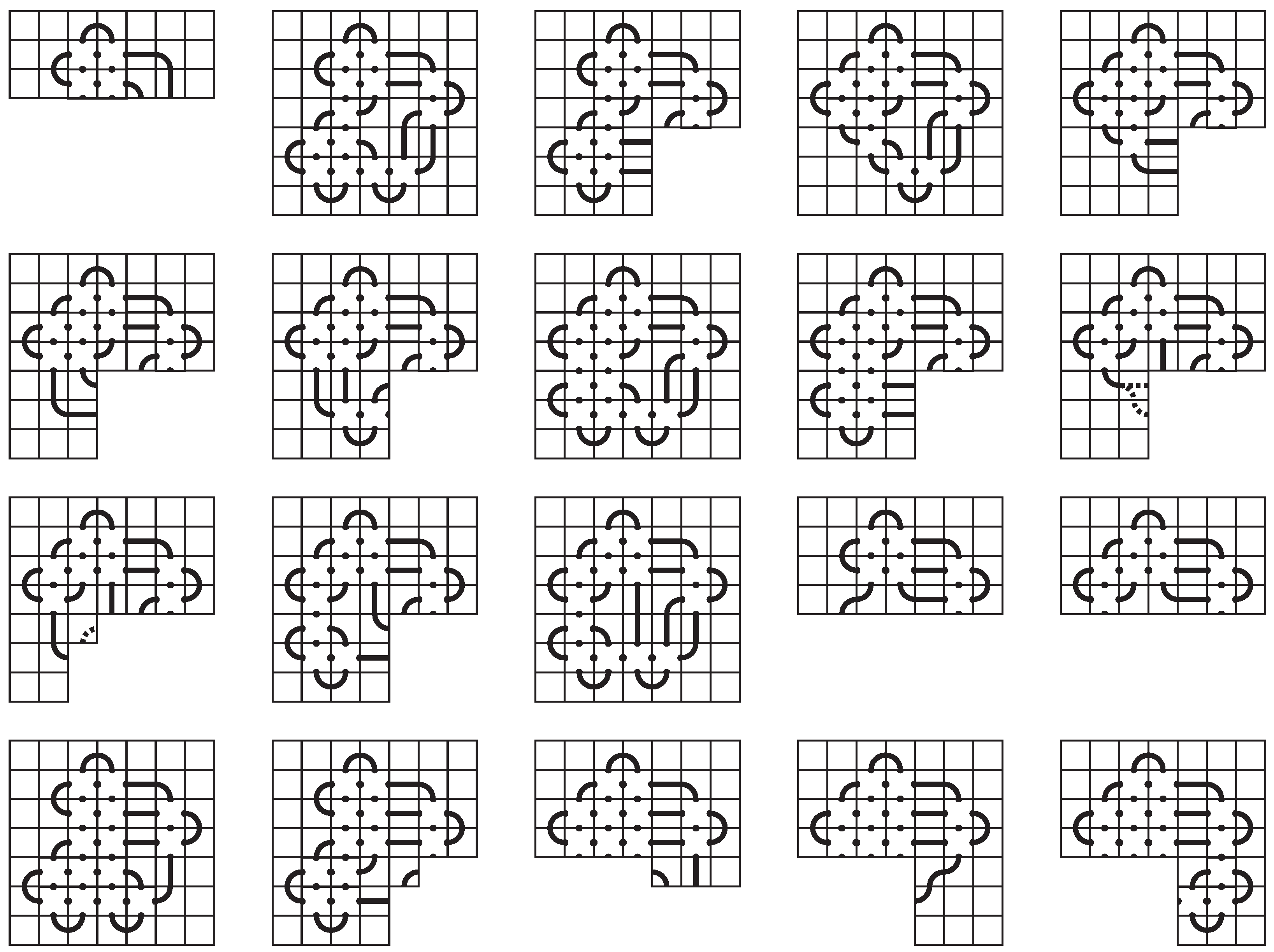
Proof. We prove the lemma for the second occupied row, and the other options follow by rotational symmetry. By Observation 3, the first occupied row only contains one or two top caps, with the rest of the positions filled by blank tiles. By Observation 2, the tile locations directly below these caps must have four connection points, and this also prevents any vertical segment tiles from occurring in the second row. The only options (up to symmetry) for the first two occupied rows are as depicted in
Figure 13. We assume that the first occupied row of the mosaic is actually the top row since, if it is not, we can simply shift all of the tiles of the mosaic upward. In each case below, we will reach a contradiction when we assume that there is a horizontal segment tile in the second row. In most cases, we construct partial mosaics for every possible tile choice until it is obvious that the mosaic is not space-efficient or does not represent a prime knot. We always base our choices on the observations stated above, knowing that the tiles sharing connection points with any cap must have four connection points and avoiding the corner tiles, reducible caps, links, composite knots, and reducible knots.
Case 1: First, we consider the case where there are two consecutive top caps. The first five tile positions in the second row are determined by Observation 2, which also prevents the sixth tile position from being a horizontal segment tile. Otherwise, there would be a cap in the seventh row, which would necessitate a tile with four connection points in the sixth position. Thus the sixth tile must be a single arc tile , and the final tile position must be blank.
Case 2: The next case has two top caps with a blank tile in between them. In this case, the second row is completely determined and must have a horizontal segment tile as seen in
Figure 13. Our claim is that any completion of this mosaic will not be space-efficient or will not represent a prime knot. To see this, we will examine the remaining rows. There is actually only one possibility for the third row as well, which can be seen in the first mosaic of
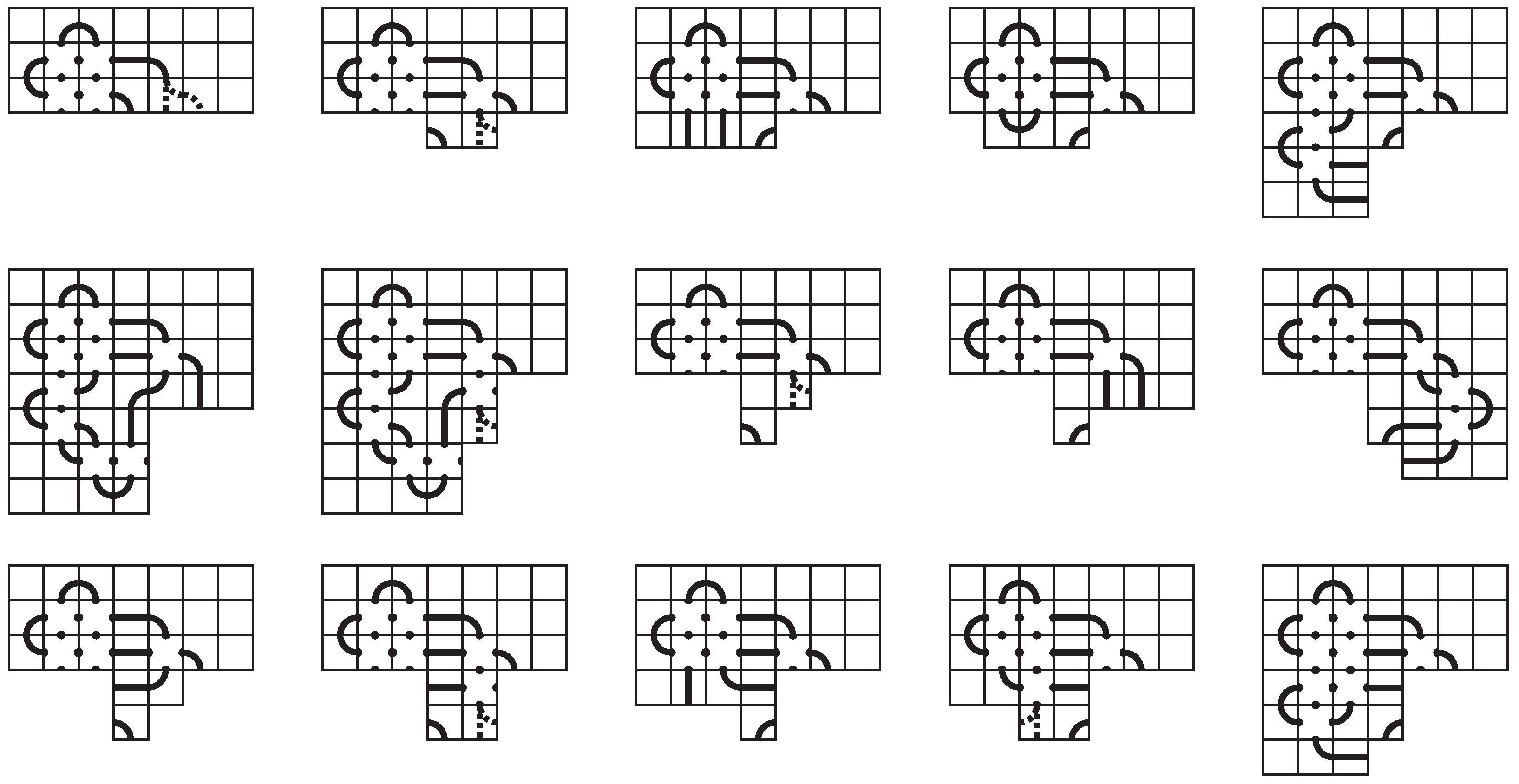
Figure 14. The first and last tiles in the third row must complete a left and right cap, respectively, and the second and sixth tiles must have four connection points. The third and fifth tile positions in the third row must also have four connection points. Otherwise, they would be single arc tiles, and according to Observation 5, any resulting space-efficient mosaic would not represent a prime knot.
We now consider the remaining positions for the middle column. The tile in the fourth position can either be blank, another horizontal tile, or a single arc tile
or
(because of symmetry, the
and
cases are equivalent). If the entire middle column has only blank or horizontal segment tiles, then the mosaic is not space-efficient, as we can collapse this column. That is, there must eventually be a
(or
) single arc tile. This tile clearly cannot be in the sixth row (by Observation 2) or the seventh row. Thus, the only options are as in the second and third mosaic of
Figure 14.
Suppose the tile in the middle position of the fourth row is the single arc tile
, as in the second mosaic of
Figure 14. Because of the locations of connection points and sides of tiles with no connection points, the options are limited. For example, the fifth position in the fourth row can only be a vertical segment tile
or single arc tile
. The vertical segment leads to the first partial mosaic in
Figure 15. If the
tile is used, the tile in the sixth position could be a single arc tile
or a tile with four connection points. The first option is the second partial mosaic in
Figure 15, and the second option leads to the remaining partial mosaics of
Figure 15. All of these depend on the tile in the fifth position of the fifth row, which can be a horizontal tile or a single arc tile
. The last three of these options depend on the third tile position in the fourth row, which can only be a single arc tile
or a tile with four connection points. Filling in a few more tiles around these make it is easy to see that none of these are space-efficient. For the first three, simply slide the right-most tiles to the left by collapsing the horizontal tiles. For the fourth, fifth, and sixth mosaics, slide the upper, left quadrant to the right by collapsing the horizontal segments.
Finally, suppose the tile in the middle position of the fourth row is either blank or a horizontal tile, and the tile in the fifth row, fourth column is the single arc tile
, as in the third mosaic of
Figure 14. There are only seven ways to complete the tile positions to the right of these, and we provide them in
Figure 16. In each case, it is easy to see that the resulting mosaics are not space-efficient. In the first six cases, we simply slide the upper, right quadrant of the mosaics to the left by collapsing all of the horizontal segment tiles. In the case of the seventh mosaic, we can lower the tile number of the mosaic using the planar isotopy given in Observation 4.
Case 3: Now let us consider the case where there is only one top cap in the first occupied row, and it is located in the first two tile positions after the corner tile, as in
Figure 17. Then the first tile in the second occupied row must be a single arc tile
, followed by two tiles with four connection points. There must also be a single arc tile
in this row, but this
tile cannot be part of a right cap (that is, the tile below it is not a
tile). To see this, assume the
tile is part of a right cap. If the
tile is in the fourth tile position of the second row, then, using Observations 2 and 5, it is easy to see that the knot mosaic is either not prime or not space-efficient. If the
tile is in the fifth, sixth, or seventh position, then Observation 2 says the preceding tile position must have four connection points, which contradicts the fact that the first row only has a single top cap.
We now examine the third row. The first tile must complete the left cap with a single arc tile , and the second tile position must have four connection points. The third position must also have four connection points. Otherwise, this tile position would be a single arc tile , and the mosaic would either not be space-efficient or would not represent a prime knot (Observation 5).
For the sake of contradiction, suppose there are horizontal segment tiles in the second row. There clearly cannot be three horizontal segment tiles because this forces the arc tile into the seventh position in this row, which is necessarily part of a right cap, and we have already ruled this out.
If there is only one horizontal segment in the second row, then it must be in the fourth tile position, and the fifth tile position is the arc tile
. We know this is not part of a right cap, and we look at the tiles below the horizontal segment. Directly below the horizontal segment must be a single arc tile
or another horizontal segment tile. The
option, shown in the first mosaic of
Figure 18, is easily simplified to reduce the number of non-blank tiles. For the horizontal segment option, the options are similar to those in Case 2. The tile below it can only be a blank, horizontal segment, or single arc (
or
) tile. Eventually there must be a
or
tile to avoid the possibility of just collapsing the entire column, and this must occur in either the fourth row or the fifth row. With each of these options in mind, the remaining fourteen partially completed mosaics shown in
Figure 18 cover all possibilities in this scenario, and it is again easy to see that none of them are space-efficient.
If there are two horizontal line segments in the second row, they must be in the fourth and fifth tile positions, and the sixth tile position is the single arc tile
. In the third row, the tile in the fourth position must be a single arc tile
or a horizontal segment tile. If it is the
tile, then the fifth position must be blank or the single arc tile
. In either case, shown in the first two mosaics of
Figure 19, it is easy to see that we can eliminate the horizontal segments in the second row without increasing the number of non-blank tiles.
If the tile in the fourth position of the third row is a horizontal segment tile, there are only two ways to complete the third row, and they are depicted in the last two mosaics of
Figure 19. The first one is easily seen to reduce to only one horizontal segment in the second row, which was covered above. The second possibility is also simple to eliminate after we examine a couple of tiles in the fourth row of the mosaic and perform a simple planar isotopy move. The sixth and seventh positions of the fourth row must complete the right cap, and there is an equivalent mosaic, with fewer non-blank tiles, in which the tiles of this right cap are moved into the position of a top cap and the horizontal segments are removed, as shown in
Figure 20.
Case 4: Now we consider the final case, shown in
Figure 21, where there is a single top cap, and it is located in the third and fourth tile positions of the first occupied row. We will assume that the first column is occupied, otherwise a shift of the mosaic to the left would reduce this to Case 3.
It is easy to see that a horizontal segment tile is not allowed in the second or sixth position of the second row, as this would necessarily violate Observation 2. Thus, if there is a horizontal segment tile, the only possibility is for it to be in the fifth position. Just as in previous cases, there must eventually be a single arc tile,
or
, in the fifth column below the horizontal segment. There are twenty possibilities, and they are given in
Figure 22. Each mosaic is either not space-efficient or does not represent a prime knot.
Having completed all four cases, we have shown that any space-efficient 7-mosaic of a prime knot can be simplified so that the second occupied row does not have a horizontal segment tile. □
Now that we have shown that all space-efficient 7-mosaics of prime knots can be created without horizontal or vertical segment tiles in the first two and last two rows and columns, we are ready to turn our focus to proving Theorem 1.
Proof of Theorem 1. We assume we have a space-efficient 7-mosaic of a prime knot for which every row is occupied. The case where every column is occupied is equivalent. Our goal is to show that the only possible layouts for the mosaic are those given in the statement of the theorem or that it is equivalent to one of them via a planar isotopy that does not increase the number of non-blank tiles. The resulting number of non-blank tiles follows immediately.
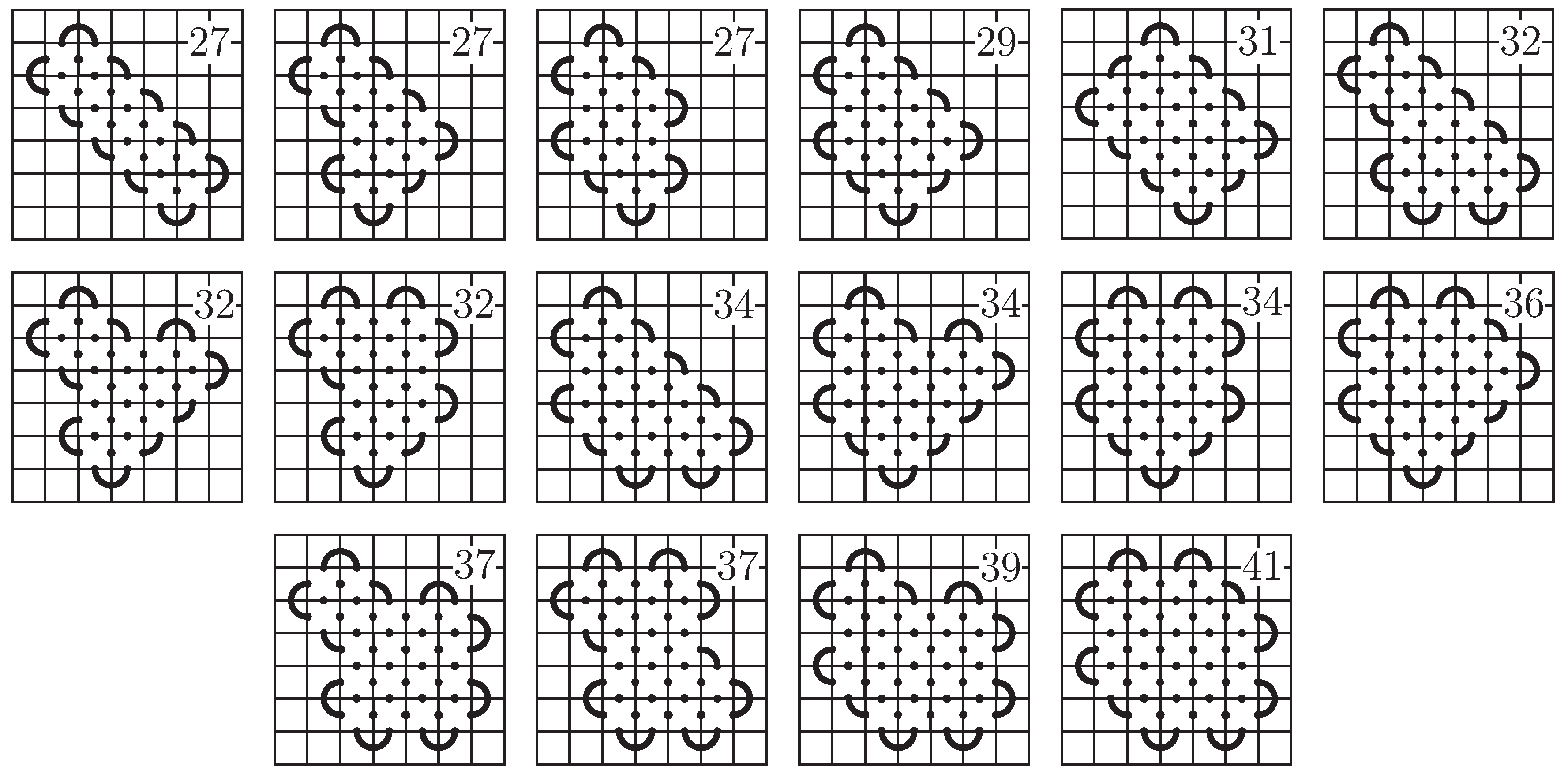
The first and seventh rows of the mosaic have either 2 or 4 non-blank tiles (one or two caps by Observation 3). In either case, we have either 4 or 6 non-blank tiles in the second and sixth rows. In the proof of Lemma 1, we show that there are only three options for the first row. These lead to only four possibilities for the first two rows (up to symmetry), and these are given in
Figure 23.
Assuming the first column is occupied, the options for the first two rows extend to the first two columns. After removing any duplicates that are equivalent up to symmetry, there are nine options for the first two rows and columns of the mosaic. See
Figure 24.
Next, we consider the bottom two rows and the two rightmost columns. We have assumed that all rows are occupied but not necessarily every column. However, in order to avoid composite knots or space-inefficiency, there must be at least four connection points between any two rows (Observation 5), except between the first two and last two rows. Removing options that are equivalent to others via symmetry, we find 20 possibilities for the two outermost rows and columns. See
Figure 25.
Now that we have a complete set of possibilities for the outer shell of a space-efficient 7-mosaic, we want to fill in the inner
block. Some of that can be accomplished using Observation 2. Using Observation 5, we need at least four connection points between each of the middle three rows and columns, and, for example, in the upper, left
block of the first mosaic in
Figure 25, the tile in the third row and third column cannot be a single arc tile
. Therefore, the tile in that location must have four connection points.
These simple observations are applied as we determine the options for filling in the inner
blocks of the mosaics in
Figure 25. For some, there is only one way to complete the mosaic, such as the first, second, third, fourth, eighth, ninth, tenth, and thirteenth mosaic. All of these, except the second one, lead to one of the desired layouts given in the statement of the theorem. The others have more than one possible way to complete them and require further consideration.
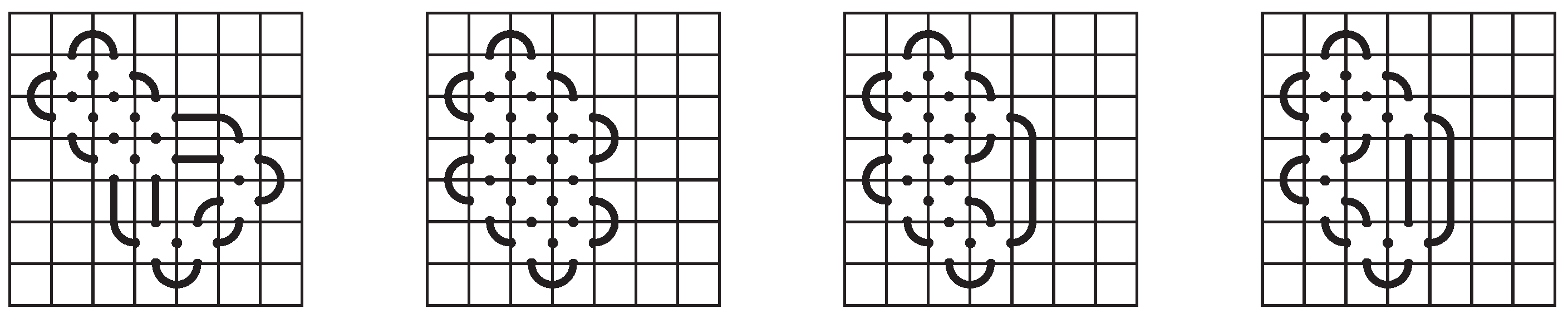
The second outer shell in
Figure 25 must be completed with horizontal or vertical segment tiles, as seen in the first mosaic of
Figure 26. The resulting mosaic is clearly not space-efficient, as we can reduce the number of non-blank tiles with a planar isotopy that shifts the upper, left
block to the right (or down).
For each of the remaining outer shells, if we fill the remaining tile positions of the inner
block, when possible, with tiles that have four connection points, we end up with the remaining layouts given in the statement of the theorem. If we assume that at least one of those tile positions does not have four connection points, there are several possibilities to consider, which we look at next, but each one is either not space-efficient or can be changed to one of the desired layouts without changing the number of non-blank tiles. For example, if we complete the fifth outer shell with tiles that have four connection points when possible, the result is the second mosaic in
Figure 26, which is the third layout given in the statement of the theorem. However, there are two alternative completions, given in the third and fourth mosaics of
Figure 26. In both cases, the vertical segment tiles can be altered by a planar isotopy that changes it to the second mosaic without changing the number of non-blank tiles.
The sixth, seventh, eleventh, twelfth, fifteenth, eighteenth, and twentieth outer shells each have one alternative completion, which are shown in
Figure 27. None of these are space-efficient as each can be simplified to one of the layouts given in the statement of the theorem using the planar isotopy shown in Observation 4.
For the fourteenth and seventeenth outer shells, there are two alternative completions, given in
Figure 28. In each case, the vertical segment tiles can be removed by a planar isotopy without changing the number of non-blank tiles.
The sixteenth outer shell has six alternative completions, and they are given in
Figure 29. The first two are easily simplified, reducing the number of non-blank tiles, using the isotopy of Observation 4. The next three are easily seen to be equivalent to the first two. For the fifth one, just slide the center tile to the right, and the resulting mosaic is identical to the fourth. The sixth alternative can be simplified, as shown, by rotating the tile in the fourth row and second column, which has four connection points, into the fourth row, third column.
Finally, we encounter six alternative completions of the nineteenth outer shell, see in
Figure 30. Each of these are handled in ways similar to the sixteenth outer shell.
This completes our discussion of filling in the outer shells given in
Figure 25. We have exhausted all possibilities of completing a space-efficient 7-mosaic in which all rows are occupied, arriving at those listed in the statement of the theorem. □