Learning the Kinematics of a Manipulator Based on VQTAM
Abstract
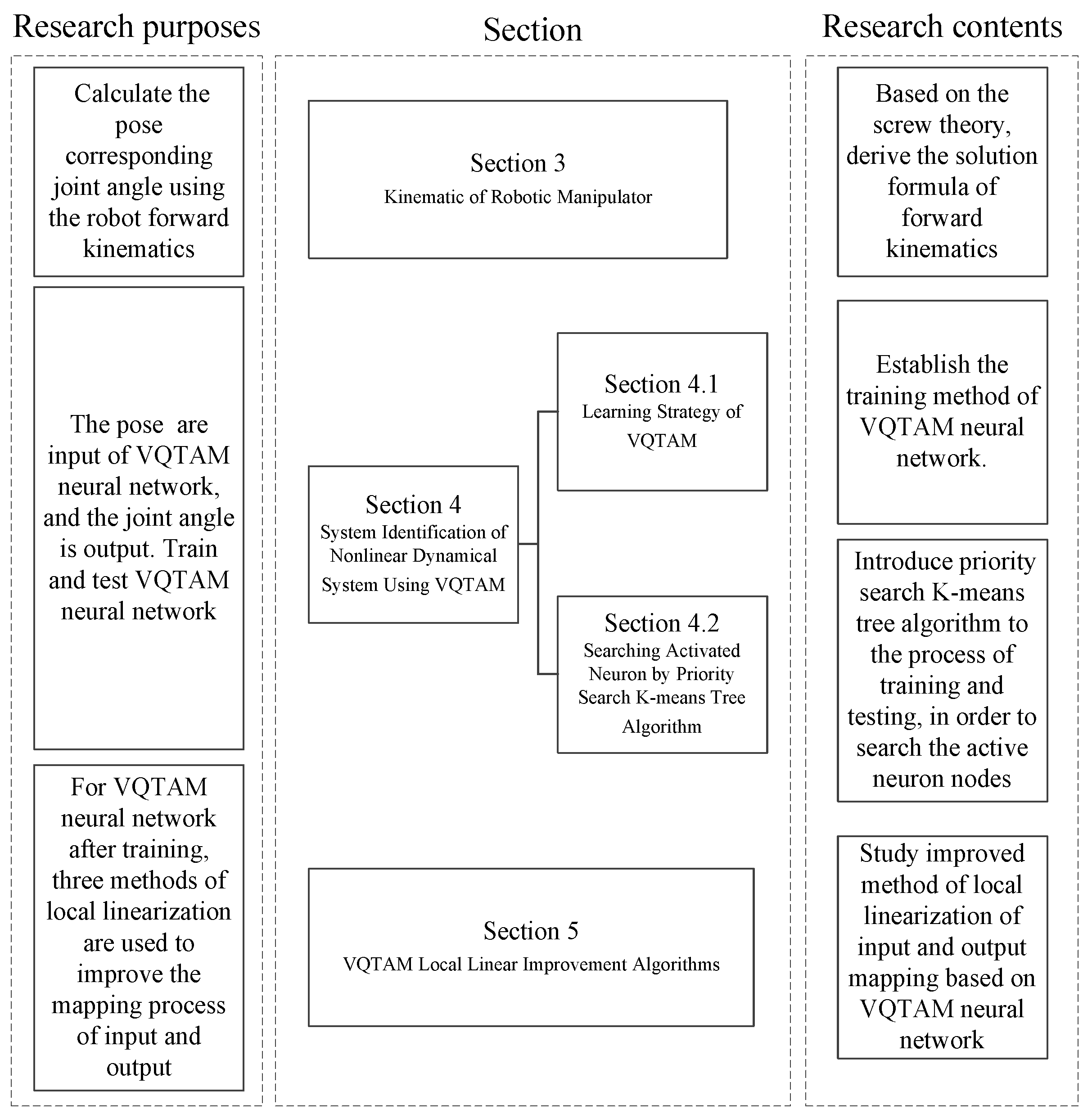
1. Introduction
2. Research Methodology
3. Kinematics of the Robotic Manipulator
- (1)
- The 6-DOF parameter is used to describe the pose relationship between two adjacent coordinate systems completely, thus avoiding the lack of completeness in the D-H model.
- (2)
- The global coordinate system is used to describe the motion state of a rigid body, which overcomes the singularity of the D-H model.
- (3)
- The motion characteristics of rigid bodies can be clearly described from a global perspective, thus simplifying the analysis of complex mechanisms and avoiding the abstraction of mathematical symbols.
4. System Identification of a Nonlinear Dynamical System Using VQTAM
4.1. Learning Strategy of VQTAM
| Algorithm 1: VQTAM Algorithm: |
| Begin |
| (training part) |
| 1 Input: Xin and Xout in training set |
| 2 Search activating neuron according to Xin |
| 3 Update the weight vector of the neuron |
| 4 Continue execution until termination conditions are met |
| (testing part) |
| 5 Input: Xtestin in testing set |
| 6 Search activating neuron according to Xtestin |
| 7 Output: |
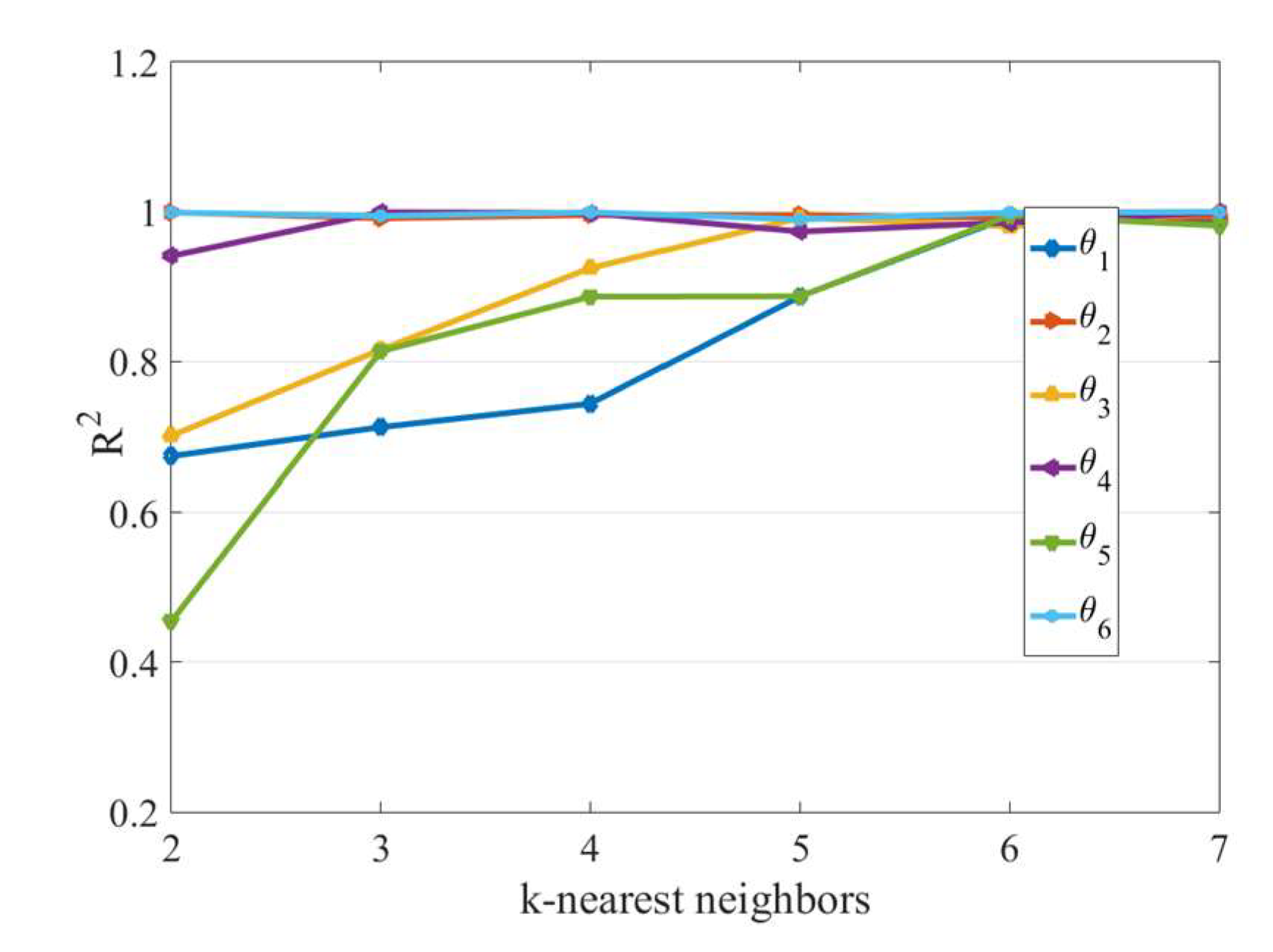
4.2. Searching the Activated Neuron by the Priority Search K-Means Tree Algorithm
| Algorithm 2: K-means tree data structure building Algorithm [32]: |
| Begin |
| 1 Input: weight vector ωiin as search data set D, branch parameter B, maximum iteration number Imax, center selection algorithm using Calg |
| 2 Compare size |D| of data set D with branch parameter B |
| 3 If |D|<B: Create leaf nodes from data sets |
| 4 else, P ← uses Calg algorithm to select B points from data set D |
| 5 start loop: |
| 6 C ← Clustering Data in D Centered on P |
| 7 Pnew ← Finding the Mean Value of Group C Data after Clustering |
| 8 if P = Pnew, Pnew is the non-leaf node, and terminate the loop |
| 9 These processes are executed on the sub-regions C until all leaf nodes are created |
| 10 Output: the entire K-means tree data structure |
| Algorithm 3: PSKMT Algorithm [32]: |
|
5. VQTAM Local Linear Improvement Algorithms
5.1. Improvement Algorithm of VQTAM with LLR
5.2. Improvement Algorithm of VQTAM with LWR
5.3. Improvement Algorithm of VQTAM with LLE
6. Simulation Results and Discussion
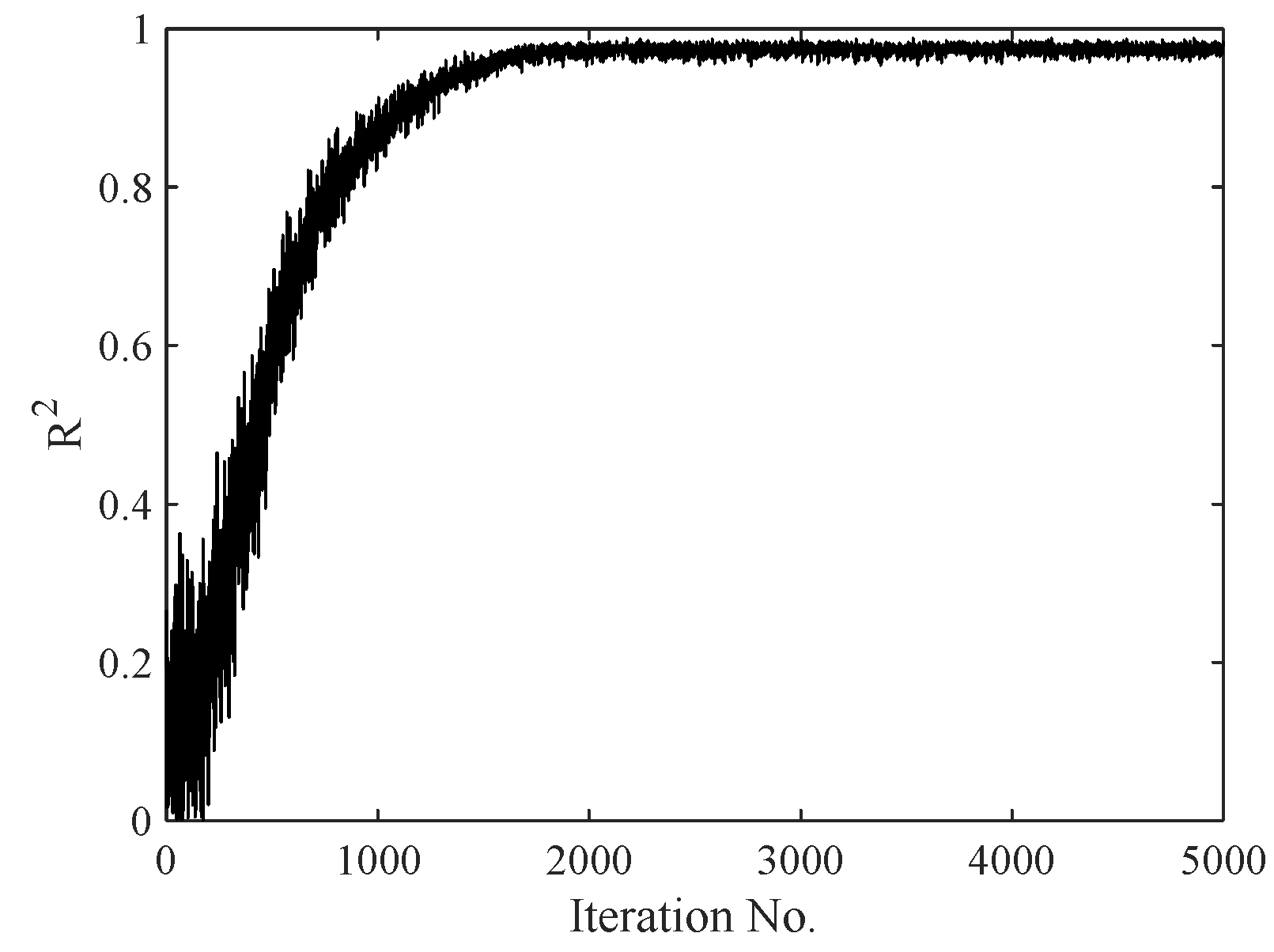
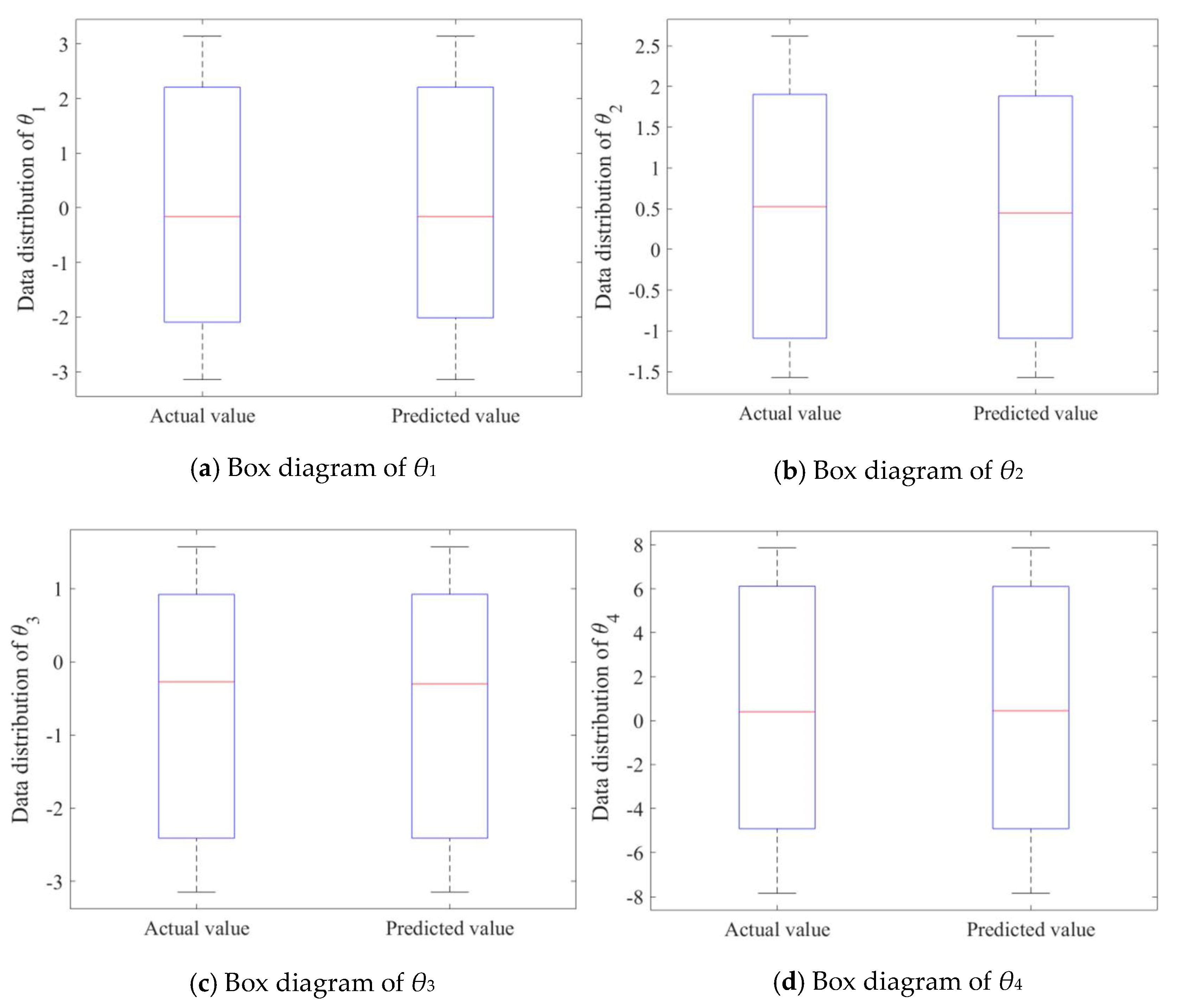
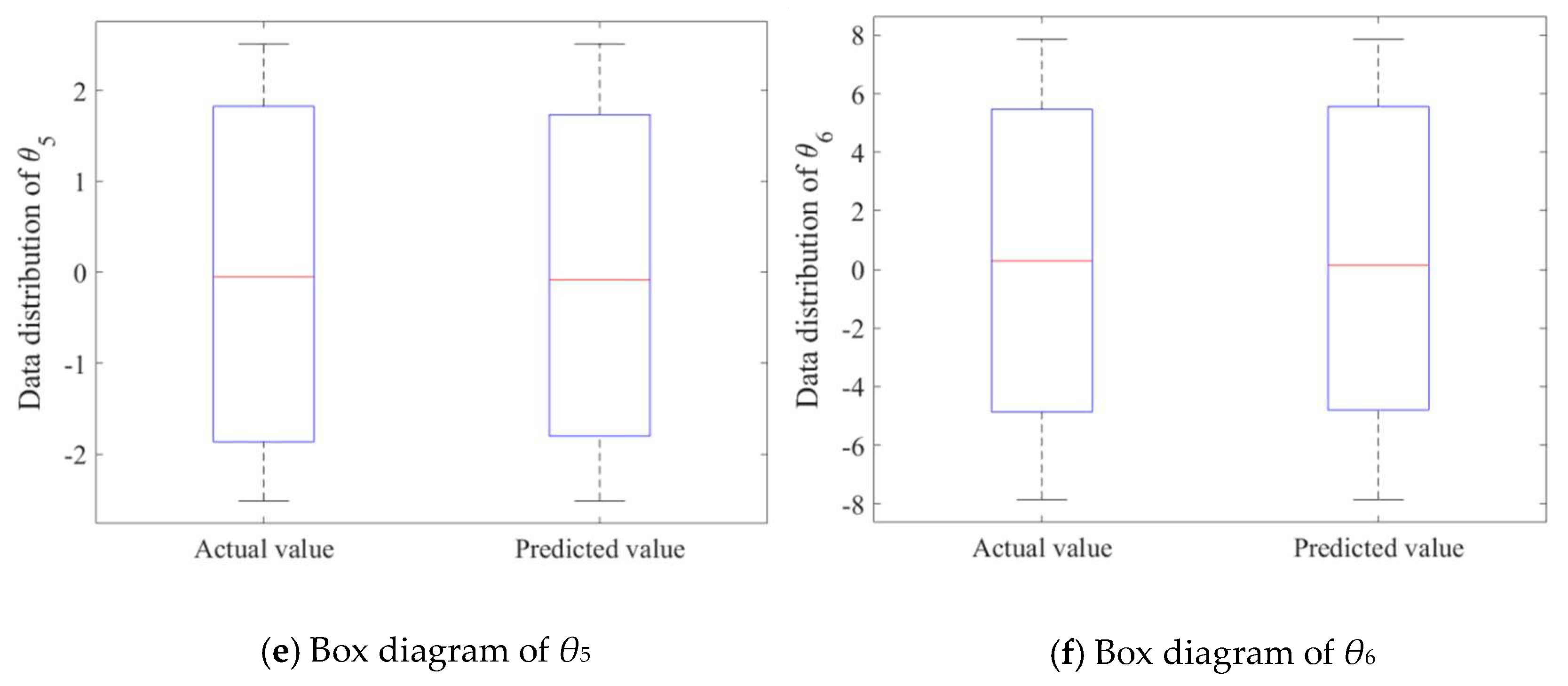
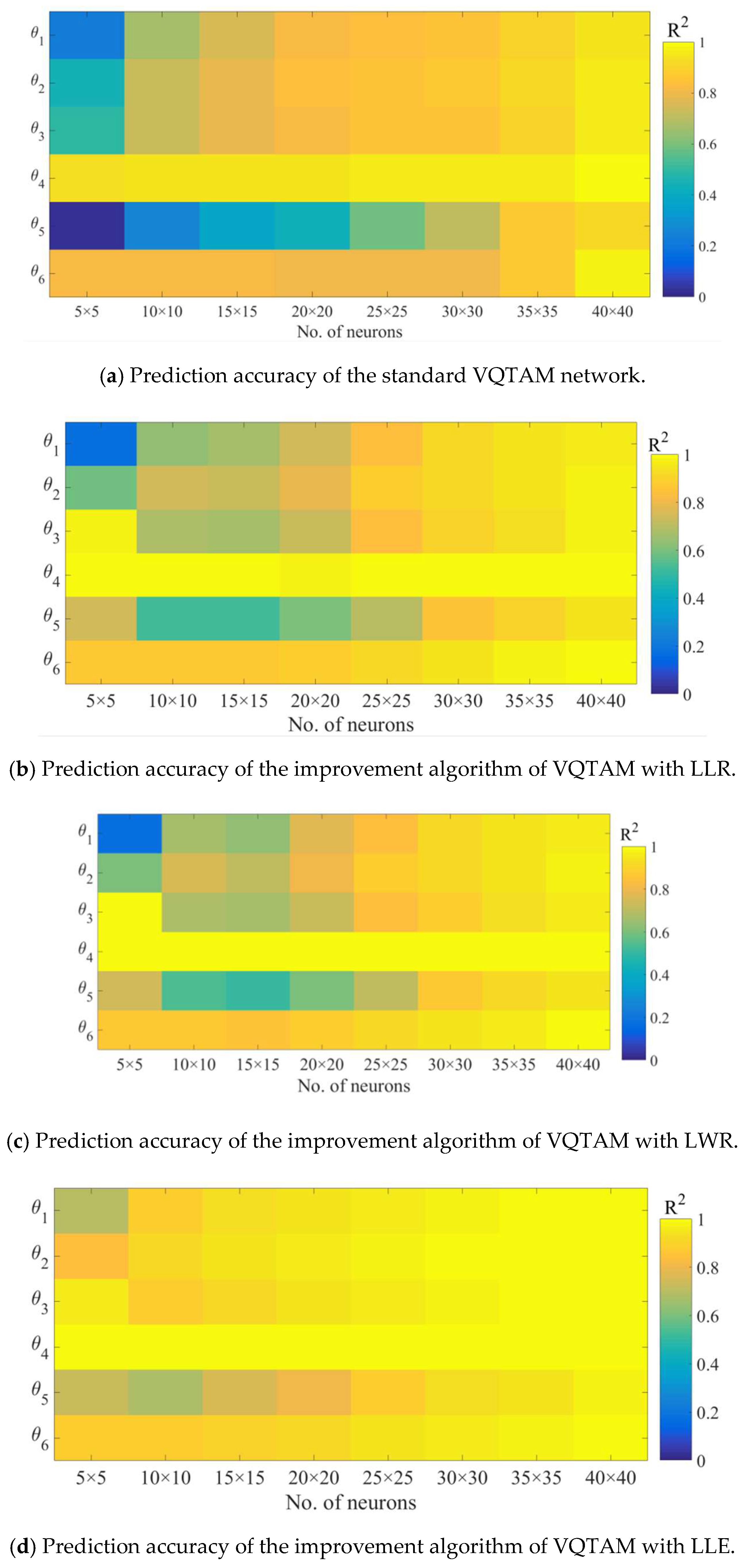
6.1. Standard VQTAM Network Test Results
6.2. VQTAM Local Linear Improvement Algorithms
6.3. Overall Examples and Test Results
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mustafa, A.; Tyagi, C.; Verma, N.K. Inverse Kinematics Evaluation for Robotic Manipulator using Support Vector Regression and Kohonen Self Organizing Map. In Proceedings of the International Conference on Industrial and Information Systems, Roorkee, India, 3–4 December 2016; pp. 375–380. [Google Scholar]
- Amouri, A.; Mahfoudi, C.; Zaatri, A.; Lakhal, O.; Merzouki, R. A Meta-heuristic Approach to Solve Inverse Kinematics of Continuum Manipulators. Available online: https://journals.sagepub.com/doi/abs/10.1177/0959651817700779 (accessed on 24 February 2020).
- Jiang, L.; Huo, X.; Liu, Y.; Liu, H. An Analytical Inverse Kinematic Solution with the Reverse Coordinates for 6-DOF Manipulators. In Proceedings of the 2013 IEEE International Conference on Mechatronics and Automation, Takamatsu, Japan, 4–7 August 2013; pp. 1552–1558. [Google Scholar]
- Sariyildiz, E.; Temeltas, H. Solution of Inverse Kinematic Problem for Serial Robot Using Quaternions. In Proceedings of the 2009 IEEE International Conference on Mechatronics and Automation, Singapore, 14–17 July 2009; pp. 26–31. [Google Scholar]
- Sariyildiz, E.; Temeltas, H. A Comparison Study of Three Screw Theory Based Kinematic Solution Methods for the Industrial Robot Manipulators. In Proceedings of the 2011 IEEEInternational Conference on Mechatronics and Automation, Beijing, China, 7–10 August 2011; pp. 52–57. [Google Scholar]
- Zhang, L.; Zuo, J.; Zhang, X.; Yao, X. A New Approach to Inverse Kinematic Solution for a Partially Decoupled Robot. In Proceedings of the 2015 International Conference on Control, Automation and Robotics, Singapore, 20–22 May 2015; pp. 55–59. [Google Scholar]
- Sun, J.-D.; Cao, G.-Z.; Li, W.-B.; Liang, Y.-X.; Huang, S.-D. Analytical Inverse Kinematic Solution Using the D-H Method for a 6-DOF Robot. In Proceedings of the 2017 14th International Conference on Ubiquitous Robots and Ambient Intelligence, Jeju, South Korea, 28 June–1 July 2017; pp. 714–716. [Google Scholar]
- Xin, S.Z.; Feng, L.Y.; Bing, H.L.; Li, Y.T. A Simple Method for Inverse Kinematic Analysis of the General 6R Serial Robot. In Proceedings of the ASME 2006 International Design Engineering Technical Conferences & Computers and Information in Engineering Conference, Philadelphia, PA, USA, 10–13 September 2006; pp. 1–8. [Google Scholar]
- Joseph, C.; Musto, A. Two-Level Strategy for Optimizing the Reliability of Redundant Inverse Kinematic Solutions. J. Intell. Robot. Syst. 2002, 33, 73–84. [Google Scholar]
- Wang, Y.; Sun, L.; Yan, W.; Liu, J. An Analytic and Optimal Inverse Kinematic Solution for a 7-DOF Space Manipulator. Robot 2014, 36, 592–599. [Google Scholar]
- Chiaverini, S.; Ecgeland, O. An efficient pseudo-inverse solution to the inverse kinematic problem for six-joint manipulators. Model. Identif. Control 1990, 11, 201–222. [Google Scholar] [CrossRef][Green Version]
- Wang, W.; Suga, Y. Hiroyasu Iwata and Shigeki Sugano, Solve Inverse Kinematics Through A New Quadratic Minimization Technique. In Proceedings of the 2012 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Kachsiung, Taiwan, 11–14 July 2012; pp. 313–360. [Google Scholar]
- Hargis, B.E.; Demirjian, W.A.; Powelson, M.W.; Canfield, S.L. Investigation of Neural-Network-Based Inverse Kinematics for A 6-DOF Serial Manipulator with Non-Spherical Wrist. In Proceedings of the ASME 2018 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Quebec City, QC, Canada, 26–29August 2018; pp. 1–14. [Google Scholar]
- Lou, Y.F.; Brunn, P. A hybrid artificial neural network inverse kinematic solution for accurate robot path control. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 1999, 213, 23–32. [Google Scholar] [CrossRef]
- Mahajan, A.; Singh, H.P.; Sukavanam, N. An unsupervised learning based neural network approach for a robotic manipulator. Int. J. Inf. Technol. 2017, 9, 1–6. [Google Scholar] [CrossRef]
- Kenwright, B. Neural Network in Combination with a Differential Evolutionary Training Algorithm for Addressing Ambiguous Articulated Inverse Kinematic Problems. In Proceedings of the 11th ACM SIGGRAPH Conference and Exhibition on Computer Graphics and Interactive Techniques in Asia, Tokyo, JAPAN, 4–7 December 2018. [Google Scholar]
- Kinoshita, K. Estimation of Inverse Model by PSO and Simultaneous Perturbation Method. In Proceedings of the 2015 Seventh International Conference of Soft Computing and Pattern Recognition, Fukuoka, Japan, 13–15 November 2015; pp. 48–53. [Google Scholar]
- Rui, T.; Zhu, J.-W.; Zhou, Y.; Ma, G.-Y.; Yao, T. Inverse Kinematics Analysis of Multi-DOFs Serial Manipulators Based on PSO. J. Syst. Simul. 2009, 21, 2930–2932. [Google Scholar]
- Shihabudheen, K.V.; Pillai, G.N. Evolutionary Fuzzy Extreme Learning Machine for Inverse Kinematic Modeling of Robotic Arms. In Proceedings of the 2015 39th National Systems Conference, Noida, India, 14–16 December 2015. [Google Scholar]
- Oyama, E.; Maeda, T.; Gan, J.Q.; Rosales, E.M.; MacDorman, K.F.; Tachi, S.; Agah, A. Inverse kinematics learning for robotic arms with fewer degrees of freedom by modular neural network systems. In Proceedings of the 2005 IEEE/RSJ International Conference on Intelligent Robots and Systems, Edmonton, AB, Canada, 2–6 August 2005; pp. 1791–1798. [Google Scholar]
- Wu, X.; Xie, Z. Forward kinematics analysis of a novel 3-DOF parallel manipulator. Sci. Iran. 2019, 26, 346–357. [Google Scholar] [CrossRef]
- Pham, D.T.; Castellani, M.; Fahmy, A.A. Learning the inverse kinematics of a robot manipulator using the Bees algorithm. In Proceedings of the 2008 6th IEEE International Conference on Industrial Informatics, Daejeon, South Korea, 13–16 July 2008; pp. 493–498. [Google Scholar]
- Giorelli, M.; Renda, F.; Calisti, M.; Arienti, A.; Ferri, G.; Laschi, C. Learning the inverse kinetics of an octopus-like manipulator in three-dimensional space. Bioinspir. Biomim. 2015, 10, 035006. [Google Scholar] [CrossRef] [PubMed]
- Karkalos, N.E.; Markopoulos, A.P.; Dossis, M.F. Optimal Model Parameters of Inverse Kinematics Solution of a 3R Robotic Manipulator Using Ann Models. Int. J. Manuf. Mater. Mech. Eng. 2017, 7, 20–40. [Google Scholar] [CrossRef]
- Rong, P.-X.; Yang, Y.-J.; Hu, L.-G.; Ma, G.-F. Inverse kinematic in SCARA manipulator based on RBF networks. Electr. Mach. 2007, 11, 303–305. [Google Scholar]
- Kumar, P.R.; Bandyopadhyay, B. The Forward Kinematic Modeling of a Stewart Platform using NLARX Model with Wavelet Network. In Proceedings of the IEEE International Conference on Industrial Informatics, Bochum, Germany, 29–31 July 2013; pp. 343–348. [Google Scholar]
- Barreto, G.D.; Araujo, A.F.R. Temporal associative memory and function approximation with the self-organizing map. In Proceedings of the Neural Networks For Signal Processing Xii, Martigny, Switzerland, 6 September 2002; pp. 109–118. [Google Scholar]
- Limtrakul, S.; Arnonkijpanich, B. Supervised learning based on the self-organizing maps for forward kinematic modeling of Stewart platform. Neural Comput. Appl. 2019, 31, 619–635. [Google Scholar] [CrossRef]
- Heskes, T. Self-organizing maps, vector quantization, and mixture modeling. IEEE Trans. Neural Netw. 2001, 12, 1299–1305. [Google Scholar] [CrossRef] [PubMed]
- Zhu, S.; Chen, Q.; Wang, X.; Liu, S. Dynamic modeling using screw theory and nonlinear sliding mode control of series robot. Int. J. Robot. Autom. 2016, 31, 63–75. [Google Scholar]
- Chen, Q.; Zhu, S.; Zhang, X. An Improved Inverse Kinematic Algorithm for 6 DOF Serial Robot Using Screw Theory. Int. J. Adv. Robot. Syst. 2015, 12, 140. [Google Scholar] [CrossRef]
- Muja, M.; Lowe, D.G. Scalable Nearest Neighbor Algorithms for High Dimensional Data. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 2227–2240. [Google Scholar] [CrossRef] [PubMed]

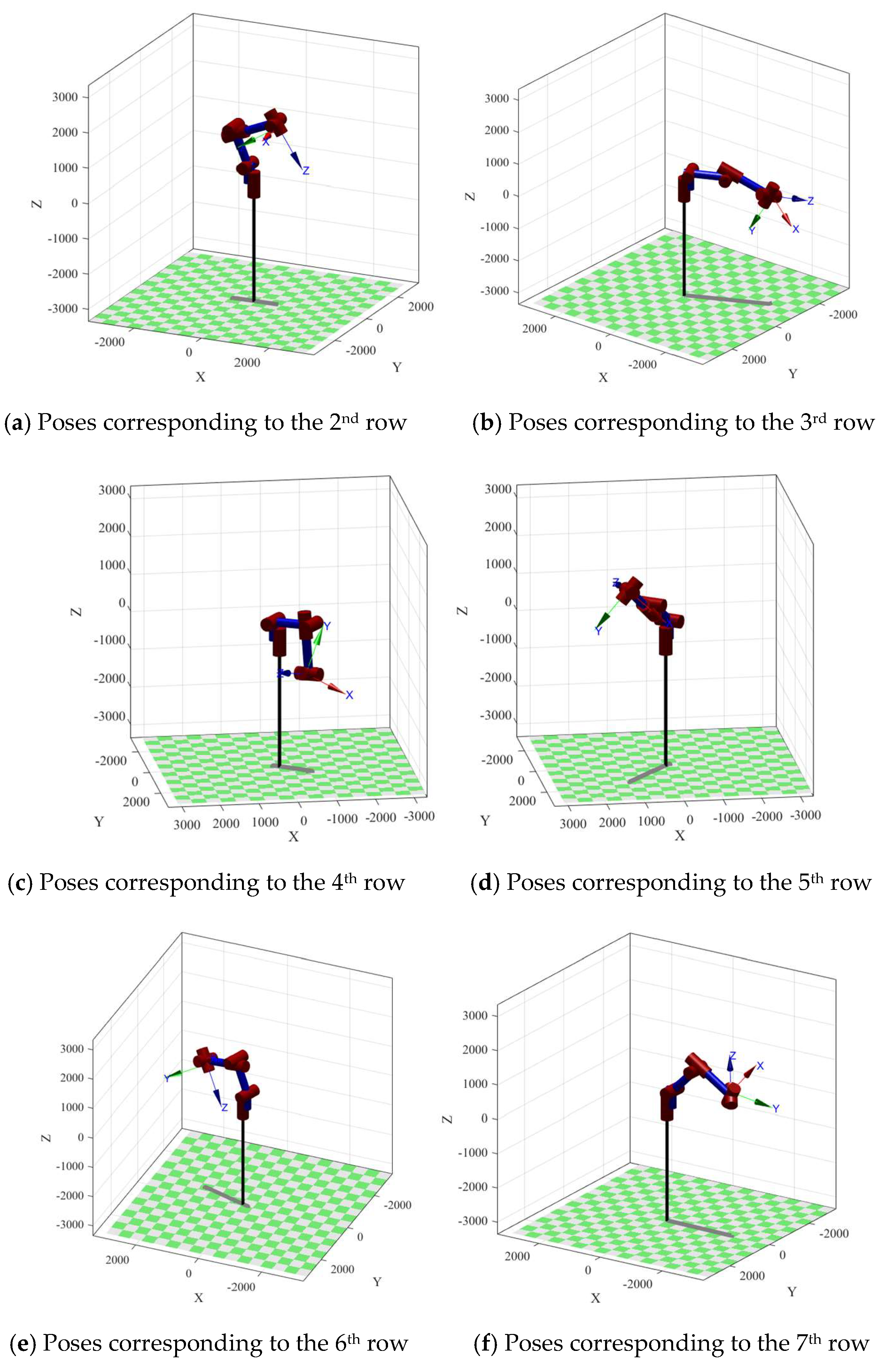





| parameter | x2 (mm) | x3 (mm) | x4 (mm) | x5 (mm) | x6 (mm) |
| value | 175 | 175 | 175 | 1445 | 1445 |
| parameter | z2 (mm) | z3 (mm) | z4 (mm) | z5 (mm) | z6 (mm) |
| value | 495 | 1590 | 1765 | 1765 | 1765 |
| θ | gst(θ) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| θ1 | θ2 | θ3 | θ4 | θ5 | θ6 | x (mm) | y (mm) | z(mm) | u | v | w |
| 0 | 0 | 0 | 0 | 0 | 0 | 1580 | 0 | 1765 | −2.81 | −1.57 | 2.81 |
| −3.14 | 0.39 | −3.14 | 0.03 | −1.41 | −4.81 | 717.58 | 9.07 | 1715.51 | −1.44 | −0.54 | 30.09 |
| −2.71 | 1.58 | −1.11 | 7.78 | 0.81 | 3.25 | −2292.10 | −1151.06 | 23.08 | 2.63 | 0.24 | −1.95 |
| −0.63 | −1.53 | −3.1 | −1.46 | −1.82 | −5.04 | −597.84 | 594.06 | −706.84 | −2.67 | −0.73 | 1.24 |
| −2.24 | −0.95 | −1.55 | 7.43 | 2.22 | 6.30 | 1152.39 | 1311.719 | 1743.21 | 2.40 | −0.15 | −1.67 |
| 2.81 | −0.42 | −2.98 | −2.90 | 2.01 | 6.95 | 1304.39 | −420.67 | 912.84 | 2.02 | 0.54 | 2.64 |
| 3.12 | 0.79 | −0.24 | −7.64 | −2.34 | −7.61 | −2057.54 | −44.10 | 822.60 | −2.44 | −0.52 | −0.97 |
| nq | np | epoch | α0 | αM | σ0 | σM |
|---|---|---|---|---|---|---|
| 3 | 3 | 5000 | 0.8 | 0.001 | 15 | 0.001 |
| θ1 | θ2 | θ3 | θ4 | θ5 | θ6 | |
|---|---|---|---|---|---|---|
| RMSE | 0.1871 | 0.1663 | 0.0895 | 0.2189 | 0.2459 | 0.5708 |
| R2 | 0.9931 | 0.9808 | 0.9972 | 0.9984 | 0.9808 | 0.9894 |
| RMAE | 0.3914 | 0.6660 | 0.4840 | 0.1734 | 0.9828 | 0.5477 |
| MLP | VQTAM (60 × 60) | VQTAM (50 × 50) | |
| RMSE | 1.5935 | 0.2901 | 0.7823 |
| VQTAM with LLR (50 × 50) | VQTAM with LWR (50 × 50) | VQTAM with LLE (50 × 50) | |
| RMSE | 0.5163 | 0.6792 | 0.3018 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lan, L.; Li, H.; Yang, W.; Yongqiao, W.; Qi, Z. Learning the Kinematics of a Manipulator Based on VQTAM. Symmetry 2020, 12, 519. https://doi.org/10.3390/sym12040519
Lan L, Li H, Yang W, Yongqiao W, Qi Z. Learning the Kinematics of a Manipulator Based on VQTAM. Symmetry. 2020; 12(4):519. https://doi.org/10.3390/sym12040519
Chicago/Turabian StyleLan, Luo, Hou Li, Wu Yang, Wei Yongqiao, and Zhang Qi. 2020. "Learning the Kinematics of a Manipulator Based on VQTAM" Symmetry 12, no. 4: 519. https://doi.org/10.3390/sym12040519
APA StyleLan, L., Li, H., Yang, W., Yongqiao, W., & Qi, Z. (2020). Learning the Kinematics of a Manipulator Based on VQTAM. Symmetry, 12(4), 519. https://doi.org/10.3390/sym12040519





