Abstract
Because digitized images are easily replicated or manipulated, copy-move forgery techniques are rendered possible with minimal expertise. Furthermore, it is difficult to verify the authenticity of images. Therefore, numerous efforts have been made to detect copy-move forgeries. In this paper, we present an improved region duplication detection algorithm based on the keypoints. The proposed algorithm utilizes the scale invariant feature transform (SIFT) and the reduced local binary pattern (LBP) histogram. The LBP values with 256 levels are obtained from the local window centered at the keypoint, which are then reduced to 10 levels. For a keypoint, a 138-dimensional is generated to detect copy-move forgery. We test the proposed algorithm on various image datasets and compare the detection accuracy with those of existing methods. The experimental results demonstrate that the performance of the proposed scheme is superior to that of other tested copy-move forgery detection methods. Furthermore, the proposed method exhibits a uniform detection performance for various types of test datasets.
1. Introduction
Copy-move forgery (CMF) is a popular image tampering method, wherein a portion of an image is copied from one section of the image and is pasted elsewhere in the same image. An image can be forged to conceal or change its meaning by the copy-move process. Therefore, it is important to verify the authenticity of the image and localize the copied and moved regions. Because the copied portion of an image is generally scaled or rotated, it is difficult to verify the authenticity of the image based on visual inspection alone. For this reason, the development of reliable copy-move forgery detection (CMFD) methods has become an important issue [1,2,3]. The common framework of CMFD comprises five steps: preprocessing (optional), feature extraction, matching, false match removal, and localization.
The optional first step of the CMFD process is preprocessing. In this step, the conversion of RGB color channels to grayscale [4,5] is often exploited to reduce the dimensionality of the input images. Alternately, RGB colors can be converted into the YCbCr [6,7] or the HSV [8] color space to use both the luminance and chrominance information. Various block division and segmentation methods can be considered for use in preprocessing. An image can be divided into overlapping square blocks [9,10,11], non-overlapping square blocks [12], or circular blocks [13,14]. Image segmentation techniques [15,16] are often included in the preprocessing step to separate the copied source region from the pasted target region.
Among these five CMFD steps, feature extraction is the main step of the CMFD process. Extracted features must be invariant to scale and rotation, and must be robust when subjected to post-processing steps, such as blurring, compression, and noise addition. Transform-based methods are frequently exploited to eliminate information that is unnecessary for detection, in addition, to enhancing the essential components. A variety of transform methods, such as the polar cosine transform [17], Fourier–Mellin transform [18,19], and polar complex exponential transform [20] were used for forgery detection, in conjunction with the popular Fourier transform [5], discrete cosine transform [7,11,21,22,23], and various wavelet transforms [7,11,24,25,26]. Recently, the local binary pattern (LBP) was successfully exploited to detect CMFs in combination with the wavelet transform [25] and singular value decomposition [27]. The center symmetric local binary pattern (CSLBP) [28], which is a variant of the LBP, was used to make CMFD more robust against noise during feature extractions. As another class of methods used to detect CMF, keypoint-based approaches have been actively studied thus far. Because keypoint features are robust under scaling, rotation, and occlusion, they are well suited to the CMFD process. Since the time that scale invariant feature transform (SIFT) was applied to forgery detection [29], various SIFT-based transforms, such as, binarized SIFT [30], opponent SIFT [31], and affine SIFT [32], have been applied to the CMFD. In addition to these schemes, histogram-based techniques [4] and statistical moment-based methods [20,33,34] have also been presented. Please refer to the referenced papers [1,2,3] for more details on these algorithms and other feature extraction methods.
Feature matching is a process of determining a candidate pair of the original section and the corresponding copy-move section using the extracted features. This process utilizes searching and similarity measurement techniques. Searching methods contain various sorting [6,7,35], nearest neighbor [31,36], and hashing methods [16]. These algorithms usually involve the use of dimension reduction techniques. During the searching process, the matching methods search for possible matches to evaluate the similarity between the selected possible matches. The Euclidean distance is the most popular and simple similarity metric employed. Several CMFD methods [4,16,20,35] use Euclidean distance. Additionally, Manhattan distance [37] and Hamming distance [30] between two features have also been employed to determine similarity.
However, even after the completion of the feature matching process, the false positive matches are not completely eliminated. To eliminate these false matches, various clustering algorithms, such as J-linkage clustering [31], distance-based clustering [38], and hierarchical clustering [39,40] have been presented to separate the authentic and tampered areas. One of the most robust and frequently used false match removal methods is the random sample consensus (RANSAC) algorithm, which can remove outliers from the matched features. The RANSAC algorithm is widely used in keypoint-based CMFD methods [15,31,35,36,39,40,41].
The final step in the CMFD process is the localization process. The detection output can be visualized as a binary image that presents the detected copy-moved regions and their corresponding authentic image parts within the target image. This process is commonly applied with various post-processing methods.
Keypoint-based CMFD algorithms have attracted a significant amount of attention in recent years. SIFT is one of the most frequently used keypoint extraction methods for the detection of CMF. SIFT generates both scale- and rotation-invariant keypoints, and each keypoint is commonly represented by a 128-dimensional descriptor. The SIFT descriptor of a keypoint is obtained from 16 4 × 4 windows around the keypoint and is generated as a set of gradient histograms representing 8 directions. However, although keypoint-based methods have been successfully applied to CMFD, their performance is degraded when the CMF implementation involves small or smooth regions [31,42]. Additionally, when a keypoint exists close to the boundary of the copy-moved portion and the authentic region or if an image has been compressed after CMF, the keypoint descriptor of the copied portion will be different from that of the moved portion.
For a single keypoint, the existing SIFT-based methods divide a 16 × 16 window into 16 sub-windows, each of size 4 × 4 pixels. The gradient values for the corresponding 8 directions in a 4 × 4 sub-window are used to generate an 8-dimensional descriptor for each sub-window. Next, the descriptors in all 16 sub-windows are arranged in series to create the final 128-dimensional descriptor. The limitation of the conventional descriptor generation method is that it only provides local information about a single keypoint. Because this method cannot represent global information around the keypoint, it may be difficult to cope with pixel changes, such as compression or differences in the background area caused by the copy-move process.
In this paper, we present an improved CMFD algorithm by adding a new descriptor. The proposed additional descriptor based on the LBP feature is capable of capturing global information associated with the keypoints. LBP is acknowledged as one of the features that is sufficiently robust to handle small pixel changes. For this reason, the proposed descriptor is generated using a histogram of LBP values for a 16 × 16 window centered on the keypoint. The LBP values are not generated at every pixel in the image but only for keypoints by the SIFT. Because a typical LBP has 256 levels for a pixel, we reduce the LBP levels to 10 to prevent an increase in the descriptor dimension. In total, the proposed descriptor for a keypoint has 138 dimensions. By means of experiments using various test datasets, we demonstrate that the proposed method generates more accurate estimation results in detecting CMFs than conventional methods.
The remainder of this paper is organized as follows. Section 2 introduces the basic process of the SIFT-based CMFD method and its limitations. Section 3 presents the proposed CMFD algorithm. In Section 4, the performance of the proposed method is compared with those of existing methods using the experimental results. Section 5 presents the discussion, and the conclusion is presented in Section 6.
2. SIFT-Based Copy-Move Forgery Detection
2.1. SIFT Descriptor
Figure 1 illustrates the basic workflow for the SIFT-based CMFD. For a given image I, SIFT features are extracted at different scales using a scale-space representation by an image pyramid. Potential keypoints are selected using scale-space extrema. All the potential keypoints are further refined according to a contrast and an edge threshold. This process is used to eliminate unstable keypoints in the SIFT algorithm. In the next step, an orientation is assigned to each keypoint to achieve invariance to image rotation. The gradient magnitude and direction are calculated in a local window centered at the SIFT keypoint. An orientation histogram with 36 bins covering 360 degrees is created. The highest peak in the histogram is considered as the dominant orientation. Furthermore, any peak above 80% of the highest peak is also considered while calculating the main orientation.

Figure 1.
Typical process of scale invariant feature transform (SIFT)-based copy-move forgery detection.
To generate a 128-dimensional descriptor for a keypoint, a 16 × 16 local window centered at the keypoint is considered. This window is divided into 16 sub-blocks each of size 4 × 4 pixels. For each sub-block, an 8-bin orientation histogram is created. A total of 128-bin values are obtained, and they are represented as a vector to form the keypoint descriptor. Let {k1, k2, …, km} be the m-keypoints extracted using the SIFT for the given image, I. Keypoint descriptors {f1, f2, …, fm} corresponding to {k1, k2, …, km} are generated using the above procedures. Figure 2 shows the generation method of a descriptor fi for a keypoint ki at the image location (xi,yi). As shown in Figure 2, the SIFT descriptor is represented as a list of gradients for the main direction in 16 4 × 4 sub-blocks around the keypoint. However, simply listing local gradients in this manner can tend to degrade the matching performance as the pixel values around the keypoints change.
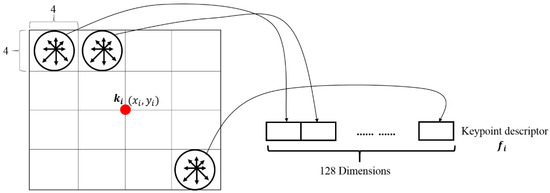
Figure 2.
Generation method of a SIFT descriptor fi for its corresponding keypoint ki.
2.2. Matching
If a pixel of an image is copied and moved, the keypoint descriptor of that pixel location, fi needs to be compared with all the other descriptors other than fi represented as fj≠i. This process is called matching. Let {d1,i, d2,i, …, dm−1,i} be the set of distances from fi and m−1 descriptors other than fi. At this point, each distance has the following relationship,
The keypoint fi is determined to be matched with the key point at distance d1,i if the following relation is satisfied, that is
where t is the threshold defined as t ∈ (1,0). In this paper, t is set to 0.65.
However, a false matching almost always exists after the completion of the matching process. Therefore, a range of methods has been studied with the aim of eliminating false matching. Mismatched keypoint pairs have been eliminated using various clustering algorithms, such as J-linage clustering [31], distance-based clustering [38], and hierarchical clustering [39,40]. In particular, the RANSAC algorithm is the most frequently used to eliminate false matches [15,31,35,36,39,40,41]. However, these algorithms can only eliminate the false matches but cannot generate the correct matched keypoint pairs.
Figure 3 illustrates an example of a false match based on the conventional SIFT descriptor [36], wherein a keypoint exists close to the boundary of the copy-moved portion and the authentic region. In Figure 3, a keypoint kA has been moved to kB. For a correct match, kA and kB should be matched by Equation (2). However, the keypoint kB is detected as the potentially matched keypoint with kA because kB has the closest distance (d1,A = 0.2684) to kA. In contrast, the distance between kA and kC is calculated as d2,A = 0.2721, and no matching occurs because d1,A/d2,A exceeds the threshold t. This is because the background (16 × 16 window centered at kA) of kA is different from that of kB. This situation may also occur if the image is compressed after CMF.
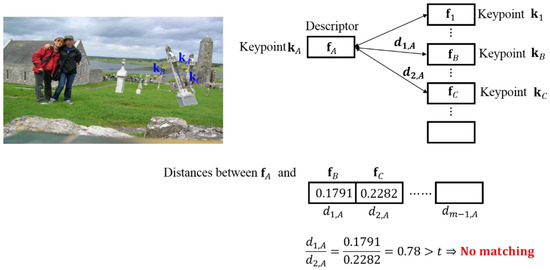
Figure 3.
Example of keypoint matching error using the conventional SIFT descriptor [36].
3. Proposed Method
In this paper, we propose an improved CMFD method by adding an LBP histogram-based descriptor. The LBP value is obtained for every pixel in the 16 × 16 window centered on the keypoint. The 256 LBP levels are reduced to 10 levels, and their histogram is used as a new descriptor. The main contribution of the proposed method is that the histogram of the reduced LBP values corresponding to a keypoint is used as an additional descriptor to increase the matched keypoint pairs.
3.1. Reduced LBP Feature
The LBP is one of the general features used to extract the texture information of an image. Owing to its discriminative performance and computational simplicity, the LBP feature is widely used in various applications. For a pixel in an image located at (p,q), the LBP value is calculated as follows.
where L(p,q) is the LBP value of the center pixel located at (p,q), In is the intensity of the neighboring pixel, I(p,q) is the intensity of the pixel at (p,q), and N is the number of neighboring pixels chosen at a given radius. In this paper, we use N = 8 (3 × 3 local window centered at (p,q)), which generates am 8-bit LBP value. In Equation (3), s(x) is defined as
Let Ω(xi,yi) be the set of pixels that exist in a 16 × 16 local window centered at the keypoint ki location, (xi,yi). Using all the pixels at (p,q) ∈ Ω(xi,yi), LBP values are calculated as depicted in Figure 4.
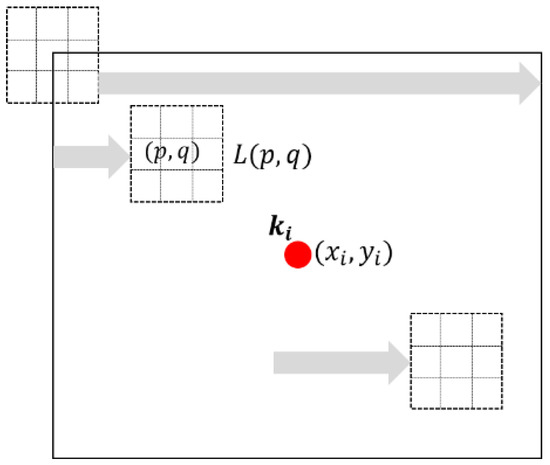
Figure 4.
Local binary pattern (LBP) generation method from all the pixels at (p,q) ∈ Ω(xi,yi).
The SIFT feature already contains a considerable amount of information for detecting CMFs. Therefore, it is not necessary to use all the LBP information. An LBP can be classified into two categories. If the binary pattern contains at most two 0→1 or 1→0 transitions, it is called a uniform pattern. For example, 00110000 (2 transitions) is a uniform pattern, but 01010100 (6 transitions) is a non-uniform pattern. Among the 256 LBP values, 58 LBP values are uniform, and the rest are non-uniform. A uniform pattern is characterized by a series of consecutive 1’s. Let Lc(p,q) (c = 0, 1, 2, …, 8) be the LBP with c consecutive 1’s. Obviously, L0(p,q) = 00000000, and L8(p,q) = 11111111. For c = 1, 2, …, 7, Lc(p,q) has 8 binary patterns that can be all be viewed as rotationally shifted versions of a single pattern. Figure 5 shows various uniform patterns. Let Lnon(p,q) be any pattern that has no consecutive 1’s except for L0(p,q). In conclusion, the 256-level LBP values can be divided into 10 groups, that is, nine types of Lc(p,q) and one Lnon(p,q).
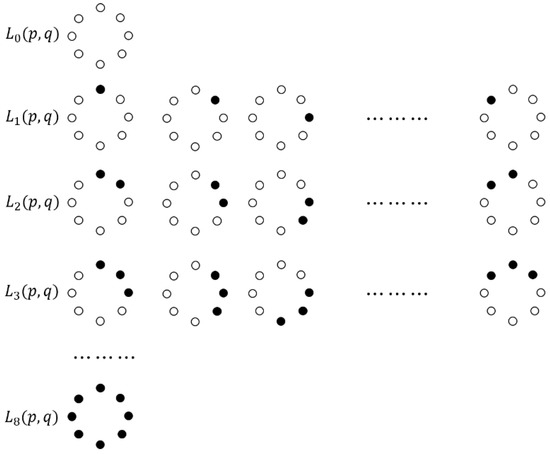
Figure 5.
Various uniform LBP patterns, ● denotes 1, and ○ indicates 0.
3.2. Proposed Descriptor
In this paper, we use the probabilities of Lc(p,q) and Lnon(p,q) as a new descriptor for CMFD. To maintain the rotation-invariant characteristic of the new descriptor, we check the occurrence of Lc(p,q) alone. Lnon(p,q) can reflect a frequent variation in a small window, which may occur because of noise, quantization errors, or small background changes. To reduce the effect of these variations, all non-uniform patterns are checked as they occur. The proposed descriptor ri corresponding to keypoint ki is obtained as
where Rc(xi,yi) and Rnon(xi,yi) are the normalized number of occurrences of Lc(p,q) and Lnon(p,q), respectively, in Ω(xi,yi). Rc(xi,yi) is calculated by
where #[Lc(p,q)] is the number of occurrences of the Lc(p,q) pattern in Ω(xi,yi), and |Ω(xi,yi)| is the cardinality of Ω(xi,yi). Rnon(xi,yi) can be obtained in a similar manner. ri is composed of the histogram of Lc(p,q) and Lnon(p,q). It is a 10 dimensional feature vector. Figure 6 illustrates the ri generation method using the reduced LBP histogram.
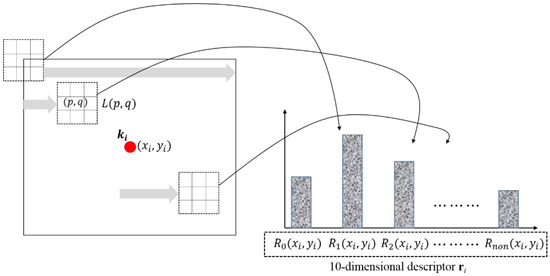
Figure 6.
New descriptor, ri generation method using the histogram of reduced LBP features.
The proposed descriptor for a keypoint, based on SIFT and the histogram of the reduced LBP, is obtained as
where gi is the proposed descriptor for CMFD and has 138 dimensional features. Because the descriptor, ri is generated for a relatively large area, unlike fi, it may be sufficiently robust to handle small pixel changes and quantization errors caused by image compression.
In Figure 4, we investigated a no-match case using the conventional SIFT descriptor. We apply the proposed descriptor to this case, and Figure 7 depicts the result of this case. As shown in Figure 7, we observe that the failed match is transformed into a successful match by using the proposed descriptor. The keypoint, kB is detected as the potentially matched keypoint with kA because kB has the closest distance (d1,A = 0.1426) to kA. The distance between kA and kC is calculated as d2,A = 0.2380. Because d1,A/d2,A does not exceed the threshold t, we can determine that kA and kB are the matched pair. Based on this result, we conclude that the proposed LBP-based descriptor plays an important role in removing the effect of a small fluctuation that occurred because there was a keypoint close to the boundary of the copy-moved portion and the authentic region.
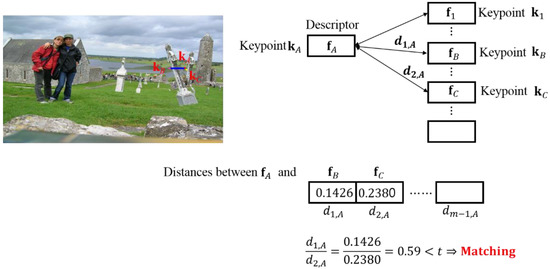
Figure 7.
Example of correct keypoint matching using the proposed descriptor.
3.3. Estimation of Affine Transform and False Match Removal
For the putative matched keypoint pairs, the geometric distortions, such as the rotation, scaling, and shearing of the duplicated regions can be estimated. Let (xi,yi) and (x’i,y’i) be the pixel locations from a region and its duplicate, respectively. These two locations are related by an affine transform as follows.
where t11, t12, t21, t22, x0, and y0 are the transform parameters. To estimate these parameters, at least three pairs of corresponding keypoints that are not collinear are required. However, the obtained parameters of the affine transform are inaccurate because of the mismatched keypoints. To eliminate unreliable keypoint matches, the widely used RANSAC scheme is employed. The parameters can be obtained using the RANSAC algorithm exhibit a high degree of accuracy. Furthermore, the affine transform parameters can also be used to determine the correlation map of the duplicated region.
After executing the RANSAC algorithm, the degree of rotation and scaling are estimated using the conventional SIFT and the proposed method. Table 1 presents the estimation results of the 10 different combinations of geometric transforms applied to the MICC-F220 dataset [36]. The MICC-F220 dataset comprises 110 tempered images and their corresponding 110 originals. The image resolution varies from 722 × 480 to 800 × 600 pixels, and the size of the forged portion covers, on average, 1.2% of the entire image. As shown in Table 1, the transform parameters using the proposed method are more accurate than those of the conventional SIFT algorithm. Thus, we conclude that the proposed descriptor based on the histogram of the reduced LBP plays a positive role in the detection of CMF.

Table 1.
Affine parameter estimation results using the conventional SIFT algorithm [36] and the proposed methods for the MICC-F220 dataset. The averaged rotation angles and scales for various attacks are presented in this table.
3.4. Localization
To localize the duplicated regions affected by CMF, the correlation map between the original image and the warped image is frequently used. Let W be the warped image obtained by transforming the image according to the affine transform. The correlation coefficient at a pixel location (x,y), ρ(x,y) is computed as
where Λ(x,y) is a 5 × 5 local window centered at (x,y), and Iμ and Wμ are the average values of I and W in the area Λ(x,y). A Gaussian filter is applied to the correlation map to reduce the noisy pixels, and a binary correlation map is obtained by a threshold. If the ρ(x,y) value for point (x,y) is greater than a threshold, this point is considered to be true, otherwise, this point is assigned a value of false.
3.5. Summary of Proposed Method
The overall algorithm of the proposed CMFD method is presented in Figure 8. SIFT is performed on the image suspected to have undergone CMF, to extract keypoints. For a keypoint ki at the image location (xi,yi), the conventional 128-dimensional descriptor fi is generated. For all the pixels in a 16 × 16 window centered at that keypoint location, pixel-wise LBP values are calculated. Next, the 256-level LBP values are reduced to 10 types of values. A histogram of the reduced LBP values is generated, and we let this 10-dimensional histogram be the additional descriptor ri. Next, gi, which is the combination of fi and ri, becomes the new descriptor for CMFD. For the final output, the false matching removal step, followed by localization using the RANSAC algorithm is performed.
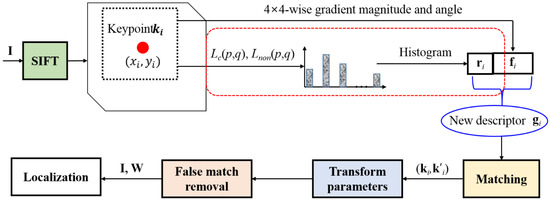
Figure 8.
Overall algorithm of the proposed method.
4. Experimental Results
To evaluate the performance of the proposed method, we first define three measures at the image level and pixel level. At the image level, the ability to correctly verify whether an images forged or not is measured, and the forgery localization accuracy performance is analyzed at the pixel level. In this paper, we use three measures, namely, true positive rate (TPR), false positive rate (FPR), and accuracy (ACC). TPR is used to measure the percentage of actual positives that are correctly identified, and it is defined as
FPR is the fraction of original images (pixels) that are not correctly identified, and it is obtained as
A well-designed CMF detector must simultaneously maintain a high TPR and low FPR. ACC is the percentage of correct decisions and is defined as
4.1. Dataset
In our simulation, we use four test datasets, namely, MICC-F220 [36], CMH [8], D [43], and COVERAGE [44]. The detailed information regarding these four datasets is summarized in Table 2. In this paper, we use the TPR and FPR values presented in the published papers for each test dataset.

Table 2.
Detailed information of five datasets.
4.2. Detection Results on Various Datasets
4.2.1. Results Obtained on MICC-F220 Dataset
Table 3 presents the detection performance using the MICC-F220 dataset. Because this dataset has no ground truth, three performance measures are obtained by at the image level. The performance of the proposed method is compared with that of various state-of-the-art CMFD methods, such as, improved DAISY descriptor (DAISY) [45], local invariant symmetry features (LISF) [46], 2-levels clustering strategy (Clustering) [47], dense filed-based method (DF) [48], Markov random field-based method (MRF) [49], iterative copy-move forgery detection (ICMFD) [35], going deeper into copy-move forgery detection (GDCMFD) [8], and hierarchical feature point matching-based method (HFPM) [42]. As presented in Table 3, HFPM exhibits the highest ACC of 99.10. The proposed CMFD algorithm achieves the second rank with an ACC of 96.82. For the MICC-F220 dataset, keypoint-based methods [42,47], including the proposed algorithm, demonstrate relatively better performance than block-based approaches.

Table 3.
True positive rate (TPR) (%), false positive rate (FPR) (%), and accuracy (%) on the MICC-F220 dataset at an image level. The number in bold indicates the highest performance, and the number in italics represents the second place.
4.2.2. Results Obtained on CMH Dataset
The CMH dataset has four types of uncompressed 108 realistic cloning images maliciously tampered with in various ways (23 plain copy-moved images (CMH1), 25 rotated images (CMH2), 25 resized images (CMH3), and 35 images that are both rotated and resized (CMH4)). Additionally, to address compressions, we compressed the full image into a JPEG format using quality factors of 70%, 80%, and 90% (CMH5). Table 4 presents the detection performance on this dataset. Every image has its own ground truth indicating the original and cloned regions in white color. For comparison, LSIF [46], SIFT-based forensic method (SIFT) [36], Helmert transform-based method (HT) [50], SIFT and J-linkage-based method (SIFTJL) [31], Zernike moment-based method (ZM) [34], GDCMFD [8], adaptive over-segmentation-based method (AO) [51], and segmentation-based CMFD (SCMFD) [15] are used.

Table 4.
TPR (%), FPR (%), and ACC (%) on the uncompressed CMH (CMH1, CMH2, CMH3, and CMH4) datasets at the pixel level. Bold numbers indicate the highest performance, and italic numbers represent the second place.
Table 4 presents the detection performance on the uncompressed CMH dataset (CMH1, CMH2, CMH3, and CMH4) at the pixel level. As shown in Table 4, all the CMFD methods except SCMFD exhibit good FPR values. However, only LSIT, HT, AO, and the proposed method exhibit valid TPR values. The proposed algorithm achieves the highest ACC, and HT exhibits the second highest performance.
Most CMFD approaches tend to degrade in their detection performance when operating on a compressed image. However, our method is considerably robust in handling compressed images during detection. To evaluate the CMFD performance for various forgery detection algorithms, three performance measures are tested on the CMH5 test dataset. Table 5 shows the detection performance on uncompressed CMH5 dataset at the pixel level. As shown in Table 5, the performance of many CMFD approaches, except those of LSIF, SIFT, and the proposed method, is degraded. In particular, the performance degradation of the block-based algorithms, such as HT, ZM, and GDCMFD, is considerable. The TPR, FPR, and ACC values of our methods are almost the same as those of the uncompressed CMH datasets. This advantage of the proposed CMFD method can be attributed to the addition of the reduced LBP descriptor.

Table 5.
TPR (%), FPR (%), and ACC (%) on the compressed CMH5 dataset at the pixel level. Bold numbers indicate the highest performance, and italic numbers represent the second place.
Figure 9 depicts the CMF region localization examples for the CMH dataset. As depicted in Figure 9, the proposed method exhibits the best localization performance. HT also demonstrates good localization results. However, this method does not reveal the details of the copied and moved regions. SIFTJL and AO demonstrate limited localization performances, whereas GDCMFD, based on statistical moments, demonstrates extremely poor localization performance.
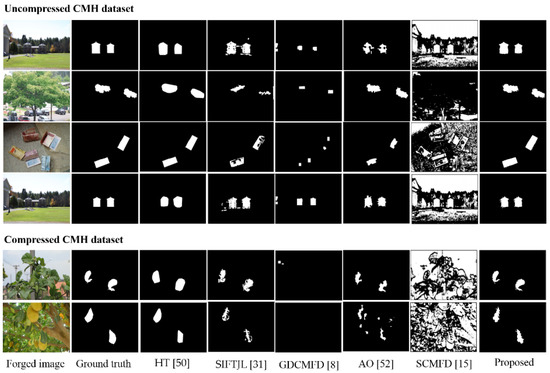
Figure 9.
Copy-move forged localization results on the CHM dataset.
4.2.3. Results on Obtained D Dataset
The D dataset comprises medium sized images (almost all of which are 1000 × 700 or 700 × 1000) and is subdivided into four datasets (D0, D1, D2, and D3). The first dataset D0 is made of 50 uncompressed images with simply translated copies. D1 is created by copy-pasting objects after rotation, and D2 is derived by of applying scaling to the copies. The subset D3 comprises 50 original images without tampering. For comparison, HT [50], SIFTJL [31], GDCMFD [8], and AO [51] are used.
Table 6 presents the detection performances on the D dataset. The proposed CMFD approach achieves the best detection performance, and HT achieves the second place with respect to ACC for the D0, D1, and D2 datasets. Because the D3 dataset contains only authentic images, only FPRs are compared in Table 6. The proposed method does not find any image to be manipulated as a copy-move image, and has an FPR value of zero. Figure 10 illustrates forged localization examples for the D dataset. As shown in Figure 10, the proposed CMFD algorithm exhibits the best localization performance.

Table 6.
TPR (%), FPR (%), and ACC (%) on D dataset at pixel level. Bold numbers indicate the highest performance, and italic numbers represent the second place.

Figure 10.
Copy-move forged localization results on the D dataset.
4.2.4. Results Obtained on COVERAGE Dataset
This dataset has 100 original and forged image pairs, with an average resolution of 400 × 486. For comparison, DF [46], SCMFD [15], ZM [34], GDCMFD [8], ICMFD [35], and HFPM [42] are used. Table 7 shows the image level detection performance on the COVERAGE dataset. Most algorithms perform poorly because each image contains similar-but-genuine objects in this dataset. HFPM exhibits the best ACC value, whereas the ACC of our method ranked third. However, the difference in the ACC between the method that achieved the first place, and the proposed method is only 1.73.

Table 7.
TPR (%), FPR (%), and ACC (%) on the COVERAGE dataset at image level. Bold numbers indicate the highest performance, and italic numbers represent the second place.
5. Discussion
In this paper, we compared the performance of our method with various CMFD methods for four datasets. Table 8 presents the ACC ranks of the CMFD methods for all the test datasets. For datasets, such as CMH and D, the proposed algorithm exhibited the highest CMFD performance. Our method achieved the second highest performance for the MIC-F220 dataset and ranked in the third place for the COVERAGE dataset. Overall, the proposed method demonstrated a high performance on average for various data. Many conventional CMFD methods exhibited performance variations depending on whether the image was compressed or not and the type of test dataset. For compressed image datasets, such as CMH5, our approach exhibited almost the same detection accuracy as that for uncompressed image datasets. In particular, our algorithm also achieved the highest rank for the dataset wherein the image was geometrically transformed. HT also exhibited a fairy good ranking, but fell short of that of the proposed method. Based on the results of Table 8, we can conclude that the proposed method results in a more uniform and consistent CMFD detection performance, regardless of the type of dataset.

Table 8.
ACC (%) ranking list on all test datasets.
6. Conclusions
In this paper, we introduced a new CMFD algorithm by adding the reduced LBP histogram-based descriptor. 256-level LBP features were first generated for a 16 × 16 window centered at a single keypoint. Next, the 256-level LBP values were reduced to 10 values to prevent an increase in the descriptor dimension. The histogram of the reduced LBP features was used as the additional descriptor to detect the CMF. In total, the proposed descriptor for a keypoint had 138 dimensions. We evaluated four types of test datasets. Additionally, the performance of the proposed method was compared with that of the existing CMFD algorithms. The simulation results showed that the proposed CMFD scheme generated more accurate estimation results while detecting CMFs than those obtained from conventional methods. The proposed method also demonstrated a relatively uniform and consistent detection performance regardless of the different types of test datasets.
Author Contributions
J.Y.P. and T.A.K. proposed the framework of this work, carried out the whole experiments, and drafted the manuscript. Y.H.M. offered useful suggestions for scale invariant transform and helped to modify the manuscript. I.K.E. initiated the main algorithm of this work, supervised the whole work, and wrote the final manuscript. All authors read and approved the final manuscript.
Funding
This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science, and Technology (NRF-2018R1D1A1B07046213).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhang, Z.; Wang, C.; Zhou, X. A survey on passive image copy-move forgery detection. J. Inf. Process. Syst. 2018, 14, 6–31. [Google Scholar] [CrossRef]
- Zheng, L.; Zhang, Y.; Thing, V. A survey on image tampering and its detection in real-world photos. J. Vis. Commun. Image Represent 2019, 58, 380–399. [Google Scholar] [CrossRef]
- Teerakanok, S.; Uehara, T. Copy-move forgery detection: A state-of-the-art technical review and analysis. IEEE Access. 2019, 7, 40550–40568. [Google Scholar] [CrossRef]
- Lee, J.C.; Chang, C.P.; Chen, W.K. Detection of copy-move image forgery using histogram of orientated gradients. Inf. Sci. 2015, 321, 250–262. [Google Scholar] [CrossRef]
- Fadl, S.M.; Semary, N.A. Robust copy-move forgery revealing in digital images using polar coordinate system. Neurocomputing. 2017, 265, 57–65. [Google Scholar] [CrossRef]
- Bi, X.; Pun, C.M.; Yuan, X.C. Multi-level dense descriptor and hierarchical feature matching for copy-move forgery detection. Inf. Sci. 2016, 345, 226–242. [Google Scholar] [CrossRef]
- Mahmood, T.; Mehmood, Z.; Shah, M.; Saba, T. A robust technique for copy-move forgery detection and localization in digital images via stationary wavelet and discrete cosine transform. J. Vis. Commun. Image Represent. 2018, 53, 202–214. [Google Scholar] [CrossRef]
- Silva, E.; Carvalho, T.; Ferreira, A.; Rocha, A. Going deeper into copy-move forgery detection: Exploring image telltales via multi-scale analysis and voting processes. J. Vis. Commun. Image Represent 2015, 29, 16–32. [Google Scholar] [CrossRef]
- Davarzani, R.; Yaghmaie, K.; Mozaffari, S.; Tapak, M. Copy-move forgery detection using multiresolution local binary patterns. Forensic Sci. Int. 2013, 231, 61–72. [Google Scholar] [CrossRef]
- Lynch, G.; Shih, F.Y.; Liao, H.-Y. An efficient expanding block algorithm for image copy-move forgery detection. Inf. Sci. 2013, 239, 253–265. [Google Scholar] [CrossRef]
- Zhao, J.; Guo, J. Passive forensics for copy-move image forgery using a method based on DCT and SVD. Forensic Sci. Int. 2013, 233, 158–166. [Google Scholar] [CrossRef]
- Sun, Y.; Ni, R.; Zhao, Y. Nonoverlapping blocks based copy-move forgery detection. Secur. Commun. Netw. 2018, 2018, 1301290. [Google Scholar] [CrossRef]
- Gao, Y.; Gao, T.; Fan, L.; Yang, Q. A robust detection algorithm for copy-move forgery in digital images. Forensic Sci. Int. 2012, 214, 33–43. [Google Scholar] [CrossRef]
- Zhong, J.; Gan, Y.; Young, J.; Huang, L.; Lin, P. A new block-based method for copy move forgery detection under image geometric transforms. Multimed. Tools Appl. 2017, 76, 14887–14903. [Google Scholar] [CrossRef]
- Li, J.; Li, X.; Yang, B.; Sun, X. Segmentation-based image copy-move forgery detection scheme. IEEE Trans. Inf. Forensics Secur. 2015, 10, 507–518. [Google Scholar] [CrossRef]
- Pun, C.M.; Chung, J.L. A two-stage localization for copy-move forgery detection. Inf. Sci. 2018, 463–464, 33–55. [Google Scholar] [CrossRef]
- Li, Y. Image copy-move forgery detection based on polar cosine transform and approximate nearest neighbor searching. Forensic Sci. Int. 2013, 224, 59–67. [Google Scholar] [CrossRef] [PubMed]
- Dixit, R.; Nakar, R. Copy–move forgery detection utilizing Fourier–Mellin transform log-polar features. J. Electron. Imaging. 2018, 27, 023007. [Google Scholar] [CrossRef]
- Bayram, S.; Sencar, H.T.; Memon, N. An efficient and robust method for detecting copy-move forgery. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Taipei, Taiwan, 9–24 April 2009; pp. 1053–1056. [Google Scholar] [CrossRef]
- Hosny, K.M.; Hamza, H.M.; Lashin, N.A. Copy-move forgery detection of duplicated objects using accurate PCET moments and morphological operators. Imag. Sci. J. 2018, 66, 330–345. [Google Scholar] [CrossRef]
- Fridrich, A.J.; Soukal, B.D.; Lukáš, A.J. Detection of copy-move forgery in digital images. In Proceedings of the Digital Forensic Research Workshop, Cleveland, OH, USA, 5–8 August 2003; pp. 55–61. [Google Scholar]
- Alkawaz, M.H.; Sulong, G.; Saba, T.; Rehman, A. Detection of copy-move image forgery based on discrete cosine transform. Neural Comput. Appl. 2018, 30, 183–192. [Google Scholar] [CrossRef]
- Kumar, S.; Desai, J.; Mukherjee, S. A fast DCT based method for copy move forgery detection. In Proceedings of the 2013 IEEE Second International Conference on Image Information Processing, Shimla, India, 9–11 December 2013; pp. 649–654. [Google Scholar] [CrossRef]
- Muhammad, G.; Hussain, M.; Bebis, G. Passive copy move image forgery detection using undecimated dyadic wavelet transform. Digit. Investig. 2012, 9, 49–57. [Google Scholar] [CrossRef]
- Mahmood, T.; Irtaza, A.; Mehmood, Z.; Mahmood, M.T. Copy–move forgery detection through stationary wavelets and local binary pattern variance for forensic analysis in digital images. Forensic Sci. Int. 2017, 279, 8–21. [Google Scholar] [CrossRef] [PubMed]
- Hashmi, M.F.; Hambarde, A.R.; Keskar, A.G. Copy move forgery detection using DWT and SIFT features. In Proceedings of the 13th International conference on intelligent systems design and applications, Bangi, Malaysia, 8–10 December 2013; pp. 188–193. [Google Scholar] [CrossRef]
- Wang, Y.; Tian, L.; Li, C. LBP-SVD based copy move forgery detection algorithm. In Proceedings of the 2017 IEEE International Symposium on Multimedia, Taichung, Taiwan, 11–13 December 2017; pp. 553–556. [Google Scholar] [CrossRef]
- Uliyan, D.M.; Jalab, H.A.; Wahab, A.W.A. Copy move image forgery detection using Hessian and center symmetric local binary pattern. In Proceedings of the 2015 IEEE Conference on Open Systems, Bandar Melaka, Malaysia, 24–26 August 2015; pp. 7–11. [Google Scholar] [CrossRef]
- Huang, H.; Guo, W.; Zhang, Y. Detection of copy-move forgery in digital images using SIFT algorithm. In Proceedings of the Pacific-Asia Workshop on Computational Intelligence and Industrial Application, Wuhan, China, 19–20 December 2008; pp. 272–276. [Google Scholar] [CrossRef]
- Muzaffer, G.; Ulutas, G. A fast and effective digital image copy move forgery detection with binarized SIFT. In Proceedings of the 2017 40th International Conference on Telecommunications and Signal Processing, Barcelona, Spain, 5–7 July 2017; pp. 595–598. [Google Scholar] [CrossRef]
- Jin, G.; Wan, X. An improved method for SIFT-based copy-move forgery detection using non-maximum value suppression and optimized J-Linkage. Signal Process. Image Commun. 2017, 57, 113–125. [Google Scholar] [CrossRef]
- Shahroudnejad, A.; Rahmati, M. Copy-move forgery detection in digital images using affine-SIFT. In Proceedings of the 2016 2nd International Conference of Signal Processing and Intelligent Systems, Tehran, Iran, 14–15 December 2016. [Google Scholar] [CrossRef]
- Mahdian, B.; Saic, S. Detection of copy–move forgery using a method based on blur moment invariants. Forensic Sci. Int. 2007, 171, 180–189. [Google Scholar] [CrossRef] [PubMed]
- Ryu, S.J.; Kirchner, M.; Lee, M.J.; Lee, H.K. Rotation invariant localization of duplicated image regions based on Zernike moments. IEEE Trans. Inf. Forensics Secur. 2013, 8, 1355–1370. [Google Scholar] [CrossRef]
- Zandi, M.; Mahmoudi-Aznaveh, A.; Talebpour, A. Iterative copy-move forgery detection based on a new interest point detector. IEEE Trans. Inf. Forensics Secur. 2016, 11, 2499–2512. [Google Scholar] [CrossRef]
- Amerini, I.; Ballan, L.; Caldelli, R.; Del Bimbo, A.; Serra, G. A sift-based forensic method for copy-move attack detection and transformation recovery. IEEE Trans. Inf. Forensics Secur. 2011, 6, 1099–1110. [Google Scholar] [CrossRef]
- Malviya, A.V.; Ladhake, S.A. Pixel based image forensic technique for copy-move forgery detection using auto color correlogram. Procedia Comput. Sci. 2016, 79, 383–390. [Google Scholar] [CrossRef]
- Uliyan, D.M.; Jalab, H.A.; Wahab, A.W.A.; Sadeghi, S. Image region duplication forgery detection based on angular radial partitioning and Harris key-points. Symmetry 2016, 8, 62. [Google Scholar] [CrossRef]
- Warif, N.B.A.; Wahab, A.W.A.; Idris, M.Y.I.; Salleh, R.; Othman, F. SIFT-symmetry: A robust detection method for copy-move forgery with refection attack. J. Vis. Commun. Image Represent. 2017, 46, 219–232. [Google Scholar] [CrossRef]
- Lee, J.C. Copy-move image forgery detection based on Gabor magnitude. J. Vis. Commun. Image Represent. 2015, 31, 320–334. [Google Scholar] [CrossRef]
- Pan, X.; Lyu, S. Region duplication detection using image feature matching. IEEE Trans. Inf. Forensics Secur. 2010, 5, 857–867. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, J. Fast and effective image copy-move forgery detection via hierarchical feature point matching. IEEE Trans. Inf. Forensics Secur. 2019, 14, 1307–1322. [Google Scholar] [CrossRef]
- Ardizzone, E.; Bruno, A.; Mazzola, G. Copy–move forgery detection by matching triangles of keypoints. IEEE Trans. Inf. Forensics Secur. 2015, 10, 2084–2094. [Google Scholar] [CrossRef]
- Wen, B.; Zhu, Y.; Subramanian, R.; Ng, T.; Shen, X.; Winkler, S. COVERAGE—A novel database for copy-move forgery detection. In Proceedings of the IEEE International Conference on Image Processing, Phoenix, AZ, USA, 25–28 September 2016; pp. 161–165. [Google Scholar] [CrossRef]
- Guo, G.M.; Liu, Y.F.; Wu, Z.J. Duplication forgery detection using improved DAISY descriptor. J. Comput. Inf. Syst. 2014, 10, 9369–9377. [Google Scholar] [CrossRef]
- Vaishnavi, D.; Subashini, T.S. Application of local invariant symmetry features to detect and localize image copy move forgeries. J. Inf. Secur. Appl. 2019, 44, 23–31. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Manogaran, G.; Fakhry, A.E.; El-Henawy, I. 2-levels of clustering strategy to detect and locate copy-move forgery in digital images. Multimed. Tools Appl. 2018, 1–19. [Google Scholar] [CrossRef]
- Cozzolino, D.; Poggi, G.; Verdoliva, L. Efficient dense-field copy-move forgery detection. IEEE Trans. Inf. Forensics Secur. 2015, 10, 2284–2297. [Google Scholar] [CrossRef]
- Elhaminia, B.; Harati, A.; Taherinia, A. A probabilistic framework for copy-move forgery detection based on Markov Random Field. Multimed. Tools Appl. 2019, 78, 25591–25609. [Google Scholar] [CrossRef]
- Huang, H.Y.L.; Ciou, A.J. Copy-move forgery detection for image forensics using superpixel segmentation and the Helmert transformation. EURASIP J. Image Video Proc. 2019, 68, 1–16. [Google Scholar] [CrossRef]
- Pun, C.M.; Yuan, X.C.; Bi, X.L. Image forgery detection using adaptive oversegmentation and feature point matching. IEEE Trans. Inf. Forensics Secur. 2015, 10, 1705–1716. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).