A GL Model on Thermo-Elastic Interaction in a Poroelastic Material Using Finite Element Method

Abstract

The purpose of this study is to provide a method to investigate the effects of thermal relaxation times in a poroelastic material by using the finite element method. The formulations are applied under the Green and Lindsay model, with four thermal relaxation times. Due to the complex governing equation, the finite element method has been used to solve these problems. All physical quantities are presented as symmetric and asymmetric tensors. The effects of thermal relaxation times and porosity in a poro-thermoelastic medium are studied. Numerical computations for temperatures, displacements and stresses for the liquid and the solid are presented graphically.

1. Introduction

The theory of poroelasticity was expanded by Biot [1]. Biot [2,3] formulated a theoretical framework for the propagation of isothermal waves in the fluid-saturated elastic porous medium for both cases of low- and high-frequency ranges. Following Biot’s model, many researchers have studied problems with the propagation of plane and surface wave in liquid-saturated porous mediums. Due to numerous applications in the fields of geophysics and similar subjects, growing attentiveness is being paid to the interactions between fluids such as water and thermo-elastic solids, a field of porothermoelasticity. Over the past four decades, thermoelastic models, which admit finite speed for thermal signals, have received a lot of attention. These models are known as generalized thermoelastic models. Lord and Shulman [4] have obtained the first generalized thermoelastic model with one thermal relaxation time, while Green-Lindsay [5] presented the second generalized thermoelastic model with two relaxation times. The field of porothermoelasticity has many applications, especially in the study of the effects of the use of waste on the disintegrations of the asphalt concrete mix. The thermo-mechanical coupling in the poroelastic material is more complex as compared to the classical cases, due to the fact that the mechanical and thermal coupling occurs between the fluid and solid phases. Following [3], many researchers including [6,7,8,9] have contributed towards various problems in porothermoelastic medium. Abbas [10] studied the natural frequencies of a poroelastic hollow cylinder. Schanz and Cheng [11] have studied the transient wave propagation in a one-dimensional poroelastic column. El-Naggar et al. [12] studied the effects of voids, initial stress, rotation and magnetic field on plane waves under generalized thermoelastic theory. Abbas et al. [13] have investigated the effects of thermal dispersion on free convection in a fluid-saturated porous media. Many researchers [14,15,16,17,18] have applied the generalized thermoelastic theories to get the numerical and analytical solutions of physical quantities. Marin et al. [19] have presented the effects of a dipolar structure under Green–Naghdi thermo-elasticity. Sur et al. [20] investigated the effects of memory on thermal wave propagations in an elastic solid with voids. Not reported in literature yet, it will be an interesting case to study the effects of thermal relaxation times in the propagations of waves in a generalized porothermoelastic medium. Many authors [21,22,23,24,25,26,27] have solved various problems under generalized thermo-elastics models and [28,29,30,31,32,33] have solved several problems for porous medium under different boundary conditions.

This paper explores the numerical solutions of the temperatures, displacements and stresses of the poro-thermoelastic medium, using the finite element method. For the considered variables, the numerical results are obtained and presented graphically, to show the effects of the porosity and the thermal relaxation times.

2. Basic Equations

Consider an isotropic, homogeneous and elastic medium with voids; the basic equations are based on [8,34], with Green-Lindsay [5] models in the absence of heat source, and body force can be expressed by

$${\mathsf{\mu }\mathrm{u}}_{\mathrm{i},\mathrm{jj}}+\left(\mathsf{\lambda }+\mathsf{\mu }\right){\mathrm{u}}_{\mathrm{j},\mathrm{ij}}+Q{U}_{i,jj}-{\mathrm{R}}_{11}\left(1+{\mathsf{\tau }}_1^{\mathrm{s}}\frac{\partial }{\partial \mathrm{t}}\right){\mathsf{\Theta }}_{,\mathrm{i}}^{\mathrm{s}}-{\mathrm{R}}_{12}\left(1+{\mathsf{\tau }}_1^{\mathrm{f}}\frac{\partial }{\partial \mathrm{t}}\right){\mathsf{\Theta }}_{,\mathrm{i}}^{\mathrm{f}}={\mathsf{\rho }}_{11}\frac{{\partial }^2{\mathrm{u}}_{\mathrm{i}}}{\partial {\mathrm{t}}^2}+{\mathsf{\rho }}_{12}\frac{{\partial }^2{\mathrm{U}}_{\mathrm{i}}}{\partial {\mathrm{t}}^2},$$

(1)

$${\mathrm{RU}}_{\mathrm{j},\mathrm{ij}}+{\mathrm{Qu}}_{\mathrm{j},\mathrm{ij}}-{\mathrm{R}}_{21}\left(1+{\mathsf{\tau }}_1^{\mathrm{s}}\frac{\partial }{\partial \mathrm{t}}\right){\mathsf{\Theta }}_{,\mathrm{i}}^{\mathrm{s}}-{\mathrm{R}}_{22}\left(1+{\mathsf{\tau }}_1^{\mathrm{f}}\frac{\partial }{\partial \mathrm{t}}\right){\mathsf{\Theta }}_{,\mathrm{i}}^{\mathrm{f}}={\mathsf{\rho }}_{12}\frac{{\partial }^2{\mathrm{u}}_{\mathrm{i}}}{\partial {\mathrm{t}}^2}+{\mathsf{\rho }}_{22}\frac{{\partial }^2{\mathrm{U}}_{\mathrm{i}}}{\partial {\mathrm{t}}^2},$$

(2)

$${\mathrm{K}}^{\mathrm{s}}{\mathsf{\Theta }}_{,\mathrm{ii}}^{\mathrm{s}}=\left(\frac{\partial }{\partial \mathrm{t}}+{\mathsf{\tau }}_{\mathrm{o}}^{\mathrm{s}}\frac{{\partial }^2}{\partial {\mathrm{t}}^2}\right)\left({\mathrm{F}}_{11}{\mathsf{\Theta }}^{\mathrm{s}}+{\mathrm{F}}_{12}{\mathsf{\Theta }}^{\mathrm{f}}\right)+\left(\frac{\partial }{\partial \mathrm{t}}+{\mathrm{n}\mathsf{\tau }}_{\mathrm{o}}^{\mathrm{s}}\frac{{\partial }^2}{\partial {\mathrm{t}}^2}\right)\left({\mathrm{T}}_{\mathrm{o}}{\mathrm{R}}_{11}{\mathrm{e}}_{\mathrm{kk}}+{\mathrm{T}}_{\mathrm{o}}{\mathrm{R}}_{21}\mathsf{ϵ}\right),$$

(3)

$${\mathrm{K}}^{\mathrm{f}}{\mathsf{\Theta }}_{,\mathrm{ii}}^{\mathrm{f}}=\left(\frac{\partial }{\partial \mathrm{t}}+{\mathsf{\tau }}_{\mathrm{o}}^{\mathrm{f}}\frac{{\partial }^2}{\partial {\mathrm{t}}^2}\right)\left({\mathrm{F}}_{21}{\mathsf{\Theta }}^{\mathrm{s}}+{\mathrm{F}}_{22}{\mathsf{\Theta }}^{\mathrm{f}}\right)+\left(\frac{\partial }{\partial \mathrm{t}}+{\mathrm{n}\mathsf{\tau }}_{\mathrm{o}}^{\mathrm{f}}\frac{{\partial }^2}{\partial {\mathrm{t}}^2}\right)\left({\mathrm{T}}_{\mathrm{o}}{\mathrm{R}}_{12}{\mathrm{e}}_{\mathrm{kk}}+{\mathrm{T}}_{\mathrm{o}}{\mathrm{R}}_{22}\mathsf{ϵ}\right).$$

(4)

The constitutive equations

$${\mathsf{\sigma }}_{\mathrm{ij}}=2{\mathsf{\mu }\mathrm{e}}_{\mathrm{ij}}+\left({\mathsf{\lambda }\mathrm{e}}_{\mathrm{kk}}+\mathrm{Q}\mathsf{ϵ}-{\mathrm{R}}_{11}\left(1+{\mathsf{\tau }}_1^{\mathrm{s}}\frac{\partial }{\partial \mathrm{t}}\right){\mathsf{\Theta }}^{\mathrm{s}}-{\mathrm{R}}_{12}\left(1+{\mathsf{\tau }}_1^{\mathrm{f}}\frac{\partial }{\partial \mathrm{t}}\right){\mathsf{\Theta }}^{\mathrm{f}}\right){\mathsf{\delta }}_{\mathrm{ij}},$$

(5)

$$\mathsf{\sigma }={\mathrm{Qe}}_{\mathrm{kk}}+\mathrm{R}\mathsf{ϵ}-{\mathrm{R}}_{21}\left(1+{\mathsf{\tau }}_1^{\mathrm{s}}\frac{\partial }{\partial \mathrm{t}}\right){\mathsf{\Theta }}^{\mathrm{s}}-{\mathrm{R}}_{22}\left(1+{\mathsf{\tau }}_1^{\mathrm{f}}\frac{\partial }{\partial \mathrm{t}}\right){\mathsf{\Theta }}^{\mathrm{f}}$$

(6)

$${\mathrm{e}}_{\mathrm{ij}}=\frac{1}{2}\left({\mathrm{u}}_{\mathrm{i},\mathrm{j}}+{\mathrm{u}}_{\mathrm{j},\mathrm{i}}\right),\mathsf{ϵ}={\mathrm{U}}_{\mathrm{i},\mathrm{i}}.$$

(7)

There are different three models as:

• (CT) points to the classical dynamical coupled theory

  $${\mathsf{\tau }}_{\mathrm{o}}^{\mathrm{s}}={\mathsf{\tau }}_{\mathrm{o}}^{\mathrm{f}}={\mathsf{\tau }}_1^{\mathrm{f}}={\mathsf{\tau }}_1^{\mathrm{s}}=\mathrm{n}=0.$$
• (LS) points to Lord and Shulman’s model

  $${\mathsf{\tau }}_{\mathrm{o}}^{\mathrm{s}}>0,{\mathsf{\tau }}_{\mathrm{o}}^{\mathrm{f}}>0,{\mathsf{\tau }}_1^{\mathrm{s}}={\mathsf{\tau }}_1^{\mathrm{f}}=0,\mathrm{n}=1.$$
• (GL) points to Green and Lindsay’s model

  $$0<{\mathsf{\tau }}_{\mathrm{o}}^{\mathrm{s}}<{\mathsf{\tau }}_1^{\mathrm{s}},0<{\mathsf{\tau }}_{\mathrm{o}}^{\mathrm{f}}<{\mathsf{\tau }}_1^{\mathrm{f}},\mathrm{n}=0,$$

  where ${\mathsf{\tau }}_{\mathrm{o}}^{\mathrm{s}},{\mathsf{\tau }}_1^{\mathrm{s}},{\mathsf{\tau }}_{\mathrm{o}}^{\mathrm{f}},{\mathsf{\tau }}_1^{\mathrm{f}}$ are the thermal relaxation times of the solid and fluid phases, respectively, ${\mathsf{\sigma }}_{\mathrm{ij}}$ are the stress components applied to the solid surface, $\mathsf{\lambda },\mathsf{\mu },\mathrm{R},\mathrm{Q}$ are the poroelastic coefficients, ${\mathrm{R}}_{11},{\mathrm{R}}_{12},{\mathrm{R}}_{21},{\mathrm{R}}_{22}$ are the thermal and mixed asymmetric coefficients, ${\mathrm{T}}_{\mathrm{o}}$ is the reference temperature, ${\mathsf{\Theta }}^{\mathrm{f}}={\mathrm{T}}^{\mathrm{f}}-{\mathrm{T}}_{\mathrm{o}}$ is the fluid temperature increment, ${\mathsf{\Theta }}^{\mathrm{s}}={\mathrm{T}}^{\mathrm{s}}-{\mathrm{T}}_{\mathrm{o}}$ is the temperature increment of the solid, ${\mathrm{u}}_{\mathrm{i}},{\mathrm{U}}_{\mathrm{i}}$ are the displacements of the solid and fluid phases, $\mathsf{\beta }$ is the porosity of the material, $\mathrm{K}$ is the interface coefficient of the interphase heat conduction, ${\mathrm{K}}^{\mathrm{f}}={\mathsf{\beta }\mathrm{K}}^{\mathrm{f}*}$ is the fluid phase thermal conductivity, ${\mathrm{K}}^{\mathrm{s}}=\left(1-\mathsf{\beta }\right){\mathrm{K}}^{\mathrm{s}*}$ is the solid thermal conductivity, ${\mathrm{K}}^{\mathrm{s}*},{\mathrm{K}}^{\mathrm{f}*}$ are the thermal conductivity of the solid and the fluid, ${\mathsf{\rho }}^{\mathrm{s}}=\left(1-\mathsf{\beta }\right){\mathsf{\rho }}^{\mathrm{s}*}$ is the solid phase density per unit volume of bulk, ${\mathsf{\rho }}^{\mathrm{f}}={\mathsf{\beta }\mathsf{\rho }}^{\mathrm{f}*}$ is the density of the solid phase per unit volume of bulk, ${\mathsf{\rho }}^{\mathrm{s}*},{\mathsf{\rho }}^{\mathrm{f}*}$ are the solid and the liquid densities, ${\mathsf{\rho }}_{12}$ is the dynamics coupling coefficient, ${\mathsf{\rho }}_{22}={\mathsf{\rho }}^{\mathrm{f}}-{\mathsf{\rho }}_{12}$ is the fluid phase mass coefficient, ${\mathsf{\rho }}_{11}={\mathsf{\rho }}^{\mathrm{s}}-{\mathsf{\rho }}_{12}$ is the solid phase mass coefficient, $\mathsf{ϵ}$ are the strain of the fluid phase components, ${\mathrm{e}}_{\mathrm{ij}}$ are the strain of the solid phase components, $\mathsf{\sigma }$ is the normal stress applied to the fluid surface, ${\mathrm{C}}_{\mathrm{E}}^{\mathrm{f}},{\mathrm{C}}_{\mathrm{E}}^{\mathrm{s}}$ are the specific heat of the fluid and the solid phases, ${\mathsf{\alpha }}^{\mathrm{fs}},{\mathsf{\alpha }}^{\mathrm{sf}}$ are the thermoelastic couplings between the phases, ${\mathsf{\alpha }}^{\mathrm{s}},{\mathsf{\alpha }}^{\mathrm{f}}$ are the thermal expansion of the phases coefficients, ${\mathrm{C}}_{\mathrm{E}}^{\mathrm{f}}$ is the specific heat couplings between the fluid and the solid phases, ${\mathsf{\eta }}^{\mathrm{f}}=\frac{{\mathsf{\rho }}^{\mathrm{f}}{\mathrm{C}}_{\mathrm{E}}^{\mathrm{f}}}{{\mathrm{K}}^{\mathrm{f}}}$ is the thermal viscosity of the fluid, ${\mathsf{\eta }}^{\mathrm{s}}=\frac{{\mathsf{\rho }}^{\mathrm{s}}{\mathrm{C}}_{\mathrm{E}}^{\mathrm{s}}}{{\mathrm{K}}^{\mathrm{s}}}$ is the thermal viscosity of the solid, $\mathsf{\eta }=\frac{{\mathsf{\rho }}_{12}{\mathrm{C}}_{\mathrm{E}}^{\mathrm{sf}}}{\mathrm{K}}$ is the couplings thermal viscosity between the phases, with the asymmetric coefficients ${\mathrm{R}}_{11}={\mathsf{\alpha }}^{\mathrm{s}}\mathrm{P}+{\mathsf{\alpha }}^{\mathrm{fs}}\mathrm{Q}$, ${\mathrm{R}}_{12}={\mathsf{\alpha }}^{\mathrm{f}}\mathrm{Q}+{\mathsf{\alpha }}^{\mathrm{sf}}\mathrm{P}$, ${\mathrm{R}}_{21}=3{\mathsf{\alpha }}^{\mathrm{s}}\mathrm{Q}+{\mathsf{\alpha }}^{\mathrm{sf}}\mathrm{R}$, ${\mathrm{R}}_{22}={\mathsf{\alpha }}^{\mathrm{f}}\mathrm{R}+3{\mathsf{\alpha }}^{\mathrm{sf}}\mathrm{Q}$, $\mathrm{P}=3\mathsf{\lambda }+2\mathsf{\mu }$, ${\mathrm{F}}_{11}={\mathsf{\rho }}^{\mathrm{s}}{\mathrm{C}}_{\mathrm{E}}^{\mathrm{s}}$, ${\mathrm{F}}_{22}={\mathsf{\rho }}^{\mathrm{f}}{\mathrm{C}}_{\mathrm{E}}^{\mathrm{f}}$, ${\mathrm{F}}_{12}=-\left(3{\mathsf{\alpha }}^{\mathrm{s}}{\mathrm{R}}_{12}+{\mathsf{\alpha }}^{\mathrm{fs}}{\mathrm{R}}_{22}\right){\mathrm{T}}_{\mathrm{o}}$ and ${\mathrm{F}}_{21}=-\left(3{\mathsf{\alpha }}^{\mathrm{sf}}{\mathrm{R}}_{11}+{\mathsf{\alpha }}^{\mathrm{f}}{\mathrm{R}}_{21}\right){\mathrm{T}}_{\mathrm{o}}$.

We shall consider an isotropic, homogeneous and porothermoelastic medium occupying the region $\mathrm{x}\ge 0$. For the one-dimensional problem, all the functions considered will depend only on the variables of space $\mathrm{x}$ and $\mathrm{t}$. The components of displacements can be written by:

$${\mathrm{u}}_{\mathrm{x}}=\mathrm{u}\left(\mathrm{x},\mathrm{t}\right),{\mathrm{u}}_{\mathrm{y}}=0,{\mathrm{u}}_{\mathrm{z}}=0,{\mathrm{U}}_{\mathrm{x}}=\mathrm{U}\left(\mathrm{x},\mathrm{t}\right),{\mathrm{U}}_{\mathrm{y}}=0,{\mathrm{U}}_{\mathrm{z}}=0$$

(8)

Then, the governing equations can be defined as

$$\left(\mathsf{\lambda }+2\mathsf{\mu }\right)\frac{{\partial }^2\mathrm{u}}{\partial {\mathrm{x}}^2}+\mathrm{Q}\frac{{\partial }^2\mathrm{U}}{\partial {\mathrm{x}}^2}-{\mathrm{R}}_{11}\left(1+{\mathsf{\tau }}_1^{\mathrm{s}}\frac{\partial }{\partial \mathrm{t}}\right)\frac{\partial {\mathsf{\Theta }}^{\mathrm{s}}}{\partial \mathrm{x}}-{\mathrm{R}}_{12}\left(1+{\mathsf{\tau }}_1^{\mathrm{f}}\frac{\partial }{\partial \mathrm{t}}\right)\frac{\partial {\mathsf{\Theta }}^{\mathrm{f}}}{\partial \mathrm{x}}={\mathsf{\rho }}_{11}\frac{{\partial }^2\mathrm{u}}{\partial {\mathrm{t}}^2}+{\mathsf{\rho }}_{12}\frac{{\partial }^2\mathrm{U}}{\partial {\mathrm{t}}^2},$$

(9)

$$\mathrm{Q}\frac{{\partial }^2\mathrm{u}}{\partial {\mathrm{x}}^2}+\mathrm{R}\frac{{\partial }^2\mathrm{U}}{\partial {\mathrm{x}}^2}-{\mathrm{R}}_{21}\left(1+{\mathsf{\tau }}_1^{\mathrm{s}}\frac{\partial }{\partial \mathrm{t}}\right)\frac{\partial {\mathsf{\Theta }}^{\mathrm{s}}}{\partial \mathrm{x}}-{\mathrm{R}}_{22}\left(1+{\mathsf{\tau }}_1^{\mathrm{f}}\frac{\partial }{\partial \mathrm{t}}\right)\frac{\partial {\mathsf{\Theta }}^{\mathrm{f}}}{\partial \mathrm{x}}={\mathsf{\rho }}_{21}\frac{{\partial }^2\mathrm{u}}{\partial {\mathrm{t}}^2}+{\mathsf{\rho }}_{22}\frac{{\partial }^2\mathrm{U}}{\partial {\mathrm{t}}^2},$$

(10)

$${\mathrm{K}}^{\mathrm{s}}\frac{{\partial }^2{\mathsf{\Theta }}^{\mathrm{s}}}{\partial {\mathrm{x}}^2}=\left(\frac{\partial }{\partial \mathrm{t}}+{\mathsf{\tau }}_{\mathrm{o}}^{\mathrm{s}}\frac{{\partial }^2}{\partial {\mathrm{t}}^2}\right)\left({\mathrm{F}}_{11}{\mathsf{\Theta }}^{\mathrm{s}}+{\mathrm{F}}_{12}{\mathsf{\Theta }}^{\mathrm{f}}\right)+\left(\frac{\partial }{\partial \mathrm{t}}+{\mathrm{n}\mathsf{\tau }}_{\mathrm{o}}^{\mathrm{s}}\frac{{\partial }^2}{\partial {\mathrm{t}}^2}\right)\left({\mathrm{T}}_{\mathrm{o}}{\mathrm{R}}_{11}\frac{\partial \mathrm{u}}{\partial \mathrm{x}}+{\mathrm{T}}_{\mathrm{o}}{\mathrm{R}}_{21}\frac{\partial \mathrm{U}}{\partial \mathrm{x}}\right),$$

(11)

$${\mathrm{K}}^{\mathrm{f}}\frac{{\partial }^2{\mathsf{\Theta }}^{\mathrm{f}}}{\partial {\mathrm{x}}^2}=\left(\frac{\partial }{\partial \mathrm{t}}+{\mathsf{\tau }}_{\mathrm{o}}^{\mathrm{f}}\frac{{\partial }^2}{\partial {\mathrm{t}}^2}\right)\left({\mathrm{F}}_{21}{\mathsf{\Theta }}^{\mathrm{s}}+{\mathrm{F}}_{22}{\mathsf{\Theta }}^{\mathrm{f}}\right)+\left(\frac{\partial }{\partial \mathrm{t}}+{\mathrm{n}\mathsf{\tau }}_{\mathrm{o}}^{\mathrm{f}}\frac{{\partial }^2}{\partial {\mathrm{t}}^2}\right)\left({\mathrm{T}}_{\mathrm{o}}{\mathrm{R}}_{12}\frac{\partial \mathrm{u}}{\partial \mathrm{x}}+{\mathrm{T}}_{\mathrm{o}}{\mathrm{R}}_{22}\frac{\partial \mathrm{U}}{\partial \mathrm{x}}\right),$$

(12)

$${\mathsf{\sigma }}_{\mathrm{xx}}=\left(\mathsf{\lambda }+2\mathsf{\mu }\right)\frac{\partial \mathrm{u}}{\partial \mathrm{x}}+\mathrm{Q}\frac{\partial \mathrm{U}}{\partial \mathrm{x}}-{\mathrm{R}}_{11}\left(1+{\mathsf{\tau }}_1^{\mathrm{s}}\frac{\partial }{\partial \mathrm{t}}\right){\mathsf{\Theta }}^{\mathrm{s}}-{\mathrm{R}}_{12}\left(1+{\mathsf{\tau }}_1^{\mathrm{f}}\frac{\partial }{\partial \mathrm{t}}\right){\mathsf{\Theta }}^{\mathrm{f}},$$

(13)

$$\mathsf{\sigma }=\mathrm{Q}\frac{\partial \mathrm{u}}{\partial \mathrm{x}}+\mathrm{R}\frac{\partial \mathrm{U}}{\partial \mathrm{x}}-{\mathrm{R}}_{21}\left(1+{\mathsf{\tau }}_1^{\mathrm{s}}\frac{\partial }{\partial \mathrm{t}}\right){\mathsf{\Theta }}^{\mathrm{s}}-{\mathrm{R}}_{22}\left(1+{\mathsf{\tau }}_1^{\mathrm{f}}\frac{\partial }{\partial \mathrm{t}}\right){\mathsf{\Theta }}^{\mathrm{f}},$$

(14)

3. Initial and Boundary Conditions

The initial can be expressed as

$$\mathrm{u}\left(\mathrm{x},0\right)=\mathrm{U}\left(\mathrm{x},\mathrm{y},0\right)=0.0,\frac{\partial \mathrm{u}\left(\mathrm{x},0\right)}{\partial \mathrm{t}}=\frac{\partial \mathrm{U}\left(\mathrm{x},0\right)}{\partial \mathrm{t}}=0.0,$$

(15)

$${\mathsf{\Theta }}^{\mathrm{s}}\left(\mathrm{x},0\right)={\mathsf{\Theta }}^{\mathrm{f}}\left(\mathrm{x},0\right)=0,\frac{\partial {\mathsf{\Theta }}^{\mathrm{s}}\left(\mathrm{x},0\right)}{\partial \mathrm{t}}=\frac{\partial {\mathsf{\Theta }}^{\mathrm{f}}\left(\mathrm{x},0\right)}{\partial \mathrm{t}},$$

(16)

While there are two types of boundary conditions, as

1. The thermal boundary conditions

The plane surface boundary of the middle at $\mathrm{x}=0$ has been thermally loaded by thermal shock by the following:

$${\mathsf{\Theta }}^{\mathrm{s}}\left(0,\mathrm{t}\right)=\left(1-\mathsf{\beta }\right){\mathsf{\Theta }}_{\mathrm{o}}\mathrm{H}\left(\mathrm{t}\right),{\mathsf{\Theta }}^{\mathrm{f}}\left(0,\mathrm{t}\right)={\mathsf{\beta }\mathsf{\Theta }}_{\mathrm{o}}\mathrm{H}\left(\mathrm{t}\right)$$

(17)

where ${\mathsf{\Theta }}_{\mathrm{o}}$ is constant and $\mathrm{H}\left(\mathrm{t}\right)$ is the Heaviside unite step function.

2. The mechanical boundary conditions

The bounding surface plane of the middle at $\mathrm{x}=0$ has been connected to tractions free on this surface, i.e.,

$${\mathsf{\sigma }}_{\mathrm{xx}}\left(0,\mathrm{t}\right)=0,\mathsf{\sigma }\left(0,\mathrm{t}\right)=0$$

(18)

For convenience, the dimensionless variables can be written by

$$\begin{gathered} \left(\mathrm{t}\prime ,{\mathsf{\tau }}_{\mathrm{o}}^{\mathrm{s}\prime },{\mathsf{\tau }}_{\mathrm{o}}^{\mathrm{f}\prime },{\mathsf{\tau }}_1^{\mathrm{s}\prime },{\mathsf{\tau }}_1^{\mathrm{f}\prime }\right)={\mathsf{\eta }\mathrm{c}}^2\left(\mathrm{t},{\mathsf{\tau }}_{\mathrm{o}}^{\mathrm{s}},{\mathsf{\tau }}_{\mathrm{o}}^{\mathrm{f}},{\mathsf{\tau }}_1^{\mathrm{s}},{\mathsf{\tau }}_1^{\mathrm{f}}\right),\left(\mathrm{x}\prime ,\mathrm{u}\prime ,\mathrm{U}\prime \right)=\mathsf{\eta }\mathrm{c}\left(\mathrm{x},\mathrm{u},\mathrm{U}\right), \\ \left({\mathsf{\Theta }}^{\mathrm{s}\prime },{\mathsf{\Theta }}^{\mathrm{f}\prime }\right)=\frac{{\mathrm{R}}_{11}\left({\mathsf{\Theta }}^{\mathrm{s}},{\mathsf{\Theta }}^{\mathrm{f}}\right)}{\left(\mathsf{\lambda }+2\mathsf{\mu }\right)},\left({\mathsf{\sigma }}_{\mathrm{xx}}^{\prime },\mathsf{\sigma }\prime \right)=\frac{\left({\mathsf{\sigma }}_{\mathrm{xx}},\mathsf{\sigma }\right)}{\left(\mathsf{\lambda }+2\mathsf{\mu }\right)}, \end{gathered}$$

(19)

where $\mathrm{c}=\sqrt{\frac{\mathsf{\lambda }+2\mathsf{\mu }}{{\mathsf{\rho }}_{11}}}$ and $\mathsf{\eta }=\frac{{\mathrm{F}}_{11}}{{\mathrm{K}}^{\mathrm{s}}}$.

In terms of these non-dimensional forms of variables in (19), the above equations can be expressed as (the script has been neglected for its suitability)

$$\frac{{\partial }^2\mathrm{u}}{\partial {\mathrm{x}}^2}+{\mathrm{f}}_1\frac{{\partial }^2\mathrm{U}}{\partial {\mathrm{x}}^2}-\left(1+{\mathsf{\tau }}_1^{\mathrm{s}}\frac{\partial }{\partial \mathrm{t}}\right)\frac{\partial {\mathsf{\Theta }}^{\mathrm{s}}}{\partial \mathrm{x}}-{\mathrm{f}}_2\left(1+{\mathsf{\tau }}_1^{\mathrm{f}}\frac{\partial }{\partial \mathrm{t}}\right)\frac{\partial {\mathsf{\Theta }}^{\mathrm{f}}}{\partial \mathrm{x}}=\frac{{\partial }^2\mathrm{u}}{\partial {\mathrm{t}}^2}+{\mathrm{f}}_3\frac{{\partial }^2\mathrm{U}}{\partial {\mathrm{t}}^2},$$

(20)

$${\mathrm{f}}_1\frac{{\partial }^2\mathrm{u}}{\partial {\mathrm{x}}^2}+{\mathrm{f}}_4\frac{{\partial }^2\mathrm{U}}{\partial {\mathrm{x}}^2}-{\mathrm{f}}_5\left(1+{\mathsf{\tau }}_1^{\mathrm{s}}\frac{\partial }{\partial \mathrm{t}}\right)\frac{\partial {\mathsf{\Theta }}^{\mathrm{s}}}{\partial \mathrm{x}}-{\mathrm{f}}_6\left(1+{\mathsf{\tau }}_1^{\mathrm{f}}\frac{\partial }{\partial \mathrm{t}}\right)\frac{\partial {\mathsf{\Theta }}^{\mathrm{f}}}{\partial \mathrm{x}}={\mathrm{f}}_7\frac{{\partial }^2\mathrm{u}}{\partial {\mathrm{t}}^2}+{\mathrm{f}}_8\frac{{\partial }^2\mathrm{U}}{\partial {\mathrm{t}}^2},$$

(21)

$$\frac{{\partial }^2{\mathsf{\Theta }}^{\mathrm{s}}}{\partial {\mathrm{x}}^2}=\left(\frac{\partial }{\partial \mathrm{t}}+{\mathsf{\tau }}_{\mathrm{o}}^{\mathrm{s}}\frac{{\partial }^2}{\partial {\mathrm{t}}^2}\right)\left({\mathsf{\Theta }}^{\mathrm{s}}+{\mathrm{f}}_9{\mathsf{\Theta }}^{\mathrm{f}}\right)+\left(\frac{\partial }{\partial \mathrm{t}}+{\mathrm{n}\mathsf{\tau }}_{\mathrm{o}}^{\mathrm{s}}\frac{{\partial }^2}{\partial {\mathrm{t}}^2}\right)\left({\mathrm{f}}_{10}\frac{\partial \mathrm{u}}{\partial \mathrm{x}}+{\mathrm{f}}_{11}\frac{\partial \mathrm{U}}{\partial \mathrm{x}}\right),$$

(22)

$$\frac{{\partial }^2{\mathsf{\Theta }}^{\mathrm{f}}}{\partial {\mathrm{x}}^2}=\left(\frac{\partial }{\partial \mathrm{t}}+{\mathsf{\tau }}_{\mathrm{o}}^{\mathrm{f}}\frac{{\partial }^2}{\partial {\mathrm{t}}^2}\right)\left({\mathrm{f}}_{12}{\mathsf{\Theta }}^{\mathrm{s}}+{\mathrm{f}}_{13}{\mathsf{\Theta }}^{\mathrm{f}}\right)+\left(\frac{\partial }{\partial \mathrm{t}}+{\mathrm{n}\mathsf{\tau }}_{\mathrm{o}}^{\mathrm{f}}\frac{{\partial }^2}{\partial {\mathrm{t}}^2}\right)\left({\mathrm{f}}_{14}\frac{\partial \mathrm{u}}{\partial \mathrm{x}}+{\mathrm{f}}_{15}\frac{\partial \mathrm{U}}{\partial \mathrm{x}}\right),$$

(23)

$${\mathsf{\sigma }}_{\mathrm{xx}}=\frac{\partial \mathrm{u}}{\partial \mathrm{x}}+{\mathrm{f}}_1\frac{\partial \mathrm{U}}{\partial \mathrm{x}}-\left(1+{\mathsf{\tau }}_1^{\mathrm{s}}\frac{\partial }{\partial \mathrm{t}}\right){\mathsf{\Theta }}^{\mathrm{s}}-{\mathrm{f}}_2\left(1+{\mathsf{\tau }}_1^{\mathrm{f}}\frac{\partial }{\partial \mathrm{t}}\right){\mathsf{\Theta }}^{\mathrm{f}},$$

(24)

$$\mathsf{\sigma }={\mathrm{f}}_1\frac{\partial \mathrm{u}}{\partial \mathrm{x}}+{\mathrm{f}}_4\frac{\partial \mathrm{U}}{\partial \mathrm{x}}-{\mathrm{f}}_5\left(1+{\mathsf{\tau }}_1^{\mathrm{s}}\frac{\partial }{\partial \mathrm{t}}\right){\mathsf{\Theta }}^{\mathrm{s}}-{\mathrm{f}}_6\left(1+{\mathsf{\tau }}_1^{\mathrm{f}}\frac{\partial }{\partial \mathrm{t}}\right){\mathsf{\Theta }}^{\mathrm{f}},$$

(25)

$$\mathrm{u}\left(\mathrm{x},0\right)=\mathrm{U}\left(\mathrm{x},\mathrm{y},0\right)=0.0,\frac{\partial \mathrm{u}\left(\mathrm{x},0\right)}{\partial \mathrm{t}}=\frac{\partial \mathrm{U}\left(\mathrm{x},0\right)}{\partial \mathrm{t}}=0.0,$$

(26)

$${\mathsf{\Theta }}^{\mathrm{s}}\left(\mathrm{x},0\right)={\mathsf{\Theta }}^{\mathrm{f}}\left(\mathrm{x},0\right)=0.0,\frac{\partial {\mathsf{\Theta }}^{\mathrm{s}}\left(\mathrm{x},0\right)}{\partial \mathrm{t}}=\frac{\partial {\mathsf{\Theta }}^{\mathrm{f}}\left(\mathrm{x},0\right)}{\partial \mathrm{t}}=0.0,$$

(27)

$${\mathsf{\Theta }}^{\mathrm{s}}\left(0,\mathrm{t}\right)=\left(1-\mathsf{\beta }\right){\mathsf{\Theta }}_{\mathrm{o}}\mathrm{H}\left(\mathrm{t}\right),{\mathsf{\Theta }}^{\mathrm{f}}\left(0,\mathrm{t}\right)={\mathsf{\beta }\mathsf{\Theta }}_{\mathrm{o}}\mathrm{H}\left(\mathrm{t}\right),$$

(28)

$${\mathsf{\sigma }}_{\mathrm{xx}}\left(0,\mathrm{t}\right)=0,\mathsf{\sigma }\left(0,\mathrm{t}\right)=0,$$

(29)

where

• ${\mathrm{f}}_1=\frac{\mathrm{Q}}{\mathsf{\lambda }+2\mathsf{\mu }}$, ${\mathrm{f}}_2=\frac{{\mathrm{R}}_{12}}{{\mathrm{R}}_{11}}$, ${\mathrm{f}}_3=\frac{{\mathsf{\rho }}_{12}}{{\mathsf{\rho }}_{11}}$, ${\mathrm{f}}_4=\frac{\mathrm{R}}{\mathsf{\lambda }+2\mathsf{\mu }}$, ${\mathrm{f}}_5=\frac{{\mathrm{R}}_{21}}{{\mathrm{R}}_{11}}$, ${\mathrm{f}}_6=\frac{{\mathrm{R}}_{22}}{{\mathrm{R}}_{11}}$, ${\mathrm{f}}_7=\frac{{\mathsf{\rho }}_{21}}{{\mathsf{\rho }}_{11}}$, ${\mathrm{f}}_8=\frac{{\mathsf{\rho }}_{22}}{{\mathsf{\rho }}_{11}}$, ${\mathrm{f}}_9=\frac{{\mathrm{F}}_{12}}{{\mathrm{F}}_{11}}$,
• ${\mathrm{f}}_{10}=\frac{{\mathrm{T}}_{\mathrm{o}}{\mathrm{R}}_{11}^2}{{\mathrm{F}}_{11}\left(\mathsf{\lambda }+2\mathsf{\mu }\right)}$, ${\mathrm{f}}_{11}=\frac{{\mathrm{T}}_{\mathrm{o}}{\mathrm{R}}_{11}{\mathrm{R}}_{21}}{{\mathrm{F}}_{11}\left(\mathsf{\lambda }+2\mathsf{\mu }\right)}$, ${\mathrm{f}}_{12}=\frac{{\mathrm{F}}_{21}}{{\mathsf{\eta }\mathrm{K}}^{\mathrm{f}}}$, ${\mathrm{f}}_{13}=\frac{{\mathrm{F}}_{22}}{{\mathsf{\eta }\mathrm{K}}^{\mathrm{f}}}$, ${\mathrm{f}}_{14}=\frac{{\mathrm{T}}_{\mathrm{o}}{\mathrm{R}}_{11}{\mathrm{R}}_{12}}{{\mathsf{\eta }\mathrm{K}}^{\mathrm{f}}\left(\mathsf{\lambda }+2\mathsf{\mu }\right)}$, ${\mathrm{f}}_{15}=\frac{{\mathrm{T}}_{\mathrm{o}}{\mathrm{R}}_{11}{\mathrm{R}}_{22}}{{\mathsf{\eta }\mathrm{K}}^{\mathrm{f}}\left(\mathsf{\lambda }+2\mathsf{\mu }\right)}$

4. Finite Element Method

In this section, the complex equations of wave propagation in a poroelastic medium are abbreviated by the finite element method (FEM). The finite element technique has been used here to obtain the solutions of Equations (20)–(23) under the boundary and initial conditions (26)–(29). This method is an originally advanced method and powerful for numerical solutions to complex problems in many fields and is the process of choice for complex systems. Another priority of this technique is that it allows the visualizing and quantifying of the physical effects, regardless of the experimental limits. The finite element equations of a porothermoelastic problem can be easily obtained by following the standard procedure, as in Abbas et al. [35,36]. In the finite element method, the corresponding nodal values of temperatures and displacements can be expressed by the forms

$${\overline{\mathsf{\Theta }}}^{\mathrm{s}}={\displaystyle \sum }_{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{N}}_{\mathrm{j}}{\overline{\mathsf{\Theta }}}_{\mathrm{j}}^{\mathrm{s}}\left(\mathrm{t}\right),{\overline{\mathsf{\Theta }}}^{\mathrm{f}}={\displaystyle \sum }_{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{N}}_{\mathrm{j}}{\overline{\mathsf{\Theta }}}_{\mathrm{j}}^{\mathrm{f}}\left(\mathrm{t}\right),\overline{\mathrm{u}}={\displaystyle \sum }_{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{N}}_{\mathrm{j}}{\overline{\mathrm{u}}}_{\mathrm{j}}\left(\mathrm{t}\right),\overline{\mathrm{U}}={\displaystyle \sum }_{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{N}}_{\mathrm{j}}{\overline{\mathrm{U}}}_{\mathrm{j}}\left(\mathrm{t}\right),$$

(30)

where n refers to the nodes number per element, while N points to the shape functions. As part of the standard Galerkin procedure, shape functions and weighting functions are identified. Three quadratic element nodes are used. So,

$${\mathsf{\delta }\overline{\mathsf{\Theta }}}^{\mathrm{s}}={\displaystyle \sum }_{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{N}}_{\mathrm{j}}{\mathsf{\delta }\overline{\mathsf{\Theta }}}_{\mathrm{j}}^{\mathrm{s}},{\mathsf{\delta }\overline{\mathsf{\Theta }}}^{\mathrm{f}}={\displaystyle \sum }_{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{N}}_{\mathrm{j}}{\mathsf{\delta }\overline{\mathsf{\Theta }}}_{\mathrm{j}}^{\mathrm{f}},\mathsf{\delta }\overline{\mathrm{u}}={\displaystyle \sum }_{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{N}}_{\mathrm{j}}{\mathsf{\delta }\overline{\mathrm{u}}}_{\mathrm{j}},\mathsf{\delta }\overline{\mathrm{U}}={\displaystyle \sum }_{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{N}}_{\mathrm{j}}{\mathsf{\delta }\overline{\mathrm{U}}}_{\mathrm{j}},$$

(31)

On the other hand, the time derivatives of unknown variables must be computed using the implicit method. Now, the weak formulation for the finite element approach corresponding to (20)–(23) can be written as follows

$${{\displaystyle \int }}_0^{\mathrm{L}}\frac{\partial \mathsf{\delta }\mathrm{u}}{\partial \mathrm{x}}\left({\mathsf{\sigma }}_{\mathrm{xx}}\right)\mathrm{dx}+{{\displaystyle \int }}_0^{\mathrm{L}}\mathsf{\delta }\mathrm{u}\left(\frac{{\partial }^2\mathrm{u}}{\partial {\mathrm{t}}^2}+{\mathrm{f}}_3\frac{{\partial }^2\mathrm{U}}{\partial {\mathrm{t}}^2}\right)\mathrm{dx}=\mathsf{\delta }\mathrm{u}{\left({\mathsf{\sigma }}_{\mathrm{xx}}\right)}_0^{\mathrm{L}},$$

(32)

$${{\displaystyle \int }}_0^{\mathrm{L}}\frac{\partial \mathsf{\delta }\mathrm{U}}{\partial \mathrm{x}}\left(\mathsf{\sigma }\right)\mathrm{dx}+{{\displaystyle \int }}_0^{\mathrm{L}}\mathsf{\delta }\mathrm{U}\left({\mathrm{f}}_7\frac{{\partial }^2\mathrm{u}}{\partial {\mathrm{t}}^2}+{\mathrm{f}}_8\frac{{\partial }^2\mathrm{U}}{\partial {\mathrm{t}}^2}\right)\mathrm{dx}=\mathsf{\delta }\mathrm{U}{\left(\mathsf{\sigma }\right)}_0^{\mathrm{L}},$$

(33)

$${{\displaystyle \int }}_0^{\mathrm{L}}\frac{\partial {\mathsf{\delta }\mathsf{\Theta }}^{\mathrm{s}}}{\partial \mathrm{x}}\frac{\partial {\mathsf{\Theta }}^{\mathrm{s}}}{\partial \mathrm{x}}\mathrm{dx}+{{\displaystyle \int }}_0^{\mathrm{L}}{\mathsf{\delta }\mathsf{\Theta }}^{\mathrm{s}}\left(\left(\frac{\partial }{\partial \mathrm{t}}+{\mathsf{\tau }}_{\mathrm{o}}^{\mathrm{s}}\frac{{\partial }^2}{\partial {\mathrm{t}}^2}\right)\left({\mathsf{\Theta }}^{\mathrm{s}}+{\mathrm{n}}_9{\mathsf{\Theta }}^{\mathrm{f}}+\mathrm{n}\left({\mathrm{f}}_{10}\frac{\partial \mathrm{u}}{\partial \mathrm{x}}+{\mathrm{f}}_{11}\frac{\partial \mathrm{U}}{\partial \mathrm{x}}\right)\right)\right)\mathrm{dx}={\mathsf{\delta }\mathsf{\Theta }}^{\mathrm{s}}{\left(\frac{\partial {\mathsf{\Theta }}^{\mathrm{s}}}{\partial \mathrm{x}}\right)}_0^{\mathrm{L}},$$

(34)

$${{\displaystyle \int }}_0^{\mathrm{L}}\frac{\partial {\mathsf{\delta }\mathsf{\Theta }}^{\mathrm{f}}}{\partial \mathrm{x}}\frac{\partial {\mathsf{\Theta }}^{\mathrm{f}}}{\partial \mathrm{x}}\mathrm{dx}+{{\displaystyle \int }}_0^{\mathrm{L}}{\mathsf{\delta }\mathsf{\Theta }}^{\mathrm{f}}\left(\left(\frac{\partial }{\partial \mathrm{t}}+{\mathsf{\tau }}_{\mathrm{o}}^{\mathrm{f}}\frac{{\partial }^2}{\partial {\mathrm{t}}^2}\right)\left({\mathrm{f}}_{12}{\mathsf{\Theta }}^{\mathrm{s}}+{\mathrm{f}}_{13}{\mathsf{\Theta }}^{\mathrm{f}}+\mathrm{n}\left({\mathrm{f}}_{14}\frac{\partial \mathrm{u}}{\partial \mathrm{x}}+{\mathrm{f}}_{15}\frac{\partial \mathrm{U}}{\partial \mathrm{x}}\right)\right)\right)\mathrm{dx}={\mathsf{\delta }\mathsf{\Theta }}^{\mathrm{f}}{\left(\frac{\partial {\mathsf{\Theta }}^{\mathrm{f}}}{\partial \mathrm{x}}\right)}_0^{\mathrm{L}},$$

(35)

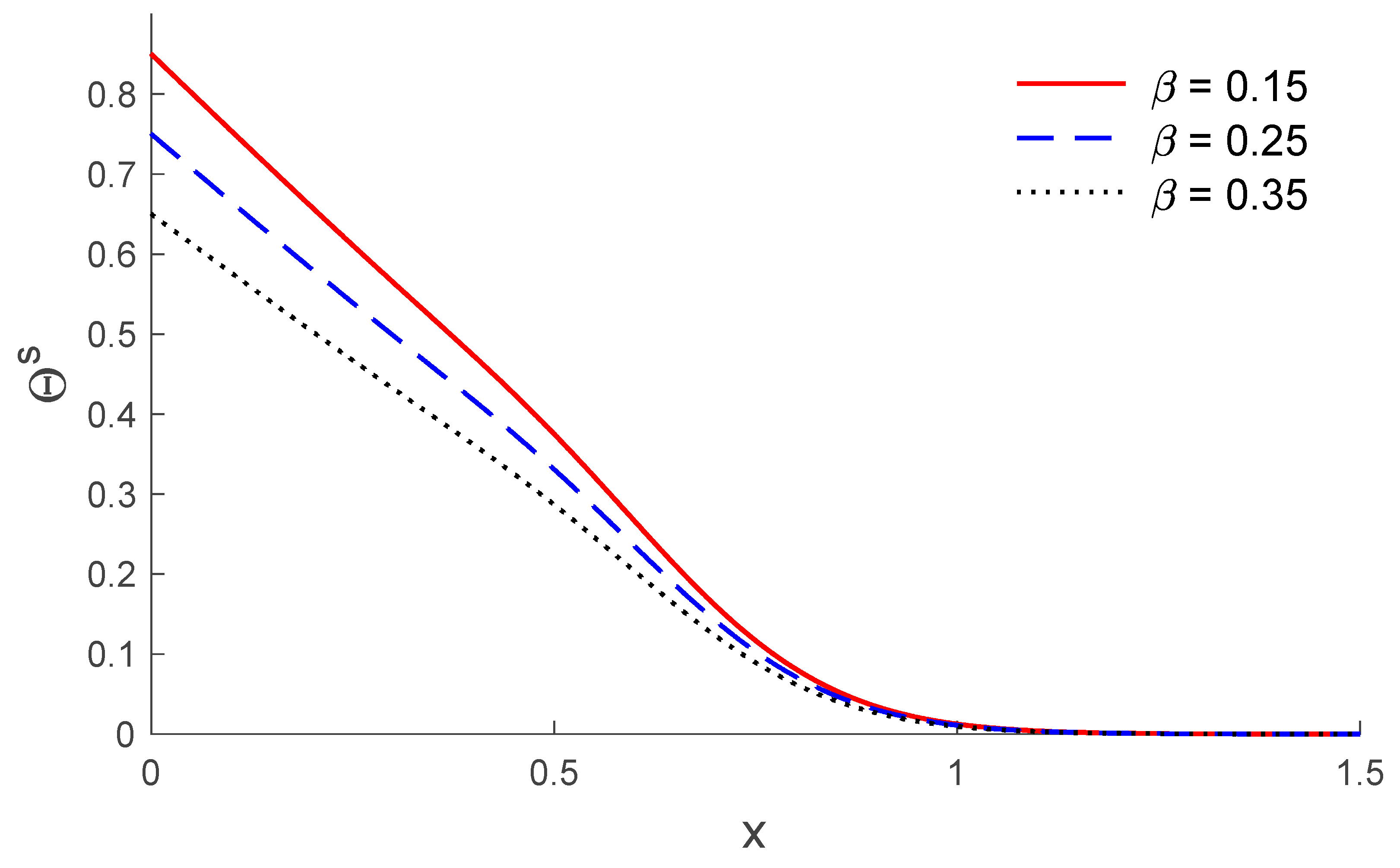
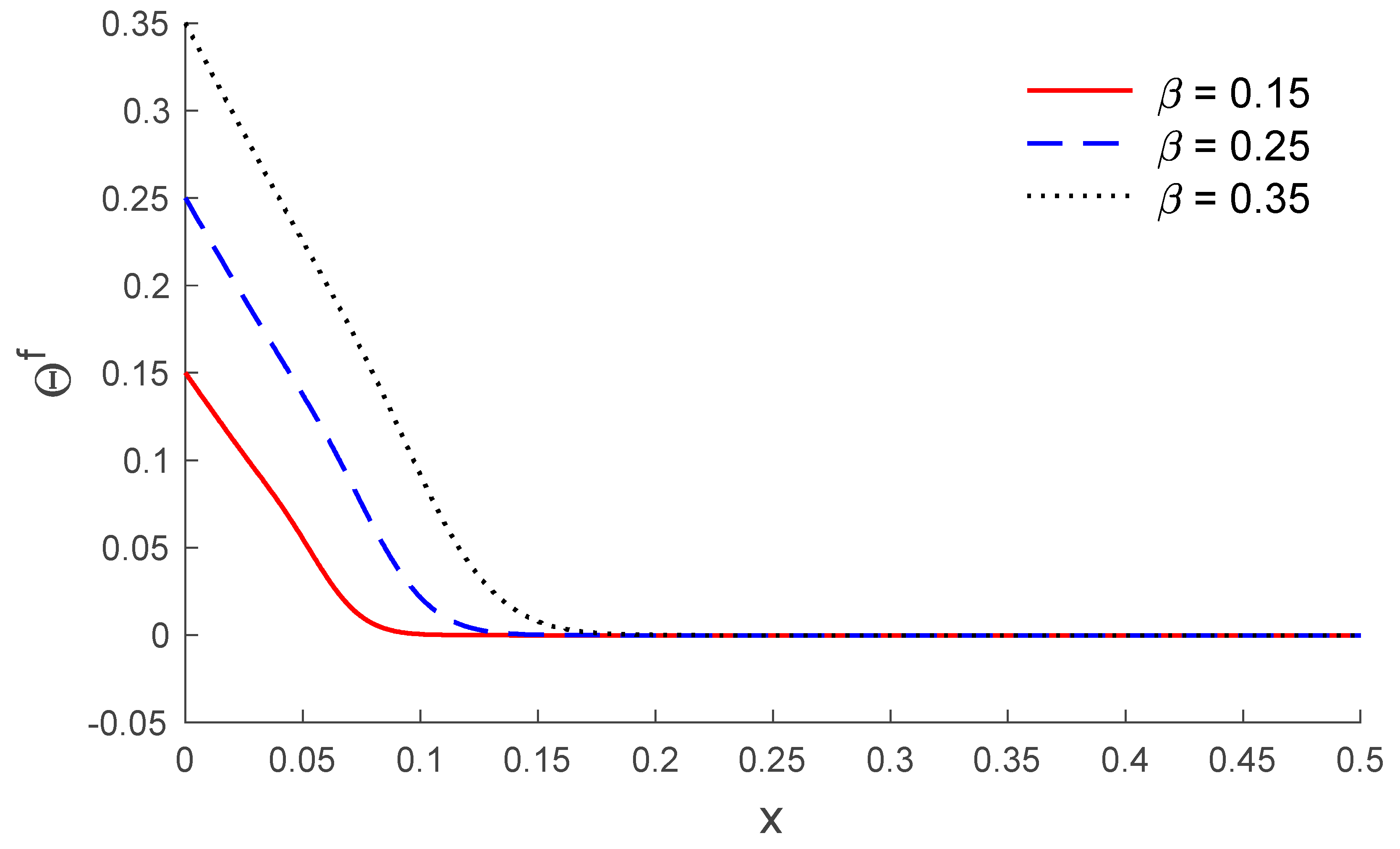
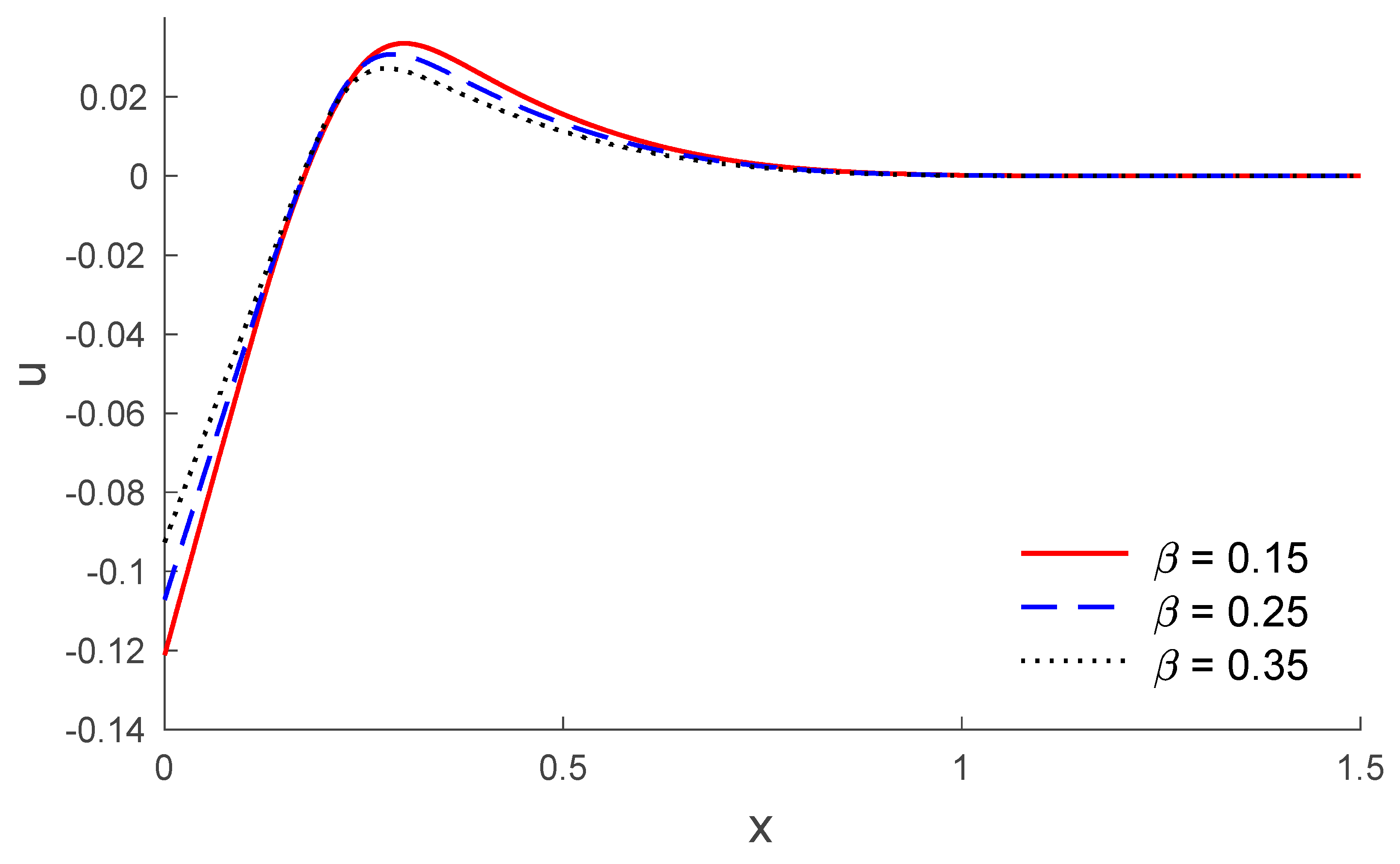
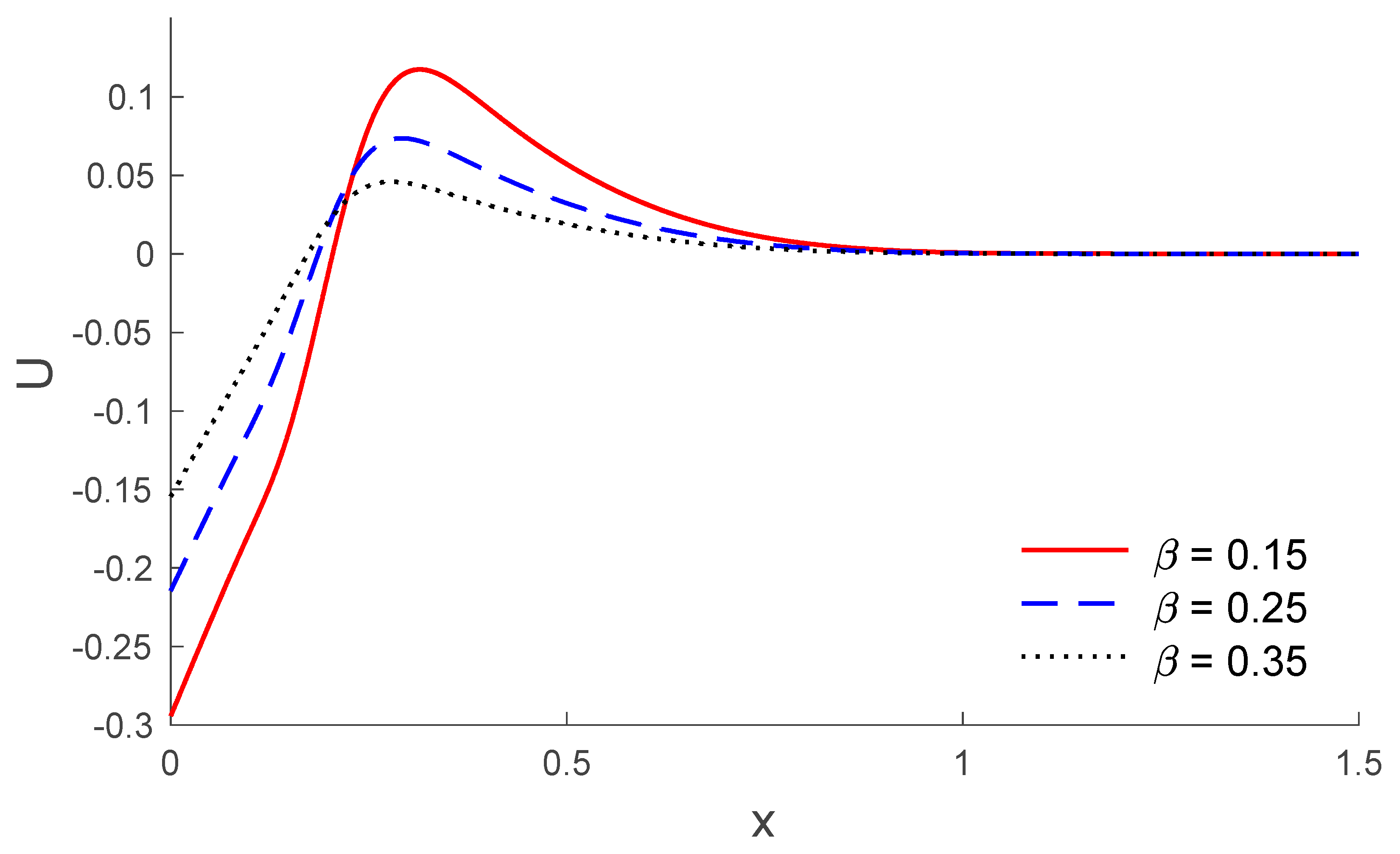
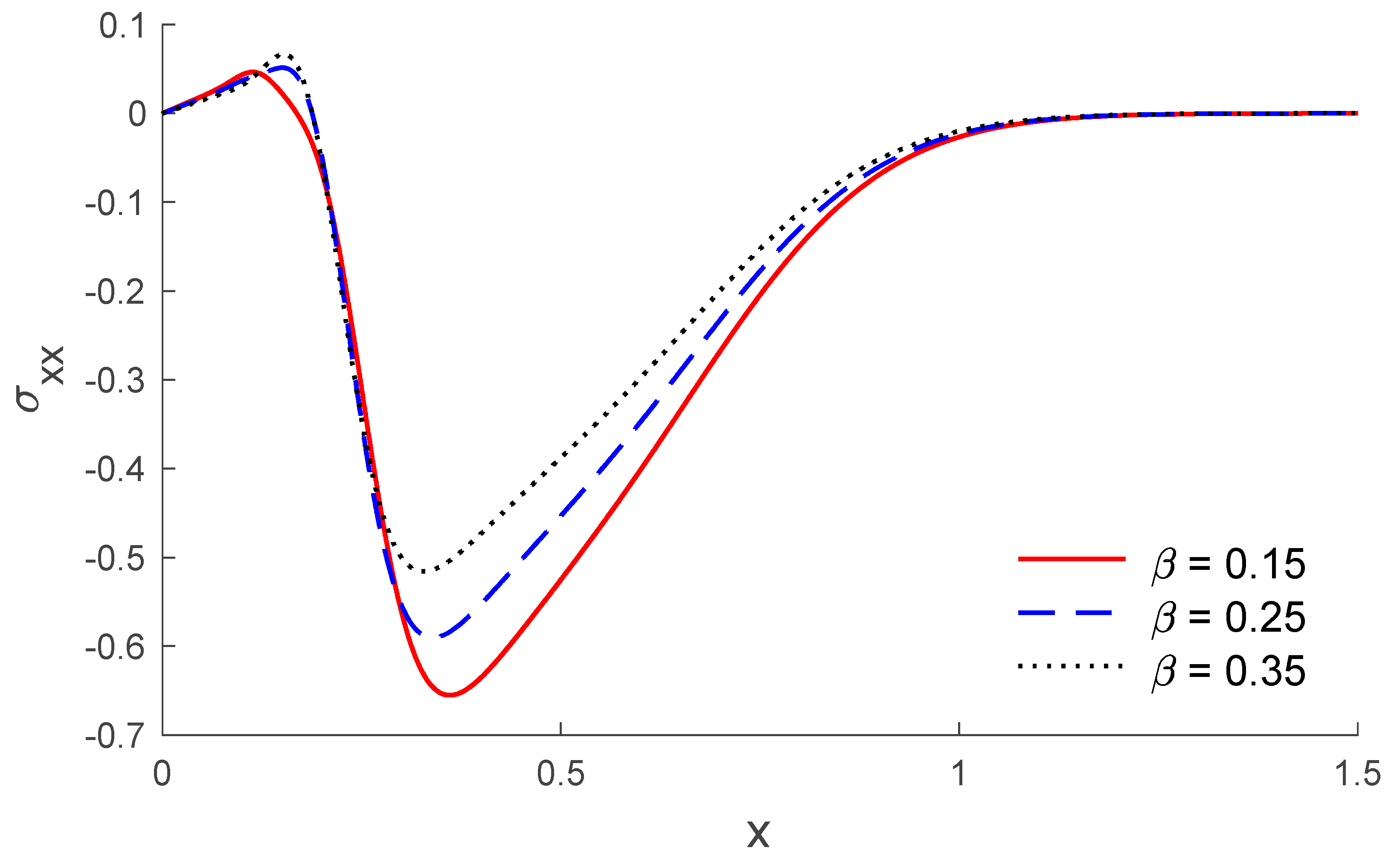
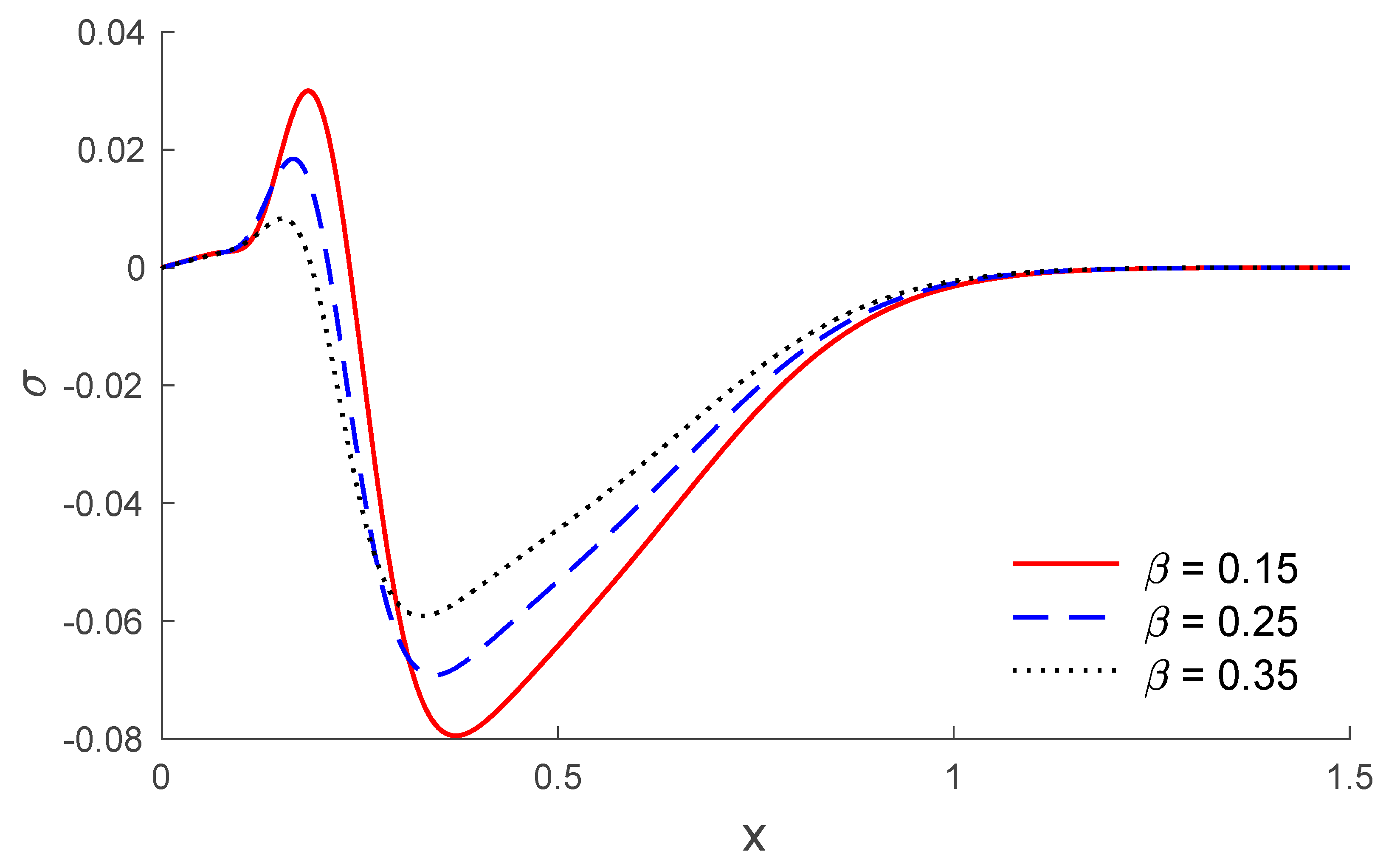
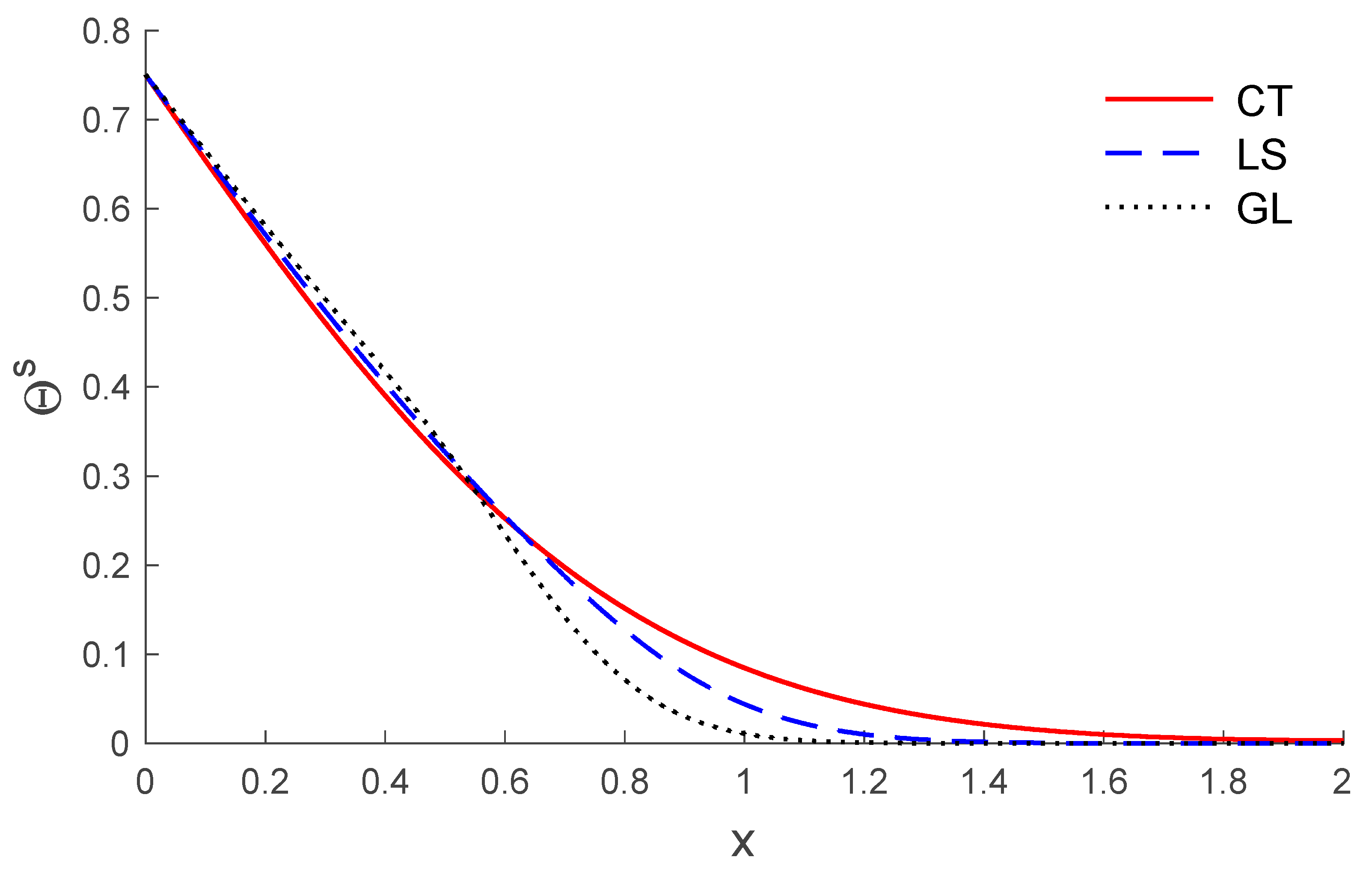
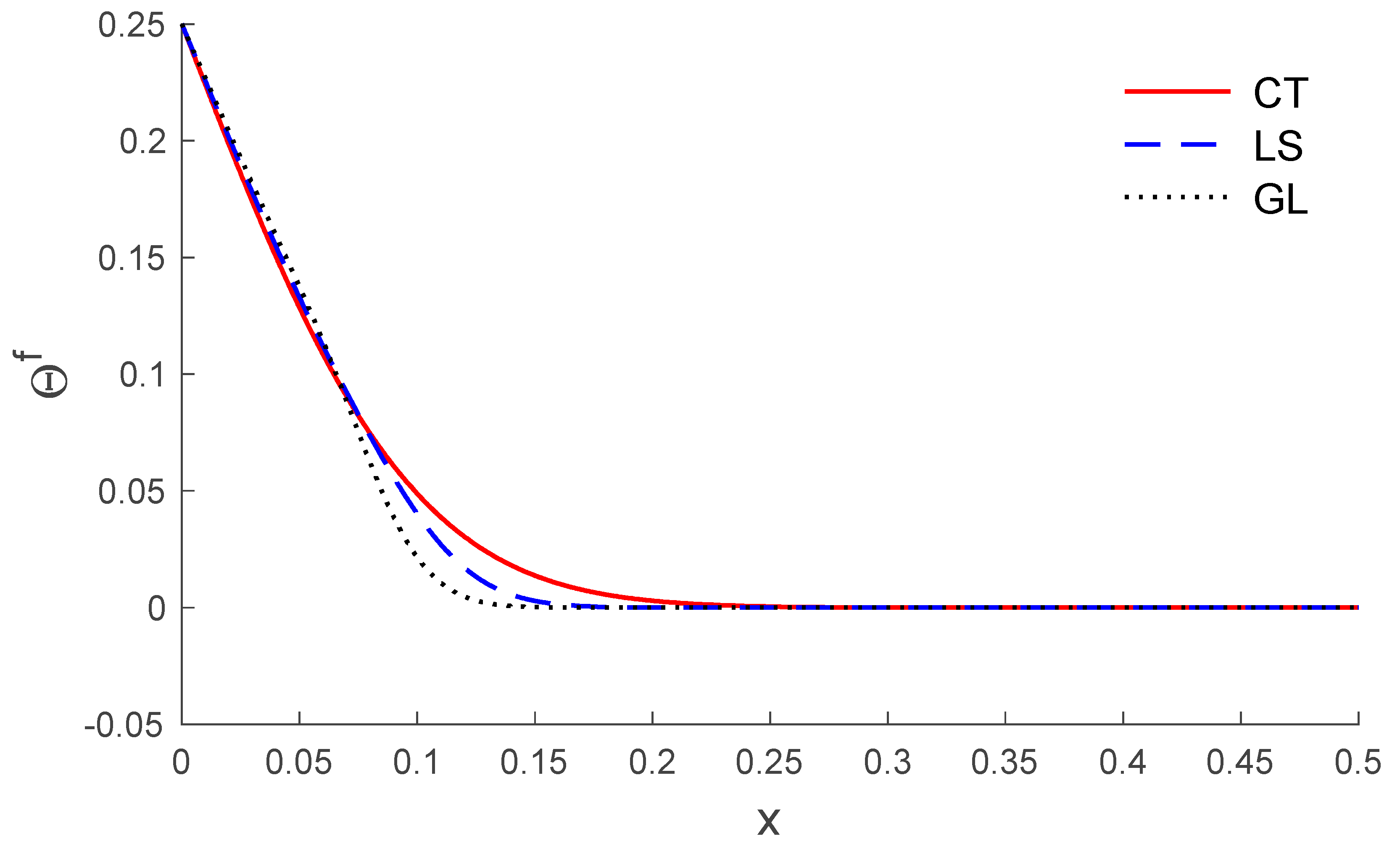
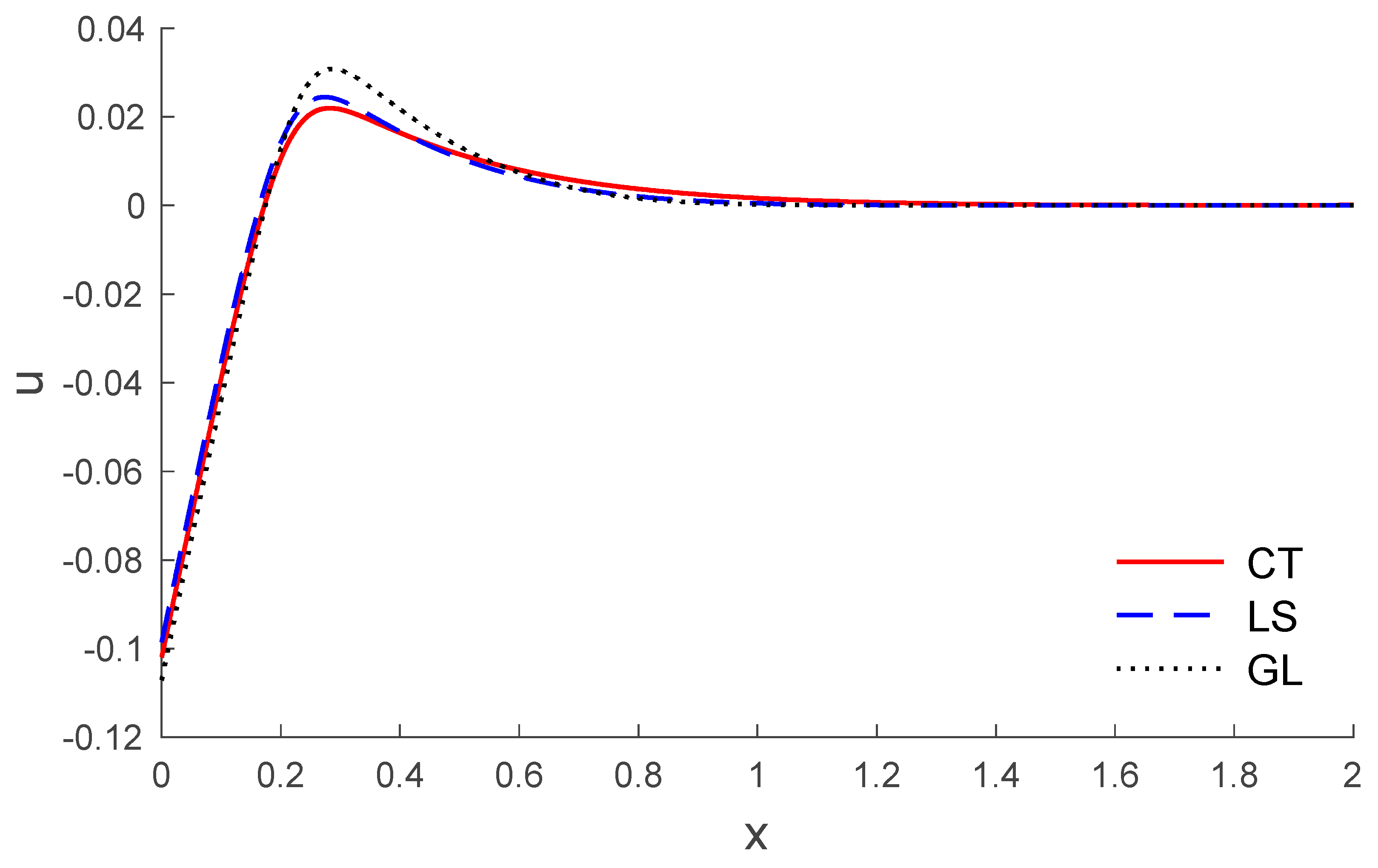
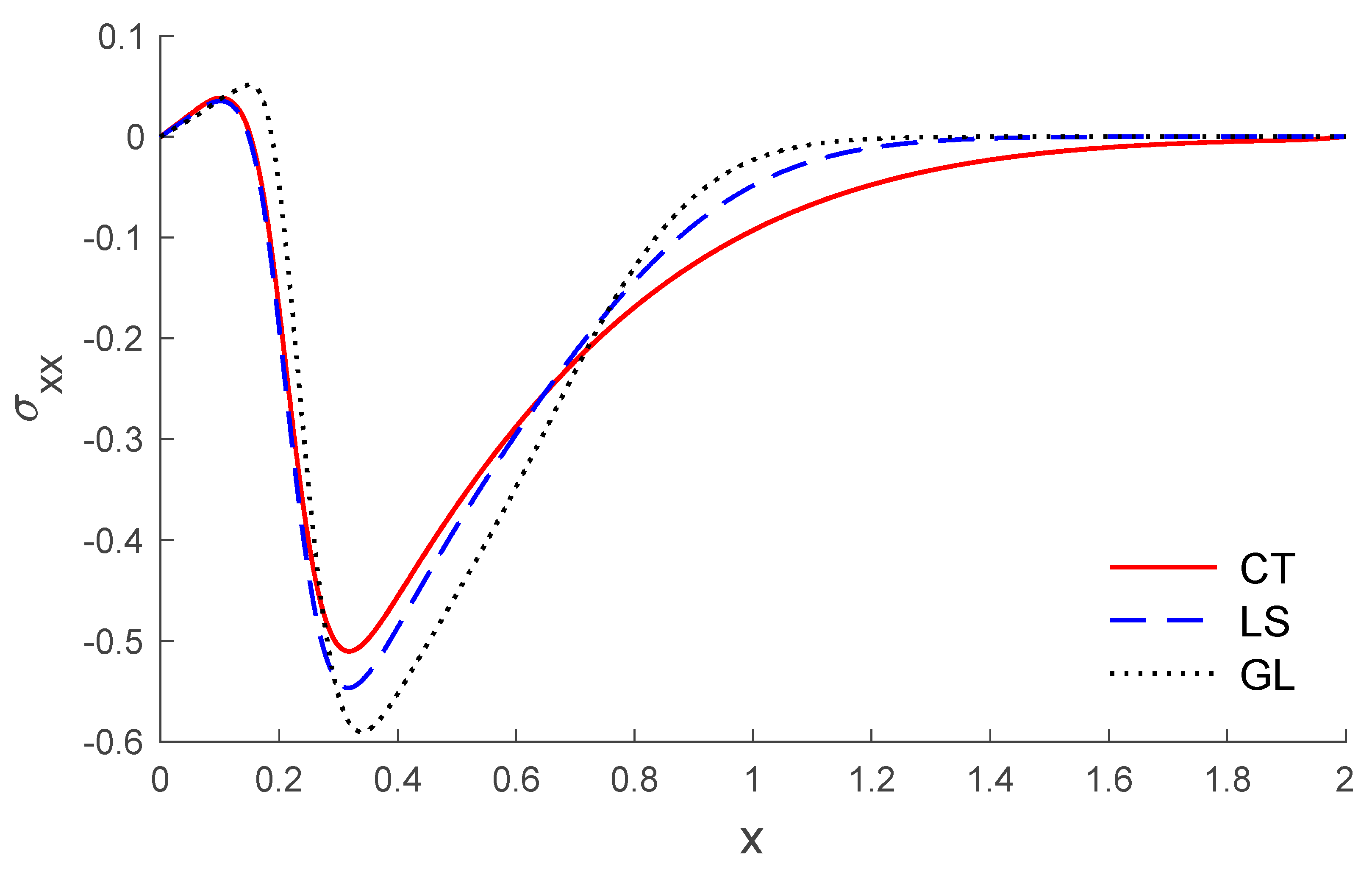
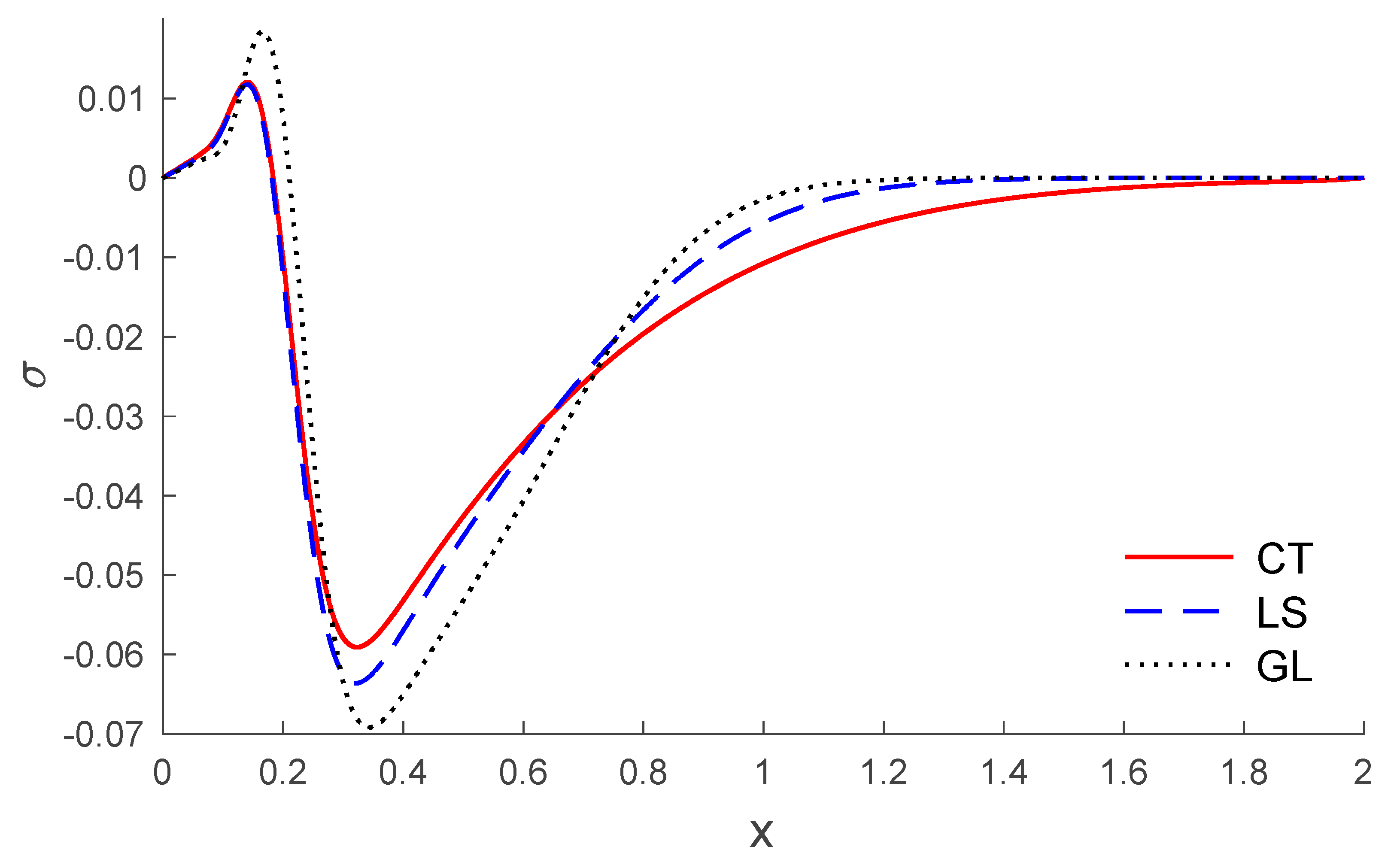
5. Results and Discussion

The physical quantities distributions in a poroelastic medium are studied. For numerical computations, the values of thermal properties for sandstone saturated with water at ${\mathrm{T}}_{\mathrm{o}}=27℃$ have been written as, in Singh [7,37]:

$$\mathrm{R}=0.07435\times {10}^{11}\left(\mathrm{dyne}\right)\left({\mathrm{cm}}^{-2}\right),\mathrm{Q}=0.99663\times {10}^{11}\left(\mathrm{dyne}\right)\left({\mathrm{cm}}^{-2}\right),$$

$${\mathrm{K}}^{\mathrm{s}}=0.4\left(\mathrm{cal}\right)\left({\mathrm{cm}}^{-1}\right)\left({\mathrm{s}}^{-1}\right)\left({℃}^{-1}\right),{\mathrm{K}}^{\mathrm{f}}=0.3\left(\mathrm{cal}\right)\left({\mathrm{cm}}^{-1}\right)\left({\mathrm{s}}^{-1}\right)\left({℃}^{-1}\right),$$

$$\mathsf{\mu }=0.2765\times {10}^{11}\left(\mathrm{dyne}\right)\left({\mathrm{cm}}^{-2}\right),\mathsf{\lambda }=0.44363\times {10}^{11}\left(\mathrm{dyne}\right)\left({\mathrm{cm}}^{-2}\right),$$

$${\mathsf{\rho }}^{\mathrm{s}*}=2.6\left(\mathrm{g}\right)\left({\mathrm{cm}}^{-3}\right),{\mathsf{\rho }}^{\mathrm{f}*}=0.82\left(\mathrm{g}\right)\left({\mathrm{cm}}^{-3}\right),{\mathsf{\rho }}_{11}=0.002137\left(\mathrm{g}\right)\left({\mathrm{cm}}^{-3}\right),$$

$${\mathrm{C}}_{\mathrm{E}}^{\mathrm{s}}=2.1\left(\mathrm{cal}\right)\left({\mathrm{g}}^{-1}\right)\left({℃}^{-1}\right),{\mathrm{C}}_{\mathrm{E}}^{\mathrm{f}}=1.9\left(\mathrm{cal}\right)\left({\mathrm{g}}^{-1}\right)\left({℃}^{-1}\right),$$

$${\mathsf{\alpha }}^{\mathrm{s}}={\mathsf{\alpha }}^{\mathrm{f}}={\mathsf{\alpha }}^{\mathrm{sf}}={\mathsf{\alpha }}^{\mathrm{fs}}=0.1\left({\mathrm{cm}}^{-3}\right)\left({\mathrm{g}}^{-1}\right).$$

Based on the above dataset, Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12 explain the physical quantities computed numerically at different values of the distance x. Numerical computations are carried out for the solid and liquid temperatures, the displacements and the stresses distributions of solid and liquid phases along the x-axis, in the context of porothermal theory, under four thermal relaxation times. Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6 represent the three curves predicted by various values of porosity considering the time $\left(\mathrm{t}=0.2\right)$, under Green and Lindsay’s model. Meanwhile, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12 represent the three curves predicted by various models, considering the time $\left(\mathrm{t}=0.2\right)$ and the porosity $\left(\mathsf{\beta }=0.25\right)$. From Figure 1 and Figure 7, it is observed that the temperature of the solid phase starts by its maximum values at $\mathrm{x}=0$ and progressively decreases with increases of the distance $\mathrm{x}$ up to zero, beyond a wave front for the porothermal theory, that satisfies the problem theoretical boundary conditions. Figure 2 and Figure 8 show the variations of the liquid temperature as a function of the distance $\mathrm{x}$. It was noted that the ${\mathsf{\Theta }}^{\mathrm{f}}$ values are the highest value on $\mathrm{x}=0$ and they decrease when the increasing distance $\mathrm{x}$ is too close to zero on $\mathrm{x}=0.08$, which depends on the porosity and the type of model. The displacement changes of solid and liquid phases versus $\mathrm{x}$ are shown in Figure 3, Figure 4, Figure 9 and Figure 10. It is clear that they attain maximum negative value and increase progressively until they reach maximum values at a particular location near $\mathrm{x}=0.0$, and then continuously decrease to zero values. Figure 5, Figure 6, Figure 11 and Figure 12 display the effects of the porosity and the thermal relaxation times in the solid and liquid stresses along the distance $\mathrm{x}$. As expected, it can be found that the porosity and the thermal relaxation times have major impacts on the values of all the studied fields.

6. Conclusions

Based on the generalized thermoelastic theory with four thermal relaxation times, the variations of temperature, the components of displacement and the components of stress in a poroelastic medium are studied. The non-dimensional resulting has been solved, employing the finite element method. The great effects of the thermal relaxation times and porosity are discussed for all physical quantities. We believe that the analysis of the present study will be useful to understand the basic features of this new model for heat conduction.