Finite Difference Approximation Method for a Space Fractional Convection–Diffusion Equation with Variable Coefficients
Abstract
1. Introduction
2. Preliminary Remarks
3. Problem Formulation of the Scheme
Crank–Nicolson Scheme for Time and Shifted Grünwald Difference Scheme for Space Discretization
4. Theoretical Analysis of Finite Difference Scheme
4.1. Boundedness of the Fractional Scheme
4.2. Stability Analysis
4.3. Convergence Analysis
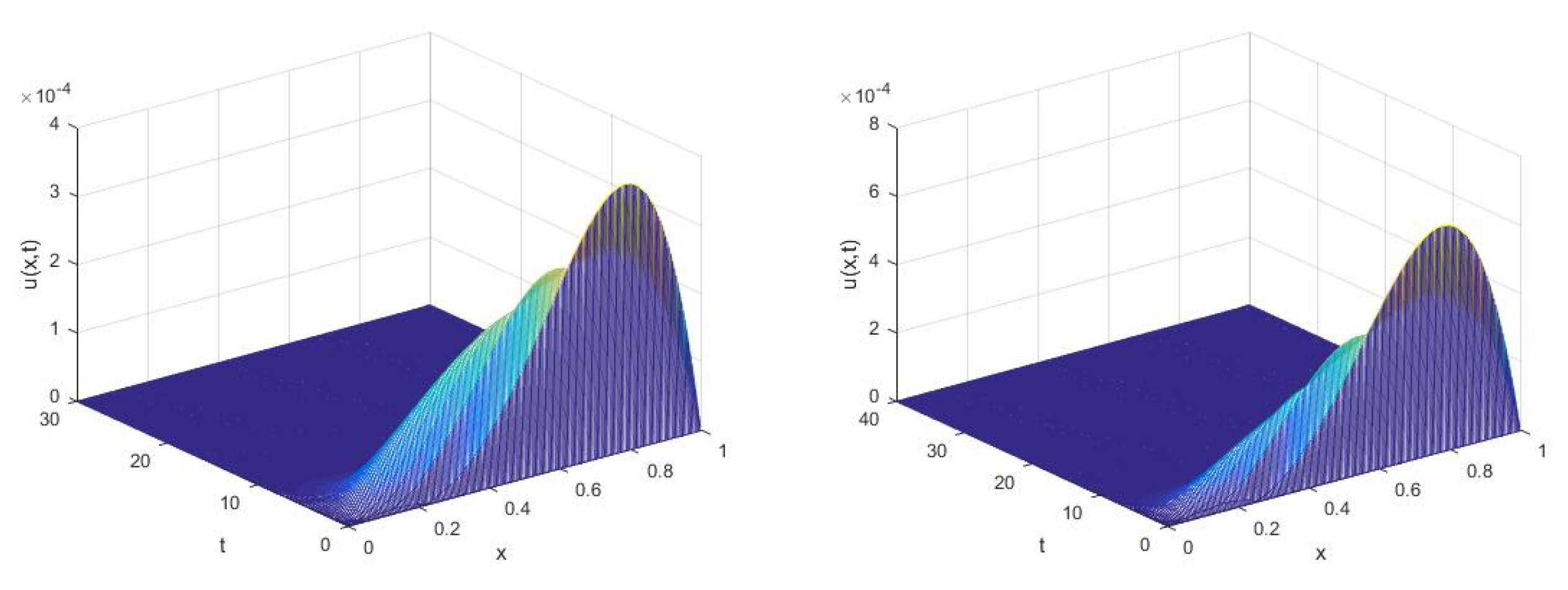
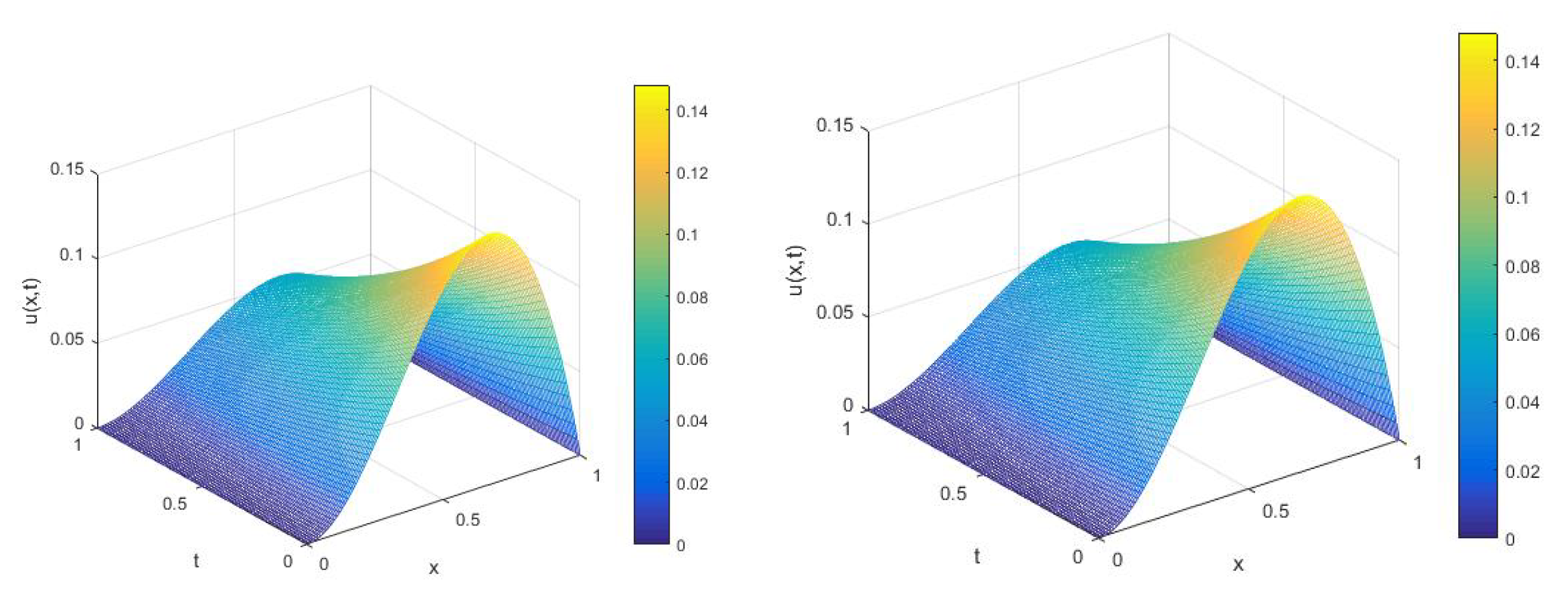
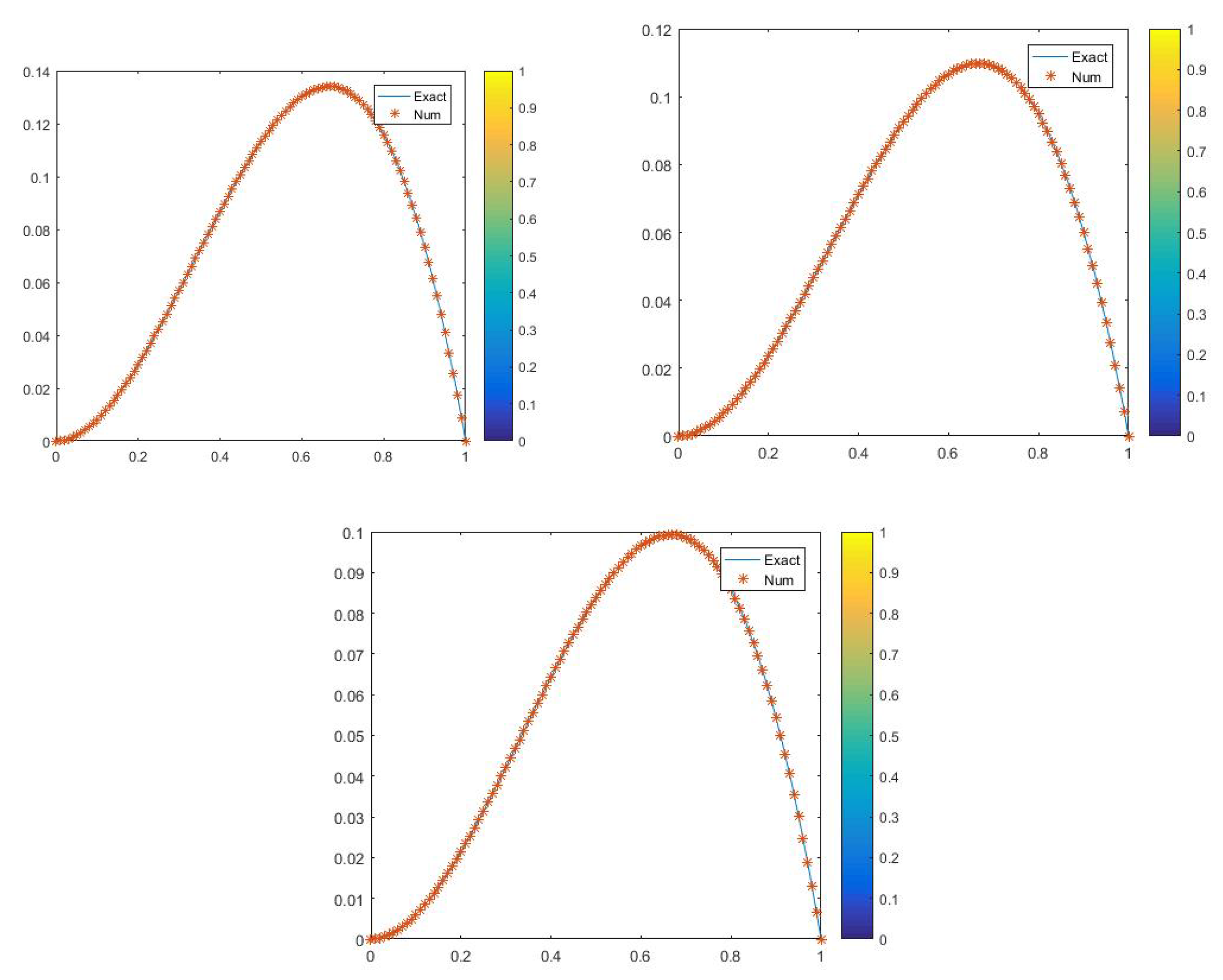
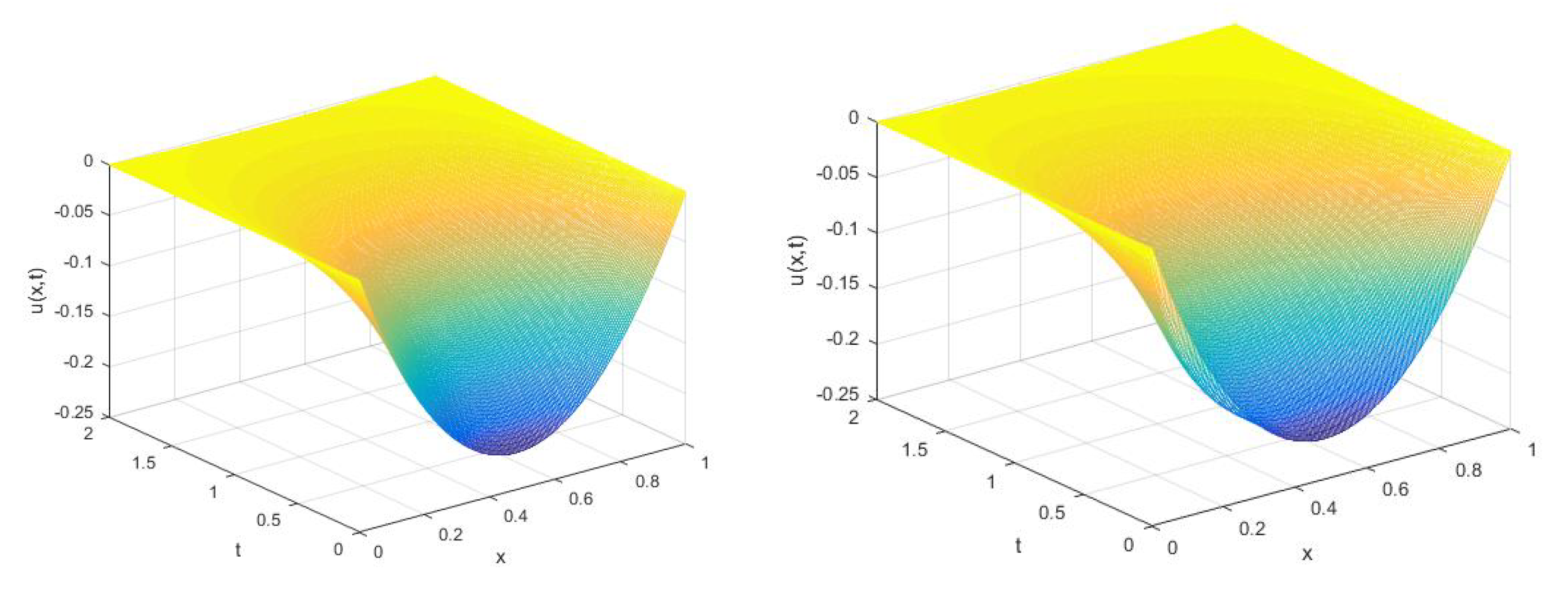
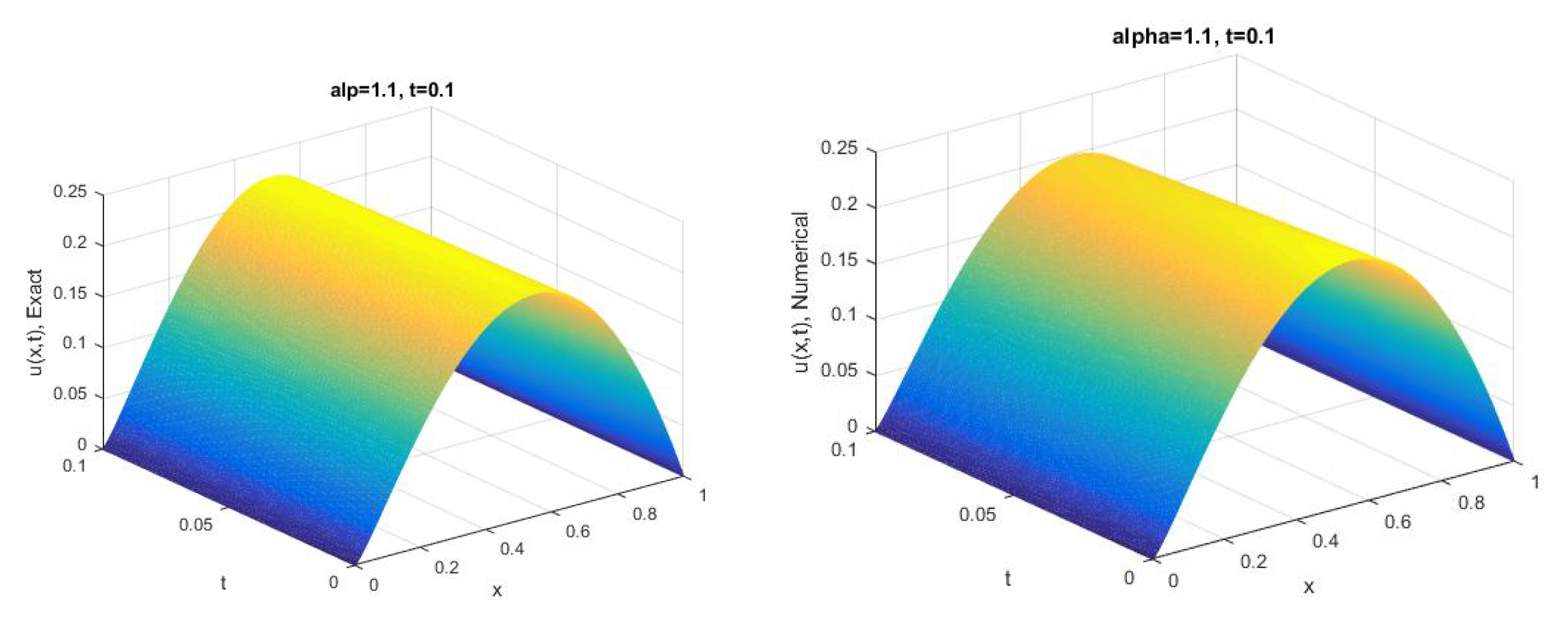
5. Numerical Tests
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Diethelm, K. The Analysis of Fractional Differential Equations; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Fomin, S.; Chugunov, V.; Hashida, T. Application of fractional differential equations for modeling the anomalous diffusion of contaminant from fracture into porous rock matrix with bordering alteration zone. Trans. Porous Med. 2010, 81, 187–205. [Google Scholar] [CrossRef]
- Guo, B.; Pu, X.; Huang, F. Fractional Partial Differential Equations and Their Numerical Solutions; World Scientific: Singapore, 2015. [Google Scholar]
- Podlubny, I. Fractional Differential Equations Academic; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: New York, NY, USA, 1998; Volume 198. [Google Scholar]
- Salman, W.; Gavriilidis, A.; Angeli, P. A model for predicting axial mixing during gas–liquid Taylor flow in microchannels at low Bodenstein number. Chem. Eng. J. 2004, 101, 391–396. [Google Scholar] [CrossRef]
- Berkowitz, B.; Cortis, A.; Dror, I.; Scher, H. Laboratory experiments on dispersive transport across interfaces. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Cortis, A.; Berkowitz, B. Computing “anomalous” contaminant transport in porous media. Ground Water 2005, 43, 947–950. [Google Scholar] [CrossRef]
- Meerschaert, M.M.; Tadjeran, C. Finite difference approximations for fractional advection–dispersion flow equations. J. Comput. Appl. Math. 2004, 172, 65–77. [Google Scholar] [CrossRef]
- Meerschaert, M.M.; Tadjeran, C. Finite difference approximations for two-sided space fractional partial differential equations. Appl. Numer. Math. 2006, 56, 80–90. [Google Scholar] [CrossRef]
- Ren, J.; Sun, Z.Z.; Zhao, X. Compact difference scheme for the fractional sub-diffusion equation with Neumann boundary conditions. J. Comput. Phys. 2013, 232, 456–467. [Google Scholar] [CrossRef]
- Wang, K.; Wang, H. A fast characteristic finite difference method for fractional advection–diffusion equations. Adv. Water. Resour. 2011, 34, 810–816. [Google Scholar] [CrossRef]
- Singh, J.; Swroop, R.; Kumar, D. A computational approach for fractional convection–diffusion equation via integral transforms. Ain Shams Eng. J. 2016, 9, 1019–1028. [Google Scholar] [CrossRef]
- Liu, F.; Zhuang, P.; Burrage, K. Numerical methods and analysis for a class of fractional advection–dispersion models. Comput. Math. Appl. 2012, 64, 2990–3007. [Google Scholar] [CrossRef]
- Tian, W.; Deng, W.; Wu, Y. Polynomial spectral collocation method for space fractional advection–diffusion equation. Numer. Methods Partial Differ. Equ. 2014, 30, 514–535. [Google Scholar] [CrossRef]
- Hejazi, H.; Moroney, T.; Liu, F. Comparison of finite difference and finite volume methods for solving the space fractional advection–dispersion equation with variable coefficients. ANZIAM J. 2013, 54, 557–573. [Google Scholar] [CrossRef][Green Version]
- Liu, F.; Zhuang, P.; Turner, I.; Burrage, K.; Anh, V. A new fractional finite volume method for solving the fractional diffusion equation. Appl. Math. Model. 2014, 38, 15–16. [Google Scholar] [CrossRef]
- Li, C.; Zeng, F. Numerical Methods for Fractional Calculus; Chapman and Hall/CRC: Boca Raton, FL, USA, 2015. [Google Scholar]
- Li, C.; Zeng, F. Finite difference methods for fractional differential equations. Int. J. Bifurcat. Chaos 2012, 22, 1230014. [Google Scholar] [CrossRef]
- Luchko, Y. Multi-dimensional fractional wave equation and some properties of its fundamental solution. Ind. Math. 2014, 6. [Google Scholar] [CrossRef]
- Lynch, V.E.; Carreras, B.A.; del-Castillo-Negrete, D.; Ferreira-Mejias, K.M.; Hicks, H.R. Numerical methods for the solution of partial differential equations of fractional order. J. Comput. Phys. 2003, 192, 406–421. [Google Scholar] [CrossRef]
- Sweilam, N.H.; Khader, M.M.; Mahdy, A.M.S. Crank–Nicolson finite difference method for solving time-fractional diffusion equation. J. Fract. Calc. Appl. 2012, 2, 1–9. [Google Scholar]
- Tadjeran, C.; Meerschaert, M.M.; Scheffler, H.P. A second-order accurate numerical approximation for the fractional diffusion equation. J. Comput. Phys. 2006, 201, 205–213. [Google Scholar] [CrossRef]
- Wang, Y.M. A compact finite difference method for a class of time fractional convection–diffusion-wave equations with variable coefficients. Num. Algor. 2015, 70, 625–651. [Google Scholar] [CrossRef]
- Wang, Y.M.; Wang, T. A compact Alternative difference implicit method and its extrapolation for time fractional sub-diffusion equations with nonhomogeneous Neumann boundary conditions. Comput. Math. Appl. 2018, 75, 721–739. [Google Scholar] [CrossRef]
- Zhou, F.; Xu, X. The third kind Chebyshev wavelets collocation method for solving the time-fractional convection–diffusion equations with variable coefficients. Appl. Math. Comput. 2016, 280, 11–29. [Google Scholar] [CrossRef]
- Jin, B.; Lazarov, R.; Zhou, Z. A Petrov–Galerkin finite element method for fractional convection–diffusion equations. SIAM J. Numer. Anal. 2016, 54, 481–503. [Google Scholar] [CrossRef]
- Gao, F.; Yuan, Y.; Du, N. An upwind finite volume element method for nonlinear convection–diffusion problem. AJCM 2011, 1, 264. [Google Scholar] [CrossRef]
- Aboelenen, T. A direct discontinuous Galerkin method for fractional convection–diffusion and Schrödinger-type equations. Eur. Phys. J. Plus 2018, 133, 316. [Google Scholar] [CrossRef]
- Xu, Q.; Hesthaven, J.S. Discontinuous Galerkin method for fractional convection–diffusion equations. SIAM J. Numer. Anal. 2014, 52, 405–423. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Baleanu, D. A spectral Legendre−Gauss–Lobatto collocation method for a space-fractional advection–diffusion equations with variable coefficients. Rep. Math. Phys. 2013, 72, 219–233. [Google Scholar] [CrossRef]
- Saadatmandi, A.; Dehghan, M.; Azizi, M.R. The Sinc-Legendre collocation method for a class of fractional convection–diffusion equations with variable coefficients. Commun. Nonlinear. Sci. Numer. Simulat. 2012, 17, 4125–4136. [Google Scholar] [CrossRef]
- Pang, G.; Chen, W.; Sze, K.Y. A comparative study of finite element and finite difference methods for two-dimensional space-fractional advection–dispersion equation. Adv. Appl. Math. Mech. 2016, 8, 166–186. [Google Scholar] [CrossRef]
- Zhang, Y. A finite difference method for fractional partial differential equation. Appl. Math. Comput. 2009, 2015, 524–529. [Google Scholar] [CrossRef]
- Gu, X.M.; Huang, T.Z.; Ji, C.C. Carpentieri B, Alikhanov AA, Fast iterative method with a second-order implicit difference scheme for time-space fractional convection–diffusion equation. J. Sci. Comput. 2017, 72, 957–985. [Google Scholar] [CrossRef]
- Benson, D.A.; Wheatcraft, S.; Meerschaert, M.M. Application of a fractional advection–dispersion equation. Water Resour. Res. 2000, 36, 1403–1412. [Google Scholar] [CrossRef]
- Tian, W.; Zhou, H.; Deng, W. A class of second order difference approximations for solving space fractional diffusion equations. Math. Comp. 2015, 84, 1703–1727. [Google Scholar] [CrossRef]
- Henrici, P. Elements of Numerical Analysis; John Wiley and Sons: New York, NY, USA, 1984. [Google Scholar]
- Tuan, V.K.; Gorenflo, R. Extrapolation to the Limit for Numerical Fractional Differentiation. Z. Angew. Math. Mech. 1995, 75, 646–648. [Google Scholar] [CrossRef]
- LeVeque, R.J. Finite Difference Methods for Ordinary and Partial Differential Equations; SIAM: Philadelphia, PA, USA, 2007; Volume 98. [Google Scholar]
- Isaacson, E.; Keller, H.B. Analysis of Numerical Methods; Courier Corporation: Chelmsford, MA, USA, 2012. [Google Scholar]

| Max-Error | Order | Max-Error | Order | Max-Error | Order | ||
|---|---|---|---|---|---|---|---|
| 1/50 | 1/50 | 4.9807e−04 | – | 4.0046e−04 | – | 1.4048e−04 | – |
| 1/100 | 1/100 | 1.0660e−04 | 2.2241 | 8.8946e−05 | 2.1707 | 3.6848e−05 | 1.9307 |
| 1/200 | 1/200 | 2.4413e−05 | 2.1265 | 2.0643e−05 | 2.1073 | 9.4393e−06 | 1.9648 |
| 1/400 | 1/400 | 5.8239e−06 | 2.0676 | 4.9592e−06 | 2.0575 | 2.3887e−06 | 1.9825 |
| 1/800 | 1/800 | 1.4211e−06 | 2.0350 | 1.2146e−06 | 2.0296 | 6.0078e−07 | 1.9913 |
| Max-Error | Order | Max-Error | Order | ||
|---|---|---|---|---|---|
| 1/50 | 1/50 | 1.4048e−04 | – | 2.5297e−05 | – |
| 1/100 | 1/100 | 3.6848e−05 | 1.9307 | 7.4748e−06 | 1.7589 |
| 1/200 | 1/200 | 9.4393e−06 | 1.9648 | 2.0122e−06 | 1.8933 |
| 1/400 | 1/400 | 2.3887e−06 | 1.9825 | 4.9017e−07 | 2.0374 |
| 1/800 | 1/800 | 6.0078e−07 | 1.9913 | 1.0620e−07 | 2.2065 |
| Max-Error | Order | ||
|---|---|---|---|
| 1/50 | 1/50 | 2.6e−03 | – |
| 1/100 | 1/100 | 7.695e−04 | 1.7563 |
| 1/150 | 1/150 | 2.144e−04 | 1.8436 |
| 1/200 | 1/200 | 5.688e−05 | 1.9143 |
| Max-Error | Order | Max-Error | Order | Max-Error | Order | |
|---|---|---|---|---|---|---|
| 1/50 | 4.5e−03 | – | 2.8e−03 | – | 1.7e−03 | – |
| 1/100 | 2.7e−03 | 0.7370 | 1.6e−03 | 0.8074 | 8.9641–04 | 0.97224 |
| 1/200 | 1.6e−03 | 0.7549 | 8.6405e−04 | 0.8889 | 4.6491e−04 | 0.8981 |
| 1/400 | 9.5896e−04 | 0.7385 | 4.7955e−04 | 0.8494 | 2.4086e−04 | 0.9488 |
| 1/800 | 5.7034e−04 | 0.7496 | 2.6609e−04 | 0.8498 | 1.2473e−04 | 0.9494 |
| Max-Error | Error-Rate | Max-Error | Error-Rate | ||
|---|---|---|---|---|---|
| 1/50 | 1/50 | 1.91e−02 | – | 1.52e−02 | – |
| 1/100 | 1/100 | 9.9e−03 | 1.93 | 7.9e−03 | 1.9 |
| 1/200 | 1/200 | 5.2e−03 | 1.90 | 4.3e−03 | 1.84 |
| 1/400 | 1/400 | 2.8e−03 | 1.86 | 2.4e−03 | 1.79 |
| 1/800 | 1/800 | 1.6e−03 | 1.75 | 1.4e−03 | 1.7 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anley, E.F.; Zheng, Z. Finite Difference Approximation Method for a Space Fractional Convection–Diffusion Equation with Variable Coefficients. Symmetry 2020, 12, 485. https://doi.org/10.3390/sym12030485
Anley EF, Zheng Z. Finite Difference Approximation Method for a Space Fractional Convection–Diffusion Equation with Variable Coefficients. Symmetry. 2020; 12(3):485. https://doi.org/10.3390/sym12030485
Chicago/Turabian StyleAnley, Eyaya Fekadie, and Zhoushun Zheng. 2020. "Finite Difference Approximation Method for a Space Fractional Convection–Diffusion Equation with Variable Coefficients" Symmetry 12, no. 3: 485. https://doi.org/10.3390/sym12030485
APA StyleAnley, E. F., & Zheng, Z. (2020). Finite Difference Approximation Method for a Space Fractional Convection–Diffusion Equation with Variable Coefficients. Symmetry, 12(3), 485. https://doi.org/10.3390/sym12030485





