Abstract
Biometrics is a scientific technology to recognize a person using their physical, behavior or chemical attributes. Biometrics is nowadays widely being used in several daily applications ranging from smart device user authentication to border crossing. A system that uses a single source of biometric information (e.g., single fingerprint) to recognize people is known as unimodal or unibiometrics system. Whereas, the system that consolidates data from multiple biometric sources of information (e.g., face and fingerprint) is called multimodal or multibiometrics system. Multibiometrics systems can alleviate the error rates and some inherent weaknesses of unibiometrics systems. Therefore, we present, in this study, a novel score level fusion-based scheme for multibiometric user recognition system. The proposed framework is hinged on Asymmetric Aggregation Operators (Asym-AOs). In particular, Asym-AOs are estimated via the generator functions of triangular norms (t-norms). The extensive set of experiments using seven publicly available benchmark databases, namely, National Institute of Standards and Technology (NIST)-Face, NIST-Multimodal, IIT Delhi Palmprint V1, IIT Delhi Ear, Hong Kong PolyU Contactless Hand Dorsal Images, Mobile Biometry (MOBIO) face, and Visible light mobile Ocular Biometric (VISOB) iPhone Day Light Ocular Mobile databases have been reported to show efficacy of the proposed scheme. The experimental results demonstrate that Asym-AOs based score fusion schemes not only are able to increase authentication rates compared to existing score level fusion methods (e.g., min, max, t-norms, symmetric-sum) but also is computationally fast.
1. Introduction
Traditional authentication methods based on passwords and identity cards still face several challenges such as passwords can be forgotten or identity cards can be faked [1,2]. A widespread technology known as biometrics was employed as an alternative to these conventional recognition mechanisms due to the growth of threats in identity management and security tasks [3]. This technology is based on human anatomical (e.g., fingerprint, face, iris, palmprint) or behavioural (e.g., gait, signature, keystroke analysis) characteristics [2]. Besides, biometric traits are inherently possessed by a human thereby it is comparatively difficult to forge or steal it. Thus, biometric attributes constitute a robust link between a human and his identity [2]. Moreover, unlike knowledge-based and token-based strategies for person recognition, biometric traits are able to guaranty that no user is able to assume more than one identity [2]. Due to above-mentioned reasons, biometrics recognition has been increasingly adopted in diverse fields such as airport checking, video surveillance, industries, commercial sectors, personal smartphone user authentication as well as forensics [4,5].
However, unimodal biometrics (i.e., utilizing only one biometric trait) are not adequate in tackling issues like noisy input data, non-universality, low interoperability and spoofing [6], which lead to lower accuracy. To alleviate some of these limitations, integration of two or more biometric traits offers many advantages compared to unimodal authentication [7]. Some of the advantages are attaining improvement in the overall accuracy, ensuring a larger population coverage, addressing the issue of non-universality, and providing greater resistance to spoofing (i.e., consolidating evidence from more than one biometric sources makes it a very difficult for an imposter to spoof simultaneously various physiological and/or behaviour attributes of an authentic user [8].
Multibiometric recognition systems that merge information from multiple biometric sources could be roughly grouped into multi-modal (i.e., employing multiple biometric traits), multi-unit (i.e., utilizing numerous units of the same modality, e.g., left and right wrist vein of a human [7]), multi-algorithm (i.e., applying various feature extraction techniques on the same biometric trait), multi-sensor (i.e., using multiple sensors to collect the same biometric modality), and multi-sample (i.e., collecting multiple samples of the same biometric modality) [2]. Moreover, information fusion in multibiometrics can be classified into four levels [9], namely, sensor level, feature level, matching score level and decision level. Although fusion of biometric data at sensor level is expected to achieve improvement accuracy, the score level fusion is generally preferred because it is easy not only to be process but also to obtain good performances.
In order to fill some of the limitations of prior unimodal and multimodal biometrics works, there is a need to formulate novel and computationally inexpensive score fusion frameworks. To this aim, in this article we proposed a novel approach of biometric score level integration scheme, i.e., Asymmetric Aggregation Operators (Asym-AOs) are exploited to combine the scores originated from different sources. The Asym-AOs are computed via the generator functions of triangular norms (t-norms). More specifically, for Asym-AOs, Aczel-Alsina, Hamcher, and Algebric product generating functions are adopted, which can lead to achieve better authentic and imposter match-scores’ discrimination compared to other score fusion methodologies such as t-norms, symmetric-sum, max and min rules. The proposed Asym-AOs based multibiometric score fusion framework were validated in different user authentication scenarios such as multiple traits (i.e., right index fingerprint and face traits were integrated in the first multimodal system, while ear and index finger’s major knuckle are combined to verify the human’s identity in the second one), multiple instances (i.e., a framework which employs left and right palmprint images), multiple algorithms or features (i.e., combining matching scores originated from two different face’s matchers), and multiple traits captured via mobile camera (i.e., face and ocular biometrics based mobile user verification).
We organize the rest of the presented work as follows. The related works on matching score combination are provided in Section 2. Section 3 provides a brief overview of the proposed score fusion rule. Section 4 discusses the obtained experimental results. while conclusions are eventually drawn in Section 5.
2. Related Work
Existing score level fusion schemes in the literature can be divided into three classes: classifier-based, density-based and transformation-based score fusion.
2.1. Transformation-Based Score Fusion
In this category, match-scores should be converted into a same domain using min-max, z-score or tanh [10] normalization approaches, then a simple rule is applied to combine the normalized scores, e.g., min, max, sum, product rules, t-norms, etc. For instance, the authors in [5] proposed 2D and 3D palmprint biometric person recognition based on bank of binarized statistical image features (B-BSIF) and self-quotient image (SQI) scheme. The scores extracted from 2D and 3D palmprints were normalized by min-max and combined using min, max and weighted sum rules. The authors in [9] investigated a finger multimodal user authentication, i.e., combining finger vein, fingerprint, finger shape and finger knuckle print using triangular norms (t-norms). While, authors in [11] have utilized t-norms to integrate the matching scores from multiple biometric traits (i.e., hand geometry, hand veins and palmprint). Cheniti et al. [12] combined the match-scores utilizing symmetric-sums (S-sum) generated via t-norms, this approach rendered good performance on National Institute of Standards and Technology (NIST)-Multimodal and NIST-Fingerprint databases.
2.2. Classifier-Based Score Fusion
In this category, the discrimination of genuine and imposter users is treated as a binary classification problem through concatenating scores from multiple matchers to form a feature vector, which is then classified into one of two classes: genuine or impostor. Towards this purpose, numerous classifiers have been utilized to this aim. For example, Kang et al. [13] applied support vector machine (SVM) for classification to combine finger vein and finger geometry. The authors in [14] used a combination of match-scores using hidden Markov model (HMM), whereas, Kang et al. [15] studied the fusion of fingerprint, finger vein and shape of finger using an SVM classifier.
2.3. Density-Based Score Fusion
In this category, the discrimination of authentic and imposter users is based on explicit estimation of authentic and impostor match score densities, which is then used to estimate likelihood ratio to produce the final output. Nandakumar et al. [16] utilized the likelihood ratio test to combine match-scores from multiple biometric traits, where densities were estimated using a mixture of Gaussian models, while authors in [17] investigated Gaussian Mixture Model to modal the authentic and impostor score densities through the combination step, attaining performance better than SVM and sum-rule based score integration methods on face, hand geometry, finger texture and palmprint datasets.
2.4. Disadvantages of Previously Proposed Methods
To sum up, transformation-based rules, like product, min, max, and weighted sum rules were observed in the literature to perform weakly, since they failed to take into account the distribution distance of different biometric traits’ match-scores. While, classifier-based fusion methods face the problem of unbalanced training set due to the unbalanced authentic and imposter training score sets. Likewise, though density-based approaches can lead to optimal performance, it is hard to estimate the density function of scores accurately because its nature is usually unknown and also limited dataset is available for the same.
In order to alleviate some of the disadvantages of prior fusion algorithms as well as to increase the overall accuracy performance of multibiometric user authentication, in this work, we present a novel score level fusion method using Asymmetric Aggregation Operators (Asym-AOs), which are built via the generator functions of t-norms.
3. Proposed Asym-AOs Score Level Fusion Technique
In this section, we describe a novel strategy for score level fusion which utilizes the generating function of t-norms. The preliminaries of Asymmetric Aggregation Operators are first discussed, then the Asym-AOs based multibiometric score fusion method is outlined.
3.1. Overview of Asymmetric Aggregation Operators
Asymmetric aggregation operators (Asym-AOs) were introduced by Mika et al. [18,19]. The Asym-AOs can be defined as a binary function .
Asym-AOs satisfy properties like asymmetry, boundary conditions and monotonicity. The general form of Asym-AO is given by:
Typically, is a generator function of t-norms, which is a continuous monotone decreasing function under the conditions:
is also a continuous monotone decreasing function under the conditions:
where
is the pseudo inverse of f and is the usual inverse of f. From the definition of t-norms, we can write:
In this paper, we have evaluated two types of Asym-AOs; the first is based on the continuous monotone decreasing function defined below:
while the second type of Asym-AOs is based on the continuous monotone decreasing function as defined below.
The three used generating functions of t-norms, i.e., Hamacher, Algebric Product and Aczel-Alsina to obtain the Asym-AOs can be given by:
Table 1 presents few typical examples of Asym-AOs. They are calculated by using various generating function of t-norms and above-mentioned continuous monotone decreasing functions. For a given continuous monotone decreasing function and the generator function of Hamacher t-norm , the Asym-AO1 is defined as:

Table 1.
Examples of Asymmetric Aggregation Operators (Asym-AOs), estimated via the generator functions of t-norms.
The Asym-AO2 is defined as:
where and is the generator function of Hamacher t-norm.
In multibiometric based individual recognition, the chosen of the combination rule is very important to attain high accuracy. Generally, the best combination rule is the one that can minimize the imposter matching scores and further maximize the authentic matching scores. To this end, we proposed Asym-AOs as a combination rule to integrate the scores because they satisfy the previously mentioned requirement of combination rule as can be observed in Figure 1, Figure 2, Figure 3 and Figure 4.
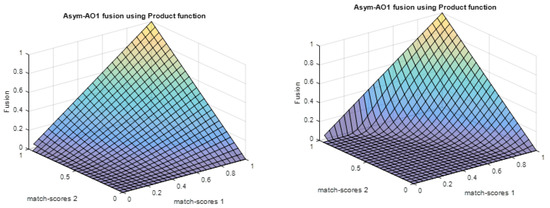
Figure 1.
Plots of matching score via Asym-AO1 with Algebric product function: (a) and (b) .
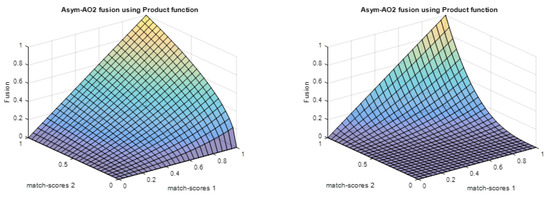
Figure 2.
Plots of matching score via Asym-AO2 with Algebric product function: (a) and (b) .
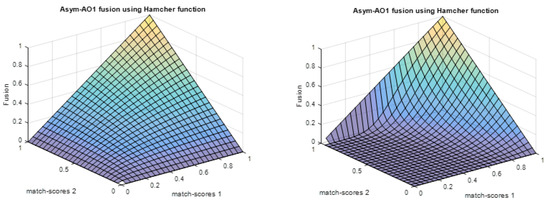
Figure 3.
Plots of matching score via Asym-AO1 with Hamacher function: (a) and (b) .
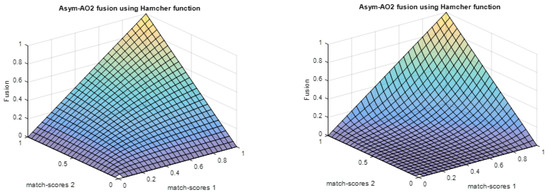
Figure 4.
Plots of matching score via Asym-AO2 with Hamacher function: (a) and (b) .
3.2. The Score Level Fusion Method Based on Asym-AOs
A biometric system is essentially a pattern recognition/matching system. The biometric recognition systems are composed of two main stages: enrollment and recognition/verification. During the enrollment stage, the biometric trait is captured using biometric sensor (e.g., camera in case of face recognition). The captured biometric trait is then used to extract salient features (i.e., template), which are then stored in a database along with user’s identity. During the recognition/verification stage, whenever the user wants to be recognized, they present their biometric trait to the system. This time the captured biometric trait from the sensor is used to extract features are compared to the features stored in the database during enrollment in order to compute match score. If the match score is greater than a threshold then the user is classified as genuine, otherwise as an impostor.
Figure 5 shows an architecture illustrating the overall procedure of a multibiometric person recognition framework that integrates information from multiple biometric sources using Asym-AOs. In a multimodal biometric verification setting, each user provides their biometric traits to the respective sensors and claims their identity. Next, the framework separately extracts individual features. In this study, binarized statistical image features method (explained below in detail) has been employed to extract the features. Then, the framework matches the captured traits’ extracted features against their corresponding features/templates in the database accumulated at the time of enrollment and produces a vector of matching score Q = [Q1, Q2, …, QN], where Qi is match-score produced via ith modality corresponding to ith sensor. The information can be fused at different levels, i.e., sensor, feature, match-score, and decision level. The match-scores level fusion is generally preferred owing to ease in combining of scores, and thus was applied in this work as well.
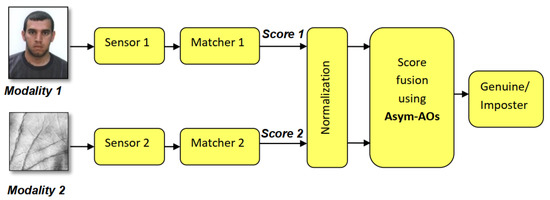
Figure 5.
Asym-AOs based scores integration framework.
Owing to the heterogeneity of match-scores, the different match-scores should be first transformed into the range [0,1] before fusion. In this work, we applied two normalization methods, which are min-max, and tanh-estimators as defined below:
where indicates the normalized score and Q represents the match-score generated by a specific matcher.
where indicates the normalized score, and Q, and are the match-score, mean and standard deviation of match scores, respectively, as given by Hampel estimators . Once the match-scores are normalized utilizing (Equation (9)) or (Equation (10)), the are applied to integrate these normalized scores. If the fused score is greater than a threshold then the user is authenticated as genuine, otherwise as an impostor.
3.3. Binarized Statistical Image Features (BSIF)
Local texture descriptors have been successfully used in various real-world applications of image texture classification [20]. Therefore, we also employed local texture descriptor in multibiometric systems. Specifically, in this study, we present an experimental analysis of a very popular descriptors named binarized statistical image features (BSIF) for accurate person authentication in multibiometric systems. BSIF features efficiently encode local texture information and represent image regions in the form of histogram. Instead of manual tuning, BSIF features employ learning technique to attain statistically significant description of the data that enables efficient information encoding using simple element-wise quantization [20,21]. Moreover, BSIF features have shown their effectiveness for different applications ranging from face, iris, ear and palmprint biometrics to face and fingerprint spoof detection [22].
The BSIF was proposed by Kannala and Rahtu [21] for texture classification and face recognition based on other methodologies like local phase quantization (LPQ) and local binary pattern (LBP) that produce a binary codes. The BSIF descriptor is based on a set of filters of fixed size, where the filters are learnt from natural images via independent component analysis (ICA). In order to effectively estimate texture properties of a given images, BSIF computes a binary code string for the pixels of the image by binarizing the response of a linear filter with a threshold at zero. The BSIF is characterized by two important factors, the filter size l and the filter length n.
For a biometric image X of size and a linear filter Wi of the same size, the response of filter is given by:
The binarized feature bi is given by:
Finally, the BSIF features are obtained as a normalized histogram of the pixel’s binary codes that can efficiently describe the texture components in biometric images.
4. Experiments
Here, we provide experimental analysis of the proposed Asym-AOs based score fusion method. In particular, we have conducted experiments on multi-modal, multi-unit, multi-algorithm and multi-modal mobile biometric systems using seven publicly available datasets.
4.1. Experimental Data
The seven publicly available databases utilized in this study are NIST-Multimodal database, NIST-Face database [23], IITDelhi Palmprint V1 database [24], IIT Delhi Ear Database [25], Hong Kong Polytechnic University Contactless Hand Dorsal Images database [26], Mobile Biometry (MOBIO) face database [27] and Visible Light Mobile Ocular Biometric (VISOB) iPhone Day Light Ocular Mobile database [28].
4.1.1. NIST-Multimodal Database
The NIST-Multimodal database is composed of four set of similarity scores from 517 subjects [23]. The scores were generated via two different face matchers (i.e., labelled as matcher C and matcher G) and from left and right index fingers.
4.1.2. NIST-Face Database
The NIST-Face database consists of two set of similarity score vectors of 6000 samples from 3000 users [23]. The scores were generated via two different face matchers (i.e., labelled as matcher C and matcher G).
4.1.3. IIT Delhi Palmprint V1 Database
The IIT Delhi Palmprint V1 database is made up of images acquired using imaging setup of 235 users [24]. The images were collected from left and right hand in the IIT Delhi campus during July 2006 to June 2007 in an indoor environment. The subjects were in the age group of 12 to 57 years. The resolution of touchless palmprint images is pixels. Besides, pixels normalized images are also available in this database.
4.1.4. PolyU Contactless Hand Dorsal Images database
In Hong Kong PolyU Contactless Hand Dorsal Images (CHDI) database, images were acquired from 712 volunteers [26]. The images were collected in the Hong Kong polytechnic university campus, IIT Delhi campus, and in some villages in India during 2006 to 2015. This database also provides segmented images of minor, second, and major knuckle of little, ring, middle, and index fingers along with segmented dorsal images.
4.1.5. IIT Delhi-2 Ear Database
In IIT Delhi Ear database, ear images acquired from 221 subjects are [25]. These images were collected from a distance in an indoor environment at IIT Delhi campus, India during October 2006 to June 2007. The subjects were in the age group 14 to 58 years. The ear images were collected using a simple imaging setup with resolution. Besides that, pixels normalized ear images are also provided.
4.1.6. MOBIO Face Database
The MOBIO face database was collected over a period of 18 months from six sites across Europe from August 2008 until July 2010. It consists of face images from 150 subjects [27]. Among them, 51 are females and 99 males. Images were collected using a handheld mobile device (i.e., the Nokia N93i).
4.1.7. VISOB iPhone Day Light Ocular Mobile database
The iPhone day light ocular mobile database is a partition of Visible Light Mobile Ocular Biometric dataset (VISOB Dataset ICIP2016 Challenge Version). It contains eye images acquired from 550 subjects using front facing (selfie) camera of mobile device, i.e., iPhone 5s (1.2 MP, fixed focus) [28]. This database provides only the eye regions with size of pixels.
4.2. Experimental Protocol
Experiments were performed in authentication mode and performance of proposed fusion scheme is reported in Receiver Operating Characteristics (ROC). The ROC curve [12] is is obtained by plotting Genuine Acceptance Rate (GAR) vs. False Acceptance Rate (FAR), where GAR = 1 − FRR. The FRR (False Rejection Rate) is the proportion at which genuine individuals are rejected by the system as imposters, FAR (False Acceptance Rate) is the proportion at which imposter individuals are accepted by the system as genuine users, and GAR is the rate of the genuine users accepted over the total of enrolled individuals. Since no finger major knuckle or mobile (face and ocular traits) multi-modal data sets are publicly available, we created chimerical multi-modal data sets. Creating chimerical data sets is a common procedure exploited in biometrics on multi-modal systems, when no real data sets are available [8]. For example, the mobile face and ocular chimerical multi-modal data set in this study was created by combining the face and ocular images of pairs of clients of the available individual MOBIO face and VISOB iPhone Day Light Ocular data sets.
Moreover, it is a very typical phenomenon that when two independent data sets that are being used to produce the chimerical multi-modal data set have different number of users, number of subjects are set to smaller number among those datasets. Thus, in this work, we set number of users equals to subjects’ number of smaller datasets. For instance, IIT Delhi-2 Ear database has 221 subjects, while PolyU-CHDI database has 712 subjects, therefore we created chimerical multi-modal data set with only 221 subjects to evaluate our proposed score fusion framework.
The abbreviations of the presented work as well as the conventional ones is described in Table 2 in order to facilitate the comparison.

Table 2.
Different methods’ abbreviations.
4.3. Experimental Results
In this section, we provide the experimental results on publicly available databases for multi-modal, multi-unit, multi-algorithm and multi-modal mobile biometric systems.
4.3.1. Performance of Asym-AOs Based Fusion on Multi-Modal Systems
• Experiment 1
Figure 6 shows an architecture illustrating the overall procedure of face and fingerprint based multi-modal person recognition framework. In this first set of experiments, the match-scores of face matcher C and right fingerprint (NIST-multimodal database) are first normalized by tanh-estimators normalization technique as in Equation (10), then they are combined via proposed Asym-AOs. Figure 7 shows performance of unimodal biometric authentication and of their integration by using Asym-AOs. At FAR = 0.01%, the GARs of face matcher C and right fingerprint are 74.30% and 85.30%,respectively. However, with Asym-AO2 using Hamacher generating function, a GAR of 97.55% is achieved with the same FAR operating point. Table 3 shows the performances of Asym-AO1 and Asym-AO2 using Hamacher, algebric product and Aczel-Alsina generating functions together with previously-proposed score fusion methods based on sum rule, min and max rules [22], algebric product [26], Frank and Hamacher t-norms [11], and S-sum based on max rule and Hamacher t-norm [12]. It can be seen from Table 2 that Asym-AOs outperformed existing score fusion methods in literature.
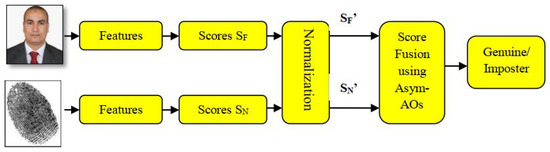
Figure 6.
Face and fingerprint based multi-modal biometric system using NIST multimodal database.
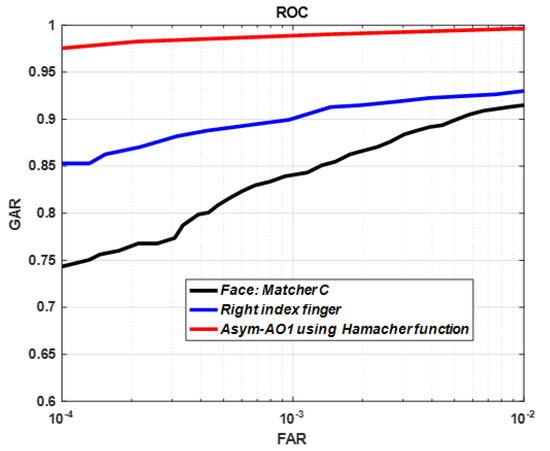
Figure 7.
Performance of individual traits (right index finger and face: matcher C) and their combination using Asym-AOs.

Table 3.
Comparison of unimodal and multi-modal fusion using various approaches on National Institute of Standards and Technology (NIST)-Multimodal database (right index and face matcher C).
• Experiment 2
Figure 8 shows an architecture illustrating the overall procedure of ear and major finger knuckles based multi-modal person recognition framework. In this second set of experiments, a multi-modal biometric framework utilizing ear and index finger’s major knuckle was analyzed. Namely, the experiments were carried out by merging two databases, i.e., IIT Delhi-2 Ear database and PolyU CHDI database. Two images per user (i.e., one train and one test image) belonging to 221 persons were randomly selected from each database. Therefore, we have 221 genuine scores and 48,620 ( ) imposter scores for each biometric trait considered.
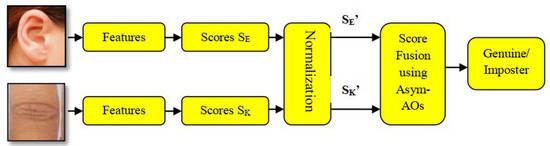
Figure 8.
Ear and major finger knuckles based multi-modal biometric system using IIT Delhi-2 Ear and PolyU-Contactless Hand Dorsal Images (CHDI) databases.
First, the match-scores of ear and index finger’s major knuckle are normalized via min-max normalization technique as in Equation (9), then they are combined utilizing Asym-AOs. Figure 9 depicts ROCs of ear and index finger’s major knuckle biometric modalities as well as of fused modalities using Asym-AO2 generated by Aczel-Alsina function. From this figure, we can observe that Asym-AOs fusion method improved the authentication rate of uni-modal systems. For example, at FAR = 0.01%, GAR’s of ear, index finger’s major knuckle and multi-modal were 40%, 75.5% and 85.00%, respectively. Other Asym-AOs such as Asym-AO1 and Asym-AO2 generated by Hamacher and Algebric product function were also tested for score level fusion and the performances attained were almost identical to those of Asym-AO2 generated by Aczel-Alsina. From Table 4, it is evident that Asym-AOs based score fusion was significantly better than by utilizing Hamacher and Frank t-norms [11], S-sum generated by Hamacher t-norm and max rule [5], algebric product [26], sum rule, min and max rules [22].
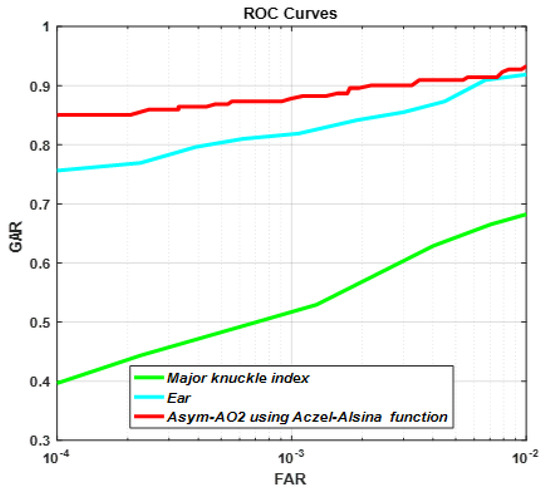
Figure 9.
Performance of individual traits (ear and index finger’s major knuckle) and their combination using Asym-AOs.

Table 4.
Comparison of unimodal and multi-modal fusion using various approaches on IIT Delhi Ear Database and Hong Kong PolyU (HKPU)-CHDI database (ear and index finger’s major knuckle).
4.3.2. Performance of Asym-AOs Based Fusion on Multi-Unit Systems
Figure 10 shows an architecture illustrating the overall procedure of left and right palmprint based multi-unit person recognition framework. For evaluation of our proposed Asym-AOs based score fusion scheme in multi-unit biometric scenario, left and right palmprint biometric traits fromIIT Delhi Palmprint V1 database were combined. From IIT Delhi Palmprint V1 database four user images (two train and two test images) of 230 persons for each modality were taken. There were 460 () genuine scores and 105,340 () imposter scores for left and right palmprint biometric traits.
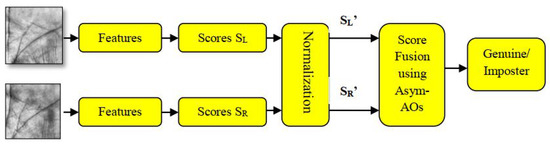
Figure 10.
Left and right palmprint based multi-unit biometric system using IITD Palmprint V1 database.
The match-scores of left and right palmprint were normalized by Equation (9) then fused using proposed score fusion technique. In Figure 11, we present the performances of unimodal and mutibiometric authentication systems in terms of ROC curves. It is easy to notice that the GARs of left and right palmprint are 91.00 and 91.50 at FAR = 0.01, respectively. However, GAR = 98.43 when Asym-AO1 based Aczel-Alsina generating function is used at 0.01 FAR operating point. We can also see in Table 5 the different Asym-AOs generated by Hamacher, Aczel-Alsina and Algebric product functions as well as previously proposed score fusion strategies, i.e., sum rule, min and max rules [22], Hamacher and Frank t-norms [11], S-sums [12] and Algebric product [26]. As previously mentioned about multi-modal biometric scenario, we can state based on Table 4 that the proposed framework outperforms prior widely adopted score fusion rules in multi-unit scenarios.
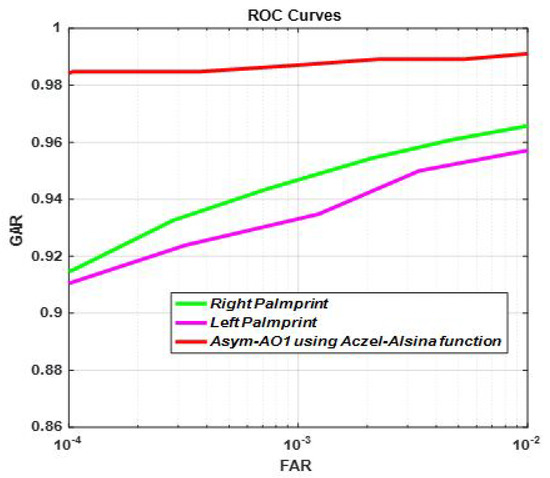
Figure 11.
Performance of individual traits (right and left palmprint) and their combination using Asym-AOs.

Table 5.
Comparison of unimodal and multi-unit fusion using various approaches on IITD Palmprint V1 database (left and right palmprint).
4.3.3. Performance of Asym-AOs Based Fusion on Multi-Algorithm Systems
In this subsection, we report performances of Asym-AOs based score fusion strategy on multi-algorithm biometric system. Figure 12 shows an architecture illustrating the overall procedure of face based multi-algorithm person recognition framework; this system applied two face matching algorithm. Specifically, we conducted experiments on NIST-face database. This database has similarity scores of 3000 subjects. The number of genuine match-scores is 6000 (), whereas the number of imposter match-score is 17,994,000 (). The match-scores of face matcher C and face matcher G were normalized by tanh-estimators normalization technique as in Equation (10).
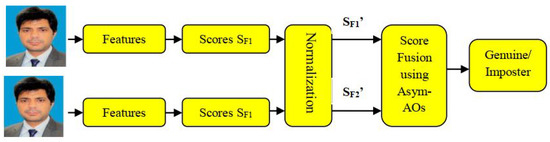
Figure 12.
Face based multi-algorithm biometric system using NIST face database.
Figure 13 shows ROC’s curves of individual biometric algorithms with proposed score level fusion method. At FAR = 0.01% operating point, the GARs of face matcher C, face matcher G and multi-algorithm using Asym-AO2 generated by Algebric product function with m = 1.2 are 64.0%, 72.1%, and 76.27%, respectively. Table 6 summarizes the obtained authentication rate based on Asym-AOs generated by Hamacher, Algebric product and Aczel-Alsina functions along with previously proposed fusion techniques like S-sum using Hamacher t-norm [12], S-sum using max rule [12], Hamcher t-norm [11], Frank t-norm [11], sum rule, min and max rules [22]. Comparing the results attained using our proposed Asym-AOs for score level with the performances of individual biometric systems, a notable improvement in terms of attainable recognition rate can be observed. Moreover, the proposed Asym-AOs outperforms not only uni-biometric systems but also existing score fusion strategies.
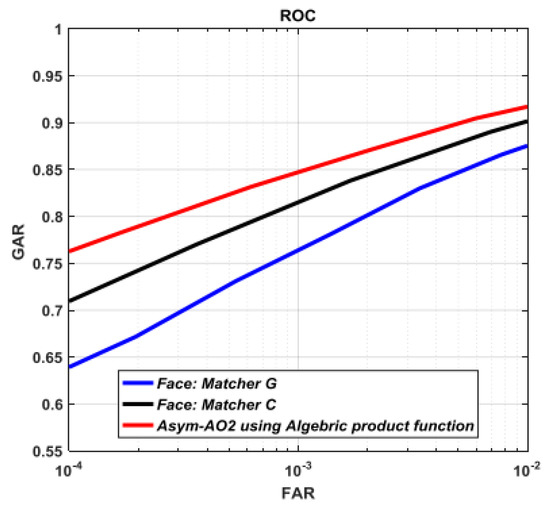
Figure 13.
Performance of individual matchers (face matcher C and face matcher G) and their combination using Asym-AOs.

Table 6.
Comparison of unimodal and multi-algorithem fusion using various approaches on NIST-Face database (Face C and Face G).
4.3.4. Performance of Asym-AOs Based Fusion on Multi-Modal Mobile Systems
Figure 14 shows an architecture illustrating the overall procedure of face based multi-modal mobile person recognition framework. Unlike previous multibiometric authentication systems that depend on samples collected using ordinary camera, we also studied a multi-modal biometric framework based on datasets collected on mobile/smart phones, i.e., multi-modal system using face and ocular biometrics (i.e., left eye) from MOBIO face and VISOB iPhone Day Light Ocular biometric databases, respectively. In this experiment, 300 images of face and 300 images of ocular biometric for 150 subjects were utilized. One image for the face and one image for ocular biometric per user were randomly selected as training set and the same thing for the testing set. The texture descriptor BSIF was extracted from face and ocular biometrics. The chi-squared distance was utilized for the generating of scores followed by min-max normalization method as in Equation (9).
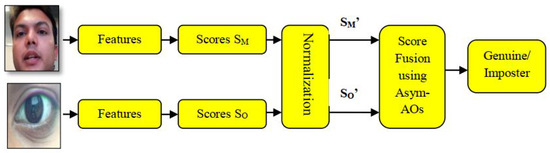
Figure 14.
Face and ocular left eye based multi-modal mobile biometric system using Mobile Biometry (MOBIO) face and Visible Light Mobile Ocular Biometric (VISOB) iPhone Day Light Ocular biometric databases.
The ROC curves of individual biometric modalities collected on mobile phones and the Asym-AO1 fusion rule generated by Hamacher function are shown in Figure 15. The Asym-AOs lead to good recognition rate compared to the best uni-biometric system. At FAR of 0.01%, GAR’s of face and ocular biometric are 95.0% and 59.0%, respectively. While, with Asym-AO1 using Hamacher function, GAR of 99.40% is attained at 0.01% FAR.The improvement in performance achieved due to Asym-AOs using Hamacher, Aczel-Alsina and Algebric product functions is also reported in Table 6. In addition, results using S-sums [12], Hamcher and Frank t-norms [11], Algebric product [26], sum rule, min and max rules [26] are also reported in Table 6 for comparison purpose.The results achieved demonstrate the effectiveness of Asym-AOs based score fusion rule. In Table 7, it is easy to observe that proposed multibiometric fusion strategy via Asym-AOs attains better performance than corresponding prior proposed score fusion rules in the literature. For instance, using Hamacher t-norm achieved GAR of 96.70%, while fusion via Asym-AO1 generated by Hamacher function resulted into GAR of 99.40%.
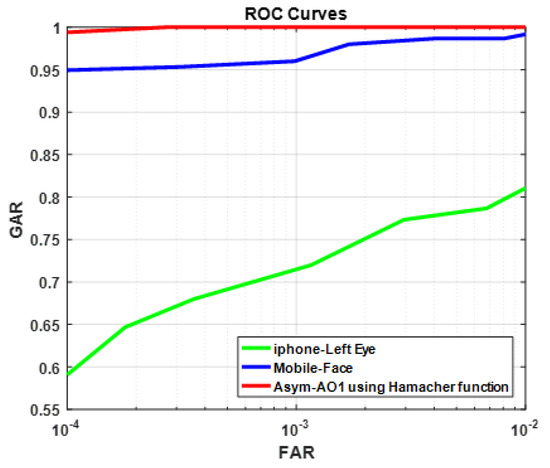
Figure 15.
Performance of individual traits(face and ocular left eye)and their combination using .

Table 7.
Comparison of unimodal and multi-modal mobile fusion using various approaches.
To sum up, our results obtained using proposed biometric fusion scheme using Asym-AOs with generating functions of t-norms show its effectiveness for person verification in different scenarios such as multi-modal, multi-unit, multi-algorithm and multimodal mobile biometric systems as well as modalities like face, major finger knuckle, palm-print, ear, fingerprint and ocular biometric. Thus, it can be stated that our presented scheme for score fusion leads to lessen inherent limitations of unibiometrics and minimizes the error rates. In addition, proposed Asym-AOs fusion framework is capable of vanquishing the drawbacks of score fusion based on density and classifier techniques owing to obstacle of score densities estimation and the unbalanced authentic and imposter training score sets, respectively. Though, our presented methodology is computationally inexpensive, estimating value of parameter m (in EContactless Hand Dorsal Imagesquations 4 and 5) can be tricky, especially when we have to empirically estimate it by way maximizing the system’s performance (i.e., brute force search).
5. Conclusions
In this work, we proposed a framework for the fusion of match-scores in a multibiometric user authentication systems based on Asymmetric Aggregation Operators (Asym-AOs). These Asym-AOs are computed utilizing the generator functions of t-norms. Extensive experimental analysis on seven publicly available databases, i.e., collected using ordinary camera and mobile phone, showed a remarkable improvement in authentication rates over uni-modal biometric systems as well as other existing score-level fusion methods like min, max, algebraic product, t-norms and S-sum using t-norms. It is hoped that the proposed Asym-AOs biometric fusion scheme will be exploited and explored for the development of information fusion systems in this field as well as in different domains. In the future, we aim to study the proposed framework under big data and fusion of mobile multibiometrics using in-built sensors. In addition, we plan to evaluate the robustness of the presented method against spoofing attacks, and subsequently, we will redesign the proposed framework to inherently enhance its robustness against attacks.
Author Contributions
Conceptualization, A.H. and Z.A.; Data curation, A.H. and M.C.; Formal analysis, K.S., N.G. and L.Z.; Funding acquisition, Z.A. and K.S.; Methodology, A.H., M.C. and K.M.; Resources, A.H., Z.A., M.C., K.S. and K.M., Validation, A.H., N.G. and L.Z.; Writing—original draft, A.H. and Z.A.; Writing—review and editing, A.H., Z.A. and K.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by Research Management Center, Xiamen University Malaysia under XMUM Research Program Cycle 3 (Grant No: XMUMRF/2019-C3/IECE/0006).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jain, A.K.; Flynn, P.; Ross, A. Handbook of Multibiometrics; Springer: Berlin, Germany, 2008. [Google Scholar]
- Jain, A.K.; Ross, A.A.; Nandakumar, K. Introduction to Biometrics; Springer Science & Business Media: Cham, Switzerland, 2011. [Google Scholar]
- Akhtar, Z.; Hadid, A.; Nixon, M.; Tistarelli, M.; Dugelay, J.; Marcel, S. Biometrics: In search of identity and security (Q & A). IEEE MultiMedia 2018. [Google Scholar] [CrossRef]
- Ross, A.; Rattani, A.; Tistarelli, M. Exploiting the “doddington zoo” effect in biometric fusion. In Proceedings of the IEEE 3rd International Conference on Biometrics: Theory, Applications, and Systems, Washington, DC, USA, 28–30 September 2009; pp. 1–7. [Google Scholar]
- Chaa, M.; Boukezzoula, N.E.; Attia, A. Score-level fusion of two-dimensional and three-dimensional palmprint for personal recognition systems. J. Electron. Imaging 2017, 26, 12–26. [Google Scholar] [CrossRef]
- Bhanu, B.; Govindaraju, V. Multibiometrics for Human Identification; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Mohamed, C.; Akhtar, Z.; Eddine, B.N.; Falk, T.H. Combining Left and Right Wrist Vein Images for Personal Verification. In Proceedings of the Seventh International Conference on Image Processing Theory, Tools and Applications (IPTA), Montreal, QC, Canada, 28 November–1 December 2017; pp. 1–6. [Google Scholar]
- Akhtar, Z.; Fumera, G.; Marcialis, G.L.; Roli, F. Robustness evaluation of biometric systems under spoof attacks. In Proceedings of the International Conference on Image Analysis and Processing, Ravenna, Italy, 14–16 September 2011; pp. 159–168. [Google Scholar]
- Peng, J.; ElLatif, A.A.A.; Li, Q.; Niu, X. Multimodal biometric authentication based on score level fusion of finger biometrics. Opt. Int. J. Light Electron Opt. 2014, 125, 6891–6897. [Google Scholar] [CrossRef]
- Ross, A.; Jain, A.; Nakumar, K. Score normalization in multimodal biometric systems. Pattern Recognit. 2005, 38, 2270–2285. [Google Scholar]
- Hanmlu, M.; Grover, J.; Gureja, A.; Gupta, H.M. Score level fusion of multimodal biometrics using triangular norms. Pattern Recognit. Lett. 2011, 32, 1843–1850. [Google Scholar] [CrossRef]
- Mohamed, C.; Eddine, B.N.; Akhtar, Z. Symmetric Sums-Based Biometric Score Fusion. IET Biom. 2018, 7, 391–395. [Google Scholar]
- Kang, B.; Park, K. Multimodal biometric method based on vein and geometry of a single finger. Comput. Vis. IET 2010, 4, 209–217. [Google Scholar] [CrossRef]
- Zheng, Y.; Blasch, E. An exploration of the impacts of three factors in multimodal biometric score fusion: Score modality, recognition method, and fusion process. J. Adv. Inf. Fusion 2014, 9, 124–137. [Google Scholar]
- Kang, B.; Park, K. Multimodal biometric method that combines veins, prints, and shape of a finger. Opt. Eng. 2011, 50, 017201. [Google Scholar]
- Nakumar, K.; Chen, Y.; Dass, S.C.; Jain, A. Likelihood ratio-based biometric score fusion. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 342–347. [Google Scholar] [CrossRef] [PubMed]
- Nanni, L.; Lumini, A.; Brahnam, S. Likelihood ratio based features for a trained biometric score fusion. Expert Syst. Appl. 2011, 38, 58–63. [Google Scholar] [CrossRef]
- Sato, M.; Sato, Y. Fuzzy Clustering Model for Asymmetry and Self-similarity. In Proceedings of the IEEEInternational Fuzzy Systems Conference, Barcelona, Spain, 1–5 July 1997; pp. 963–968. [Google Scholar]
- Sato, M.; Sato, Y. Asymmetric aggregation operator and its application to fuzzy clustering model. Comput. Stat. Data Anal. 2000, 32, 379–394. [Google Scholar] [CrossRef]
- Singh, A.K.; Dolly, C.D.; Tiwari, S. Feature Extraction and Classification Methods of Texture Images; Lap Lambert Academic Publishing: Saarbrücken, Germany, 2013. [Google Scholar]
- Kannala, J.; Rahtu, E. BSIF: Binarized statistical image features. In Proceedings of the International Conference Pattern Recognition, Tsukuba, Japan, 11–15 November 2012; pp. 1363–1366. [Google Scholar]
- Herbadji, A.; Guermat, N.; Ziet, L.; Cheniti, M.; Herbadji, D. Personal authentication based on wrist and palm vein images. Int. Biom. 2019, 11, 309–327. [Google Scholar] [CrossRef]
- NIST: ‘National Institute of Standards and Technology: NIST Biometric Scores Set’. 2004. Available online: https://wwwnistgov/itl/iad/ig/biometricscores (accessed on 14 January 2020).
- Kumar, A.; Shekhar, S. Personal Identification using Rank-level Fusion. IEEE Trans. Syst. Man Cybern. Part 2011, 41, 743–752. [Google Scholar] [CrossRef]
- Ajay, K.; Chenye, W. Automated human identification using ear imaging. Pattern Recogn. 2012, 41, 956–968. [Google Scholar]
- Kumar, A.; Kwong, Z.X. Personal identification using minor knuckle patterns from palm dorsal surface. IEEE Trans. Inf. Forensics Secur. 2016, 11, 2338–2348. [Google Scholar] [CrossRef]
- McCool, C.; Marcel, S.; Hadid, A.; Pietikäinen, M.; Matejka, P.; Cernocký, J.; Poh, N.; Kittler, J.; Larcher, A.; Levy, C.; et al. Bi-Modal Person Recognition on a Mobile Phone: Using mobile phone data. In Proceedings of the IEEE ICME Workshop on Hot Topics in Mobile Mutlimedia, Melbourne, Australia, 9–13 July 2012; pp. 635–640. [Google Scholar]
- Rattani, A.; Derakhshani, R.; Saripalle, S.K.; Gottemukkula, V. ICIP 2016 competition on mobile ocular biometric recognition. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Phoenix, AZ, USA, 25–28 September 2016; pp. 320–324. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).