Abstract
Although the Poisson distribution is appropriate for modelling equi-dispersed distributions, it reflects bimodality less well. In this paper, we propose a distribution which is more suitable for the latter purpose. It can be fitted to both positively and negatively skewed data and appears to represent overdispersion phenomena correctly in count data models obtained using a Poisson distribution. Furthermore, the distribution can be normalised in terms of its mean value, and therefore covariates can be included. Our empirical results are based on tourists’ length of stay in the Canary Islands (Spain), a popular holiday destination. The study analyses data supplied by the Canary Islands Tourist Expenditure Survey. Our findings show that the model presented is valid and that the fit obtained is reasonably good.
Keywords:
bimodality; covariate; overdispersion; shifted Poisson distribution; length of tourist stay MSC:
62-07; 62E99; 62P20
1. Introduction
Bimodal and multimodal distributions are found in many continuous and discrete data sets; for example, in aggregate counts of responses to Likert scale questions, as in online ratings of movies or hotels [1]; in the durations of intervals between the eruptions of certain geysers; in the distributions of male and female body weights; in student test scores, distinguishing between those who studied for the test and those who did not; and in tourism analysis, regarding the number of nights that tourists spend at a given destination [2,3]. However, these distributions have received little attention in theoretical and empirical literature, with the exceptions of classical distributions based on continuous data, such as exponential or normal distributions [4]; discrete data frameworks, such as censored count data (where an additional mode might be used for the highest category; see [5]); latent class models for count data which account for heterogeneity using a finite mixture of unimodal Poisson distributions (i.e., the latent class truncated Poisson regression [6]); and flexible models that capture both over and underdispersion, such as the mixed Conway–Maxwell–Poisson distribution, which can reflect a wide range of truncated discrete data, and can exhibit either unimodal or bimodal behaviour [1] (the Conway–Maxwell–Poisson (CMP) distribution is a two-parameter generalisation of the Poisson distribution that allows for either over or underdispersion.). An important feature of multimodal data sets is that they can reveal when two or more types of individuals are represented in a data set (for example, consumer segments and preferences). The discrete data observed in the specific case of the length of tourist stay at a major “sun and sand” destination present not only bimodality but also overdispersion (the variance is greater than the mean). The length of stay is considered to be multimodal because tourists usually structure their trips in weekly blocks (for holidays in the Canary Islands, periods of one, two or three weeks are the most common options). However, there is also some heterogeneity of tourist preferences as regards shorter or longer stays, which may depend on socioeconomic and demographic characteristics, the time available to tourists and their prior familiarity with the destination, among other things. Reflecting on these diverse possibilities, empirical studies in this field have used several types of count data models, for example, latent class truncated Poisson models, to define different segments of tourists’ preferences [3] or count data quantile regression models to analyse the quantiles of the distribution of overall length of tourist stay [7], based on the Poisson distribution. More recently, [2] two newly proposed statistical distributions with which to explicitly incorporate bimodality, including a flexible discrete distribution and a mixture model based on the Poisson distribution (discrete choice models, have also been used, which redefine the variable by taking weekly intervals; see [8,9,10]). However, although the latter models are suitable and provide a reasonably good fit, they also present certain drawbacks. Following [2], we obtain a flexible distribution for modelling bimodal behaviour in a count data framework based on the Poisson distribution. As an anonymous reviewer pointed out, a finite mixture (non-latent) of two Poisson distributions could produce bimodality. However, these models of finite mixtures are known to present some difficulty regarding identifying and estimating the parameters. Moreover, this problem may be aggravated if covariates are included. This research contributes to the literature in two main respects. First, we present a discrete distribution characterised by overdispersion, and also by either unimodality or bimodality, according to the parameter values selected. This distribution is obtained by means of a shifted version of a classical discrete Poisson distribution. Our proposal accounts for some of the heterogeneity observed, and moreover, facilitates the inclusion of covariates; therefore, determinants to explain the bimodal variable can be considered. Second, the approach described overcomes problems that may arise in estimating the models described by [2], with respect to the existence of multiple points which maximise the logarithm function of the likelihood, thus impeding identification of the global maximum. The rest of this paper is organised as follows. Section 2 presents the model proposed for length of tourist stay, and describes its most important properties. The estimations of the parameters for the proposed distribution are discussed in Section 3, after which we present the empirical analysis performed, based on the length of stay. The results obtained are then discussed. Finally, in Section 6 we summarise the main conclusions drawn.
2. The Bimodal Shifted Poisson Model
According to the standard literature in this field, briefly presented above, the length of tourist stay, T, like most expressions of the frequency of occurrence of an event, can be described by a Poisson distribution in which . This is the standard distribution for modelling random counts. In many cases, however, a model based on the Poisson distribution will be inadequate. Thus, in some situations counts may occur in clusters, giving rise to heterogeneity among individuals and provoking contagion (i.e., a degree of association between discrete events). When this happens, the count data may become overdispersed (i.e., the variance is greater than the mean), making the Poisson assumption very restrictive. On the other hand, if the parameter fits a gamma distribution with shape and scale , , the unconditional distribution of T produces a negative binomial distribution with parameters r (dispersion parameter) and . Nevertheless, although this distribution overcomes the problem of overdispersion, it still fails to reflect the bimodality observed in empirical data, such as that for the length of tourist stay (usually expressed in days). The following theorem, crucially, obtains a distribution that is appropriate for modelling the length of tourist stay.
Theorem 1.
Let be a discrete (or continuous distribution) with finite mean μ and variance . Then, it is verified that
for , where
is a genuine probability mass function (density function in the continuous case).
Proof.
The result is obtained by taking into account that and summing (integrating in the continuous case) over the support of the random variable Y in order to have (). ☐
Parameter controls the unimodality or bimodality of the family given in (1). Here is the parent distribution from which we can construct a distribution that can be unimodal or bimodal. From the construction established in the previous result, it is apparent that this same result can be applied to obtain generalisations of classical distributions. The first candidates for this application, which rely on just a single parameter, would be the exponential distribution, for the continuous case, and the geometric and Poisson distributions, for the discrete case. In this paper, we consider the latter case. In other words, our starting point is that of a shifted Poisson distribution with parameter . This situation is illustrated in the following result.
Proposition 1.
The expression given by
where , and
is a genuine probability mass function for .
Proof.
The proposition is an immediate consequence of applying the result provided in Theorem to the shifted Poisson distribution with the pf given by
Hence the result. ☐
In order to achieve a more elegant expression for the above probability function (pf), it is convenient to take and . The expression given in (2) can then be rewritten as
where
with . Figure 1 shows that the proposed distribution properly represents the unimodal or bimodal nature of empirical data. In this situation, the shifted Poisson distribution is a special case for . Furthermore, it seems that as tends to infinity and , the normal distribution is an excellent approximation of the pf (4). Some tedious but simple computations then provide the probability generating function of the distribution, which is given by
for . From (5) the moments of the distribution can be obtained. In particular, the mean and the variance are given by
respectively.
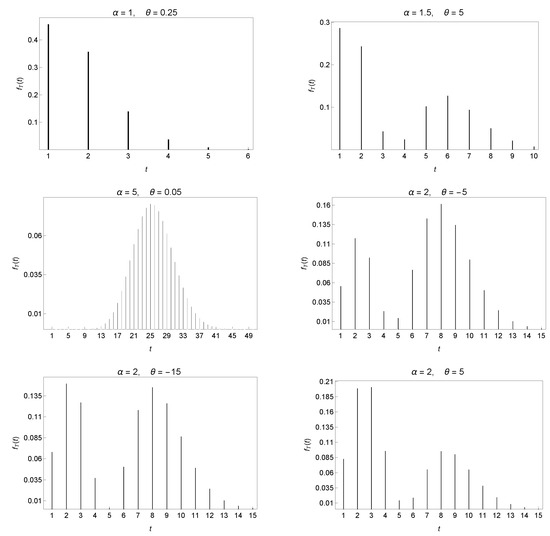
Figure 1.
Graphs of the pf given in (4) for special cases of parameters and .
By determining the index of dispersion (ID) of a probability distribution, we can quantify the extent to which a set of occurrences is dispersed, compared to a standard pattern such as the Poisson distribution. The ID is defined as the variance of a distribution divided by its mean. If the ID is greater than one, the corresponding distribution is said to be overdispersed, and if it is less than one, the distribution is underdispersed. Figure 2 represents the ID plot of the proposed bimodal distribution for some supports of the two parameters of the distribution. The ID can take values greater or less than 1, and so the distribution is appropriate for fitting empirical data which present over or underdispersion. The probabilities can be computed by using the recursive formula
where . Furthermore, the expression given in (6) can be used to obtain the mode or modes of the distribution, by solving, for , the third-degree polynomial equation given by
where represents the integer part. Equation (7) supplies either one real solution (the unimodal case) or three such solutions (two modes and the corresponding anti-mode). The cumulative distribution function, which is not reproduced here, can also be obtained in closed form.
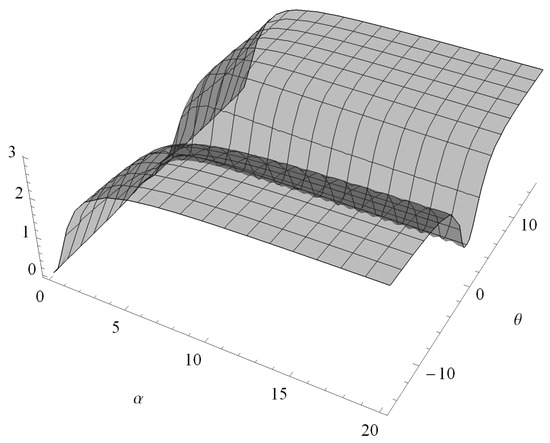
Figure 2.
Index of dispersion of the proposed distribution.
3. Model Estimation
Consider a sample with n observations , taken from the pf (2). As a first approximation, the parameters and can be estimated by the method of moments, assuming , where is the sample mean. The estimation is then obtained by the maximum likelihood method. To do so, we first consider the model without covariates. Here, the log-likelihood function is proportional to
The normal equations for estimating the parameters and are given by
Equations (9) and (10) can be solved numerically for and using the Newton–Raphson iteration; for example, starting from the seed point near to zero, with .
Simulation Study
The accept-reject sampling method can be used to generate random values of a variable following the pf (4) (see, for instance, [11]). Table 1 shows the results of simulation studies performed to illustrate the behaviour of the maximum likelihood (ML) estimators for 1000 samples, with n = 50, 100, 150 and 200, from a population distributed as in (4). For each of these samples, ML estimators are computed numerically according to the Newton–Raphson method. Means, standard deviations (SD) and coverage (C) are reported, and as expected, the bias decreases in inverse proportion to the sample size n.

Table 1.
Empirical mean, standard deviation (SD) and coverage (C) values for different values of parameters and .
4. Including Covariates
Let us now assume that covariates are to be included in the model. First, consider that
where and where . Under this assumption, the mean of the pf given in (4) is just the parameter , as is usually assumed when covariates must be included in the model. Now, let be a vector of covariates or factors associated with the length of stay of the i-th tourist and where is the j-th factor for the i-th observation, . This vector of linearly independent regressors will determine . The model provides great simplicity and the mean is straightforwardly expressed in terms of . Therefore, in order to introduce the covariates, we need only assume a translated one unit logit link, defined by
where denotes the corresponding vector of regression coefficients. Furthermore, this logit link ensures that lies within the interval . The log-likelihood of the model with covariates is similar to that given in (8) except that is replaced by , given in (11). Thus we have
The normal equations are now given by
for , where,
Finally, can easily be computed by means of the chain rule.
Marginal Effects
The marginal effect can be defined as the variation in the conditional mean of T caused by a one-unit change in the j-th covariate. It is calculated as
for and . The marginal effect indicates that a one-unit change in the j-th regressor will increase or decrease the expectation of the length of stay. The effect is determined by the sign, positive or negative, of the regressor for each mean. For indicator variables such as , which only take the value 0 or 1, the marginal effect in terms of the odds ratio is approximately . Therefore, when the indicator variable is one, the conditional mean is approximately times greater than when the indicator is zero.
5. Empirical Analysis
5.1. Literature Review on Length of Tourist Stay
Previous analyses of the length of tourist stay at a given destination have mainly focused on the factors which may determine or influence this duration. Two types of econometric method have been proposed to address this question. On the one hand, the survival analysis method, which has been discussed by [12,13,14,15,16,17,18,19], among others. However, this technique has been criticised by [20], who observed that various justifications for survival models as an alternative to traditional OLS regression do not bear close scrutiny. According to this critic, the OLS regression model describes the association between a set of independent variables and length of stay at least as effectively as the various survival models that have been proposed. In the second approach, an empirical statistical property is addressed, such as the presence of various modes in the distribution of the length of stay. Thus, [8,9,10] have proposed estimating binary and/or multinomial logit models for various time periods: up to seven days, 7 to 14 days and so on. However, a drawback of this type of modelling is that segmentation into weekly categories is rather arbitrary [3]. To overcome this objection, [3] proposed estimating a latent class Poisson regression model for the length of stay. This model assigns individuals endogenously to categories presenting homogeneous preferences, such that each latent class corresponds to a segment of the sample with a unique set of preferences. For each class, the model estimates the impacts of other variables relevant to the final length of stay. Finally, [7] used a count data quantile regression to analyse the multimodality of tourists’ length of stay. In this paper, the authors used micro-level data to calculate price and income elasticities for the length of tourist stay at various holiday destinations in Italy. In a related study, [2] examined two distributions which may incorporate bimodality. The first was a flexible discrete distribution that can be applied to bimodal or unimodal data sets, while the second was an infinite mixture model that explained the unobserved heterogeneity in the main parameter, reflecting the heterogeneity of tourists’ preferences. Covariates may be included in either of these models.
5.2. Data
In the present study, the data were obtained from the Canary Islands Tourist Expenditure Survey (Encuesta de Gasto Turístico), carried out by the Canary Islands Institute of Statistics (ISTAC). This survey was based on interviews conducted with tourists on the day of their departure and provides quarterly information on total tourist expenditure in the Canary Islands. The survey population comprises Spanish and foreign tourists who enter the Canary Islands by air. The study excludes tourists whose expenditure in their country of origin (i.e., flights and accommodation paid in advance) is zero. It includes both those who booked a package holiday and those who travelled independently. The tourists comprising the study population were from Germany, Austria, Belgium, Denmark, mainland Spain, Finland, France, the Netherlands, Ireland, Italy, Norway, Poland, Portugal, the United Kingdom, Czech Republic, Russia, Sweden, Switzerland and Luxembourg. They stayed for at least one night and for no more than 30 consecutive nights. The study variables considered were household income expenditure at origin concerning the vacation and other characteristics regarding Spanish and foreign tourists who visited the Canary Islands during 2011 (17,923 observations) (see Appendix A Annex for definitions of variables). Table 2, with the descriptive statistics obtained for the dependent and explanatory variables used, shows that the average tourist spent 1473 euros at origin, preferred a “sun and beach” type holiday and was travelling in an average group size of two persons. On average, these tourists had visited the Canary Islands three times, had a household income of 36,000 to 48,000 euros, were 42 years old and had booked the trip through a tour operator. Almost half (47%) stayed in a 4 or 5 star hotel, and 36% had booked their flight with a low cost carrier.

Table 2.
Descriptive statistics for all tourists. Filtered database.
As can be seen in Figure 3, the statistical distribution for the variable length of stay, in all cases, is distinctly bimodal, with the vast majority of stays being for seven or fourteen days, the typical duration of package holidays in the Canary Islands. The mean length of stay was around eight nights. This bimodality was tested by the Pearson coefficient for unimodal versus bimodal distribution, which is calculated as -kurtosis. The value obtained, , confirmed the bimodality of the distribution. In addition, Hartigan’s dip test was conducted to determine whether the distribution was other than unimodal. The test result of (p-value = ) indicated significant multimodality.
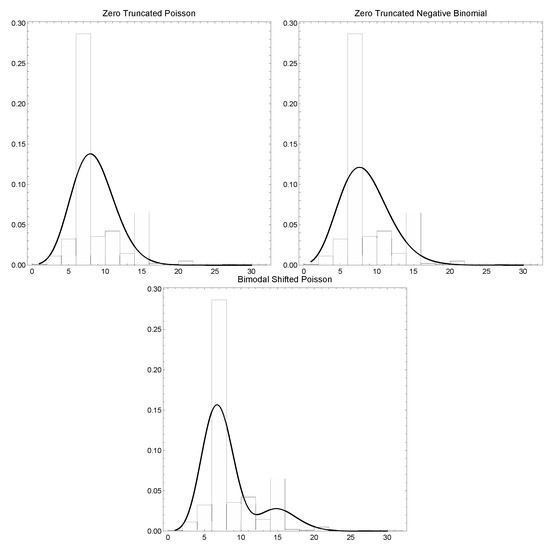
Figure 3.
Observed and expected counts under the basic model without covariates.
5.3. Model Results
The proposed model was evaluated by ML, the BFGS algorithm and Poisson regression, incorporating the survey information obtained for all tourists. Table 3 shows the results obtained for the model without covariates, the corresponding p-values (in brackets), the maximum value of the log-likelihood function for distribution (4) and the number of observations. Comparisons were made with the zero truncated Poisson (ZTP) and zero truncated negative binomial (ZTNB) distributions and the following probability functions:
where and , with and .

Table 3.
Maximum likelihood estimates for models without covariates: Zero truncated Poisson (ZTP), zero truncated negative binomial (ZTNB) and bimodal shifted Poisson. The p-values are shown in parentheses.
Table 3 shows that all these parameters are statistically significant at 5%. This table also includes the maximum value of the log-likelihood function (), the number of observations actually used and some measures of goodness-of-fit evaluated at the maximum likelihood estimates and based on the information-criterion approach. These measures are the Akaike information criterion (AIC), the Bayesian information criterion (BIC) and the consistent Akaike information criterion (CAIC) [21]. The latter overcomes the tendency of the AIC to overestimate the complexity of the underlying model, since it lacks certain properties of asymptotic consistency and does not directly depend on the sample size. The expressions for these measures are as follows:
where k is the number of parameters and n is the sample size. The lower the value of these measures, the better. Figure 3 shows a smooth kernel distribution based on empirical data and on the fitted pf. The pattern of empirical data is clearly captured by the proposed distribution.
Table 4 shows the results obtained with covariates, with ordinary least squares (OLS) estimates and also the ML estimation for TP, TNB and Bimodal Shifted Poisson regressions. The table includes the corresponding coefficients and p-values. The coefficients for covariates in the non-linear models should be interpreted with caution, because the estimated coefficients are not the marginal effects, and so the marginal effects are computed using the formula: , where k represents the k-th covariate, is a vector of covariates included in the mean equation and is a vector of estimated parameters. These effects can be evaluated at the mean or at each observation. For this reason, Table 4 includes the marginal effects evaluated at the mean (ME).

Table 4.
Ordinary least squares (OLS) and maximum likelihood (ML) estimates for TP, TNB and the bimodal shifted Poisson models with the inclusion of covariates.
A notable aspect of the ML results is that the parameter in Table 4 is statistically significant at 5%. Some coefficients in the zero-truncated Poisson and negative binomial models present important changes in magnitude and sign. Moreover, in terms of information criteria (AIC, BIC and CAIC), the shifted Poisson model outperforms the TP and TNB models. In the following, therefore, we comment on the results obtained for the Shifted Poisson model. The constant term represents a tourist with the following characteristics: someone who visits the Canary Islands in the spring, who is staying in their own home or with family/friends or who has other non-hotel accommodation, whose trip is for reasons other than a “sun and beach” holiday, whose transport and accommodation were not booked via a tour operator and who did not book in advance. Most of the parameters observed are statistically significant at 5%. Only one coefficient is significant at 10%. The proxy for cost of travel and accommodation in the country of origin, described as “expenditure at origin”, has a positive coefficient. In other words, the greater the expenditure, the longer the stay. However, contrasting results have been reported in previous research. For example, [17] obtained negative coefficients for tourism in Madeira. Reference [22] reported positive results in their study of Chinese tourism, but the coefficients for the income variables, although close to zero, were negative, and thus contrary to expectations. Our review of the literature revealed varying signs in this respect. For example, [23] obtained a negative value, although it was not statistically significant; this finding contrasts with those of [22], who obtained positive results. Regarding the influences of individual characteristics, such as the nature of the vacation, positive effects were found for the dummy variable “sun and beach” (motivation for the trip), but also for accommodation-related variables (i.e., whether the tourist stayed in a 4 or 5 star or a 1–3 star hotel). According to our analysis, repetition of the trip was positively associated with length of stay, although [20] measured a negative effect for this parameter. Statistically negative effects were found for the coefficients low-cost carrier, nationality and prebooked transport and accommodation. In addition, there was a significant positive association between the respondent’s age and the length of stay. Finally, with regard to seasonal effects, the summer season (Q4) is positively associated with the length of stay, while the winter (Q1) and autumn (Q3) have a negative effect.
6. Conclusions
This paper proposes a count data model based on the Poisson distribution, taking into account both bimodality and overdispersion. The model proposed is the shifted Poisson distribution, in the view that it is suitable for modelling the length of tourist stay, taking bimodality into account. This model was applied to the Canary Islands, a popular holiday destination, and would also be suitable with respect to tourism in the Balearic Islands, another major tourist destination in Spain. Using data from the Canary Islands Tourist Expenditure Survey for the year 2011, and taking into account information for all tourists, our shifted Poisson model provided a reasonable fit. Only the coefficient of income did not appear to be coherent with the expenditure literature, although this outcome has also been reported by previous studies of the duration of tourist visits. Finally, several variables corresponding to vacation characteristics were found to have statistically significant effects on the length of stay, as were some individual characteristics, such as age.
Author Contributions
All authors contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
E.G.D. was partially funded by grant ECO2017-85577-P (Ministerio de Economía, Industria y Competitividad. Agencia Estatal de Investigación). The research of H. W. Gómez and J. Reyes was supported by MINEDUC-UA project, Code ANT 1755. E.G.D. also acknowledges the Departamento de Matemáticas, Facultad de Ciencias Básicas, Universidad de Antofagasta, Antofagasta (Chile) for their special support, as part of this paper was written while EGD was visiting the university in 2018 supported by MINEDUC-UA project, code ANT1755.
Acknowledgments
The authors wish to acknowledge the Associate Editor and two anonymous referees for the constructive comments that helped to improve the quality of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Annex: Brief Description of Variables Used
This annex includes a brief description of the variables used in the empirical analysis section.
- Length of tourist stay (days) in the Canary Islands.
- Expenditure at origin (€). Flights and accommodation for the travel party, paid in advance. This is usually the main expenditure by each tourist, and is effected in the country of origin.
- Some individual characteristics.
- 3.1
- Household income. Measured as an ordered categorical variable, not as a continuous one. This variable takes the following values: , from 12,000 to 24,000€; , from 24,001 to 36,000€; , from 36,001 to 48,000€; , from 48,001 to 60,000€; , from 60,001 to 72,000€; , from 72,001 to 84,000€; and , higher than 84,000€. Medium income is a dummy variable which takes the value one when categories are 3, 4 or 5, and 0 otherwise. High income is a dummy variable that takes the value 1 for categories 6 and 7, and 0 otherwise.
- 3.2
- Age of the survey respondent. Finally, we controlled for seasonal variables, considering three dummies: summer, autumn and winter. Summer was taken as June to September, autumn as October to December and winter as January to March. In winter, there is much less competition in the sun-and-beach tourism market than in summer, as there are few good alternatives for tourists in this demand segment (in many cases, too, tourists prefer to repeat their visits) [24].
- Some vacation characteristics.
- 4.1
- Type of accommodation. The following types of variable were considered: a dummy variable, taking the value 1 if the tourist accommodation is a 4 or 5 star hotel/aparthotel, and 0 otherwise; a second dummy variable, taking the value 1 if the tourist accommodation is a 1, 2 or 3 star hotel/aparthotel, and 0 otherwise; and a third dummy variable taking the value 1 if the tourist stays in non-hotel accommodation and the value 0 otherwise. The reference categories considered are own home or staying at the home of friends or family, or other types of accommodation.
- 4.2
- Travel party size or family size. The number of persons booking the holiday package paid for in the country of origin.
- (a)
- Repetition. The number of previous visits to the Canary Islands. A value of 0 is possible, indicating that at the moment of the interview, this is the tourist’s first visit to the Canary Islands.
- 4.3
- Transport (return flight) and accommodation booked via a tour operator.
- 4.4
- Low cost. This is a dummy variable, taking the value 1 if the travel arrangements were made with a low-cost carrier, and 0 otherwise.
- 4.5
- Sun and beach. A dummy variable, taking the value 1 if the tourist’s motive for travel is a “sun and beach” holiday, and 0 otherwise.
References
- Sur, P.; Shmueli, G.; Bose, S.; Dubey, P. Modeling bimodal discrete data using Conway-Maxwell-Poisson mixture models. J. Bus. Econ. Stat. 2015, 33, 352–365. [Google Scholar]
- Gómez-Déniz, E.; Pérez-Rodríguez, J.V. Modeling bimodality of tourist length of stay. Ann. Tour. Res. 2019, 75, 131–151. [Google Scholar]
- Alegre, J.; Mateo, S.; Pou, L. A latent class approach to tourists’ length of stay. Tour. Manag. 2011, 32, 555–563. [Google Scholar]
- Little, K.R.; DelHomme-Little, B. A graphical technique for determining the number of components in a mixture of normals. J. Am. Stat. Assoc. 1994, 89, 487–495. [Google Scholar]
- Bose, S.; Shmueli, G.; Sur, P.; Dubey, P. Fitting Com-Poisson mixtures to bimodal count data. In Proceedings of the 2013 International Conference on Information, Operations Management and Statistics (ICIOMS2013), Kuala Lumpur, Malaysia, 1–3 September 2013; pp. 1–8. [Google Scholar]
- Wedel, M.; Desarbo, W.S.; Bult, J.R.; Ramaswamy, V.J. A latent class Poisson regression model for heterogeneous count data. J. Appl. Econom. 1993, 8, 397–411. [Google Scholar]
- Salmasi, L.; Celidoni, M.; Procidano, I. Length of stay: Price and income semi-elasticities at different destinations in Italy. Int. J. Tour. Res. 2012, 14, 515–530. [Google Scholar]
- Alegre, J.; Pou, L. Microeconomic Determinants of the Duration of Stay of Tourists; Physica-Verlag: Heidelberg, Germany, 2007; pp. 181–206. [Google Scholar]
- Alegre, J.; Pou, L. The length of stay in the demand for tourism. Tour. Manag. 2006, 27, 1343–1355. [Google Scholar]
- Nicolau, J.L.; Más, F.J. A Random Parameter Logit Approach to the Two-Stage Tourist Choice Process: Going on Holidays and Length of Stay; Working Papers; Serie AD 2004-46; Instituto Valenciano de Investigaciones Económicas: Valencia, Spain, 2004. [Google Scholar]
- von Newmann, J. Various Techniques used in Connection With Random Digits. Stand. Appl. Math. Ser. 1951, 12, 36–38. [Google Scholar]
- Alegre, J.; Mateo, S.; Pou, L. Determinants of the length of stay in Latin American tourism destinations. Tour. Anal. 2011, 13, 329–340. [Google Scholar]
- Barros, C.P.; Butler, R.; Correia, A. The length of stay of golf tourism: A survival analysis. Tour. Manag. 2010, 31, 13–21. [Google Scholar]
- Barros, C.P.; Correia, A.; Crouch, G. The length of stay in tourism. Ann. Tour. Res. 2010, 37, 692–706. [Google Scholar]
- Gokovali, U.; Bahar, O.; Kozak, M. Determinants of length of stay: A practical use of survival analysis. Tour. Manag. 2011, 28, 736–746. [Google Scholar]
- Hong, S.K.; Jang, H. Factors influencing purchasing time of a new casino product and its managerial implications: An exploratory study. J. Travel Res. 2005, 43, 395–403. [Google Scholar]
- Machado, L.P. Does destination image influence the length of stay in a tourism destination? Tour. Econ. 2010, 16, 443–456. [Google Scholar]
- Menezes, A.G.; Moniz, A.; Vieira, J.C. The determinants of length of stay of tourists in the Azores. Tour. Econ. 2008, 14, 205–222. [Google Scholar]
- Peypoch, N.; Randriamboarison, R.; Rasoamananjara, F.; Solonandrasana, B. The length of stay of tourists in Madagascar. Tour. Manag. 2012, 33, 1230–1235. [Google Scholar]
- Thrane, C. Analyzing tourists’ length of stay at destinations with survival models: A constructive critique based on a case study. Tour. Manag. 2004, 33, 126–132. [Google Scholar]
- Bozdogan, H. The general theory and its analytical extension. Psychometrika 1987, 52, 345–370. [Google Scholar]
- Wang, E.; Little, B.; DelHomme-Little, B. Factors contributing to tourists’ length of stay in Dalian northeastern China-A survival model analysis. Tour. Manag. Perspect. 2012, 4, 67–72. [Google Scholar]
- Hellström, J. A bivariate count data model for household tourism demand. J. Appl. Econom. 2013, 21, 213–226. [Google Scholar]
- Ledesma-Rodríguez, F.; Navarro-Ibáñez, M.; Pérez-Rodríguez, J.V. Return to tourist destination. Is it reputation, after all? Appl. Econ. 2005, 37, 2055–2065. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).