Convergence and Dynamics of a Higher-Order Method

Abstract

Solving problems in various disciplines such as biology, chemistry, economics, medicine, physics, and engineering, to mention a few, reduces to solving an equation. Its solution is one of the greatest challenges. It involves some iterative method generating a sequence approximating the solution. That is why, in this work, we analyze the convergence in a local form for an iterative method with a high order to find the solution of a nonlinear equation. We extend the applicability of previous results using only the first derivative that actually appears in the method. This is in contrast to either works using a derivative higher than one, or ones not in this method. Moreover, we consider the dynamics of some members of the family in order to see the existing differences between them.

1. Introduction

Mathematics is always changing and the way we teach it also changes, as can be seen in the literature. Moreover, in advanced mathematics we need to use different alternatives since we all know the different problems that students encounter. In this paper, we present a study on iterative methods that can be used in postgraduate studies in order to teach them.

In the present work, we are focused on the problem of solving the equation

$$g(x)=0,$$

(1)

giving an approximating solution $x^{*}$, where $g:\mathsf{\Omega }\subseteq S\to S$ is differentiable and $S=\mathbb{R}$ or $\mathbb{C}$. There exist several studies related to this problem, since we need to use iterative methods to find the solution. We refer the reader to the book by Petkovic et al. [1] for a collection of relevant methods. The method of interest is in this case:

$$\begin{array}{ccc}\hfill y_n& =& x_n-\frac{g(x_n)}{g^{\prime }(x_n)},\hfill \\ \hfill t_n& =& y_n-\frac{g(y_n)(g(x_n)+\rho g(y_n))}{g^{\prime }(x_n)(g(x_n)+(\rho -2)g(y_n))},\hfill \\ \hfill x_{n+1}& =& t_n-\delta \frac{K(t_n)}{g^{\prime }(x_n)},\hfill \end{array}$$

(2)

where a starting point $x_0$ is chosen, parameters $\rho$, $\delta \in S$, and

$$\begin{array}{c}K(t_n)=g(x_n)+g^{\prime }(x_n){\displaystyle \frac{{(t_n-y_n)}^2(t_n-x_n)}{(y_n-x_n)(x_n+2y_n-3t_n)}}\hfill \\ +g^{\prime }(t_n){\displaystyle \frac{(t_n-y_n)(x_n-t_n)}{x_n+2y_n-3t_n}}-g[x_n;y_n]{\displaystyle \frac{{(t_n-x_n)}^3}{(y_n-x_n)(x_n+2y_n-3t_n)}}.\hfill \end{array}$$

If we consider only the first two steps of the method in Equation (2), we obtain the King’s class of methods. This method has an order of 4 [2]. However, Equation (2) has limited usage, since its convergence assumes the existence of fifth order derivatives not appearing in the method. Moreover, no computable error bounds on $\left|\right|x_n-x_{*}\left|\right|$ or uniqueness results are given. Furthermore, the initial point $x_0$ is a shot in the dark. As an example consider function

$$g(x)=\left\{\begin{array}{cc}{x}^{3}ln{x}^2+x^5-x^4,\hfill & x\ne 0\hfill \\ x=0.\hfill \end{array}\right.$$

Then $g^{‴}(x)$ is unbounded on $\mathsf{\Omega }=[-\frac{1}{2},\frac{3}{2}]$. Hence, there is no guarantee that the method in Equation (2) converges to $x_{*}=1$ under the results in [2].

Our technique can also be used to extend the applicability of other methods defined in [1,2,3]. The novelty of our work, compared to other such as [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18], is that we give weaker conditions, only in the first derivative, to guarantee the convergence of the described method. Those conditions are given in Section 2 and the dynamical study appears in the Section 3.

2. Local Convergence Analysis

In this section we study the local convergence analysis of the method in Equation (2). If $v\in \mathrm{I}\parallel \mathrm{R}$ and $\mu >0$, we can define $U(v,\mu )$ and $\overline{U}(v,\mu )$, respectively, the open and closed balls in R. Besides, we require the parameters $L_0>0$, $L>0$, $M_0>0$, $M>0$, ${\gamma }_0>0$, $\mu$, and $\delta \in \mathrm{I}\parallel \mathrm{R}$. We need to define some parameters and functions to analyze the local convergence. Consider functions on the interval $\left[0,{\displaystyle \frac{1}{L_0}}\right)$ by

$$g_1(t)=\frac{Lt}{2(1-L_{0}t)}$$

$$\overline{g_1}(t)=\frac{L_0}{2}t+M|\rho -2|g_1(t)$$

$$h_1(t)=\overline{g_1}(t)-1$$

Then, $h_1(0)=-1<0$ and $h_1(t)\to +\infty$ as $t\to {\frac{1}{L_0}}^{-}$. Function $h_1$ has zeros in the interval $\left(0,{\displaystyle \frac{1}{L_0}}\right)$ by the intermediate value theorem. Let $r_1$ be the smallest such zero. Define functions $g_2$ and $h_2$ on the interval $[0,r_1)$ by

$$g_2(t)=\left[1+\frac{M^2(1+|\rho |g_1(t))}{(1-L_{0}t)(1-g(t))}\right]g_1(t)$$

and

$$h_2(t)=g_2(t)-1.$$

By these definitions, $h_2(0)=-1<0$ and $h_2(t)\to +\infty$ as $t\to r_1^{-}$. For this reason, function $h_2$ has a smallest zero $r_2\in (0,r_1)$. Moreover, define functions on $[0,r_2)$ by

$$\begin{array}{ccc}\hfill g_3(t)& =& g_2(t)+M\left|\delta \right|[\frac{1}{1-L_{0}t}\hfill \\ \hfill & +& \frac{\beta \gamma M^3{g}_1^2(t)(1+|\rho |g_1(t))}{(1-L_{0}t)(1-\frac{L_0}{2}t){(1-\overline{g_1}(t))}^2}+\frac{\beta \gamma M^2{g}_1(t)(1+|\rho |g_1(t))}{{(1-L_{0}t)}^2(1-\overline{g_1}(t))}\hfill \\ \hfill & +& \frac{\beta M_0{M}^3(1+|\rho -1|g_1(t)+\left|\rho \right|g_1^2{(t))}^2}{{(1-L_{0}t)}^2(1-\frac{L_0}{2}t){(1-\overline{g_1}(t))}^2}],\hfill \\ \hfill \end{array}$$

and

$$h_3(t)=g_3(t)-1.$$

Suppose that

$$M\left|\delta \right|(1+\beta M_0{M}^3)<1.$$

(3)

We can see that $h_3(0)=M\left|\delta \right|(1+\beta M_0{M}^3)-1<0$ and $h_3(t)\to +\infty$ as $t\to r_1^{-}$.

Characterize by $r_3$ the smallest such zero of $h_3(t)=0$ in $(0,r_1^{-1})$. Set $r=$ min$\{r_1,r_2,r_3\}$. Then, we have that

$$0\le g_1(t)<1$$

(4)

$$0\le \overline{g_1}(t)<1$$

(5)

$$0\le g_2(t)<1$$

(6)

and

$$0\le g_3(t)<1\mathrm{for}\mathrm{each}t\in [0,r).$$

(7)

We can express the method in Equation (2) in a different way as

$$\begin{array}{ccc}\hfill y_n& =& x_n-\frac{g(x_n)}{g^{\prime }(x_n)}\hfill \\ \hfill t_n& =& y_n-\frac{g(y_n)}{g^{\prime }(x_n)}\frac{(g(x_n)+\rho g(y_n))}{(g(x_n)+(\rho -2)g(y_n))}\hfill \\ \hfill x_{n+1}& =& t_n-\delta (A_n+B_n+C_n+D_n),\hfill \\ \hfill \end{array}$$

provided

$$\begin{array}{ccc}\hfill A_n& =& -\frac{g(x_n)}{g^{\prime }(x_n)},\hfill \\ \hfill B_n& =& -\frac{{(t_n-y_n)}^2(t_n-x_n)}{(y_n-x_n)(x_n+2y_n-3t_n)},\hfill \\ \hfill C_n& =& -\frac{g(t_n)(t_n-y_n)(x_n-t_n)}{g^{\prime }(x_n)(x_n+2y_n-3t_n)}\hfill \\ \hfill \end{array}$$

(8)

and

$$\begin{array}{ccc}\hfill D_n& =& \frac{g[x_n;y_n]{(t_n-x_n)}^3}{g^{\prime }(x_n)(y_n-x_n)(x_n+2y_n-3t_n)}.\hfill \end{array}$$

Moreover, by simple algebraic manipulations we can write the previous $B_n$, $C_n$ and $D_n$ in view of the definition of $x_n$, $y_n$, $t_n$, $B_n$, and $C_n$ as

$$\begin{array}{c}\hfill B_n=\frac{g{(y_n)}^2{(g(x_n)+\rho g(y_n))}^2(f^2(x_n)+(\rho -1)g(x_n)g(y_n)+\rho f^2(y_n))}{g(x_n){(g(x_n)+(\rho -2)g(y_n))}^2(f^2(x_n)+(\rho +1)g(x_n)g(y_n)+3\rho f^2(y_n))}\end{array}$$

(9)

$$\begin{array}{c}\hfill C_n=\frac{g^{\prime }(t_n)g(y_n)(g(x_n)+\rho g(y_n))(f^2(x_n)+(\rho -1)g(x_n)g(y_n)+\rho f^2(y_n))}{g^{\prime }(x_n)(g(x_n)+(\rho -2)g(y_n))(f^2(x_n)+(\rho +1)g(x_n)g(y_n)+3\rho f^2(y_n))}\end{array}$$

(10)

and

$$\begin{array}{c}\hfill D_n=\frac{g[x_n;y_n]{(f^2(x_n)+(\rho -1)g(x_n)g(y_n)+\rho f^2(y_n))}^3}{g(x_n)g^{\prime }{(x_n)}^2{(g(x_n)+(\rho -2)g(y_n))}^2(f^2(x_n)+(\rho +1)g(x_n)g(y_n)+3\rho f^2(y_n))}·\end{array}$$

(11)

Next, we can give the local convergence result for the method in Equation (2) using the preceding notation.

Theorem 1. 

Let $D\subseteq \mathrm{I}\mathrm{R}$ be a convex subset and $f:D\to \mathrm{I}\mathrm{R}$ a differentiable function. Consider the divided difference of order one $g[.;.]:D\times D\to L(D)$, $x^{*}\in D$ and for each $x,y\in D$ the constants $L_0>0$, $L>0$, $M_0>0$, $M>0$, $\gamma >0$, ρ, $\delta \in \mathrm{I}\mathrm{R}$, and $\beta >1$ such that

$$M\left|\delta \right|(1+\beta M_0{M}^3)<1,$$

(12)

$$0<{\rho }_0\le \rho ,max\{{\rho }_0,3-2\sqrt{2}\}\le \rho \le 3+2\sqrt{2},$$

(13)

$$g(x^{*})=0,g^{\prime }(x^{*})\ne 0,\left|\right|g^{\prime }{(x*)}^{-1}\left|\right|\le \gamma ,$$

(14)

$$\left|\right|g^{\prime }{(x^{*})}^{-1}(g^{\prime }(x)-g^{\prime }(x^{*}))\left|\right|\le L_0\left|\right|x-x^{*}\left|\right|,$$

(15)

$$\left|\right|g^{\prime }{(x^{*})}^{-1}(g^{\prime }(x)-g^{\prime }(y))\left|\right|\le L\left|\right|x-y\left|\right|,$$

(16)

$$\left|\right|g^{\prime }{(x^{*})}^{-1}{g}^{\prime }(x)\left|\right|\le M$$

(17)

$$\left|\right|g^{\prime }{(x^{*})}^{-1}g[x;y]\left|\right|\le M_0$$

(18)

and

$$\overline{U}(x^{*},r)\subseteq D,$$

(19)

where the radius r is given previously

$${\rho }_0=\frac{{(1+\beta )}^2}{(\beta -1)(2\sqrt{2(\beta -1)(3\beta -1)}+(5\beta -3))}.$$

(20)

Then, for $x_0\in U(x^{*},r)-\left\{x^{*}\right\}$ the method in Equation (2) generates a well defined sequence $\left\{x_n\right\}$, all its terms are in $U(x^{*},r)$ ($n=0,1,2,\dots$), and the sequence converges to $x^{*}$. Furthermore, the following estimates are verified

$$\begin{array}{ccc}\hfill \left|\right|y_n-x^{*}\left|\right|& \le & g_1(||x_n-x^{*}\left|\right|)||x_n-x^{*}\left|\right|<\left|\right|x_n-x^{*}\left|\right|<r,\hfill \end{array}$$

(21)

$$\begin{array}{ccc}\hfill \left|\right|t_n-x^{*}\left|\right|& \le & g_2(||x_n-x^{*}\left|\right|)||x_n-x^{*}\left|\right|<\left|\right|x_n-x^{*}\left|\right|\hfill \end{array}$$

(22)

and

$$\begin{array}{ccc}\hfill \left|\right|x_{n+1}-x^{*}\left|\right|& \le & g_3(||x_n-x^{*}\left|\right|)||x_n-x^{*}\left|\right|<\left|\right|x_n-x^{*}\left|\right|,\hfill \end{array}$$

(23)

using the functions $g_1$, $g_2$ and $g_3$ is defined above Theorem 1. Besides, $x^{*}$ is the only solution of $F(x)=0$ in $\overline{U}(x^{*},T)$ for $T\in \left[r,\frac{2}{L_0}\right)$ such that $\overline{U}(x^{*},T)\subseteq D$.

Proof. 

We shall show estimates of Equations (21)–(23) using mathematical induction. We get, through hypothesis $x_0\in U(x^{*},r)-\left\{x^{*}\right\}$, the definition of r and Equation (15) that

$$\left|\right|g^{\prime }{(x^{*})}^{-1}(g^{\prime }(x_0)-g^{\prime }(x^{*}))\left|\right|\le L_0\left|\right|x_0-x^{*}\left|\right|<L_{0}r<1.$$

(24)

From the Banach Lemma on invertible operators and Equation (24) it follows that $g^{\prime }(x_0)$ is invertible and

$$\left|\right|g^{\prime }{(x_0)}^{-1}{g}^{\prime }(x^{*})\left|\right|\le \frac{1}{1-L_0\left|\right|x_0-x^{*}\left|\right|}·$$

(25)

Then, $y_0$ is well defined by the method in Equation (2) for $n=0$. Then, we can write

$$y_0-x^{*}=x_0-x^{*}-g^{\prime }{(x_0)}^{-1}g(x_0)$$

(26)

So, we get, using Equations (4), (16), (25), and (26) that

$$\begin{array}{c}\left|\right|y_0-x^{*}\left|\right|\le \left|\right|g^{\prime }{(x_0)}^{-1}{g}^{\prime }(x^{*})\left|\right|\parallel {\int }_0^1{g}^{\prime }{(x^{*})}^{-1}(g^{\prime }(x^{*}+\theta (x_0-x^{*}))-g^{\prime }(x_0))(x_0-x^{*})d\theta \parallel \\ \le \frac{L\left|\right|x_0-x^{*}{\left|\right|}^2}{2(1-L_0||x_0-x^{*}||)}=g_1(||x_0-x^{*}\left|\right|)||x_0-x^{*}\left|\right|\\ <\left|\right|x_0-x^{*}\left|\right|<r,\end{array}$$

(27)

which shows $y_0\in U(x^{*},r)$ and Equation (21) for $n=0$.

Using Equation (14), we can express

$$g(x_0)=g(x_0)-g(x^{*})={\int }_0^1{g}^{\prime }(x^{*}+\theta (x_0-x^{*}))(x_0-x^{*})d\theta .$$

(28)

We get, in view of Equations (17) and (28), that

$$\left|\right|g^{\prime }{(x^{*})}^{-1}g(x_0)\left|\right|=\parallel {\int }_0^1{g}^{\prime }{(x^{*})}^{-1}{g}^{\prime }(x^{*}+\theta (x_0-x^{*}))(x_0-x^{*})d\theta \parallel \le M\left|\right|x_0-x^{*}\left|\right|,$$

(29)

and similarly

$$\left|\right|g^{\prime }{(x^{*})}^{-1}g(y_0)\left|\right|\le M\left|\right|y_0-x^{*}\left|\right|.$$

(30)

At this point, we have that, by Equation (18),

$$\left|\right|g^{\prime }{(x^{*})}^{-1}g[x_0;y_0]\left|\right|\le M_0.$$

(31)

Hence, $g(x_0)+(\rho -2)g(y_0)$ is invertible. We get, using Equations (5), (14), (15), (27), and (30), that

$$\begin{array}{c}\left|\right|{(g^{\prime }(x^{*})(x_0-x^{*}))}^{-1}(g(x_0)-g(x^{*})-g^{\prime }(x^{*})(x_0-x^{*})+(\rho -2)g(y_0))\left|\right|\\ \le \left|\right|x_0-x^{*}{\left|\right|}^{-1}\left[\parallel {\int }_0^1{g}^{\prime }{(x^{*})}^{-1}{g}^{\prime }(x^{*}+\theta (x_0-x^{*})-g^{\prime }(x^{*}))(x_0-x^{*})d\theta \left|\right|+\left|\right|g^{\prime }{(x^{*})}^{-1}g(y_0)\parallel \right]\\ \le \left|\right|x_0-x^{*}{\left|\right|}^{-1}\left(\frac{L_0}{2}\left|\right|x_0-x^{*}{\left|\right|}^2+|\rho -2|M\left|\right|y_0-x^{*}\left|\right|\right)\\ \le \left|\right|x_0-x^{*}{\left|\right|}^{-1}\left(\frac{L_0}{2}\left|\right|x_0-x^{*}{\left|\right|}^2+|\rho -2|M{g}_1(||x_0-x^{*}\left|\right|)||x_0-x^{*}\left|\right|\right)\\ =\overline{g_1}(||x_0-x^{*}\left|\right|)<1.\end{array}$$

(32)

Then, by Equation (32) the function $g(x_0)+(\rho -2)g(y_0)$ is invertible and

$$\left|\right|{(g(x_0)+(\rho -2)g(y_0))}^{-1}{g}^{\prime }(x^{*})\left|\right|\le \frac{1}{\left|\right|x_0-x^{*}\left|\right|(1-\overline{g_1}(||x_0-x^{*}\left|\right|))}·$$

(33)

It also follows that $t_0$ is well defined from the method in Equation (2) for $n=0$. Then, using the method in Equation (2) for $n=0$, Equations (6), (25), (29), (30), and (33), we have that

$$\begin{array}{c}\left|\right|t_0-x^{*}\left|\right|\le \left|\right|y_0-x^{*}\left|\right|+\parallel \frac{g^{\prime }{(x^{*})}^{-1}g(y_0)g^{\prime }{(x^{*})}^{-1}(g(x_0)+\rho g(y_0))}{g^{\prime }{(x^{*})}^{-1}g(x_0)g^{\prime }{(x^{*})}^{-1}(g(x_0)+(\rho -2)g(y_0))}\parallel \\ \le \left|\right|y_0-x^{*}\left|\right|+\frac{M^2\left|\right|y_0-x^{*}\left|\right|(||x_0-x^{*}\left|\right|+\left|\rho \right|\left|\right|y_0-x^{*}\left|\right|)}{(1-L_0\left|\right|x_0-x^{*}\left|\right|)||x_0-x^{*}\left|\right|(1-\overline{g_1}(||x_0-x^{*}\left|\right|))}\\ \le \left[1+\frac{M^2(||x_0-x^{*}\left|\right|+\left|\rho \right|g_1(||x_0-x^{*}\left|\right|)||x_0-x^{*}\left|\right|)}{(1-L_0\left|\right|x_0-x^{*}\left|\right|)||x_0-x^{*}\left|\right|(1-\overline{g_1}(||x_0-x^{*}\left|\right|))}\right]\left|\right|y_0-x^{*}\left|\right|\\ =g_2(||x_0-x^{*}\left|\right|)||x_0-x^{*}\left|\right|<\left|\right|x_0-x^{*}\left|\right|<r,\end{array}$$

(34)

which shows Equation (22) for $t_0\in U(x^{*},r)$ and $n=0$. Next, we define estimates on $\left|\right|A_0\left|\right|$, $\left|\right|B_0\left|\right|$, $\left|\right|C_0\left|\right|$, and $\left|\right|D_0\left|\right|$. Assume that $g(x_0)\ne 0$. We take into account the expressions $f^2(x_0)+(\rho +1)g(x_0)g(y_0)+3\rho f^2(y_0)$ and $f^2(x_0)+(\rho -1)g(x_0)g(y_0)+\rho f^2(y_0)$ as quadratic polynomials in $g(y_0)$ (or $g(x_0)$). At this point, the discriminants are formed, respectively, by $({\rho }^2-10\rho +1)f^2(x_0)$ and $({\rho }^2-6\rho +1)f^2(x_0)$, which are less than zero by Equation (13). Consequently,

$$f^2(x_0)+(\rho +1)g(x_0)g(y_0)+3\rho f^2(y_0)>0$$

(35)

and

$$f^2(x_0)+(\rho -1)g(x_0)g(y_0)+\rho f^2(y_0)>0.$$

(36)

Then, $x_1$ is well defined. Besides, we have, by Equations (35) and (36), that

$$\begin{array}{c}\left|\frac{f^2(x_0)+(\rho -1)g(x_0)g(y_0)+\rho f^2(y_0)}{f^2(x_0)+(\rho +1)g(x_0)g(y_0)+3\rho f^2(y_0)}\right|\\ =\frac{f^2(x_0)+(\rho -1)g(x_0)g(y_0)+\rho f^2(y_0)}{f^2(x_0)+(\rho +1)g(x_0)g(y_0)+3\rho f^2(y_0)}\le \beta ,\end{array}$$

(37)

so Equation (37) reduces to exhibiting that for $\lambda =\frac{g(y_0)}{g(x_0)}$

$$\phi (\lambda )\le 0,$$

(38)

where

$$\phi (t)=(1-3\beta )\rho t^2+(\rho -1-\beta (\rho +1))t+1-\beta .$$

The inequality of Equation (38) is satisfied for all $t\in \mathrm{I}\mathrm{R}$, if $1-3\beta <0$ (i.e., $\beta >\frac{1}{3}$), and the discriminant $\Delta$ of $\phi$ is

$$\Delta \le 0$$

or

$$\psi (\rho )\le 0,$$

where,

$$\psi (t)={(\beta -1)}^2{t}^2-2(\beta -1)(5\beta -3)t+{(\beta +1)}^2.$$

But the discriminant ${\Delta }_1$ of $\psi$ is given by

$${\Delta }_1=32{(\beta -1)}^3(3\beta -1)>0,\mathrm{if}\beta >1.$$

Moreover, we have $(\beta -1)(5\beta -3)>0$ for $\beta >1$. Then, by the Descartes rule of signs $\psi$ has two positive zeros. Denote by ${\rho }_0$ the smallest such zero, which can be given in closed form using the quadratic formula to arrive at the definition of ${\rho }_0$ given in Equation (20). Hence, Equation (38) holds for all $\lambda \in \mathrm{I}\mathrm{R}$ provided that Equation (13) is satisfied. Then, $x_1$ is well defined by the method in Equation (2) for $n=0$ and we get, using Equations (8), (25), and (29), that

$$\left|\right|A_0\left|\right|\le \frac{M\left|\right|x_0-x^{*}\left|\right|}{1-L_0\left|\right|x_0-x^{*}\left|\right|}.$$

(39)

Next, using inequalities from Equations (9), (14), (25), (27), (30), (33), and (37), we have that

$$\begin{array}{c}\left|\right|B_0\left|\right|\le \frac{\gamma \beta M^4\left|\right|y_0-x^{*}\left|\right|(||x_0-x^{*}\left|\right|+\left|\rho \right|\left|\right|y_0-x^{*}{\left|\right|)}^2}{\left|\right|x_0-x^{*}\left|\right|(1-\frac{L_0\left|\right|x_0-x^{*}\left|\right|}{2})\left|\right|x_0-x^{*}{\left|\right|}^2(1-\overline{g_1}(||x_0-x^{*}{\left|\right|))}^2(1-L_0\left|\right|x_0-x^{*}\left|\right|)}\\ \le \frac{\gamma \beta M^4{g}_1^2(||x_0-x^{*}\left|\right|)(1+\left|\rho \right|g_1(||x_0-x^{*}\left|\right|))\left|\right|x_0-x^{*}\left|\right|}{(1-\frac{L_0}{2}\left|\right|x_0-x^{*}\left|\right|)(1-\overline{g_1}(||x_0-x^{*}{\left|\right|))}^2(1-L_0\left|\right|x_0-x^{*}\left|\right|)}.\end{array}$$

(40)

Through Equations (10), (14), (25), (27), (30), (33), and (37), we obtain that

$$\begin{array}{c}\left|\right|C_0\left|\right|\le \frac{\gamma \beta M^3\left|\right|y_0-x^{*}\left|\right|(||x_0-x^{*}\left|\right|+\left|\rho \right|\left|\right|y_0-x^{*}\left|\right|)}{(1-L_0\left|\right|x_0-x^{*}{\left|\right|)}^2\left|\right|x_0-x^{*}\left|\right|(1-\overline{g_1}(||x_0-x^{*}\left|\right|))}\\ \le \frac{\gamma \beta M^3{g}_1(||x_0-x^{*}\left|\right|)(1+\left|\rho \right|g_1(||x_0-x^{*}\left|\right|))\left|\right|x_0-x^{*}\left|\right|}{(1-L_0\left|\right|x_0-x^{*}{\left|\right|)}^2(1-\overline{g_1}(||x_0-x^{*}\left|\right|))}\end{array}$$

(41)

Then, we obtain, by Equations (11), (14), (18), (25), (27), (30), (33), and (37) that

$$\begin{array}{c}\left|\right|D_0\left|\right|\le \frac{\beta M_0{M}^4(||x_0-x^{*}{\left|\right|}^2+|\rho -1|\left|\right|x_0-x^{*}\left|\right|\left|\right|y_0-x^{*}\left|\right|+\left|\rho \right|\left|\right|y_0-x^{*}{\left|\right|}^2{)}^2}{(1-L_0\left|\right|x_0-x^{*}{\left|\right|)}^2\left|\right|x_0-x^{*}{\left|\right|}^3(1-\frac{L_0\left|\right|x_0-x^{*}\left|\right|}{2})(1-\overline{g_1}(||x_0-x^{*}{\left|\right|))}^2}\\ \le \frac{\beta M_0{M}^4(1+|\rho -1|g_1(||x_0-x^{*}\left|\right|)+\left|\rho \right|g_1^2(||x_0-x^{*}{\left|\right|))}^2\left|\right|x_0-x^{*}\left|\right|}{(1-L_0\left|\right|x_0-x^{*}{\left|\right|)}^2(1-\frac{L_0\left|\right|x_0-x^{*}\left|\right|}{2})(1-\overline{g_1}(||x_0-x^{*}{\left|\right|))}^2}\end{array}$$

(42)

Then, using Equations (7), (34) and (39)–(42), and the method in Equation (2) for $n=0$, we obtain that

$$\begin{array}{c}\left|\right|x_1-x^{*}\left|\right|\le \left|\right|t_0-x^{*}\left|\right|+\left|\delta \right|(||A_0\left|\right|+\left|\right|B_0\left|\right|+\left|\right|C_0\left|\right|+\left|\right|D_0\left|\right|)\\ \le g_3(||x_0-x^{*}\left|\right|)||x_0-x^{*}\left|\right|<\left|\right|x_0-x^{*}\left|\right|<r,\end{array}$$

(43)

which shows the inequality in Equation (23) for $n=0$. By simply replacing $x_0,y_0,t_0,x_1$ by $x_k,y_k,t_k,x_{k+1}$ in the previous estimates we have that the estimates in Equations (21)–(23) hold. Then, from $\left|\right|x_{k+1}-x^{*}\left|\right|\le a$, $a=g_3(||x_0-x^{*}\left|\right|)\in [0,1)$, $\left|\right|x_k-x^{*}\left|\right|<r$, we get that $\underset{k\to \infty }{lim}{x}_k=x^{*}$ and $x_{k+1}\in U(x^{*},r)$. At last, to show the uniqueness part, let us suppose that there exists $y^{*}\in \overline{U}(x^{*},T)$ with $g(y^{*})=0$. Define $Q={\int }_0^1{g}^{\prime }(y^{*}+\theta (x^{*}-y^{*}))d\theta .$ We get, using Equation (15), that

$$\begin{array}{c}\left|\right|g^{\prime }{(x^{*})}^{-1}(Q-g^{\prime }(x^{*}))\left|\right|\le L_0{\int }_0^1\left|\right|y^{*}+\theta (x^{*}-y^{*})-x^{*}\left|\right|d\theta \\ \le L_0{\int }_0^1(1-\theta )\left|\right|x^{*}-y^{*}\left|\right|d\theta \\ =\frac{L_0}{2}T<1.\end{array}$$

(44)

It follows from Equation (44) that Q is invertible. Then, we conclude that $x^{*}=y^{*}$ from the estimate $0=g(x^{*})-g(y^{*})=Q(x^{*}-y^{*})$. □

As an example, consider $g(x)=e^{*}-1$, $\mathsf{\Omega }=U(0,1)$ with $x^{*}=0$ and $g[x;y]={\int }_0^1{g}^{\prime }(y+\theta (x-y))d\theta$. Then, we have $\gamma =1$, $L_0=e-1$, $L=e$, $M=e$, $M_0=\frac{e}{2}$. Then choosing $\rho =2.0$, $\delta =0.001$, $\beta =1.01$ conditions Equations (12) and (13) are satisfied. The radii obtained are: $r_1=1.16395$, $r_2=0.0585945$, and $r_3=0.0530484$, so as a consequence we obtain $r=r_3=0.0530484$.

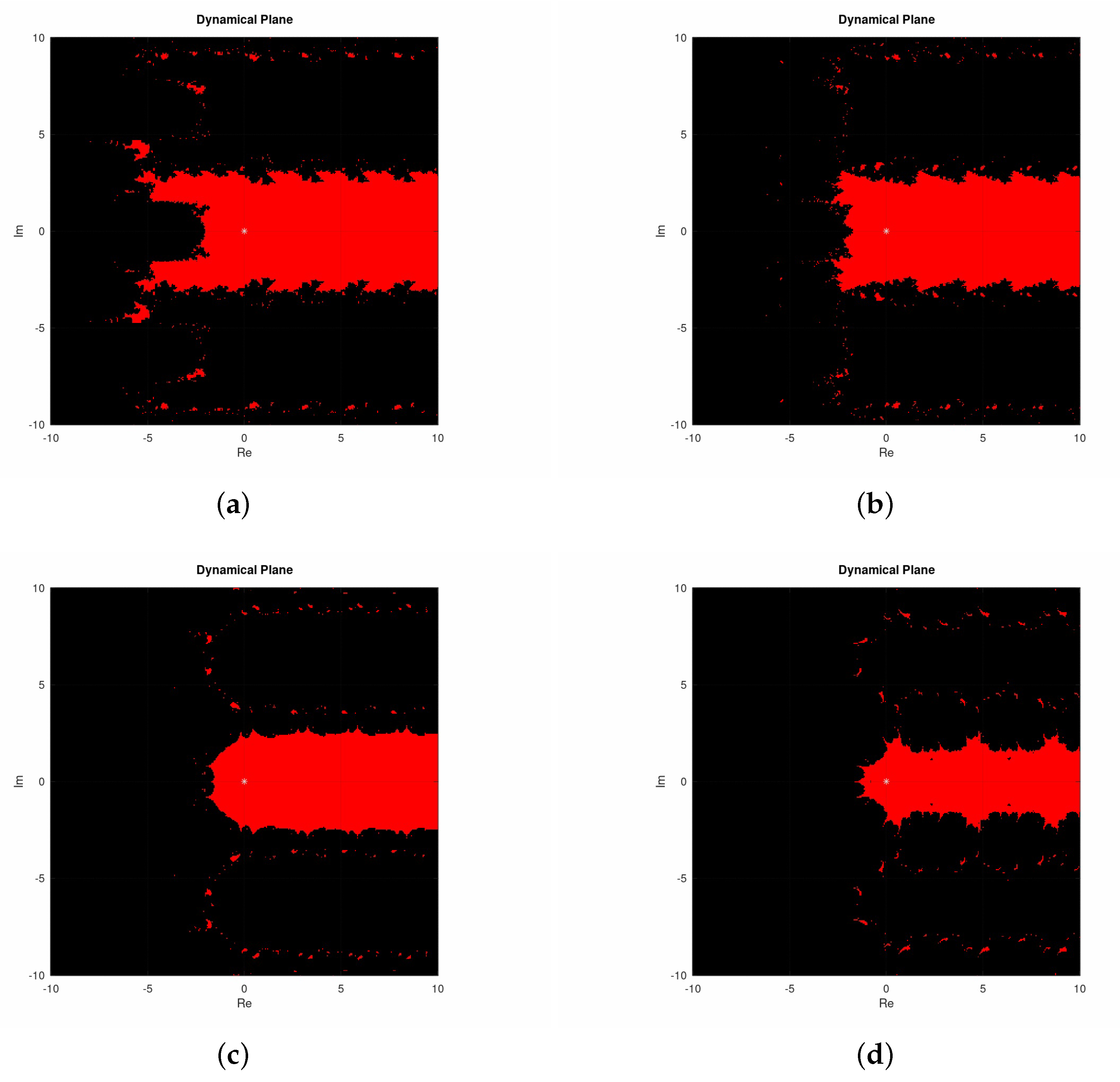
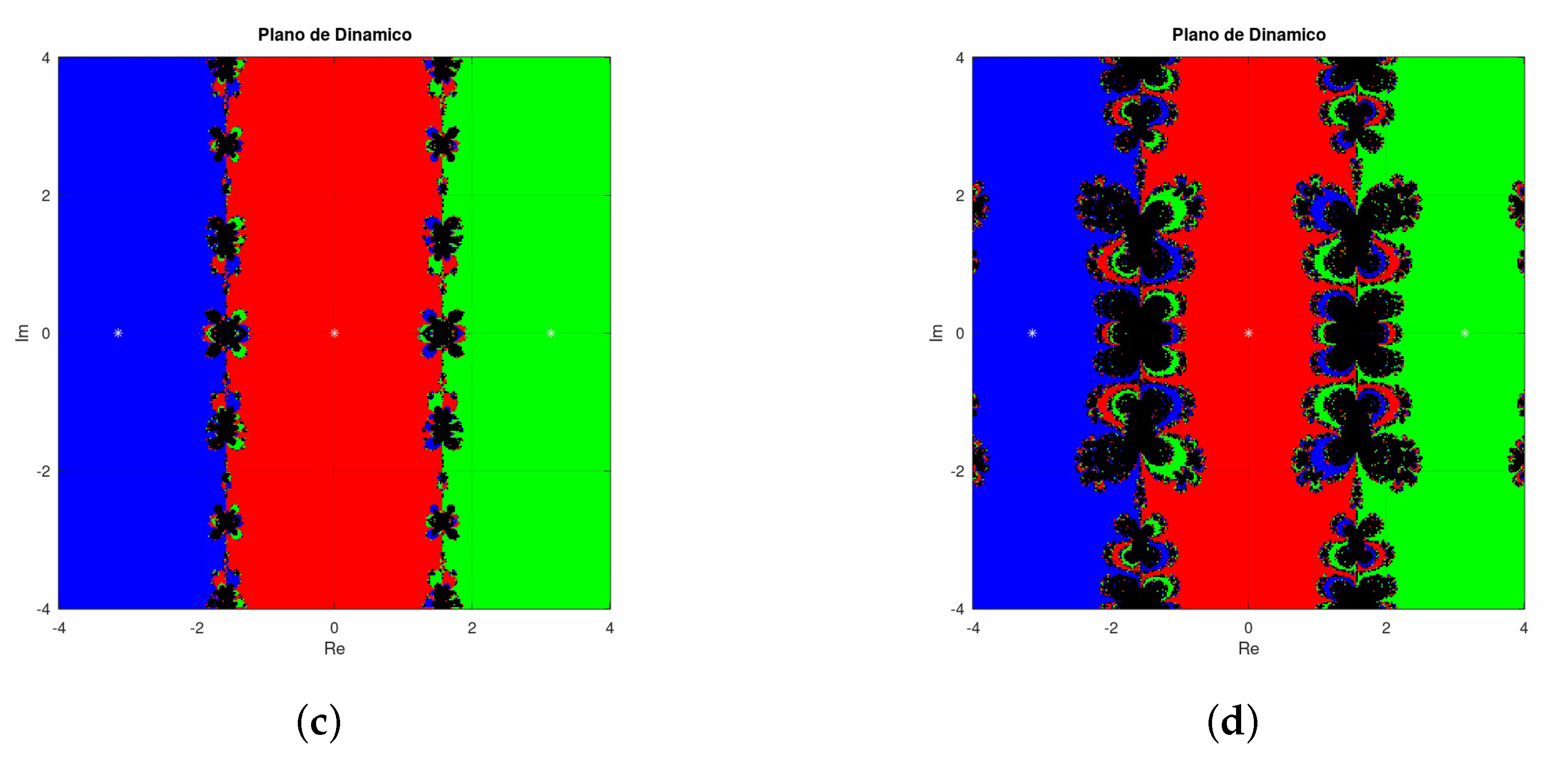
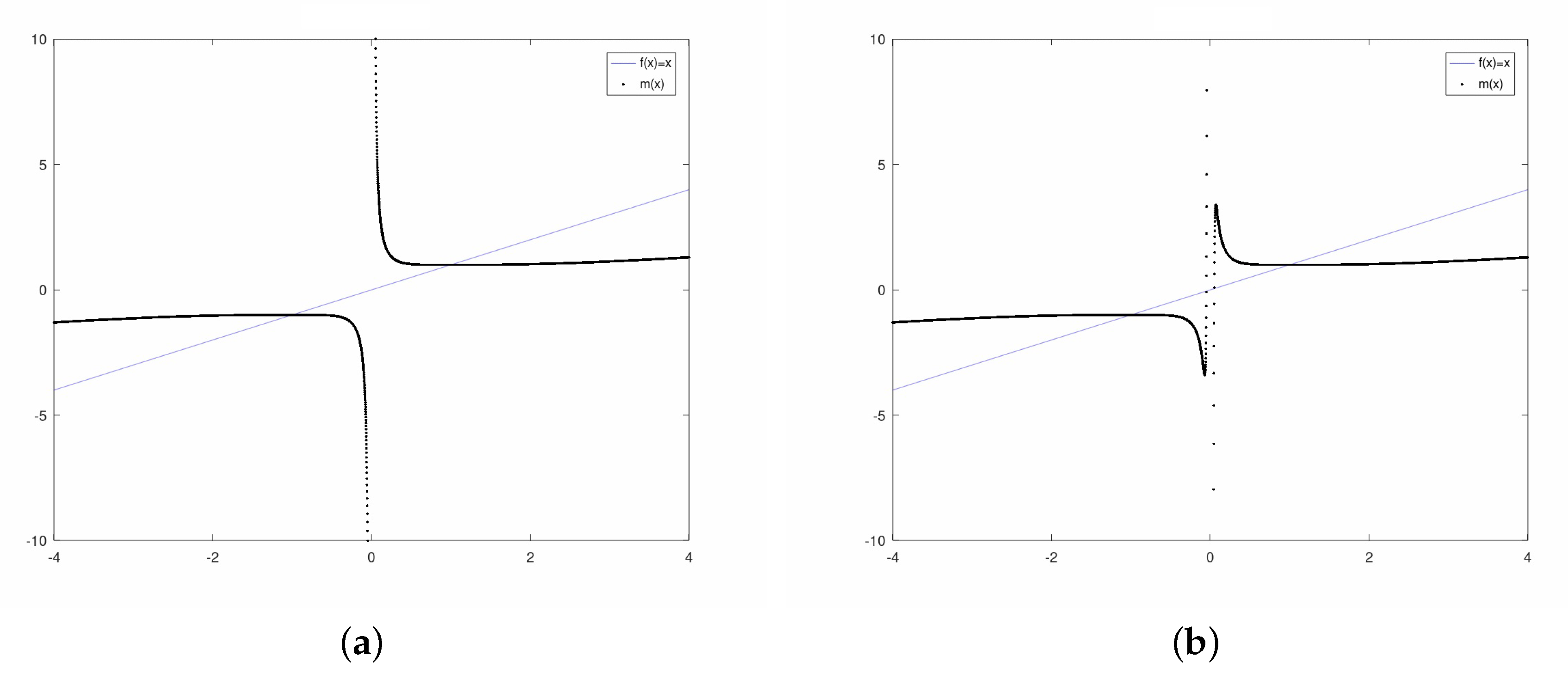
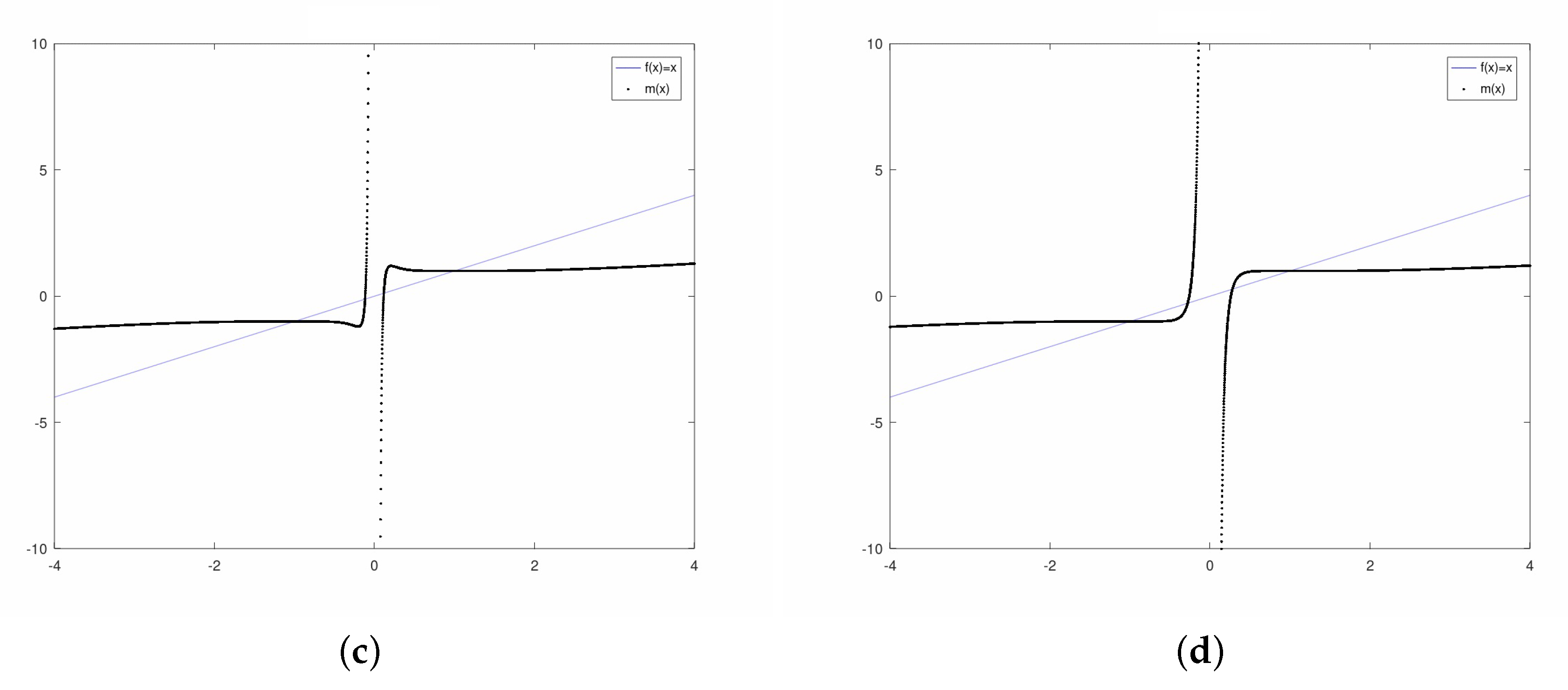
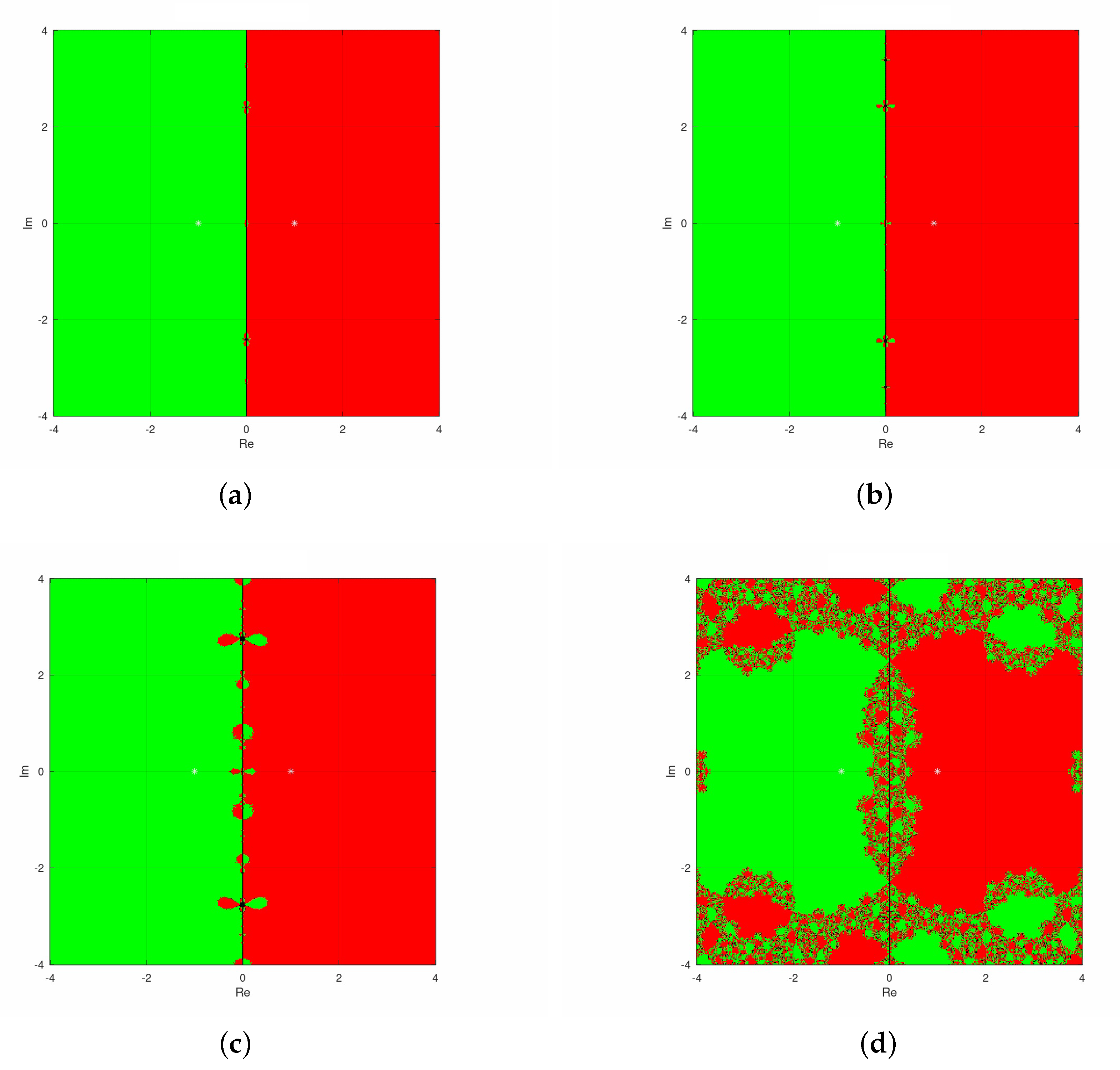
3. Dynamical Analysis

In this section, the method in Equation (2) is applied to three different families of functions and its behavior has been analyzed by changing the $\delta$ parameter using techniques that appear in [19,20,21,22].

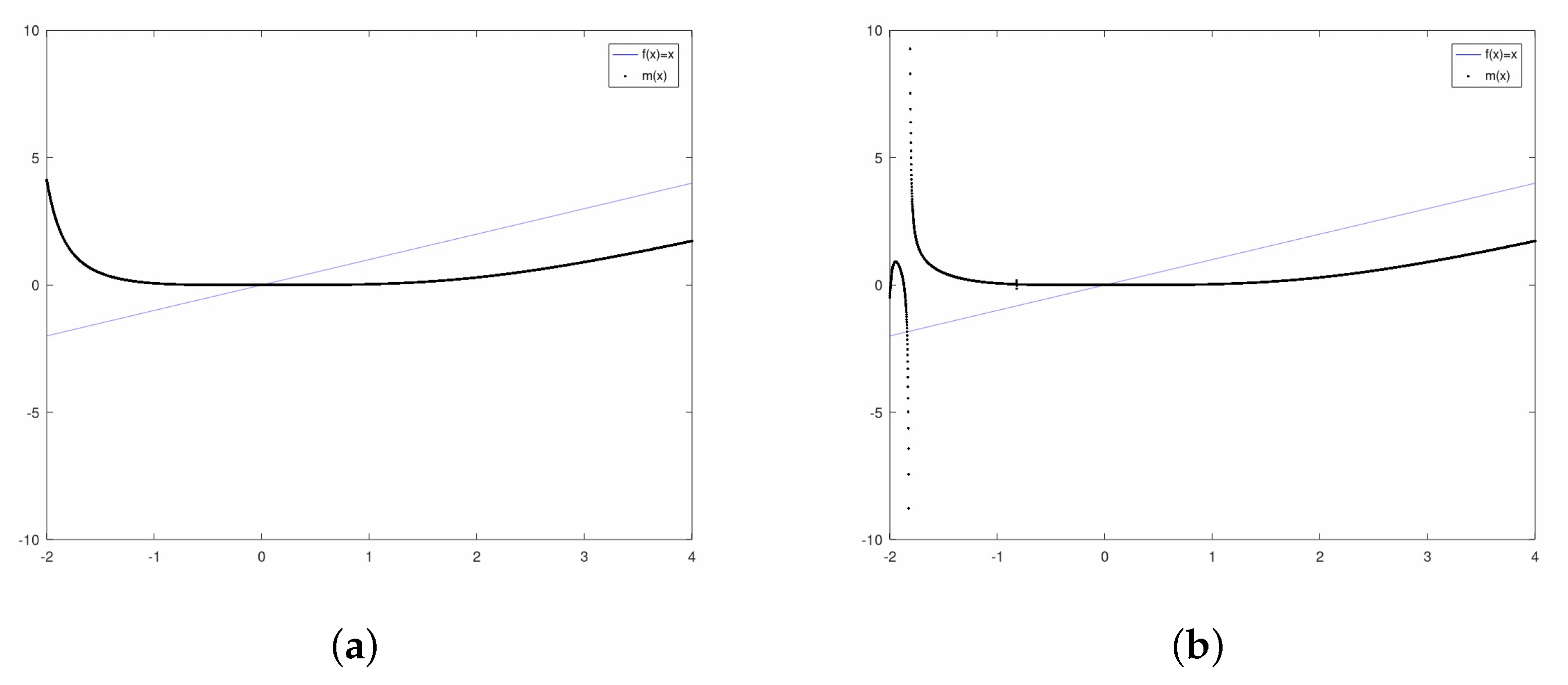
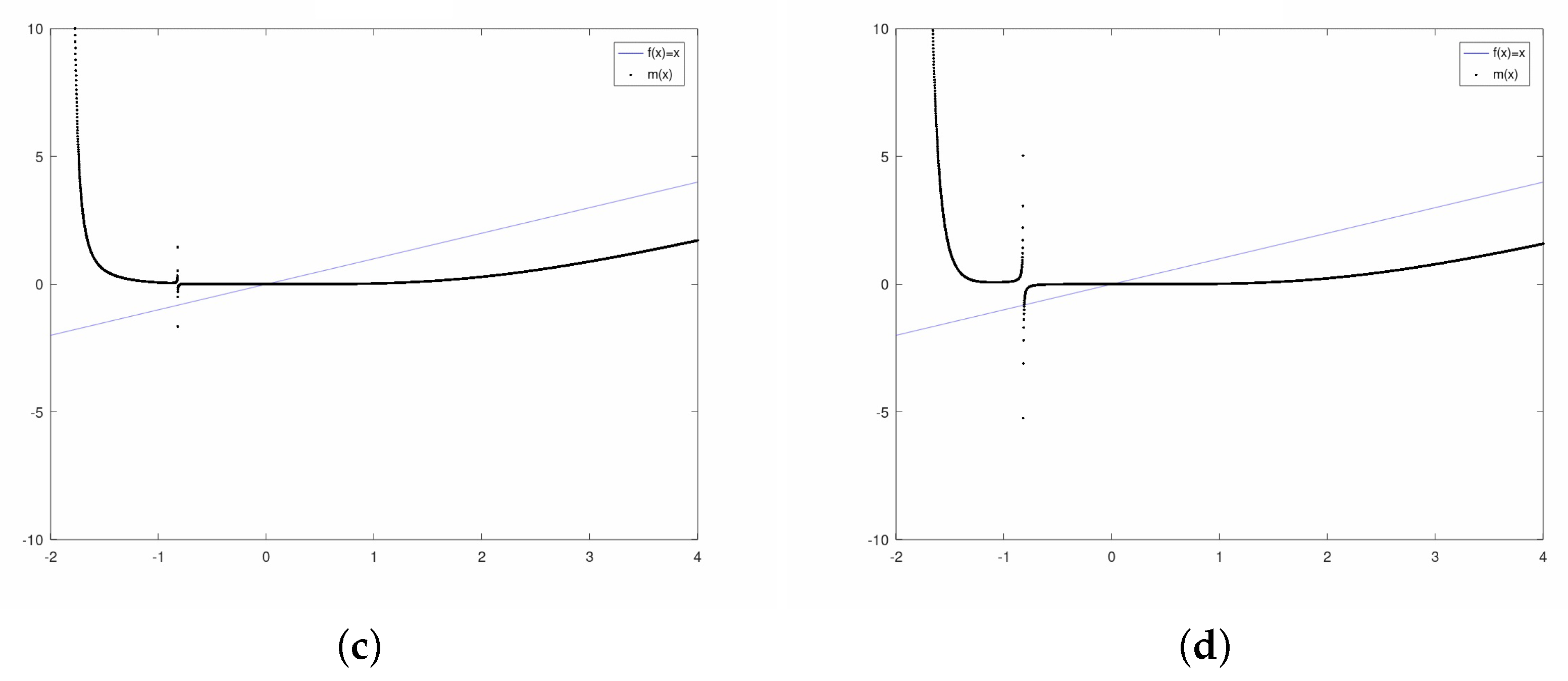
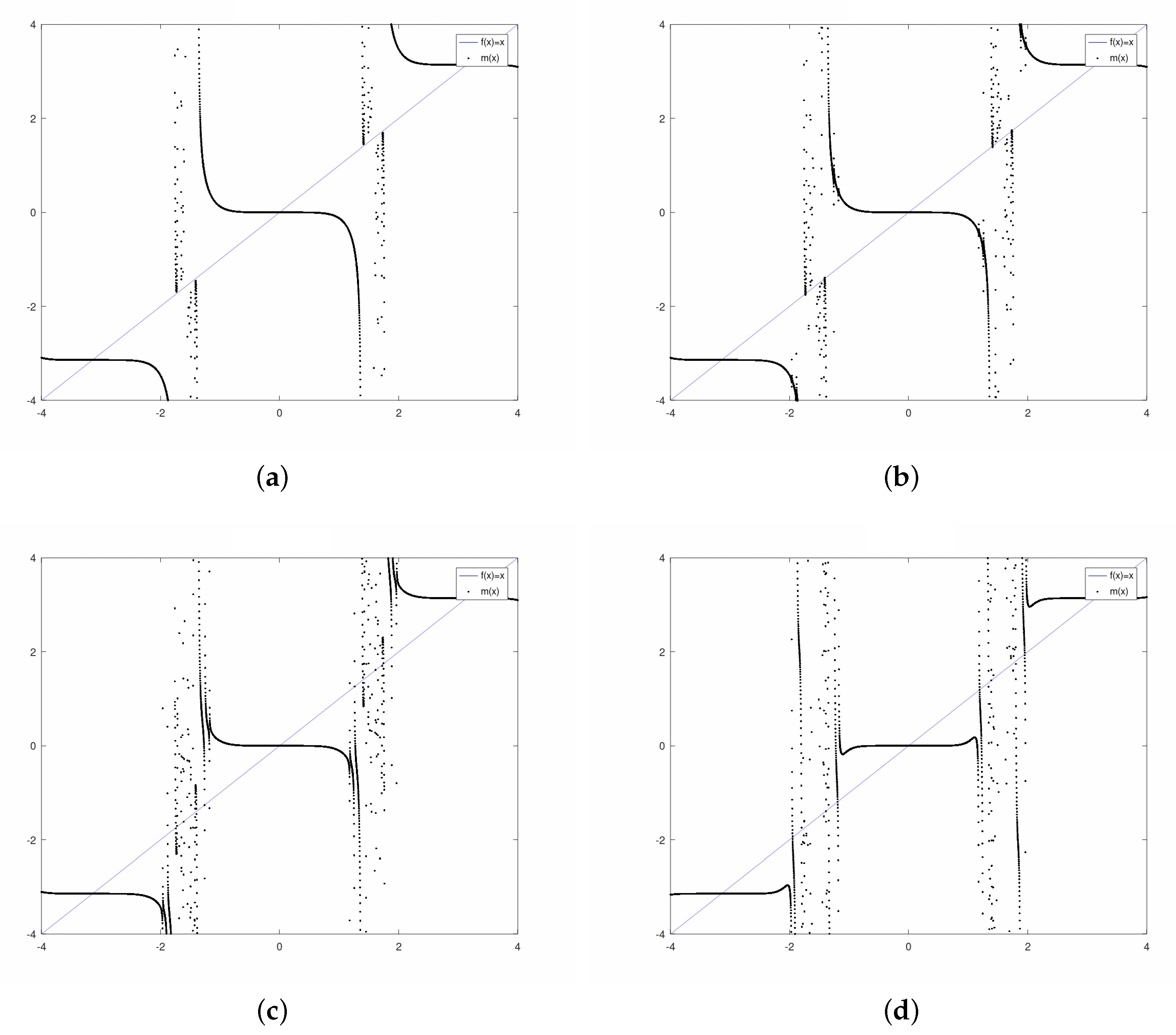
3.1. Exponential Family

The method has been applied to the function $g(x)=e^x-1$ by considering the corresponding equation $g(x)=0$. This equation has a solution at the point $x=0$, which is the only one attractive fixed point of the method. In Figure 1 we observe how the method changes with the $\delta$ parameter. Dynamical planes represent the behavior of the method in the complex domain.

In Figure 2 the symmetry of the region of convergence to the solution $x=0$ with respect to the imaginary axis is observed. Small islands of convergence appear out of the main region. It is necessary to increase the maximum number of iterations to achieve convergence with high values of $\delta$.

3.2. Sinus Family

The method can be applied to the function $g(x)=sin(x)$ with equation $g(x)=0$. In this case, the equation has a periodical solutions $x=-\pi$, $x=0$, $x=\pi$, and …, coinciding with the fixed points of the method. In Figure 3 how the method changes with the $\delta$ parameter is shown. Dynamical planes represent the behavior of the method in the complex domain as it appears in Figure 4, where with high values of $\delta$ the region of convergence is reduced.

3.3. Polynomial Family

The method was applied to the function $g(x)=(x-1)(x+1)$ with equation $g(x)=0$. The sink fixed points obtained in this case using the method are $x=-1$, $x=1$, the solutions of the previous equation. In Figure 5 how the method changes with the $\delta$ parameter is shown. Dynamical planes represent the behavior of the method in the complex domain as it appears in Figure 6, where with larger values of $\delta$ the region of convergence is more complex.

4. Conclusions

The study of high-order iterative methods is very important, since problems from all disciplines require the solution of some equations. This solution is found as the limit of sequences generated by such methods, since closed form solutions can rarely be found in general. The convergence order is usually found in the literature using expensive Taylor expansions, high-order derivatives, and without computable error estimates on $\left|\right|x_n-x^{*}\left|\right|$ or uniqueness results. It is worth noticing that the high-order derivatives do not appear in these methods. Moreover, the initial point is a “shot in the dark”. Hence, the applicability of these methods is very limited. To address all these problems, we have developed a technique using hypotheses only on the first derivative that actually appears on the method and Lipschitz-type conditions. This allows us to: extend the applicability of the method; find a radius of convergence as well as computable error estimates and uniqueness results based on Lipschitz constants. Although we demonstrated our technique on the method in Equation (2), clearly it can be used to extend the applicability of other methods along the same lines. In view of the involvement of parameters on the method, the dynamics of it have also been explored in many interesting cases.