Abstract
Aiming at the problem that the banana de-handing device has poor radial deployment to the banana bunch stalk during the mechanized banana de-handing procedure, this paper presented a ring deployable mechanism based on a set of planar seven-bar linkages. It consists of multiple basic deployable units, which has great folding/deploying performance and is suitable for manufacturing a banana de-handing device, the diameter of which can be variably larger. The kinematics analysis of the mechanism was done, and the trajectory in space was obtained. When the mechanism is fully deployed, the diameter is 164 mm. The ratio of the folded height to the deployed diameter is 0.732, the ratio of the folded diameter to the deployed diameter is 0.262, and the ratio of the folded volume to the maximum of the deployed volume is 0.069. An experimental prototype of 500, 500, and 768 mm in length, width, and height was manufactured, and the deploying performance was analyzed to show the feasibility. Finally, experimental results show that 71.43% of the banana hands are de-handed successfully. The mechanism has a great deploying effect on banana bunch stalk, and the quality of the banana crown incision is good.
1. Introduction
The banana (Musa spp.), is the most consumed fruit in the world, and one of the most important crops in tropical and subtropical regions. The planting areas and yields have continued to increase in recent years [1]. Banana de-handing is one part of the banana post-harvesting procedure, which is between field picking, ropeway transportation, and cleaning disinfection, and packaging for sale. At present, the degree of mechanization of banana de-handing in banana orchards and post-harvesting factories at home and abroad is very low, basically relying on employees with simple de-handing tools to work. The manual de-handing banana by a worker is shown in Figure 1a, the de-handing tools are shown in Figure 1b, and the banana bunch stalk after de-handing is shown in Figure 1c. Banana de-handing purely by human is inefficient, and the time and labor costs are high, which is not conducive to the development of the mechanization of the banana post-harvesting industry.
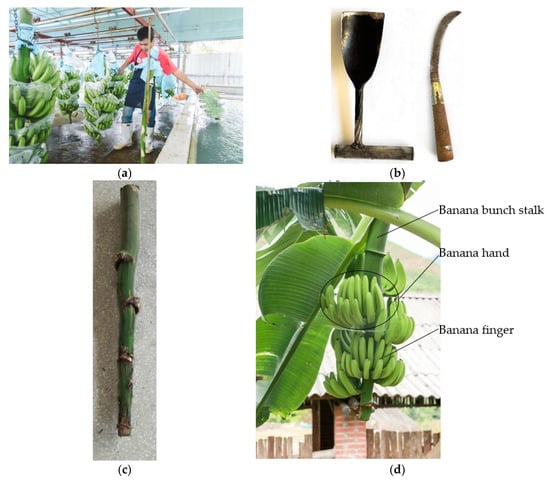
Figure 1.
Current status of banana de-handing by human. (a) Banana de-handing by human, (b) Typical de-handing tools, (c) Banana bunch stalk after de-handing, (d) Banana bunch before de-handing.
As shown in Figure 1c, the diameters of the two ends of the banana bunch stalk are different. If the curvature changes of the entire central axis of the bunch stalk are omitted, the geometric shape of the banana stalk can be simplified to a round table. In order to solve the key technical problems such as the poor profiling ability and the low self-adaptive performance of the banana de-handing device in banana mechanical de-handing, and further to manufacture practical mechanical de-handing devices, Yang Zhou and Xu Zeyu explored two types of mechanical de-handing mechanisms for single banana hand de-handing based on the manual de-handing method. One of them is an impact insert-type banana de-handing mechanism with ring cutters [2], and the other is a vibration-cutting mechanism with arc cutters [3]. In the mechanical banana de-handing procedure, the whole banana bunch needs to be fixed vertically for convenience of de-handing. In order to meet this operation, Yang Zhou [4] designed a banana bunch stalk clamping device and analyzed the effects of clamping force with different types of clamping hands to banana bunch stalk.
The banana hands are spirally distributed on the bunch stalk, and the quality and volume of the banana hand are becoming larger with the diameter of the bunch stalk increasing. Therefore, the de-handing tool is designed to fit the banana bunch stalk for cutting banana hands, and the tools need to be deployable to prevent cutting incorrectly and inaccurately. In the procedure of the whole banana de-handing one by one, with the diameter of the bunch stalk increasing, the clamping force on the bunch stalk of the impact insert-cutting tool also increases gradually, which is not conducive to the subsequent banana hands de-handing. For this purpose, Yang Zhou [5] designed a ring-shaped enveloping device based on constant force mechanism, which can provide a constant clamping force between the de-handing tools and the bunch stalk during the whole banana de-handing procedure and can improve the self-adaptive performance of the device to the diameter of the banana bunch stalk. Eventually, it finished the whole banana de-handing work continuously.
The design of the ring de-handing cutter based on the impact insert-cutting mechanism not only requires the enveloping circle formed by all blades to have a stable center and variable diameter, but also requires the adjacent blades to be connected closely during the procedure of changing the diameter, to prevent cutting the banana hands and banana crowns inaccurately in the de-handing operation. The aim of this study is to improve the self-adaptive performance of the de-handing mechanism on the banana bunch stalk, make the procedure of banana de-handing one by one smoother, and improve the efficiency of mechanized banana de-handing. It is very urgent to design and manufacture a banana de-handing device which can expand its diameter. According to the impact insert-cutting de-handing mechanism, we designed and manufactured a banana de-handing device based on a symmetrical-shape deployable mechanism after analyzing the existing mechanical de-handing devices at home and abroad. It can expand its diameter, and meanwhile, it can fill the gap among the adjacent main cutting blades in deploying procedure because of the setting of the auxiliary cutting blades, which can prevent cutting the banana hands and banana crowns inaccurately.
In our daily life, in order to pursue the harmony of patterns and enhance the beauty, symmetry is applied to the designs of art and engineering and the corresponding theories of symmetry are widely used in mechanical engineering, electrical engineering, civil engineering, and computer engineering [6]. In the field of mechanical engineering, the deployable mechanism is composed of a number of basic deployable units, which is with a certain degree of symmetry, and the deploying procedure is similar to origami [7,8]. The deployable mechanism refers to a kind of mechanism that can transform from a compact folded state to an expected deployed state. After deploying, the mechanism become stable because of its built-in adaptive supporting components. The representative deployable mechanisms are divided into two types; one is the cylindrical deployable mechanism [9,10], and the other is the cone deployable mechanism [11]. In the field of aerospace applications, deployable mechanisms are widely used to build large space mechanisms, such as deployable masts and antennas, etc., which play a significant role in space missions, such as earth observation, telecommunication, scientific research, and so on. Researchers have proposed two types of double-ring deployable truss concepts based on a parallelogram structure, and the structural stiffness is verified by prototype experiments [12,13,14,15].
In the banana de-handing device is based on the symmetrical shape deployable mechanism. The deployable de-handing tool is composed of six basic deployable units. The unit model consists of seven-bar linkages, one of which is a common connecting linkage between adjacent units. The shape of the banana de-handing device in this paper is based on a deployable mechanism is symmetrical, and the center axis of the enveloping circle formed by the ring deployable mechanism is always consistent with the center axis of the banana bunch stalk during its passively adaptive deploying procedure. The diameter of the enveloping circle enclosed by the ring deployable mechanism is self-adaptive to the banana bunch stalk. The first and second hard blades are set in the deployable mechanism, and they are connected to form a parallelogram structure by short connecting rods. When the first hard blade moves outward radially, the second hard blade connected by the short connecting rods does a composite movement including vertical upward movement and radial outward movement. The “boat-shaped” auxiliary blades installed on the upper end of the hard blades can fill the gap of adjacent hard blades during moving outward radially, which makes sure to seamlessly cut the banana crown in the actual de-handing work and improves the quality of banana de-handing. The deployable mechanism has a small mass and folded volume, high rigidity, high stability, and a great deploying reliability, which meets the practical demands of banana de-handing. Constant force components are installed in the banana de-handing device, which can provide constant clamping force between the de-handing mechanism and the banana bunch stalk during the de-handing procedure, and the de-handing cutter can be reset automatically to the direction of the circle after all banana hands in one bunch stalk are de-handed completely. The design and research of the deployable banana de-handing mechanism in this paper can provide references for the designs of other variable diameter mechanisms and stalk plant debranching devices.
The rest of this paper consists of the following four sections. In Section 2, the design concept of the basic deployable units and the geometric modeling of the ring deployable mechanism are presented. In Section 3, the kinematics analysis of the ring deployable mechanism is carried out. In Section 4, an experimental prototype based on the ring deployable mechanism is manufactured, by which the deployable performance of the prototype is verified. Finally, in Section 5, the works of this paper are summarized.
2. Proposal of Ring Deployable Mechanism
In order to adapt changes in diameter of the banana bunch stalk and complete the banana de-handing work, the design of the de-handing mechanism is mainly composed of flexible ring deployable units. In the ring deployable mechanism, the first and second hard blades are cut by pentagonal prism, and the “boat-type” auxiliary blades are installed on the upper end of the hard blades. The geometric size, installing position and manufacturing accuracy of the “boat-type” auxiliary blades directly determine the performance of the de-handing mechanism and affect the quality of banana crown incision. The slider and linear guide supporting the first hard blade to move radially are used to adapt the diameter change of banana bunch stalk passively. In this paper, a module with planar seven-bar mechanism is proposed as the basic unit of large deployable mechanism, which can be used to manufacture banana de-handing devices with fixed center and continuously variable diameter characteristics.
2.1. Basic Deployable Unit
As shown in Figure 2, the basic deployable unit contains three vertical rods and four short connecting rods. The three vertical rods are divided into two first vertical rods and one second vertical rod according to their geometric dimensions, of which the one first vertical rod is shared between two adjacent deployable units. The short connecting rods and vertical rods are connected by rotational joints, which form two closed loops in whole. The lengths l, m, n, o, p, q, r of seven rods within the mechanism satisfy the following geometrical relationships:
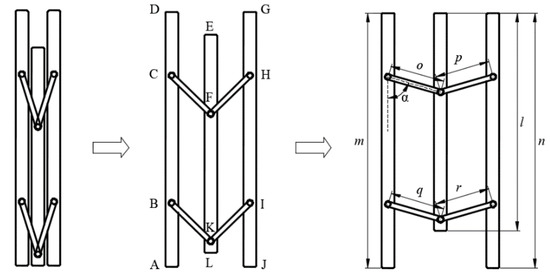
Figure 2.
Schematic diagram of the basic deployable unit.
From Figure 2, when the basic unit is folded, the bottom ends AD, EL, and GJ of the three vertical rods are on the same horizontal plane, and the four short connecting rods CF, BK and FH, KI are parallel to each other. Then the two first vertical rods AD, GJ move towards the left and right, respectively, at the same time; the second vertical rod EL moves upward; and the hinges F, K at the short connecting rods move upward. When the top of the second vertical rod EL moves to the same plane with those of the first vertical rods AD, GJ, it will be locked. The unit achieves the maximum deployable configuration, and each closed loop is nearly a rectangle.
Adjacent basic deployable units are connected by a shared first vertical rod, as shown in Figure 3. In order to achieve the synchronization of the movement between the basic units, the crank-slider mechanisms are formed respectively by four short connecting rods CF, BK, FH, KI and the second vertical rod EL. Due to sharing the first vertical rod between the basic units, the second vertical rod and the short connecting rods of the adjacent units can realize the synchronous deploying or folding. Multiple basic units can be assembled by the same method, and a ring deployable mechanism can be formed.
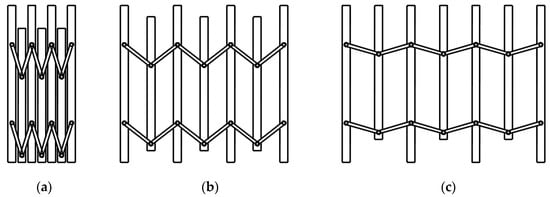
Figure 3.
Schematic diagram of assembly deploying procedure of basic deployable units. (a) Folded configuration, (b) Deploying configuration, (c) Deployed configuration.
2.2. Geometric Modeling of Ring Deployable Mechanism
According to the special geometric shape of the banana bunch stalk, the diameters of the banana bunch stalk are different of different banana hands on one banana bunch. Although the central axis of some banana bunch stalks has a certain degree of curvature, there are few banana hands on it where the central axis of the banana bunch stalk is bent. Therefore, the geometric characteristic of banana bunch stalk can be simplified as a round table approximately, as shown in Figure 4. The diameter of the cross section in different positions of the round table is different, and the planar top view is a set of concentric circles with a fixed center and variable diameters. A series of centering cylinders of different diameters are set to simulate the enveloping effect of the banana de-handing cutter on the banana bunch stalk at the different positions. The banana bunch stalk is simplified to a round table, and the ring banana de-handing cutters at different positions are simplified to concentric cylinders of variable diameters.
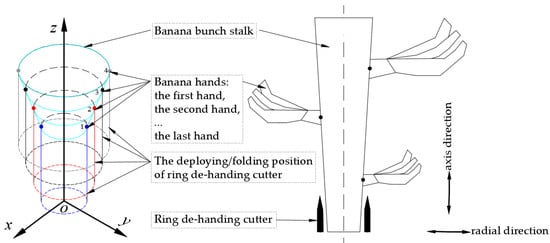
Figure 4.
Schematic diagram of the envelope of ring de-handing cutters on banana bunch stalk.
Generally, each basic unit is designed to have the same geometric parameters to form the whole ring deployable mechanism. The basic assembly principle is to make a regular polygon as close to a circle as possible. The design parameters are simple and the angles between adjacent units are equal. As shown in Figure 5, a circle is inscribed in a regular hexagon. The number of basic units is n, the angle between adjacent units is γ, the external angle of a regular polygon is β, the radius of the banana bunch stalk is r, and the length of short connecting rod in the basic unit is c. Then the angle between adjacent units can be obtained as follows,
γ = 180° − β = 180° − 360°/n
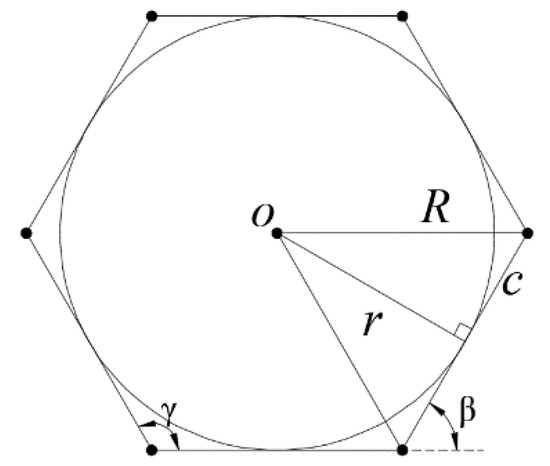
Figure 5.
Regular polygon inscribed in the circle.
According to Equation (2), the angle between the adjacent units of the ring cutter under different basic deployable units can be obtained. When the number of basic units n is determined, the connecting angle between adjacent units can be obtained.
As shown in Figure 5, when the angle α is 90° between the short connecting rod and the first vertical rod, the distance R from the center to the first vertical rod in the basic deployable unit can be obtained,
According to Equation (3), the deployment area of the ring deployable mechanism is proportional to the length c of the short connecting rod, and the deployable surface will increase with the increase of the number n of basic deployable units. In Figure 6, it shows the aperture of the ring deployable mechanisms when the number n of basic units is different, and the red part represents the basic deployable unit.
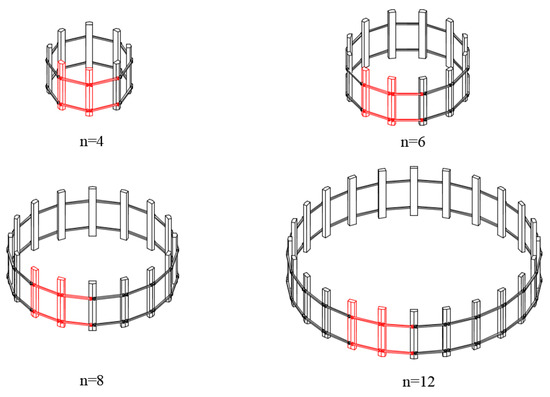
Figure 6.
Ring deployable mechanisms with different number n of units.
The first vertical rod of the basic deployable unit in the ring deployable mechanism connected with a slider on the side deviating from the center of the circle. The slider is mounted on a linear guide. By moving the slider on the linear guide, the geometric size of the entire ring deployable mechanism can be changed. The linear guides are evenly distributed in a circular array on the mounting plate, as shown in Figure 7. At the same height, the amplitude of variable diameter of the ring mechanism formed by the above units is larger. Similarly, using such deployable units to manufacture a circular cutter with the same enveloped circular surface can effectively reduce the number of basic units.
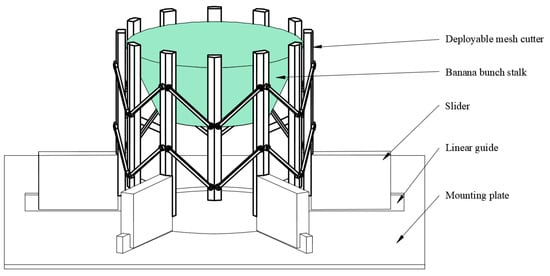
Figure 7.
Deployable mesh cutter in enveloping net for banana de-handing.
In order to better evaluate the performance of the ring deployable mechanism in central enveloping volume and deployment surface, three evaluation indexes of the deployable mechanism are established, as shown in Figure 8:
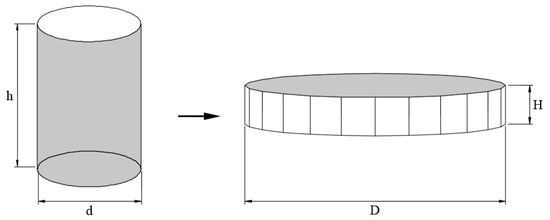
Figure 8.
Evaluation parameters of ring deployable mechanism.
Height ratio, the ratio of folded height h to deployed diameter D, named HR = h/D;
Diameter ratio, the ratio of folded diameter d to deployed diameter D, named DR = d/D;
Volume ratio, the ratio of folded volume v to the maximum deployed enveloping volume V, named VR = (d2h)/(D2H).
The surface coverage area of the deployed ring mechanism is similar to a circle, and the diameter D of the deployed round surface can be calculated by Equation (3). The folded height h and deployed height H are consistent, which is about three times of the length c of the short connecting rod, and named h = 3c. Assuming that, when folded, the vertical rods are parallelly arranged in a circular manner, the diameter of the vertical rod is d′, and each basic unit contains an average of six rods; hence, the maximum value of the ring diameter d can be approximately calculated as follows,
The height ratio, diameter ratio, and volume ratio of the mechanism can be calculated, respectively, as
As shown in Equation (5), we can see that the height ratio of the mechanism decreases with the increase of basic unit number n, and the diameter ratio and volume ratio have constant values and do not change with the change of unit number n. The change trend is shown in Figure 9. We can see that when the height of the mechanism is at a certain value, the ring deployable mechanism can be used to manufacture a banana de-handing device with larger deploying surface and smaller folding volume. The proposed ring deployable mechanism is composed of multiple deployable units of seven-bar linkage, which is very simple at the aspect of structure. The geometric shape of the banana bunch stalk is simplified into a round table. In the procedure of banana de-handing, each basic unit of the ring deployable mechanism can deploy passively and synchronously with the change of the diameter of the banana bunch stalk. The traditional banana de-handing device does not have a fixed center and changes in diameter; therefore, the mechanized development of the banana de-handing is very limited. The banana de-handing device based on a deployable mechanism in this paper has the function of deploying into large area and has great folding/deploying performance; therefore, it can be used to manufacture banana mechanical de-handing devices which can adapt to a larger diameter of banana bunch stalk.
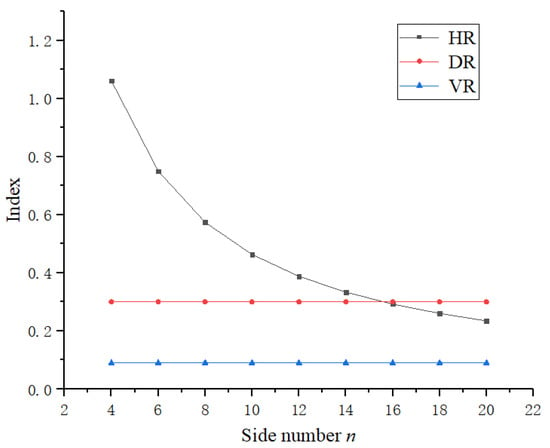
Figure 9.
Evaluation indices changed with basic unit number n.
3. Kinematics Analysis
3.1. Degree of Freedom of the Basic Unit
For a ring deployable mechanism with multiple closed loops, the basic unit of the mechanism contains multiple rods and motion pairs. In order to analyze the kinematics of the mechanism, a basic unit model of the deployable mechanism is established in this paper, as shown in Figure 10. The unit model contains three vertical rods and four short connecting rods. The first vertical rod on the left is fixed, and this unit contains three movable rods and four low joints, including three rotating joints and one mobile joint. The degree of freedom of the basic unit can be obtained as follows:
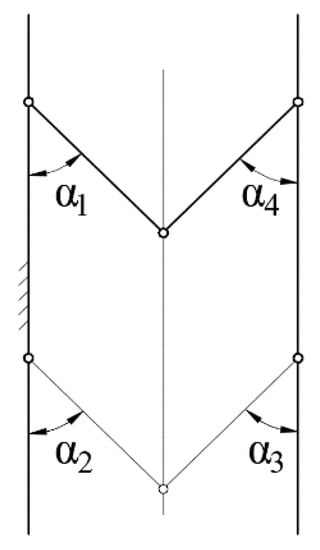
Figure 10.
Schematic diagram of basic unit module.
In this paper, four parametric variables α1, α2, α3, and α4 of the rods are selected to analyze the kinematic configuration of the mechanism during the deploying procedure. From Equation (6), we know that the degree of freedom of the basic unit model is 1, which means that there is only one independent parametric variable in Figure 10. In other words, when it meets α1 = α2 = α3 = α4, the mechanism can achieve the desired kinematic configuration and can deploy stably. Therefore, its movement procedure is determined, which means that only one motion configuration exists and the first vertical rod on the right side can be ensured to move horizontally.
3.2. Kinematic Model
Firstly, the global coordinate system O-XYZ is established as shown in Figure 11a, Z direction is upward along the first vertical rod, Y direction is along the diameter of the ring deployable mechanism and points to the center O, and X direction is determined by the right-hand rule. Each first vertical rod of the basic unit is marked from 0 to 5 in a counterclockwise direction. At the same time, the local coordinate system i-xyz is established, y direction of each system points to the center O, all z directions are upward, and x direction can be determined by the right-hand rule. There are only translation and rotation around the z-axis between adjacent coordinate systems, and the rotational angle is the exterior angle β of the adjacent units. In Figure 11b, it is the local coordinate system in the basic unit model. According to the geometric relationship, the coordinates of joints A, B, C, D, E, F, G, H, I, J, K, L in the local coordinate system can be obtained,
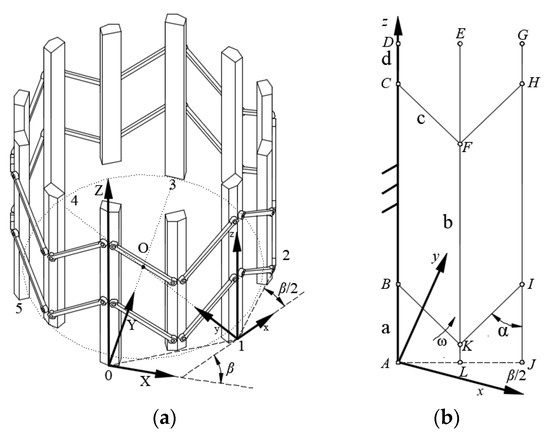
Figure 11.
Coordinate system of the ring deployable mechanism. (a) Global coordinate system, (b) Local coordinate system.
The homogeneous transformation matrix between adjacent coordinate systems is as follows,
All transformation matrices between the local coordinate system and the global coordinate system can be obtained by using Equation (8). For example, the homogeneous transformation matrix Ti represents a homogeneous transformation matrix which is from the i-th local coordinate system to the global coordinate system,
The spatial coordinates of each basic unit can be transformed into the global coordinate system, and the relationship between input and output parameters in the ring mechanism can be quickly worked out.
3.3. Simulation Example
Taking the ring mechanism composed of six basic deployable units as an example, the kinematics of the mechanism is analyzed. The length m of the first vertical rod is 120 mm, and the length c of the short connecting rod is 40 mm. The input parameter during the deploying procedure satisfies α = ωt, and ω = π/180 rad/s, so the mechanism can be fully deployed in 90 s, and the angle α between the short connecting rod and the vertical rod changes 1° per second. As shown in Figure 12, with the center of banana bunch stalk enveloped by the ring mechanism as the base point, the movement trajectory and outer contour of the first and second hard blades can be obtained. We can see that the ring mechanism is fully symmetrically deployed, and all the hard blades move radially along the certain fixed straight lines. With the first vertical rod of the basic unit on the diagonal of the ring mechanism as the base point, the movement contour and the deploying space of the first and second hard blades can be obtained as shown in Figure 13, and we can see that the deployed maximum diameter is approximately 160 mm.
Figure 12.
Schematic diagram of symmetrical developed ring mechanism.
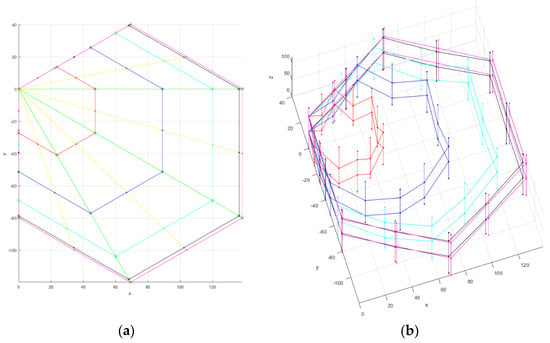
Figure 13.
Schematic diagram of deployed diagonal of the ring mechanism. (a) Contour and trajectory of deployed diagonal of ring mechanism. (b) Motion trajectory of ring mechanism during deploying procedure.
Figure 14 shows a CAD model of a ring deployable mechanism composed of 6 basic units. The mechanism can be deployed from the folded state to a ring structure, and the diameters of the corresponding enveloping circles are 43, 103, 141, 161, and 164 mm. The deployed diameter is 164 mm, the folded height is 120 mm, the folded diameter is 43 mm, and then HR is 0.732, DR is 0.262, and VR is 0.069, which are very close to the theoretical values. We can conclude that a bigger area of the deployable mechanism can be manufactured by increasing the unit numbers.
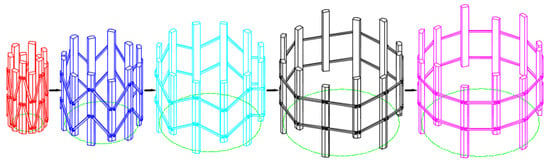
Figure 14.
CAD model of ring deployable mechanism composed of 6 basic units.
4. Prototype and Experiments
4.1. Device Structure and Working Principle
A schematic diagram of the deployable banana de-handing device based on symmetrical shape is shown in Figure 15. The length, width, and height of the device are 500, 500, and 768 mm, respectively. The whole device is mainly composed of mounting plate, constant force components, sliders, linear guides, and cutting blades which are made of 304 stainless steel.
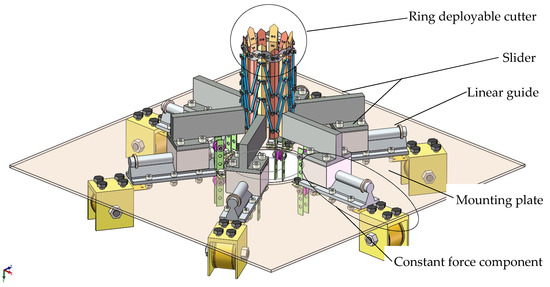
Figure 15.
Three-dimensional model diagram of the deployable banana de-handing device.
During banana de-handing, the whole banana bunch is removed from the transport ropeway in banana orchards, and the thicker end of the banana bunch stalk is fixed vertically to the lifting mechanism, to ensure that the central axis of the banana bunch stalk and the axis of the center of the mounting plate of the mechanism basically coincide. The lifting mechanism can drive the banana bunch move downward slowly, as shown in Figure 16. When the first banana hand on the bunch stalk contacts the de-handing cutter and continues to move downward, the ring deployable cutter shown in Figure 15 envelops the banana bunch stalk and cuts the banana crown slowly, after which the banana hand is separated from the banana bunch stalk successfully. With the banana de-handing works going ahead, when the subsequent banana hands at bunch stalk with a larger diameter move into the working space, circularly installed blades will deploy outward passively along the radial to adapt to the change of the diameter of the banana bunch stalk. The constant force components are fixed under the mounting plate to make sure that the ring de-handing cutter can generate the almost constant clamping force to the banana bunch stalk during the procedure of banana de-handing. Therefore, the purpose of radial self-adaption of the banana bunch stalk is achieved, and it is conducive to subsequent bananas de-handing smoothly until the last banana hand is de-handed. Figure 17 shows a working schematic diagram of constant force component. The constant force spring is made of sheet metal around the central axis and is installed on the sheet storage roller; only its outer end is connected with other parts. When the diameter of the banana bunch stalk becomes larger, the cutter deploys outward passively. Meanwhile, the slider pulls the constant force spring by nylon rope and makes a radial movement deviating from the center of the circle. When all banana hands in the banana bunch stalk are de-handed, remove the bunch stalk. Then the ring cutter can be reset under the automatic winding function of the spring and the initial working state is realized to prepare for the next de-handing operation.

Figure 16.
Schematic diagram of the whole operation of the banana de-handing device.
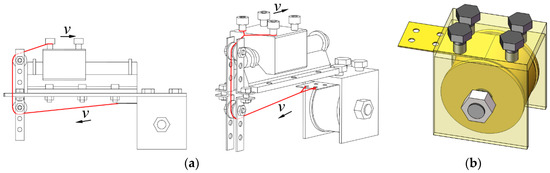
Figure 17.
Working schematic diagram of constant force component. (a) Mechanism of constant force generation, (b) 3D model of constant force spring.
4.2. Evaluation Experiment of the Deployable Performance of Ring Cutter
The change of the diameter of the banana bunch stalk makes the ring deployable cutter move passively along the radius during the whole banana bunch de-handing procedure. The performance of the ring deployable cutter directly determines the efficiency of de-handing. The diameters of both ends of the banana bunch stalk range from 40 to 100 mm, and the diameters of the banana bunch stalks with banana hands range from 41.8 to 81.0 mm. Therefore, the deploying procedure of the ring cutter with diameters changed from 40 to 84 mm is simulated, as shown in Figure 18. We can see that the ring cutter has great folding/deploying performance, and the “boat-shaped” auxiliary blades fill the gap between the adjacent first and second hard blades during the deploying procedure, ensuring the seamless cutting of the banana crown in actual banana de-handing operation.
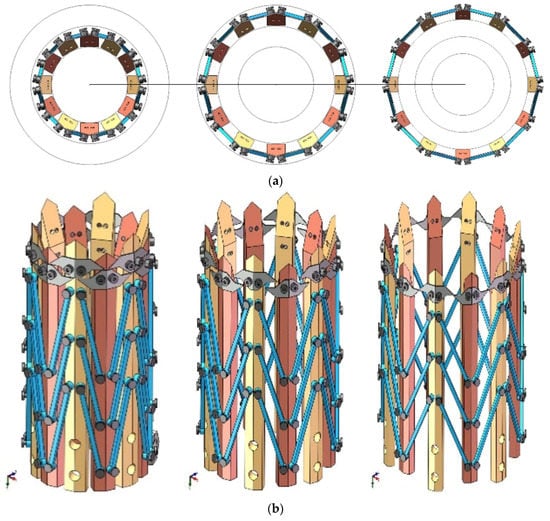
Figure 18.
Schematic diagram of the ring cutter deploying procedure. (a) Top view of the ring cutter deploying procedure, (b) Side view of the ring cutter deploying procedure.
In order to verify the deployability performance of the ring deployable mechanism to the large-diameter geometry, acrylic sheets of different diameters were designed, as shown in Figure 19. Figure 20 shows the enveloping effects of ring deployable cutter on cylinders with diameters of 60, 70, 80, and 90 mm, respectively. Figure 21 shows the self-adaptive deploying effects of the ring deployable cutter on the round table. We can see that the ring cutter has great deploying effects, which can provide references for the feasibility of subsequent banana de-handing experiments.

Figure 19.
Cylinders of different diameters.

Figure 20.
Enveloping schematic diagram of the ring cutter on cylinders of different diameters. (a) Diameter is 60 mm, (b) Diameter is 70 mm, (c) Diameter is 80 mm, (d) Diameter is 90 mm.

Figure 21.
Enveloping schematic diagram of ring cutter self-adaptive on round table.
4.3. Experiment of Banana De-Handing
4.3.1. Experimental Evaluation Indexes
The banana de-handing experiments were done at Engineering Fundamental Teaching and Training Center of South China Agricultural University, China. The banana de-handing device based on the deployable mechanism was used as the experimental platform. The banana species used in experiments was Brazil banana, which is the main species of Guangdong province. The sampling location was a typical banana orchard in Zengcheng District, Guangzhou, Guangdong Province. The sampling time was December 2019. The number of samples in de-handing experiments is five banana bunches, totaling thirty-five banana hands. The samples were free of diseases and insect pests, and there was no obvious mechanical damage. The banana de-handing experimental time was within 3 to 4 days after sampling from the banana orchard.
At present, there is no explicit index for the evaluation of banana hands after banana de-handing at home and abroad. In this paper, we proposed experimental evaluation indexes including the de-handing success rate, self-adaptability, and the quality of banana incision, based on the research experience of banana farmers in Huizhou, Dongguan, Nansha, and Zengcheng Districts of Guangzhou during earlier investigations, with the combination of design concepts of the banana de-handing device. The de-handing success rate refers to cutting the whole banana hand by the de-handing tool at one time and no secondary cut is required, and it is defined as the ratio of the number of banana hands cut at one time to the total number of banana samples. Self-adaptability means that when the previous banana hand is de-handed, the remaining part of the banana crown on the bunch stalk does not affect the next banana hand de-handing. The de-handing cutter can continue to finish the de-handing work of the remaining banana hands. The quality of banana crown incision refers to the banana hands not being cut separately and to the epidermis of the banana bunch stalk not being obviously torn during the banana de-handing procedure. After the banana hand de-handing, there is no large area with banana bunch stalk fiber at the position of banana crown.
4.3.2. Analysis of Results of Banana De-Handing Experiment
Figure 22a shows the enveloping effect of the ring deployable cutter on banana bunch stalk during the experiments of banana de-handing, and the incision of the banana crown after de-handing is shown in Figure 22b. In the banana de-handing experiments, the number of banana hands successfully cut at one time is twenty-five, and the success rate of de-handing is 71.43%. The self-adaptive deployable performance of the ring cutter enveloping to the bunch stalk is great, and the quality of the crown incision of de-handed banana hands are good. The disadvantage is that the experiment time of banana de-handing was beyond 24 hours of the sampling time in the banana orchard, and the banana bunch stalk fibers’ toughness increases and the brittleness reduces because of water evaporation in the sample of banana bunch stalk, which makes banana de-handing difficult to a certain degree.

Figure 22.
Schematic diagram of banana de-handing. (a) Enveloping schematic diagram of ring cutter on bunch stalk, (b) Banana crown incision after de-handing.
5. Conclusions
This paper proposed and studied a ring deployable mechanism based on a set of planar seven-bar linkages, and the results proved that it is feasible to manufacture a banana de-handing cutter with a fixed center and larger variable diameters. In addition, the geometric modeling method of the symmetrical shape deployable cutter is introduced in detail. The height ratio of the mechanism decreases with the increase of the number of basic units, and the diameter ratio and volume ratio have constant values and do not change with the number of units. Based on the working space of the banana de-handing cutter and the geometric parameters of the deployable unit, we determined that the number of basic units assembling the deployable mechanism is 6.
The kinematics analysis and simulation of the deploying procedure of ring cutter along the circle center and the diagonal were carried out through the calculation of the degree of freedom in the basic unit. The height of the folded ring deployable mechanism is 120 mm, and the diameter is 43 mm when the mechanism folded and becomes 164 mm when fully deployed. The ratio of the folded height to the deployed diameter is 0.732, the ratio of the folded diameter to the deployed diameter is 0.262, and the ratio of the folded volume to the maximum deployed volume is 0.069. We found that the mechanism can be fully deployed in 90 seconds and the movement trajectory and the outer contour of the mechanism can be obtained at the 20th, 40th, 60th, 80th and 90th second during the deploying procedure. The results show that all hard blades move radially along certain fixed straight lines and meet practical demands of banana de-handing.
An experimental prototype of 500, 500, and 768 mm in length, width, and height was manufactured of 304 stainless steel. Experiments of banana de-handing were carried out to verify the deployable performance of the ring cutter. The enveloping effects of the ring deployable cutter on cylinders with different diameters of 60, 70, 80, and 90 mm were tested, respectively. The self-adaptive deploying effects of the ring deployable cutter on the round table with diameters of 40 mm and 100 mm at both ends were tested. The banana species used in experiments was Brazil banana, a main species in Guangdong province, and the success rate of banana de-handing was 71.43%. The results show that the ring cutter has a great deployable performance, and the quality of banana crown incision de-handed by the ring deployable cutter is good. In future work, through de-handing experiments of other banana species, the structural parameters of the banana de-handing device based on the deployable mechanism can be optimized to improve the applicability.
6. Patent
The symmetrical shape deployable mechanism designed in this paper has applied for a Chinese invention patent, and the number is 201911297728.4.
Author Contributions
Conceptualization, J.G. and M.J.; methodology, J.G. and M.J.; software, J.G. and H.F.; validation, Z.Y., J.L. and J.D.; formal analysis, J.G.; investigation, J.G. and J.L.; resources, Z.Y.; writing—original draft preparation, J.G.; writing—review and editing, H.F., J.G. and Z.X.; visualization, J.G.; supervision, L.Z., Y.D. and Y.J.; project administration, Z.Y. and J.D.; funding acquisition, Z.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grant No. 51675189), the China Agriculture Research System (CARS-31) and the Innovative Research Team of Guangdong Province Agriculture Research System (2017LM2153). The authors wish to thank their generous financial assistance.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| l | length of the second vertical rod (mm) |
| m | length of the first vertical rod (mm) |
| c | length of the short connecting rod (mm) |
| r | radius of banana bunch stalk (mm) |
| R | radius of the enveloping circle (mm) |
| h | folded height (mm) |
| H | deployed height (mm) |
| d | folded diameter (mm) |
| D | deployed diameter (mm) |
| α | deploying angle (°) |
| β | external angle of regular polygon (°) |
| γ | the angle between adjacent units (°) |
| n | number of basic units |
| F | degree of freedom of basic unit |
| T | homogeneous transformation matrix |
References
- Mohapatra, D.; Mishra, S.; Singh, C.B. Post-harvest processing of banana: Opportunities and challenges. Food Bioprocess Technol. 2011, 4, 327–339. [Google Scholar] [CrossRef]
- Xu, Z.Y.; Yang, Z.; Zhu, Z.B. Parameter optimization of banana crown-cutting machine using combined cutters. Curr. Sci. 2019, 117, 492. [Google Scholar] [CrossRef]
- Xu, Z.Y.; Yang, Z.; Duan, J.L. Design and experiment of symmetrical shape deployable arc profiling mechanism based on composite multi-cam structure. Symmetry 2019, 11, 958. [Google Scholar] [CrossRef]
- Yang, Z.; Xu, Z.Y.; Jin, M.H. Experimental study on clamping safety margin of a banana stem gripper. IFAC-PapersOnLine 2018, 51, 560–564. [Google Scholar] [CrossRef]
- Yang, Z.; Guo, J.; Jin, M.H. Design and analysis of self-adaptability in banana crown-cutting device based on constant-force mechanism. Trans. Chin. Soc. Agric. Mach. 2019, 50, 148–155. [Google Scholar]
- Montoya, F.G.; Baños, R.; Alcayde, A. Symmetry in engineering sciences. Symmetry 2019, 11, 797. [Google Scholar] [CrossRef]
- Chen, Y.; Yan, J.; Feng, J. Geometric and kinematic analyses and novel characteristics of origami-inspired structures. Symmetry 2019, 11, 1101. [Google Scholar] [CrossRef]
- Lee, D.; Kim, S.; Kim, J. Origami wheel transformer: A variable-diameter wheel drive robot using an origami structure. Soft Robot. 2017, 4, 163–180. [Google Scholar] [CrossRef] [PubMed]
- Qi, X.; Huang, H.; Li, B. A large ring deployable mechanism for space satellite antenna. Aerosp. Sci. Technol. 2016, 58, 498–510. [Google Scholar] [CrossRef]
- Xu, Y.; Guan, F.; Xu, X. Development of a novel double-ring deployable mesh antenna. Int. J. Antennas Propag. 2012, 2012, 1–10. [Google Scholar] [CrossRef]
- Cao, W.; Yang, D.; Ding, H. Topological structural design of umbrella-shaped deployable mechanisms based on new spatial closed-loop linkage units. J. Mech. Design 2018, 140, 23–26. [Google Scholar] [CrossRef]
- Qi, X.; Huang, H.; Miao, Z. Design and mobility analysis of large deployable mechanisms based on plane-symmetric rod linkage. J. Mech. Design 2017, 139, 20–23. [Google Scholar] [CrossRef]
- Huang, H.; Li, B.; Zhang, T. Design of large single-mobility surface-deployable mechanism using irregularly shaped triangular prismoid modules. J. Mech. Design 2019, 141, 1. [Google Scholar] [CrossRef]
- Han, B.; Xu, Y.; Yao, J. Configuration synthesis of hoop truss deployable mechanisms for space antenna based on screw theory. AIP Adv. 2019, 9, 85–90. [Google Scholar] [CrossRef]
- Han, B.; Xu, Y.; Yao, J. Design and analysis of a scissors double-ring truss deployable mechanism for space antennas. Aerosp. Sci. Technol. 2019, 93, 105–112. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).