Abstract
Software defect prediction (SDP) is the technique used to predict the occurrences of defects in the early stages of software development process. Early prediction of defects will reduce the overall cost of software and also increase its reliability. Most of the defect prediction methods proposed in the literature suffer from the class imbalance problem. In this paper, a novel class imbalance reduction (CIR) algorithm is proposed to create a symmetry between the defect and non-defect records in the imbalance datasets by considering distribution properties of the datasets and is compared with SMOTE (synthetic minority oversampling technique), a built-in package of many machine learning tools that is considered a benchmark in handling class imbalance problems, and with K-Means SMOTE. We conducted the experiment on forty open source software defect datasets from PRedict or Models in Software Engineering (PROMISE) repository using eight different classifiers and evaluated with six performance measures. The results show that the proposed CIR method shows improved performance over SMOTE and K-Means SMOTE.
1. Introduction
Most important activity in the testing phase of software development process is the software defect prediction (SDP) [1]. SDP identifies defect prone modules which need rigorous testing. By identifying defect prone modules well in advance, testing engineers can use testing resources efficiently without violating the constraints. Although, the SDP is most useful in the testing phase, it is not always easy to predict the defect prone modules. There are different issues which obstruct the algorithm performance as well as use of the defect prediction methods. The quality of the software is correlated directly with the number of defects in the software module. So, the defect prediction is considerable part in measuring the software quality. To minimize the number of defects, thorough testing is required, but the implicit disadvantage is that it is most expensive in terms of man hours. Accurate identification of defective modules in initial phases of testing can decrease the overall testing time. There are several algorithms available in machine learning for model building. Users can choose appropriate algorithm for regression or classification problems and calculate accuracy of the model. However, most of the defect prediction methods proposed in the literature suffers with the problem of class imbalance. Machine learning algorithms tend to oscillate when the datasets are imbalanced and lead to misleading accuracies. In an imbalanced dataset, samples of one class contain less number compared to other class samples and the former is termed as minority class and the other is termed as majority class. When the dataset is imbalanced, classification algorithm doesn’t have the sufficient information relating to the minority class to get accurate prediction. So, it is advantageous to have balanced datasets with a symmetry of defect and non-defect records to apply classification algorithms.
Datasets with disparity in dependent variable are called as imbalanced. Classification (or) prediction with imbalanced datasets is a supervised learning method where the percentage of one class differs with other class in large proportion. This is the frequent problem occurred in binary classification. With the imbalance nature of the datasets, machine learning algorithms results in poor accuracy. The reasons for poor accuracy of classification algorithms with imbalanced datasets can be uneven distribution of values in class label attributes. This leads to biased performance of the classifier towards majority class
To balance the imbalanced data, various sampling methods are proposed in the literature and are used to change imbalanced data into balanced data. By balancing the datasets, the accuracy of classification is improved. The main approaches used to handle the imbalanced data are undersampling, oversampling, and synthetic data generation.
In the undersampling method, some samples of majority class are reduced to balance the data. Undersampling can be random or informative. In random undersampling, the samples to be deleted are chosen randomly. Informative undersampling uses a pre-specified condition which selects the samples from majority class. EasyEnsemble [2] and BalanceCascade [2] are popular algorithms for informative undersampling.
EasyEnsemble extracts numerous subsets from majority class which are independent samples (with replacement) and it create multiple classifiers by considering combination of every subset with the minority class, whereas BalanceCascade works on the supervised learning method where it creates an ensemble of classifiers and selects systematically which majority class to ensemble. But with this method, valuable information relating to majority class is lost.
In oversampling, samples of minority class are replicated to create symmetry between the number of defect and non-defect records to balance the data. Oversampling method is of two types: (i) informative oversampling and (ii) random oversampling. A pre-specified criterion is used in Informative Oversampling and it generates synthetically minority class samples. In Random Oversampling data is balanced by oversampling the samples of minority class randomly. Oversampling avoids the problem of information loss. But it suffers with replication of data. The synthetic data generation method generates synthetic data in minority class. The synthetic minority oversampling technique (SMOTE) [3] is powerful and most widely used technique. It creates random set of samples to balance minority class. New synthetic data samples are generated between randomly chosen minority class sample and its nearest neighbor samples. SMOTE is considered as a benchmark in learning from imbalanced datasets. Chawla et al. [4] discussed the current research progress using SMOTE and applications of SMOTE in different fields. There are different variants of SMOTE are proposed by many researchers and their implementations in python is discussed in [5]. K-Means SMOTE [6] is the variation of SMOTE in which the data samples are divided into k number of clusters by using K-Means algorithm. Next, the clusters which are to be oversampled are identified by using filtering method and finally the SMOTE is applied to identified clusters to balance the samples.
In the present work, we propose a novel class imbalance reduction (CIR) technique for reducing the imbalance between defective and non-defective samples for achieving improved accuracy in software defect prediction and our technique is compared with baseline method SMOTE and latest variant K-Means SMOTE. The organization of the paper is as follows. In Section 2, various classification methods used in this work are explained. Related work is mentioned in Section 3; Section 4 describes the proposed algorithm. In Section 5, experimentation results are outlined. The paper is concluded with Section 6 by including the possible scope for future enhancements.
2. Background
There are many classifiers used in the literature for prediction. In this work, we used below mentioned classifiers to test our new approach.
2.1. AdaBoost
AdaBoost [7] is the ensemble boosting classification method which merges various classifiers to increase classifier accuracy. Multiple weak classifiers are merged to create a strong classifier with high accuracy. The AdaBoost algorithm works as follows:
- AdaBoost randomly selects a subset from training data.
- It trains the chosen machine learning model iteratively by selecting the training dataset based on the accurate prediction of the last training.
- It assigns weights to samples such that the wrongly classified samples get higher weight than correctly classified samples. With this the wrongly classified samples will get highest classification probability in the next iteration.
- In every iteration, the algorithm assigns the weight to the classifier based on the accuracy of the classifier, so that more accurate classifier will have the highest weight.
- This process will be terminated when all the training data classified correctly or reach the specified threshold of a maximum number of estimators.
- Finally it performs a “vote” among all of the learning algorithms built.
2.2. Decision Tree
The decision tree [8] is a tree structure, where each non-terminal (non-leaf) node represents an attribute, each branch of the non-terminal node represents an outcome of the condition on that node, and each terminal (leaf) node represents a class label. The tree is constructed by identifying the best splitting attribute as the root node. Each possible value of splitting attribute leads to one branch of the tree. This process is recursively repeated to identify attributes at next levels of the tree and is terminated when all the attributes are added to the tree. These trees handle high dimensional data with good accuracy. It classifies new instances by traversing the decision tree from the root to leaf node. At each level of the decision tree, the new instance is tested against the attribute of that node, and traversing the branch corresponding to the value of new instance attribute. This procedure will be repeated until the search reaches to the leaf node.
2.3. Extra Tree
The extra tree [9] is an ensemble learning technique in which the classification result represents the aggregated results of different de-correlated decision trees. It is mostly analogous to the Random Forest technique but it differs in the construction process of the decision trees in the forest. Decision Trees in the Extra Trees are constructed by considering all the training samples. For each test node, every tree is provided with a random sample of n features. Each decision tree will select the best feature from n features. Then, the data are partitioned by using mathematical criteria. Finally, multiple de-correlated decision trees are created from this random sample of features.
2.4. Gradient Boosting
Gradient boosting [10] is used to generate a classification model with the collection of weak prediction models. This method builds the model in a stage-wise manner, and an arbitrary differentiable loss function is used to generalize them by allowing optimization. It trains number of models in additive, gradual, and sequential fashion. Gradient boosting uses gradients in the loss function (y = ax + b + e, e is the error term) to identify weak classifiers. The loss function used in gradient boosting indicates how best the model’s coefficients are fitting the underlying data.
2.5. KNN
The KNN algorithm [11] works on the assumption that similar samples exist in the close proximity. KNN consider every training sample with its associated class label as a vector in the multidimensional space. While training the model, KNN stores the feature vectors and their class labels. While classifying, class label is assigned to the new instance by considering the majority class label value of k nearest samples of that new instance (k is a user parameter).
2.6. Logistic Regression
Logistic regression [12] is a statistical method used to analyze the given dataset which contains more than one independent variables (features) which determine dependent variable’s (Class Label) value. The dependent variable’s value is binary (either zero or one) or dichotomous.
Logistic regression aims to find the model with best fitting which describes the association between the class label and set of independent variables. Logistic regression generates the coefficients shown in the Equation (1), which predicts a logit transformation of the probability of presence of the characteristic of interest:
where, the variable p is the probability of presence of the characteristic of interest.
The logit transformation is described as the logged odds given by Equations (2) and (3).
and
2.7. Naïve Bayes Classifier
Naïve Bayesian classifier [13] is built based on Bayes’ theorem which assumes the predictor attributes are independent and is called class conditional independence. According to the Bayes’ theorem, the class label (c) of the data instance (x) is identified by calculating the posterior probability of value P(c|x) as given in Equation (4).
where P(c|x) is posterior probability of class c conditioned on data instance x. P(x|c) is posterior probability of data instance x conditioned on class c. P(c) is prior probability of class c. P(x) is prior probability of data instance x.
2.8. Random Forest
Random forest [14] model is the collection of many decision trees. This algorithm extracts random sample from training data while constructing the trees and extract random subset from the features while splitting the nodes. While training, each tree in a RF learns from the randomly selected samples of training data points. The sampling technique used is random sampling with replacement. So that same samples can be used number of times in a single tree. While testing, each tree’s prediction is taken and the average of these predicted values are considered as final prediction. The other concept in RF is that only some features (sqrt of n features) of the dataset are considered for splitting each node in each decision tree.
3. Related Work
Class imbalance problem in software defect prediction is addressed by various methods based on data and algorithm levels [15,16]. Data-level methods address the issue by means of re-sampling techniques, which may balance datasets by deleting majority class data samples or by replicating minority class samples. Methods like random undersampling, random oversampling, SMOTE [3], and their variants [17,18,19,20,21,22] are widely used in literature. But, these kinds of methods have the risk of discarding useful data or duplicate the existing data.
Ensemble learning and cost-sensitive learning are examples for algorithm-level methods. Bagging and boosting are classic ensemble learning techniques, which demonstrated handling class imbalanced problem effectively [23]. Variants of bagging and boosting have been proposed to address this problem in the SDP [15,24,25,26]. Cost sensitive (CS) learning works on assigning big misclassification cost for defective instance and small misclassification cost for non-defective instances. Khoshgotaar et al. [27] introduced CS learning into SDP and proposed a cost-boosting method. Zheng J. [28] proposed cost-sensitive boosting neural networks for SDP. Similarly, CS neural network was studied by Arar and Ayan [29]. Liu et al. [30] proposed two-stage CS learning for SDP, which includes CS feature selection and CS neural network classifier. Li et al. [31] used three-way decision-based CS for SDP. Some researchers combined CS with other machine learning methods, such as dictionary learning and random forest [18,20]. Furthermore, CS also has been used in the CPDP scenario [16,32]. However, how to set suitable cost values is still an unsolved problem for the cost-sensitive learning method. Divya Tomar et al. [33], developed SDP system using weighted least squares twin support vector machine (WLSTSVM). In this method, they assigned a high cost of misclassification to the defective class samples and low cost to non-defective class samples. Lina Gong et al. [34], proposed KMFOS method which generates new samples that spread diversely in the defective space. KMFOS applies K-means clustering method to divide defective samples into K number of clusters. Then, new instances are generated by using interpolation between different instances belong to each two clusters. Finally, it uses CLNI filtering technique to clean the noise instances. Sohan et al. [35], assessed the imbalance learning effect on CPDP by using eight different classifiers. Q. Song et al. [36], conducted experiments which explores the effect of the presence of imbalanced data, its nature, use of different classifiers, using software metrics as input. They evaluated twenty seven data sets, using seven classifiers on seven types of input metrics and various imbalanced learning methods and concluded that imbalanced learning could be considered only for moderate or highly imbalanced software defect prediction datasets. Sohan et al. [37] conducted a study to know the inconsistency in the performance among imbalanced dataset and balanced dataset. In this study, eight public data sets were examined with seven classification methods to conclude that the imbalance nature of defective and non-defective classes plays a major role in SDP and among seven classifiers, the voting results in best performer among the classifiers. S. Huda et al. [38], proposed two novel hybrid SDP models to choose significant attributes by combining wrapper and filter methods.
4. Proposed Method
Our proposed approach class imbalance reduction (CIR) is based on calculating the centroid of all attributes of minority class samples for synthesizing new samples. Our approach is outperforming the popular SMOTE oversampling technique in six mostly used performance measures. The general framework for implementing our approach is described as follows:
Let the imbalanced defect dataset DSi = {r1, r2, r3,…, rn} where ri (1 ≤ i ≤ n) is a ith record representing ith module in the project. Each ri contains m number of attributes where each attribute is a software metric and one additional class label attribute. The value of class label represents number of bugs occurred in that module. The zero value in class label attribute represents a non-defective module and the value greater than zero represents a defective module. The binary classifier requires the class label values to be zero or one, so with pre-processing, we changed class label values to either zero or one. The proposed framework is depicted in Figure 1.
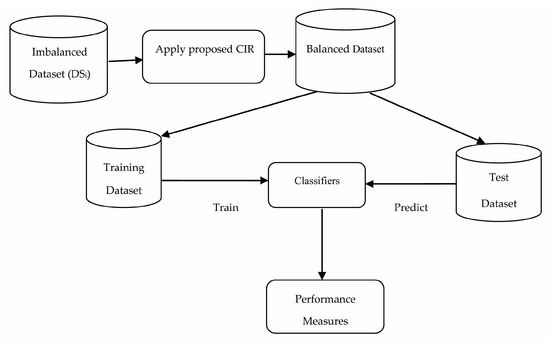
Figure 1.
Proposed framework.
Algorithm for Class Imbalance Reduction (CIR)
The input dataset DSi is divided based on the value of the class label into two groups. The group with less number of samples is designated as minority class and the group with more number of samples as majority class as shown in Figure 2. In our approach, as described in Algorithm 1, synthetic data is generated to increase the samples of minority class to match number of samples of majority class. The centroid (C) of the minority class samples is computed and its nearest neighbor sample is identified. A new sample is generated by applying scalar multiplication of centroid and random number generated within the range of 0 to 1 and adding it to its nearest neighbor. The generated synthetic sample is appended to minority class samples. This procedure of generating new samples is terminated when both minority and majority classes are balanced so as to create symmetry between the number of defect and non-defect records. For example, consider three data samples (1,2), (2,5), (3,5). The centroid (C) of these data sampless is (2,4) and the nearest neighbor to centroid is (2,5). The algorithm generates synthetic data samples by (2,5) + (random number between 0 and 1) * C.
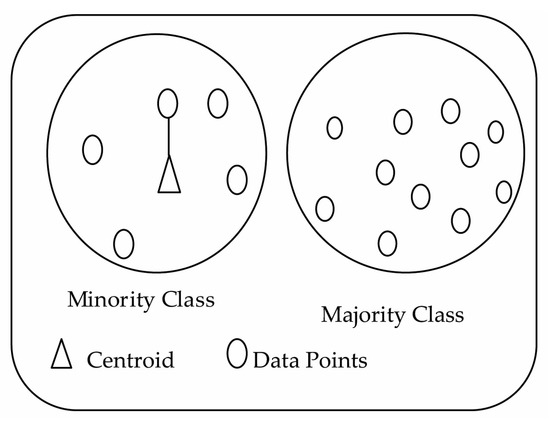
Figure 2.
Demonstration of proposed CIR method.
As shown in Figure 1, from the balanced data, random 70% records are considered as training data and remaining 30% records are considered as test data. The classification models are generated and tested by using 10-fold cross validation on training and test datasets with various classifiers like AdaBoost (AB), decision tree (DT), extra tree (ET), GradientBoost (GB), K-nearest neighbor (KNN), logistic regression (LR), Naïve Bayes (NB) and random forest (RF).
| Algorithm1: Class Imbalance Reduction (CIR) |
| Input: Imbalanced Dataset (DSi) with X1, X2, X3,…, Xm attributes which represent features (software metrics) with class label and r1, r2, r3,…, rn are records |
| Output: Balanced Dataset (BD) with symmetry of number of defect and non-defect records |
| Step-1: Divide the DSi into two groups based on class label value representing defect and non-defect classes |
| Step-2: Class which contains less number of records is denoted as minority class (Do) |
| Step-3: Class which contains more number of records is denoted as majority class (Dj) |
| Step-4: Calculate the centroid (C) of Do using C ={mean(X1), mean(X2), mean(X3),…, mean(Xm)} |
| Step-5: For each record ri in Do Step-5.1 Calculate the distance dist(ri, C) using Euclidian distance |
| Step-6: Sort the records in increasing order of their distances |
| Step-7: Choose the record with minimum distance (Dmin) |
| Step-8: Generate n random numbers k0, k1, k2,…, kn, between 0 and 1, where n = |Dj|-|Do| such that symmetry is created between the number of defect and non-defect records Step-8.1 For each random number kj Step-8.1.1 Generate a new record as Dmin + kj * C Step-8.1.2 Append new record to Do |
5. Experimentation and Results
For experimentation, we considered forty open source datasets relating to the defect prediction from tera-PROMISE repository [39]. The list and the class imbalance percentages of datasets are shown in Table 1. All the datasets are containing data of twenty software metrics such as McCabes cyclomatic complexity, weighted methods per class, and others. The description of each metric is given in Table 2.

Table 1.
Datasets used for experimentation.

Table 2.
Description of Software Metrics.
5.1. Performance Measures
There are several classifier performance measures that are proposed in the literature as given by Equations (5)–(10). Sensitivity or recall is the measure to check the proportion of positives which are correctly classified. Specificity is the ability of the test to correctly identify true negatives. Geometric mean combines rate of true negative and true positive at a specific threshold. Precision measures the proportion of predicted positives over all positives. F-Measure is the harmonic mean of precision and recall. Accuracy measures the proportion of true results over total cases. The confusion matrix which is used to compute these performance measures is shown in Table 3.

Table 3.
Confusion Matrix.
The comparative analysis of our approach with SMOTE and K-means SMOTE for above mentioned performance measures by using AdaBoost (AB), decision tree (DT), extra tree (ET), GradientBoost (GB), K-nearest neighbor (KNN), logistic regression (LR), Naïve Bayes (NB) and random forest (RF) classifiers is shown in Table 4 in the format of “Mean ± Standard Deviation (SD)”. The analysis shows that the proposed CIR method exhibits an improvement over SMOTE as well as K-Means SMOTE for all the performance measures (Depicted in bold faced values). CIR is performing very well over SMOTE when applied with frequently used eight machine algorithms like AdaBoost, decision tree, extra tree, gradient boost, K-nearest neighbors, logistic regression, Naïve Bayes classifier and random forest.

Table 4.
Comparison of Accuracy, Precision, Recall, F-Measure, Specificity and Geometric Mean measures for SMOTE, K-Means SMOTE and proposed CIR techniques using six classifiers with Mean ± SD.
Table 5 is showing the comparison of improvement of CIR over SMOTE using eight classifiers with six performance measures. Each row in Table 5 shows the number of datasets in which the performance improvement is seen using CIR over SMOTE. For example the first row is showing that 27 out of 40 datasets is showing improvement in performance with CIR over SMOTE and 6 datasets is showing equal performance with CIR over SMOTE in accuracy for AdaBoost classifier. Table 6 is showing the comparison of improvement of CIR over K-means SMOTE using eight classifiers with six performance measures. Each row in Table 6 is showing the number of datasets in which the performance improvement is seen using CIR over K-means SMOTE. For example the first row is showing that 26 out of 40 datasets is showing improvement in performance with CIR over K-means SMOTE and 5 datasets is showing equal performance with CIR over K-means SMOTE in accuracy for AdaBoost classifier. Table 7 is showing the comparison of performance improvement with CIR over SMOTE and K-means SMOTE using different classifiers. Every row in Table 7 is showing the performance improvement of CIR over SMOTE and K-means SMOTE for each classifier. KNN performance is better than other classifiers in accuracy, precision and specificity whereas logistic regression is performing well in recall, F-measure and geometric mean. Overall, logistic regression is performing close to or better than all other classifiers.

Table 5.
Comparison of CIR over SMOTE using eight classifiers with six performance measures for forty datasets. (X = number of datasets showing improved performance over SMOTE, Y = number of datasets showing equal performance over SMOTE).

Table 6.
Comparison of CIR over K-Means SMOTE using eight classifiers with six performance measures for forty datasets. (X = number of datasets showing improved performance over K-Means SMOTE, Y = number of datasets showing equal performance over K-Means SMOTE).

Table 7.
Comparison of Performance improvement (in percentage) with CIR over SMOTE and K-Means SMOTE using different classifiers.
5.2. Statistical Significance
Post hoc Analysis
The post hoc analysis is done by using SPSS 20.0 tool [40] with multiple comparison single factor ANOVA to compare three algorithms, SMOTE, K-means SMOTE and proposed CIR algorithm. By post hoc analysis, the proposed CIR algorithm showed significance in precision, recall, and specificity using AdaBoost classifier, in geometric mean using extra tree. K-nearest neighbors, logistic regression and Naïve Bayes classifiers are showed high significance in all six performance measures and Random Forest classifier showed high significance in precision, F-measure and specificity when compared with SMOTE and K-Means SMOTE since p-values are significant at 0.05 level the results of which are shown in Table 8.

Table 8.
Result of post hoc analysis.
6. Conclusions
In this paper, we proposed a novel technique class imbalance reduction (CIR) to handle class imbalance in software defect prediction by considering distribution properties of dataset. The proposed method uses the centroid and nearest neighbor based approach to generate synthetic data. Several experiments are conducted by applying the proposed approach on forty open source datasets and the results of the experiment obtained using proposed approach are compared with the results obtained by applying the SMOTE, which is a benchmark model in reducing class imbalance, and with K-means SMOTE algorithms. Our experiment results prove that the proposed approach CIR is outperforming the SMOTE and K-Means SMOTE in terms of six standard prediction measures. CIR is performing very well over SMOTE and K-means SMOTE when applied with frequently used eight machine algorithms like AdaBoost, decision tree, extra tree, gradient boost, K-nearest neighbors, logistic regression, naïve Bayes and random forest. KNN performance is better than other classifiers in accuracy, precision and specificity whereas logistic regression is performing well in recall, F-measure and geometric mean. Overall, logistic regression performs close to or better than all other classifiers.
Post hoc analysis is done by using SPSS 20.0 tool with multiple comparison single factor ANOVA to compare three algorithms, SMOTE, K-means SMOTE and proposed CIR algorithm. By post hoc analysis, proposed CIR algorithm showed significance in precision, recall and specificity using AdaBoost classifier, in geometric mean using extra tree. K-Nearest neighbors, Logistic regression and naïve Bayes classifiers are showed high significance in all six performance measures and Random Forest classifier showed high significance in precision, f-measure and specificity when compared with SMOTE and K-means SMOTE since p-values are significant at 0.05 levels. The proposed work can be extended to cross project defect prediction (CPDP) and also can be integrated with other optimization techniques such as ant colony optimization.
Author Contributions
K.K.B. has implemented CIR algorithm, collected data sets and verified results. J.G. has proposed CIR algorithm along with other authors and given suggestions to improve the paper. N.G. has helped in validating the results of CIR algorithm by comparing it with SMOTE technique. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Deanship of Scientific Research at Majmaah University under grant number [R-1441-84]. And The APC was funded by Deanship of Scientific Research at Majmaah University.
Acknowledgments
The author would like to thank Deanship of Scientific Research at Majmaah University for supporting this work under Project Number No. R-1441-84. The author is also thankful to the anonymous reviewers for their useful comments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Arora, I.; Tetarwal, V.; Saha, A. Open Issues in Software Defect Prediction. Proc. Comput. Sci. 2015, 46, 906–912. [Google Scholar] [CrossRef]
- Liu, X.; Wu, J.; Zhou, Z. Exploratory Undersampling for Class-Imbalance Learning. IEEE Trans. Syst. Man Cybern. Part B 2009, 39, 539–550. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Fernández, A.; Garcia, S.; Herrera, F.; Chawla, N.V. SMOTE for Learning from Imbalanced Data: Progress and Challenges, Marking the 15-year Anniversary. J. Artif. Intell. Res. 2018, 61, 863–905. [Google Scholar] [CrossRef]
- Kovacs, G. Smote-variants: A python implementation of 85 minority oversampling techniques. Neurocomputing 2019, 366, 352–354. [Google Scholar] [CrossRef]
- Douzas, G.; Bacao, F.; Last, F. Improving Imbalanced Learn-ing Through a Heuristic Oversampling Method Based on K-Means and SMOTE. Inf. Sci. 2018, 465, 1–20. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R. A Decision-Theoretic Generalization of on-Line Learning and an Application to Boosting. J. Comp. Syst. Sci. 1995, 55, 119–139. [Google Scholar] [CrossRef]
- Quinlan, J.R. C4.5: Programs for Machine Learning; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1993. [Google Scholar]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Friedman, J. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1–39. [Google Scholar]
- Altman, N.S. An introduction to kernel and nearest-neighbor nonparametric regression. Am. Stat. 1992, 46, 175–185. [Google Scholar] [CrossRef]
- Peng, C.Y.J.; Lee, K.L.; Ingersoll, G.M. An Introduction to Logistic Regression Analysis and Reporting. J. Educ. Res. 2002, 96, 3–14. [Google Scholar] [CrossRef]
- Rish, I. IBM Research Report, An Empirical Study of the Naive Bayes Classifier. In Proceedings of the JCAI 2001 Workshop on Empirical Methods in Artificial Intelligence, Seattle, WA, USA, 4–6 August 2001; Volume 3, pp. 41–46. [Google Scholar]
- Liaw, A.; Wiener, M. Classification and Regression by RandomForest. R News 2002, 2, 18–22. [Google Scholar]
- Laradji, I.H.; Alshayeb, M.; Ghouti, L. Software defect prediction using ensemble learning on selected features. Inf. Softw. Technol. 2015, 58, 388–402. [Google Scholar] [CrossRef]
- Li, Z.; Jing, X.Y.; Wu, F.; Zhu, X.; Xu, B.; Ying, S. Cost-sensitive transfer kernel canonical correlation analysis for heterogeneous defect prediction. Autom. Softw. Eng. 2018, 25, 201–245. [Google Scholar] [CrossRef]
- Aman, H.; Amasaki, S.; Sasaki, T.; Kawahara, M. Lines of comments as a noteworthy metric for analyzing fault-proneness in methods. IEICE Trans. Inf. Syst. 2015, 12, 2218–2228. [Google Scholar] [CrossRef]
- Gao, K.; Khoshgoftaar, T.M.; Napolitano, A. The use of ensemble-based data preprocessing techniques for software defect prediction. Int. J. Softw. Eng. Knowl. Eng. 2014, 24, 1229–1253. [Google Scholar] [CrossRef]
- Chen, L.; Fang, B.; Shang, Z.; Tang, Y. Negative samples reduction in cross-company software defects prediction. Inf. Softw. Technol. 2015, 62, 67–77. [Google Scholar] [CrossRef]
- Siers, M.J.; Islam, M.Z. Software defect prediction using a cost sensitive decision forest and voting, and a potential solution to the class imbalance problem. Inf. Syst. 2015, 51, 62–71. [Google Scholar] [CrossRef]
- Khoshgoftaar, T.M.; Gao, K.; Napolitano, A.; Wald, R. A comparative study of iterative and non-iterative feature selection techniques for software defect prediction. Inf. Syst. Front. 2014, 16, 801–822. [Google Scholar] [CrossRef]
- Zhang, Z.W.; Jing, X.Y.; Wang, T.J. Label propagation based semi-supervised learning for software defect prediction. Autom. Softw. Eng. 2016, 24, 1–23. [Google Scholar] [CrossRef]
- Galar, M.; Fernandez, A.; Barrenechea, E.; Bustince, H.; Herrera, F. A Review on Ensembles for the Class Imbalance Problem: Bagging-, Boosting-, and Hybrid-Based Approaches. IEEE Trans. Syst. Man Cybern. Part C 2012, 42, 463–484. [Google Scholar] [CrossRef]
- Tong, H.; Liu, B.; Wang, S. Software defect prediction using stacked denoising autoencoders and two-stage ensemble learning. Inf. Softw. Technol. 2018, 96, 94–111. [Google Scholar] [CrossRef]
- Wang, S.; Yao, X. Using class imbalance learning for software defect prediction. IEEE Trans. Reliab. 2013, 62, 434–443. [Google Scholar] [CrossRef]
- Sun, Z.; Song, Q.; Zhu, X. Using coding-based ensemble learning to improve software defect prediction. IEEE Trans. Syst. Man Cybern. Part C 2012, 46, 1806–1817. [Google Scholar] [CrossRef]
- Khoshgoftaar, T.M.; Geleyn, E.; Nguyen, L.; Bullard, L. Cost-sensitive boosting in software quality modeling. In Proceedings of the 7th IEEE International Symposium on High Assurance Systems Engineering, Tokyo, Japan, 23–25 October 2002; pp. 51–60. [Google Scholar] [CrossRef]
- Zheng, J. Cost-sensitive boosting neural networks for software defect prediction. Exp. Syst. Appl. 2010, 37, 4537–4543. [Google Scholar] [CrossRef]
- Arar, Ö.F.; Ayan, K. Software defect prediction using cost-sensitive neural network. Appl. Soft Comput. 2015, 33, 263–277. [Google Scholar] [CrossRef]
- Liu, M.; Miao, L.; Zhang, D. Two-stage cost-sensitive learning for software defect prediction. IEEE Trans. Reliab. 2014, 63, 676–686. [Google Scholar] [CrossRef]
- Li, W.; Huang, Z.; Li, Q. Three-way decisions based software defect prediction. Knowl.-Based Syst. 2016, 91, 263–274. [Google Scholar] [CrossRef]
- Ryu, D.; Jang, J.I.; Baik, J. A transfer cost-sensitive boosting approach for cross-project defect prediction. Softw. Qual. J. 2017, 25, 235–272. [Google Scholar] [CrossRef]
- Tomar, D.; Agarwal, S. Prediction of Defective Software Modules Using Class Imbalance Learning. Appl. Comput. Intell. Soft Comput. 2016, 2016, 1–12. [Google Scholar] [CrossRef]
- Gong, L.; Jiang, S.; Jiang, L. Tackling Class Imbalance Problem in Software Defect Prediction Through Cluster-Based Over-Sampling with Filtering. IEEE Access 2019, 7, 145725–145737. [Google Scholar] [CrossRef]
- Sohan, M.F.; Jabiullah, M.I.; Rahman, S.S.M.M.; Mahmud, S.H. Assessing the Effect of Imbalanced Learning on Cross-project Software Defect Prediction. In Proceedings of the 10th International Conference on Computing, Communication and Networking Technologies (ICCCNT), Kanpur, India, 6–8 July 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Song, Q.; Guo, Y.; Shepperd, M. A Comprehensive Investigation of the Role of Imbalanced Learning for Software Defect Prediction. IEEE Trans. Softw. Eng. 2019, 45, 1253–1269. [Google Scholar] [CrossRef]
- Sohan, M.F.; Kabir, M.A.; Jabiullah, M.I.; Rahman, S.S.M.M. Revisiting the Class Imbalance Issue in Software Defect Prediction. In Proceedings of the 2019 International Conference on Electrical, Computer and Communication Engineering (ECCE), Cox’sBazar, Bangladesh, 7–9 February 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Huda, S.; Alyahya, S.; Ali, M.M.; Ahmad, S.; Abawajy, J.; Al-Dossari, H.; Yearwood, J. A Framework for Software Defect Prediction and Metric Selection. IEEE Access 2018, 6, 2844–2858. [Google Scholar] [CrossRef]
- Ferenc, R.; Toth, Z.; Ladányi, G.; Siket, I.; Gyimóthy, T. A Public Unified Bug Dataset for Java. In Proceedings of the 14th International Conference on Predictive Models and Data Analytics in Software Engineering, Oulu, Finland, 10 October 2018; pp. 12–21. [Google Scholar] [CrossRef]
- IBM_SPSS_Advanced_Statistics.pdf. Available online: ftp://public.dhe.ibm.com/software/analytics/spss/documentation/statistics/20.0/en/client/Manuals/IBM_SPSS_Advanced_Statistics.pdf (accessed on 12 February 2020).
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).