Earthquake Vulnerability Mapping Using Different Hybrid Models
Abstract
1. Introduction
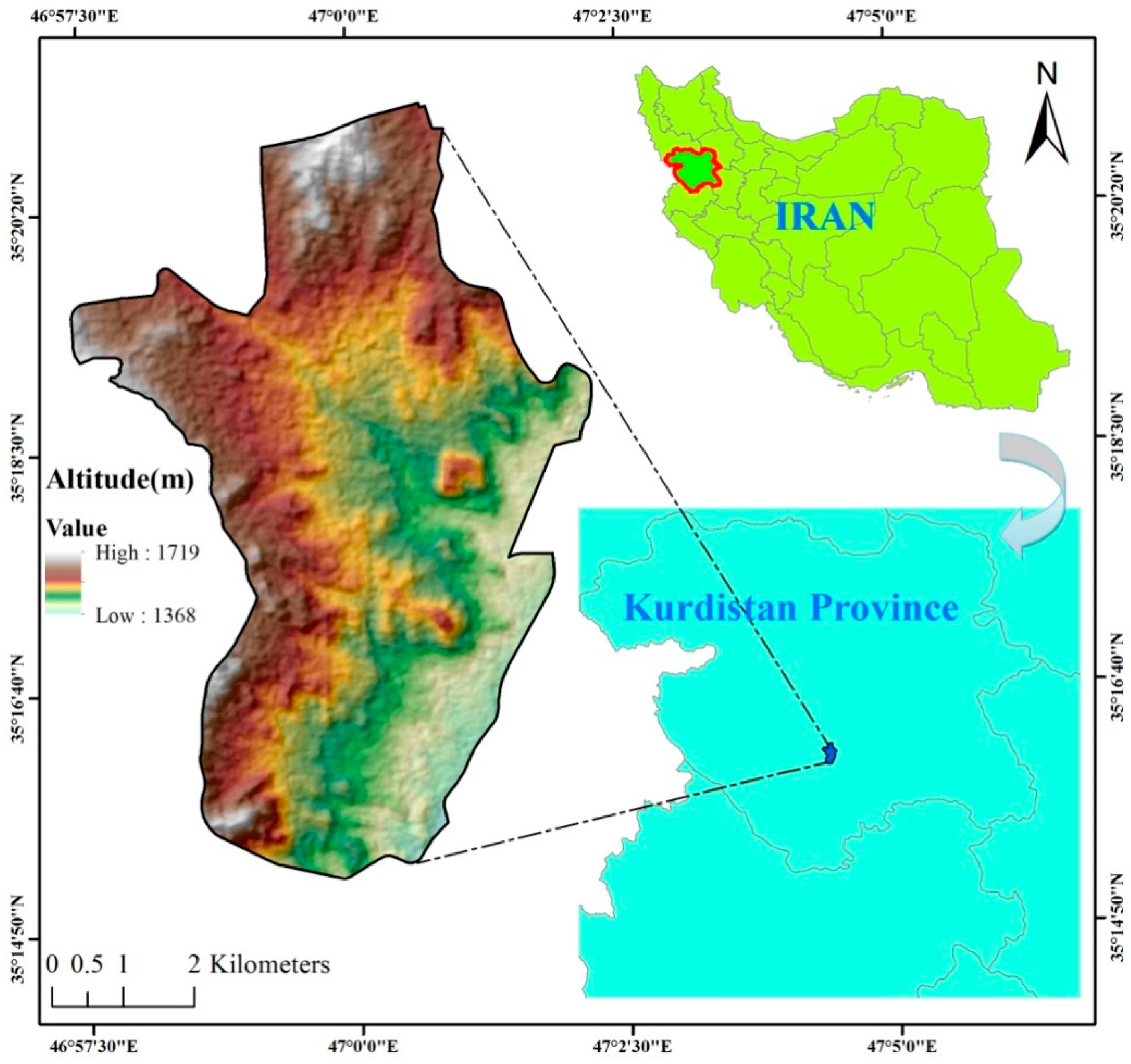
2. Overview of the Study Area
Data Used
3. Earthquake Vulnerability Mapping
3.1. Background of the Multi-Criteria Decision and Statistical Models Used
3.1.1. Fuzzy Logic
- i.
- Rules Base: This section covers all the rules and conditions that are specified “if … then” by an expert to be able to control the decisions of a “decision system”.
- ii.
- Fuzzy inference: In this section, the degree of fuzzy inputs′ compliance with the basic rules is determined. Thus, based on the percentage of adaptation, different decisions are produced as a result of fuzzy inference.
- iii.
- Aggregation: Because decisions are made on the basis of testing all the rules in parallel, as a result, all the rules calculated by the above method are brought together and a fuzzy set of output is created.
- iv.
- Defuzzification: In the last step, the results of fuzzy inference, which are fuzzy sets, are converted into quantitative data and information. A variety of methods are used for defuzzification, but the COG (relation 1) method provided by the Center of Gravity (COG) is most used [59].
3.1.2. Analytical Hierarchical Process (AHP)
3.1.3. Analytic Network Process (ANP)
3.1.4. Ordered Weight Average (OWA)
3.1.5. Logistic Regression (LR)
3.2. Validation and Accuracy Assessment
3.2.1. Relative Operating Characteristic (ROC)
3.2.2. Seismic Relative Index (SRI)
3.2.3. Frequency Ratio (FR)
4. Experiment Results and Analysis
Selection of Training Sites Used in Modeling
5. Results
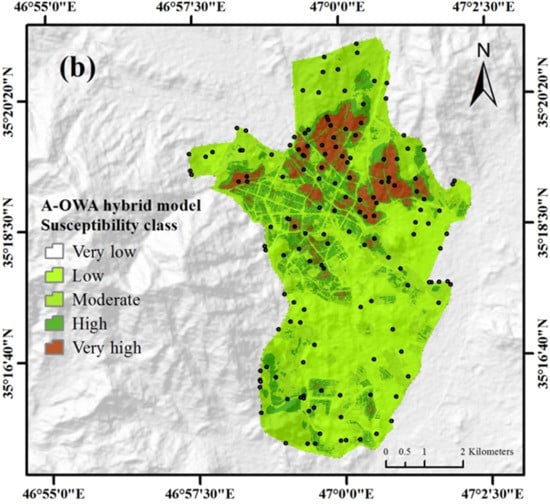
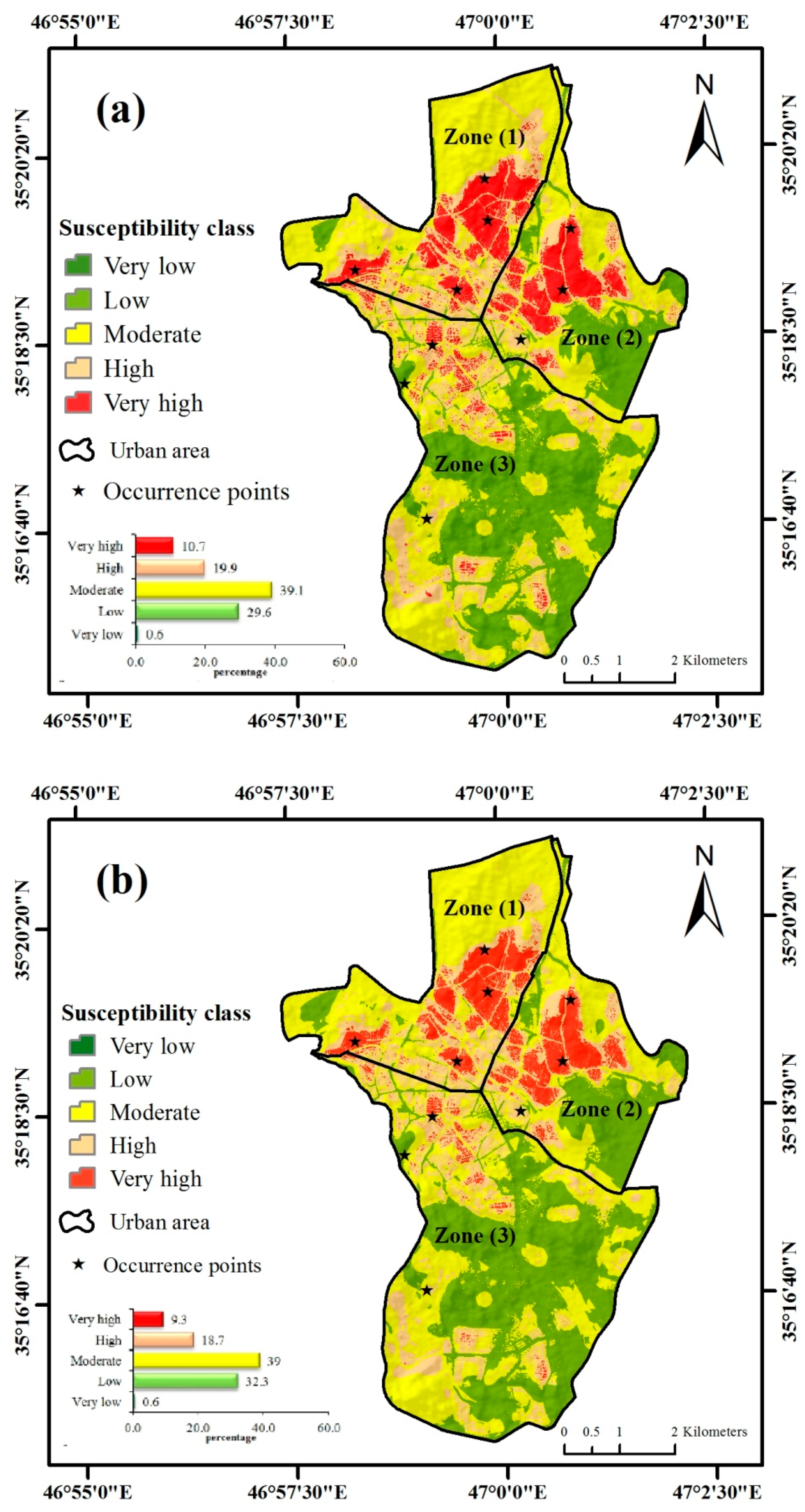
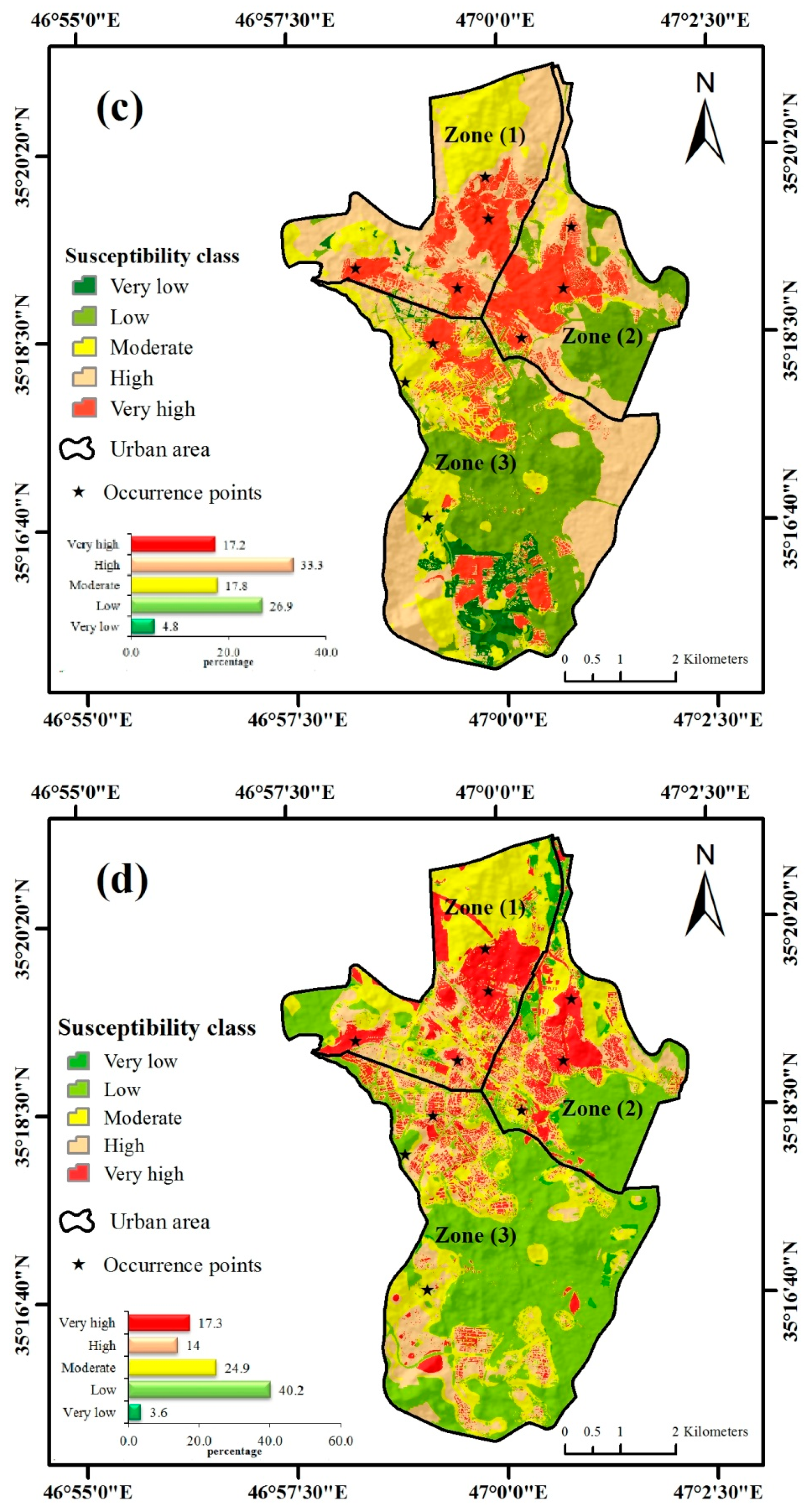
5.1. Seismic Vulnerability Map
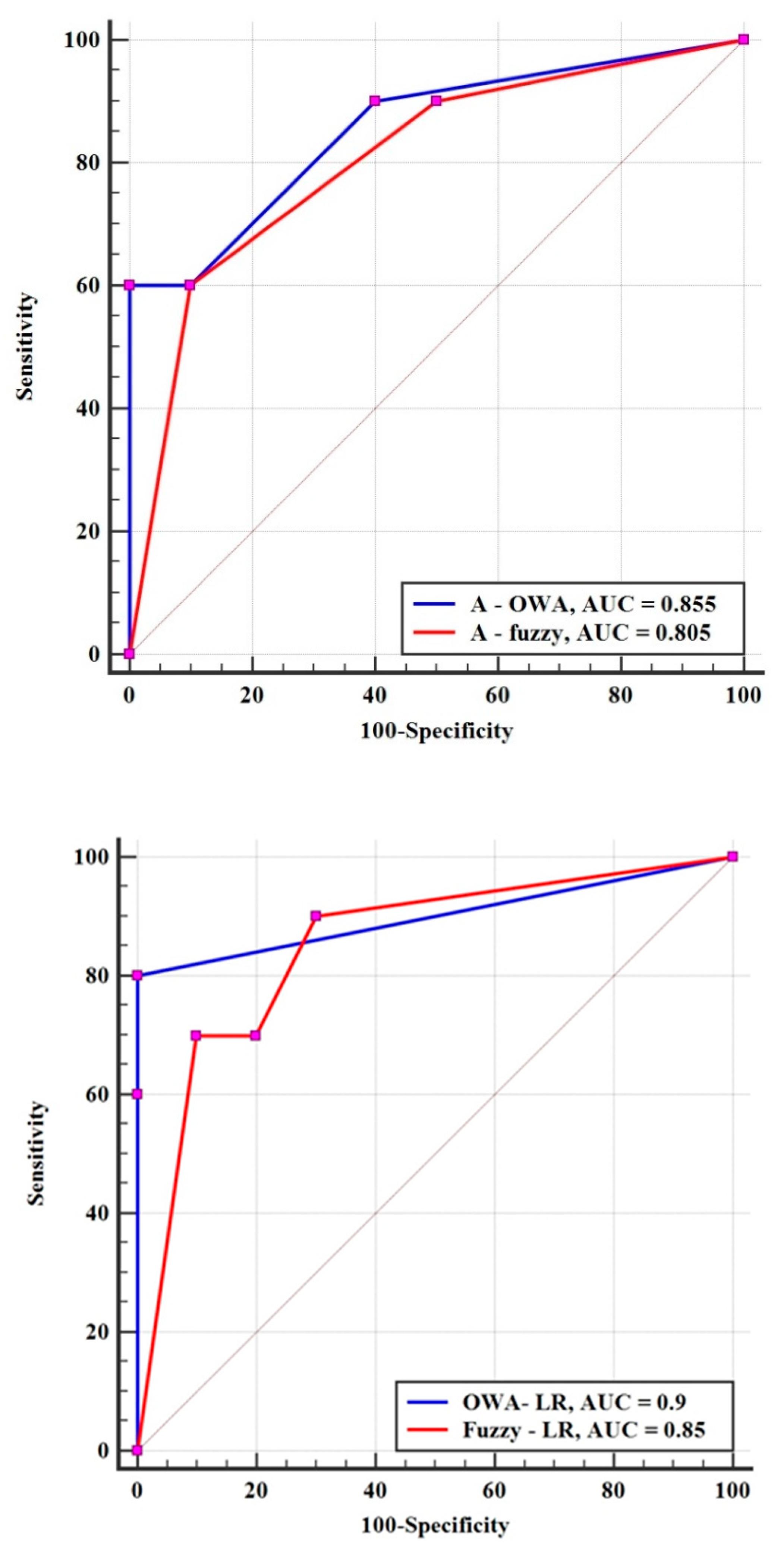
5.2. Validation of the Seismic Susceptibility Maps
6. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lantada, N.; Pujades, L.G.; Barbat, A.H. Vulnerability index and capacity spectrum based methods for urban seismic risk evaluation. Nat. Hazards 2009, 51, 501–524. [Google Scholar] [CrossRef]
- Rashed, T.; Weeks, J. Assessing vulnerability to earthquake hazards through spatial multicriteria analysis of urban areas. Int. J. Geogr. Inf. Sci. 2003, 17, 547–576. [Google Scholar] [CrossRef]
- Ebert, A.; Kerle, N. Urban Social Vulnerability Assessment Using Object-Oriented Analysis of Remote Sensing and GIS Data. A Case Study for Tegucigalpa, Honduras. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 1307–1312. [Google Scholar]
- Asadi, Y.; Samany, N.N.; Ezimand, K. Seismic vulnerability assessment of urban buildings and traffic networks using fuzzy ordered weighted average. J. Mt. Sci. 2019, 16, 677–688. [Google Scholar] [CrossRef]
- Wald, D.; Jaiswal, K.; Marano, K.; Bausch, D. Earthquake impact scale. Nat. Hazards Rev. 2011, 12, 125–139. [Google Scholar] [CrossRef]
- Linares, R.; Alejandra, R. Panama Prepares the City of david for Earthquakes, project highlights. Panama 2012, 9, 1–4. Available online: http://siteresources.worldbank.org/INTLACREGTOPURBDEV/Resources/840343-1319570618921/PH_Issue_9_CITY_DAVID_PRINT.pdf (accessed on 4 March 2020).
- Xing, H.; Zhonglin, Z.; Shaoyu, W. The prediction model of earthquake casuailty based on robust wavelet v-SVM. Nat. Hazards 2015, 77, 717–732. [Google Scholar] [CrossRef]
- Merciu, C.; Ianos, I.; Merciu, G.; Jones, R.; Pomeroy, G. Mapping accessibility for earthquake hazard response in the historic urban centre of Bucharest. Nat. Hazards Earth Syst. Sci. 2018, 18, 2011–2026. [Google Scholar] [CrossRef]
- Frigerio, I.; De Amicis, M. Mapping social vulnerability to natural hazards in Italy: A suitable tool for risk mitigation strategies. Environ. Sci. Policy 2016, 63, 187–196. [Google Scholar] [CrossRef]
- Martins, V.N.; e Silva, D.S.; Cabral, P. Social vulnerability assessment to seismic risk using multicriteria analysis: The case study of Vila Franca do Campo (São Miguel Island, Azores, Portugal). Nat. Hazards 2012, 62, 385–404. [Google Scholar] [CrossRef]
- Kumlu, K.B.Y.; Tüdeş, Ş. Determination of earthquake-risky areas in Yalova City Center (Marmara region, Turkey) using GIS-based multicriteria decision-making techniques (analytical hierarchy process and technique for order preference by similarity to ideal solution). Nat. Hazards 2019, 96, 999–1018. [Google Scholar] [CrossRef]
- Carreño, M.L.; Cardona, O.D.; Barbat, A.H. New methodology for urban seismic risk assessment from a holistic perspective. Bull. Earthq. Eng. 2012, 10, 547–565. [Google Scholar] [CrossRef]
- McClure, J.; Johnston, D.M.; Henrich, L.; Milfont, T.L.; Becker, J. When a hazard occurs where it is not expected: Risk judgments about different regions after the Christchurch earthquakes. Nat. Hazards 2015, 75, 635–652. [Google Scholar] [CrossRef]
- Kumamoto, T.; Masataka, T. Multivariate statistical analysis for seismotectonic zonation by the use of earthquake, active fault and crustal structure. In Proceedings of the Japan Geosciences Union Meeting, Takayama, Japan, 26–28 October 2011. [Google Scholar]
- Asim, K.M.; Idris, A.; Iqbal, T.; Martinez-Alvarez, F. Earthquake prediction model using support vector regressor and hybrid neural networks. PLoS ONE 2018, 13. [Google Scholar] [CrossRef] [PubMed]
- Dehghani, R.; Mohammadzadeh, N.; Salehi, M.; Kassiri, H. Earthquake planning and crisis management with an emphasis on the facilities, utilities, and services of the health care centers of Tiran and Karvan County, Isfahan Province, Iran: A case study. J. Acute Dis. 2018, 7, 115. [Google Scholar]
- Miano, A.; Jalayer, F.; De Risi, R.; Prota, A.; Manfredi, G. A case-study on scenario-based probabilistic seismic loss assessment for a portfolio of bridges. In Proceedings of the 12th International Conference on Applications of Statistics and Probability in Civil Engineering (ICASP12), Vancouver, BC, Canada, 12–15 July 2015; pp. 12–15. [Google Scholar]
- De Silva, S.; De Silva, G.S.; Padmal, H. Assessment method for seismic vulnerability of old masonry buildings in Sri Lanka. Procedia Eng. 2018, 212, 61–68. [Google Scholar] [CrossRef]
- Banica, A.; Rosu, L.; Muntele, I.; Grozavu, A. Towards urban resilience: A multi-criteria analysis of seismic vulnerability in Iasi City (Romania). Sustainability 2017, 9, 270. [Google Scholar] [CrossRef]
- Dou, J.; Yunus, A.P.; Tien Bui, D.; Sahana, M.; Chen, C.W.; Zhu, Z.; Wang, W.; Thai Pham, B. Evaluating GIS-based multiple statistical models and data mining for earthquake and rainfall-induced landslide susceptibility using the LiDAR DEM. Remote Sens. 2019, 11, 638. [Google Scholar] [CrossRef]
- Tian, Y.; Xu, C.; Hong, H.; Zhou, Q.; Wang, D. Mapping earthquake-triggered landslide susceptibility by use of artificial neural network (ANN) models: An example of the 2013 Minxian (China) Mw 5.9 event. Geomat. Nat. Hazards Risk 2019, 10, 1–25. [Google Scholar] [CrossRef]
- Ghorbanzadeh, O.; Blaschke, T.; Gholamnia, K.; Aryal, J. Forest fire susceptibility and risk mapping using social/infrastructural vulnerability and environmental variables. Fire 2019, 2, 50. [Google Scholar] [CrossRef]
- Bagheri, V.; Uromeihy, A.; Aghda, S.M.F. Evaluation of ANFIS and LR models for seismic rockfalls’ susceptibility mapping: A case study of Firooz Abad-Kojour, Iran, Earthquake (2004). Environ. Earth Sci. 2018, 77, 800. [Google Scholar] [CrossRef]
- Ghorbanzadeh, O.; Valizadeh Kamran, K.; Blaschke, T.; Aryal, J.; Naboureh, A.; Einali, J.; Bian, J. Spatial prediction of wildfire susceptibility using field survey gps data and machine learning approaches. Fire 2019, 2, 43. [Google Scholar] [CrossRef]
- Tavakkoli Piralilou, S.; Shahabi, H.; Jarihani, B.; Ghorbanzadeh, O.; Blaschke, T.; Gholamnia, K.; Meena, S.R.; Aryal, J. Landslide Detection Using Multi-Scale Image Segmentation and Different Machine Learning Models in the Higher Himalayas. Remote Sens. 2019, 11, 2575. [Google Scholar] [CrossRef]
- Abdollahi, S.; Pourghasemi, H.R.; Ghanbarian, G.A.; Safaeian, R. Prioritization of effective factors in the occurrence of land subsidence and its susceptibility mapping using an SVM model and their different kernel functions. Bull. Eng. Geol. Environ. 2019, 78, 4017–4034. [Google Scholar] [CrossRef]
- Ghorbanzadeh, O.; Blaschke, T.; Gholamnia, K.; Meena, S.R.; Tiede, D.; Aryal, J. Evaluation of Different Machine Learning Methods and Deep-Learning Convolutional Neural Networks for Landslide Detection. Remote Sens. 2019, 11, 196. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Beheshtirad, M.; Pradhan, B. A comparative assessment of prediction capabilities of modified analytical hierarchy process (M-AHP) and Mamdani fuzzy logic models using Netcad-GIS for forest fire susceptibility mapping. Geomat. Nat. Hazards Risk 2016, 7, 861–885. [Google Scholar] [CrossRef]
- Ghorbanzadeh, O.; Rostamzadeh, H.; Blaschke, T.; Gholaminia, K.; Aryal, J. A new GIS-based data mining technique using an adaptive neuro-fuzzy inference system (ANFIS) and k-fold cross-validation approach for land subsidence susceptibility mapping. Nat. Hazards 2018, 94, 497–517. [Google Scholar] [CrossRef]
- Termeh, S.V.R.; Kornejady, A.; Pourghasemi, H.R.; Keesstra, S. Flood susceptibility mapping using novel ensembles of adaptive neuro fuzzy inference system and metaheuristic algorithms. Sci. Total Environ. 2018, 615, 438–451. [Google Scholar] [CrossRef]
- Ziemba, P. Towards strong sustainability management—A generalized PROSA method. Sustainability 2019, 11, 1555. [Google Scholar] [CrossRef]
- Guan, X.; Qian, L.; Li, M.; Chen, H.; Zhou, L. Earthquake relief emergency logistics capacity evaluation model integrating cloud generalized information aggregation operators. J. Intell. Fuzzy Syst. 2017, 32, 2281–2294. [Google Scholar] [CrossRef]
- Gudiyangada Nachappa, T.; Tavakkoli Piralilou, S.; Ghorbanzadeh, O.; Shahabi, H.; Blaschke, T. Landslide Susceptibility Mapping for Austria Using Geons and Optimization with the Dempster-Shafer Theory. Appl. Sci. 2019, 9, 5393. [Google Scholar] [CrossRef]
- Shahabi, H.; Khezri, S.; Ahmad, B.B.; Hashim, M. Landslide susceptibility mapping at central Zab basin, Iran: A comparison between analytical hierarchy process, frequency ratio and logistic regression models. Catena 2014, 115, 55–70. [Google Scholar] [CrossRef]
- Ghorbanzadeh, O.; Blaschke, T. Wildfire Susceptibility Evaluation by Integrating an Analytical Network Process Approach into Gis-Based Analyses. Int. J. Adv. Sci. Eng. Technol. 2018, 6, 48–53. [Google Scholar]
- Pirnazar, M.; Karimi, A.Z.; Feizizadeh, B.; Ostad-Ali-Askari, K.; Eslamian, S.; Hasheminasab, H.; Ghorbanzadeh, O.; Hamedani, M.H. Assessing flood hazard using gis based multi-criteria decision making approach; Study area: East-azerbaijan province (kaleybar chay basin). J. Flood Eng. 2017, 8, 203–223. [Google Scholar]
- Rahmati, O.; Ghorbanzadeh, O.; Teimurian, T.; Mohammadi, F.; Tiefenbacher, J.P.; Falah, F.; Pirasteh, S.; Ngo, P.-T.T.; Bui, D.T. Spatial Modeling of Snow Avalanche Using Machine Learning Models and Geo-Environmental Factors: Comparison of Effectiveness in Two Mountain Regions. Remote Sens. 2019, 11, 2995. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Rahmati, O. Prediction of the landslide susceptibility: Which algorithm, which precision? Catena 2018, 162, 177–192. [Google Scholar]
- Shahabi, H.; Hashim, M. Landslide susceptibility mapping using GIS-based statistical models and Remote sensing data in tropical environment. Sci. Rep. 2015, 5, 9899. [Google Scholar] [CrossRef]
- Razandi, Y.; Pourghasemi, H.R.; Neisani, N.S.; Rahmati, O. Application of analytical hierarchy process, frequency ratio, and certainty factor models for groundwater potential mapping using GIS. Earth Sci. Inform. 2015, 8, 867–883. [Google Scholar] [CrossRef]
- Ghodrati Amiri, G.; Andisheh, K.; Razavian Amrei, S.A. Probabilistic seismic hazard assessment of Sanandaj, Iran. Struct. Eng. Mech. 2009, 32, 563–581. [Google Scholar] [CrossRef]
- Alizadeh, M.; Hashim, M.; Alizadeh, E.; Shahabi, H.; Karami, M.R.; Beiranvand Pour, A.; Pradhan, B.; Zabihi, H. Multi-criteria decision making (MCDM) model for seismic vulnerability assessment (SVA) of urban residential buildings. ISPRS Int. J. Geo-Inf. 2018, 7, 444. [Google Scholar] [CrossRef]
- Hassanzadeh, R.; Nedović-Budić, Z.; Razavi, A.A.; Norouzzadeh, M.; Hodhodkian, H. Interactive approach for GIS-based earthquake scenario development and resource estimation (Karmania hazard model). Comput. Geosci. 2013, 51, 324–338. [Google Scholar] [CrossRef]
- Rahman, N.; Ansary, M.A.; Islam, I. GIS based mapping of vulnerability to earthquake and fire hazard in Dhaka city, Bangladesh. Int. J. Disaster Risk Reduct. 2015, 13, 291–300. [Google Scholar] [CrossRef]
- Karimzadeh, S.; Miyajima, M.; Hassanzadeh, R.; Amiraslanzadeh, R.; Kamel, B. A GIS-based seismic hazard, building vulnerability and human loss assessment for the earthquake scenario in Tabriz. Soil Dyn. Earthq. Eng. 2014, 66, 263–280. [Google Scholar] [CrossRef]
- Sivakumar, N.; Karthik, S.; Thangaraj, S.; Saravanan, S.; Shidhardhan, C.K. Seismic vulnerability of open ground floor columns in multi storey buildings. Int. J. Sci. Eng. Res. (IJSER) 2013, 1, 52–58. [Google Scholar]
- Cole, G.L.; Dhakal, R.P.; Chouw, N. Building Pounding Damage Observed in the 2011 Christchurch earthquake Christchurch Earthquake. Earthq. Eng. Struct. Dyn. 2011, 41, 893–913. [Google Scholar] [CrossRef]
- Sinha, N.; Priyanka, N.; Joshi, P.K. Using spatial multi-criteria analysis and ranking tool (SMART) in earthquake risk assessment: A case study of Delhi region, India. Geomat. Nat. Hazards Risk 2016, 7, 680–701. [Google Scholar] [CrossRef]
- Rimal, B.; Baral, H.; Stork, N.E.; Paudyal, K.; Rijal, S. Growing city and rapid land use transition: Assessing multiple hazards and risks in the Pokhara Valley, Nepal. Land 2015, 4, 957–978. [Google Scholar] [CrossRef]
- Hosseini, K.A.; Hosseini, M.; Jafari, M.K.; Hosseinioon, S. Recognition of vulnerable urban fabrics in earthquake zones: A case study of the Tehran metropolitan area. J. Seismol. Earthq. Eng. 2009, 10, 175–187. [Google Scholar]
- Armaş, I.; Toma-Danila, D.; Ionescu, R.; Gavriş, A. Vulnerability to earthquake hazard: Bucharest case study, Romania. Int. J. Disaster Risk Sci. 2017, 8, 182–195. [Google Scholar] [CrossRef]
- Duzgun, H.S.B.; Yucemen, M.S.; Kalaycioglu, H.S.; Celik, K.; Kemec, S.; Ertugay, K.; Deniz, A. An integrated earthquake vulnerability assessment framework for urban areas. Nat. Hazards 2011, 59, 917. [Google Scholar] [CrossRef]
- Potter, S.H.; Becker, J.S.; Johnston, D.M.; Rossiter, K.P. An overview of the impacts of the 2010–2011 Canterbury earthquakes. Int. J. Disaster Risk Reduct. 2015, 14, 6–14. [Google Scholar] [CrossRef]
- Yariyan, P.; Karami, M.R.; Ali Abbaspour, R. Exploitation of mcda to learn the radial base neural network (rbfnn) aim physical and social vulnerability analysis versus the earthquake (case study: Sanandaj city, iran). Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019. [Google Scholar] [CrossRef]
- Pachauri, A.K.; Pant, M. Landslide hazard mapping based on geological attributes. Eng. Geol. 1992, 32, 81–100. [Google Scholar] [CrossRef]
- Chen, W.; Shahabi, H.; Shirzadi, A.; Li, T.; Guo, C.; Hong, H.; Li, W.; Pan, D.; Hui, J.; Ma, M. A novel ensemble approach of bivariate statistical-based logistic model tree classifier for landslide susceptibility assessment. GeoIn 2018, 33, 1398–1420. [Google Scholar] [CrossRef]
- Moslem, S.; Ghorbanzadeh, O.; Blaschke, T.; Duleba, S. Analysing Stakeholder Consensus for a Sustainable Transport Development Decision by the Fuzzy AHP and Interval AHP. Sustainability 2019, 11, 3271. [Google Scholar] [CrossRef]
- Theodoridou, P.; Varouchakis, E.; Karatzas, G. Spatial analysis of groundwater levels using Fuzzy Logic and geostatistical tools. J. Hydrol. 2017, 555, 242–252. [Google Scholar] [CrossRef]
- Negnevitsky, M.; Intelligence, A. Artificial Intelligence: A Guide to Intelligent Systems, 2nd ed.; Addison-Wesley Inc.: New York, NY, USA, 2005. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Mamdani, E.H. Application of fuzzy algorithms for control of simple dynamic plant. In Proceedings of the Institution of Electrical Engineers; IET: London, UK, 1974; pp. 1585–1588. [Google Scholar]
- Ghorbanzadeh, O.; Moslem, S.; Blaschke, T.; Duleba, S. Sustainable Urban Transport Planning Considering Different Stakeholder Groups by an Interval-AHP Decision Support Model. Sustainability 2018, 11, 9. [Google Scholar] [CrossRef]
- Duleba, S.; Moslem, S. Examining Pareto optimality in analytic hierarchy process on real Data: An application in public transport service development. Expert Syst. Appl. 2019, 116, 21–30. [Google Scholar] [CrossRef]
- Saaty, T.L. Relative measurement and its generalization in decision making why pairwise comparisons are central in mathematics for the measurement of intangible factors the analytic hierarchy/network process. RACSAM 2008, 102, 251–318. [Google Scholar] [CrossRef]
- Ghorbanzadeh, O.; Feizizadeh, B.; Blaschke, T. An interval matrix method used to optimize the decision matrix in AHP technique for land subsidence susceptibility mapping. Environ. Earth Sci. 2018, 77, 584. [Google Scholar] [CrossRef]
- Tang, A.; Wen, A. An intelligent simulation system for earthquake disaster assessment. Comput. Geosci. 2009, 35, 871–879. [Google Scholar] [CrossRef]
- Asghar Pour, M.J. Multi-Criteria Decision Making; University of Tehran Publications: Tehran, Iran, 2008. [Google Scholar]
- Ghorbanzadeh, O.; Feizizadeh, B.; Blaschke, T. Multi-criteria risk evaluation by integrating an analytical network process approach into GIS-based sensitivity and uncertainty analyses. Geomat. Nat. Hazards Risk 2018, 9, 127–151. [Google Scholar] [CrossRef]
- Saaty, L. An analytical hierarchy and network processes approach for the measurement in tangible criteria and for decision making; Multiple Criteria Decision, Analysis: State of The Art Surveys, Edited by Jose Figueira et. al. State Art Surv. 2005, 345–406. [Google Scholar] [CrossRef]
- Saaty, T.L. Fundamentals of the analytic network process. In Proceedings of the 5th International Symposium on the Analytic Hierarchy Process, Kobe, Japan, 12–14 August 1999; pp. 12–14. [Google Scholar]
- Zebardast, E. Constructing a social vulnerability index to earthquake hazards using a hybrid factor analysis and analytic network process (F’ANP) model. Nat. Hazards 2013, 65, 1331–1359. [Google Scholar] [CrossRef]
- Yager, R.R. On ordered weighted averaging aggregation operators in multicriteria decisionmaking. IEEE Trans. Syst. Man Cybern. 1988, 18, 183–190. [Google Scholar] [CrossRef]
- Malczewski, J. GIS and Multicriteria Decision Analysis; John Wiley & Sons: Hoboken, NJ, USA, 1999. [Google Scholar]
- Liu, X.; Han, S. Orness and parameterized RIM quantifier aggregation with OWA operators: A summary. Int. J. Approx. Reason. 2008, 48, 77–97. [Google Scholar] [CrossRef]
- Shafapour Tehrany, M.; Shabani, F.; Neamah Jebur, M.; Hong, H.; Chen, W.; Xie, X. GIS-based spatial prediction of flood prone areas using standalone frequency ratio, logistic regression, weight of evidence and their ensemble techniques. Geomat. Nat. Hazards Risk 2017, 8, 1538–1561. [Google Scholar] [CrossRef]
- Ayalew, L.; Yamagishi, H. The application of GIS-based logistic regression for landslide susceptibility mapping in the Kakuda-Yahiko Mountains, Central Japan. Geomorphology 2005, 65, 15–31. [Google Scholar] [CrossRef]
- Wright, R.E. Logistic regression. In Reading and Understanding Multivariate Statistics; Grimm, L.G., Yarnold, P.R., Eds.; American Psychological Association: Washington, DC, USA, 1995; pp. 217–244. [Google Scholar]
- Avand, M.; Janizadeh, S.; Naghibi, S.A.; Pourghasemi, H.R.; Khosrobeigi Bozchaloei, S.; Blaschke, T. A comparative assessment of Random Forest and k-Nearest Neighbor classifiers for gully erosion susceptibility mapping. Water 2019, 11, 2076. [Google Scholar] [CrossRef]
- Shahabi, H.; Jarihani, B.; Tavakkoli Piralilou, S.; Chittleborough, D.; Avand, M.; Ghorbanzadeh, O. A Semi-Automated Object-Based Gully Networks Detection Using Different Machine Learning Models: A Case Study of Bowen Catchment, Queensland, Australia. Sensors 2019, 19, 4893. [Google Scholar] [CrossRef]
- Achour, Y.; Pourghasemi, H.R. How do machine learning techniques help in increasing accuracy of landslide susceptibility maps? Geosci. Front. 2019. [Google Scholar] [CrossRef]
- Jaafari, A.; Zenner, E.K.; Panahi, M.; Shahabi, H. Hybrid artificial intelligence models based on a neuro-fuzzy system and metaheuristic optimization algorithms for spatial prediction of wildfire probability. Agric. For. Meteorol. 2019, 266, 198–207. [Google Scholar] [CrossRef]


| Row | Fault Name | Fault Type | Fault Length (Km) | Minimum Distance from the Site (km) | Maximum Distance from the Site (km) |
|---|---|---|---|---|---|
| 1 | Morvarid | strike-slip fault | 23 | 29 | 43 |
| 2 | Sartakht | strike-slip fault | 75 | 39 | 71 |
| 3 | Piranshahr | strike-slip fault | 149 | 34 | 150 |
| 4 | Dinoor | strike-slip fault | 52 | 66 | 111 |
| 5 | Sahneh | strike-slip fault | 47 | 103 | 150 |
| 6 | Nahavand | strike-slip fault | 16 | 133 | 150 |
| 7 | Zagros | Rivers fault | 250 | 91 | 150 |
| 8 | Garun | strike-slip fault | 47 | 133 | 138 |
| 9 | Takht soleaman | strike-slip fault | 30 | 130 | 150 |
| Unit | Description | Percent |
|---|---|---|
| k2av | Andesite volcano | 1 |
| kpef | Limestone and conglomerate | 1 |
| kupl | Limestone | 8 |
| kussh | Dark gray hose and Sandstone | 68 |
| peEf | Sandstone and calcareous ash | 2 |
| Qft2 | Quaternary formation | 20 |
| Operator | Mathematical Expression |
|---|---|
| X AND Y | Min (X, Y) |
| X OR Y | Max (X, Y) |
| not X | 1-X |
| Definition | The Intensity of Relative Importance |
|---|---|
| Extremely Preferred | 9 |
| Very strongly Preferred | 7 |
| Strongly Preferred | 5 |
| Moderately Preferred | 3 |
| Equally Preferred | 1 |
| Intermediate Values Between | 2, 4, 6, 8 |
| Group | Factors | Class | Pixels in Domain | Percentage of Domain | Weight of AHP-ANP | Eigenvalue AHP-ANP |
|---|---|---|---|---|---|---|
| Physical | Area | <100 | 2549 | 0.60 | 0.05945 | 0.006 |
| 100–200 | 341,103 | 80.72 | 0.807 | |||
| 200–300 | 9554 | 2.26 | 0.023 | |||
| 300–400 | 27331 | 6.47 | 0.065 | |||
| 400< | 42051 | 9.95 | 0.100 | |||
| Inappropriate materials | <20 | 2549 | 0.60 | 0.05944 | 0.006 | |
| 20–40 | 390,554 | 92.42 | 0.924 | |||
| 40–60 | 21947 | 5.19 | 0.052 | |||
| 60–80 | 6281 | 1.49 | 0.015 | |||
| 80< | 1257 | 0.30 | 0.003 | |||
| Land use | Group 1 | 2698 | 0.64 | 0.07825 | 0.006 | |
| Group 2 | 6532 | 1.55 | 0.015 | |||
| Group 3 | 4909 | 1.16 | 0.012 | |||
| Group 4 | 314,582 | 74.44 | 0.744 | |||
| Group 5 | 93867 | 22.21 | 0.222 | |||
| Distance from hospital | <1000 | 2613 | 0.62 | 0.06863 | 0.006 | |
| 1000–2000 | 115,241 | 27.27 | 0.273 | |||
| 2000–3000 | 154,422 | 36.54 | 0.365 | |||
| 3000–4000 | 85,553 | 20.25 | 0.202 | |||
| 4000< | 64759 | 15.32 | 0.153 | |||
| Distance from fire station | <1300 | 2613 | 0.62 | 0.06889 | 0.006 | |
| 1300–2400 | 88,341 | 20.90 | 0.209 | |||
| 2500–3600 | 89,141 | 21.09 | 0.211 | |||
| 3700–4800 | 97,463 | 23.06 | 0.231 | |||
| 4800< | 145,030 | 34.32 | 0.343 | |||
| Number of floors | 1 Floor | 320,809 | 75.92 | 0.06866 | 0.759 | |
| 2 Floor | 32,503 | 7.69 | 0.077 | |||
| 3 Floor | 46,257 | 10.95 | 0.109 | |||
| 4 Floor | 16,548 | 3.92 | 0.039 | |||
| 5 Floor | 6471 | 1.53 | 0.015 | |||
| Distance from the Street | <100 | 2578 | 0.61 | 0.06054 | 0.006 | |
| 100–200 | 27,649 | 6.54 | 0.065 | |||
| 200–300 | 15,473 | 3.66 | 0.037 | |||
| 300–400 | 30,891 | 7.31 | 0.073 | |||
| 400< | 345,997 | 81.88 | 0.819 | |||
| Environmental | Altitude | <1400 | 2560 | 0.61 | 0.03929 | 0.006 |
| 1400–1500 | 13124 | 3.11 | 0.031 | |||
| 1500–1600 | 175,334 | 41.49 | 0.415 | |||
| 1600–1700 | 182,582 | 43.21 | 0.432 | |||
| 1700< | 48,988 | 11.59 | 0.116 | |||
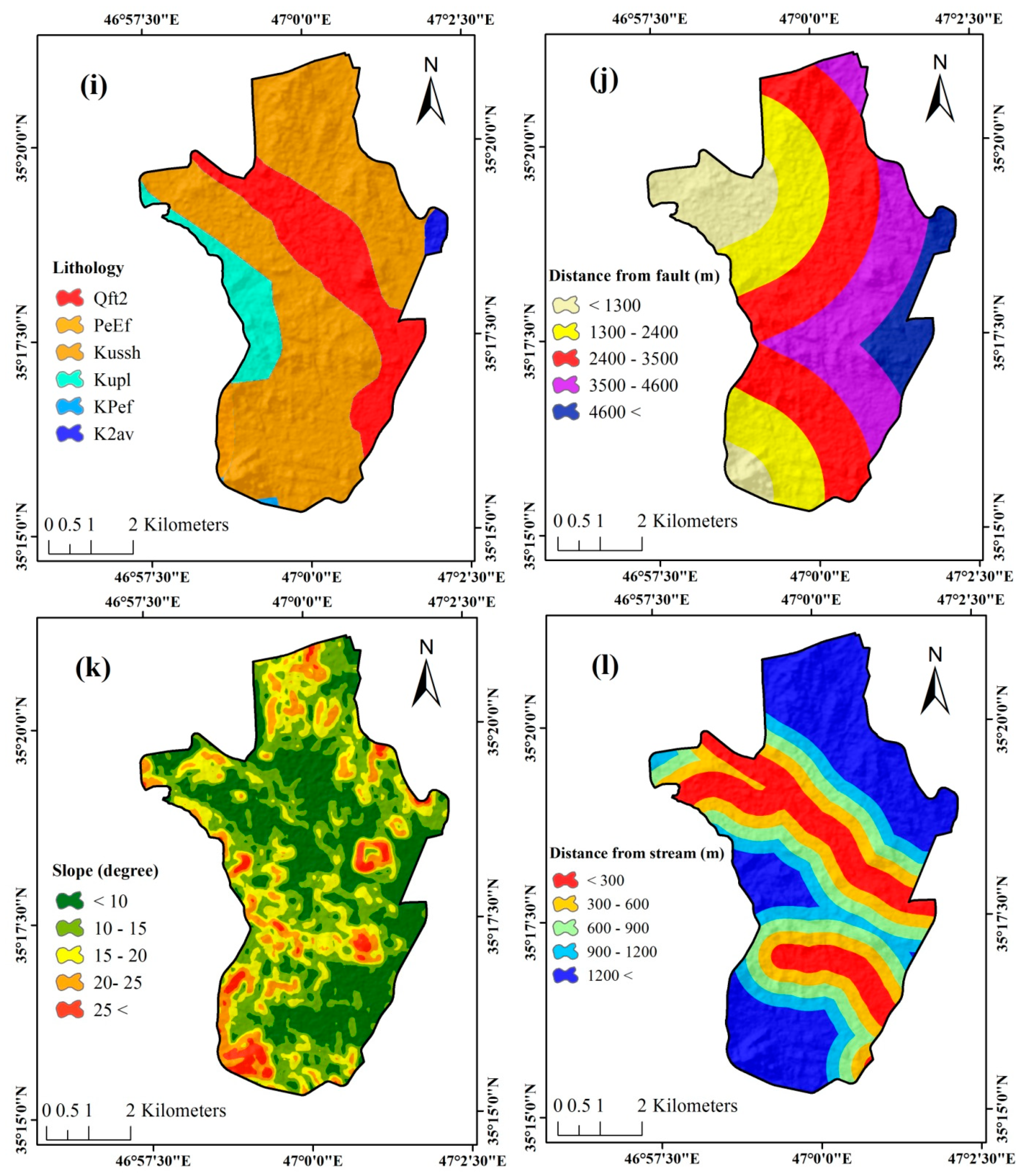
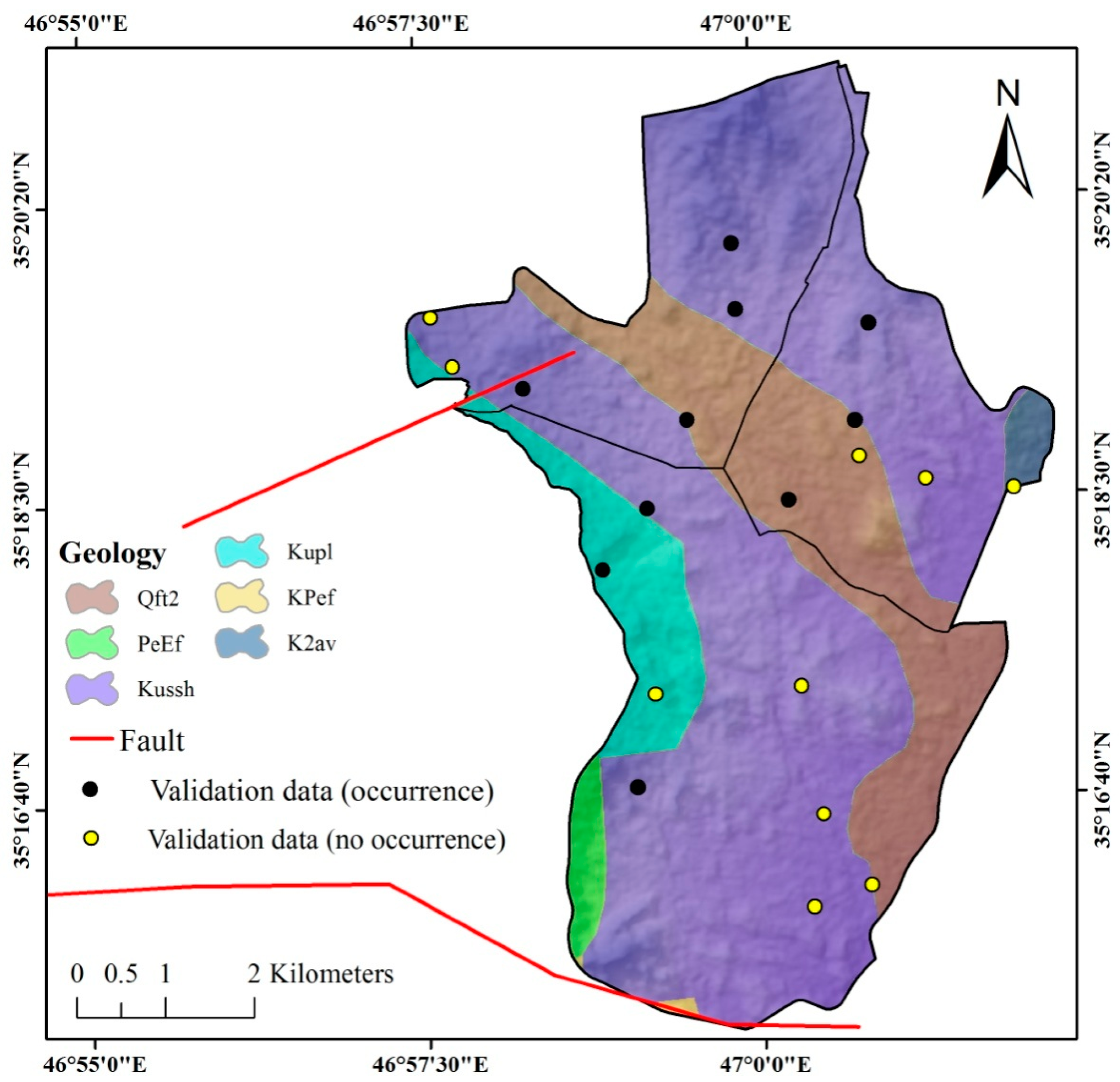
| Lithology | K2av | 1484 | 0.35 | 0.07935 | 0.004 | |
| Kupl | 4601 | 1.09 | 0.011 | |||
| Kussh | 33,517 | 7.93 | 0.079 | |||
| PeEf | 288,315 | 68.23 | 0.682 | |||
| Qft2 | 94,671 | 22.40 | 0.224 | |||
| Distance from Fault | <1300 | 2549 | 0.60 | 0.08766 | 0.006 | |
| 1300–2400 | 56,655 | 13.41 | 0.134 | |||
| 2400–3500 | 100,967 | 23.89 | 0.239 | |||
| 3500–4600 | 113,184 | 26.78 | 0.268 | |||
| 4600< | 149,233 | 35.31 | 0.353 | |||
| Slope | <10 | 2560 | 0.61 | 0.04609 | 0.006 | |
| 10–15 | 32850 | 7.77 | 0.078 | |||
| 15–20 | 149,963 | 35.49 | 0.355 | |||
| 20–25 | 118,412 | 28.02 | 0.280 | |||
| 25 < | 118,803 | 28.11 | 0.281 | |||
| Distance from stream | < 300 | 2558 | 0.61 | 0.06054 | 0.006 | |
| 300–600 | 322,256 | 76.26 | 0.763 | |||
| 600–900 | 47,553 | 11.25 | 0.113 | |||
| 900–1200 | 24,051 | 5.69 | 0.057 | |||
| 1200< | 26,170 | 6.19 | 0.062 | |||
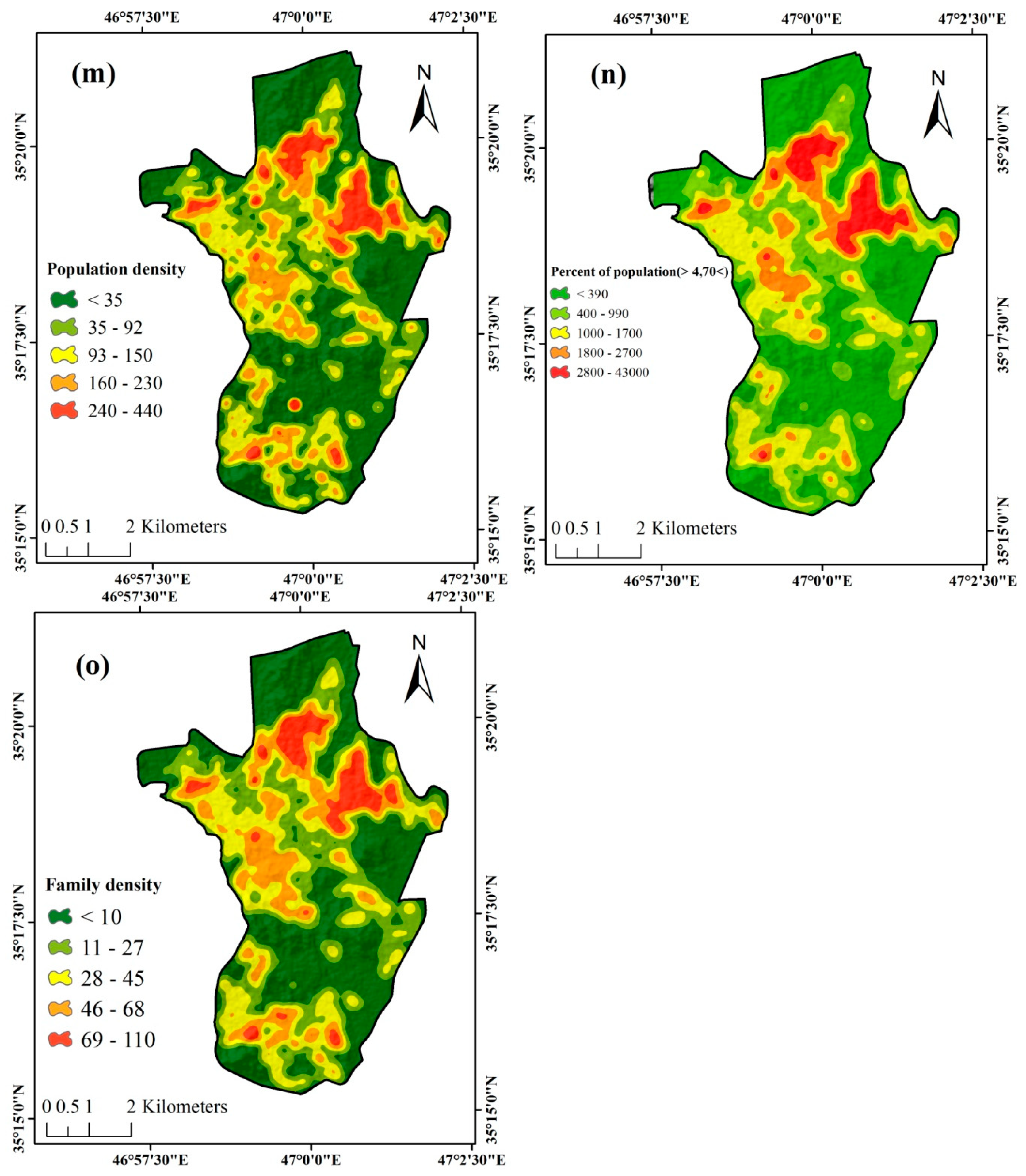
| Social | Population density | <35 | 2549 | 0.60 | 0.08810 | 0.006 |
| 35–92 | 193,194 | 45.72 | 0.457 | |||
| 93–150 | 77,680 | 18.38 | 0.184 | |||
| 160–230 | 71,061 | 16.82 | 0.168 | |||
| 240–440 | 78,104 | 18.48 | 0.185 | |||
| Percent of population | <390 | 2549 | 0.60 | 0.07809 | 0.006 | |
| 400–990 | 160,639 | 38.01 | 0.380 | |||
| 1000–1700 | 107,761 | 25.50 | 0.255 | |||
| 1800–2700 | 90,444 | 21.40 | 0.214 | |||
| 2800–43000 | 61,195 | 14.48 | 0.145 | |||
| Family density | <10 | 2708 | 0.64 | 0.04879 | 0.006 | |
| 11–27 | 212,088 | 50.19 | 0.502 | |||
| 28–45 | 107,093 | 25.34 | 0.253 | |||
| 46–48 | 63,093 | 14.93 | 0.149 | |||
| 69–110 | 37,606 | 8.90 | 0.089 |
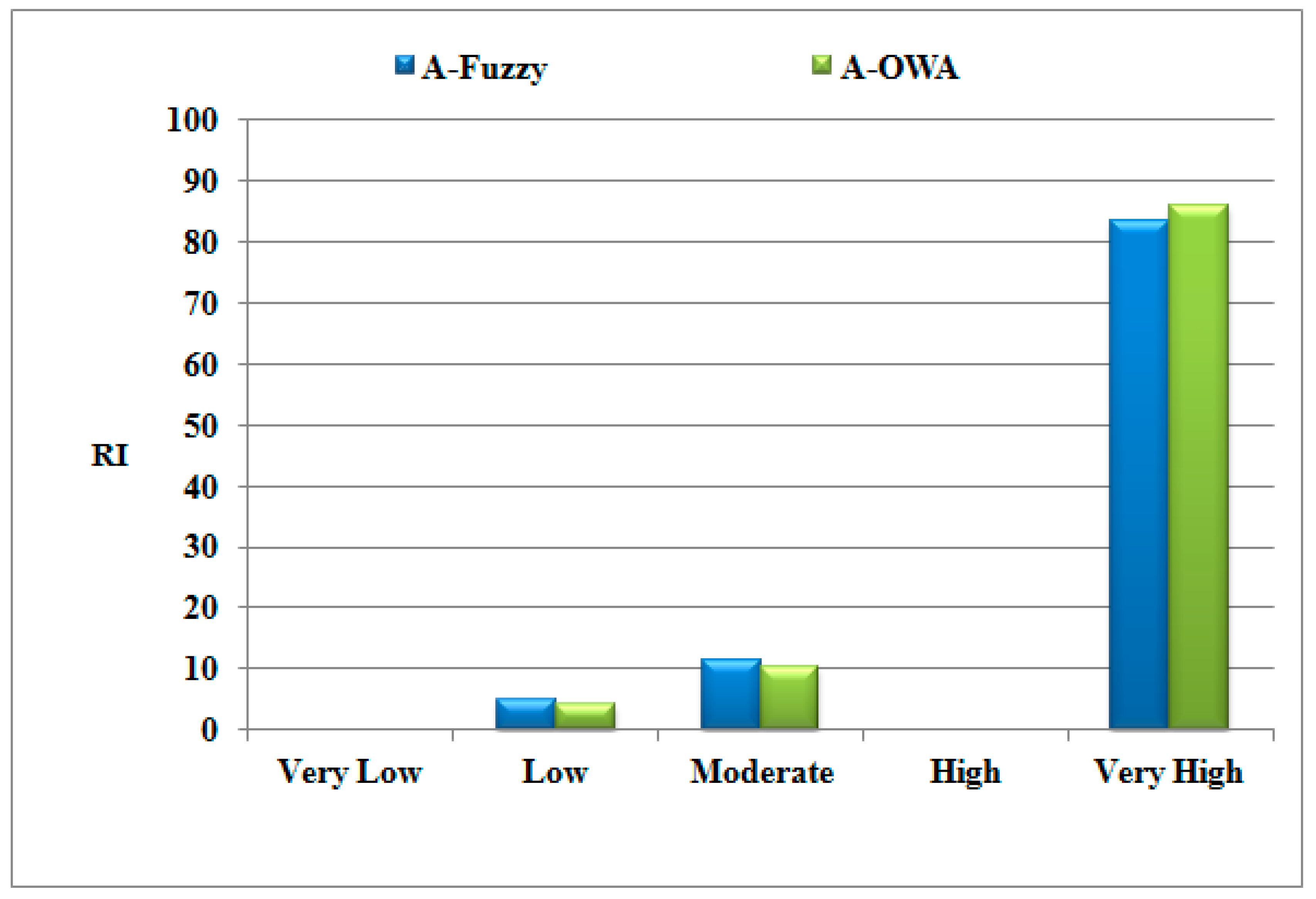
| Hybrid Model | Class | Pixel | pi | SV (Occurrence) | Pi | RI |
|---|---|---|---|---|---|---|
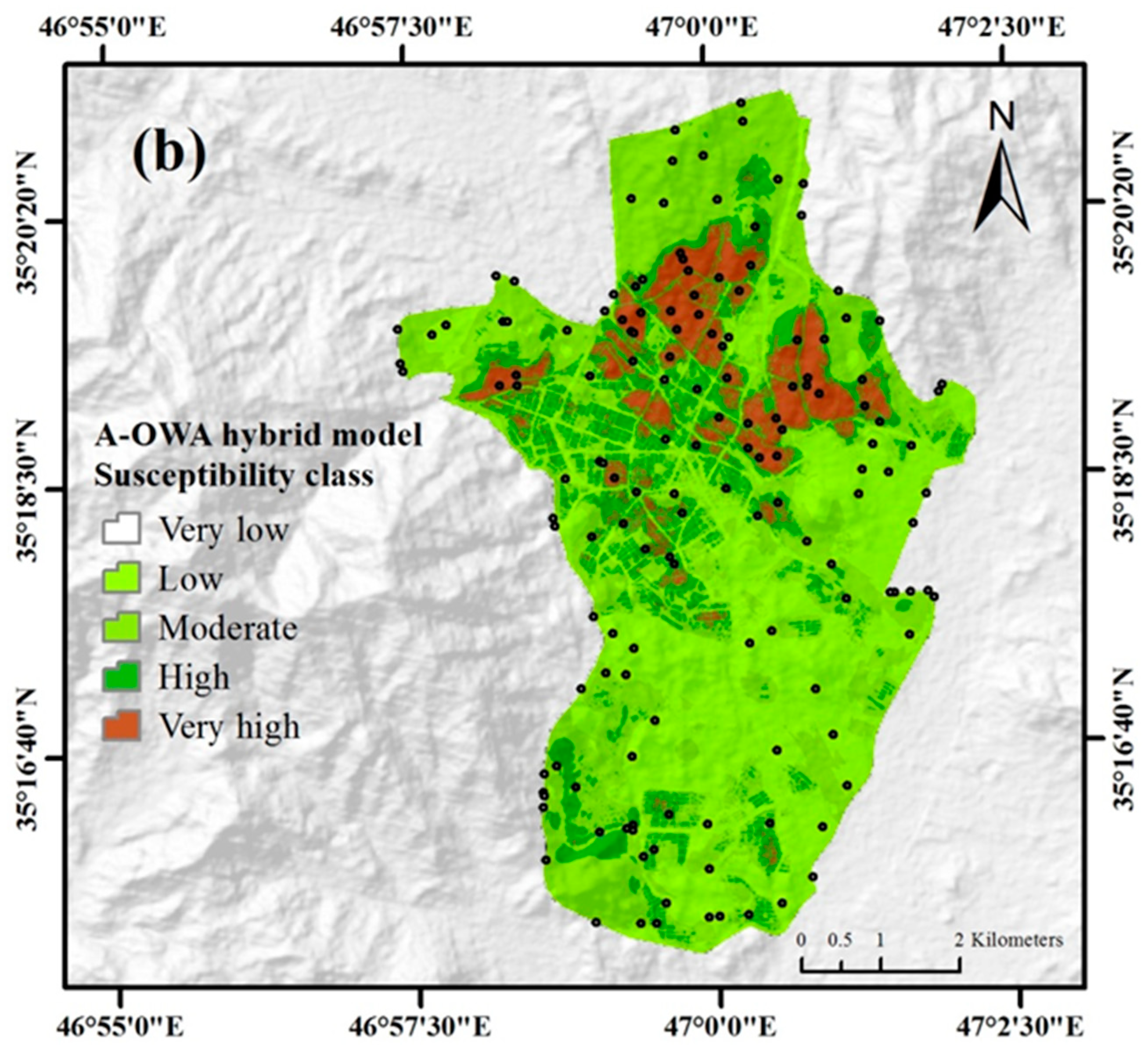
| A-OWA | Very Low | 2553 | 0.60 | 0 | 0.00 | 0 |
| Low | 136,693 | 32.35 | 1 | 10.00 | 4 | |
| Moderate | 165,176 | 39.09 | 3 | 30.00 | 10 | |
| High | 79,187 | 18.74 | 0 | 0.00 | 0 | |
| Very High | 38979 | 9.22 | 6 | 60.00 | 86 | |
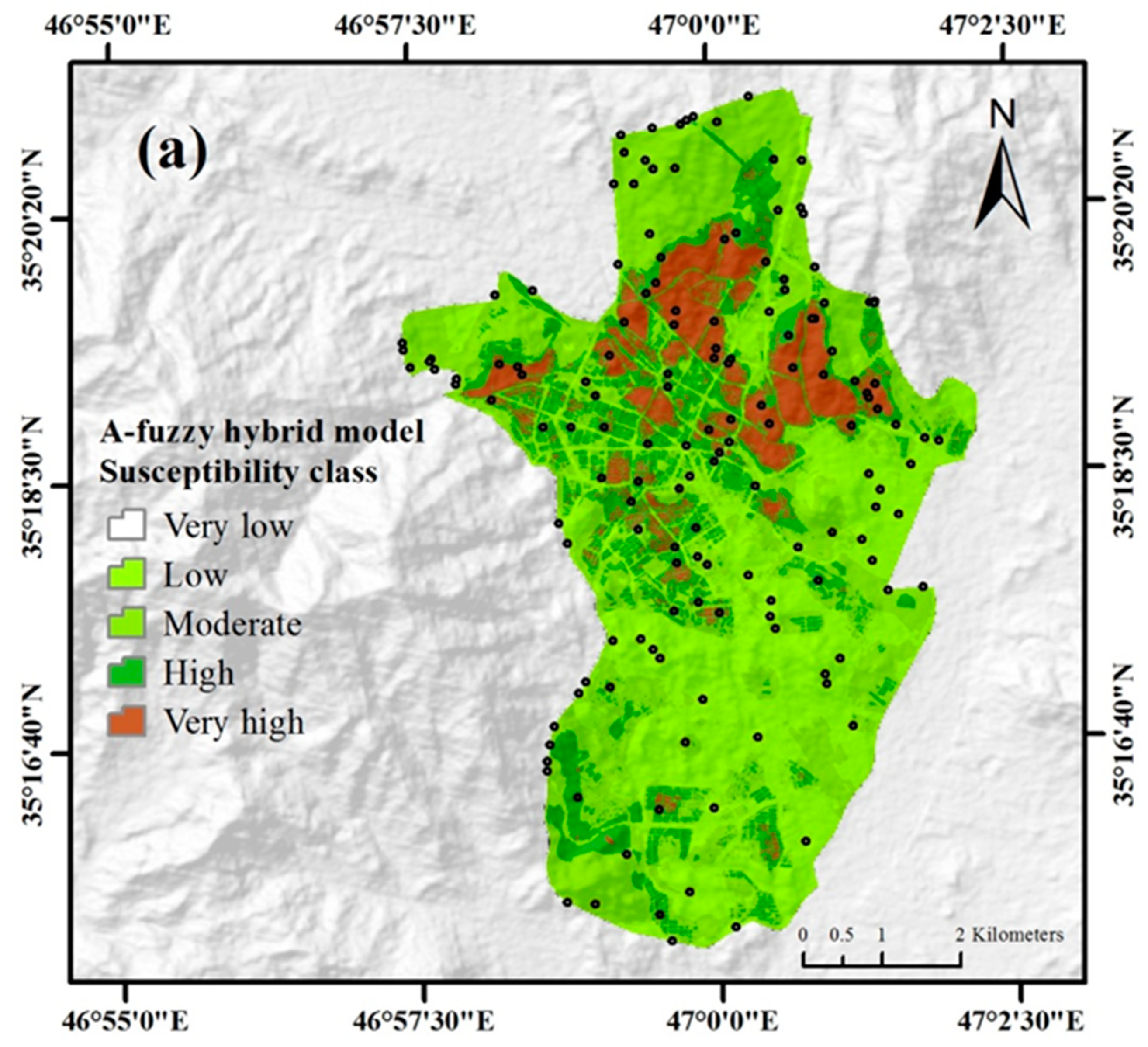
| A-fuzzy | Very Low | 2551 | 0.60 | 0 | 0.00 | 0 |
| Low | 125,175 | 29.62 | 1 | 10.00 | 5 | |
| Moderate | 165,388 | 39.14 | 3 | 30.00 | 11 | |
| High | 84,126 | 19.91 | 0 | 0.00 | 0 | |
| Very High | 45,348 | 10.73 | 6 | 60.00 | 84 |
| Hybrid Model | AUC | Std. Error | Confidence Interval (95%) | |
|---|---|---|---|---|
| Lower | Upper | |||
| A-fuzzy | 0.805 | 0.0966 | 0.569 | 0.945 |
| A-OWA | 0.855 | 0.0830 | 0.627 | 0.970 |
| Fuzzy-LR | 0.850 | 0.0872 | 0.621 | 0.968 |
| OWA-LR | 0.9 | 0.0667 | 0.683 | 0.988 |
| Hybrid Model | Class | No. Pixels in Domain | Percentage of Domain | No. of SV | Percentage of SV | FR |
|---|---|---|---|---|---|---|
| Fuzzy-LR | Very Low | 20,068 | 4.75 | 0 | 0 | 0 |
| Low | 113,849 | 26.94 | 2 | 10 | 2.20 | |
| Moderate | 75,272 | 17.81 | 2 | 10 | 3.32 | |
| High | 140,599 | 33.27 | 0 | 0 | 0.00 | |
| Very high | 72,800 | 17.23 | 6 | 30 | 10.30 | |
| OWA-LR | Very Low | 15,254 | 3.61 | 0 | 0 | 0.00 |
| Low | 169,861 | 40.20 | 1 | 5 | 0.74 | |
| Moderate | 105,310 | 24.92 | 2 | 10 | 2.37 | |
| High | 59,440 | 14.07 | 0 | 0 | 0.00 | |
| Very high | 72,723 | 17.21 | 7 | 35 | 12 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yariyan, P.; Avand, M.; Soltani, F.; Ghorbanzadeh, O.; Blaschke, T. Earthquake Vulnerability Mapping Using Different Hybrid Models. Symmetry 2020, 12, 405. https://doi.org/10.3390/sym12030405
Yariyan P, Avand M, Soltani F, Ghorbanzadeh O, Blaschke T. Earthquake Vulnerability Mapping Using Different Hybrid Models. Symmetry. 2020; 12(3):405. https://doi.org/10.3390/sym12030405
Chicago/Turabian StyleYariyan, Peyman, Mohammadtaghi Avand, Fariba Soltani, Omid Ghorbanzadeh, and Thomas Blaschke. 2020. "Earthquake Vulnerability Mapping Using Different Hybrid Models" Symmetry 12, no. 3: 405. https://doi.org/10.3390/sym12030405
APA StyleYariyan, P., Avand, M., Soltani, F., Ghorbanzadeh, O., & Blaschke, T. (2020). Earthquake Vulnerability Mapping Using Different Hybrid Models. Symmetry, 12(3), 405. https://doi.org/10.3390/sym12030405