Abstract
In this paper, the effect of Magneto Hydro-Dynamics (MHD) on a polymer chain in the micro channel is studied by employing the Dissipative Particle Dynamics simulation (DPD) method. First, in a simple symmetric micro-channel, the results are evaluated and validated for different values of Hartmann (Ha) Number. The difference between the simulation and analytical solution is below 10%. Then, two types of polymer chain including short and long polymer chain are examined in the channel and the effective parameters such as Ha number, the harmony bond coefficient or spring constant (K), and the length of the polymer chain (N) are studied in the MHD flow. It is shown that by increasing harmony bond constant to 10 times with Ha = 20, the reduction of about 80% in radius of gyration squared, and half in polymer length compared to Ha = 1 would occur for both test cases. For short and long length of polymer, proper transfer of a polymer chain through MHD particles flow is observed with less perturbations (80%) and faster polymer transfer in the symmetric micro-channel.
1. Introduction
Understanding the behavior of polymer chains in micro/nano-scale flows is an important issue, as it is the gateway to different scientific and technological research activities in different fields of study such as biology, genetics, etc. The translocation of polymers through nano/micro-scale passages is encountered in many biological processes in living cells or chemical processes such as DNA (Deoxyribonucleic acid) motion through narrow pores, protein translocation through cell membranes, and penetration of viruses into the cell nucleus. Knowledge of such processes can be beneficial in developing some technical analysis procedures concerning genomic partitioning and rapid DNA sequencing [1,2,3]. There are several ways to transfer polymer through narrow pores or micro channel including electroosmotic micro pump, magneto hydrodynamic method, and pressure driven flow [3]. Due to high controllability on fluid flow using electrical field or magnetic field, they are proper methods for fluid pumping [3,4].
The difficulties and costs associated with the experimental studies promote the researchers to use the computational simulation methods as the preliminary design and analysis tools to narrow down the design parameters’ envelopes before getting into the actual manufacturing process. Regarding the small scale of simulated systems, molecular simulation methods would be the best choices. Such simulation methods have been successfully applied to different nano-scale flow problems. Researches have used different numerical simulation methods such as computational fluid dynamics [5,6,7], molecular dynamics [8], Langevin dynamics [9,10], and Brownian dynamics [11] to study prediction of polymer chains behavior in fluid flows. Based on the Lagrangian methods such as Molecular Dynamics [12,13,14,15], lattice Boltzmann method [16,17] or smoothed particle hydrodynamics method [18,19,20,21], the dissipative particle dynamics (DPD) method is a mesoscopic method [12,13,22] which has been vastly used in micro/nano-scale simulations. It benefits from the lower computational cost compared with the molecular dynamics method via using the clusters of molecules, known as beads, instead of considering all actual molecules.
There are several studies in relation of DPD and polymer chain motion in nano/micro flows. Zhang and Manke [23] used the DPD method to study the motion of polymers and polymer solutions rheology in the spherical particles with adsorbed polymers. They found that Newtonian behavior is governing on polymer solutions or polymer in sphere suspensions at low shear rates, but shear-thinning behavior is formed at higher shear rates. Willemsen et al. [24] used the DPD method to investigate the motion of a polymer within a square capillary and the effect of polymers on melting process in a shear flow. Pastorino et al. [25] compared the dynamics of Langevin and DPD as a thermostat term in non-equilibrium simulations of polymeric systems. They studied polymer brushes in different systems including the relative sliding motion, Poiseuille and Couette flows of polymeric liquids, and brush-melt interfaces to compare these two different thermostats. Based on the DPD method, Duong-Hong et al. [26] introduced an electrophoresis model for DNA, which they simulated the coupled DNA electro-osmotic and electrophoretic motion in micro/nano-scale passages. Using this model, they were able to capture the free-draining mobility of DNA while avoiding the expensive electrostatic interactions in the molecular simulations. They also computed DNA mobilities in realistic geometries with a good accuracy. Their results indicated that the Ti-channel has a better separating performance than the Tp-channel. Pan et al. [27] used the DPD method to study the DNA separation in a micro-device using an entropic trapping mechanism. They showed that longer DNA strands have a higher speed than shorter ones. They concluded that the entropic trapping is the consequence of delayed entrance. Moreover, they concluded that corner trapping does not contribute to DNA separation. Masoud and Alexeev [28] used the DPD method to design nano-structured surfaces capable of selective regulation of collision between microchannel walls and polymer, which is suspended in fluid though the microchannel. By utilizing different geometries for nanoscopic posts attached to the internal channel surfaces, they could attract the suspended nanoparticles and polymeric chains to the walls or repel them. Guo et al. [29] studied the translocation of polymers in fluid through a microchannel using the DPD method. They predicted the relation between shear stress and length of polymer chain for the average translocation time. Moreover, they observed two different mechanisms for translocation including single-file and double-folded translocation. They also mentioned the possibility of clogging at the entrance of the channel for polymers longer than a critical length.
All of the mentioned studies used pressure driven flow for transfer of polymer through microchannel. However, lack of studies in the area of different body forces are observed. Yang et al. [30] studied the motion of a polymer chain through a hole using DPD method. They considered two different driving forces, namely the uniform hydrostatic force implemented to whole solvent particles and polymer chains, and also uniform electrostatic force which is employed as a body force, applied to selected charged particles in the chain and some ions in the solvent which were charged oppositely. They found that the power-law correlations should be used for coil-like chains and it is not proper for globular chains. Ranjith et al. [31] used the DPD method to investigate the effect of finite slip at hydrophobic microchannel walls on the hydrodynamics and the dynamics of the DNA chain. They showed that an asymmetric velocity profile caused by hydrophobic and hydrophilic walls can affect the location of the DNA molecules. They used this effect to propose a simple arrangement for separation of short and long DNA chains. Zakeri [32] used the DPD method to simulate the performance of a soft polymer micro-actuator in electro-osmotic flow in a simple micro-channel and a convergent–divergent one. The results indicated that the amplitude of reciprocating motion of polymer increases as the electric field is enhanced, the number of beads is decreased, the spring constant is increased, or more length of a polymer chain is exposed against the fluid flow motion.
A thorough review on the literature shows that there were studies in which the electrical field is used as the transport driving force for polymer chains, e.g., [26,32,33]. Base on the Zakeri [32,34], electroosmotic is a proper external force to move DPD particles in a micro channel, However, the transport of polymer chains using the magnetic forces is not regarded frequently. Magnetic force [35,36] is also another body force capable of inducing fluid flow. This driving force plays an important role in micro pumps (e.g., see [37,38,39,40,41,42]). Kefayati [43] employed LBM method to simulate the effect of MHD flow in a lid-driven cavity problem for various Hartman numbers. Ghahderijani [44] used LBM method to simulate MHD flow in simple micro channels. Javaherdeh and Najjarnezami [45] used LBM to investigate natural convection in a porous cavity with sinusoidally heated walls considering the effects of magnetic field. They investigated the effects of Hartmann number, porosity and Darcy number on the fluid flow, and heat transfer. Chaabane and Jemni [46] used the LBM to study the convection heat transfer in a 2D enclosure containing a conductive fluid. They examined the effects of Hartmann number, Rayleigh number, Prandtl number on the flow, and temperature fields. Although LBM is a proper simulation method in microscale, the freedom degree of DPD method is higher and it treats more realistically based on the real physics of particles interaction [17,47]. Based on the several references [32,34], the effect of polymer chain from electroosmotic flow was presented, but polymer transfer from in MHD flow requires more investigation.
In this paper, the DPD simulation method is employed to simulate MHD flow in simple symmetric micro channel, also the motion of a polymer chain through micro channel is studied to investigate the various physical properties of polymer chain influenced from MHD flow.
2. Numerical Simulation
To present the simulation of MHD in micro channels which affects the polymer chain transfer through fluid particles, we discuss in the three main subjects in the Section 2.1, Section 2.2 and Section 2.3, including the magneto-hydrodynamics equations, the details of DPD method, and the molecular model of polymer chain.
2.1. Magneto-Hydrodynamics
Magneto-Hydro-Dynamics (MHD) equations consist of equations of electromagnetics and hydrodynamics. Electromagnetics equation relates the current density J to the magnetic field strength H [48,49,50].
In the case that the substance such as fluid has a velocity, J is calculated as follows:
where is the electrical conductivity, is the velocity of flow, is the magnetic permeability, and is the electric field intensity. The body force or external force which will be used in DPD equations, Section 2.2 (as hydrodynamic equations) is calculated as follows:
2.1.1. Analytical Solution for MHD in Simple Channel
By using the source term calculated in Equation (4) in the steady equation of fluid motion, applying the assumption of uniform conductivity of liquid between two parallel walls (simple channel), implementing perpendicular to the walls in z-direction while implementing E in y-direction, and ignoring the gravity effect, a fluid motion should occur in x-direction satisfying the following momentum equation [47,51].
where is pressure term, is the dynamic viscosity, and .
Substituting the in Equation (5) and assuming that velocity is zero at the walls and shear stress is zero at the middle of channel, would result in the following solution of MHD flow in the simple channel.
where, and .
If the parameter varies while the other parameters are kept constant, the value of Ha (or Hartmann number) will change linearly. Hartmann number or Ha is the ratio of magnetic force to viscous force.
If we assume that = 1 then and .
2.2. Dissipative Particle Dynamics Method
The DPD method treats the simulated system as a cloud of beads each having the mass, , position vector , and velocity vector . The evolution of beads’ velocity vectors follows the basic kinematic and dynamic laws of motion [47].
The net force exerted on bead i and , can be decomposed in two parts, namely the force exerted by an external force-field like gravitational, electrical, or magnetic fields, and the intermolecular forces exerted by polymer and fluid particles :
In DPD method, it is assumed that the intermolecular force exerted by bead j on bead i and , consists of three parts, namely the conservative force, the dissipative force, and the random force [52].
Of course, would be equal to , as the third law of motion indicates. is the external force such a electro-osmotic force or magnetic force [32].
The conservative force can be described using the following force filed:
where is the maximum repulsion force between beads i and j, is the distance between those beads, i.e., , and is the unit vector pointing from bead j to bead i, and is the cut-off radius beyond which, the intermolecular forces are assumed to diminish effectively.
The dissipative intermolecular force is calculated as follows:
where is a constant that determines the strength of dissipative force. The weighting function is calculated as follows:
On the other hand, the random force is calculated as follows:
in which, the constant determines the strength of random force. is the relative velocity vector between beads i and j. is a random number chosen from a symmetric Gaussian distribution having the zero mean and unit variance. and relate to and as follows:
where is the Boltzmann constant and is the temperature.
In this study, the modified velocity-Verlet algorithm is used for time integration of position and velocity of each particle is calculated explicitly. The Ref. [53] is suggested for more information. Implementation of wall boundary condition has been follow based on the ref [48,54,55,56].
2.3. Polymer Chain
Polymer chain model consists of a number of masses and springs which are connected together. The mechanism of polymer chain motion influenced from interaction of fluid particles and polymer beads is depicted in Figure 1. According to number of different types of particles, we have different interactions. In this case, we have three types of interactions, including fluid to fluid particles, polymer and fluid, and polymer and polymer beads interactions. Each mass has its own repulsion force to fluid particles or other masses. Thus, the conservative force Fc should be modified for this type of simulation. In this paper, the harmonic spring force, , or is used between beads which is added to Fc in DPD formulation. For the beads consisting a polymer chain, the following conservative harmonic force presents the intermolecular bonds [32,34,53].
where is the equilibrium (zero-force) distance between two beads in the polymer chain and K is the harmonic bond constant.
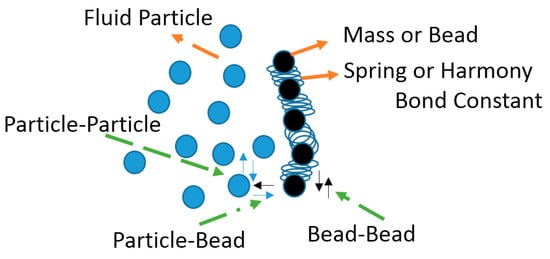
Figure 1.
Mechanism of polymer and fluid particles interaction and motion of polymer chain.
Due to difficulty of studying the properties of polymer chain in motion, some physical properties such as mean square radius of gyration and velocity of mass center are employed for finding effect of MHD on polymer chain motion.
In equilibrium, the radius of gyration is defined as [30,51]:
where, and N is the number of beads of polymer chain. The end to end distance (Ee) is defined as . Also, the center of mass velocity of system is calculated as follows:
where is the mass of bead i. Also, the average kinetic temperature is calculated as follows [51].
where n is the number of particles.
3. Results
In this section, the results of numerical simulations of MHD flow in micro channel are presented regarding the polymer chain motion under the influence of magnetic field (MHD flow) using DPD method. We developed our DPD code for current simulation. First, the DPD results for the simple channel flow with the results of the analytical solution are compared to evaluate the accuracy of suggested method for this type of simulation. Then, the study by embedding the polymer chain in a simple channel is extended to study the effect of MHD flow on polymer chain and the related motion characteristics. Different conditions have been considered including changing the magnetic field or Ha-value, spring constant (harmonic bond constant of polymer), or K parameter and the number of polymer beads in the polymer chain.
3.1. Validation of MHD-DPD Results with Analytical Solution
In order to evaluate and validate the results, the simple microchannel flow under external force of magnetic field is simulated. The simulation parameters are presented in Table 1, Table 2 and Table 3. The analytical velocity profiles are also calculated in accordance with Equation (6) in Section 2.1.1 with the assumption of . As can be seen in Figure 2 (left), by increasing the value of parameter Ha Number, dimensionless velocity profiles not only increase to a certain extent in terms of value, but they also flatten more in plug like shape and tend to remain constant thereafter. For example, there is a dramatic change of about 80% for maximum value of dimensionless velocity when the value Ha Number is increased from 1.0 to 2.0. However, the changes are much less evident from Ha = 10 to Ha = 20. For a better study of variation of MHD flow, the dimensionless average velocity of particles in channel considering different values of Ha is compared with the analytical calculation in Figure 2 (right). As it is expected, increasing the value of Ha, the differences would decrease remarkably and would approach the constant value of unity. Also, the results show a proper agreement with the analytical results. The range of discrepancy between DPD solution and analytical solution is between 3% to 7%. The level of accuracy depends on time steps and number of iterations. Therefore, the parameter of Ha number is a suitable criterion for studying the velocity profile behavior in micro-channels and DPD method is a proper method for this type of fluid simulation.

Table 1.
Setting parameters for particles of DPD.

Table 2.
Setting parameters for polymer chain.

Table 3.
Setting parameters for magnetic parameter.
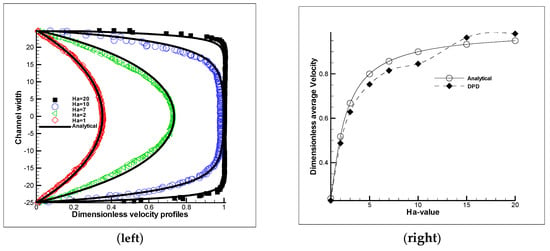
Figure 2.
Comparison of dimensionless velocity profiles of DPD particles (left) and dimensionless average velocities (right) with analytical results under influence of MHD in simple channel by changing values of Ha.
3.2. Short Polymer Chain Transfer in MHD Flow
In order to extend the results to the case of polymer translocation in microchannel, the movement of a short no charge polymer chain consisting of 20 beads in a microchannel has been analyzed under influence of MHD flow. Figure 3 illustrates the movement of the polymer chain under different magnetic field strengths (or Ha-values) as well as different polymer harmonic bond coefficients (or spring constants), considering periodic boundary condition at inlet/outlet boundaries. As can be observed, by increasing the Ha values from 1 to Ha = 20, the relative movement of the short polymer would be more with respect to the hardness coefficient (spring constant) of 500. It has been simulated that conspicuous differences in x-direction for the cases of Ha = 1 and 20 with the harmonic bond constant of K = 500 (red lines with circular symbol and blue lines with diamond symbol) is occurred compared to the cases of K = 5000 (green lines with triangle symbols and black lines with gradient symbols). By increasing the harmonic bond constant from 500 to 5000 (10 times), the length of polymers is decreased almost to the half. Results show that choosing the higher Ha values and higher harmonic bond constants provides proper polymer chain transfer for low length of polymer cases.
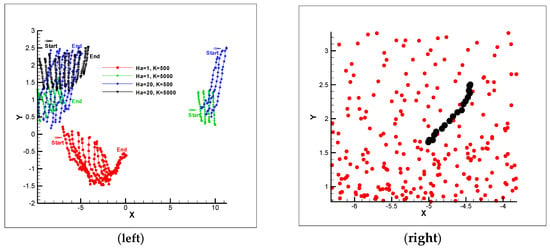
Figure 3.
Motion of polymer chain with different values for Ha parameter and harmonic bond constant (K) from number of time steps 1 to 15000 for 20 beads (left) and a chain polymer through DPD particles at number of time step 14000 with K = 5000 and Ha = 20 (right).
In the following, the effects of magnetic field and hardness of polymers on the properties of polymer chain are investigated. The variation of dimensionless velocity of mass center of the polymer during the time is depicted in the Figure 4 (left). As can be seen, the oscillations decrease over time and, in the case of more severe magnetic field and higher spring coefficient value, the oscillation is greatly reduced. Therefore, in the condition of Ha = 20 and K = 5000 causes the polymer to move with less velocity changes. As is evident from Figure 4 (right), temporal evolutions of the average kinetic temperature for all cases reach to unity and fluid condition approaches the equilibrium. Also, by examining the radius of gyration squared for the polymer chain in Figure 5 (left), it is observed that the amount of distortion and perturbation is greatly reduced around the 80% by increasing the harmonic bond constant from 500 to 5000. Changing the magnetic field has little effect on the polymer chain perturbations. Such behavior can be expected by studying the end-to-end distance of the polymer chain as shown in Figure 5 (right). Results indicate that in the non-equilibrium situation, the amount of perturbation for a short polymer chain is high for a short period of time, and in the case of higher Ha and K values, low oscillation is resulted for those mentioned parameters. Therefore, again, having a chain with a higher harmonic bond constant has about 80% lower oscillation in this study.
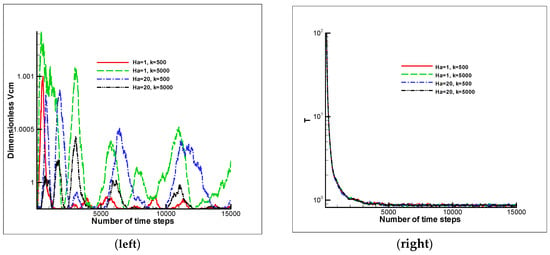
Figure 4.
Dimensionless velocity of polymer mass center for different Ha and K values for a polymer chain consisting of 20 beads (left) and temporal variation of average kinetic temperature (right).
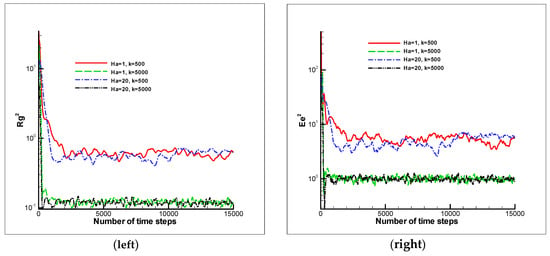
Figure 5.
Temporal evolution of radius of gyration squared (left) and end-end distance (right) for different Ha and K values for a polymer chain consisting of 20 beads.
3.3. Long Polymer Chain Transfer in MHD Flow
One of the significant factors in polymer chain transfer is the length of polymer chain. In this study, the effect of MHD is investigated on no charge polymer chain motion and consequently, the length of chain would be influenced from magnetic field. By consideration of previous results, the motion of a polymer chain consisting of 50 beads having different harmonic bond constant values is depicted in Figure 6. As can be expected, higher magnetic field has more effect on the motion in the case of the higher spring constant or K = 5000 compared to K = 500. Also, by increasing the harmonic bond constant, the polymer prefers to collapse and in higher magnetic field, compression is enhanced compared to other conditions. In the maximum circumstance, 40% compression is observed in the case of Ha = 20 and K = 5000. It can be concluded that the proper selection of parameters for transfer of polymer chain are the higher Ha and K values.
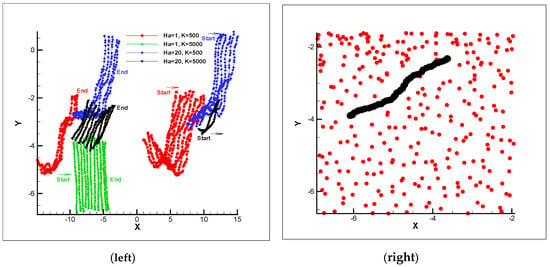
Figure 6.
Motion of polymer chain with different Ha parameter and harmonic bond constant (K) from time step 1 to time step 15000 for a 50-beads polymer chain (left) and a snapshot of polymer chain among DPD particles at time step14000 for K = 5000 and Ha = 50 (right).
It can also be concluded from the study of the dimensionless velocity of mass center the rate of velocity variation would greatly decrease as the harmonic bond constant and chain length increase. As Figure 7 indicates, more reduction would be resulted for the magnetic field with Ha = 20 and K = 5000. Similar to the previous results, the average kinetic temperature would converge to unity over the time and fluid would move towards the equilibrium condition. In these cases, for high length of polymer chain, the higher magnetic field and the higher polymer hardness has a proper result.
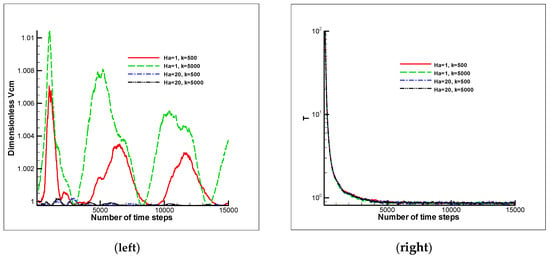
Figure 7.
Dimensionless velocity of polymer mass center for different Ha and K values for a 50-beads polymer chain (left) and the temporal evolution of average kinetic temperature (right).
By examining the radius of gyration squared and the end-to-end distance, it can be concluded from Figure 8 that a significant decrease of about 75% would occur by increasing the harmonic bond constant from 500 to 5000. It should be noted that higher length of polymer chain delays the equilibrium condition. In this case, higher Ha value along with a higher harmonic bond constant present proper polymer chain transfer. In Figure 9, these transfers for both cases of short and long polymer chain with Ha = 20 and K = 5000 as a high Ha and K values are shown as a proper polymer chain transfer in this study. For more information from quantity aspect, average properties of radius of gyration squared, dimensionless velocity of polymer mass center, temporal evolution of average kinetic temperature, and the length of polymer chain by consideration of Figure 2 to 8 and different input DPD variable are presented in Table 4. As can be seen again, test case of Ha = 20 and K=5000 show less perturbation and less strength in polymer chain through transfer in the micro channel.
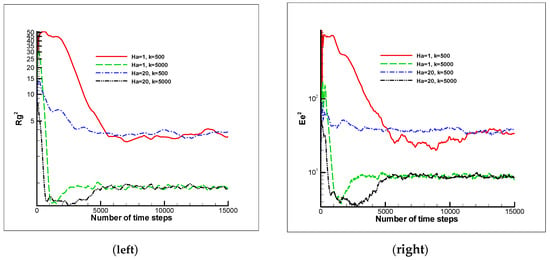
Figure 8.
Radius of gyration squared (left) and end-end distance (right) for different Ha and K values for a 50-beads polymer chain.
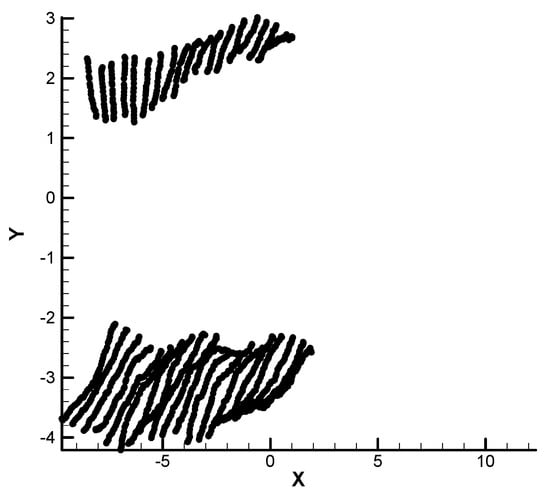
Figure 9.
Short (N = 20) and long (N = 50) polymer chain transfer in microchannel for Ha = 20 and K = 5000 from number of time steps from 1 to 20000.

Table 4.
Average values of test cases calculation from number of time steps from 1 to 15000 with different effective input parameters.
4. Conclusions
In this paper, the DPD simulation of a polymer chain through micro channel was investigated by consideration of Magneto Hydro-Dynamics (MHD) body force. The validation of results with analytical solution was presented and accuracy of simulation was in proper range (max. discrepancy was below 10%). Various physical properties of polymer chain in transition were studied, such as radius of gyration squared, velocity of mass center, and average kinetic temperature for short (20 beads) and long polymer chain (50 beads). For all cases, enhancing the Ha-value and K parameters provide less perturbations for both short and long length of polymer chains, in the case of Ha = 20 and K = 5000 around the 80% reduction in radius of gyration squared was resulted in this paper.
Author Contributions
R.Z. conducted modeling; the writing and revising of the article was carried out by R.Z. and M.S.; R.Z., A.M. and Z.A. supervised the research and edited it. All authors have read and agree to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Li, X.; Pivkin, I.V.; Liang, H. Hydrodynamic effects on flow-induced polymer translocation through a microfluidic channel. Polymer 2013, 54, 4309–4317. [Google Scholar] [CrossRef]
- Xu, Z.; Yang, Y.; Zhu, G.; Chen, P.; Huang, Z.; Dai, X.; Hou, C.; Yan, L.T. Simulating Transport of Soft Matter in Micro/Nano Channel Flows with Dissipative Particle Dynamics. Adv. Theory Simul. 2019, 2, 1800160. [Google Scholar] [CrossRef]
- Li, P.C. Microfluidic Lab-on-A-Chip for Chemical and Biological Analysis and Discovery; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Darbandi, M.; Zakeri, R.; Schneider, G.E. Simulation of Polymer Chain Driven by DPD Solvent Particles in Nanoscale Flows. In Proceedings of the ASME 2010 8th International Conference on Nanochannels, Microchannels, and Minichannels Collocated with 3rd Joint US-European Fluids Engineering Summer Meeting, Montreal, QC, Canada, 1–5 August 2010; pp. 1035–1040. [Google Scholar]
- Chen, C.-W.; Jiang, Y. Computational Fluid Dynamics Study of Magnus Force on an Axis-Symmetric, Disk-Type AUV with Symmetric Propulsion. Symmetry 2019, 11, 397. [Google Scholar] [CrossRef]
- Irandoost Shahrestani, M.; Maleki, A.; Safdari Shadloo, M.; Tlili, I. Numerical Investigation of Forced Convective Heat Transfer and Performance Evaluation Criterion of Al2O3/Water Nanofluid Flow inside an Axisymmetric Microchannel. Symmetry 2020, 12, 120. [Google Scholar] [CrossRef]
- Maleki, A.; Elahi, M.; Assad, M.E.H.; Nazari, M.A.; Shadloo, M.S.; Nabipour, N. Thermal conductivity modeling of nanofluids with ZnO particles by using approaches based on artificial neural network and MARS. J. Therm. Anal. Calorim. 2020. [Google Scholar] [CrossRef]
- Guillouzic, S.; Slater, G.W. Polymer translocation in the presence of excluded volume and explicit hydrodynamic interactions. Phys. Lett. A 2006, 359, 261–264. [Google Scholar] [CrossRef]
- Muthukumar, M.; Kong, C. Simulation of polymer translocation through protein channels. Proc. Natl. Acad. Sci. USA 2006, 103, 5273–5278. [Google Scholar] [CrossRef]
- Liu, S.; Ban, X.; Wang, B.; Wang, X. A Symmetric Particle-Based Simulation Scheme towards Large Scale Diffuse Fluids. Symmetry 2018, 10, 86. [Google Scholar] [CrossRef]
- Ikonen, T.; Bhattacharya, A.; Ala-Nissila, T.; Sung, W. Unifying model of driven polymer translocation. Phys. Rev. E 2012, 85, 051803. [Google Scholar] [CrossRef]
- Jin, H.; Chen, B.; Zhao, X.; Cao, C. Molecular dynamic simulation of hydrogen production by catalytic gasification of key intermediates of biomass in supercritical water. J. Energy Resour. Technol. 2018, 140, 041801. [Google Scholar] [CrossRef]
- Xu, B.; Jin, H.; Li, H.; Guo, Y.; Fan, J. Investigation on the evolution of the coal macromolecule in the process of combustion with Molecular dynamics method. J. Energy Resour. Technol. 2020, 142. [Google Scholar] [CrossRef]
- Hoogerbrugge, P.; Koelman, J. Simulating microscopic hydrodynamic phenomena with dissipative particle dynamics. EPL (Europhys. Lett.) 1992, 19, 155. [Google Scholar] [CrossRef]
- Zakeri, R.; Lee, E.S. Similar Region in Electroosmotic Flow Rate for Newtonian and non-Newtonian Fluids using dissipative particle dynamics (DPD). In Proceedings of the ASME 2014 International Mechanical Engineering Congress and Exposition, Montreal, QC, Canada, 14–20 November 2014. [Google Scholar]
- Safdari Shadloo, M. Numerical simulation of compressible flows by lattice Boltzmann method. Numer. Heat Transf. Part A Appl. 2019, 75, 167–182. [Google Scholar] [CrossRef]
- Vasheghani Farahani, M.; Foroughi, S.; Norouzi, S.; Jamshidi, S. Mechanistic Study of Fines Migration in Porous Media Using Lattice Boltzmann Method Coupled With Rigid Body Physics Engine. J. Energy Resour. Technol. 2019, 141. [Google Scholar] [CrossRef]
- Almasi, F.; Shadloo, M.; Hadjadj, A.; Ozbulut, M.; Tofighi, N.; Yildiz, M. Numerical simulations of multi-phase electro-hydrodynamics flows using a simple incompressible smoothed particle hydrodynamics method. Comput. Math. Appl. 2019. [Google Scholar] [CrossRef]
- Fatehi, R.; Rahmat, A.; Tofighi, N.; Yildiz, M.; Shadloo, M.S. Density-based smoothed particle hydrodynamics methods for incompressible flows. Comput. Fluids 2019, 185, 22–33. [Google Scholar] [CrossRef]
- Hopp-Hirschler, M.; Shadloo, M.S.; Nieken, U. A smoothed particle hydrodynamics approach for thermo-capillary flows. Comput. Fluids 2018, 176, 1–19. [Google Scholar] [CrossRef]
- Shadloo, M.S.; Oger, G.; Le Touzé, D. Smoothed particle hydrodynamics method for fluid flows, towards industrial applications: Motivations, current state, and challenges. Comput. Fluids 2016, 136, 11–34. [Google Scholar] [CrossRef]
- Hopp-Hirschler, M.; Shadloo, M.S.; Nieken, U. Viscous fingering phenomena in the early stage of polymer membrane formation. J. Fluid Mech. 2019, 864, 97–140. [Google Scholar] [CrossRef]
- Zhang, K.; Manke, C.W. Simulation of polymer solutions by dissipative particle dynamics. Mol. Simul. 2000, 25, 157–166. [Google Scholar] [CrossRef]
- Willemsen, S.; Hoefsloot, H.; Iedema, P. Mesoscopic simulation of polymers in fluid dynamics problems. J. Stat. Phys. 2002, 107, 53–65. [Google Scholar] [CrossRef]
- Pastorino, C.; Kreer, T.; Müller, M.; Binder, K. Comparison of dissipative particle dynamics and Langevin thermostats for out-of-equilibrium simulations of polymeric systems. Phys. Rev. E 2007, 76, 026706. [Google Scholar] [CrossRef] [PubMed]
- Duong-Hong, D.; Han, J.; Wang, J.S.; Hadjiconstantinou, N.G.; Chen, Y.Z.; Liu, G.R. Realistic simulations of combined DNA electrophoretic flow and EOF in nano-fluidic devices. Electrophoresis 2008, 29, 4880–4886. [Google Scholar] [CrossRef] [PubMed]
- Pan, H.; Ng, T.; Li, H.; Moeendarbary, E. Dissipative particle dynamics simulation of entropic trapping for DNA separation. Sens. Actuators A Phys. 2010, 157, 328–335. [Google Scholar] [CrossRef]
- Masoud, H.; Alexeev, A. Selective control of surface properties using hydrodynamic interactions. Chem. Commun. 2011, 47, 472–474. [Google Scholar] [CrossRef]
- Guo, J.; Li, X.; Liu, Y.; Liang, H. Flow-induced translocation of polymers through a fluidic channel: A dissipative particle dynamics simulation study. J. Chem. Phys. 2011, 134, 134906. [Google Scholar] [CrossRef] [PubMed]
- Yang, K.; Vishnyakov, A.; Neimark, A.V. Polymer translocation through a nanopore: DPD study. J. Phys. Chem. B 2013, 117, 3648–3658. [Google Scholar] [CrossRef]
- Ranjith, S.K.; Patnaik, B.; Vedantam, S. Transport of DNA in hydrophobic microchannels: A dissipative particle dynamics simulation. Soft Matter 2014, 10, 4184–4191. [Google Scholar] [CrossRef]
- Zakeri, R. Dissipative particle dynamics simulation of the soft micro actuator using polymer chain displacement in electro-osmotic flow. Mol. Simul. 2019, 45, 1488–1497. [Google Scholar] [CrossRef]
- Mao, J.; Yao, Y.; Zhou, Z.; Hu, G. Polymer translocation through nanopore under external electric field: Dissipative particle dynamics study. Appl. Math. Mech. 2015, 36, 1581–1592. [Google Scholar] [CrossRef]
- Zakeri, R.; Lee, E.S. Simulation of nano polymer chain sensor in electroosmotic flow using dissipative particle dynamics (DPD) method. In Proceedings of the ASME 2014 International Mechanical Engineering Congress and Exposition, Montreal, QC, Canada, 14–20 November 2014. [Google Scholar]
- Alarifi, I.M.; Abokhalil, A.G.; Osman, M.; Lund, L.A.; Ayed, M.B.; Belmabrouk, H.; Tlili, I. MHD flow and heat transfer over vertical stretching sheet with heat sink or source effect. Symmetry 2019, 11, 297. [Google Scholar] [CrossRef]
- Khan, I.; Alqahtani, A.M. MHD Nanofluids in a Permeable Channel with Porosity. Symmetry 2019, 11, 378. [Google Scholar] [CrossRef]
- Laser, D.J.; Santiago, J.G. A review of micropumps. J. Micromech. Microeng. 2004, 14, R35. [Google Scholar] [CrossRef]
- Lim, S.; Choi, B. A study on the MHD (magnetohydrodynamic) micropump with side-walled electrodes. J. Mech. Sci. Technol. 2009, 23, 739–749. [Google Scholar] [CrossRef]
- Kang, H.-J.; Choi, B. Development of the MHD micropump with mixing function. Sens. Actuators A Phys. 2011, 165, 439–445. [Google Scholar] [CrossRef]
- Ito, K.; Takahashi, T.; Fujino, T.; Ishikawa, M. Influences of channel size and operating conditions on fluid behavior in a MHD micro pump for micro total analysis system. J. Int. Counc. Electr. Eng. 2014, 4, 220–226. [Google Scholar] [CrossRef]
- Khan, M.A.; Hristovski, I.R.; Marinaro, G.; Kosel, J. Magnetic Composite Hydrodynamic Pump With Laser-Induced Graphene Electrodes. IEEE Trans. Magn. 2017, 53, 1–4. [Google Scholar] [CrossRef]
- Zhou, X.; Gao, M.; Gui, L. A Liquid-Metal Based Spiral Magnetohydrodynamic Micropump. Micromachines 2017, 8, 365. [Google Scholar] [CrossRef]
- Kefayati, G.R.; Gorji-Bandpy, M.; Sajjadi, H.; Ganji, D. Lattice Boltzmann simulation of MHD mixed convection in a lid-driven square cavity with linearly heated wall. Sci. Iran. 2012, 19, 1053–1065. [Google Scholar] [CrossRef]
- Ghahderijani, M.J.; Esmaeili, M.; Afrand, M.; Karimipour, A. Numerical simulation of MHD fluid flow inside constricted channels using lattice Boltzmann method. J. Appl. Fluid Mech. 2017, 10, 1639–1648. [Google Scholar] [CrossRef]
- Javaherdeh, K.; Najjarnezami, A. Lattice Boltzmann simulation of MHD natural convection in a cavity with porous media and sinusoidal temperature distribution. Appl. Math. Mech. 2018, 39, 1187–1200. [Google Scholar] [CrossRef]
- Chaabane, R.; Jemni, A. Lattice Boltzmann approach for MagnetoHydroDynamic convective heat transfer. Energy Procedia 2019, 162, 181–190. [Google Scholar] [CrossRef]
- Jafari, S.; Zakeri, R.; Darbandi, M. DPD simulation of non-Newtonian electroosmotic fluid flow in nanochannel. Mol. Simul. 2018, 44, 1444–1453. [Google Scholar] [CrossRef]
- Elmars, B.; Yu, M.; Ozols, R. Heat and Mass Transfer in MHD Flows; World Scientific: Singapore, 1987; Volume 3. [Google Scholar]
- Gold, R.R. Magnetohydrodynamic pipe flow. Part 1. J. Fluid Mech. 1962, 13, 505–512. [Google Scholar] [CrossRef]
- Asma, M.; Othman, W.; Muhammad, T.; Mallawi, F.; Wong, B. Numerical Study for Magnetohydrodynamic Flow of Nanofluid Due to a Rotating Disk with Binary Chemical Reaction and Arrhenius Activation Energy. Symmetry 2019, 11, 1282. [Google Scholar] [CrossRef]
- Karniadakis, G.; Beskok, A.; Aluru, N. Microflows and Nanoflows: Fundamentals and Simulation; Springer Science & Business Media: Berlin, Germany, 2006; Volume 29. [Google Scholar]
- Jehser, M.; Zifferer, G.; Likos, C.N. Scaling and Interactions of Linear and Ring Polymer Brushes via DPD Simulations. Polymers 2019, 11, 541. [Google Scholar] [CrossRef]
- Nikunen, P.; Karttunen, M.; Vattulainen, I. How would you integrate the equations of motion in dissipative particle dynamics simulations? Comput. Phys. Commun. 2003, 153, 407–423. [Google Scholar] [CrossRef]
- Duong-Hong, D.; Phan-Thien, N.; Fan, X. An implementation of no-slip boundary conditions in DPD. Comput. Mech. 2004, 35, 24–29. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Shehzad, S. Magnetohydrodynamic nanofluid convection in a porous enclosure considering heat flux boundary condition. Int. J. Heat Mass Transf. 2017, 106, 1261–1269. [Google Scholar] [CrossRef]
- Yapici, M.K.; Al Nabulsi, A.; Rizk, N.; Boularaoui, S.M.; Christoforou, N.; Lee, S. Alternating magnetic field plate for enhanced magnetofection of iron oxide nanoparticle conjugated nucleic acids. J. Magn. Magn. Mater. 2019, 469, 598–605. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).