The Pauli Exclusion Principle and the Problems of Its Experimental Verification
Abstract
1. Introduction: Discovery of the Pauli Exclusion Principle and Its Generalized Formulation for all Elementary Particles
“According to this point of view, the doublet structure of alkali spectra… is due to a particular two-valuedness of the quantum theoretic properties of the electron, which cannot be described from the classical point of view.”
“Physicists found it difficult to understand the exclusion principle, since no meaning in terms of a model was given to the fourth degree of freedom of the electron.”
“An antisymmetric eigenfunction vanishes identically when two of the electrons are in the same orbit. This means that, in the solution of the problem with antisymmetric eigenfunctions, there can be no stationary states with two or more electrons in the same orbit, which is just Pauli’s exclusion principle.”
The only possible states of a system of identical particles possessing spin s are those for which the total wave function transforms upon interchange of any two particles as
That is, it is symmetric for integer values of s (the Bose–Einstein statistics) and antisymmetric for half-integer values of s (the Fermi–Dirac statistics).
2. Experimental Verifications of the Pauli Exclusion Principle
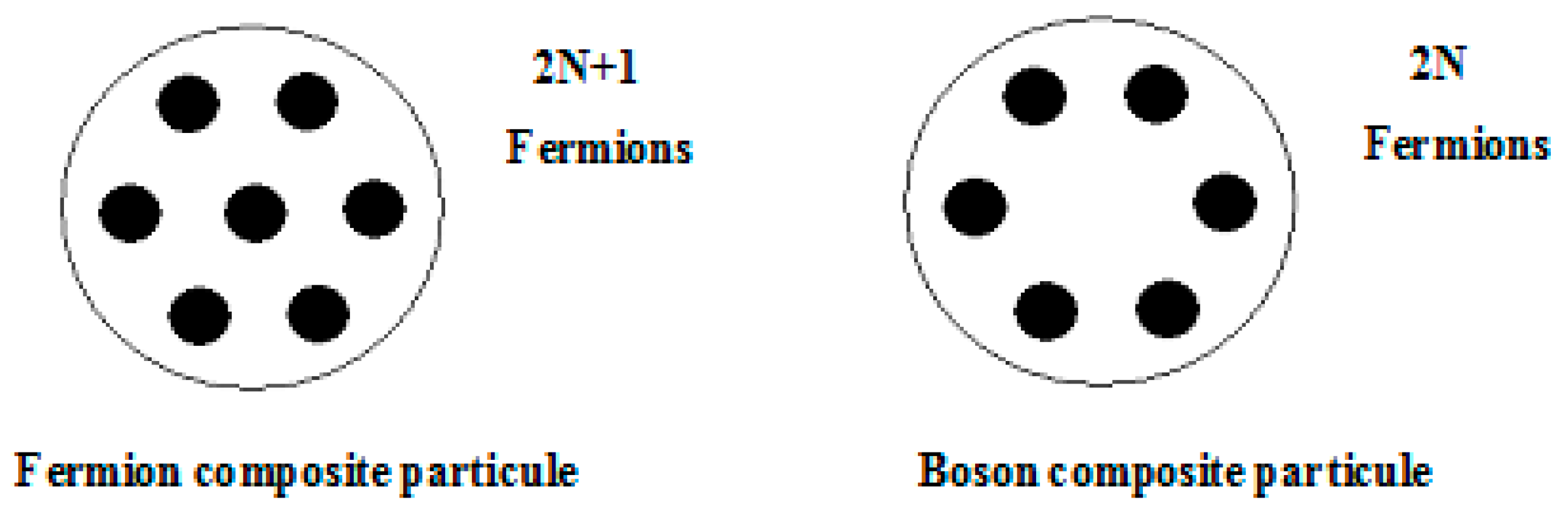
2.1. Motivation: Theoretical Conceptions on the PEP Violations
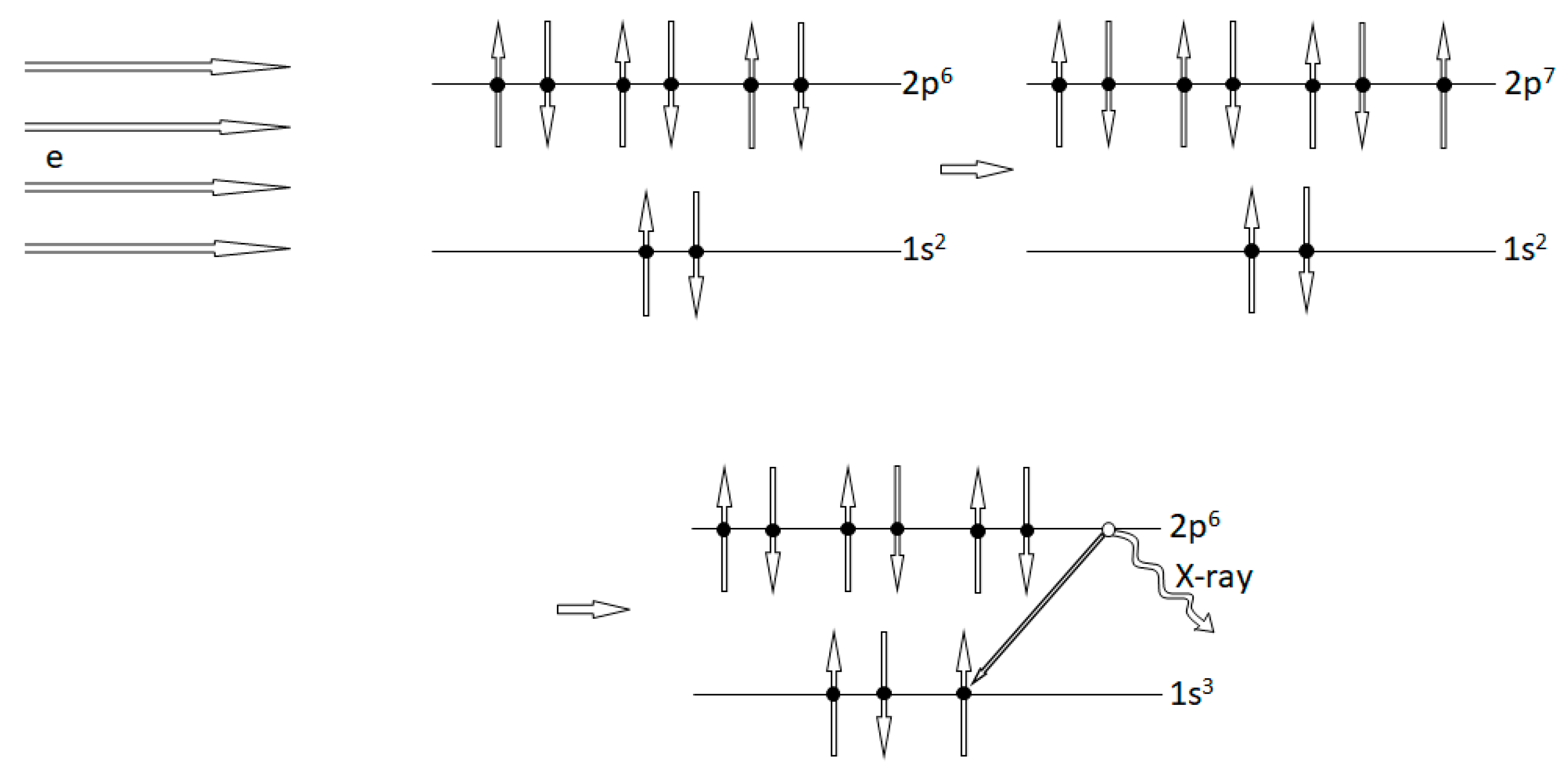
2.2. Experimental Tests of the PEP Violations: What Is Measured
2.3. Comments on the Experimental Tests of the Pauli-Forbidden Electron Transitions
- (a)
- Mallon et al. [83] applied the Desclaux method for heavy atoms. For these atoms, the relativistic approach is appropriate; however, in this case, the j–j coupling should be used (as they did), and spin ceases to be a good quantum number. On the other hand, the elements of the fourth period of the periodical table, with 3d-electrons, can be calculated with good precision at the non-relativistic level (see very precise MR CI calculations in References [84,85]). Thus, Cu can be calculated at the non-relativistic level using the Russel-Saunders (L–S) coupling and without the Breit–Pauli, Lamb shift, and others relativistic corrections. It is worthwhile to mention that, in this case, the non-relativistic Greenberg quon model [46] is quite justified.
- (b)
- If, in analogy with muons, it can be assumed that a non-Pauli electron can be attached to atoms in solids, it is quite doubtful that it will be located on the same atomic shells as the “normal” Pauli electrons and then to the K-shell. This is a crucial point in the treatment of experiments for detecting the Pauli forbidden transition, and it must be argued more carefully.
3. Concluding Remarks
Funding
Acknowledgments
Conflicts of Interest
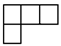
Appendix A. Some Necessary Knowledge on the Permutation Group
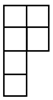
| [λ] = [22 12]. |
|  |
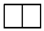
| [2] | [12] |
| 
|  |
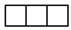
| [3] | [2.1] | [13] |
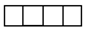
| 
| 
| 
|  |
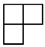
| [4] | [3 1] | [22] | [2 12] | [14] |
References
- Heisenberg, W. Quantum-theoretical re-interpretation of kinematic and mechanical relations. Z. Phys. 1925, 33, 879–893. [Google Scholar] [CrossRef]
- Born, M.; Jordan, P. Zur Quantenmechanik. Z. Phys. 1925, 34, 858–888. [Google Scholar] [CrossRef]
- De Broglie, L. Recherches sur la théorie des quanta. Ann. Phys. 1925, 3, 22–128. [Google Scholar] [CrossRef]
- Schrödinger, E. On the relation between the Quantum Mechanics of Heisenberg, Born, and Jordan, and that of Schrödinger. Ann. Phys. 1926, 79, 361–376, 489–527, 734–756. [Google Scholar] [CrossRef]
- Schrödinger, E. An Undulatory Theory of the Mechanics of Atoms and Molecules. Phys. Rev. 1926, 28, 1049–1070. [Google Scholar] [CrossRef]
- Pauli, W. Über den Einfluß der Geschwindigkeitsabhängigkeit der Elektronenmasse auf den Zeemaneffekt. Z. Phys. 1925, 31, 373–385. [Google Scholar] [CrossRef]
- Pauli, W. Über den Zusammenhang des Abschlusses der Elektronengruppen im Atom mit der Komplexstruktur der Spektren. Z. Phys. 1925, 31, 765–783. [Google Scholar] [CrossRef]
- Pauli, W. Exclusion principle and quantum mechanics. Nobel Lecture. In Nobel Lectures, Physics 1942–1962; Elsevier: Amsterdam, The Netherlands, 1964. [Google Scholar]
- Kaplan, I.G. The Pauli Exclusion Principle: Origin, Verifications and Applications; Wiley: Chichester, UK, 2017. [Google Scholar]
- Heisenberg, W. Mehrkörperproblem und Resonanz in der Quantenmechanik. Z. Phys. 1926, 38, 411–426. [Google Scholar] [CrossRef]
- Dirac, P.A.M. On the theory of quantum mechanics. Proc. R. Soc. Lond. A 1926, 112, 661–677. [Google Scholar]
- Slater, J.C. The Theory of Complex Spectra. Phys. Rev. 1929, 34, 1293–1322. [Google Scholar] [CrossRef]
- Fowler, R.H. On dense matter. Mon. Not. R. Astron. Soc. 1926, 87, 114–122. [Google Scholar] [CrossRef]
- Dirac, P.A.M. The quantum theory of the Electron. Proc. R. Soc. Lond. A 1928, 117, 610–624. [Google Scholar]
- Schrödinger, E. Ueber die kraeftefreie Bewegung in der relativistischen Quantenmechanik Sitzungsber. Preuss. Akad. Wiss. Phys. Math. Kl. 1930, 24, 418–428. [Google Scholar]
- Chadwick, J. Possible Existence of a Neutron. Nature 1932, 129, 312. [Google Scholar] [CrossRef]
- Heisenberg, W. Über den Bau der Atomkerne. I. Z. Phys. 1932, 77, 1–11. [Google Scholar] [CrossRef]
- Wigner, E. On the Consequences of the Symmetry of the Nuclear Hamiltonian on the Spectroscopy of Nuclei. Phys. Rev. 1937, 51, 106–119. [Google Scholar] [CrossRef]
- Ehrenfest, P.; Oppenheimer, J.R. Note on the Statistics of Nuclei. Phys. Rev. 1931, 37, 333–338. [Google Scholar] [CrossRef]
- Kaplan, I.G. The Pauli Exclusion Principle. Can It Be Proved? Found. Phys. 2013, 43, 1233–1251. [Google Scholar] [CrossRef]
- Kaplan, I.G. Is the Pauli exclusive principle an independent quantum mechanical postulate? Int. J. Quantum Chem. 2002, 89, 268–276. [Google Scholar] [CrossRef]
- Wu, C.S.; Ambler, E.; Hayward, R.W. Experimental Test of Parity Conservation in Beta Decay. Phys. Rev. 1957, 105, 1413–1415. [Google Scholar] [CrossRef]
- Christensen, J.H.; Cronin, J.W.; Fitch, V.L. Evidence for the 2π Decay of the Meson. Phys. Rev. Lett. 1964, 13, 138–140. [Google Scholar] [CrossRef]
- Okun’, L.B. Tests of electric charge conservation and the Pauli principle. Sov. Phys. Uspekhi 1989, 32, 543–547. [Google Scholar] [CrossRef]
- Okun’, L.B. Comments on Testing Charge Conservation and the Pauli Exclusion Principle. Comments Nucl. Part. Phys. 1989, 19, 99–116. [Google Scholar]
- Okun, L.B.; Zeldovich, Y.B. Paradoxes of unstable electron. Phys. Lett. B 1978, 78, 597–600. [Google Scholar] [CrossRef]
- Voloshin, M.B.; Okun, L.B. Conservation of electric charge. JETP Lett. 1978, 28, 145–149. [Google Scholar]
- Ignatiev, A.Y.; Kuzmin, V.A.; Shaposhnikov, M.E. Is the electric charge conserved? Phys. Lett. B 1979, 84, 315–318. [Google Scholar] [CrossRef]
- Huang, J.C. Stability of the electron in the SU (5) and GWS models. J. Phys. G 1987, 13, 273–283. [Google Scholar] [CrossRef]
- Mohapatra, R.N. Possible nonconservation of electric charge. Phys. Rev. Lett. 1987, 59, 1510–1512. [Google Scholar] [CrossRef]
- Mohapatra, R.N.; Nusinov, S. Electric charge nonconservation and minicharged particles-phenomenological implications. Int. J. Mod. Phys. A 1992, 7, 3817–3834. [Google Scholar] [CrossRef]
- Greenberg, O.W. On the surprising rigidity of the Pauli exclusion principle. Nucl. Phys. B Proc. Suppl. 1986, 6, 83–89. [Google Scholar] [CrossRef]
- Greenberg, O.W.; Mohapatra, R.N. Phenomenology of small violations of Fermi and Bose statistics. Phys. Rev. D 1989, 39, 2032–2038. [Google Scholar] [CrossRef] [PubMed]
- Ignatiev, A.Y. X rays test the Pauli exclusion principle. Radiat. Phys. Chem. 2006, 75, 2090–2096. [Google Scholar] [CrossRef]
- Barabash, A.S. Experimental test of the Pauli Exclusion Principle. Found. Phys. 2010, 40, 703–718. [Google Scholar] [CrossRef][Green Version]
- Dirac, P.A.M. The Principles of Quantum Mechanics, 4th ed.; Clarendon Press: Oxford, UK, 1958. [Google Scholar]
- Amado, R.D.; Primakoff, H. Comments on testing the Pauli principle. Phys. Rev. C 1980, 22, 1338–1340. [Google Scholar] [CrossRef]
- Reines, F.; Sobel, H.W. Test of the Pauli Exclusion Principle for Atomic Electrons. Phys. Rev. Lett. 1974, 32, 954. [Google Scholar] [CrossRef]
- Logan, B.A.; Ljubicic, A. Validity of the Pauli exclusion principle for nucleons. Phys. Rev. C 1979, 20, 1957–1958. [Google Scholar] [CrossRef]
- Ignatiev, A.Y.; Kuzmin, V.A. Is small violation of the Pauli principle possible? Sov. J. Nucl. Phys. 1987, 46, 444–446. [Google Scholar]
- Greenberg, O.W.; Mohapatra, R.N. Local Quantum Field Theory of Possible Violation of the Pauli Principle. Phys. Rev. Lett. 1987, 59, 2507–2510. [Google Scholar] [CrossRef]
- Okun’, L.B. Possible violation of the Pauli principle in atoms. JETP Lett. 1987, 46, 529–532. [Google Scholar]
- Govorkov, A.B. Parastatistics and parafields. Theor. Math. Phys. 1983, 54, 361–371. [Google Scholar] [CrossRef]
- Govorkov, A.B. Can the Pauli principle be deduced with local quantum field theory? Phys. Lett. A 1989, 137, 7–10. [Google Scholar] [CrossRef]
- Greenberg, O.W. Theories of violation of statistics. AIP Conf. Proc. 2000, 545, 113–127. [Google Scholar]
- Greenberg, O.W. Example of infinite statistics. Phys. Rev. Lett. 1990, 64, 705–708. [Google Scholar] [CrossRef] [PubMed]
- Greenberg, O.W. Particles with small violations of Fermi or Bose statistics. Phys. Rev. D 1991, 43, 4111–4120. [Google Scholar] [CrossRef] [PubMed]
- Hilborn, R.C. Connecting q-mutator theory with experimental tests of the spin-statistics connection. AIP Conf. Proc. 2000, 545, 128–141. [Google Scholar]
- Gavrin, V.N.; Ignatiev, A.Y.; Kuzmin, V.Z. Search for small violation of the Pauli principle. Phys. Lett. B 1988, 206, 343–345. [Google Scholar] [CrossRef]
- Novikov, V.M.; Pomansky, A.A. Experimental test of a possible violation of the Pauli principle. JETP Lett. 1989, 49, 81–83. [Google Scholar]
- Novikov, V.M.; Pomansky, A.A. Test of the Pauli exclusion principle for atomic electrons. Phys. Lett. B 1990, 240, 227–231. [Google Scholar] [CrossRef]
- Nolte, E. Test of the Pauli exclusion principle for nucleons and atomic electrons by accelerator mass spectrometry. Z. Phys. A 1991, 340, 411–413. [Google Scholar] [CrossRef]
- Müller, D. AMS measurements at the Munich tandem with a time-of-flight setup. Nucl. Instrum. Methods B 1990, 52, 366–369. [Google Scholar] [CrossRef]
- Nolte, E. Search for a violation of the Pauli exclusion principle for atomic electrons and for nucleons. Nucl. Instrum. Methods Phys. Res. B 1990, 52, 563–567. [Google Scholar] [CrossRef]
- Deilamian, K.; Gilaspy, J.D.; Kelleher, D.E. Search for Small Violations of the Symmetrization Postulate in an Excited State of Helium. Phys. Rev. Lett. 1995, 74, 4787–4790. [Google Scholar] [CrossRef] [PubMed]
- Barabash, A.S. Search for anomalous carbon atoms-evidence of violation of the Pauli principle during the period of nucleosynthesis. JETP Lett. 1998, 68, 112–116. [Google Scholar] [CrossRef]
- Javorsek, D. New Experimental Test of the Pauli Exclusion Principle Using Accelerator Mass Spectrometry. Phys. Rev. Lett. 2000, 85, 2701–2704. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, Y. Study of invisible nucleon decay, n→vvv and a forbidden nuclear transition in the Kamiokande detector. Phys. Lett. B 1993, 311, 357–361. [Google Scholar] [CrossRef]
- Arnold, R. Testing the Pauli exclusion principle with the NEMO-2 detector. Eur. Phys. J. A 1999, 6, 361–366. [Google Scholar] [CrossRef][Green Version]
- Bernabei, R. New search for processes violating the Pauli exclusion principle in sodium and in iodine. Eur. Phys. J. C 2009, 62, 327–332. [Google Scholar] [CrossRef]
- Bernabei, R. Search for non-paulian transitions in 23Na and 127I. Phys. Lett. B 1997, 408, 439–444. [Google Scholar] [CrossRef]
- Kishimoto, T. Search for violation of the Pauli principle through spontaneous neutron emission from lead. J. Phys. G 1992, 18, 443–448. [Google Scholar] [CrossRef]
- Kekez, D.; Ljubičić, A.A.; Logan, B.A. An upper limit to violations of the Pauli exclusion principle. Nature 1990, 348, 224. [Google Scholar] [CrossRef]
- Miljanić, D. Test of the Pauli principle in nuclear reactions. Phys. Lett. B 1990, 252, 487–490. [Google Scholar] [CrossRef]
- Bellini, G. New experimental limits on the Pauli-forbidden transitions in 12C nuclei obtained with 485 days Borexino data. Phys. Rev. C 2010, 81, 034317. [Google Scholar] [CrossRef]
- Akama, K.; Terazawa, H.; Yasuè, M. Superficial violation of the Pauli principle due to the possible substructure of electrons. Phys. Rev. Lett. 1992, 68, 1826–1829. [Google Scholar] [CrossRef] [PubMed]
- Gillaspy, D. High precision experimental tests of the symmetrization postulate for fermions. AIP Conf. Proc. 2000, 545, 241–252. [Google Scholar]
- Elliott, S.R. An Improved Limit on Pauli-Exclusion-Principle Forbidden Atomic Transitions. Found. Phys. 2012, 42, 1015–1030. [Google Scholar] [CrossRef]
- Ramberg, E.; Snow, G.A. Experimental limit on a small violation of the Pauli principle. Phys. Lett. B 1990, 238, 438–441. [Google Scholar] [CrossRef]
- Ignatiev, A.Y.; Kuzmin, V.A. Quarks’86. In Proceedings of the 229 Seminar, Tbilisi, 15–17 April 1986; Tarkhelidze, A.N., Matveev, V.A., Pivovarov, A.A., Tkachev, I.I., Eds.; VNU Science Press BV: Utecht, The Nederlands, 1987; pp. 263–268. [Google Scholar]
- Bartalucci, S. New experimental limit on the Pauli exclusion principle violation by electrons. Phys. Lett. B 2006, 641, 18–22. [Google Scholar] [CrossRef]
- Curceanu (Petrascu), C. Experimental tests of quantum mechanics—Pauli exclusion principle violation (the VIP experiment) and future perspective. J. Phys. Conf. Ser. 2011, 306, 012036. [Google Scholar] [CrossRef]
- Bartalucci, S. The VIP Experimental Limit on the Pauli Exclusion Principle Violation by Electrons. Found. Phys. 2010, 40, 765–775. [Google Scholar] [CrossRef]
- Curceanu (Petrascu), C. Experimental tests of quantum mechanics: Pauli Exclusion Principle Violation (the VIP experiment) and future perspectives. Phys. Procedia 2011, 17, 40–48. [Google Scholar] [CrossRef][Green Version]
- Shi, H. Searches for the violation of Pauli exclusion principle at LNGS in VIP-2 experiment. J. Phys. Conf. Ser. 2016, 718, 042055. [Google Scholar] [CrossRef]
- Curceanu, C. Test of the Pauli Exclusion Principle in the VIP-2 Underground Experiment. Entropy 2017, 19, 300. [Google Scholar] [CrossRef]
- Shi, H. Experimental search for the violation of Pauli exclusion principle. Eur. Phys. J. C 2019, 78, 319. [Google Scholar] [CrossRef] [PubMed]
- Milotti, E. On the Importance of Electron Diffusion in a Bulk-Matter Test of the Pauli Exclusion Principle. Entropy 2018, 20, 515. [Google Scholar] [CrossRef]
- Piscicchia, K. High Precision Test of the Pauli Exclusion Principle for Electrons. Condens. Matter 2019, 4, 45. [Google Scholar] [CrossRef]
- Kaplan, I.G.; Rodimova, O.B. Matrix Elements of General Configuration of Nonorthogonal Orbital in State with Definite Spin. Int. J. Quantum Chem. 1973, 7, 1203–1220. [Google Scholar] [CrossRef]
- Kaplan, I.G. Symmetry of Many-Electron Systems; Academic Press: New York, NY, USA, 1975. [Google Scholar]
- Desclaux, J.P. Relativistic Multiconfiguration Dirac–Fock Package. Available online: http://dirac.spectro.jussieu.fr/mcdf/mcdf_theory/Mettec/mettec.html (accessed on 2 January 2020).
- Mallow, J.V. Dirac-Fock method for muonic atoms: Transition energies, wave functions, and charge densities. Phys. Rev. A 1978, 17, 1804–1809. [Google Scholar] [CrossRef]
- Tzeli, D. First principles study of the electronic structure and bonding of Mn2. J. Chem. Phys. 2008, 129, 154310. [Google Scholar] [CrossRef]
- Miranda, U.; Kaplan, I.G. The nature of binding in the ground state of the scandium dimer. Eur. Phys. J. D 2011, 63, 263–270. [Google Scholar] [CrossRef]

© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaplan, I.G. The Pauli Exclusion Principle and the Problems of Its Experimental Verification. Symmetry 2020, 12, 320. https://doi.org/10.3390/sym12020320
Kaplan IG. The Pauli Exclusion Principle and the Problems of Its Experimental Verification. Symmetry. 2020; 12(2):320. https://doi.org/10.3390/sym12020320
Chicago/Turabian StyleKaplan, Ilya G. 2020. "The Pauli Exclusion Principle and the Problems of Its Experimental Verification" Symmetry 12, no. 2: 320. https://doi.org/10.3390/sym12020320
APA StyleKaplan, I. G. (2020). The Pauli Exclusion Principle and the Problems of Its Experimental Verification. Symmetry, 12(2), 320. https://doi.org/10.3390/sym12020320



