Extraction of Frictional Vibration Features with Multifractal Detrended Fluctuation Analysis and Friction State Recognition
Abstract
1. Introduction
2. Experiments
2.1. Tribological Pair
2.2. Apparatus
2.3. Methods
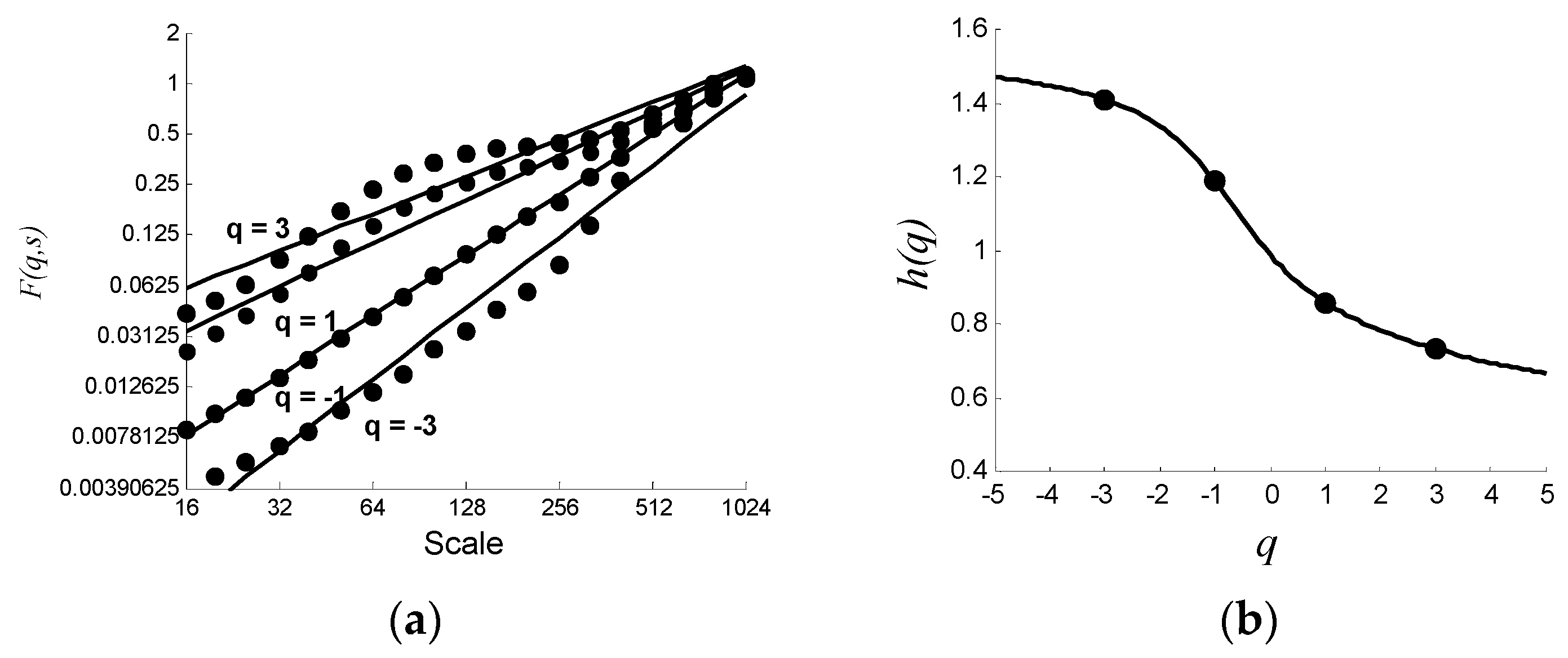
3. MFDFA Algorithm
4. Applying MFDFA to Signals
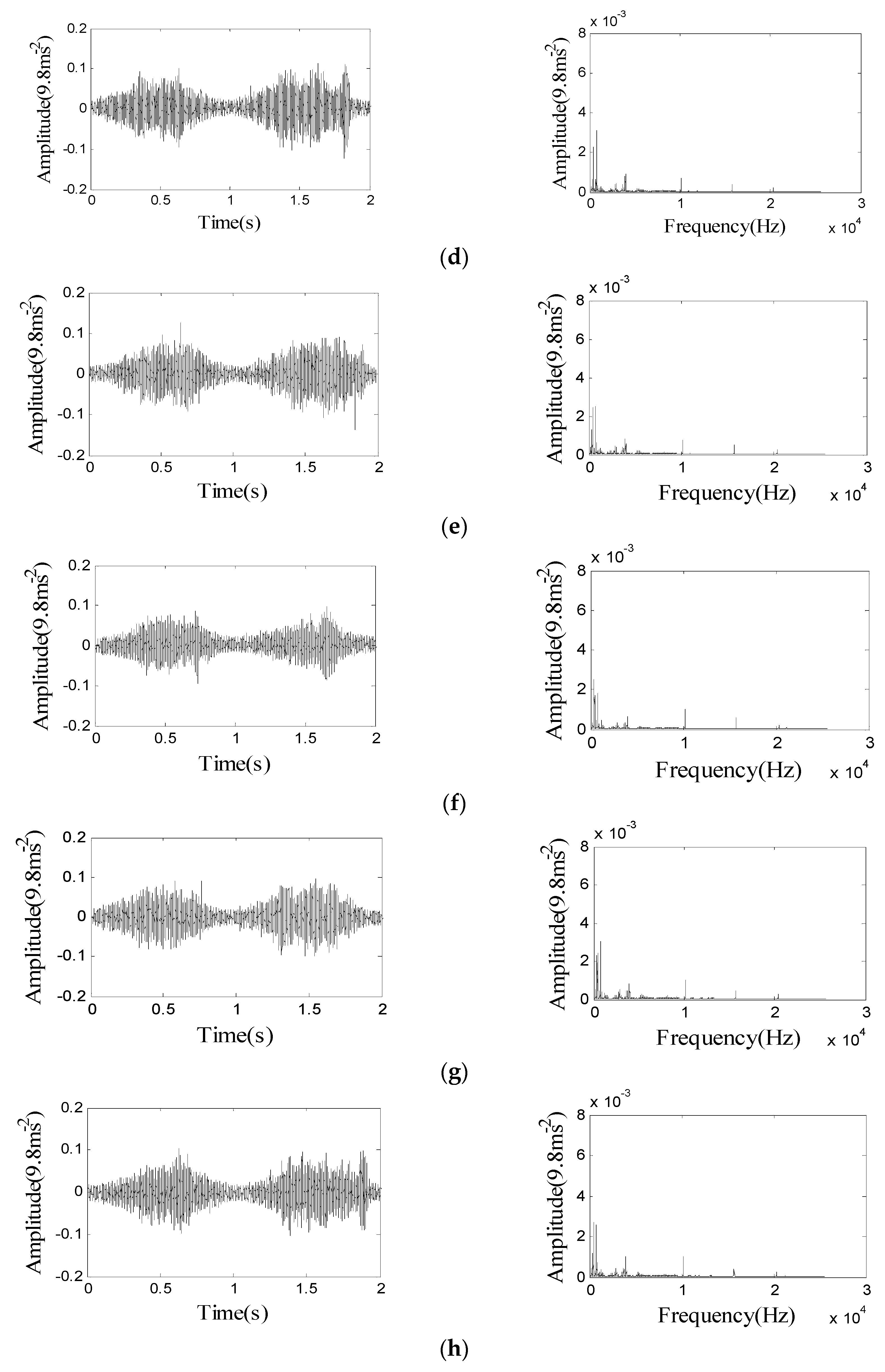
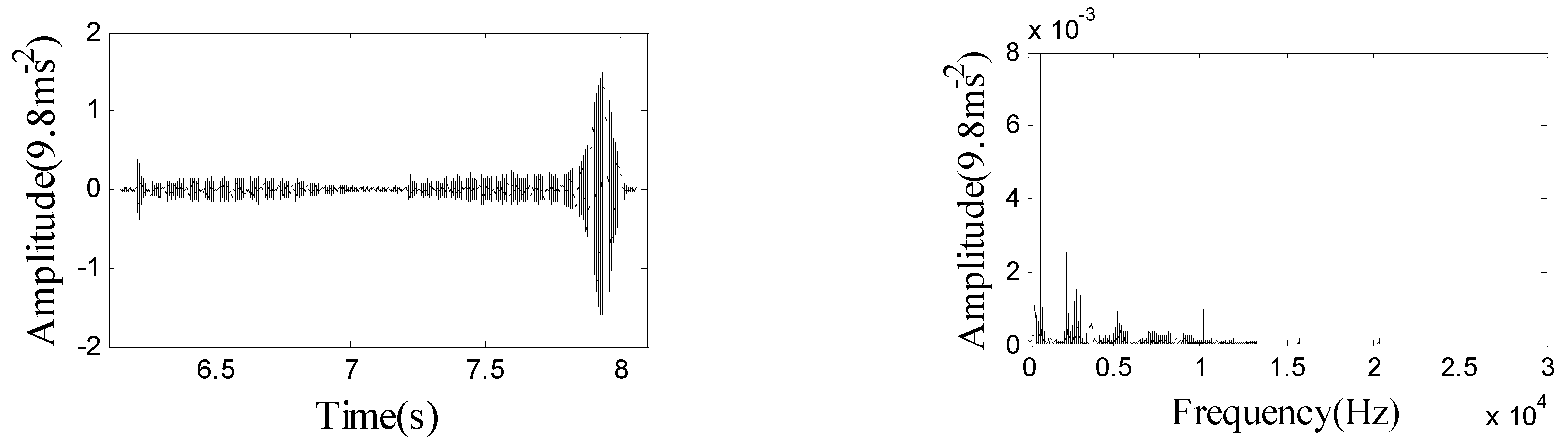
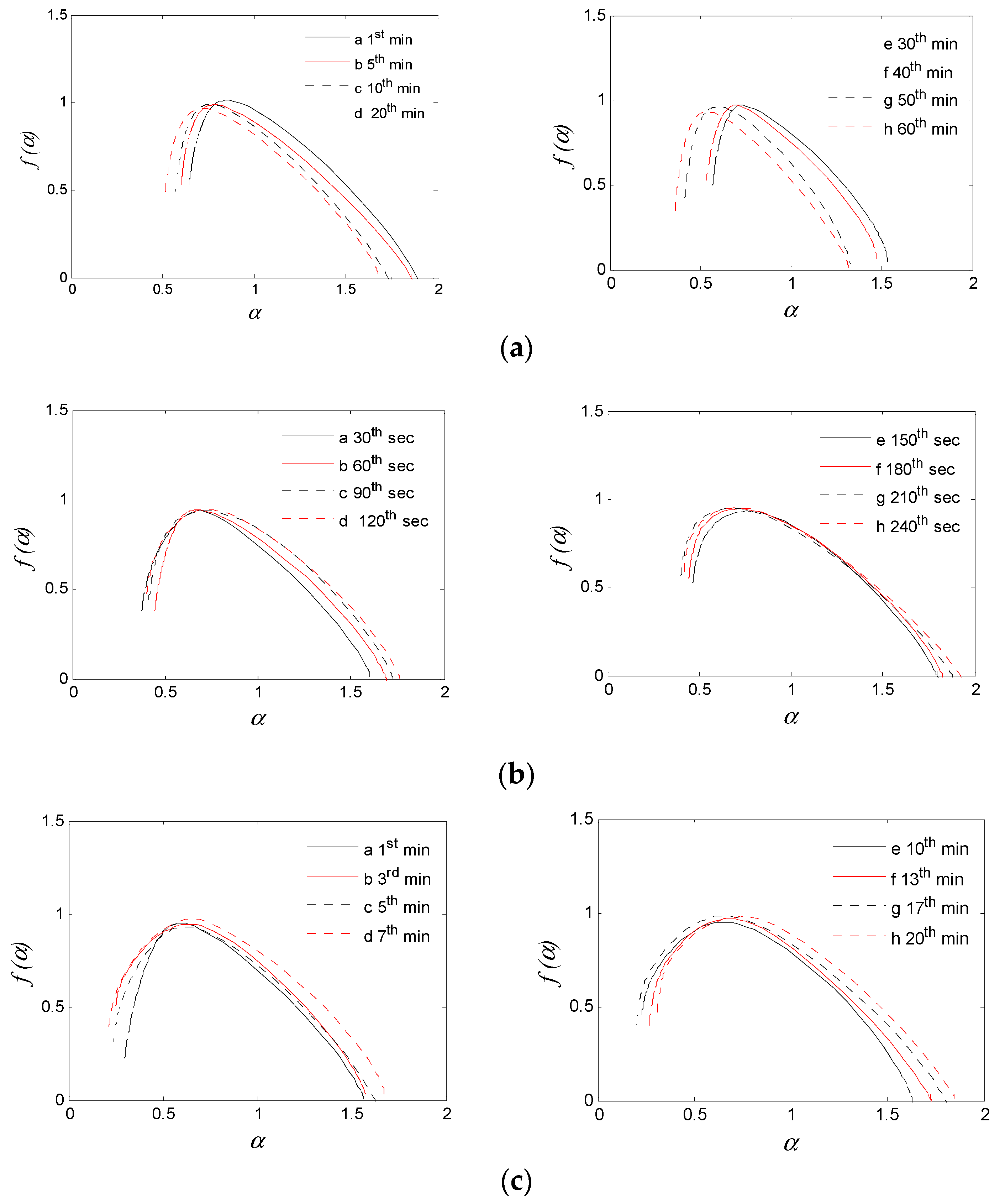
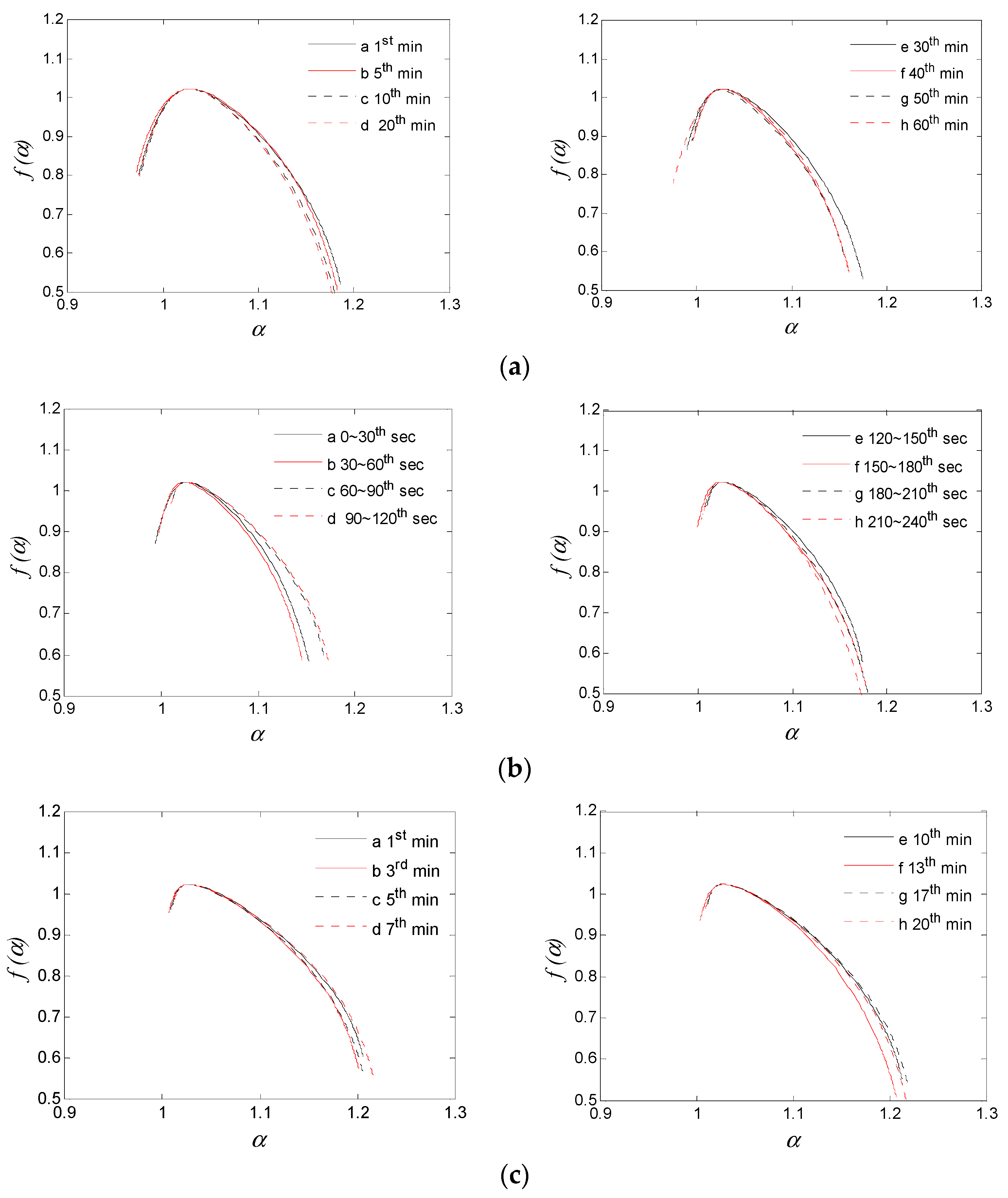
4.1. Applying MFDFA to Frictional Vibration Time-Domain Signals
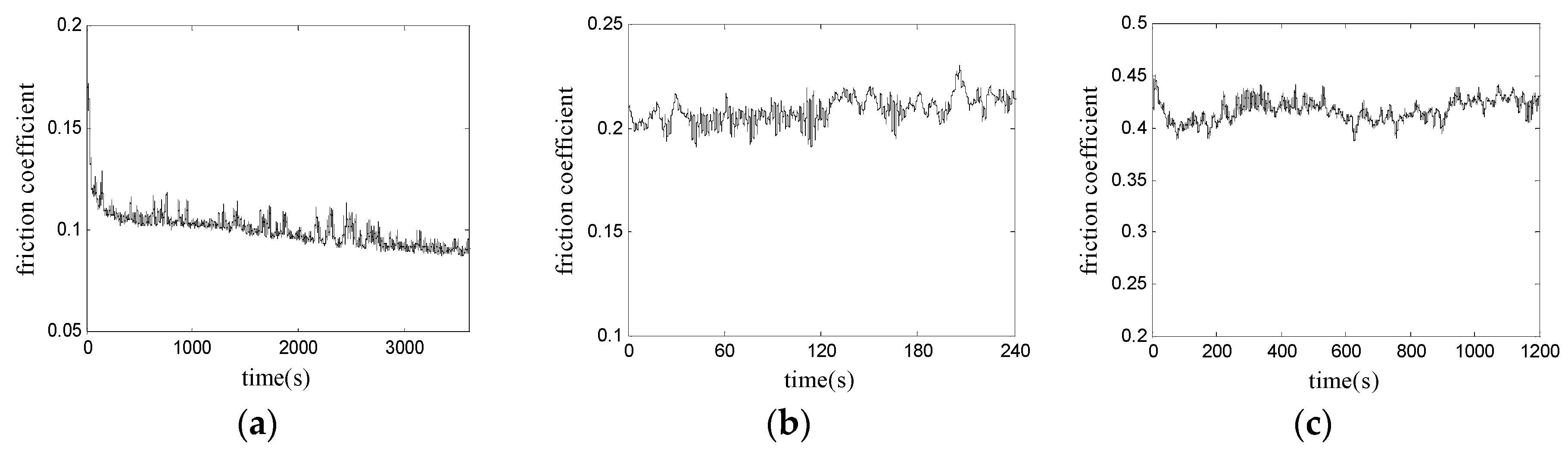
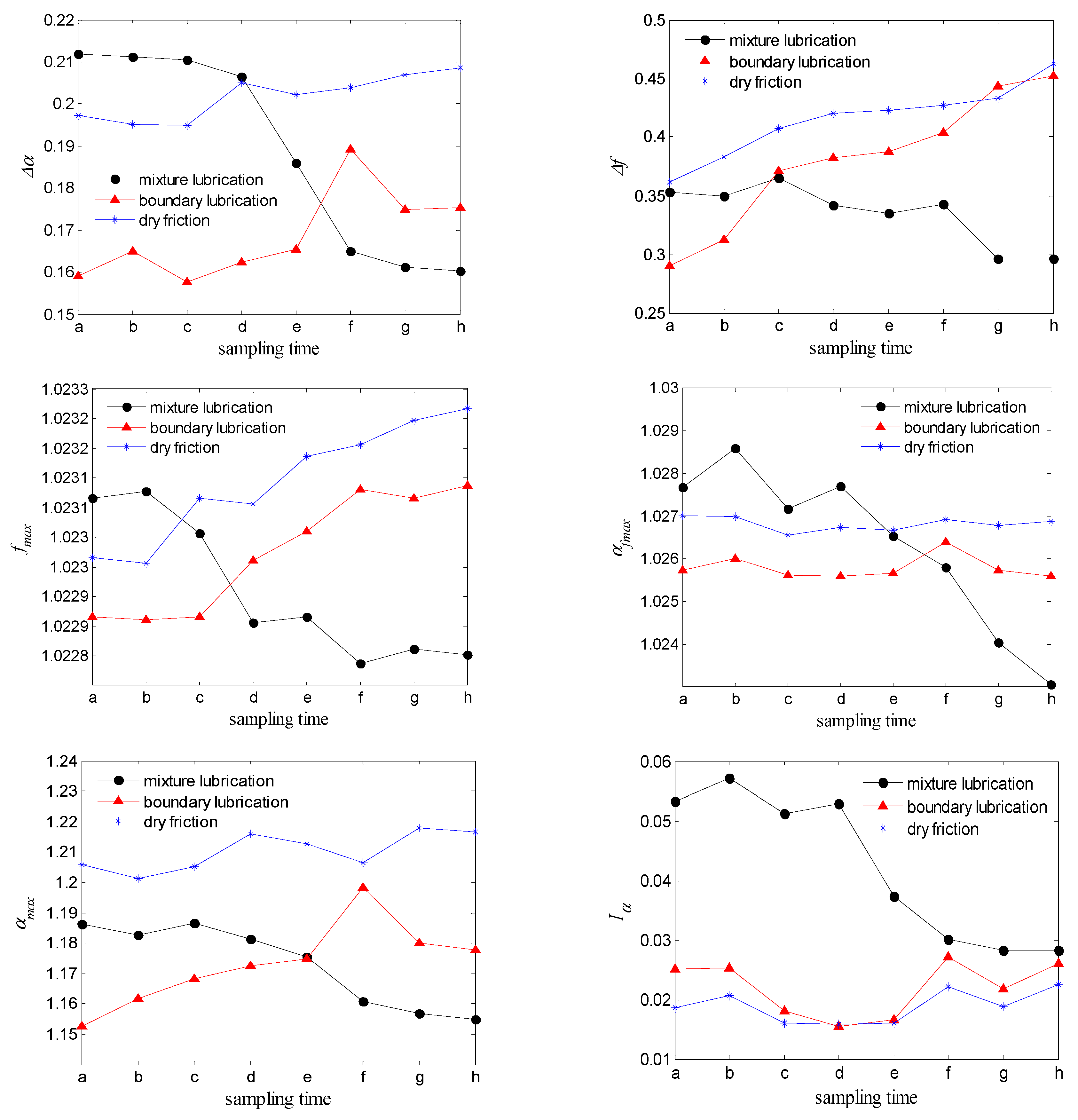
4.2. Applying MFDFA to Friction Coefficient Data
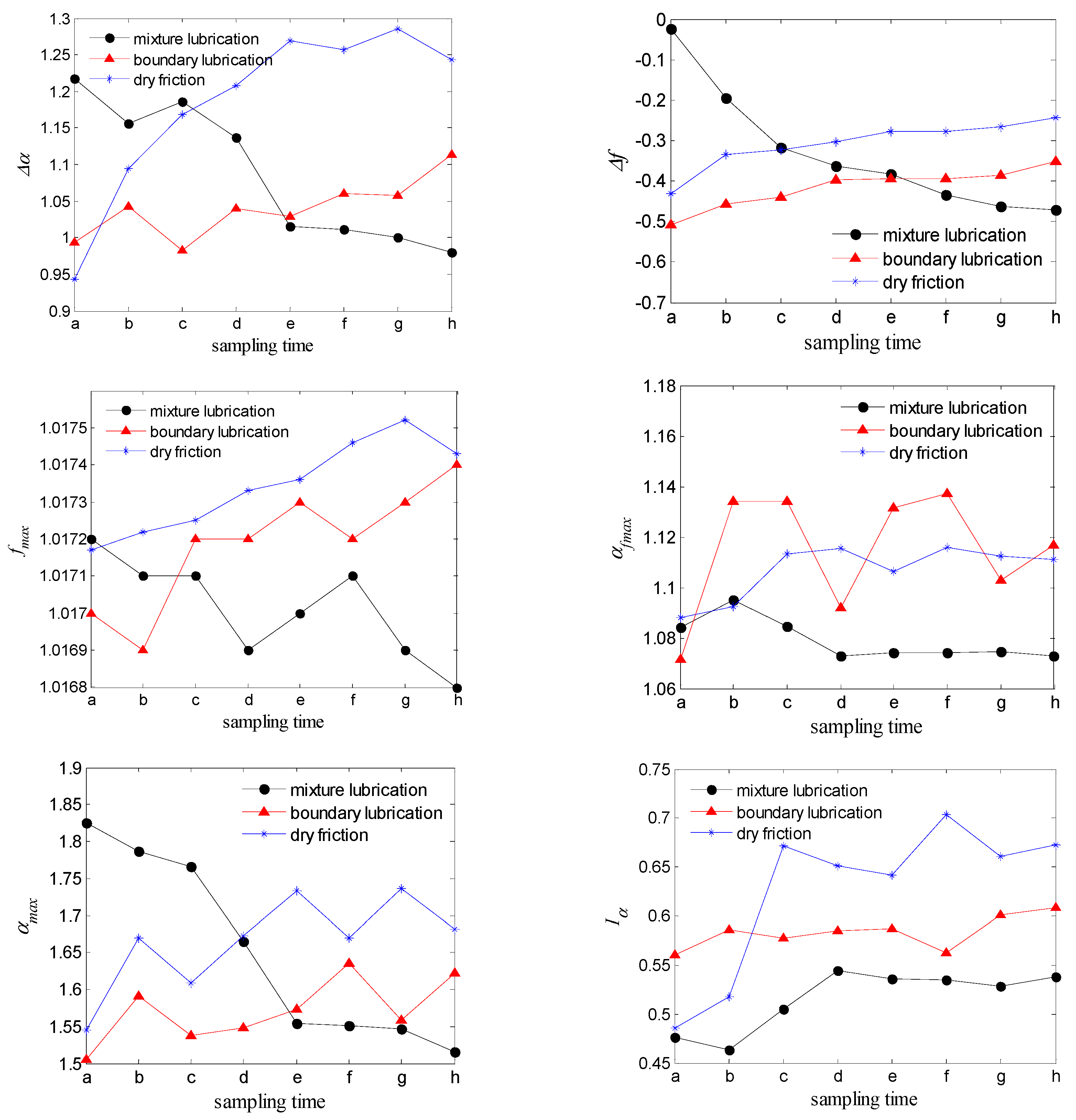
4.3. Applying MFDFA to Frictional Vibration Frequency-Domain Signals
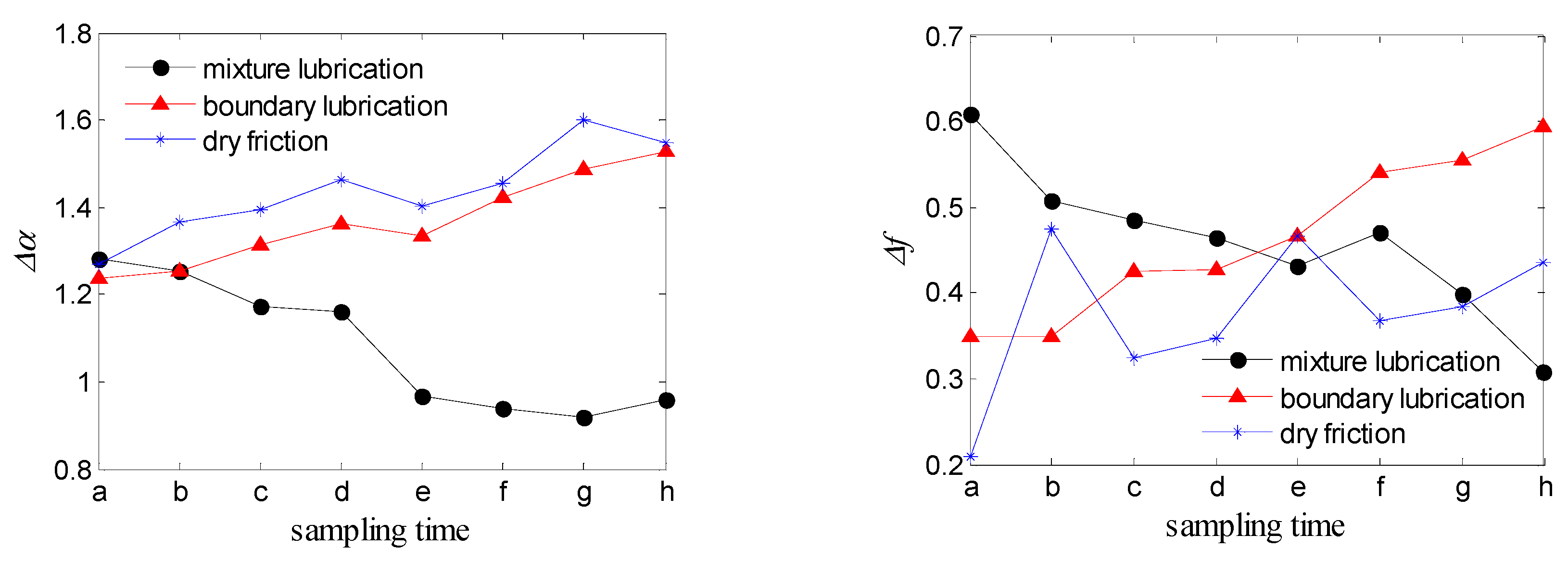
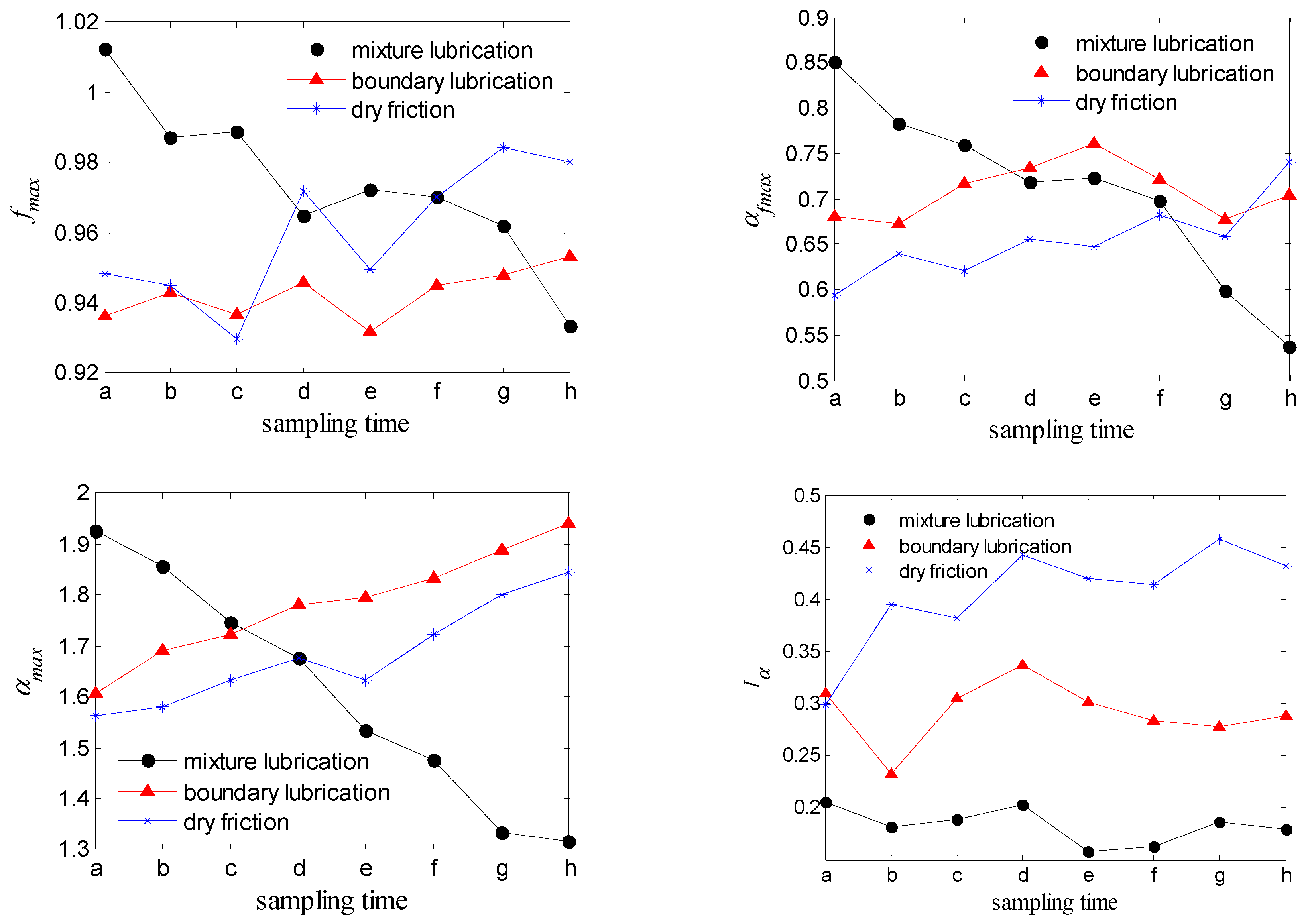
4.4. Analysis and Discussions
5. Friction State Recognition
5.1. Principal Component Analysis Algorithm
5.2. Analysis and Discussions
6. Conclusions
- (1)
- The multifractal detrended fluctuation analysis algorithm can extract the fractal characteristics of the frictional vibration signals effectively. In different friction states, the multifractal spectrum parameters of the frictional vibrations have different parameter ranges and present different trends. The analysis shows that it is symmetric in the variation trends of the multifractal spectrum parameters of the frictional vibrations and the friction coefficients within the same lubrications. The multifractal spectra and their parameters can characterize the nonlinear characteristics of the frictional vibrations.
- (2)
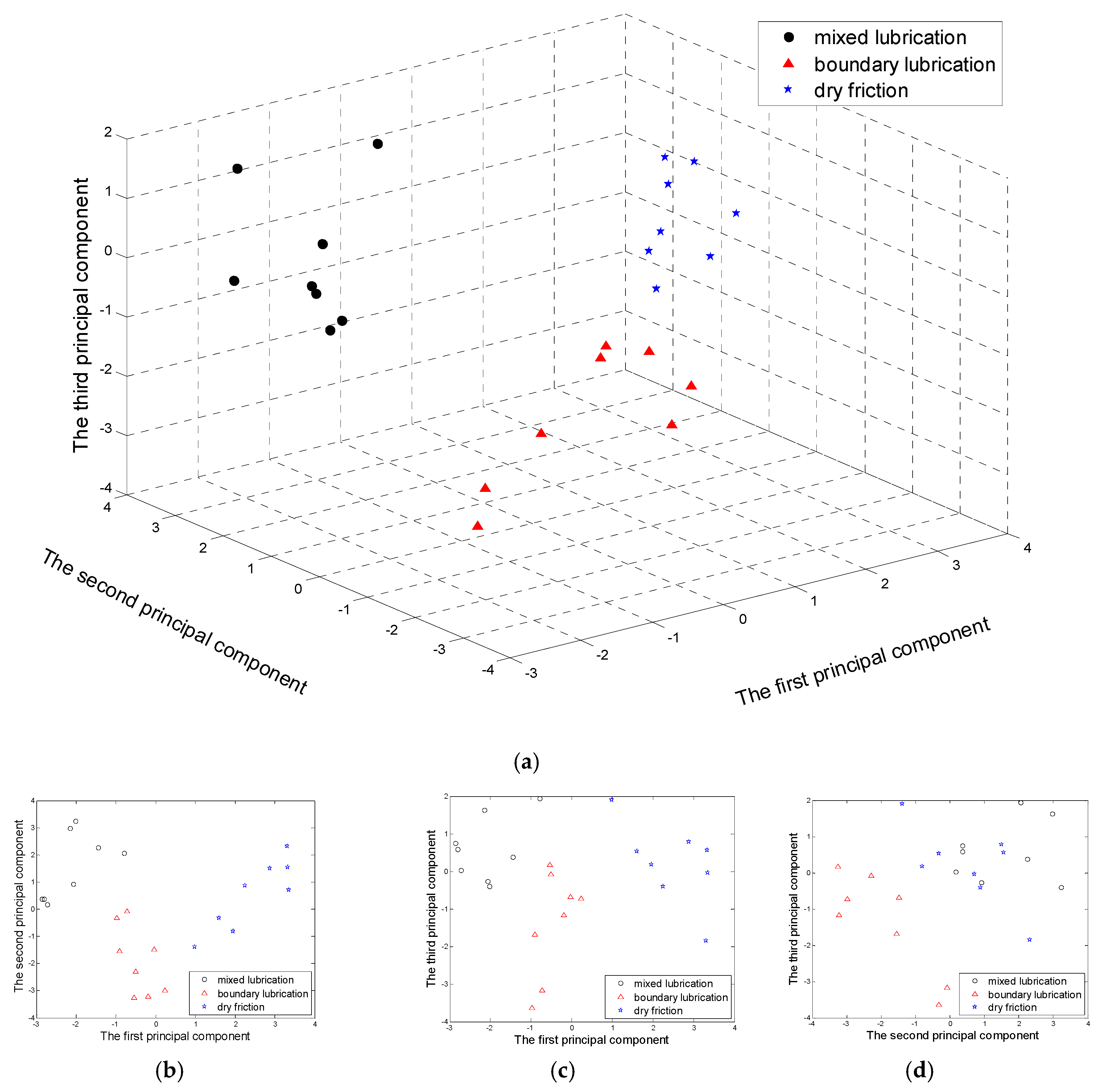
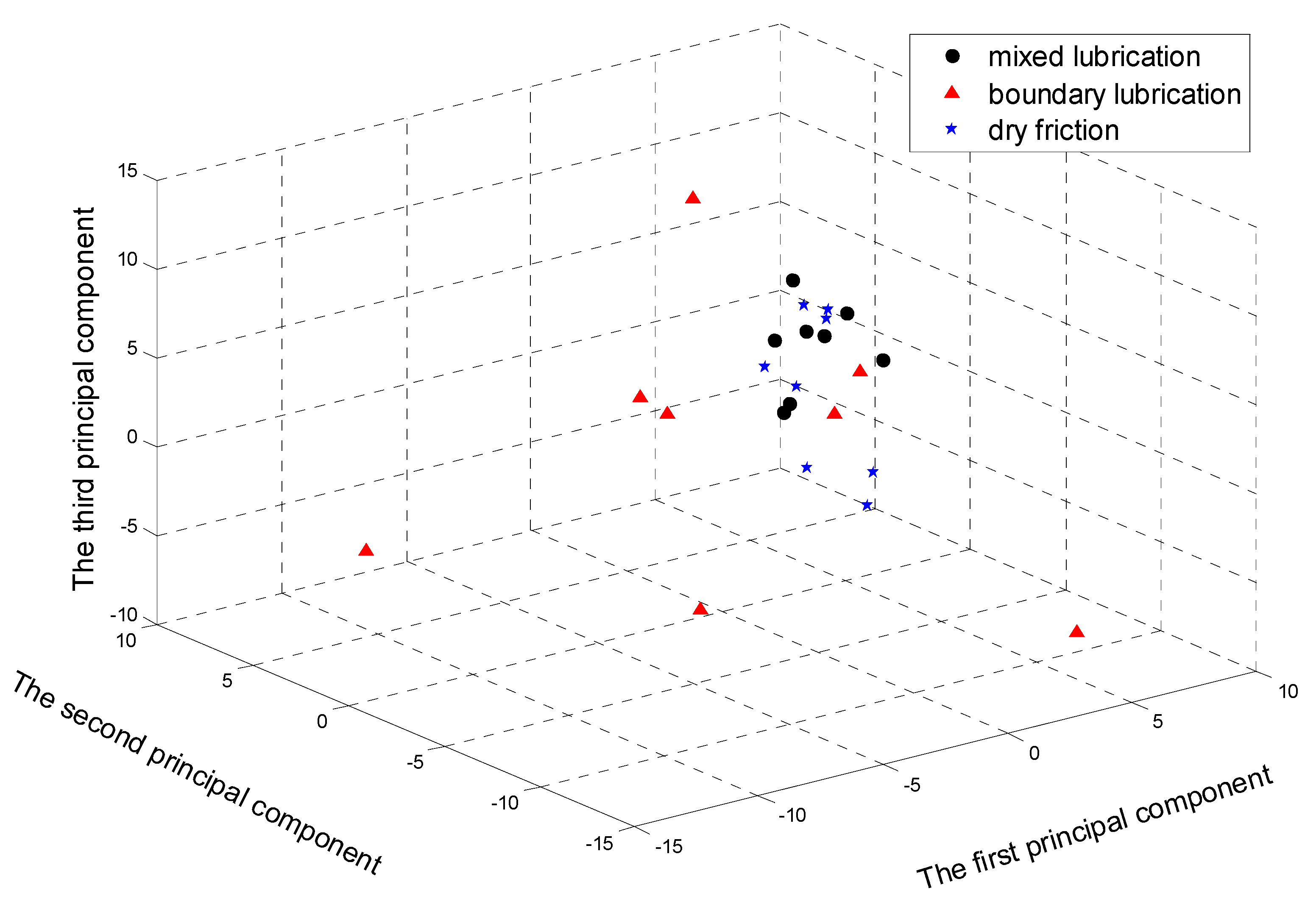
- The principal component analysis based on the multifractal spectrum parameters of the frictional vibrations can realize the friction state recognition. The first three components of the frictional vibration multifractal spectrum parameters of the mixed lubrication, boundary lubrication and dry friction have their respective positions in a three-dimensional space and close to each other with different states in different spatial zones. The multifractal spectrum parameters of the frictional vibrations can be used to identify the friction states of the friction pair.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Miler, D.; Hoic, M.; Domitran, Z.; Zezelj, D. Prediction of friction coefficient in dry-lubricated polyoxymethylene spur gear pairs. Mech. Mach. Theory 2019, 138, 205–222. [Google Scholar] [CrossRef]
- Zhou, C.J.; Hu, B.; Qian, X.L.; Han, X. A novel prediction method for gear friction coefficients based on a computational inverse technique. Tribol. Int. 2018, 127, 200–208. [Google Scholar] [CrossRef]
- Goncalves, D.; Cousseau, T.; Gama, A.; Gampos, A.V.; Seabra, J.H.O. Friction torque in thrust roller bearings lubricated with greases, their base oils and bleed-oils. Tribol. Int. 2017, 107, 306–319. [Google Scholar] [CrossRef]
- Zhu, H.; Ge, S.R.; Huang, X. Experimental study on the characterization of worn surface topography with characteristic roughness parameter. Wear 2003, 255, 309–314. [Google Scholar] [CrossRef]
- Ge, S.R.; Chen, G.X.; Zhang, X.Y. Fractal characterization of wear particle accumulation in the wear process. Wear 2001, 251, 1227–1233. [Google Scholar]
- Li, J.M.; Wei, H.J.; Mei, L.Q.; Xu, D.Z. Frictional vibration signal analysis using empirical mode decomposition and rescaled range analysis. J. Shanghai Mari. Univ. 2016, 2, 89–93. [Google Scholar]
- Ge, S.R.; Zhu, H. Complicate Tribological Systems and Quantitative Study Methods of Their Problems. Tribology 2002, 22, 405–408. [Google Scholar]
- Jaeyoung, K. Lyapunov exponent of friction-induced vibration under smooth friction curve. J. Mech. Sci. Technol. 2018, 32, 3563–3567. [Google Scholar]
- Liu, T.; Li, G.B.; Wei, H.J.; Sun, D. Experimental observation of cross correlation between tangential friction vibration and normal friction vibration in a running-in process. Tribol. Int. 2016, 97, 77–88. [Google Scholar] [CrossRef]
- Sun, D.; Li, G.B.; Wei, H.J.; Liao, H.F.; Liu, T. Investigation on frictional vibration behavior of friction pair under different wear state. J. Tribol. Trans. ASME 2015, 137, 021606. [Google Scholar] [CrossRef]
- Rouzic, J.; Bot, A.; Perret-Liaudet, J. Friction-Induced Vibration by Stribeck’s Law: Application to Wiper Blade Squeal Noise. Tribol. Lett. 2013, 49, 563–572. [Google Scholar] [CrossRef]
- Wernitz, B.A.; Hoffmann, N.P. Recurrence analysis and phase space reconstruction of irregular vibration in friction brakes. Signatures of chaos in steady sliding. J. Sound Vibr. 2012, 331, 3887–3896. [Google Scholar] [CrossRef]
- Nadim, A.E.; Hamzeh, T.M.; Montasser, S.T. Stick-slip detection through measurement of near field noise. J. Mech. Eng. Res. 2011, 3, 96–102. [Google Scholar]
- Zhu, H.; Lu, B.B.; Li, J.Q.; Ji, C.C. Nonlinear theory and methods of researching tribological problems. J. Mech. Eng. 2010, 46, 82–88. [Google Scholar] [CrossRef]
- Li, G.B.; Huang, Y.H.; Lin, Y.H.; Pan, X.X. Multifractal analysis of frictional vibration in the running-in process. Tribol. Trans. 2013, 56, 284–289. [Google Scholar] [CrossRef]
- Zhu, H.; Ge, S.R. Chaotic characteristics of tribological systems. Chin. J. Mech. Eng. 2004, 40, 10–13. [Google Scholar] [CrossRef]
- Sun, D.; Li, G.B.; Wei, H.J. Experimental study on the chaotic attractor evolvement of the friction vibration in a running-in process. Tribol. Int. 2015, 88, 290–297. [Google Scholar] [CrossRef]
- Zhu, H.; Ge, S.R.; Cao, X.C. The changes of fractal dimensions of frictional signals in the running-in wear process. Wear 2007, 263, 1502–1507. [Google Scholar] [CrossRef]
- Zuo, X.; Tan, Y.; Zhou, Y.K.; Zhu, H.; Fang, H.F. Multifractal analysis of three-dimensional surface topographies of GCr15 steel and H70 brass during wear process. Measurement 2018, 125, 196–218. [Google Scholar] [CrossRef]
- Philippopoulos, K.; Kalamaras, N.; Tzanis, C.G.; Deligiorgi, D.; Koutsogiannis, I. Multifractal detrended fluctuation analysis of temperature reanalysis data over Greece. Atmosphere 2019, 10, 336. [Google Scholar] [CrossRef]
- Laib, M.; Telesca, L.; Kanevski, M. Long-range fluctuations and multifractality in connectivity density time series of a wind speed monitoring network. Chaos 2018, 28, 033108. [Google Scholar] [CrossRef] [PubMed]
- Gunay, S. Performance of the multifractal model of asset returns (MMAR): Evidence from emerging stock markets. Int. J. Financial Stud. 2016, 4, 11. [Google Scholar] [CrossRef]
- Shang, P.J.; Lu, Y.B.; Kamae, S. Detecting long-range correlations of traffic time series with multifractal detrended fluctuation analysis. Chaos Solitons Fractals 2008, 36, 82–90. [Google Scholar] [CrossRef]
- Li, J.M.; Wei, H.J.; Wei, L.D.; Fan, L. Multifractal Detrended Fluctuation Analysis of Frictional Vibration Signals in the Running-in Wear Process. Tribol. Lett. 2017, 65, 50. [Google Scholar] [CrossRef]
- Subhakar, D.; Chamdrasekhar, E. Reservoir characterization using multifractal detrended fluctuation analysis of geophysical well-log data. Physica A 2016, 445, 57–65. [Google Scholar] [CrossRef]
- Dutta, S. Multifractal properties of ECG patterns of patients suffering from congestive heart failure. J. Stat. Mech. 2010, 12, 1–14. [Google Scholar] [CrossRef]
- Vitanov, N.K.; Hoffmann, N.P.; Wernitz, B. Nonlinear time series analysis of vibration data from a friction brake: SSA, PCA, and MFDFA. Chaos Solitons Fractals 2014, 69, 90–99. [Google Scholar] [CrossRef]
- McMahan, W.; Kuchenbecker, K.J. Spectral subtraction of robot motion noise for improved event detection in tactile acceleration signals. EuroHaptics 2012, 7282, 326–337. [Google Scholar]
- Chen, R.X.; Tang, B.P.; Ma, J.H. Adaptive de-noising method based on ensemble empirical mode decomposition for vibration signal. J. Vibr. Shock 2012, 31, 82–86. [Google Scholar]
- Wen, S.Z.; Huang, P.; Tian, Y. Principles of Tribology; Tsinghua University Press: Beijing, China, 2018. [Google Scholar]
- Peng, C.K.; Buldyrev, S.V.; Havlin, S.; Simons, M.; Goldberger, A.L. Mosaic organization of dna nucleotides. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 1994, 49, 1685–1689. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny, E. Multifractal detrended fluctuation analysis of nonstationary time series. Physica A 2002, 316, 87–114. [Google Scholar] [CrossRef]
- Ihlen, E.A.F. Introduction to multifractal detrended fluctuation analysis in Matlab. Front. Physiol. 2012, 141, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Feder, J. Fractals; Plenum Press: New York, NY, USA, 1988. [Google Scholar]
- Zia, R.K.P.; Redish, E.F.; McKay, S.R. Making sense of the Legendre transform. Am. J. Phys. 2009, 7, 614–622. [Google Scholar] [CrossRef]
- Bai, X.Q.; Xie, G.T.; Fan, H.; Peng, Z.X.; Yuan, C.Q.; Yan, X.P. Study on biomimetic preparation of shell surface microstructure for ship antifouling. Wear 2013, 306, 285–295. [Google Scholar] [CrossRef]
- Li, W.; Peng, M.J.; Wang, Q.Z. False alarm reducing in PCA method for sensor fault detection in a nuclear power plant. Ann. Nucl. Energy 2018, 118, 131–139. [Google Scholar] [CrossRef]
- Valle, S.; Li, W.H.; Qin, S.J. Selection of the number of principal components: The variance of the reconstruction error criterion with a comparison to other methods. Ind. Eng. Chem. Res. 1999, 38, 4389–4401. [Google Scholar] [CrossRef]
- Li, G.; Hu, Y. An enhanced PCA-based chiller sensor fault detection method using ensemble empirical mode decomposition based denoising. Energy Build. 2019, 183, 311–324. [Google Scholar] [CrossRef]
- Zhang, S.; Tang, Q.; Lin, Y.; Tang, Y. Fault detection of feed water treatment process using PCA-WD with parameter optimization. ISA Trans. 2017, 68, 313–326. [Google Scholar] [CrossRef]



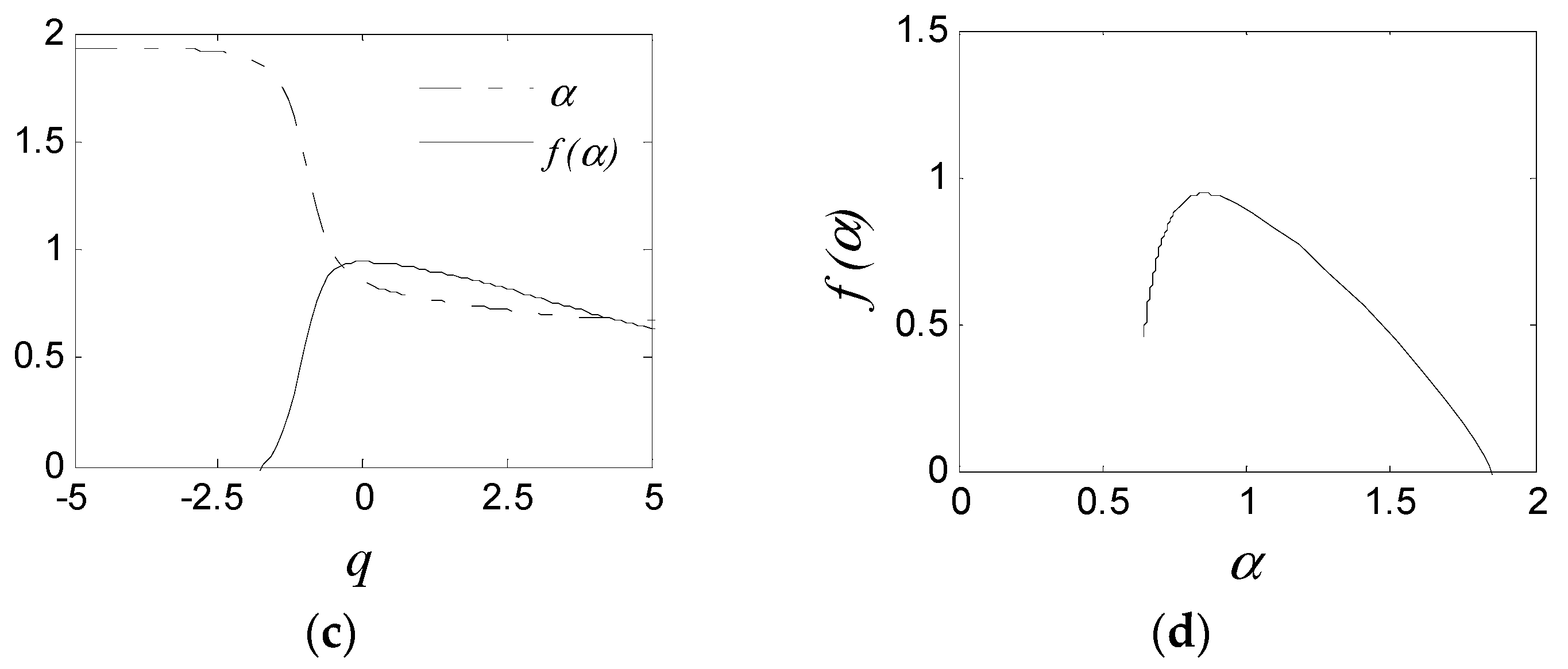

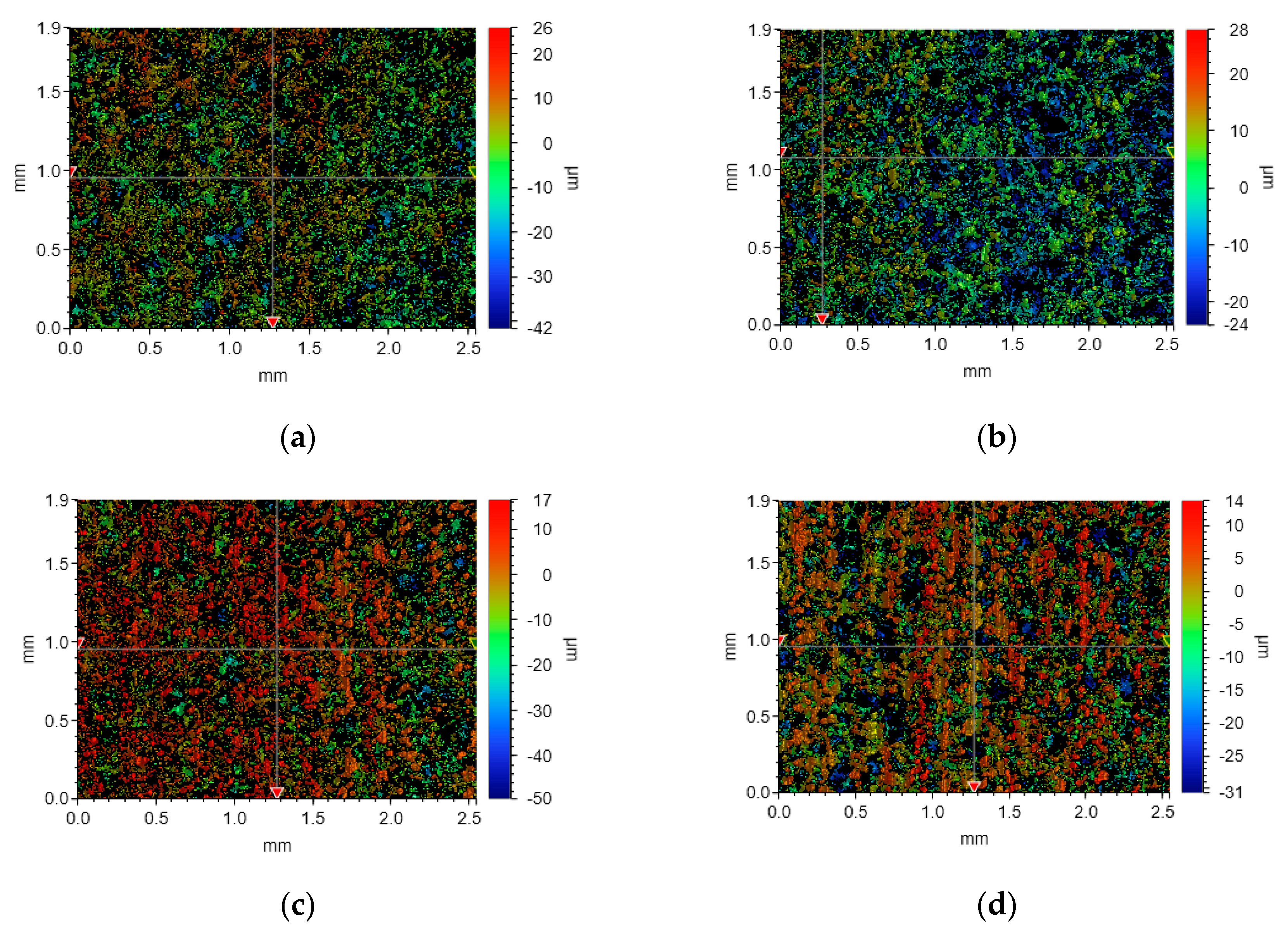
| Parameters | Block Specimen Initial | End of Mixed Lubrication | End of Boundary Lubrication | End of Dry Friction |
|---|---|---|---|---|
| Sa (μm) | 4.749 | 3.185 | 2.524 | 2.787 |
| Ssk | −0.693 | −0.51 | −1.376 | −1.833 |
| Sz (μm) | 63.785 | 54.635 | 36.367 | 37.756 |
| Principal Component | Eigenvalues | Percent Variance% |
|---|---|---|
| The first | 5.8786 | 48.9889 |
| The second | 3.4176 | 28.4801 |
| The third | 1.7415 | 14.5121 |
| Principal Component | Cumulative Percent Variance (CPV)% |
|---|---|
| The first | 48.9889 |
| The first + the second | 77.4690 |
| The first + the second + the third | 91.9811 |
| Mixed Lubrication | Boundary Lubrication | Dry Friction | ||||||
|---|---|---|---|---|---|---|---|---|
| The First Principal Component | The Second Principal Component | The Third Principal Component | The First Principal Component | The Second Principal Component | The Third Principal Component | The First Principal Component | The Second Principal Component | The Third Principal Component |
| −0.7896 | 2.0636 | 1.9273 | −0.9732 | −0.3196 | −3.6385 | 0.9897 | −1.3864 | 1.9019 |
| −1.4366 | 2.2550 | 0.3800 | −0.7220 | −0.0861 | −3.1720 | 1.9564 | −0.8116 | 0.1820 |
| −2.1462 | 2.9779 | 1.6202 | −0.9069 | −1.5494 | −1.6859 | 2.2432 | 0.8836 | −0.3994 |
| −2.0151 | 3.2316 | −0.4073 | −0.5071 | −2.2932 | −0.0743 | 1.5996 | −0.3241 | 0.5384 |
| −2.0641 | 0.9125 | −0.2715 | −0.0323 | −1.4850 | −0.6901 | 3.3515 | 0.7103 | −0.0342 |
| −2.7968 | 0.3663 | 0.5866 | −0.1894 | −3.2170 | −1.1709 | 3.3065 | 2.3175 | −1.8440 |
| −2.8594 | 0.3683 | 0.7395 | 0.2357 | −2.9844 | −0.7245 | 3.3298 | 1.5562 | 0.5675 |
| −2.7226 | 0.1705 | 0.0153 | −0.5426 | −3.2542 | 0.1757 | 2.8816 | 1.5018 | 0.7907 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.-M.; Wei, H.-J.; Wei, L.-D.; Zhou, D.-P.; Qiu, Y. Extraction of Frictional Vibration Features with Multifractal Detrended Fluctuation Analysis and Friction State Recognition. Symmetry 2020, 12, 272. https://doi.org/10.3390/sym12020272
Li J-M, Wei H-J, Wei L-D, Zhou D-P, Qiu Y. Extraction of Frictional Vibration Features with Multifractal Detrended Fluctuation Analysis and Friction State Recognition. Symmetry. 2020; 12(2):272. https://doi.org/10.3390/sym12020272
Chicago/Turabian StyleLi, Jing-Ming, Hai-Jun Wei, Li-Dui Wei, Da-Ping Zhou, and Ye Qiu. 2020. "Extraction of Frictional Vibration Features with Multifractal Detrended Fluctuation Analysis and Friction State Recognition" Symmetry 12, no. 2: 272. https://doi.org/10.3390/sym12020272
APA StyleLi, J.-M., Wei, H.-J., Wei, L.-D., Zhou, D.-P., & Qiu, Y. (2020). Extraction of Frictional Vibration Features with Multifractal Detrended Fluctuation Analysis and Friction State Recognition. Symmetry, 12(2), 272. https://doi.org/10.3390/sym12020272





