Variable Viscosity Effects on Unsteady MHD an Axisymmetric Nanofluid Flow over a Stretching Surface with Thermo-Diffusion: FEM Approach
Abstract
1. Introduction
2. Mathematical Formulation
3. Finite Element Method Solutions
3.1. Variational Formulations
3.2. Finite Element Formulations
4. Results and Discussion
5. Conclusions
- The velocity of fluid declines with the increasing values of suction, Hartmann number, stretching sheet, and unsteadiness parameters.
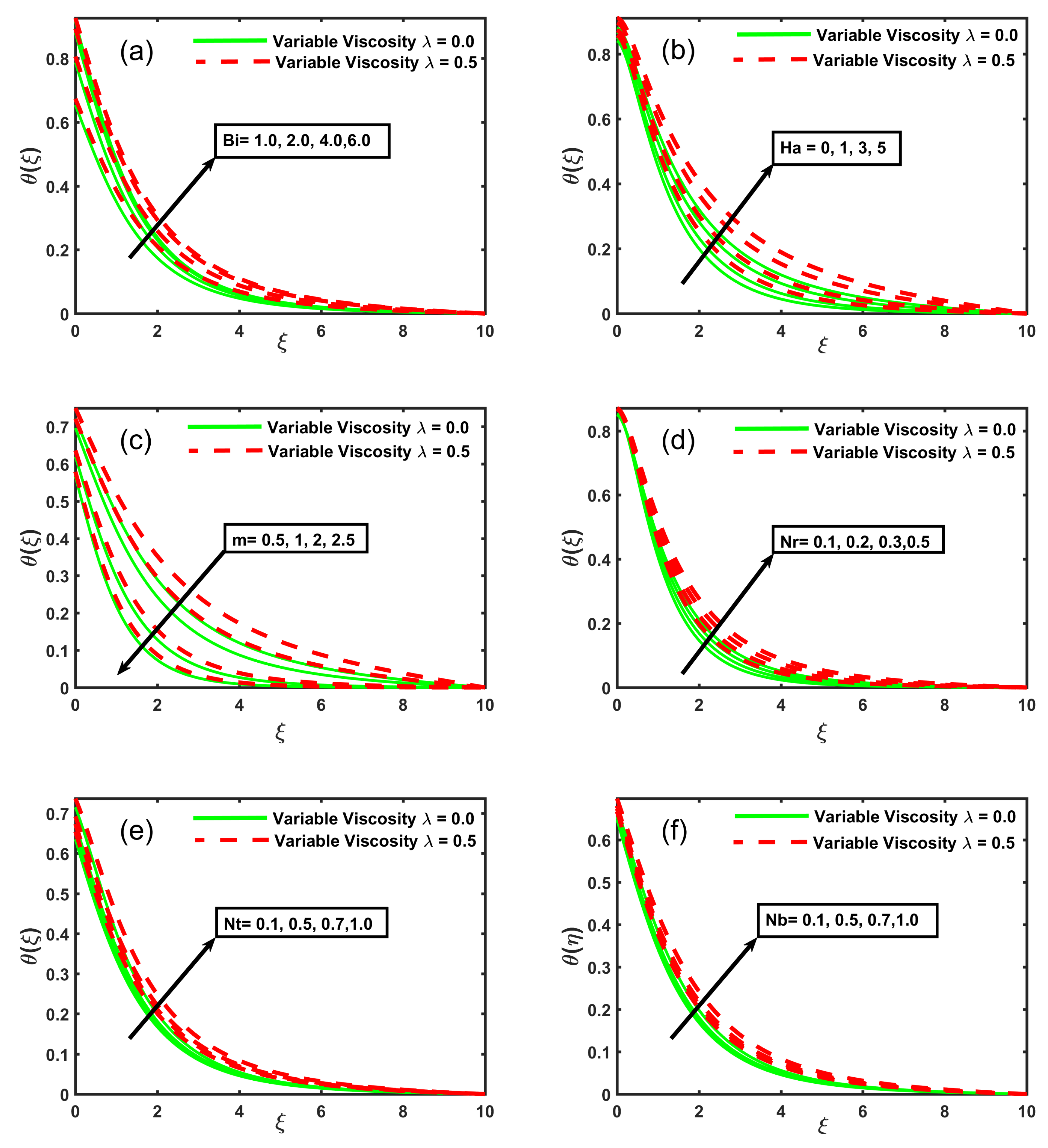
- The temperature rises with the increasing values of Hartmann number, radiation, thermophoresis, Brownian motion, and Biot number parameters.
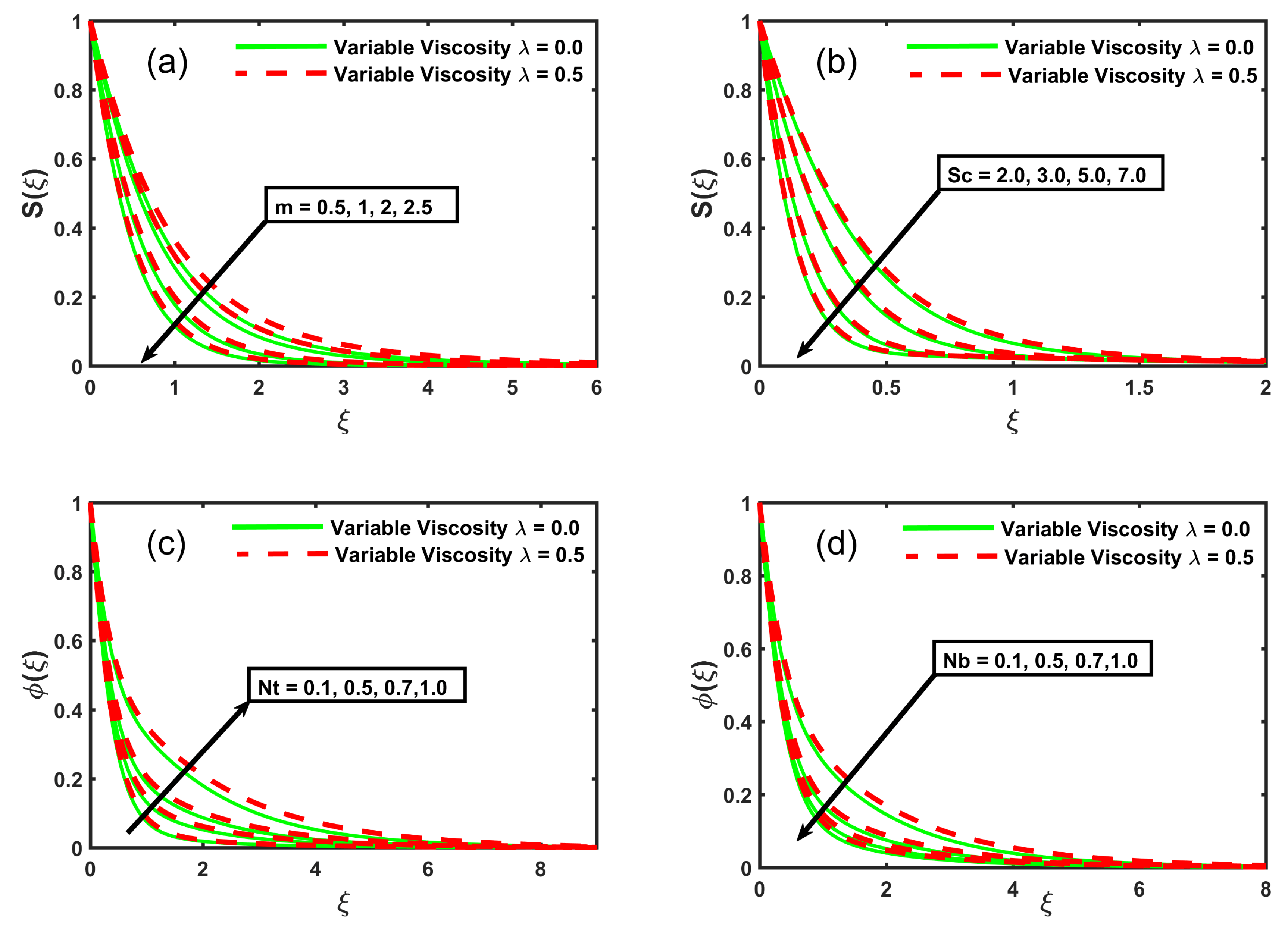
- The solutal concentration profile illustrates a decreasing impact with the growing of the stretching sheet parameter and the Schmidt number.
- The concentration profile of nanoparticles indicates a decline with the growing values of the Brownian motion, Moreover, the elevation of the thermophoresis parameter enhances the concentration profile of nanoparticles.
- The growing values of the viscosity parameter decline the velocity of nanofluid but elevates the concentration and temperature profiles.
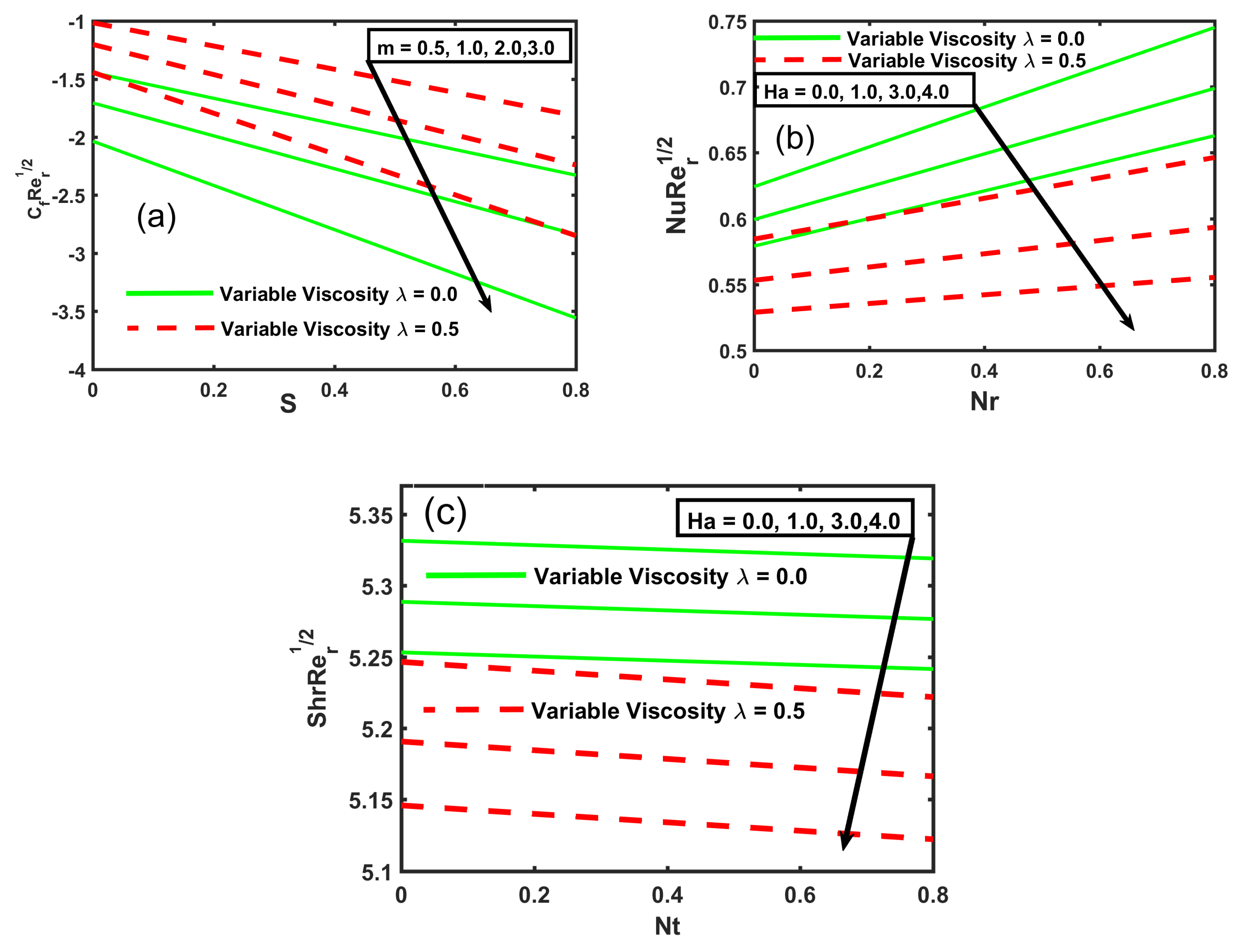
- An increase in the magnitude of skin friction coefficient, Nusselt number, and Sherwood number can be detected with the growing viscosity parameter values, stretching sheet parameter, and Hartmann number; however, for the magnitude of Nusselt and Sherwood numbers against Hartman number, an opposite behavior was noted.
- The decline in Nusselt number and Sherwood number magnitude was recorded with the increasing viscosity parameter values and Biot number, but an opposite behavior was recorded for the magnitude of Nusselt and Sherwood numbers against Schmidt number.
- The present study was restricted to the unsteady state flow and neglected the slip effects at the sheet. For future study, stagnation point flow with viscous dissipation effects at the sheet will be examined.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Magnetic parameter | |
| Brownian motion parameter | |
| Thermophoresis parameter | |
| Prandtl number | |
| Lewis number | |
| Dufour parameter | |
| Soret parameter | |
| Schmidt number | |
| S | Mass transfer rate at the surface |
| Variable viscosity | |
| Electrical conductivity | |
| Thermal diffusivity | |
| T | Temperature |
| unsteadiness parameter | |
| Biot number | |
| Sheet temperature | |
| Ambient temperature | |
| Solutal concentration | |
| Ambient solutal concentration | |
| Velocity of sheet | |
| Nanoparticle volume fraction | |
| Thermal diffusivity | |
| Molecular diffusivity | |
| Brownian diffusivity | |
| Soret diffusivity | |
| Dufour diffusivity | |
| Dynamic viscosity | |
| Fluid density | |
| Velocity components | |
| test functions |
References
- Aziz, A.; Khan, W.A.; Pop, I. Free convection boundary layer flow past a horizontal flat plate embedded in porous medium filled by nanofluid containing gyrotactic microorganisms. Int. J. Therm. Sci. 2012, 56, 48–57. [Google Scholar] [CrossRef]
- Choi, S. Enhancing thermal conductivity of fluids with nanoparticle, development and applications of non-newtonian flow. ASME Fluids Eng. Div. 1995, 231, 99–105. [Google Scholar]
- Ariel, P.D. Axisymmetric flow of a second grade fluid past a stretching sheet. Int. J. Eng. Sci. 2001, 39, 529–553. [Google Scholar] [CrossRef]
- Mustafa, M.; Hayat, T.; Alsaedi, A. Axisymmetric flow of a nanofluid over a radially stretching sheet with convective boundary conditions. Curr. Nanosci. 2012, 8, 328–334. [Google Scholar] [CrossRef]
- Akbari, O.A.; Toghraie, D.; Karimipour, A.; Marzban, A.; Ahmadi, G.R. The effect of velocity and dimension of solid nanoparticles on heat transfer in non-Newtonian nanofluid. Phys. E Low-Dimens. Syst. Nanostruct. 2017, 86, 68–75. [Google Scholar] [CrossRef]
- Mohyud-Din, S.T.; Khan, U.; Ahmed, N.; Rashidi, M.M. A study of heat and mass transfer on magnetohydrodynamic (MHD) flow of nanoparticles. Propuls. Power Res. 2018, 7, 72–77. [Google Scholar] [CrossRef]
- Raza, J. Thermal radiation and slip effects on magnetohydrodynamic (MHD) stagnation point flow of Casson fluid over a convective stretching sheet. Propuls. Power Res. 2019. [Google Scholar] [CrossRef]
- Ashraf, M.; Bashir, S. Numerical simulation of MHD stagnation point flow and heat transfer of a micropolar fluid towards a heated shrinking sheet. Int. J. Numer. Methods Fluids 2012, 69, 384–398. [Google Scholar] [CrossRef]
- Chen, C.H. Laminar mixed convection adjacent to vertical, continuously stretching sheets. Heat Mass Transf./Waerme- und Stoffuebertragung 1998, 33, 471–476. [Google Scholar] [CrossRef]
- Sankara, K.K.; Watson, L.T. Micropolar flow past a stretching sheet. Z. Angew. Math. Phys. 1985, 36, 845–853. [Google Scholar] [CrossRef]
- Hamza, E. The magnetohydrodynamic squeeze film. J. Tribol. 1988, 110, 375–377. [Google Scholar] [CrossRef]
- Shahzad, A.; Ali, R.; Hussain, M.; Kamran, M. Unsteady axisymmetric flow and heat transfer over time-dependent radially stretching sheet. Alex. Eng. J. 2017, 56, 35–41. [Google Scholar] [CrossRef]
- Shahzad, A.; Ahmed, J.; Khan, M. On heat transfer analysis of axisymmetric flow of viscous fluid over a nonlinear radially stretching sheet. Alex. Eng. J. 2016, 55, 2423–2429. [Google Scholar] [CrossRef]
- Rana, P.; Bég, O.A. Mixed convection flow along an inclined permeable plate: Effect of magnetic field, nanolayer conductivity and nanoparticle diameter. Appl. Nanosci. 2015, 5, 569–581. [Google Scholar] [CrossRef]
- Thumma, T.; Anwar Bég, O.; Kadir, A. Numerical study of heat source/sink effects on dissipative magnetic nanofluid flow from a nonlinear inclined stretching/shrinking sheet. J. Mol. Liquids 2017, 232, 159–173. [Google Scholar] [CrossRef]
- Seth, G.S.; Sarkar, S. MHD natural convection heat and mass transfer flow past a time dependent moving vertical plate with ramped temperature in a rotating medium with hall effects, radiation and chemical reaction. J. Mech. 2015, 31, 91–104. [Google Scholar] [CrossRef]
- Takhar, H.S.; Agarwal, R.S.; Bhargava, R.; Jain, S. Mixed convection flow of a micropolar fluid over a stretching sheet. Heat Mass Transf./Waerme- und Stoffuebertragung 1998, 34, 213–219. [Google Scholar] [CrossRef]
- Qiu, L.; Zhu, N.; Feng, Y.; Michaelides, E.E.; Żyła, G.; Jing, D.; Zhang, X.; Norris, P.M.; Markides, C.N.; Mahian, O. A review of recent advances in thermophysical properties at the nanoscale: From solid state to colloids. Phys. Rep. 2019. [Google Scholar] [CrossRef]
- Dhanai, R.; Rana, P.; Kumar, L. Critical values in slip flow and heat transfer analysis of non-Newtonian nanofluid utilizing heat source/sink and variable magnetic field: Multiple solutions. J. Taiwan Inst. Chem. Eng. 2016, 58, 155–164. [Google Scholar] [CrossRef]
- Nayak, B.; Mishra, S.R.; Krishna, G.G. Chemical reaction effect of an axisymmetric flow over radially stretched sheet. Propuls. Power Res. 2019, 8, 79–84. [Google Scholar] [CrossRef]
- Ashraf, M.; Batool, K. Mhd Flow and Heat Transfer of a Micropolar Fluid Over a Stretchable Disk. J. Theor. Appl. Mech. 2013, 51, 25–38. [Google Scholar]
- Faraz, F.; Imran, S.M.; Ali, B.; Haider, S. Thermo-diffusion and multi-slip effect on an axisymmetric Casson flow over a unsteady radially stretching sheet in the presence of chemical reaction. Processes 2019, 7, 851. [Google Scholar] [CrossRef]
- Khan, S.A.; Nie, Y.; Ali, B. Multiple Slip Effects on Magnetohydrodynamic Axisymmetric Buoyant Nanofluid Flow above a Stretching Sheet with Radiation and Chemical Reaction. Symmetry 2019, 11, 1171. [Google Scholar] [CrossRef]
- Uddin, M.; Rana, P.; Bég, O.A.; Ismail, A.M. Finite element simulation of magnetohydrodynamic convective nanofluid slip flow in porous media with nonlinear radiation. Alex. Eng. J. 2016, 55, 1305–1319. [Google Scholar] [CrossRef]
- Kumar, L. Finite-element analysis of transient heat and mass transfer in microstructural boundary layer flow from a porous stretching sheet. Comput. Therm. Sci. Int. J. 2014, 6. [Google Scholar] [CrossRef]
- Shankar, B.; Yirga, Y. Unsteady heat and mass transfer in MHD flow of nanofluids over stretching sheet with a non-uniform heat source/sink. Int. J. Math. Comput. Stat. Nat. Phys. Eng. 2013, 7, 1248–1255. [Google Scholar]
- Sajid, M.; Hayat, T.; Asghar, S.; Vajravelu, K. Analytic solution for axisymmetric flow over a nonlinearly stretching sheet. Arch. Appl. Mech. 2008, 78, 127–134. [Google Scholar] [CrossRef]
- Khan, M.; Malik, R.; Munir, A.; Shahzad, A. MHD flow and heat transfer of Sisko fluid over a radially stretching sheet with convective boundary conditions. J. Braz. Soc. Mech. Sci. Eng. 2016, 38, 1279–1289. [Google Scholar] [CrossRef]
- Disu, A.; Dada, M. Reynold’s model viscosity on radiative MHD flow in a porous medium between two vertical wavy walls. J. Taibah Univ. Sci. 2017, 11, 548–565. [Google Scholar] [CrossRef][Green Version]
- Gupta, D.; Kumar, L.; Bég, O.A.; Singh, B. Finite element analysis of MHD flow of micropolar fluid over a shrinking sheet with a convective surface boundary condition. J. Eng. Thermophys. 2018, 27, 202–220. [Google Scholar] [CrossRef]
- Bhargava, R.; Rana, P. Finite element solution to mixed convection in MHD flow of micropolar fluid along a moving vertical cylinder with variable conductivity. Int. J. Appl. Math. Mech. 2011, 7, 29–51. [Google Scholar]
- Rana, P.; Bhargava, R.; Bég, O.A. Finite element simulation of unsteady magneto-hydrodynamic transport phenomena on a stretching sheet in a rotating nanofluid. Proc. Inst. Mech. Eng. Part N J. Nanoeng. Nanosyst. 2013, 227, 77–99. [Google Scholar] [CrossRef]
- Reddy, J.N. Solutions Manual for an Introduction to the Finite Element Method; McGraw-Hill: New York, NY, USA, 1993; p. 41. [Google Scholar]
- Ali, L.; Liu, X.; Ali, B.; Mujeed, S.; Abdal, S. Finite Element Simulation of Multi-Slip Effects on Unsteady MHD Bioconvective Micropolar nanofluid Flow Over a Sheet with Solutal and Thermal Convective Boundary Conditions. Coatings 2019, 9, 842. [Google Scholar] [CrossRef]
- Ali, L.; Liu, X.; Ali, B.; Mujeed, S.; Abdal, S. Finite Element Analysis of Thermo-Diffusion and Multi-Slip Effects on MHD Unsteady Flow of Casson Nano-Fluid over a Shrinking/Stretching Sheet with Radiation and Heat Source. Appl. Sci. 2019, 9, 5217. [Google Scholar] [CrossRef]
- Ibrahim, W.; Gadisa, G. Finite Element Method Solution of Boundary Layer Flow of Powell-Eyring Nanofluid over a Nonlinear Stretching Surface. J. Appl. Math. 2019, 2019. [Google Scholar] [CrossRef]
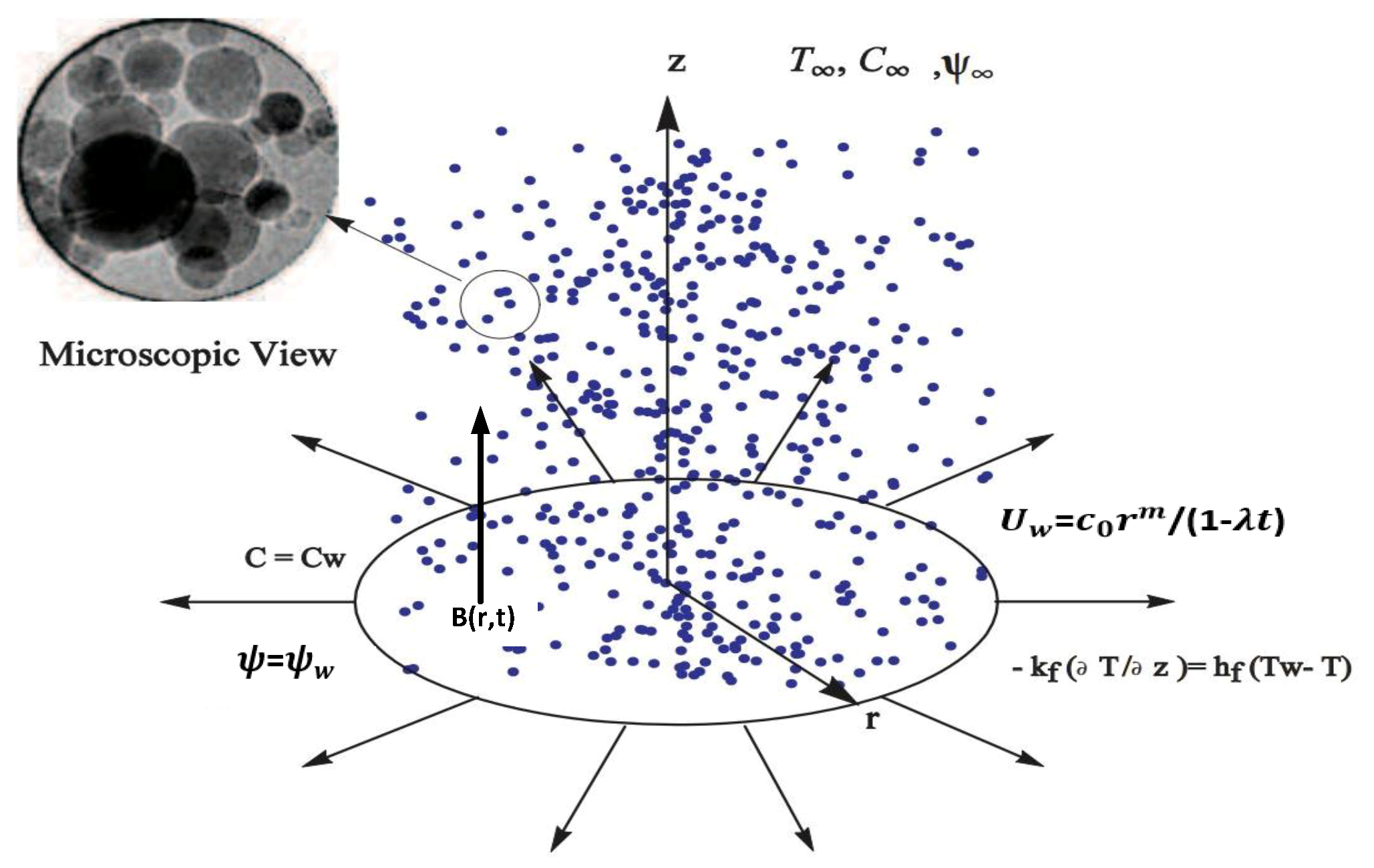

| Number of Elements | |||||
|---|---|---|---|---|---|
| 100 | 0.643350 | 0.031597 | 0.019678 | 0.389363 | 0.130666 |
| 200 | 0.644363 | 0.031894 | 0.019659 | 0.388431 | 0.130627 |
| 400 | 0.644616 | 0.031968 | 0.019656 | 0.388199 | 0.130617 |
| 600 | 0.644663 | 0.031982 | 0.019655 | 0.388156 | 0.130616 |
| 700 | 0.644673 | 0.031984 | 0.019655 | 0.388147 | 0.130615 |
| 1000 | 0.644687 | 0.031989 | 0.019654 | 0.388134 | 0.130615 |
| 1200 | 0.644691 | 0.031989 | 0.019654 | 0.388130 | 0.130615 |
| 1300 | 0.644692 | 0.031990 | 0.019654 | 0.388130 | 0.130615 |
| S | Azeem et al. [12] | Faraz et al. [22] | (Our Results) | |
|---|---|---|---|---|
| (HAM) | (KBM) | (FEM) | ||
| −1.0 | 0.5 | 0.620400 | 0.620436 | 0.620437 |
| −0.5 | 0.887200 | 0.887247 | 0.887247 | |
| 0.0 | 1.308999 | 1.308670 | 1.308668 | |
| 0.5 | 1.907999 | 1.907973 | 1.907973 | |
| 1.0 | 2.655999 | 2.655591 | 2.655588 | |
| 0.5 | 0.0 | 1.798999 | 1.798668 | 1.798667 |
| 0.5 | 1.907999 | 1.907973 | 1.907972 | |
| 1.0 | 2.016999 | 2.016665 | 2.016667 |
| Mustafa et al. [4] | FEM (Present Results) | |||||
|---|---|---|---|---|---|---|
| 0.1 | 1.0 | 1.00 | 0.088980 | 0.793545 | 0.088980 | 0.793541 |
| 0.4 | 0.266901 | 0.676928 | 0.266900 | 0.676926 | ||
| 1.0 | 0.443452 | 0.561546 | 0.443450 | 0.561546 | ||
| 2.0 | 0.567859 | 0.480446 | 0.567857 | 0.480448 | ||
| 0.5 | 0.4 | 1.00 | 0.310557 | 0.193614 | 0.310540 | 0.195635 |
| 0.7 | 0.308900 | 0.446367 | 0.308899 | 0.446420 | ||
| 2.0 | 0.305905 | 1.160300 | 0.305904 | 1.160294 | ||
| 10.0 | 0.303021 | 3.222890 | 0.303021 | 3.222894 | ||
| 0.5 | 1.00 | 0.40 | 0.230078 | 0.710803 | 0.230424 | 0.711456 |
| 0.72 | 0.281948 | 0.671917 | 0.281951 | 0.671938 | ||
| 2.00 | 0.353934 | 0.605337 | 0.353933 | 0.605334 | ||
| 10.0 | 0.422650 | 0.515390 | 0.422649 | 0.515386 | ||
| m | Variable Viscosity | Variable Viscosity | |||||||
|---|---|---|---|---|---|---|---|---|---|
| , | , | ||||||||
| 1.0 | 1.0 | 1.0 | 5.0 | 1.917015 | 0.197352 | 1.966102 | 1.500390 | 0.160016 | 1.887431 |
| 3.0 | 2.531770 | 0.249901 | 2.677550 | 2.030868 | 0.222542 | 2.586780 | |||
| 5.0 | 3.066937 | 0.282943 | 3.365334 | 2.500620 | 0.260220 | 3.268914 | |||
| 1.0 | 1.0 | 1.0 | 5.0 | 1.917015 | 0.197352 | 1.966102 | 1.500390 | 0.160016 | 1.887431 |
| 3.0 | 2.445511 | 0.161933 | 1.897593 | 1.886349 | 0.117210 | 1.812817 | |||
| 5.0 | 2.868619 | 0.137579 | 1.853265 | 2.187080 | 0.091258 | 1.768997 | |||
| 1.0 | 1.0 | 1.0 | 5.0 | 1.917015 | 0.197352 | 1.966102 | 1.500390 | 0.160016 | 1.887431 |
| 2.0 | 1.917015 | 0.234919 | 1.939081 | 1.460656 | 0.181408 | 1.858082 | |||
| 4.0 | 1.917015 | 0.259440 | 1.921454 | 1.436016 | 0.193590 | 1.840234 | |||
| 1.0 | 1.0 | 1.0 | 5.0 | 1.917015 | 0.197352 | 1.966102 | 1.500390 | 0.160016 | 1.887431 |
| 7.0 | 1.917015 | 0.148547 | 2.018283 | 1.472408 | 0.105062 | 1.932371 | |||
| 9.0 | 1.917015 | 0.100783 | 2.070145 | 1.443607 | 0.050675 | 1.976854 | |||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, B.; Naqvi, R.A.; Nie, Y.; Khan, S.A.; Sadiq, M.T.; Rehman, A.U.; Abdal, S. Variable Viscosity Effects on Unsteady MHD an Axisymmetric Nanofluid Flow over a Stretching Surface with Thermo-Diffusion: FEM Approach. Symmetry 2020, 12, 234. https://doi.org/10.3390/sym12020234
Ali B, Naqvi RA, Nie Y, Khan SA, Sadiq MT, Rehman AU, Abdal S. Variable Viscosity Effects on Unsteady MHD an Axisymmetric Nanofluid Flow over a Stretching Surface with Thermo-Diffusion: FEM Approach. Symmetry. 2020; 12(2):234. https://doi.org/10.3390/sym12020234
Chicago/Turabian StyleAli, Bagh, Rizwan Ali Naqvi, Yufeng Nie, Shahid Ali Khan, Muhammad Tariq Sadiq, Ateeq Ur Rehman, and Sohaib Abdal. 2020. "Variable Viscosity Effects on Unsteady MHD an Axisymmetric Nanofluid Flow over a Stretching Surface with Thermo-Diffusion: FEM Approach" Symmetry 12, no. 2: 234. https://doi.org/10.3390/sym12020234
APA StyleAli, B., Naqvi, R. A., Nie, Y., Khan, S. A., Sadiq, M. T., Rehman, A. U., & Abdal, S. (2020). Variable Viscosity Effects on Unsteady MHD an Axisymmetric Nanofluid Flow over a Stretching Surface with Thermo-Diffusion: FEM Approach. Symmetry, 12(2), 234. https://doi.org/10.3390/sym12020234









