Abstract
In view of the problems such as low efficiency, difficulty in resolving local conflicts and lack of practical application scenarios, existing in the interaction model of multi-agent systems in a distributed environment, a multi-master multi-slave interaction model was designed based on the Stackelberg game, which is applied to the interaction game problem between the controller and the participant in the command and control process. Through optimizing the Stackelberg game model and multi-attribute decision-making, the multi-master, multi-slave, multi-agent system of the Stackelberg game was designed, and the closed loop problem under the Stackelberg game is solved for dimension reduction and optimal function value. Finally, through the numerical derivation simulation and the training results of related system data, the high efficiency and strong robustness of the model were verified from multiple perspectives, and this model algorithm was proved to be true and highly efficient.
1. Introduction
With the rapid development of network information technology, intelligent command and control is widely applied in military, network, biological and other fields to realize intelligent control, and it has a high degree of sensitivity and accuracy in information task management and command control [1]. In this paper, a multi-master and multi-slave Stackelberg game model was proposed. Command and control behavior modeling is an important part of military analysis simulation [2]. In the current dynamically changing battlefield environment, whether command and control can meet the requirements of rapid information collection and real-time decision-making is a crucial link [3]. A command and control software system enables commanders, staff officers, and other participants to exchange the information about mission information (commands) and situational awareness status (reports) [4]. In order to effectively manage emergencies, crises and disasters, different organizations and their command and control and sensing systems must continuously cooperate, exchange and share data information [5]. As the technologies including network physical system, pervasive computing, embedded systems, mobile ad-hoc network, wireless sensor networks, cellular networks, wearable computing, cloud computing, big data analysis and intelligent agent have created an environment with various heterogeneous functions and protocols, adaptive control is required to realize useful links and modification of users. In military applications, completely different IoT devices need to be integrated into a common platform that must interoperate with dedicated military protocols, data structures and systems [6]. The effectiveness of military organizations mainly depends on the command and control structure. Sun, Y [7] et al. studied the C2 structure design of distributed military organizations, established a multi-objective optimization model to balance and minimize the relative load of decision-makers, and proposed a multi-objective genetic algorithm. Evans J et al. [8] mainly studied how to meet the requirements of the rapid decision-making cycle of tactical command and control. We discussed the security requirements of security packages and how named data networks meet these requirements.
The Stackelberg game is a classic example of the double-level optimization problem, which is often encountered in game theory and economics. These are complex problems with a hierarchical structure, in which one optimization task is nested in another. In recent years, because of the advantages of multi-master multi-slave Stackelberg game, it has been studied deeply in many fields. Emerging mobile cloud computing technologies provide great potentials for mobile terminals to support highly complex applications. Wang Y et al. [9], based on the two-stage Stackelberg game model of multi-master and multi-slave, adopted an acceptable QoE to solve the resource management problem of MCC networks which maximized the utility function of the network. Modern communication networks are becoming highly virtualized, with a two-layer hierarchical structure. Zheng Z et al. [10] combined the optimization method with game theory and proposed an alternate direction multiplier based on multi-master and multi-slave games. This method excites multiple agents to execute the tasks of the controller, so as to meet the corresponding goals of the controller and the agent. Sinha A et al. [11] studied a special case of a multi-cycle, multi-master and multi-slave Stackelberg competition model with nonlinear cost and demand functions and discrete production variables. In literature [12], an asymmetric explicit model was proposed. The framework of Stackelberg game was used to capture the self-interested and hierarchical competitive properties of nodes, which proved the existence and uniqueness of Stackelberg equilibrium. Akbarid et al. proposed a new coordinated structure for a power generation system whereby power generation capacity was deregulated by transmission departments and decentralized capacity expansion planning of the transmission network. In this paper, a two-level Stackelberg game problem with multiple leaders and followers was solved by the diagonalization method [13]. Chen F et al. [14] studied the multi-master and multi-slave coordination problem based on neighborhood network topology. Scheme [15] mainly studied the problem of anti-interference transmission in a UAV (unmanned aerial vehicle) communication network, and a Bayes Stackelberg game method was proposed to describe the competitive relationship between a UAV (user) and jammer, namely, the jammer acts as a leader, and the user acts as a follower of the proposed game, and the jammer and user choose the optimal power control strategy according to their own utility function. Yuan Y et al. [16] studied elastic control under denial of service attack initiated by intelligent attackers. The elastic control system was modeled as a multi-stage hierarchical game with decision levels at the network and physical levels, respectively. Specifically, the interaction between different security agents in the network layer was modeled as a static infinite Stackelberg game.
Aiming at the above two game roles, the interaction model was constructed based on the game relationship, and the optimization model based on the Stackelberg game and the multi-attribute decisions discuss how the accuser and the participant interacted in the distributed collaborative environment. The current multi-agent model of leader-follower architecture still has a closed loop solution that cannot be explained. In fact, many studies have performed a preliminary investigation of it, which provided some insight for this paper. Thai C N et al. [17] studied the performance of closed-loop identification technology and chose an optimal closed-loop identification solution. The flexible transmission system used two recursive closed-loop identification methods and proposed an optimal closed-loop control scheme for the flexible transmission system. In reference [18], the dynamic mean-variance combinatorial optimization problem with deterministic coefficients was studied, and an inherent property of the closed-loop equilibrium solution was obtained for the first time, which proved that this optimization problem really had a unique equilibrium solution. Due to the limitations of the above studies, this paper will demonstrate the existence of the closed-loop solution from the perspective of mathematical derivation and solve the closed-loop solution, prove the reliability and rationality of the closed-loop solution with numerical simulation, and verify the model algorithm through the results of data training.
Based on the command and control model of multi-agent system under the distributed cooperative engagement, the game theories within the multi-agent system were discussed and studied, a multi-master and multi-slave Stackelberg game model was proposed [19]. It took two types of major decisions in the process of operation command as the research objects, one is accuser, namely leader, who is responsible for the command and control of the combat process; The other is the participant, namely, the follower, who is responsible for executing the decision scheme generated by the accuser. Aiming at the above two kinds of game roles, the interaction model was constructed based on the game relationship, and the optimization model based on Stackelberg game and the multi-attribute decisions discuss how the accuser and the participant interacted in the distributed collaborative environment.
Considering the problem presented by the limited individual capability of a single agent, the ability to deal with complex tasks can be enhanced through cooperation among individuals [20], so the multi-agent system has more advantages in dealing with complex tasks. First of all, the multi-agent system has a better battlefield situational awareness than the single-agent system. It can obtain global situational information and has the ability of parallel perception and parallel charge decision-making [21]. Secondly, the ability of a cooperative agent system is stronger than that of a single agent, so a multi-agent system has excellent expansibility and robustness. Finally, based on reasonable battlefield resource deployment and cooperative control between combat units, the multi-agent system with low resource loss was used to replace a single complex system with high resource loss, so as to achieve higher benefits.
2. Relevant Work
2.1. Multi-Agent Interaction Model for Multi-Master and Multi-Slave Stackelberg Game
Due to the low global coupling degree of distributed environments, the strategies are diversified, behavior planning is more complex, and solution space index level is high [22]. As the number of external access agents increases, the behavior of each agent will have a huge impact on the maximization of global benefits [23]. From the perspective of economics, both the accuser and the participant of the task tend to pursue the maximization of their own benefits in the process. Based on this principle, a balanced interaction model of multiple agents must be studied to make each agent meet its own goals on the premise of satisfying the maximum global benefits.
In this section, an agent interaction model based on multi-master and multi-slave Stackelberg game was proposed. In the process that the agent system dealt with complex tasks, the agent was divided into two roles: leader and follower. Based on these two roles, the game interaction model in the command and control system was studied in depth, and the validity and robustness of the game interaction model were demonstrated through numerical calculation and simulation [24]. In addition, the existence and uniqueness of the Stackelberg equilibrium solution in an interactive game were also deduced, and the closed-loop expression of the equilibrium solution was provided.
2.1.1. Optimization Model of Stackelberg Game
Game theory, as a commonly used model method, is used to deal with the issues of competition with multiple participants [25]. Game theory mainly studies the theory that various the decision-makers influence the behavior of each other under competition as well as decision-making equalization, and it is the mathematical theories and methods of the decision-making process to maximize their own profits.
Generally, according to whether there is a binding agreement between game participants, the game mode can be divided into a cooperative game and non-cooperative game. The two parties of a cooperative game [26] have a consistent income direction and a constraint agreement is reached. Otherwise, it is called a non-cooperative game. According to whether the sum of the cost functions of the two sides of the game has a loss, it can be divided into a zero-sum game and a non-zero-sum game. The game can be classified as either a complete information game or incomplete information game according to the players’ mastery of global situation information. According to the different status of each participating member in the Game process, the Game is divided into Nash Game, master slave Game (Stackelberg Game), etc. [27].
The Stackelberg game is a dynamic game, which is used where there is a level of decision behavior between two types of game players [28], one being the leader, and the other a follower. After leading the action, the followers make their own decision plans according to the action plan of the leader, so as to ensure the maximization of the decision benefits of the leader. However, in this paper, the original model was improved, and based on the relevant concept of distributed collaboration, a multi-master and multi-slave game model was established, wherein leader was redefined as the accuser, and the followers were defined as the participants so as to make the accuser adjust the follow-up action plan according to the participants’ decision-making scheme and maintain the benefits of participants to the greatest degree, thus obtaining the maximization of global income. Therefore, the optimal decision-making and response decision-making corresponding to participants constituted the equilibrium of the game [29].
Two types of game participants were defined. The accuser was , and its performance index function was . The participant was , and its performance index function was . The purpose of both parties was to minimize , so as to maximize the benefits of both parties and maximize the global benefits. For any decision made by the accuser, the participants had a unique decision to minimize its performance index function . The mapping relationship between the two parties’ decision choices can be expressed as follows:
At this time, considering the performance index of the accuser , it was assumed that there was a unique solution , i.e., . At this time, was the unique Stackelberg solution.
2.1.2. Multi-Attribute Decision-Making
The multi-attribute decision-making problem is a multi-criterion decision problem. Another multi-criterion decision problem is the multi-objective optimization or multi-objective decision-making problem [30]. The criterion of MADM is often invisible and indirect. Even in many cases, it cannot be accurately described in a quantitative way, while the constraint of MODM must be direct and accurate. MADM’s constraint on the target is often hidden in the attribute, while MODM does not have this feature due to the accuracy of the constraint. In addition, MADM alternatives are often limited, while MODMs can have an infinite number of alternatives [31].
where represents the set of alternatives represents one of the alternatives in , and represents the attributes of the multi-attribute decision problem. Let be the alternative scheme set, the attribute set, and set , where is the attribute value of for . Then, a multi-attribute decision matrix can be constructed, i.e.,. are shown in the following Table 1:

Table 1.
Decision matrix.
At this time, the property value is an estimate. The solving process of the multi-attribute decision-making problem is as follows. First of all, the decision matrix was listed. Ssecondly, according to whether the weight was known, the weight determination method was selected. Thirdly, based on the attribute values of decision matrix, the aggregation operator of the property matrix was determined, and according to the solving target and the form of decision matrix, the appropriate multi-attribute decision-making method was chosen to calculate. The calculation results were carried out with weight distribution and gathering, and eventually the score of each scheme was obtained, and the decisions were made according to the score situation [32].
In this paper, every member of the multi-master and multi-slave Stackelberg game model used multi-attribute decision making as the basic method to generate the decision-making scheme, optimized the weights of the method according to the roles of the decision-makers, and generated the optimal decision scheme according to the final score.
3. Multi-Master and Multi-Slave Stackelberg Game Model in a Distributed Environment
Game theory is widely used in the field of interactive multi-agent systems. The Stackelberg game [33] is a classic game model, and the strategy of various participants in the game is usually made on the basis of the maximization of self-interest, and there is cooperation or non-cooperation between each other. When all participants achieve maximum interests and global interests tend to be steady, this state is called equilibrium state.
The Stackelberg game is a game problem between upper and lower levels, in which each participant belongs to the relationship between upper and lower levels, namely leader and followers [34]. In the game model, the leader generates a decision scheme according to the state prediction of the task objective and the followers, and the followers respond according to the decision scheme of the leader. In the game process, information between leader and followers is not fully shared, that is, the leader’s information is partially shared with followers, but the followers’ information is fully shared with the leader. Considering such a design, the leader’s decision-making scheme constraint is based on the maximization of followers’ revenue, so in Stackelberg game [35], the leader doesn’t need to design a response function.
The main problem of the current multi-master and multi-slave Stackelberg game model is the difficulty in solving the closed loop solution, so the open-loop solution of Stackelberg game is usually the mainstream research object [36]. This section aims to obtain Stackelberg game equilibrium through reasoning, namely, the closed-loop solution of the Stackelberg game. Therefore, in this paper, the retrieval process of the open-loop solution won’t be demonstrated in detail. The closed-loop solution of multi-master and multi-slave Stackelberg game model under the accuser participants has the nonlinear characteristics, there is no explicit solution, so under certain conditions, this paper will use the regularity of a positive semidefinite matrix to give a closed-loop solution to the Stackelberg game, obtain the optimal decision through the accuser, optimize the participants’ decision-making, obtain the optimal decision scheme of participants, and eventually maximize the overall revenue.
3.1. A Closed-Loop Solution of Multi-Master and Multi-Slave Stackelberg Game Model
Under the distributed environment with a certain complexity, the optimal regularity of positive semidefinite quadratic performance index was used to give a closed-loop solution of multi-master and multi-slave Stackelberg game. In this section, a regular Riccati equation was introduced to solve positive semi-definite multi-master and multi-slave Stackelberg game problems, and the main contribution is that it gave a closed loop solution to the Stackelberg game. The general process is as follows: First of all, the optimal decision was obtained in the decision optimization of the accuser. When the decision resulted in the maximum value of the accuser, the value of was the minimum. At this time, the weighted matrix of the control performance index was positive semi-definite, so there were arbitrary terms in the performance index function. Secondly, the participants’ decisions were optimized by continuously using arbitrary terms in , and finally, combined with the solution of the regular Riccati equation, and according to the decision-making optimization process of the accuser and participants, the closed-loop solution of multi-master and multi-slave Stackelberg game problem.
3.2. Problem Description
The linear discrete time system is defined as follows:
where is the state variable of game participants and there is an initial value and it can be determined; is the interference that can be quantified; is the output item; is the input item; and the interference attenuation factor is defined as , whose value range is , then the following performance index function can be obtained:
where is the interference attenuation factor defined above and ; , where is the variance matrix of the initial state .
In this section, the accuser’s optimization and the participants’ decision-making optimization were carried out simultaneously. During the decision-making optimization of the accuser, under any initial environmental conditions , meets . During the decision-making optimization of the participants, for any initial environmental condition , the optimal value was sought to minimize , that is, .
3.3. Closed-Loop Solution of Semidefinite Control in Stackelberg Game
This section will describe the closed-loop solution process in the optimization of the multi-master multi-slave Stackelberg game, and the optimization process of this problem is mainly divided into two parts. The first part is the accuser’s decision-making optimization. By adjusting the value of , the performance index function is minimized, and at the same time, by adjusting , the performance index function is maximized. According to the positive definiteness of the weighted matrix, value contains arbitrary terms. In order to ensure the only decision-making of the accuser, arbitrary terms are used as new decision-making to be solved, and it is obtained from the participants’ decision-making optimization, so as to obtain the accuser’s optimal decision.
- Decision optimization of accuser
As can be seen from the above, the accuser’s decision-making optimization is carried out, that is , where:
where . Firstly, the existence of the accuser’s optimal decision-making scheme is proved:
If the above equation is satisfied, it can be proven that the accuser has an optimal decision, that is, has a definite value, and the optimal solution satisfies Equations (10) and (11). The proof process can be seen in the literature [37].
According to Equations (3) and (9), it can be known that there is a non-secondary linear relationship between variable and , so it is defined as follows:
where and will be defined below.
Substitute Equation (12) into Equation (11), then Equation (11) can be written as follows:
Substitute Equation (12) into Equation (10), and Equation (10) can be written as follows:
where . Since there is an optimal solution for the accuser’s decision making, it can be seen that the weighting matrix is determined, that is , then Equation (14) can be written as follows:
Substitute Equation (15) into Equation (13), the following formula can be obtained:
where in , , and . Assuming that when the weighted matrix is semi-positive definite, may have more than one optimal solution. At this time, it is necessary to introduce the regular Riccati equation to make satisfy the Riccati equation, which can be expressed as follows:
At this time, and , is the pseudo-inverse matrix of . Then it can be obtained , so Equation (12) is true at time . Assuming Equation (12) is true at time k, then , when the range of the two accords with , the following formula can be obtained from Equation (16):
where is an arbitrary term. By substituting Equation (18) into Equation (15), the following formula can be obtained:
By substituting Equations (18), (19), and (12) into (9), the following equation can be obtained:
As meets Equation (17), and , the following formula can be obtained:
It can be concluded from the above that . As can be seen from the above, when (1) ; (2) ; (3) , the following formulas can be obtained:
where is arbitrary vector with appropriate dimension, . Then the optimal decision indicator function is as follows:
The specific proof process can be seen in Appendix A.
- Accuser’s strategy optimization
It was found that there is an arbitrary term in the optimal decision scheme. In order to further optimize the arbitrary item in the optimal decision scheme, we first carry out matrix transformation to transform the arbitrary item into the participants to be solved. An elementary row transformation matrix is introduced to make:
is defined, where , and the following formula can be obtained:
Based on the above analysis, and are rewritten as follows:
By substituting the above formula into the definition of , the following equation can be obtained:
where , . By substituting and into , the following equation can be obtained:
At this time, the decision-making scheme optimization problem of the participants is solved, namely:
The participants’ decision scheme optimization is a standard linear quadratic optimization problem. First of all, the necessary conditions for a solution are given:
If the above equation is true, it indicates that there is an optimal solution to the participants’ decision-making scheme optimization problem. The specific proof process is as follows:
Firstly, the inhomogeneous relation between and is defined as follows:
where and are defined in the following lemma. By combining the definition of and , the following equilibrium equation can be obtained:
where
In order to obtain the explicit solution of the optimal controller , we consider the following situation, that is, the following hypothesis is obtained:
When the control matrix in the performance index of the decision-making scheme of the participants is a semi-positive definite matrix, has no unique solution. Here, the regular Riccati equation is introduced. Under the above regular hypothesis, this paper solves the solution of the regular Riccati equation and verifies the homogeneous relationship between the state variable and the adjoint state variable . Under the above hypothesis, , where:
At this time, , and and . Namely, . If is true at time k, so , and the following formula is obtained:
where is the arbitrary terms with the appropriate dimension. By substituting this formula and into , the following formula can be obtained:
where is applied to the derivation of the above formula, and the following formula can be obtained:
As , it can be concluded that .
Next, the state-space model and the indicator function of the decision scheme are considered. When meets the above assumptions, there is an optimal solution to the optimization problem, when the following conditions are satisfied: (1) ; (2) . The problem is solvable when the optimal solution is met, and the optimal solution is as follows.
where is the arbitrary vector with the appropriate dimension. Then the performance index of the corresponding optimal decision scheme is as follows:
The specific proof process is shown in Appendix B.
At this time, and . Therefore, the optimal decision-making scheme of participants exists, and the optimal accuser-participant decision-making scheme, i.e., the global optimal decision-making scheme, is as follows:
Thus, a closed-loop solution to the Stackelberg game is obtained, and the optimal decision scheme of the accuser, the participant is obtained, and global profit maximization is finally achieved.
3.4. Model Performance Comparison
In this paper, a multi-master, multi-slave Stackelberg game model is designed. Under the same resource deployment situation, the optimization effect and model complexity of the model designed in this paper, and the unimproved model under the same time limit are compared, as shown in the Table 2 and Table 3.

Table 2.
Model iteration efficiency comparison.

Table 3.
Comparison of complexity between time and space of model.
According to the experimental data, after the learning rate is improved adaptively, the function value and the time-space complexity of the model are analyzed under the condition of the same number of iterations, and it is found that the model in this paper can achieve lower objective function values with better convergence and higher efficiency [38].
By comparing the performance of the model, this paper sets the same initial function value and iteration times between the literature model and the model. Finally, under the same iteration times, it can be seen that the model in this paper has better convergence from Table 4.

Table 4.
The comparison of model performance.
4. Numerical Simulation
To verify the validity of the above results, a numerical example is given in this section. Some parameters of the multi-agent system are assumed as follows:
is equal to 4, is equal to . The initial state is . Let , . First of all, the optimization process of is analyzed. Through algebraic iterative operation, the solution of the regular Riccati Equation (17) is obtained as follows:
where . By combining with the results obtained from the above operation, (20) and (21) are calculated, and the optimal controller described in theorem 1 can be obtained as follows:
In the optimization, the solution of the regular Riccati Equation (27) is shown as follows:
The arbitrary term in the decision-making scheme of the participants obtained in the previous optimization process can be transformed into through matrix transformation. The value of obtained by calculating Equation (32) is as follows:
The arbitrary term in Equation (32) is as follows:
Substituting into , and then according to Equation (3), we can get the optimal controller (Equations (52) and (53), respectively):
After calculation, the optimal performance index of norm form is . The optimal performance index of norm form is .
5. The Experimental Simulation
In this section, the air defense of important places in the field of air defense and anti-missile defense is taken as the experimental scene, constraint conditions and objective functions are designed as the simulation environment, and a multi-agent system based on edge Laplace matrix is constructed to analyze the system complexity and verify the reliability and robustness of the system.
5.1. The Description of Simulation Scenario
This chapter will be based on the air defense of important place as the background. Considering the influence of mountains, the algorithm in this chapter will be used to model the multi-agent system, and the system will be used to deploy the battlefield fire unit to verify whether the key points can be defended and the target function value can be achieved under the specified incoming fire.
5.1.1. Parameters Definition
(1) Battlefield environment:
Terrain: mainly flat terrain, some areas for undulating mountains
Area: 300 km × 300 km
Object of protection: important place
(2) Strength formation:
Security object: important place
Security forces: 8 launching vehicles with a running speed of 40 km/h, which can stop shooting for a short time. Each vehicle is equipped with a number of medium range bombs with a range of 50 km and an average speed of 800 m/s; 20 short range bombs with a range of 20 km and an average speed of 600 m/s. There are five radar vehicles with a detection distance of 50 km for cruise missile, 120 km for fighter, 100 km for helicopter, and 80 km for UAV.
(3) Tactical purpose:
The coverage of detection area of one layer shall be more than 85%, that of two layers shall be more than 55%, and that of key areas shall be at least two layers; that of fire area of one layer shall be more than 80%, that of two layers shall be more than 70%, and that of key areas shall be at least three layers.
Resources are the operational objects that command and control the deployment behavior of resources. They are physical resource entities. Resources include fire units and detection units. The set of resources is , and is the number of resources. In this chapter, the platform resources are mainly radar vehicle, launch vehicle, medium range missile and short-range missile.
Command entity: the command entity is the entity that receives situation information, makes decisions, and completes the deployment of fire units, task allocation, situation information interaction, command and decision-making, etc. The collection of charged entities is , and is the number of charged entities. In this model, the command entity is radar vehicle, which belongs to scheme release agent. Each radar vehicle is the same level of command entity, but there is a logic center at some time, which is distributed deployment.
There are four capability parameters of the accusing entity:
- (1)
- How many launching vehicles can each radar vehicle control at the same time is called the control and management ability of the command entity .
- (2)
- How many identical tasks each radar vehicle performs with other radar vehicles is called the cooperation capability of the command entity .
- (3)
- How many tasks can each radar vehicle handle at the same time is called the task processing capacity of decision entity .
- (4)
- How many identical tasks each radar vehicle performs with other radar vehicles is called the decision entity ’s cooperation capability .
5.1.2. Element Definition and Load Design
The following elements need to be defined to describe the deployment of command and control resources:
- (1)
- task to resource assignment capability if task t is assigned to resource , then , otherwise . In this model, the ability variable of task to resource allocation belongs to known quantity.
- (2)
- the control ability of decision-making entity over resources , if resource belongs to decision-making entity , then , otherwise .
- (3)
- assignment ability from task to decision entity. If task is assigned to decision entity , then , otherwise .
Internal workload of decision entity.
The workload that decision entity controls its platform to perform tasks is called ’s internal workload, which is recorded as , and its calculation formula is ’s internal workload, which is recorded as , and its calculation formula is as follows:
where is the execution time of task Ti; is the final completion time of all tasks; is the difficulty of the task; is the weighting coefficient of execution time factor; is the weighting coefficient of task difficulty degree.
Collaborative load between decision entities.
The collaboration load of any two decision entities h and is the workload that and must cooperate to complete the task, which is recorded as , and its calculation formula is as follows:
5.2. Constraint Analysis and Objective Function Design
5.2.1. Constraint Analysis
The constraints of the command and control resource deployment model are analyzed as follows:
The decision entity performs tasks through the platform it controls. Therefore, when at least one platform in the platform controls the variable and , then , otherwise, , that is:
There is an upper capacity limit for the control management ability of each decision-making entity, that is:
In the formula, is the upper limit of control management capacity, and the constraint value of all decision entities is set to be the same in this paper. There is an upper capacity limit for the task processing capacity of each decision entity, namely:
In the formula, is the upper limit of cooperative ability capacity, and the constraint value of all decision entities is set to be the same in this paper. There is an upper capacity limit for the task processing capacity of each decision entity, namely:
In the formula, is the upper limit of cooperation ability. In this paper, all decision entities are set with the same constraint value.
5.2.2. Objective Function Design
As can be seen from the above, the sum of workload of all agents remains the same during the task assignment, while the workload varies with the assignment. According to this characteristic, we want to achieve the optimal, then the total load should be minimized. Let the amount of tasks assigned to each agent be , and the amount of tasks received by each agent be . The workload for all agents is . So if is the smallest, the smaller the total cost, the more reasonable the assignment. Then the objective function is:
After using and in the boundary, the group which makes the smallest is selected.
5.3. System Training Data Demonstration
This section will demonstrate and analyze the system from the perspective of a reinforcement learning network, global gain function and global loss function. When the number of iterations is between 2500 k and 3000 k, the maximum global gain is basically reached and becomes stable.
Experimental background is set to be the deployment of battlefield resources. Figure 1 is the iterative curve map of the stability of multi-agent system, where the horizontal axis is the number of iterations, and the vertical axis is the revenue function of multi-agent system. With the increase of the number of iterations, when the number of iterations reaches 2500 times, the revenue function tends to be stable, which proves that the multi-agent system tends to be stable and has excellent robustness. The details are shown in the following figure:
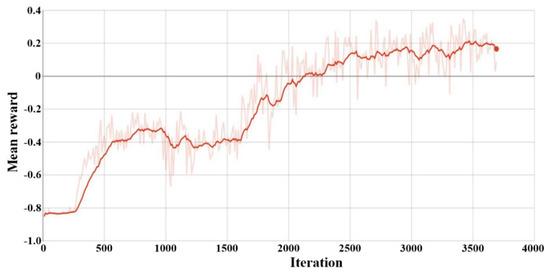
Figure 1.
Global revenue function.
It can be concluded from Figure 1 that, as the training iteration proceeds, the global return gradually increases after a period of time from a low level, during which there is a small range of ups and downs, finally reaches the optimal global return, and tends to converge.
Figure 2 is the graphical display of reinforcement learning network. The 3D coordinate system of reinforcement learning network is established, and every point in the figure represents a performance index of the intelligent agent, and the location represents the index’s specific parameter value and the state function of the intelligent agent at that time. With the increase of the number of iterations, the state transfer of the intelligent agent is carried out, and the coordinate information also changes. There are more than 2000 parameters for the multi-agent system in the command and control system of this paper, and the specific details are shown in Figure 2:
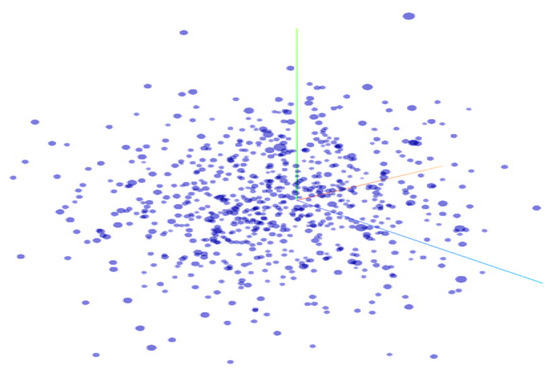
Figure 2.
Training learning network.
As the number of iterations increases, the global gain increases, and as the corresponding global loss gradually decreases, when the algorithm approaches the global optimization, the loss function tends to be stable, with a small range of fluctuations. The change trajectory of the function corresponds to Figure 1, so as to ensure that the total battlefield situation remains unchanged. Figure 3 is the consistency analysis diagram of the multi-agent system. It can be seen from the figure that, with the increase of the number of iterations, when it reaches about 1000 k, the edge state of the intelligent agent tends to balance. Meanwhile, it can be seen that after a certain number of iterative training, the multi-agent system is locally Lipschitz continuous and has excellent consistency. The change trend of the specific loss value function is shown in the figure below:
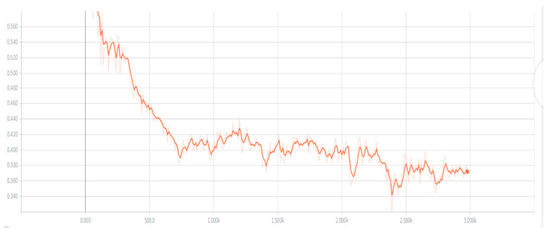
Figure 3.
Global loss function.
It can be concluded from Figure 3 that, at the beginning of the iteration, that the loss value shows a rapid decline. When the number of iterations reaches 500–1000 k, the loss value starts to drop slightly, but the average value declines slowly. When the number of iterations reaches about 1500 k, the loss value starts to become stable and reaches the minimum value of the global loss function.
6. Conclusions
This paper analyzes and solves the game interaction model of the multi-agent system in distributed combat environment, and provides a solution to the accuser participant game problem in the multi-agent system with a semi-positive definite weighted matrix based on the performance index. In order to solve this problem, the optimal decision is first obtained in the accuser’s optimization, in which the size of is controlled to obtain the optimal value of . Due to its semi-positive definite nature and the existence of arbitrary term item in , the arbitrary term obtained before is transformed into the item to be solved in to further optimize after matrix transformation. Based on the above optimization process, the Riccati equation is solved and the closed-loop solution of the multi-master and multi-slave Stackelberg game model is given, which solves the problem of data interaction and local conflict resolution between various intelligent agents in the command and control system. The research of this paper not only broadens the depth of the academic theory of distributed command and control, but also satisfies the interactive game model mechanism in distributed multi-agent systems, which lays a theoretical foundation for intelligent warfare.
Author Contributions
Conceptualization, G.W. and Y.S. Methodology, J.Z. and Y.S. Validation, Y.S. and G.W. Writing—Original Draft Preparation, J.Z. Writing—Review and Editing, X.Y., Y.S., S.Y., J.L. Funding Acquisition, Y.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation, grant number 61703412, the China Postdoctoral Science Foundation fund, grant number 2016 M602996 and National Natural Science Foundation, grant number 61503407.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Based on equation and , the following equation can be obtained:
By summing the above equation from 0 to N in sequence, the following equation can be obtained:
The performance index function of control is updated as follows:
Combined with the previous content, this equation can be rewritten as follows:
At this time, , , and . Combining with the previous content, the optimal decision scheme of the accuser can be obtained, and the optimal performance index can be calculated as shown in the above equation.
Appendix B
Proof of necessity: Suppose the problem has a solution. The optimal decision scheme is verified and obtained by induction. Equation (30) can be written as follows:
When , can be written as the expression of and , as follows:
where
where has a quadratic term, which is a semi-positive definite matrix for any non-zero . At this time, , and the following formula can be obtained:
That is . By combining with the previous formula and , the following formula can be obtained:
At this time, the optimal decision-making scheme parameters of the participants can be defined as follows:
So far, we’ve verified at time . By induction, any k in is selected, and assuming and the optimal decision scheme parameter is consistent with the derivation above when . Then, when , the conditions in this paper are still valid, so has an optimal decision for all . It needs to verify that is a semi-positive definite matrix. Supposing , the quadratic form of in is solved. At this time, the following formula can be obtained:
The two sides of the equation are carried out with summation:
To sum up, can be written as follows:
Assuming that the optimal decision scheme of the participants exists, the minimum value of can be obtained for any . Therefore, . By combining with , the following formula can be obtained:
So can be written as . Combined with the previous text, the following formula can be obtained:
At this point, it is verified that is true at time :
Proof of sufficiency:
The total sum of squares is used to obtain the following formula:
Sum over the above equation from , then:
By substituting into the above equation and combining with Riccati equation, can be described as follows:
Ends.
References
- Wang, F.Y. CC 5.0: Intelligent Command and Control Systems in the Parallel Age. J. Command Control. 2015, 1, 107–120. [Google Scholar]
- Sun, L.; Zha, Y.; Jiao, P.; Xu, K.; Liu, X. Mission-based command and control behavior model. In Proceedings of the IEEE International Conference on Mechatronics & Automation, Harbin, China, 7–10 August 2016. [Google Scholar]
- Li, N.; Huai, W.; Wang, S. The solution of target assignment problem in command and control decision-making behaviour simulation. Enterp. Inf. Syst. 2016, 11, 1–19. [Google Scholar] [CrossRef]
- Pullen, J.M. Enabling Military Coalition Command and Control with Interoperating Simulations, 5th International Conference on Simulation and Modeling Methodologies. Technol. Appl. 2015, 442, 157–174. [Google Scholar]
- Ciano, M.D.; Morgese, D.; Palmitessa, A. Profiling Approach for the Interoperability of Command and Control Systems in Emergency Management: Pilot Scenario and Application. In Recent Trends in Control and Sensor Systems in Emergency Management; Springer: Cham, Switzerland, 2018; pp. 23–30. [Google Scholar]
- Raglin, A.; Metu, S.; Russell, S.; Budulas, P. Implementing Internet of Things in a military command and control environment. In Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, Proceedings of the SPIE Defense + Security, Los Angeles, CA, USA, 9 April 2017; SPIE: Los Angeles, CA, USA, 1955. [Google Scholar]
- Sun, Y.; Yao, P.Y.; Wan, L.J.; Jia, W. A Quantitative Method to Design Command and Control Structure of Distributed Military Organization. In Proceedings of the International Conference on Information System & Artificial Intelligence, Tianjin, China, 14–16 July 2017. [Google Scholar]
- Evans, J.; Ewy, B.J.; Pennington, S.G. Named data networking protocols for tactical command and control. In Proceedings of the Open Architecture/Open Business Model Net-Centric Systems and Defense Transformation 2018, Houston, TX, USA, 22–26 April 2018. [Google Scholar]
- Wang, Y.; Meng, S.; Chen, Y.; Sun, R.; Wang, X.; Sun, K. Multi-leader Multi-follower Stackelberg Game Based Dynamic Resource Allocation for Mobile Cloud Computing Environment. Wirel. Pers. Commun. 2017, 93, 461–480. [Google Scholar] [CrossRef]
- Zheng, Z.; Song, L.; Han, Z.; Li, G.Y.; Poor, H.V. Game Theory for Big Data Processing: Multileader Multifollower Game-Based ADMM. IEEE Trans. Signal Process. 2018, 99, 1. [Google Scholar] [CrossRef]
- Sinha, A.; Malo, P.; Frantsev, A.; Deb, K. Finding optimal strategies in a multi-period multi-leader–follower Stackelberg game using an evolutionary algorithm. Comput. Oper. Res. 2014, 41, 374–385. [Google Scholar] [CrossRef]
- Leng, S.; Yener, A. Relay-Centric Two-Hop Networks with Asymmetric Wireless Energy Transfer: A Multi-Leader-Follower Stackelberg Game. In Proceedings of the 2018 IEEE International Conference on Communications (ICC), Kansas City, MO, USA, 20–24 May 2018; pp. 1–6. [Google Scholar]
- Akbari, T.; Zolfaghari Moghaddam, S.; Poorghanaat, E.; Azimi, F. Coordinated planning of generation capacity and transmission network expansion: A game approach with multi-leader-follower. Int. Trans. Electr. Energy Syst. 2017, 27, e2339. [Google Scholar] [CrossRef]
- Chen, F.; Ren, W.; Lin, Z. Multi-leader multi-follower coordination with cohesion, dispersion, and containment control via proximity graphs. Sci. China (Inf. Sci.) 2017, 11, 109–128. [Google Scholar] [CrossRef][Green Version]
- Xu, Y.; Ren, G.; Chen, J.; Luo, Y.; Jia, L.; Liu, X.; Yang, Y.; Xu, Y. A One-leader Multi-follower Bayesian-Stackelberg Game for Anti-jamming Transmission in UAV Communication Networks. IEEE Access 2018, 6, 21697–21709. [Google Scholar] [CrossRef]
- Yuan, Y.; Sun, F.; Liu, H. Resilient control of cyber-physical systems against intelligent attacker: A hierarchal stackelberg game approach. Int. J. Syst. Sci. 2016, 47, 11. [Google Scholar] [CrossRef]
- Thai, C.N.; That, L.T.; Cao, H.T.L. Evaluation of maintained effect of hypertonic saline solution in Guyton’s closed-loop model. In Proceedings of the 2018 2nd International Conference on Recent Advances in Signal Processing, Telecommunications & Computing (SigTelCom), Da Nang, Vietnam, 9–11 January 2018; pp. 142–145. [Google Scholar]
- Huang, J.; Li, X.; Wang, T. Characterizations of closed-loop equilibrium solutions for dynamic mean–variance optimization problems. Syst. Control Lett. 2017, 110, 15–20. [Google Scholar] [CrossRef]
- Chen, L.; Shen, Y. Stochastic Stackelberg differential reinsurance games under time-inconsistent mean–variance framework. Insur. Math. Econ. 2019, 88, 120–137. [Google Scholar] [CrossRef]
- Song, Y.; Wang, X.; Quan, W.; Huang, W. A new approach to construct similarity measure for intuitionistic fuzzy sets. Soft Comput. 2019, 23, 1985–1998. [Google Scholar] [CrossRef]
- Song, Y.; Wang, X.; Zhu, J.; Lei, L. Sensor dynamic reliability evaluation based on evidence and intuitionistic fuzzy sets. Appl. Intell. 2018, 48, 3950–3962. [Google Scholar] [CrossRef]
- Song, Y.; Wang, X.; Lei, L.; Xue, A. A novel similarity measure on intuitionistic fuzzy sets with its applications. Appl. Intell. 2015, 42, 252–261. [Google Scholar] [CrossRef]
- Wen, G.; Wang, P.; Huang, T.; Yu, W.; Sun, J. Robust Neuro-Adaptive Containment of Multileader Multiagent Systems with Uncertain Dynamics. IEEE Trans. Syst. Man Cybern. Syst. 2017, 49, 1–12. [Google Scholar] [CrossRef]
- Wang, X.; Song, Y. Uncertainty measure in evidence theory with its applications. Appl. Intell. 2018, 48, 1672–1688. [Google Scholar] [CrossRef]
- Macua, S.V.; Zazo, J.; Zazo, S. Learning Parametric Closed-Loop Policies for Markov Potential Games. Comput. Sci. 2018, 25, 26–33. [Google Scholar]
- Dalapati, P.; Agarwal, P.; Dutta, A.; Bhattacharya, S. Dynamic process scheduling and resource allocation in distributed environment: An agent-based modelling and simulation. Math. Comput. Model. Dyn. Syst. 2018, 24, 485–505. [Google Scholar] [CrossRef]
- Wu, Q.; Ren, H.; Gao, W.; Ren, J. Benefit allocation for distributed energy network participants applying game theory based solutions. Energy 2017, 119, 384–391. [Google Scholar] [CrossRef]
- Fele, F.; Maestre, J.M.; Camacho, E.F. Coalitional Control: Cooperative Game Theory and Control. IEEE Control Syst. 2017, 37, 53–69. [Google Scholar]
- Setoodeh, P.; Haykin, S. Game Theory; Wiley: Hoboken, NJ, USA, 2017. [Google Scholar]
- Song, Y.; Fu, Q.; Wang, Y.-F.; Wang, X. Divergence-based cross entropy and uncertainty measures of Atanassov’s intuitionistic fuzzy sets with their application in decision making. Appl. Soft Comput. 2019, 84, 1–15. [Google Scholar] [CrossRef]
- Le Cadre, H. On the efficiency of local electricity markets under decentralized and centralized designs: A multi-leader Stackelberg game analysis. Cent. Eur. J. Oper. Res. 2018, 27, 953–984. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, M.; Song, Y.; Zhang, L. Combining evidence sources in time domain with decision maker’s preference on time sequence. IEEE Access 2019, 7, 174210–174218. [Google Scholar] [CrossRef]
- Clempner, J.B.; Poznyak, A.S. Using the extraproximal method for computing the shortest-path mixed Lyapunov equilibrium in Stackelberg security games. Math. Comput. Simul. 2017, 138, 14–30. [Google Scholar] [CrossRef]
- Joshi, R.; Kumar, S. An (R, S)-norm fuzzy information measure with its applications in multiple-attribute decision-making. Comput. Appl. Math. 2017, 37, 1–22. [Google Scholar] [CrossRef]
- Wang, W.; Hoang, D.T.; Niyato, D.; Wang, P.; Kim, D.I. Stackelberg Game for Distributed Time Scheduling in RF-Powered Backscatter Cognitive Radio Networks. IEEE Trans. Wirel. Commun. 2018, 17, 5606–5622. [Google Scholar] [CrossRef]
- Yang, D.; Jiao, J.R.; Ji, Y.; Du, G.; Helo, P.; Valente, A. Joint optimization for coordinated configuration of product families and supply chains by a leader-follower Stackelberg game. Eur. J. Oper. Res. 2015, 246, 263–280. [Google Scholar] [CrossRef]
- Zhang, H.; Li, L.; Xu, J.; Fu, M. Linear quadratic regulation and stabilization of discrete-time systems with delay and multiplicative noise. IEEE Trans. Autom. Control 2015, 60, 2599–2613. [Google Scholar] [CrossRef]
- Wu, C.; Gao, B.; Tang, Y.; Wang, Q. Master-slave Game Based Bilateral Contract Transaction Model for Generation Companies and Large Consumers. Autom. Electr. Power Syst. 2016, 40, 56–62. [Google Scholar]
- El Moursi, M.S.; Zeineldin, H.H.; Kirtley, J.L.; Alobeidli, K. A Dynamic Master/Slave Reactive Power-Management Scheme for Smart Grids with Distributed Generation. IEEE Trans. Power Deliv. 2014, 29, 1157–1167. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).