Binomial Regression Models with a Flexible Generalized Logit Link Function

Abstract

In binomial regression, a link function is used to join the linear predictor variables and the expectation of the response variable. This paper proposes a flexible link function from a new class of generalized logistic distribution, namely a flexible generalized logit (glogit) link. This approach considers both symmetric and asymmetric models, including the cases of lighter and heavier tails, as compared to standard logistic. The glogit is created from the inverse cumulative distribution function of the exponentiated-exponential logistic (EEL) distribution. Using a Bayesian framework, we conduct a simulation study to investigate the model performance compared to the most commonly used link functions, e.g., logit, probit, and complementary log–log. Furthermore, we compared the proposed model with several other asymmetric models using two previously published datasets. The results show that the proposed model outperforms the existing ones and provides flexibility fitting the experimental dataset. Another attractive aspect of the model are analytically tractable and can be easily implemented under a Bayesian approach.

1. Introduction

Binomial regression is a general term of a regression model in which the dependent variable has binomial distribution. The binomial distribution is formed from a number of successes in some repeated trials of a binomial experiment, where each trial has a probability of success. Binomial regression belongs to the generalized linear models (GLM) class, which uses a link function to connect linear predictor variables to the expectation of response variables. In binomial regression, predictor variables relate the probability of success from a series of independent Bernoulli trials. The link function for the binomial regression is formed from inverse cumulative distribution functions (c.d.f.) of a random distribution, for instance, the logit link function that corresponds to the inverse c.d.f. of the standard logistic distribution, the probit link function uses the inverse c.d.f. of standard normal distribution, and the complementary log–log (cloglog) link function is formed from the inverse c.d.f. of the Gumbel distribution. For more information about GLM and binomial regression, see McCullagh and Nelder [1] or Agresti [2].

The logit, probit, and cloglog links are the three commonly used link functions in a binomial regression. The first link is preferable due to its easy interpretation of the regression coefficients and the odds ratio. The logit model is a linear model for the canonical or natural parameter of the underlying exponential family that was obtained, and it has a closed form [3]. However, the logit model cannot always guarantee a good fit for all binomial regressions, especially for asymmetric models [4]. Czado and Santner [5], Tiku and Vaughan [6], Dobson and Barnett [7] indicated that misspecification of the link function in binomial regression could produce significant bias and increase mean squared error of parameter estimates and the predicted probabilities.

Both logit and probit links are symmetric links. Symmetric links assume that the probability of a given binomial response approaches 0 at the same rate as it approaches 1. This implies that the probability curve has a symmetric form of about 0.5. It is supported by the symmetrical probability density function (p.d.f.), which corresponds to the inverse c.d.f. of the link function. This assumption may not be reasonable in various cases. Many studies found that these symmetric link functions have some limitations. Nagler [8] indicated how sensitive the inferences are if a symmetric link was incorrectly used in the direction of an asymmetric model. Chen et al. [9] concluded that when the probability of a given binomial response approaches 0 at a different rate than it approaches 1 (depending on the covariate) or vice versa, the symmetric link function is inappropriate.

Collet [10] showed that an asymmetric link function could be more fitting than symmetric for binomial regression in some specific situations. One of the asymmetric links that is frequently used in binomial regression is the cloglog link function. However, the cloglog link has a fixed left or negative skewness, which means the probability of a given binomial response rises slowly from 0 but then tapers off more quickly as it approaches 1 and not the other way around [11]. As a result, the cloglog may produce an inaccurate inference for a symmetric model and a positive skewness model, and hence, it is not a flexible link function for binomial regression, although it is an asymmetric link. Binomial regression will be better modeled with flexible link functions that allow for symmetric and asymmetric (both positive and negative skewness) models and that allows the model to determine the required skewness level.

There have been many types of studies proposed that include skewness into the link function. Stukel [12] presented a two-parameter class of generalized logistic models that can approximate many link functions, including probit, logit, and complementary log–log. However, in a Bayesian analysis, it may not be straightforward to be implemented, because of a problem of multiple covariates and noninformative improper priors. Chen et al. [9] proposed skew-probit links using a latent variable approach of Albert and Chib [13], which can lead to proper posterior distributions using standard improper priors. Kim et al. [14] introduced a new link function based on the class of generalized skewed t-link models with the constraint on the shape parameter. Bazan et al. [15] presented the skewed probit link function and some variants with different parameterizations. Naranjo et al. [16] presented asymmetric link function based on the asymmetric exponential power (AEP) distribution. More recently, Caron et al. [17] proposed a skewed Weibull link function for categorical response data arising from the binomial model as well as the multinomial model and showed that logit, probit, and complementary log–log can be obtained as limiting cases.

In this paper, we propose a flexible generalized logit (glogit) link function for the binomial regression model. The link function is created from inverse cumulative distribution function (c.d.f.) of a new class of generalized logistic based on the exponentiated-exponential logistic (EEL) distribution that was introduced by Ghosh and Alzaatreh [18]. The EEL distribution has similar characteristics to Type IV generalized logistic distribution (GLD). The distributions consider both symmetric and asymmetric models, including the case of lighter and heavier tails, simultaneously as compared to standard logistic. The logistic distribution, Type I GLD, and Type II GLD can be obtained as special cases of both distributions. However, the EEL distribution differs from the Type IV GLD in the c.d.f. which is algebraically more tractable, so that it is more easily to be implemented. Some of the researchers use the previous GLD as the link function in binary regression, e.g., Tiku and Vaughan [6] that use Type I GLD and Oral [19] extended the work of Tiku and Vaughan [6] with a stochastic covariate, Valle et al. [20] use the Type III GLD and show that the model has ability to capture heavy and light tails, and Prentice [21] applies Type IV GLD model for Dose-Response Curves.

A Bayesian estimation technique using Markov chain Monte Carlo (MCMC) is provided for implementations of the proposed model. We present a simple syntax for the computation of the model using the JAGS (Just Another Gibbs Sampler) program shown as an attractive aspect. A simulation study to investigate the model performance of the proposed model in comparison with the most commonly used link functions, i.e., logit, probit, and complementary log–log is conducted. We also compare the proposed model with several other asymmetric models using two previously published datasets, i.e., the beetle mortality dataset [22] that was analyzed by Naranjo et al. [16] and potency of three different poisons dataset [23] analyzed by Caron et al. [17].

The rest of the paper is organized as follows: Section 2 describes the binomial regression model and the role of the link function in the model. In Section 3, we introduce the flexible generalized logit (glogit) link based on the c.d.f. corresponding to the exponentiated-exponential logistic (EEL) distribution, and we show the graphs of the distribution in various schemes. Section 4 demonstrates the flexibility of the glogit model compared with logit, probit, and complementary log–log by simulated datasets. Section 5 contains the application and comparison of the glogit model using the beetle mortality and potency of three different poisons datasets. The conclusion and discussion are given in Section 6.

2. Binomial Regression Model

The general notation of the binomial regression model is given as follows. Suppose $\mathit{y}=\left(y_1,y_2,\dots ,y_n\right)\prime$ is an $n\times 1$ vector of independent binary random variables that took value 1 for success and 0 for failure. Let X denote $n\times \left(k+1\right)$ design matrix with rows ${\mathit{x}}_{\mathit{i}}^{\prime }$, where ${\mathit{x}}_{\mathit{i}}=\left(1,x_{i1},x_{i2},\dots ,x_{ik}\right)\prime$ is a $\left(k+1\right)\times 1$ vector of the predictor variable, where value 1 corresponds to an intercept. Furthermore, we consider $\mathit{\beta }=\left({\beta }_0,{\beta }_1,\dots ,{\beta }_k\right)\prime$ as a $\left(k+1\right)\times 1$ corresponding the intercept and regression coefficient.

In binomial regression models, the probability $p_i=P\left(y_i=1\right)$ is predicted by applying link functions to a linear combination of predictor variables that leads to the following model:

$$F^{-1}\left(p_i\right)={\mathit{x}}_{\mathit{i}}^{\prime }\mathit{\beta },$$

(1)

where $F^{-1}(·)$ is called as a link function. Link function $F^{-1}$ can be formed from inverse c.d.f. of a random distribution $F$. When $F$ is a c.d.f. of a symmetric distribution, the resulting link is also symmetric. The most common symmetric links include logit and probit, whereas an asymmetric link is obtained when $F$ is an asymmetric c.d.f., for example, the cloglog link.

The likelihood function $ℒ\left(\mathit{\beta }|\mathit{y},\mathit{X}\right)$ is derived from the likelihood of binomial distribution as follows:

$$ℒ\left(\mathit{\beta }|\mathit{y},\mathit{X}\right)={{\displaystyle \prod }}_{i=1}^{n}F{\left({\mathit{x}}_{\mathit{i}}^{\prime }\mathit{\beta }\right)}^{y_i}{\left(1-F\left({\mathit{x}}_i^{\prime }\mathit{\beta }\right)\right)}^{1-y_i},$$

(2)

thus, the log-likelihood function $\ell \left(\mathit{\beta }|\mathit{y},\mathit{X}\right)$ is given by:

$$\ell \left(\mathit{\beta }|\mathit{y},\mathit{X}\right)={\displaystyle \sum }_{i=1}^n{y}_i\log \left(F\left({\mathit{x}}_{\mathit{i}}^{\prime }\mathit{\beta }\right)\right)+{\displaystyle \sum }_{i=1}^n\left(1-y_i\right)\log \left(1-F\left({\mathit{x}}_{\mathit{i}}^{\prime }\mathit{\beta }\right)\right).$$

(3)

The $\mathit{\beta }$ parameters in the model (3) can be estimated by using a maximum likelihood method or using the Bayesian method. The numerical method, such as the Newton–Raphson algorithm or the Nelder–Mead algorithm, can be applied for estimation with maximum likelihood estimation (MLE). While in the Bayesian framework, inferences about model parameters are typically summarized by random draws from a posterior density, which is proportional to the likelihood function for the data multiplied by a prior for the parameters.

3. Flexible Generalized Logit Link

The flexible generalized logit link function for the binomial regression model proposed in this paper is developed from inverse c.d.f. of a new class of generalized logistic. We start this section with a brief review of the new class of generalized logistic based on the exponentiated-exponential logistic (EEL) distribution given by Ghosh and Alzaatreh [18]. The EEL distribution is obtained using the technique of mixing two distributions of exponentiated-exponential and logistic distribution. For a more detailed discussion about this method, see Alzaatreh et al. [24] as well as Gupta and Kundu [25].

3.1. Exponentiated-Exponential Logistic Distribution

A random variable X is an EEL distribution, with parameter $\theta =\left(\mu ,s,\alpha ,\lambda \right)$, where $\mu \in \Re$ and $s>0$ are the locations and the scale parameter of logistic distribution, $\alpha >0$ and $\lambda >0$ are the shapes and the scale parameter of exponentiated-exponential distribution. The probability density function (p.d.f.) of X is given by:

$$f_{gl}\left(x\right)=\frac{\alpha \lambda e^{\left(x-\mu \right)/s}}{s{\left(1+e^{\left(x-\mu \right)/s}\right)}^{\lambda +1}}{\left(1-{\left(1+e^{\left(x-\mu \right)/s}\right)}^{-\lambda }\right)}^{\alpha -1}.$$

(4)

We denote hereafter as $\mathit{X}~\mathrm{EEL}\left(\mu ,s,\alpha ,\lambda \right)$. If $\alpha =\lambda =1$, the p.d.f. of X in (4) is reduced to the p.d.f. of the logistic distribution. In the special case of $\lambda =1$, the p.d.f. in (4) is the Type I GLD. Moreover, when $\alpha =1$, the p.d.f. reduces to the Type II GLD. The illustrations of some typical standard EEL p.d.f.s for different values of $\alpha$ and $\lambda$ in $\mu =0$ and $s=1$ are provided in Figure 1. Figure 1 shows that the density function of the EEL distribution can take different shapes. It has negative skewness for $\alpha <\lambda$, positive skewness for $\alpha >\lambda$, and symmetric for $\alpha =\lambda$. The greater skewness can be achieved when the difference between $\alpha$ and $\lambda$ is higher. Furthermore, the standard EEL p.d.f. has lighter tails compared to standard logistic p.d.f. when $\alpha >1$ and $\lambda >1$, otherwise if $\alpha <1$ and $\lambda <1$ then heavier tails are achieved.

Based on the p.d.f. in (4), the c.d.f. for the EEL distribution is given by:

$$F_{gl}\left(x\right)={\left(1-{\left(1+e^{\left(x-\mu \right)/s}\right)}^{-\lambda }\right)}^{\alpha }.$$

(5)

Suppose $F_{gl}^{-1}\left(p\right)$ denotes the quantile function for the EEL distribution, where $0<p<1$. Then, the quantile function, which is an inverse of the EEL c.d.f. can be written as

$$F_{gl}^{-1}\left(p\right)=\mu +s \log \left(1-{\left(1-p^{1/\alpha }\right)}^{-1/\lambda }\right).$$

(6)

The result is obtained by using $F_{gl}\left(F_{gl}^{-1}\left(p\right)\right)=p$ in (4) and then solving it for $F_{gl}^{-1}\left(p\right)$.

3.2. Binomial Regression Model with Glogit Link Function

A binomial regression model, applying the inverse of the EEL c.d.f. as a link function, namely glogit, is presented in this section. The glogit link function is formed from the quantile function of the standard EEL distribution at $\mu =0$ and $s=1$. The glogit link function $F_{gl}^{-1}$ can be defined as:

$$F_{gl}^{-1}\left(p\right) = \mathrm{glogit}\left(p\right)=\log \left(1-{\left(1-p^{1/\alpha }\right)}^{-1/\lambda }\right).$$

(7)

When $\alpha =\lambda =1$, the glogit link function in (7) will be reduced to the logit link function. Figure 2 depicts different EEL c.d.f. curves for the different values of $\alpha$ and $\lambda$.

The glogit class for the binomial regression model is obtained by considering $F_{gl}^{-1}$ in the specification of the binomial regression model given in (1), which is expressed as:

$$\mathrm{glogit}\left(p_i\right)=\log \left(1-{\left(1-p_i{}^{1/\alpha }\right)}^{-1/\lambda }\right)={\mathit{x}}_{\mathit{i}}^{\prime }\mathit{\beta } , i=1,2,\dots ,n.$$

(8)

We can rewrite the formula in (8) as:

$$\begin{gathered} p_i=F_{gt}\left({\mathit{x}}_{\mathit{i}}^{\prime }\mathit{\beta }\right) , i=1,2,\dots ,n. \\ \hspace{1em}={\left(1-{\left(1+e^{\left({\mathit{x}}_{\mathit{i}}^{\prime }\mathit{\beta }\right)}\right)}^{-\lambda }\right)}^{\alpha }, \end{gathered}$$

(9)

where $F_{gt}(·)$ is the c.d.f. of the EEL distribution given in (5) in case $\mu =0$ and $s=1$. The likelihood function for the glogit model can be formed by substituting (9) in (2) as:

$$\begin{array}{ll}ℒ\left(\mathit{\beta },\alpha ,\lambda |\mathit{y},\mathit{X}\right)& ={\displaystyle \prod _{i=1}^n}{F}_{gt}{\left({\mathit{x}}_{\mathit{i}}^{\prime }\mathit{\beta }\right)}^{y_i}{\left(1-F_{gt}\left({\mathit{x}}_{\mathit{i}}^{\prime }\mathit{\beta }\right)\right)}^{1-y_i}\\ & ={\displaystyle \prod _{i=1}^n}{\left({\left(1-{\left(1+e^{\left({\mathit{x}}_{\mathit{i}}^{\prime }\mathit{\beta }\right)}\right)}^{-\lambda }\right)}^{\alpha }\right)}^{y_i}{\left(1-{\left(1-{\left(1+e^{\left({\mathit{x}}_{\mathit{i}}^{\prime }\mathit{\beta }\right)}\right)}^{-\lambda }\right)}^{\alpha }\right)}^{1-y_i}.\end{array}$$

(10)

Thus, the log-likelihood function $\ell \left(\mathit{\beta },\alpha ,\lambda |\mathit{y},\mathit{X}\right)$ is given as:

$$\ell \left(\mathit{\beta },\alpha ,\lambda |\mathit{y},\mathit{X}\right)={\displaystyle \sum }_{i=1}^n{y}_i\alpha \log \left(1-{\left(1+e^{\left({\mathit{x}}_{\mathit{i}}^{\prime }\mathit{\beta }\right)}\right)}^{-\lambda }\right)+{\displaystyle \sum }_{i=1}^n\left(1-y_i\right)\log \left(1-{\left(1-{\left(1+e^{\left({\mathit{x}}_{\mathit{i}}^{\prime }\mathit{\beta }\right)}\right)}^{-\lambda }\right)}^{\alpha }\right),$$

(11)

where $\mathit{\beta }$, $\alpha$, and $\lambda$ in the model (11) are the parameters to be estimated by using a maximum likelihood estimation (MLE) method, or a Bayesian method as previously mentioned in Section 2.

In this paper, we conduct a Bayesian method for the simulation and applications. The Bayesian analysis requires the joint posterior density $\pi \left(\mathit{\beta },\alpha ,\lambda |\mathit{y},\mathit{X}\right)$ that is defined by:

$$\pi \left(\mathit{\beta },\alpha ,\lambda |\mathit{y},\mathit{X}\right)\propto ℒ\left(\mathit{\beta },\alpha ,\lambda |\mathit{y},\mathit{X}\right)\pi \left(\mathit{\beta }\right)\pi \left(\alpha \right)\pi \left(\lambda \right),$$

(12)

where $\pi \left(\mathit{\beta }\right)$ is the join prior of regression coefficients, $\pi \left(\alpha \right)$ is prior for the $\alpha$ parameter, and $\pi \left(\lambda \right)$ is prior for the $\lambda$ parameter. For the priors of the intercept and regression coefficients, we can adopt the typical proper priors for $\mathit{\beta }$, a normal prior, and thus ${\beta }_j~\mathrm{N}\left({\mu }_j^{*},{\tau }_j^{*}\right)$, where $j=0,1,\dots ,k$, ${\mu }_j^{*}=0$, and ${\tau }_j^{*}$ denotes the precision ($1/{\sigma }_j^{2*}$) with a small value representing the common situation that is a lack of information available for the priors. Alternatively, informative priors are obtained when ${\mu }_j^{*}$ and ${\tau }_j^{*}$ are elicited based on historical information, expert opinion or validation from datasets. For $\alpha$ and $\lambda$, we can use a proper lognormal prior with the mean 0 and variance 1 $\left(\alpha ~\mathrm{LN}\left(0,1\right); \lambda ~\mathrm{LN}\left(0,1\right)\right)$, for the reasons that their value is positive and around to 1 (get near to the logit model).

With the model setup of prior distributions as shown above, the joint posterior distribution of the model is given by:

$$\begin{array}{ll}\pi \left(\mathit{\beta },\alpha ,\lambda |\mathit{y},\mathit{X}\right)\propto & {\displaystyle \prod _{i=1}^n}{\left({\left(1-{\left(1+e^{\left({\mathit{x}}_{\mathit{i}}^{\prime }\mathit{\beta }\right)}\right)}^{-\lambda }\right)}^{\alpha }\right)}^{y_i}{\left(1-{\left(1-{\left(1+e^{\left({\mathit{x}}_{\mathit{i}}^{\prime }\mathit{\beta }\right)}\right)}^{-\lambda }\right)}^{\alpha }\right)}^{1-y_i}\\ & \times {\displaystyle \prod _{j=0}^k}\left(\frac{\sqrt{{\tau }_{\left(\beta \right)j}}}{\sqrt{2\pi }}{e}^{-\frac{{\tau }_{\left(\beta \right)j}}{2}{\left({\beta }_j-{\mu }_{\left(\beta \right)j}\right)}^2}\right)\times \frac{\sqrt{{\tau }_{\left(\alpha \right)}}}{\alpha \sqrt{2\pi }}{e}^{-\frac{{\tau }_{\left(\alpha \right)}}{2}{\left(\ln \left(\alpha \right)-{\mu }_{\left(\alpha \right)}\right)}^2}\\ & \times \frac{\sqrt{{\tau }_{\left(\lambda \right)}}}{\lambda \sqrt{2\pi }}{e}^{-\frac{{\tau }_{\left(\lambda \right)}}{2}{\left(\ln \left(\lambda \right)-{\mu }_{\left(\lambda \right)}\right)}^2}\end{array}$$

(13)

Using the proportionality follows from Bayes’ theorem, the joint posterior distribution (13) can be rewritten as:

$$\begin{array}{ll}\pi \left(\mathit{\beta },\alpha ,\lambda |\mathit{y},\mathit{X}\right)\propto & {\displaystyle \prod _{i=1}^n}{\left({\left(1-{\left(1+e^{\left({\mathit{x}}_{\mathit{i}}^{\prime }\mathit{\beta }\right)}\right)}^{-\lambda }\right)}^{\alpha }\right)}^{y_i}{\left(1-{\left(1-{\left(1+e^{\left({\mathit{x}}_{\mathit{i}}^{\prime }\mathit{\beta }\right)}\right)}^{-\lambda }\right)}^{\alpha }\right)}^{1-y_i}\\ & \times {\displaystyle \prod }_{j=1}^k\left(\frac{1}{\alpha \lambda }{e}^{-\frac{1}{2}\left({\tau }_{\left(\beta \right)j}{\left({\beta }_j-{\mu }_{\left(\beta \right)j}\right)}^2+{\tau }_{\left(\alpha \right)}{\left(\ln \left(\alpha \right)-{\mu }_{\left(\alpha \right)}\right)}^2+{\tau }_{\left(\lambda \right)}{\left(\ln \left(\lambda \right)-{\mu }_{\left(\lambda \right)}\right)}^2\right)}\right)\end{array}$$

(14)

The analysis of Bayesian models is using MCMC, which sampling from the posterior is done using the Gibbs sampling algorithm. The full conditional distributions for all parameters must be derived to implement the algorithm for the joint posterior distribution (14). The full conditional distributions for $\mathit{\beta }$ are easy to obtain:

$$\begin{gathered} \pi \left({\beta }_j|\mathit{y},\mathit{X},\alpha ,\lambda ,{\mathit{\beta }}_{\left(-j\right)}\right)\propto {\displaystyle \prod }_{i=1}^n{\left({\left(1-{\left(1+e^{\left({\mathit{x}}_{\mathit{i}}^{\prime }\mathit{\beta }\right)}\right)}^{-\lambda }\right)}^{\alpha }\right)}^{y_i}{\left(1-{\left(1-{\left(1+e^{\left({\mathit{x}}_{\mathit{i}}^{\prime }\mathit{\beta }\right)}\right)}^{-\lambda }\right)}^{\alpha }\right)}^{1-y_i} \\ \times e^{-\frac{1}{2}\left({\tau }_{\left(\beta \right)j}{\left({\beta }_j-{\mu }_{\left(\beta \right)j}\right)}^2\right)}, \end{gathered}$$

(15)

where ${\mathit{\beta }}_{\left(-j\right)}^{\prime }=\left({\beta }_0,{\beta }_1,\dots ,{\beta }_{j-1},{\beta }_{j+1},\dots ,{\beta }_k\right)$ and the subscript $\left(-j\right)$ denotes the j-th element has been removed. The full conditional distributions for $\alpha$ and $\lambda$ are given by:

$$\begin{gathered} \pi \left(\mathit{\alpha }|\mathit{y},\mathit{X},\mathit{\beta },\lambda \right)\propto {\displaystyle \prod }_{i=1}^n{\left({\left(1-{\left(1+e^{\left({\mathit{x}}_{\mathit{i}}^{\prime }\mathit{\beta }\right)}\right)}^{-\lambda }\right)}^{\alpha }\right)}^{y_i}{\left(1-{\left(1-{\left(1+e^{\left({\mathit{x}}_{\mathit{i}}^{\prime }\mathit{\beta }\right)}\right)}^{-\lambda }\right)}^{\alpha }\right)}^{1-y_i} \\ \times \frac{1}{\alpha }{e}^{-\frac{1}{2\alpha }\left({\tau }_{\left(\alpha \right)}{\left(\ln \left(\alpha \right)-{\mu }_{\left(\alpha \right)}\right)}^2\right)} \end{gathered}$$

(16)

$$\begin{gathered} \pi \left(\lambda |\mathit{y},\mathit{X},\mathit{\beta },\alpha \right)\propto {\displaystyle \prod }_{i=1}^n{\left({\left(1-{\left(1+e^{\left({\mathit{x}}_{\mathit{i}}^{\prime }\mathit{\beta }\right)}\right)}^{-\lambda }\right)}^{\alpha }\right)}^{y_i}{\left(1-{\left(1-{\left(1+e^{\left({\mathit{x}}_{\mathit{i}}^{\prime }\mathit{\beta }\right)}\right)}^{-\lambda }\right)}^{\alpha }\right)}^{1-y_i} \\ \times \frac{1}{\lambda }{e}^{-\frac{1}{2\lambda }\left({\tau }_{\left(\lambda \right)}{\left(\ln \left(\lambda \right)-{\mu }_{\left(\lambda \right)}\right)}^2\right)} \end{gathered}$$

(17)

Each draw can be done using the adaptive rejection metropolis algorithm implemented in JAGS. JAGS is a program for Bayesian graphical modeling, which has compatibility with classic BUGS (Bayesian inference using Gibbs sampling), developed by Martyn Plummer [26]. We can express the models for $k=2$ in JAGS using the following simple syntax:

model {

for (i in 1:n) {

y[i]~dbin(p[i], 1)

omega[i] < -beta0 + beta1*x1[i] + beta2*x2[i]

p[i] < -pow((1-pow((1+exp(omega[i])),-lambda)),alpha)

}

#Prior

beta0~dnorm(0, 0.001)

beta1~dnorm(0, 0.001)

beta2~dnorm(0, 0.001)

alpha~dlnorm(0, 1)

lambda~dlnorm(0, 1)

}

We implemented the models using the function autojags in the jagsUI package developed by Kellner [27] in the R software. The autojags applies the convergence diagnostic based on Gelman and Rubin [28] and Brooks and Gelman [29] called Gelman–Rubin diagnostic tests. To compute the Gelman–Rubin statistic, we must run two chains in JAGS using two different sets of initial values. If the MCMC chain has reached convergence, the Gelman–Rubin statistics, namely Rhat, are lower than 1.05, and it concludes that burn-in is adequate, whereas the value in excess of 1.05 indicates a lack of convergence. Another convergence diagnostic method of Raftery and Lewis [30] was considered in autojags. The method estimates and applies the number of iterations needed for a given level of precision in posterior samples when quantiles are the posterior summaries of interest.

4. Simulation

A simulation study was carried out to evaluate the performance of the glogit link function for the binomial regression models compared to logit, probit, and cloglog. For this purpose, several datasets were generated by the following steps:

• Step 1: Specify a binomial regression model with one predictor variable and set a vector of the regression coefficients $\mathit{\beta }=\left({\beta }_0,{\beta }_1\right)=\left(0.1, 1\right)$;
• Step 2: Generate $x_{i1}~\mathrm{Normal}\left(0,1\right)$, then we create $x_i={\left(1,x_{i1}\right)}^{\prime }$;
• Step 3: Compute $p_i$ from a given link, so that $p_i=F(x_i^{\prime }\mathit{\beta }$);
• Step 4: Generate $n_i~\mathrm{Poisson}\left(\delta \right)$ with $\delta$ = 100, and $Y_i~\mathrm{Binomial}\left(n_i,p_i\right)$, which is the binomial distribution with $p_i$ as the probability of success and $n_i$ is the sample size for the repeated Bernoulli trials.

We consider seven simulations to accommodate into seven scenarios for symmetric and asymmetric models and lighter and heavier tails (compared to the logit model). The scenarios were considered by applying the different inverse of link functions $F(·)$. The scenarios are as follows:

• Scenario 1: $F^{-1}\left(p_i\right)=\mathrm{glogit}(p_i|\alpha =1, \lambda =1)$, same with $F^{-1}\left(p_i\right)=\mathrm{logit}\left(p_i\right)$;
• Scenario 2: $F^{-1}\left(p_i\right)=\mathrm{glogit}(p_i|\alpha =4, \lambda =4)$, represent the lighter tails compared to the logit;
• Scenario 3: $F^{-1}\left(p_i\right)=\mathrm{glogit}(p_i|\alpha =0.5, \lambda =0.5)$, represent the heavier tails compared to the logit;
• Scenario 4: $F^{-1}\left(p_i\right)=\mathrm{glogit}(p_i|\alpha =3, \lambda =0.3)$, represent the positive skewness;
• Scenario 5: $F^{-1}\left(p_i\right)=\mathrm{glogit}(p_i|\alpha =0.3, \lambda =3)$, represent the negative skewness;
• Scenario 6: $F^{-1}\left(p_i\right)=\mathrm{cloglog}\left(p_i\right)$;
• Scenario 7: $F^{-1}\left(p_i\right)=\mathrm{probit}\left(p_i\right)$.

The comparison of graph visualizations for scenarios 1 to 5 represented specifically for the glogit can be seen in Figure 1 and Figure 2. For each scenario, we generated 100 datasets, and for each dataset, we generated $m=100$ binomial response variables, thus, $y_i~\mathrm{Binomial}\left(n_i,p_i\right)$ for $i=1,\dots ,100$. Furthermore, we fit all of the models for each simulated dataset, respectively, to find the best performance in terms of model comparisons. We conducted a Bayesian analysis on the above seven simulated datasets and set with the uninformative prior for each model given in Section 3.2.

To compare the performance of the models under different link functions, we use two model comparisons. The first is the deviance information criterion (DIC) proposed by Spiegelhalter et al. [31], which represents a goodness-of-fit criterion. It is an estimate of expected predictive error. Therefore, the lower value of DIC is better. DIC is given by $\mathrm{DIC}=\overline{D\left(\eta \right)}+\widehat{pD}$, where $D\left(\eta \right)=-2\log L\left(\eta \right)$ is deviance of model, $L\left(\eta \right)$ is the likelihood, and $\overline{D\left(\eta \right)}=\mathrm{E}\left(D\left(\eta \right)|\mathrm{data}\right)$ is the deviance posterior mean. The number of parameters is given as $p$, and $\widehat{pD}=\overline{D\left(\eta \right)}-D\left(\overline{\eta }\right)$ is defined as the effective number of parameters, while $D\left(\overline{\eta }\right)$ is the deviance posterior means of the parameters of interest, with $\overline{\eta }=\mathrm{E}\left(\eta |\mathrm{data}\right)$. Another criterion for the model comparison is absolute errors (AE). Absolute error is defined as the absolute value of the difference between the prediction value and the true value of a measurement and is commonly given as the maximum possible error given a model's degree of accuracy. AE is defined by $AE={\displaystyle \sum }_{i=1}^n\left|p_i-\widehat{p_i}\right|$. The smaller values of AE indicate better models.

Table 1. Model comparison using average of deviance information criterion (DIC) and absolute errors (AE) corresponding to the link functions at several scenarios.

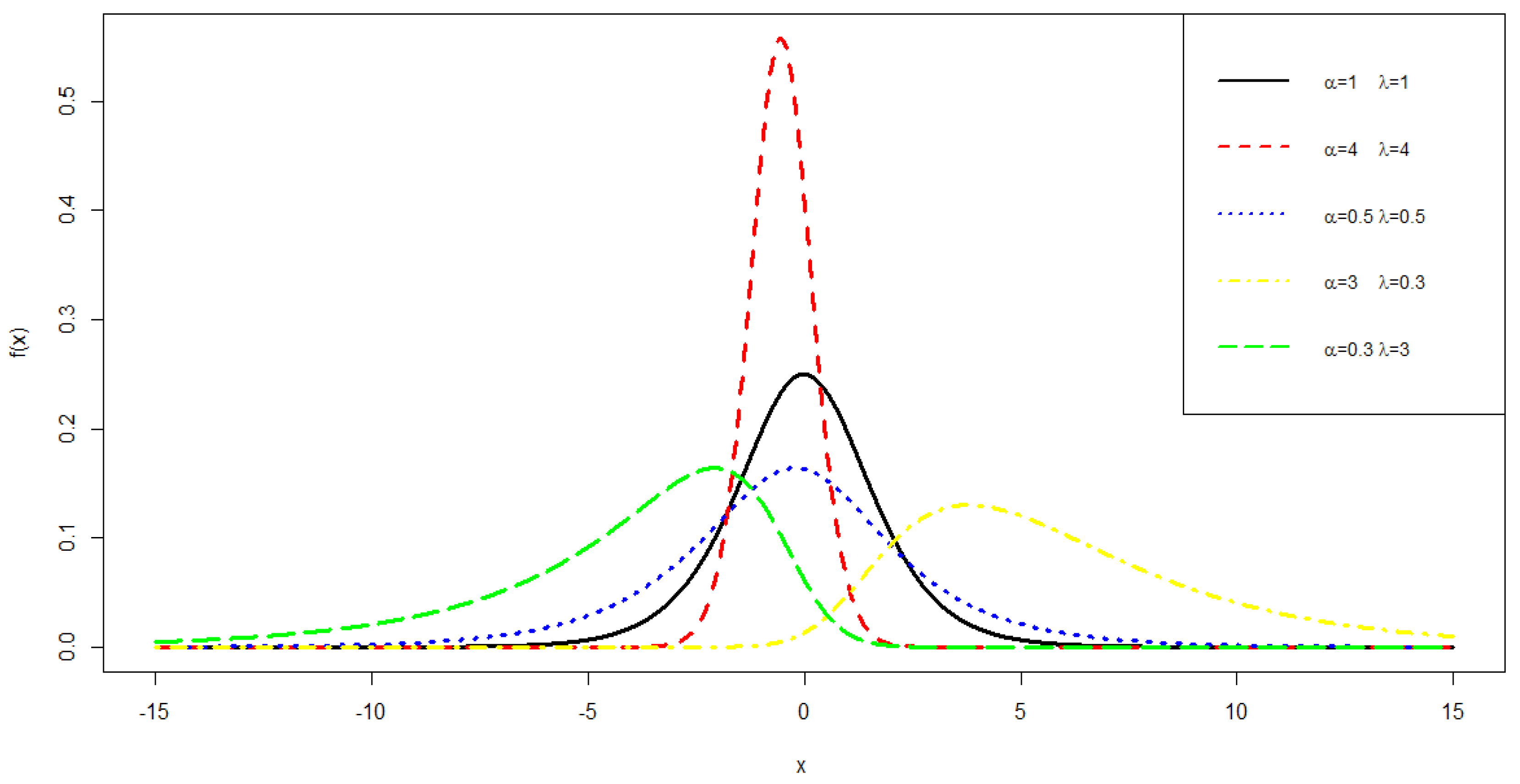
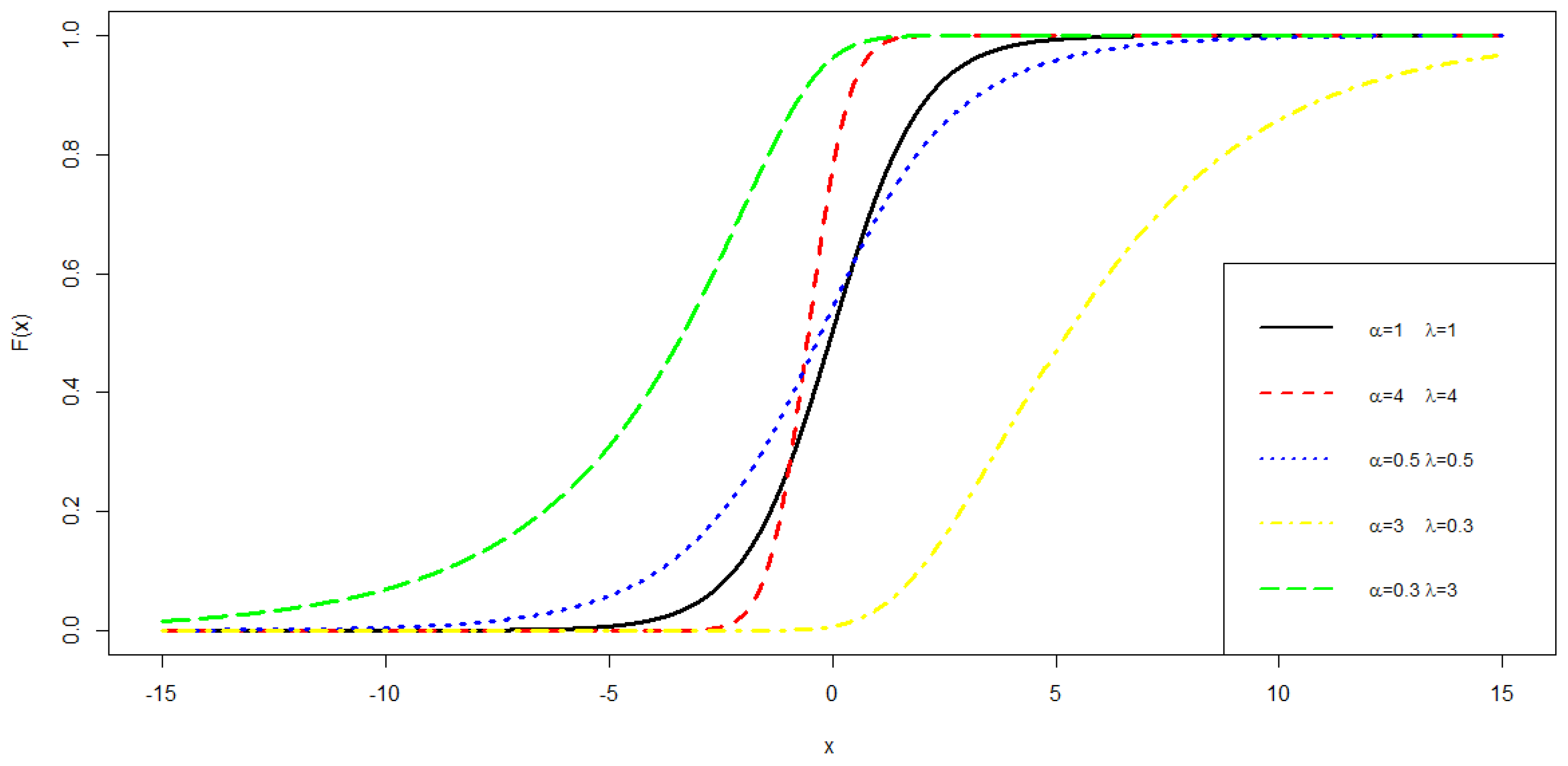
Scenarios	Glogit Link		Logit Link		Cloglog Link		Probit Link
	DIC	AE	DIC	AE	DIC	AE	DIC	AE
1	815.21 **	0.1903 **	813.74 *	0.1589 *	1116.61	1.7661	824.27	0.3413
2	697.04 *	0.1409 *	746.97	0.5093	1903.64	2.5617	712.61 **	0.2909 **
3	826.91 *	0.1980 *	827.74 **	0.2021 **	916.40	0.9986	833.12	0.2904
4	462.63 *	0.0545 *	539.94	0.2971	557.11	0.3286	477.06 **	0.1396 **
5	597.04 *	0.0895 *	822.00	0.8047	599.08 **	0.1038 **	655.23	0.4173
6	745.41 **	0.1934 **	1613.28	2.4169	742.98 *	0.1369 *	1378.13	2.0713
7	776.19 **	0.2139 **	825.32	0.6017	1611.83	2.4673	771.02 *	0.1249 *

Scenario 1 = glogit$\left(\alpha =1;\lambda =1\right)$; Scenario 2 = glogit$\left(\alpha =4;\lambda =4\right)$; Scenario 3 = glogit$\left(\alpha =0.5;\lambda =0.5\right)$; Scenario 4 = glogit$\left(\alpha =3;\lambda =0.3\right)$; Scenario 5 = glogit$\left(\alpha =0.3;\lambda =3\right)$; Scenario 6 = cloglog; Scenario 7 = probit. * indicates the smallest value; ** indicates the next smallest value.

shows the result of the simulation for the seven scenarios. Scenarios 1 to 3 are symmetrical models in which the first one is generated from $\mathrm{glogit}\left(\alpha =1;\lambda =1\right)$, or same with the logit. The second one represents the lighter tails compared to the logit, and the third one represents the heavier tails compared to the logit. The fourth and fifth scenarios are used to represent the asymmetric models in which the fourth one has a positive direction of skewness, while the fifth one has a negative direction. In addition, the sixth and seventh scenarios belong to the cloglog and probit link function. We evaluate each scenario by DIC and AE values to compare the models, i.e., glogit, logit, cloglog, and probit.

First, we focus on the results of the first scenario. When the datasets generated from the logit link that equaled the glogit link for $\alpha = \lambda =1$, then the logit model is the best, followed by the glogit. However, the DIC and AE values of both models are very close compared to the other. For the second to fifth scenario that used datasets generated from the glogit model for the several values of $\alpha$ and $\lambda$, the glogit model performs best. In the second scenario, which has lighter tails compared to the standard logistic, the second-best fit model is the probit model. For the third scenario, the logit model gives almost identical values of DIC and AE, with the result that it is the second-best fit model. In the fourth scenario, the second-best fit is the probit model, whereas, in the fifth one, the second-best fit is the cloglog model. This result is consistent with the fact that the cloglog model also has negative skewness. When the datasets are generated from cloglog and probit models (Scenario 6 and 7), the second-best fit is the glogit model after them. However, the differences in the model comparison values are quite similar. In summary, the simulation results show that the glogit model is quite flexible and performs better than the standard link function.

5. Application

This section discusses the result of applying the proposed method to the empirical cases. It aims to study the performance of the flexible generalized logit link function, compared with other recent asymmetric link functions. Two datasets are considered, i.e., beetle mortality dataset of Bliss [22] and potency of three different poison datasets of Finney [23].

5.1. Beetle Mortality Dataset

The beetle mortality dataset in

Table 2. Beetles toxicological experiment of $C{S}_2$ exposure at various concentrations.

log(dose)	n	ndead	p
49.1	59	6	0.102
53.0	60	13	0.217
56.9	62	18	0.290
60.8	56	28	0.500
64.8	63	52	0.825
68.7	59	53	0.898
72.6	62	61	0.984
76.5	60	60	1

is taken from Bliss [22]. The data consist of the toxicological experiment results based on the number of flour beetles dead after several hours of carbon disulfide $\left(C{S}_2\right)$ exposure at various concentrations (transformed to ten base logarithm of dose). More information about the data can be found in Bliss [22].

The dataset in Table 2 was previously analyzed by Naranjo et al. [16], who proposed the AEP-based link model to analyze a binomial regression by using the inverse of the Asymmetric Exponential Power (AEP) c.d.f. as the link function. Furthermore, they compared the model with some symmetric and asymmetric link models, such as the probit and t-link (T(8)) models that are proposed by Albert and Chib [13], the skewed probit (SP) model that are proposed by Chen et al. [9], and the skewed generalized t-link (SGT) model proposed by Kim et al. [14]. The model is given by

$${\eta }_i=F^{-1}\left(p_i\right)={\beta }_0+{\beta }_1\log \left({\mathrm{dose}}_i\right), i=1,2,\dots ,8,$$

(18)

where the response variable is binary with $(y_i=1)$ representing the dead and $(y_i=0)$ representing the beetles that survived, $p_i$ is the proportion of dead beetles (${\mathrm{ndead}}_i$) to the number of beetles exposed ($n_i$) under the i^th dose. A comparison of the five models was considered by using different link functions $F^{-1}$.

Five models were fitted to the data, and four different criteria of model comparison were used, e.g., the deviance information criterion (DIC), the Bayesian information criterion (BIC), the Akaike information criterion (AIC), and the absolute errors (AE). However, in this paper, only DIC and AE are used to compare with the flexible generalized logit (glogit) model because the DIC, BIC, and AIC give the same conclusions. The formulas of DIC and AE are given in Section 4. All of the estimation and comparison criteria values for the models, except the glogit model, are adopted from Naranjo et al. [16] that applied Bayesian analysis to estimate the parameters. For the glogit model, we also used a Bayesian framework, whose join posterior is given in (12), including the settings for the prior.

The posterior estimates (mean and standard deviation), the DIC value, and the AE value for the fitted models are reported in

Table 3. Summary of posterior estimations and model comparison for the several models fitted to the beetle mortality dataset.

Parameters	Model [Posterior Mean (Standard Deviation)]
	Probit	T(8)	SP	SGT	AEP	Glogit
${\beta }_0$	−33.88 (1.91)	−35.17 (2.03)	−34.45 (2.06)	−8.3 (1.73)	−35.16 (0.36)	−16.56 (5.08)
${\beta }_1$	19.14 (1.04)	19.86 (1.14)	19.43 (1.14)	4.69 (0.98)	19.69 (0.21)	0.25 (0.08)
-			$\delta = 0.08 \left(0.45\right)$	$v_{1 }= 9.4 \left(14.8\right)$	${\theta }_1 = 1.04 \left(0.15\right)$	$\alpha = 0.86 \left(0.59\right)$
-				$\delta = 0.22 \left(0.1\right)$	${\theta }_1 = 0.47 \left(0.07\right)$	$\lambda = 2.61 \left(2.37\right)$
DIC	39.26	41.22	40.22	36.72	36.43 **	35.09 *
AE	0.35	0.37	0.35	0.25	0.15 *	0.18 **

* indicates the smallest value; ** indicates the next smallest value.

. The glogit model is fitted to the dataset, and the result is compared with those for the probit, T(8), SP, SGT, and AEP-based link models processed by Naranjo et al. [16]. These results presented in Table 3 show that the glogit model provides the best fit, followed by the AEP-based link model indicated by the smallest value of DIC. For criterion AE, we note that the AEP-based link model has the smallest value so that the AEP-based link model is superior, followed by the glogit model. Furthermore, the glogit and AEP-based link models have similar values of model comparison compared with the other in this dataset.

5.2. The Potency of Three Different Poisons Dataset

In the second application, we take the potency of three different poisons dataset from Finney [23] and the analysis results from Caron et al. [17]. The data consist of the test results of the different doses and the different poisons to know the potency of the poisons to kill insects. The poisons are rotenone, deguelin, and a mixture of rotenone and deguelin. The data are provided in

Table 4. Relative potency of three different poisons (rotenone, deguelin, and a mixture of the two) to kill insects.

Rotenone			Deguelin			Mixture
log(dose)	dead	n	log(dose)	dead	n	log(dose)	dead	n
1.01	44	50	1.7	48	48	1.4	48	50
0.89	42	49	1.61	47	50	1.31	43	46
0.71	24	46	1.48	47	49	1.18	38	48
0.58	16	48	1.31	34	48	1	27	46
0.41	6	50	1	18	48	0.71	22	46
			0.71	16	49	0.4	7	47

, where n is the number of observations. More information about this data can be found in Finney [23].

Caron et al. [17] proposed a skewed Weibull (SW) link function and analyzed the dataset in Table 4 in MLE and Bayesian framework. In the Bayesian method, they compared the proposed model with another skewed link function, such as the AEP-based link (AEP) model presented by Naranjo et al. [16] and the skewed probit (SP) model proposed by Chen et al. [9]. The model that was used is:

$${\eta }_i=F^{-1}\left(p_i\right)={\beta }_0+{\beta }_1\log \left({\mathrm{dose}}_i\right)+{\beta }_2\mathrm{Rotenone}+{\beta }_3\mathrm{Deguelin}, i=1,2,\dots ,8,$$

(19)

where the $p_i$ is the proportion of dead insects (${\mathrm{dead}}_i$) to the number of observation ($n_i$) under the i^th log(dose), rotenone dummy variable, and deguelin dummy variable. The mixture variable is considered as the reference poison (rotenone = 0 and deguelin = 0). A comparison to the models was considered by applying different $F^{-1}$ (link functions). They are the SP, AEP, SW, and glogit models.

In this section, we applied the DIC and the mean absolute error (MAE) for model comparison. The MAE is defined as $\mathrm{MAE}=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$n$}\right.{\displaystyle \sum }_{i=1}^n\left|p_i-\widehat{p_i}\right|$. The estimation and the model comparison values for the models, except the glogit model, were taken from Caron et al. [17]. More detail about their methods can be found in Caron et al.’s study [17]. For the glogit model, we used the model presented in (12), including the settings for the prior.

The model comparison results of DIC and MAE for the fitted models are presented in

Table 5. Summary of posterior estimations and model comparison for the several models fitted to the potency of three different poisons dataset.

Parameters	Model [Posterior Mean (Standard Deviation)]
	SP	AEP	SW	glogit
${\beta }_0$	−2.19 (0.40)	−4.98 (1.51)	0.27 (0.20)	−10.78 (0.81)
${\beta }_1$	2.65 (0.22)	5.27 (1.48)	0.78 (0.23)	9.08 (0.74)
${\beta }_2$	0.38 (0.13)	1.23 (0.46)	0.12 (0.04)	1.89 (0.37)
${\beta }_3$	−0.50 (0.13)	−1.01 (0.38)	−0.15 (0.06)	−1.74 (0.40)
-	$\delta = -0.04 \left(0.55\right)$	${\theta }_1 = 0.45 \left(0.12\right)$	$\gamma = 4.03 \left(1.20\right)$	$\alpha = 0.26 \left(0.03\right)$
-		${\theta }_1 =0.91 \left(0.19\right)$		$\lambda = 1.17 \left(0.72\right)$
DIC	751.92	749.01 **	751.38	747.75 *
MAE	0.0662	0.0564 **	0.0644	0.0497 *

* indicates the smallest value; ** indicates the next smallest value.

. The glogit model is fitted to the dataset, and the result is compared with SP, AEP, and SW models analyzed by Caron et al. [17]. The results reported in Table 5 show that the glogit model provides the best fit, followed by the AEP-based link model, indicated by the smallest value of DIC and MAE. Overall, we see the superiority of the glogit against other link functions for the datasets. The mean and standard deviation of posterior estimates values for all of the models are also given in Table 5.

6. Conclusions

A flexible generalized logit (glogit) link function for analyzing binomial regression is proposed in this paper. The link function is based on a new class of generalized logistic distribution, exponentiated-exponential logistic (EEL) distribution. This distribution considers both symmetric and asymmetric models to accommodate positive or negative skewness. Moreover, this allows for the case of a lighter or heavier tails behavior compared to the standard logistic.

The paper provides a simulation of binomial regression using seven scenarios to indicate the flexibility and superiority of the glogit compared with common link functions, i.e., logit, probit, and cloglog in the Bayesian framework. The simulation result show that the glogit model always gave the best fit for the datasets generated from the glogit link function and the second-best fit for the datasets generated from another correspond link function. It also shows the second-best fit model when the datasets generated from the glogit was the model that related to the shape of EEL p.d.f. curve determined from $\alpha$ and $\lambda$ value.

In addition, applying the model for the datasets from previous studies indicates that the glogit fits the data well and outperforms the other asymmetric link functions, such as the probit and t-link (T(8)) models proposed by Albert and Chib [13], the skewed probit (SP) model proposed by Chen et al. [9], the skewed generalized t-link (SGT) model proposed by Kim et al. [14], AEP-based link (AEP) model presented by Naranjo et al. [16], and finally, a skewed Weibull (SW) model presented by Caron et al. [17]. The proposed model is evidently flexible and capable of handling the datasets. The performance of the glogit is very good, indicated by the smallest value of DIC, followed by the AEP-based link model for both of the datasets. We are convinced that the glogit model is a good option and could be used in practice due to its flexibility. Other attractive aspects of the model are that it is analytically tractable and can be easily implemented under a Bayesian approach using the simple syntax.

This study adopted the typical priors for the Bayesian analysis with non-informative priors. Priors with other distributions can also be considered. The prior selection is an important activity that was not analyzed in this paper and hence, can be considered in future research.