Multiple Lump Novel and Accurate Analytical and Numerical Solutions of the Three-Dimensional Potential Yu–Toda–Sasa–Fukuyama Equation
Abstract
:1. Introduction
2. Analytical and Numerical Matching for the 3-Dp-YTSF Equation
- Applying ESE and MKud schemes to Equation (2) to get lump wave solutions then getting the initial and boundary conditions to investigate semi-analytical and numerical solutions trough the SBS and VI techniques.
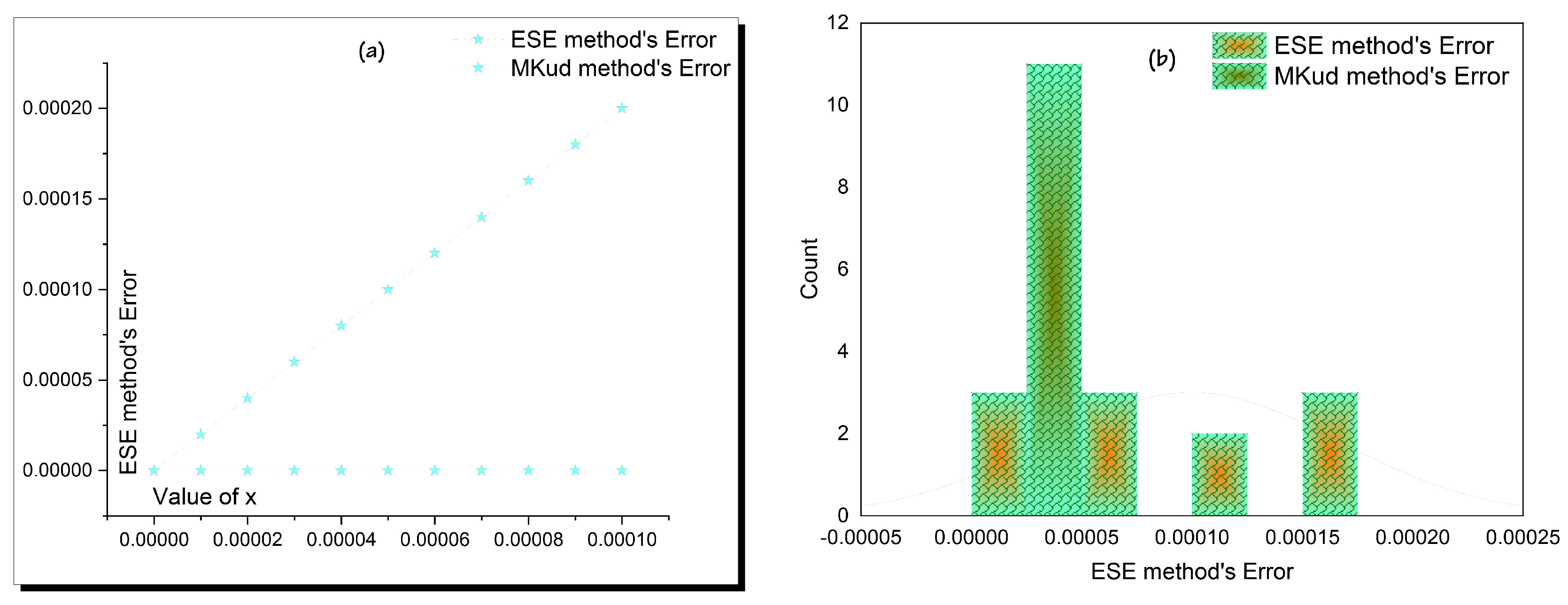
- Checking the accuracy of the obtained solutions along calculating the absolute value of error between exact and semi-analytical & numerical solutions.
2.1. ESE Analytical vs. SBS and VI Numerical Techniques along 3-Dp-YTSF Equation
Matching between Analytical and Numerical
- Applying the SBS numerical technique with the following initial condition gets the following shown analytical and numerical solutions’ values with respect to different values of x in Table 1
- Applying the VI method to Equation (1), gets the following semi-analytical solutions:Using same steps we can get
2.2. Kud Analytical vs. SBS and VI Numerical Techniques along 3-Dp-YTSF Equation
Matching between Analytical, Semi-Analytical and Numerical Solutions
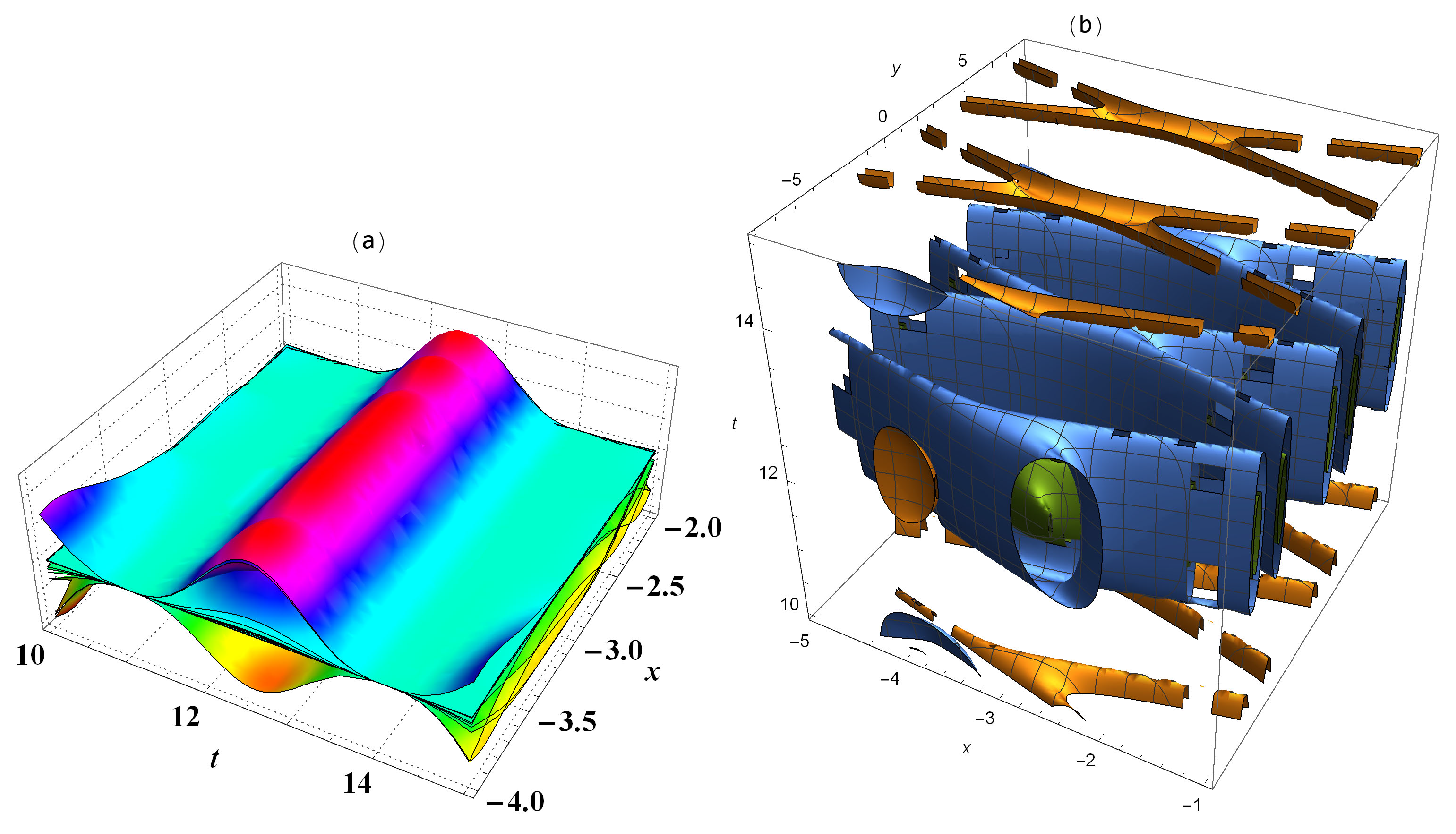
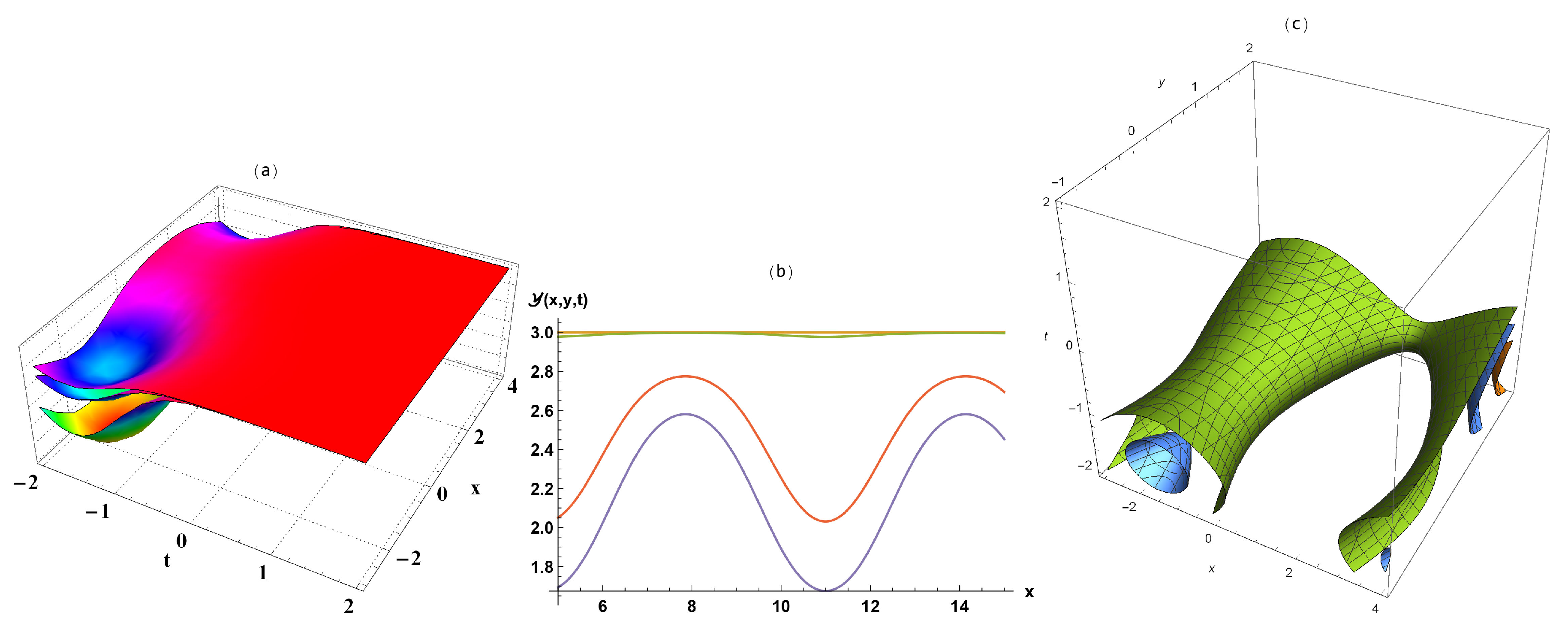
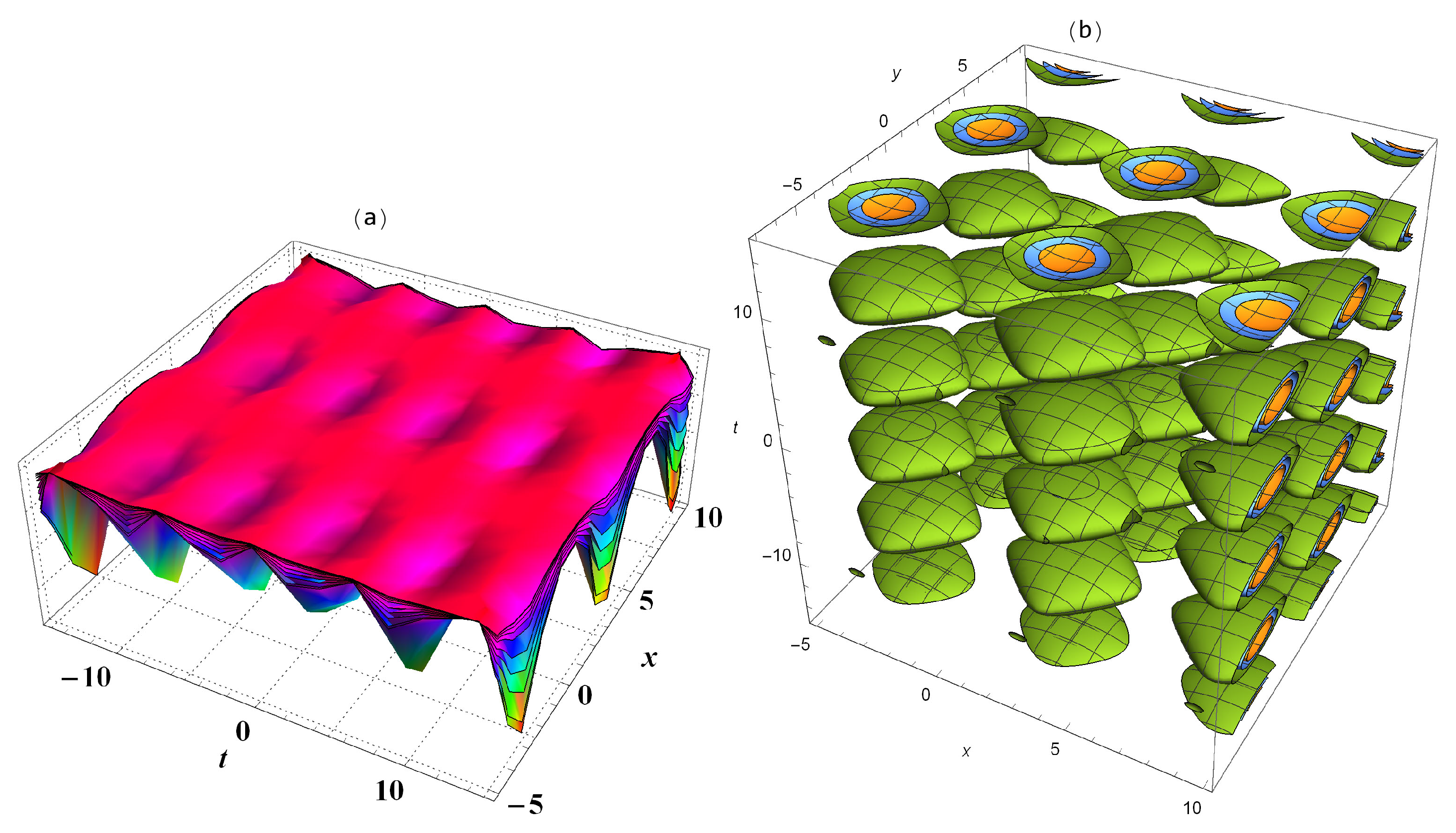
3. Results’ Interpretation
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Availability of Data and Materials
References
- Shen, B.; Chang, L.; Liu, J.; Wang, H.; Yang, Q.F.; Xiang, C.; Wang, R.N.; He, J.; Liu, T.; Xie, W.; et al. Integrated turnkey soliton microcombs. Nature 2020, 582, 365–369. [Google Scholar] [CrossRef] [PubMed]
- Ni, G.; Wang, H.; Jiang, B.Y.; Chen, L.; Du, Y.; Sun, Z.; Goldflam, M.; Frenzel, A.; Xie, X.; Fogler, M.; et al. Soliton superlattices in twisted hexagonal boron nitride. Nat. Commun. 2019, 10, 1–6. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dudley, J.M.; Genty, G.; Mussot, A.; Chabchoub, A.; Dias, F. Rogue waves and analogies in optics and oceanography. Nat. Rev. Phys. 2019, 1, 675–689. [Google Scholar] [CrossRef]
- Su, J.J.; Gao, Y.T.; Deng, G.F.; Jia, T.T. Solitary waves, breathers, and rogue waves modulated by long waves for a model of a baroclinic shear flow. Phys. Rev. E 2019, 100, 042210. [Google Scholar] [CrossRef]
- Dematteis, G.; Grafke, T.; Onorato, M.; Vanden-Eijnden, E. Experimental evidence of hydrodynamic instantons: The universal route to rogue waves. Phys. Rev. X 2019, 9, 041057. [Google Scholar] [CrossRef] [Green Version]
- Kannan, R.; Wang, Z. A high order spectral volume solution to the Burgers’ equation using the Hopf–Cole transformation. Int. J. Numer. Methods Fluids 2012, 69, 781–801. [Google Scholar] [CrossRef]
- Lan, Z.Z.; Su, J.J. Solitary and rogue waves with controllable backgrounds for the non-autonomous generalized AB system. Nonlinear Dyn. 2019, 96, 2535–2546. [Google Scholar] [CrossRef]
- Marcucci, G.; Pierangeli, D.; Conti, C. Theory of neuromorphic computing by waves: Machine learning by rogue waves, dispersive shocks, and solitons. Phys. Rev. Lett. 2020, 125, 093901. [Google Scholar] [CrossRef]
- Kannan, R. A high order spectral volume formulation for solving equations containing higher spatial derivative terms: Formulation and analysis for third derivative spatial terms using the LDG discretization procedure. Commun. Comput. Phys. 2011, 10, 1257–1279. [Google Scholar] [CrossRef]
- Ilhan, O.A.; Manafian, J.; Shahriari, M. Lump wave solutions and the interaction phenomenon for a variable-coefficient Kadomtsev–Petviashvili equation. Comput. Math. Appl. 2019, 78, 2429–2448. [Google Scholar] [CrossRef]
- Kannan, R. A high order spectral volume formulation for solving equations containing higher spatial derivative terms II: Improving the third derivative spatial discretization using the LDG2 method. Commun. Comput. Phys. 2012, 12, 767–788. [Google Scholar] [CrossRef]
- Kannan, R.; Wang, Z.J. LDG2: A variant of the LDG flux formulation for the spectral volume method. J. Sci. Comput. 2011, 46, 314–328. [Google Scholar] [CrossRef]
- Khater, M.M.; Baleanu, D. On abundant new solutions of two fractional complex models. Adv. Differ. Equ. 2020, 2020, 1–14. [Google Scholar] [CrossRef]
- Abdel-Aty, A.H.; Khater, M.M.; Dutta, H.; Bouslimi, J.; Omri, M. Computational solutions of the HIV-1 infection of CD4+ T-cells fractional mathematical model that causes acquired immunodeficiency syndrome (AIDS) with the effect of antiviral drug therapy. Chaos Solitons Fractals 2020, 139, 110092. [Google Scholar] [CrossRef]
- Khater, M.M.; Attia, R.A.; Park, C.; Lu, D. On the numerical investigation of the interaction in plasma between (high & low) frequency of (Langmuir & ion-acoustic) waves. Results Phys. 2020, 18, 103317. [Google Scholar]
- Qin, H.; Khater, M.; Attia, R.A. Inelastic Interaction and Blowup New Solutions of Nonlinear and Dispersive Long Gravity Waves. J. Funct. Spaces 2020, 2020, 5362989. [Google Scholar] [CrossRef]
- Khater, M.M.; Ghanbari, B.; Nisar, K.S.; Kumar, D. Novel exact solutions of the fractional Bogoyavlensky–Konopelchenko equation involving the Atangana-Baleanu-Riemann derivative. Alex. Eng. J. 2020, 59, 2957–2967. [Google Scholar] [CrossRef]
- Yue, C.; Lu, D.; Khater, M.M.; Abdel-Aty, A.H.; Alharbi, W.; Attia, R.A. On explicit wave solutions of the fractional nonlinear DSW system via the modified Khater method. Fractals 2020. [Google Scholar] [CrossRef]
- Abdel-Aty, A.H.; Khater, M.; Attia, R.A.; Eleuch, H. Exact Traveling and Nano-Solitons Wave Solitons of the Ionic Waves Propagating along Microtubules in Living Cells. Mathematics 2020, 8, 697. [Google Scholar] [CrossRef]
- Qin, H.; Khater, M.; Attia, R.A. Copious Closed Forms of Solutions for the Fractional Nonlinear Longitudinal Strain Wave Equation in Microstructured Solids. Math. Probl. Eng. 2020, 2020, 3498796. [Google Scholar] [CrossRef]
- Li, J.; Attia, R.A.; Khater, M.M.; Lu, D. The new structure of analytical and semi-analytical solutions of the longitudinal plasma wave equation in a magneto-electro-elastic circular rod. Mod. Phys. Lett. B 2020, 34, 2050123. [Google Scholar] [CrossRef]
- Khater, M.M.; Attia, R.A.; Alodhaibi, S.S.; Lu, D. Novel soliton waves of two fluid nonlinear evolutions models in the view of computational scheme. Int. J. Mod. Phys. B 2020, 34, 2050096. [Google Scholar] [CrossRef]
- Günerhan, H.; Khodadad, F.S.; Rezazadeh, H.; Khater, M.M. Exact optical solutions of the (2+ 1) dimensions Kundu–Mukherjee–Naskar model via the new extended direct algebraic method. Mod. Phys. Lett. B 2020, 34, 2050225. [Google Scholar] [CrossRef]
- Yue, C.; Khater, M.M.; Inc, M.; Attia, R.A.; Lu, D. Abundant analytical solutions of the fractional nonlinear (2+ 1)-dimensional BLMP equation arising in incompressible fluid. Int. J. Mod. Phys. B 2020, 34, 2050084. [Google Scholar] [CrossRef]
- Yue, C.; Elmoasry, A.; Khater, M.; Osman, M.; Attia, R.; Lu, D.; Elazab, N.S. On complex wave structures related to the nonlinear long–short wave interaction system: Analytical and numerical techniques. AIP Adv. 2020, 10, 045212. [Google Scholar] [CrossRef] [Green Version]
- Yue, C.; Khater, M.M.; Attia, R.A.; Lu, D. Computational simulations of the couple Boiti–Leon–Pempinelli (BLP) system and the (3+ 1)-dimensional Kadomtsev–Petviashvili (KP) equation. AIP Adv. 2020, 10, 045216. [Google Scholar] [CrossRef] [Green Version]
- Khater, M.M.; Attia, R.A.; Lu, D. Computational and numerical simulations for the nonlinear fractional Kolmogorov–Petrovskii–Piskunov (FKPP) equation. Phys. Scr. 2020, 95, 055213. [Google Scholar] [CrossRef]
- Khater, M.M.; Alzaidi, J.; Attia, R.A.; Lu, D. Analytical and numerical solutions for the current and voltage model on an electrical transmission line with time and distance. Phys. Scr. 2020, 95, 055206. [Google Scholar] [CrossRef]
- Dong, M.J.; Tian, S.F.; Wang, X.B.; Zhang, T.T. Lump-type solutions and interaction solutions in the (3+ 1)-dimensional potential Yu–Toda–Sasa–Fukuyama equation. Anal. Math. Phys. 2019, 9, 1511–1523. [Google Scholar] [CrossRef]
- Hu, Y.; Chen, H.; Dai, Z. New kink multi-soliton solutions for the (3+ 1)-dimensional potential-Yu–Toda–Sasa– Fukuyama equation. Appl. Math. Comput. 2014, 234, 548–556. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, H.Q. A transformed rational function method for (3+ 1)-dimensional potential Yu–Toda–Sasa–Fukuyama equation. Pramana 2011, 76, 561–571. [Google Scholar] [CrossRef]
- Liu, W. Rogue waves of the (3+ 1)-dimensional potential Yu–Toda–Sasa–Fukuyama equation. Rom. Rep. Phys. 2017, 69, 16. [Google Scholar]
- Roshid, H.O. Lump solutions to a (3+ 1)-dimensional potential-Yu–Toda–Sasa–Fukuyama (YTSF) like equation. Int. J. Appl. Comput. Math. 2017, 3, 1455–1461. [Google Scholar] [CrossRef]
- Zayed, E.; Arnous, A. Exact solutions of the nonlinear ZK-MEW and the potential YTSF equations using the modified simple equation method. AIP Conf. Proc. 2012, 1479, 2044–2048. [Google Scholar]
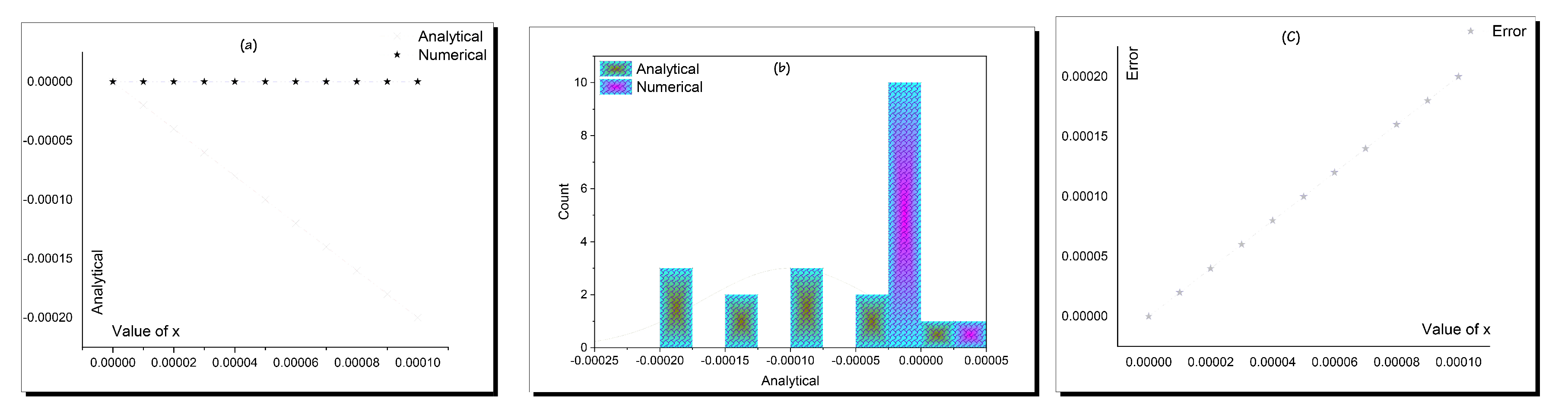

| Value of x | Analytical | Numerical | Absolute Error |
|---|---|---|---|
| 0 | 0 | 2.59953 | 2.59953 |
| 0.00001 | −0.00002 | −4.94237 | 0.00002 |
| 0.00002 | −0.00004 | −6.43149 | 0.00004 |
| 0.00003 | −0.00006 | −1.08723 | 0.00006 |
| 0.00004 | −0.00008 | −1.13736 | 0.00008 |
| 0.00005 | −0.0001 | −1.48758 | 0.0001 |
| 0.00006 | −0.00012 | −1.44334 | 0.00012 |
| 0.00007 | −0.00014 | −1.69924 | 0.00014 |
| 0.00008 | −0.00016 | −1.56069 | 0.00016 |
| 0.00009 | −0.00018 | −1.72219 | 0.00018 |
| 0.0001 | −0.0002 | −1.49012 | −0.0002 |
| Value of x | Analytical | Numerical | Error |
|---|---|---|---|
| 0 | 0 | 2.98907 | 2.98907 |
| 0.00001 | 5 | 1.02496 | 5 |
| 0.00002 | 0.00001 | 1.31139 | 0.00001 |
| 0.00003 | 0.000015 | 2.19425 | 0.000015 |
| 0.00004 | 0.00002 | 2.28909 | 0.00002 |
| 0.00005 | 0.000025 | 2.98536 | 0.000025 |
| 0.00006 | 0.00003 | 2.89309 | 0.00003 |
| 0.00007 | 0.000035 | 3.40231 | 0.000035 |
| 0.00008 | 0.00004 | 3.12301 | 0.00004 |
| 0.00009 | 0.000045 | 3.44501 | 0.000045 |
| 0.0001 | 0.00005 | 2.98023 | 0.00005 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khater, M.M.A.; Baleanu, D.; Mohamed, M.S. Multiple Lump Novel and Accurate Analytical and Numerical Solutions of the Three-Dimensional Potential Yu–Toda–Sasa–Fukuyama Equation. Symmetry 2020, 12, 2081. https://doi.org/10.3390/sym12122081
Khater MMA, Baleanu D, Mohamed MS. Multiple Lump Novel and Accurate Analytical and Numerical Solutions of the Three-Dimensional Potential Yu–Toda–Sasa–Fukuyama Equation. Symmetry. 2020; 12(12):2081. https://doi.org/10.3390/sym12122081
Chicago/Turabian StyleKhater, Mostafa M. A., Dumitru Baleanu, and Mohamed S. Mohamed. 2020. "Multiple Lump Novel and Accurate Analytical and Numerical Solutions of the Three-Dimensional Potential Yu–Toda–Sasa–Fukuyama Equation" Symmetry 12, no. 12: 2081. https://doi.org/10.3390/sym12122081
APA StyleKhater, M. M. A., Baleanu, D., & Mohamed, M. S. (2020). Multiple Lump Novel and Accurate Analytical and Numerical Solutions of the Three-Dimensional Potential Yu–Toda–Sasa–Fukuyama Equation. Symmetry, 12(12), 2081. https://doi.org/10.3390/sym12122081






