Abstract
Saving money and time are very important in any research project, so we must find a way to decrease the time of the experiment. This method is called the accelerated life tests (ALT) under censored samples, which is a very efficient method to reduce time, which leads to a decrease in the cost of the experiment. This research project includes inference on Lindley distribution in a simple step-stress ALT for the Type II progressive censored sample. The paper contains two major sections, which are a simulation study and a real-data application on the experimental design of an industry experiment on lamps. These sections are used to conduct results on the study of the distribution. The simulation was done using Mathematica 11 program. To use real data in the censored sample, we fitted them to be compatible with the Lindley distribution using the modified Kolmogorov–Smirnov (KS) goodness of fit test for progressive Type II censored data. We used the tampered random variable (TRV) acceleration model to generate early failures of items under stress. We also found the values of the distribution parameter and the accelerating factor using the maximum likelihood estimation of (MLEs) and Bayes estimates (BEs) using symmetric loss function for both simulated data and real data. Next, we estimated the upper and lower bounds of the parameters using three methods, namely approximate confidence intervals (CIs), Bootstrap CIs, and credible CIs, for both parameters of the distribution, and . Finally, we found the value of the parameter for the real data set under normal use conditions and stress conditions and graphed the reliability functions under normal and accelerated use.
1. Introduction
Due to the use of high technology in manufacturing products, the reliability of products has become very high, thus it is very hard nowadays to find a sufficient number of failure times in classical life testing experiments and reliability experiments; most products have exponential life time and it may be thousands of hours. Our aim is find a suitable way to produce early failures, because, under normal use conditions for products, producing failures in the lifetime experiments with a limited testing time may produce very few failures and it is not sufficient to study the data and make a very good model for them. Thus, we use the best way for decreasing the lifetime of the products: Accelerated life tests (ALT). In ALT, units or products are exposed to tough conditions and high stress levels (humidity, temperature, pressure, voltage, etc.) according to the conditions of manufacturing. There are many methods and models of ALT; products are exposed to stress according to the purpose of the experiment and the type of products. Scientists apply different types and methods of acceleration, e.g., constant ALT, step stress ALT, and progressive stress ALT. Nelson [1] discussed these different types of ALT. The main purpose of using ALT is to drive items to failure quickly, because some items may have a long lifetime under normal operating conditions. Therefore, in ALT, we put products under higher stress than the usual stress conditions, e.g. by increasing operating temperatures, pressures, or voltages, according to the physical use of the product, to generate failures more quickly.
There are several different forms of applying stress to products, e.g. step-stress (see, e.g., [1]). Two other common types are constant stress, where the test is conducted under a constant degree of stress for the entire experiment, and progressive stress, where all test units are subjected to stress as a function of time, and the stress increases on the experimented items as the time of the experiment increases (see El-Din et al. [2,3] for more details about acceleration and its models).
In step-stress ALT, we first apply a certain value of stress on the items under testing for certain time . Then, after this time, the stress load is increased by a fixed value for a certain period and so on until all the units have failed or the experiment ends. One of the most common methods of simple step-stress ALT has two levels (see, e.g., El-Din et al. [2,3,4].) Two types of censoring approaches can be applied to units: Type I censoring and Type II censoring. Recently, Type II censoring has been shown to make perfect use of time because it presets the number of failures. This means that the experiment does not end until the required number of failures has been achieved. Type II censoring can be explained as follows. If, for example, we have several independent and identical products and the sample number is n products under lifetime observation, the experiment then reaches its end by achieving m number of failure, which is preset before the experiment begins. With a fixed censoring scheme, let us denote them as . For more extensive reading about this subject, see the works done by alBalakrishnan [5], Fathi [6], and Abd El-Raheem [7].
This paper aims to make a full study on the Lindley distribution under ALT using progressive Type II censored samples and apply an experimental application to introduce the importance of this distribution in fitting many real data applications in many fields of life. We refer to different recent studies to explain the difference kinds of ALT; for more reading about constant, step, and progressive ALT, see the works of El-din et al. [8,9,10,11].
This paper is organized as follows. In Section 2, a brief literature review about the Lindley distribution and its applications in many fields of life, as well as the assumptions of the acceleration model used in this study, is presented. In Section 3, the maximum likelihood estimation (MLEs) of the parameters are obtained. We present another updated type of estimation, the Bayes estimation (BEs), using a symmetric loss function for model parameters in Section 4. We introduce three different types of intervals, namely asymptotic, bootstrap, and credible confidence intervals (CIs), for the parameters of the model in Section 5. In Section 6, a real data example for reliability engineering data is fitted and studied to apply the proposed methods (for more reading about reliability engineering modelling and applications, see [12,13,14]). Section 6 also includes the graphs of the reliability function and some elaboration about these graphs. Simulation study and some results and observations are presented in Section 7. Finally, the major findings are concluded in Section 8.
2. Lindley Distribution and Its Importance
This section identifies the importance of the Lindley distribution in the fields of business, pharmacy, biology, and so on. For example, Gomez et al. [15], applied the Lindley distribution to the application of strength systems’ reliability. Ghitany et al. [16] created a new bounded domain probability density feature in view of the generalized Lindley distribution.
The novelty of this paper is that no one jas used the tampered random variable (TRV) ALT model under progressive Type II censoring for the Lindley distribution and applied a real data experiment on censored sample, not complete sample, using the modified Kolmogorov–Smirnov (KS) algorithm, we compared it with the two-parameter Weibull distribution and we proved that it provides better fitting to the real data experiment. This inspires us to work on implementing the SSALT model and estimating the parameters involved under Lindley distribution for simulated data and real data application. The first one introduced the Lindley distribution was Lindley [17], who combined exponential distribution with parameter () and Gamma (2,). In 2012, Bakouch et al. [18] introduced an extended Lindley distribution that now has many applications in finance and economics. Ghitany et al. [19] proved that the Lindley distribution is a weighted distribution of gamma distribution and exponential distribution. Therefore, in many cases, the Lindley distribution is more flexible than these two and distributions, as he studied its properties, and showed through a numerical study that Lindley distribution is a better fit to lifetime data than exponential distribution. One of the major advantage of the Lindley distribution over many distributions, as an example of exponential distribution, is that it has an increased risk rate. Gomez et al. [15] introduced an improvement on the Lindley distribution named the Log Lindley distribution, which was used as a replacement for the beta regression model. Now, the probability density function (PDF) can be written of the Lindley distribution as follows:
Its cumulative distribution function (CDF) is as Equation (2). By graphing the Lindsey’s PDF and CDF we can deduce that they have asymmetric shapes. As the Lindley distribution has a failure-rate function, which is called the hazard rate function (HRF), and can be introduced by:
For more details about real data applications using the Lindley distribution, see [17].
Assumptions and the Test Procedure and the Steps Used
- Let us assume that we have n identical and independent products that follows the Lindley distribution and these were subject to a lifetime examination in a lifetime experiment;
- The examination of the products ends as soon as the failure happens such that: ;
- All units run in normal-use conditions and after a prefixed time , the stress is increased by a certain value;
- From the physical experiments on products, engineers have stated that the following law controls the connection between the stress on the products S and scale parameter . Thus, the law can be stated as follows: The model of inverse power law (IPL) is given by: , where , and voltage is denoted by S, and a is the model parameter;
- We will apply progressive Type II censoring, as discussed above, on the units of this experiment;
- After running the test on the products, the number of units that failed before stress is . In addition, is the total number of failed items after applying the stress at time ;
- We used the tampered random variable (TRV) model provided by [20]. This model states that under step stress partially accelerated life test (SSPALT), the lifetime of a unit can be written as:where z refers to the time of the product under the use conditions, is the time that we change the stress, and is the factor that we use to accelerate the failure time (> 1);
- The PDF is divided as follows:
3. Estimation Using the Maximum Likelihood Function
Maximum likelihood estimation (MLE) in statistics is a method of estimating the parameters of a probability distribution by maximizing the probability function so that the observed data is most likely under the assumed statistical model. The maximum likelihood estimate gives a point estimation of the distribution parameter and this estimate makes the likelihood function maximum, one of the advantages of this method being that it is versatile and provides a good estimates for the distribution parameter.
This method works on finding the first derivatives for the log-likelihood function with respect to the distribution parameters and solving the equations simultaneously and finding the estimates that make the log-likelihood function at maximum value, this value is called the estimates of the distribution.
In this section, we used this method for estimating the parameters of the distribution and the accelerating factor. Thus, by using Equations (4) and substituting with it in Equation (5), we get the likelihood function under the progressive Type II censored sample. In the next subsection, we will introduce the procedures of this method.
Point Estimation
Let be the times that the items the failing occurred times the products under SSPALT, with censored scheme then the likelihood function is as expressed below, see [4] for more reading:
By taking the log for both sides for Equation (6), we then get the log-likelihood function, as shown below:
By finding the first derivative for the distribution parameters and as follows:
4. Bayes Estimation
Bayesian estimation is a modern efficient approximation for estimating the parameters compared with the maximum likelihood estimates method. As it takes into account both previous information and sample information and estimates the unspecified interest parameters. Bayesian estimation can be performed using symmetric and asymmetric loss function, according to the necessity of the experiment, and sometimes symmetric loss functions are better than asymmetric loss functions. There are different types of asymmetric loss functions, two being the linear exponential loss function and the general entropy loss function.
In this section, we proposed the Bayes estimators of the unknown parameters of the Lindley distribution using the symmetric loss function. In Bayesian estimation we must assign a prior distribution to the data, and in order to choose the prior density function that covers our belief on the data, we must choose appropriate values hyper-parameters. In this part of the paper, based on Type II progressive censored sample, we used the square error (SE) loss function to obtain the model parameters estimations for and , as we deduced that both and are independent, we choose a gamma priors as a prior distribution for the two parameters because it is versatile for adjusting different shapes of the distribution density. It also has another merit which is that it provides conjugacy and mathematical ease and has closed expressions for moments type. The two independent priors are as follows:
and
As the gamma prior is very common, many authors have used it because it encourages researchers to feel confident in the data. For more information about BE, see Nassar and Eissa [21], and Singh et al. [22]. If we do not have any belief about the data, we must use non-informative priors, we do this by setting the following values so that tends to zero, and tends to infinity, . In this way, we can change informative priors into non-informative priors, see Singh et al. [22]. After this, we can find the form of the joint PDF prior of , and as below:
By multiplying Equation (11) with Equation (5), we get equation the posterior function in Equation (12):
By making some simplifications on Equation (12) we get Equation (13).
The posterior density function in (14) for the two parameters and can be formed by the multiplication of Equations (6) with (11) and making some simplification, and its final form is as below:
According to the SE loss function, the Bayes estimator for , (for more details see Ahmadi et al. [23]):
where is given by Equation (14).
In a fact we cannot find a result for integrals in Equation (15). Thus, we used the Markov chain Monte Carlo (MCMC) technique to approximate these integrals, and used the the Metropolis—Hasting algorithm as an example of the MCMC technique to find the estimates.
4.1. Using MCMC Method in Bayesian Estimation
In this section, we use the MCMC method because we do not have a well-known distribution for the posterior density function, and we then calculate the BEs of and . From Equation (14), the conditional posterior distribution functions for and are as shown below, respectively:
Therefore, we do not have a closed form for the conditional posterior distribution and in (16) and (17) as it does not represent any known distribution. We therefore used the Metropolis–Hasting algorithm (for more information about this, see Upadhyay and Gupta [24]). The algorithm below explains the steps required to compute Bayes estimators for under the SE loss function.
4.2. The Metropolis—Hasting Algorithm
The Metropolis—Hastings algorithm and sometimes we call it the random walk algorithm, this kind of algorithm can be considered as a Markov Chain Monte Carlo (MCMC) method for generating data from any CDF as it used for normal distribution to generate data because it has the symmetric property that ensures that all other distribution are covered under the symmetric normal graph. This generated samples can be used to approximate the distribution or to compute an integral (e.g., an expected value), we use Algorithm 1 because sometimes obtaining samples is difficult, that is because the posterior we have is from an unknown distribution. We can use this algorithm with one dimension and two dimensions data. For more reading see [24,25,26,27,28,29,30,31].
| Algorithm 1 MCMC algorithm |
where is the burn-in period. |
5. Interval Estimation
In this part, we tried to estimate the upper and lower bounds of the following parameters and using the following three methods: The first method is approximate CIs, the second method is the Bootstrap CIs, and the third method is credible CIs
5.1. Finding Confidence Intervals for the Parameters
In statistics, a confidence interval (CI) is a type of estimate computed from the statistics of the observed data. This interval identifies the range of for the unknown parameters, it changes according to the confidence level chosen by the investigator, confidence interval for an unknown parameter is based on sampling the distribution of a corresponding estimator.
In this part of the paper, we will try to find the upper and lower bounds for using the MLEs of the two parameters. Where the asymptotic distributions for the MLEs are is given by [32]:
where is the variance covariance matrix of the unknown parameters
The approximate s for is given by:
5.2. Bootstrap Confidence Intervals
Bootstrapping assigns measures of accuracy (bias, variance, confidence intervals, prediction error, etc.) to sample estimates. This technique allows an estimation of the sampling distribution of almost any statistic using random sampling methods. In this part of the paper, we find the values of bootstrap CIs for (see Efron and Tibshirani [33] for more information). Algorithm 2 below specifies the steps for obtaining lower and upper bounds using bootstrap CIs.
| Algorithm 2 Bootstrap algorithm |
Thus, we can get bootstrap CIs for , given by: |
5.3. Credible Confidence Intervals
In Bayesian statistics, a credible interval is an interval in which the distribution parameter value falls between the lower and upper bounds of it with a certain confidence level. It is an interval in the domain of a posterior probability distribution. Credible intervals are symmetric in meaning to the approximate confidence interval, Bayesian intervals treat their bounds as fixed and the estimated parameter as a random variable, whereas frequentest confidence intervals treat their bounds as random variables and the parameter as a fixed value. In addition, Bayesian credible intervals use knowledge of the situation-specific prior distribution, while the frequentest confidence intervals do not. Algorithm 3 below was used to get credible CIs of and .
| Algorithm 3 Credible interval |
Thus, we can get credible CIs for is given by: |
6. Application on Real Data Set for Lindley Distribution
Here, we used real data to serve as a real-life example for the step stress model with a real data set, and fitted this data set and then made a statistical inference on this data to assess the performance of the Lindley distribution.
6.1. Example
The data set that we used in the application were collected from Chapter 5 of Zhu [26]. These data represent an experiment on some light bulbs with working-use stress of 2 voltage. Here, a sample of size n = 64 light bulbs were lit at 2.25 voltage for a period of 96 h before increasing the voltage to 2.44 voltage. This means the time of stress change was at h. This lifetime experiment was performed on a sample of size n = 64 light bulbs under stress; in our experiment, we removed 11 bulbs when they were still working and functioning before they had reached their failure point. Consequently, we observed only failures, as only had failed on the stress voltage V, and the scheme used in progressive censoring is , :
From practical experiments, we deduced that the best model to represents the acceleration and voltage relationship is the inverse power model. Thus, the acceleration model can be expressed as:
We use modified Kolmogorov–Smirnov goodness of fit test for progressive Type-II censored data to determine the goodness of fit for the data in the experiment, this method was suggested by Pakyari and Balakrishnan [34].
6.2. Comparison with Competitive Distribution
The importance of the Lindley distribution in this paper is that it provides more fit than its traditional competitor, the two-parameter Weibull distribution, as we checked for the p-value for both distributions for fitting the real data application and found that the Lindley distribution has p-value greater than 0.05 for both levels of stress in the experiment, while in case of the Weibull distribution it makes a poor-fitting for the real data set because the p-value of the first level of acceleration is less than 0.05, while it provides good fitting for the second level, so we can deduce that the Lindley distribution makes better fitting than the Weibull distribution for both levels of experiment so we can use it instead of the Weibull distribution by fitting the two levels of the Lindley distribution which has a merit over the two parameters Weibull distribution in fitting this kind of experiment. For more information about the reliability of engineering data, please see references [12,13,14].
The following table contains the value of test statistic and the p-values of each stress level for the Lindley distribution and Weibull two parameters distribution.
6.3. Important Results Conducted from Real Data
The following points illustrate briefly the work we have done in this real data example. According to the results in Table 1, Table 2 and Table 3.

Table 1.
The table below shows how our distribution makes a good fit for the real data set as we see the value of test statistic and the corresponding p-values of each stress level for Lindley distribution.

Table 2.
The table below shows value of test statistic and the corresponding p-values for each stress level for the Weibull distribution, we can see that the Weibull distribution makes a poor fitting for the real data set because the p-value of the first level of acceleration is less than 0.05, while it provides good fitting for the second level, on the other hand the Lindley distribution makes better than Weibull for both levels of experiment and we used one distribution to fit the whole experiment with both levels of acceleration, so we can use the Lindley distribution instead of the Weibull distribution for modeling the whole experiment according to the results in Table 2.

Table 3.
The lengths of confidence intervals (CIs), maximum likelihood estimation (MLEs), and Bayes estimates (BEs) using non-informative prior of the parameters , are introduced in the table below, where , . For this data set, Bayesian analysis is carried out in case of non-informative priors.
- In the experiment with real data, we used a modified K-S method to ensure that our data was a good fit for our distribution;
- According to the p-values in Table 1, we deduced that our distribution made a good fit for the failure times of the experiment. After that, we first estimated the parameters using this real data, and then we concluded the CIs;
- By using the estimated parameters and the acceleration model estimates , we deduced , where is the scale parameter under normal use. From Equation (27), we can evaluate the MLE of the scale parameter under normal conditions . Which is the scale parameter under normal use;
- By estimating the parameter under normal use we can use it to find the following:
- The mean time to failure (MTTF) under normal conditions is
- The failure rates (hazard rate function ) under normal conditions is:
- The reliability function under normal conditions is:
- By graphing the reliability function we deduced the following: Reliability function under normal use, at time, equals zero the reliability function equal one, see Figure 1. Under stress conditions, we concluded that the reliability function decreases, as time increases, see Figure 2. As the stress increase once more it approaches zero see Figure 3.
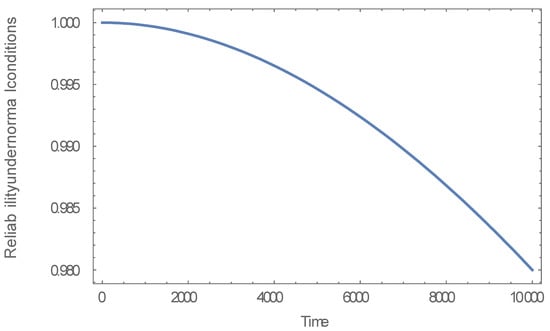 Figure 1. The graph above is for the reliability function under normal conditions, we can see that from the graph that the reliability function at time = 0, it approaches to one, and it approaches to zero by increasing the time, and that is very rational under normal use for any item.
Figure 1. The graph above is for the reliability function under normal conditions, we can see that from the graph that the reliability function at time = 0, it approaches to one, and it approaches to zero by increasing the time, and that is very rational under normal use for any item.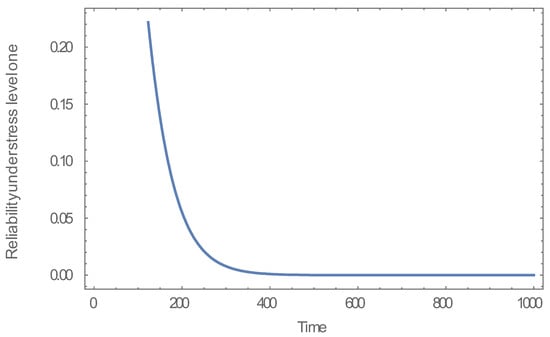 Figure 2. The graph above is for the reliability function under stress level S = 2.25 volt conditions, we can deduce from the graph that the reliability function decreases rapidly by increasing time, and that result is very rational under stress use for any item as it was subjected to high voltage greater than the use conditions, which leads to early failure.
Figure 2. The graph above is for the reliability function under stress level S = 2.25 volt conditions, we can deduce from the graph that the reliability function decreases rapidly by increasing time, and that result is very rational under stress use for any item as it was subjected to high voltage greater than the use conditions, which leads to early failure.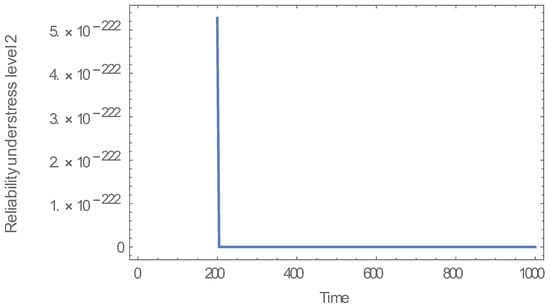 Figure 3. The graph above is for the reliability function under stress level S = 2.44 volt conditions, we can deduce from the graph that the reliability function, decreases very rapidly by increasing the time and stress, and that is very rational under stress use for any item as it if any item was subjected to high voltage greater than the use conditions, which leads to early failure.
Figure 3. The graph above is for the reliability function under stress level S = 2.44 volt conditions, we can deduce from the graph that the reliability function, decreases very rapidly by increasing the time and stress, and that is very rational under stress use for any item as it if any item was subjected to high voltage greater than the use conditions, which leads to early failure.
7. Simulation Studies
This part of the paper contains the simulation for the data in order to estimate the parameters by using both the MLEs and BEs (under square error loss (SEL) function), according to the mean square errors (MSEs) results in the tables below we can make a decision on the parameters, and in this simulation we used different values of n, m, and , . Table 4 and Table 5 gives us the results deduced from the simulation. The censoring schemes (CS) vector used in the simulation is defined below.

Table 4.
The table below contains the values of MSEs for MLEs and BEs (under square error loss function (SEL)) of ( and with true values and values of the prior parameters ( 14,400, , 12,100, and ), time of changing stress .

Table 5.
The results in this table is the coverage probabilities of approximate, credible, and bootstrap CIs for .
To make a complete simulation, we used the following algorithm to clarify the steps used in the whole simulation.
Important Results Conducted from Simulated Data
The following points illustrate briefly the observed results from simulation Algorithm 4. According to the results in Table 4 and Table 5:
- As the sample size increased, the MSEs of BEs and MLEs estimation for the parameters and decreased. Sometimes this situation did not occur because of small disturbances in data generation;
- The MSEs for BEs of and are smaller than the MSEs of MLEs, and this is rational because the BE is the updated method, and more accurate than MLE;
- When the sample size increases, the length of the approximate, Bootstrap, and credible CIs reduced, except in some small iterations, and that is due to the randomization in the generation of data using the Mathematica package;
- The shortest interval is the credible CIs of and according to the length, and credible CIs had the highest coverage probability;
- The length of Bootstrap CIs is shorter than the approximate CIs in most cases.
- We deduced that the credible CIs was the shortest one and had the highest coverage probability among all intervals.
| Algorithm 4 The complete algorithm for all simulation in the paper |
|
8. Conclusions on Real Data and Simulation Results
In this paper, we made a statistical inference on step stress accelerated life tests under progressive Type II censoring when the lifetimes of the data follow the Lindley distribution. First, we used our simulation studies to find the estimation of the model parameters by using the classical method, which is MLEs and the other method is the Metropolis Hasting algorithm method to get the BEs. We conclude that the Bayesian method was better than the classical method because it had a smaller MSE compared with the other method. CIs, including approximate CIs, Bootstrap CIs, and credible CIs, were estimated for the parameters of the model, and we conclude that the credible interval was the best one according to the shortness of the interval length, and it had the highest coverage probability. All the calculations were worked out based on different sample sizes and using censoring Scheme 1. In Section 6, we introduce a real data application on a Lindley distribution to see whether the data made a good fit to it or not. This application consisted of two levels of acceleration, the first being complete and the second being censored and exposed to higher stress than the first. We fitted the data using the Lindley distribution and the two-parameter Weibull distribution. We deduced that the data are a good fit for the Lindley distribution based on the p-values in both levels, but they were poorly fit to the Weibull distribution in the first level and well fit in the second level, thus we could use the Lindley distribution as a good candidate to model this application while the Weibull distribution could not be used. We then made statistical inference using this application and estimate the parameters of the distribution by using the above two methods, but we used non-informative priors in the BEs and also estimated the three CIs for the model parameters.
Author Contributions
Formal analysis, F.H.R. and S.A.M.M.; Funding acquisition, E.H.H. and M.S.M.; Investigation, S.A.M.M. and M.S.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Taif University researchers supporting project number (TURSP-2020/160), Taif University, Taif, Saudi Arabia. This paper was funded by “Taif University Researchers Supporting Project number (TURSP-2020/160), Taif University, Taif, Saudi Arabia”.
Acknowledgments
The authors are thankful for the Taif University researchers supporting project number TURSP-2020/160, Taif University, Taif, Saudi Arabia. This paper was funded by “Taif University Researchers Supporting Project number TURSP-2020/160, Taif University, Taif, Saudi Arabia”.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| Probability density function | |
| CDF | Cumulative distribution function |
| SSPALT | Step Stress Partially Accelerated Life Test |
| CIs | Credible confidence intervals |
| BEs | Bayes estimates |
| MLEs | Maximum Likelihood |
| TRV | Tampered Random Variable |
| KS | Kolmogorov–Smirnov |
| ALT | Accelerated Life Test |
| IPL | inverse power law |
| SE | Square error |
| MCMC | Markov chain Monte Carlo |
| MTTF | The mean time to failure |
| SEL | Square error loss |
| CS | The censoring schemes |
References
- Nelson, W. Accelerated Testing: Statistical Models, Test Plans and Data Analysis; Wiley: New York, NY, USA, 1990. [Google Scholar]
- El-Din, M.M.M.; Amein, M.M.; El-Attar, H.E.; Hafez, E.H. Symmetric and Asymmetric Bayesian Estimation For Lindley Distribution Based on Progressive First Failure Censored Data. Math. Sci. Lett. 2017, 6, 255–261. [Google Scholar] [CrossRef]
- El-Din, M.M.M.; Amein, M.M.; Abd El-Raheem, A.M.; Hafez, E.H.; Riad, F.H. Bayesian inference on progressive-stress accelerated life testing for the exponentiated Weibull distribution under progressive Type II censoring. J. Stat. Appl. Probab. Lett. 2020, 7, 109–126. [Google Scholar]
- El-Din, M.M.M.; Abu-Youssef, S.E.; Ali, N.S.A.; Abd El-Raheem, A.M. Estimation in step-stress accelerated life tests for Weibull distribution with progressive first-failure censoring. J. Stat. Appl. Probab. 2015, 3, 403–411. [Google Scholar]
- Balakrishnan, N.; Cramer, E. The Art of Progressive Censoring: Applications to Reliability and Quality; Birkhäuser: New York, NY, USA, 2014. [Google Scholar]
- Fathy, H.; Riad, E.; Hafez, H. Point and Interval Estimation for Frechet Distribution Based on Progressive First Failure Censored Data. J. Stat. Appl. Probab. 2020, 9, 181–191. [Google Scholar]
- Abd El-Raheem, A.M.; Abu-Moussa, M.H.; Hafez, M.M. Accelerated life tests under Pareto-IV lifetime distribution: Real data application and simulation study. Mathematics 2020, 8, 1786. [Google Scholar] [CrossRef]
- El-Din, M.M.M.; Abu-Youssef, S.E.; Ali, N.S.A.; Abd El-Raheem, A.M. Optimal plans of constant-stress accelerated life tests for the Lindley distribution. J. Test. Eval. 2017, 45, 1463–1475. [Google Scholar]
- El-Din, M.M.M.; Amein, M.M.; El-Raheem, A.M.A.; El-Attar, H.E.; Hafez, E.H. Estimation of the Coefficient of Variation for Lindley Distribution based on Progressive First Failure Censored Data. J. Stat. Appl. Probab. 2019, 8, 83–90. [Google Scholar]
- El-Din, M.M.M.; Amein, M.M.; El-Attar, H.E.; Hafez, E.H. Estimation in Step-Stress Accelerated Life Testing for Lindley Distribution with Progressive First-Failure Censoring. J. Stat. Appl. Probab. 2016, 5, 393–398. [Google Scholar] [CrossRef]
- El-Din, M.M.M.; Abu-Youssef, S.E.; Ali, N.S.A.; El-Raheem, A.M.A. Estimation in constant-stress accelerated life tests for extension of the exponential distribution under progressive censoring. Metron 2016, 74, 253–273. [Google Scholar] [CrossRef]
- Ling, M.H.; Hu, X.W. Optimal design of simple step-stress accelerated life tests for one-shot devices under Weibull distributions. Reliab. Eng. Syst. Saf. 2020, 193, 1–20. [Google Scholar] [CrossRef]
- Cheng, Y.; Elsayed, E.A. Reliability modeling of mixtures of one-shot units under thermal cyclic stresses. Reliab. Eng. Syst. Saf. 2017, 167, 58–66. [Google Scholar] [CrossRef]
- Wang, J. Data Analysis of Step-Stress Accelerated Life Test with Random Group Effects under Weibull Distribution. Math. Probl. Eng. 2020, 2020, 4898123. [Google Scholar] [CrossRef]
- Gmez-Déniz, E.; Sordo, M.A.; Calderín-Ojeda, E. The log–Lindley distribution as an alternative to the beta regression model with applications in insurance. Insur. Math. Econ. 2014, 54, 49–57. [Google Scholar] [CrossRef]
- Ghitany, M.E.; Al-Mutairi, D.K.; Aboukhamseen, S.M. Estimation of the Reliability of a Stress-Strength System from Power Lindley Distributions. Commun. Stat. Simul. Comput. 2015, 44, 118–136. [Google Scholar] [CrossRef]
- Lindley, D.V. Fudicial distributions and Bayes’ theorem. J. R. Stat. Soc. 1958, 20, 102–107. [Google Scholar]
- Bakouch, H.S.; Al-Zahrani, B.M.; Al-Shomrani, A.A.; Marchi, V.A.; Louzada, F. An extended Lindley distribution. J. Korean Stat. Soc. 2012, 41, 75–85. [Google Scholar] [CrossRef]
- Ghitany, M.E.; Atieh, B.; Nadarajah, S. Lindley distribution and its application. Math. Comput. Simul. 2008, 78, 493–506. [Google Scholar] [CrossRef]
- DeGroot, M.H.; Goel, P.K. Bayesian and optimal design in partially accelerated life testing. Nav. Res. Logist. 1979, 16, 223–235. [Google Scholar] [CrossRef]
- Nassar, M.M.; Eissa, F.H. Bayesian estimation for the generalized Weibull model. Commun. Stat. Theor. 2004, 33, 2343–2362. [Google Scholar] [CrossRef]
- Singh, S.K.; Singh, U.; Sharma, V.K. Bayesian estimation and prediction for the generalized Lindley distribution under asymmetric loss function, Hacet. J. Math. Stat. 2014, 43, 661–678. [Google Scholar]
- Ahmadi, J.; Jozani, M.J.; Marchand, E.; Parsian, A. Bayes estimation based on k-record data from a general class of distributions under balanced type loss functions. J. Stat. Plan. Inference 2009, 139, 1180–1189. [Google Scholar] [CrossRef]
- Upadhyay, S.K.; Gupta, A. A Bayes analysis of modified Weibull distribution via Markov chain Monte Carlo simulation. J. Stat. Comput. Simul. 2010, 80, 241–254. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Sandhu, R.A. A simple simulation algorithm for generating progressively type-II censored samples. Am. Stat. 1995, 49, 229–230. [Google Scholar]
- Zhu, Y. Optimal Design and Equivalency of Accelerated Life Testing Plans. Ph.D. Thesis, The State University of New Jersey, New Brunswick, NJ, USA, 2010. [Google Scholar]
- El-Din, M.M.M.; Abu-Youssef, S.E.; Ali, N.S.A.; El-Raheem, A.M.A. Parametric inference on step-stress accelerated life testing for the extension of exponential distribution under progressive Type II censoring. Commun. Stat. Appl. Methods 2016, 23, 269–285. [Google Scholar] [CrossRef]
- El-Din, M.M.M.; Abu-Youssef, S.E.; Ali, N.S.A.; El-Raheem, A.M.A. Classical and Bayesian inference on progressive-stress accelerated life testing for the extension of the exponential distribution under progressive Type II censoring. Qual. Reliab. Eng. Int. 2017, 33, 2483–2496. [Google Scholar]
- El-Din, M.M.M.; Abd El-Raheem, A.M.; Abd El-Azeem, S.O. On Step-Stress Accelerated Life Testing for Power Generalized Weibull Distribution Under Progressive Type-II Censoring. Ann. Data Sci. 2020. [Google Scholar] [CrossRef]
- Gepreel, K.A.; Mahdy, A.M.S.; Mohamed, M.S.; Al-Amiri, A. Reduced differential transform method for solving nonlinear biomathematics models. Comput. Mater. Contin. 2019, 61, 979–994. [Google Scholar] [CrossRef]
- Mahdy, A.M.S.; Mohamed, M.S.; Gepreel, K.A.; AL-Amiri, A.; Higazy, M. Dynamical characteristics and signal flow graph of nonlinear fractional smoking mathematical model. Chaos Solitons Fractals 2020, 141, 110308. [Google Scholar] [CrossRef]
- Miller, R. Survival Analysis; Wiley: New York, NY, USA, 1981. [Google Scholar]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; Chapman & Hall: London, UK, 1993. [Google Scholar]
- Pakyari, R.; Balakrishnan, N. A general purpose approximate goodness-of-fit test for progressively Type II censored data. IEEE Trans. Reliab. 2012, 61, 238–243. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).