miRID: Multi-Modal Image Registration Using Modality-Independent and Rotation-Invariant Descriptor
Abstract
:1. Introduction
2. The Proposed Method
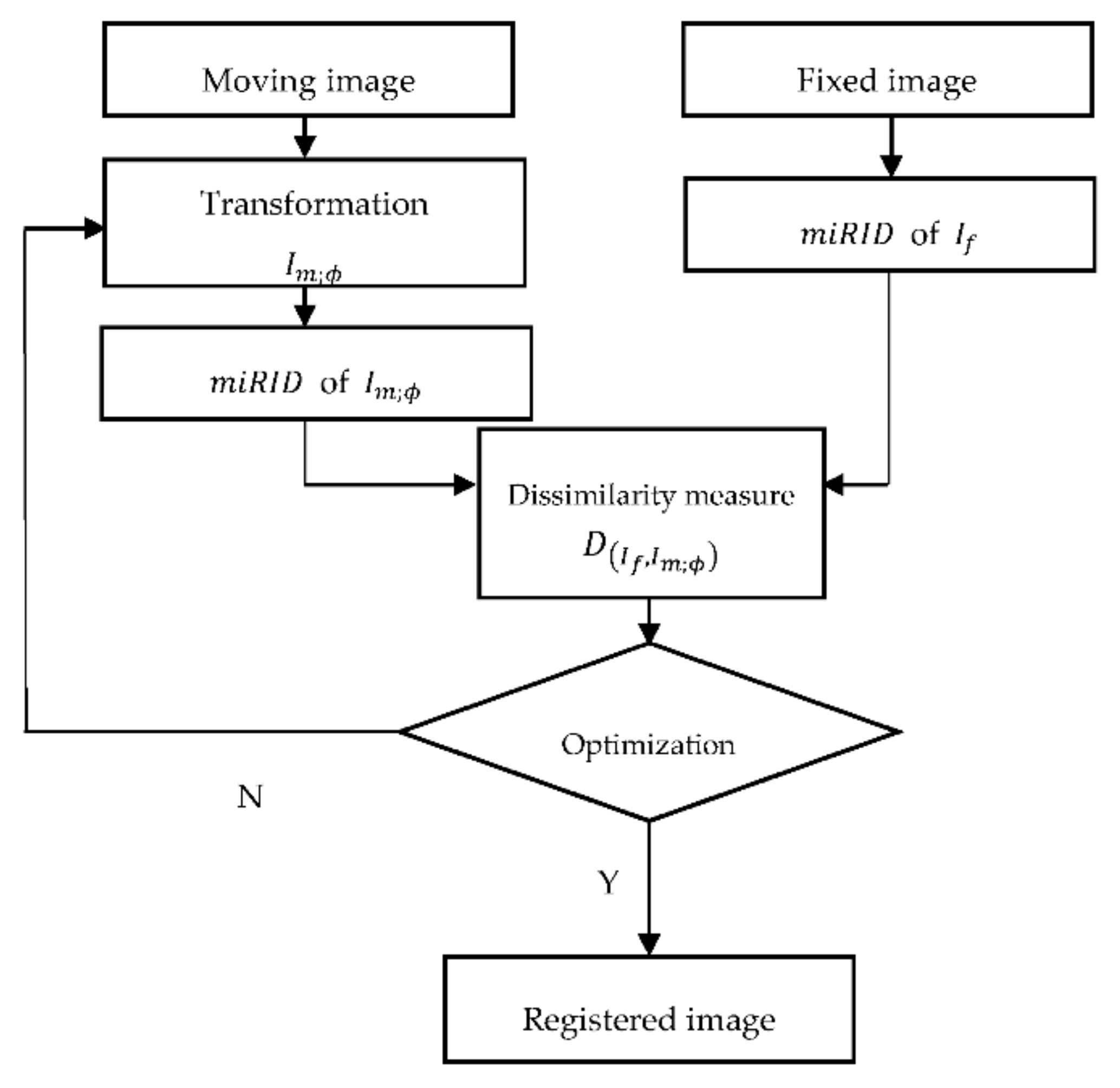
2.1. Registration Framework
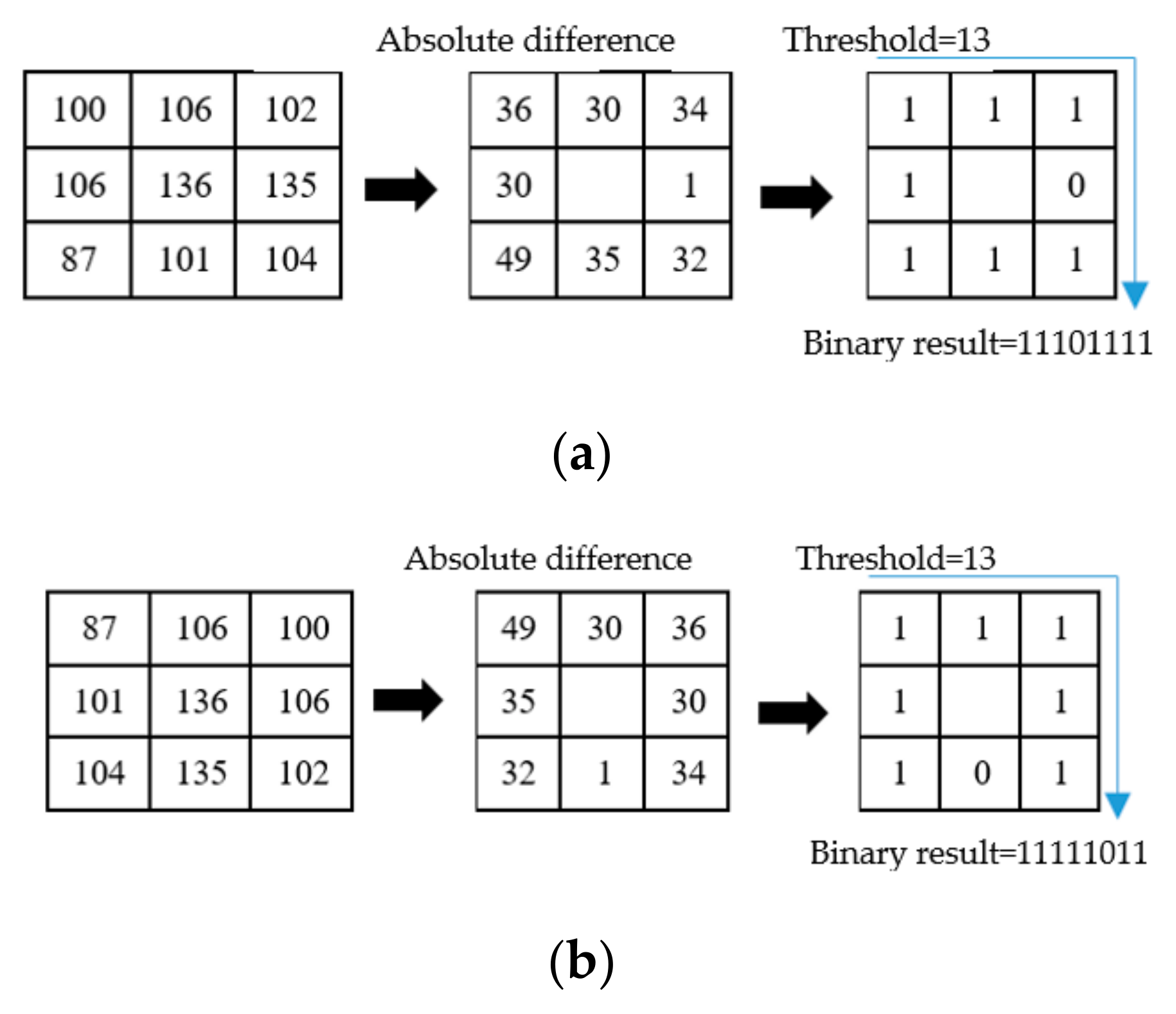
2.2. miLBP
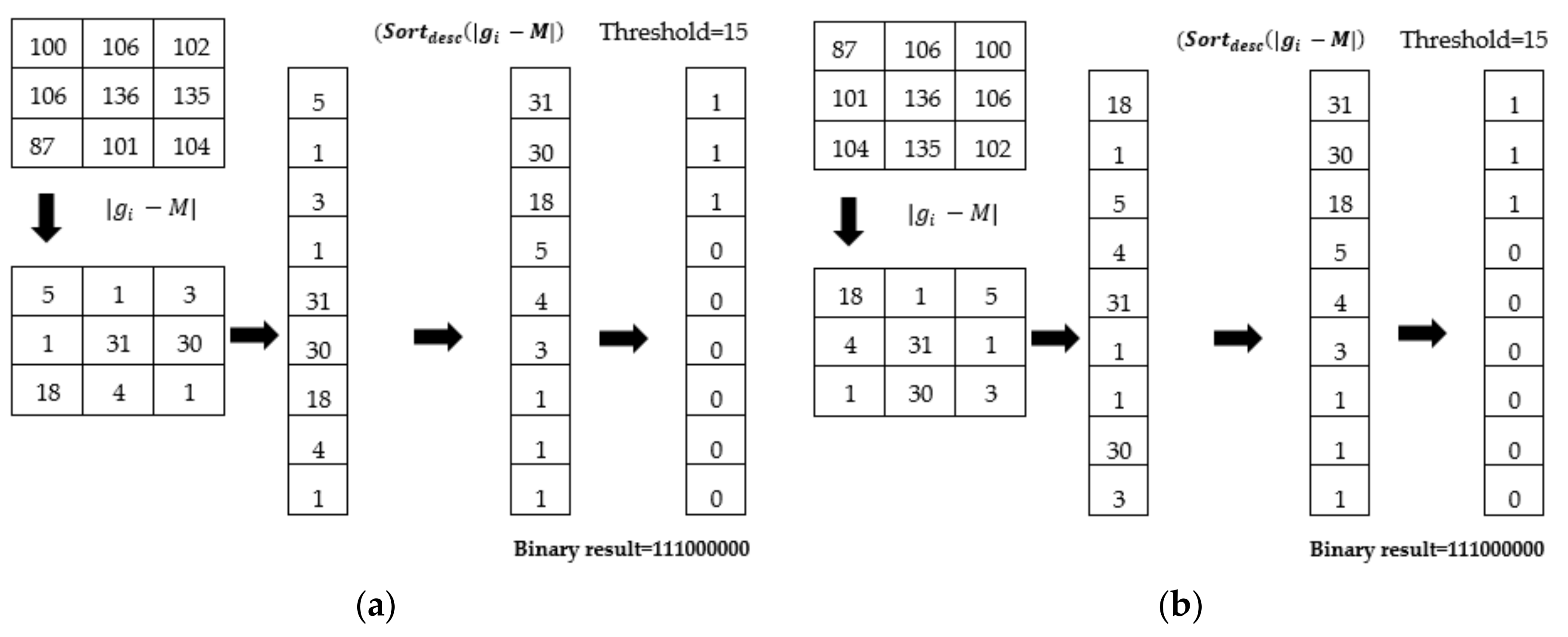
2.3. miRID
| Algorithm 1.The Calculation of Our Descriptor |
| Input: image patch at position of |
| Output: |
| (1) |
| (2) Calculate , δ |
| (3) For ; ; |
| (4) ID[i] = |
| (5) End for |
| (6) |
| (7) For ; ; |
| (8) If ID[i] > δ then ID[i] = 1 else ID[i] = 0 |
| (9) End for |
| (10) = ID[1…G] |
| (11) Return |
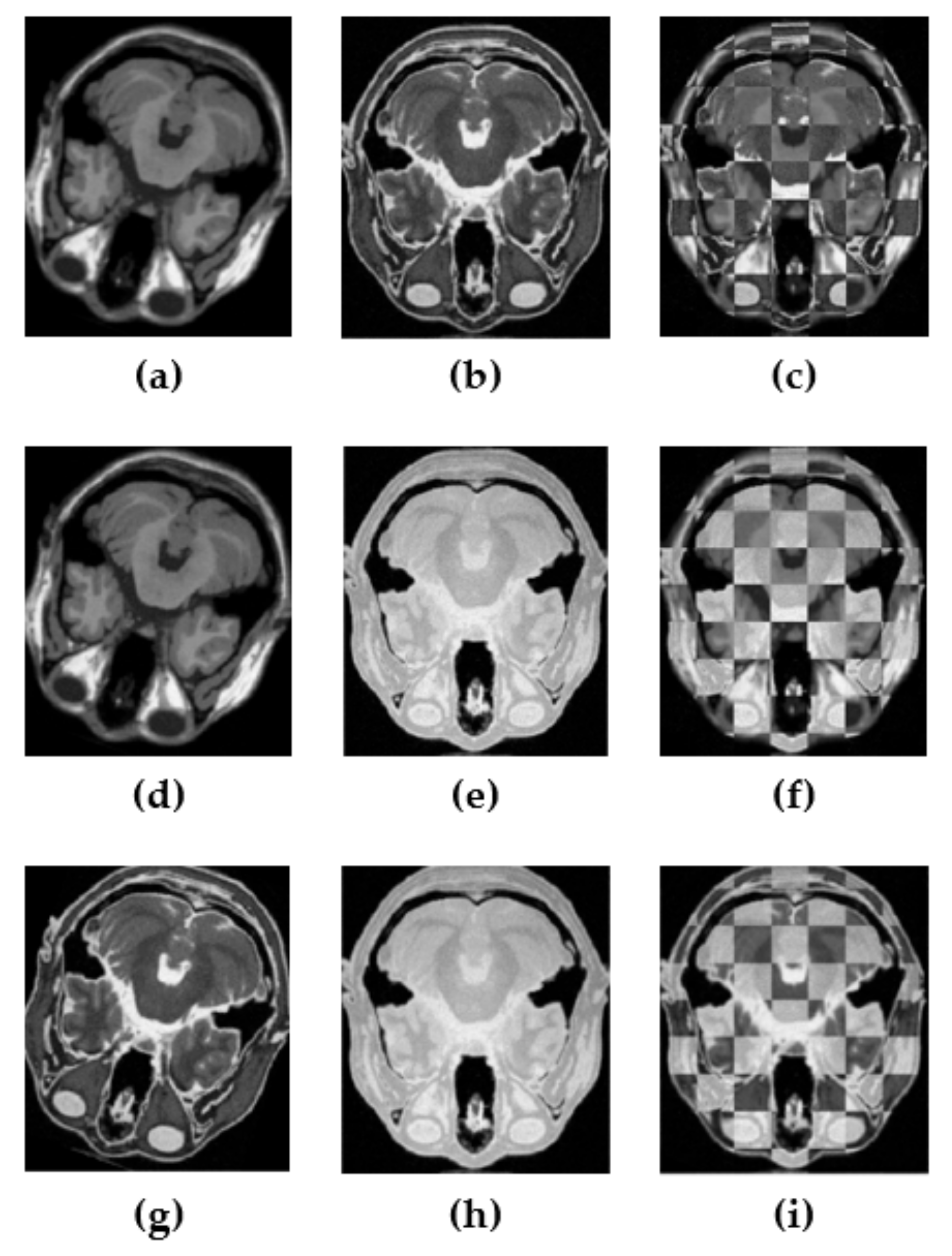
3. Experimental Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ou, Y. Development and Validations of a Deformable Registration Algorithm for Medical Images: Applications to Brain, Breast and Prostate Studies; University of Pennsylvania: Philadelphia, PA, USA, 2012. [Google Scholar]
- Hill, D.L.; Batchelor, P.G.; Holden, M.; Hawkes, D.J. Medical image registration. Phys. Med. Biol. 2001, 46, R1. [Google Scholar] [CrossRef] [PubMed]
- Mani, V. Survey of medical image registration. J. Biomed. Eng. Technol. 2013, 1, 8–25. [Google Scholar]
- Sotiras, A.; Davatzikos, C.; Paragios, N. Deformable medical image registration: A survey. IEEE Trans. Med. Imaging 2013, 32, 1153–1190. [Google Scholar] [CrossRef] [Green Version]
- De Nigris, D.; Collins, D.L.; Arbel, T. Multi-modal image registration based on gradient orientations of minimal uncertainty. IEEE Trans. Med. Imaging 2012, 31, 2343–2354. [Google Scholar] [CrossRef]
- Maes, F.; Collignon, A.; Vandermeulen, D.; Marchal, G.; Suetens, P. Multimodality image registration by maximization of mutual information. IEEE Trans. Med. Imaging 1997, 16, 187–198. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jin, S.; Li, D.; Wang, H.; Yin, Y. Registration of PET and CT images based on multiresolution gradient of mutual information demons algorithm for positioning esophageal cancer patients. J. Appl. Clin. Med. Phys. 2013, 14, 50–61. [Google Scholar] [CrossRef] [PubMed]
- Korsager, A.S.; Carl, J.; Østergaard, L.R. Comparison of manual and automatic MR-CT registration for radiotherapy of prostate cancer. J. Appl. Clin. Med. Phys. 2016, 17, 294–303. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Degen, J.; Modersitzki, J.; Heinrich, M.P. Dimensionality reduction of medical image descriptors for multimodal image registration. Curr. Dir. Biomed. Eng. 2015, 1, 201–205. [Google Scholar] [CrossRef]
- Schroeder, M.J.J.P. Analogy in Terms of Identity, Equivalence, Similarity, and Their Cryptomorphs. Philosophies 2019, 4, 32. [Google Scholar] [CrossRef] [Green Version]
- Borvornvitchotikarn, T.; Kurutach, W. A taxonomy of mutual information in medical image registration. In Proceedings of the 2016 International Conference on Systems, Signals and Image Processing (IWSSIP), Bratislava, Slovakia, 23–25 May 2016; pp. 1–4. [Google Scholar]
- Sahoo, S.; Nanda, P.K.; Samant, S. Tsallis and Renyi’s embedded entropy based mutual information for multimodal image registration. In Proceedings of the 2013 Fourth National Conference Computer Vision, Pattern Recognition, Image Processing and Graphics (NCVPRIPG), Jodhpur, India, 18–21 December 2013; pp. 1–4. [Google Scholar]
- He, Y.; Hamza, A.B.; Krim, H. A generalized divergence measure for robust image registration. IEEE Trans. Signal Process. 2003, 51, 1211–1220. [Google Scholar]
- Rueckert, D.; Clarkson, M.; Hill, D.; Hawkes, D.J. Non-rigid registration using higher-order mutual information. In Proceedings of the Medical Imaging 2000, San Diego, CA, USA, 13–15 February 2000; pp. 438–447. [Google Scholar]
- Russakoff, D.B.; Tomasi, C.; Rohlfing, T.; Maurer, C.R., Jr. Image similarity using mutual information of regions. In Computer Vision-ECCV 2004, Proceedings of the European Conference on Computer Vision, Prague, Czech Republic, 11–14 May 2004; Springer: Berlin/Heidelberg, Germany, 2004; pp. 596–607. [Google Scholar]
- Chen, Y.-W.; Lin, C.-L. PCA based regional mutual information for robust medical image registration. In Advances in Neural Networks–ISNN 2011, Proceedings of the International Symposium on Neural Networks, Guilin, China, 29 May–1 June 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 355–362. [Google Scholar]
- Loeckx, D.; Slagmolen, P.; Maes, F.; Vandermeulen, D.; Suetens, P. Nonrigid image registration using conditional mutual information. IEEE Trans. Med. Imaging 2010, 29, 19–29. [Google Scholar] [CrossRef] [PubMed]
- Rivaz, H.; Karimaghaloo, Z.; Collins, D.L. Self-similarity weighted mutual information: A new nonrigid image registration metric. Med. Image Anal. 2014, 18, 343–358. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rivaz, H.; Karimaghaloo, Z.; Fonov, V.S.; Collins, D.L. Nonrigid registration of ultrasound and MRI using contextual conditioned mutual information. IEEE Trans. Med. Imaging 2014, 33, 708–725. [Google Scholar] [CrossRef] [PubMed]
- Heinrich, M.P.; Jenkinson, M.; Bhushan, M.; Matin, T.; Gleeson, F.V.; Brady, M.; Schnabel, J.A. MIND: Modality independent neighbourhood descriptor for multi-modal deformable registration. Med. Image Anal. 2012, 16, 1423–1435. [Google Scholar] [CrossRef] [PubMed]
- Heinrich, M.P.; Jenkinson, M.; Papiez, B.W.; Brady, S.M.; Schnabel, J.A. Towards realtime multimodal fusion for image-guided interventions using self-similarities. Med. Image Comput. Comput. Assist. Interv. 2013, 16, 187–194. [Google Scholar] [PubMed] [Green Version]
- Kasiri, K.; Fieguth, P.; Clausi, D.A. Self-similarity measure for multi-modal image registration. In Proceedings of the 2016 IEEE International Conference on Image Processing (ICIP), Phoenix, AZ, USA, 25–28 September 2016; pp. 4498–4502. [Google Scholar]
- Kasiri, K.; Fieguth, P.; Clausi, D.A. Sorted self-similarity for multi-modal image registration. In Proceedings of the 2016 IEEE 38th Annual International Conference of the Engineering in Medicine and Biology Society (EMBC), Lake Buena Vista (Orlando), FL, USA, 16–20 August 2016; pp. 1151–1154. [Google Scholar]
- Ojala, T.; Pietikainen, M.; Maenpaa, T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 971–987. [Google Scholar] [CrossRef]
- Jiang, D.; Shi, Y.; Yao, D.; Wang, M.; Song, Z. miLBP: A robust and fast modality-independent 3D LBP for multimodal deformable registration. Int. J. Comput. Assist. Radiol. Surg. 2016, 11, 997–1005. [Google Scholar] [CrossRef] [Green Version]
- Borvornvitchotikarn, T.; Kurutach, W. Robust Self-Similarity Descriptor for Multimodal Image Registration. In Proceedings of the 2018 25th International Conference on Systems, Signals and Image Processing (IWSSIP), Maribor, Slovenia, 20–22 June 2018; pp. 1–4. [Google Scholar]
- Crum, W.R.; Hartkens, T.; Hill, D. Non-rigid image registration: Theory and practice. Br. J. Radiol. 2014. [Google Scholar] [CrossRef]
- Klein, S.; Staring, M.; Pluim, J.P.W. Evaluation of optimization methods for nonrigid medical image registration using mutual information and B-splines. IEEE Trans. Image Process. 2007, 16, 2879–2890. [Google Scholar] [CrossRef]
- Myronenko, A.; Song, X. Intensity-based image registration by minimizing residual complexity. IEEE Trans. Med. Imaging 2010, 29, 1882–1891. [Google Scholar] [CrossRef]
- BrainWeb, B. Simulated Brain Database. 2010. Available online: http://brainweb.bic.mni.mcgill.ca/cgi/brainweb2 (accessed on 23 May 2018).
- Yaniv, Z.; Lowekamp, B.C.; Johnson, H.J.; Beare, R. SimpleITK image-analysis notebooks: A collaborative environment for education and reproducible research. J. Digit. Imaging 2018, 31, 290–303. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ojala, T.; Pietikäinen, M.; Harwood, D. A comparative study of texture measures with classification based on featured distributions. Pattern Recognit. 1996, 29, 51–59. [Google Scholar] [CrossRef]
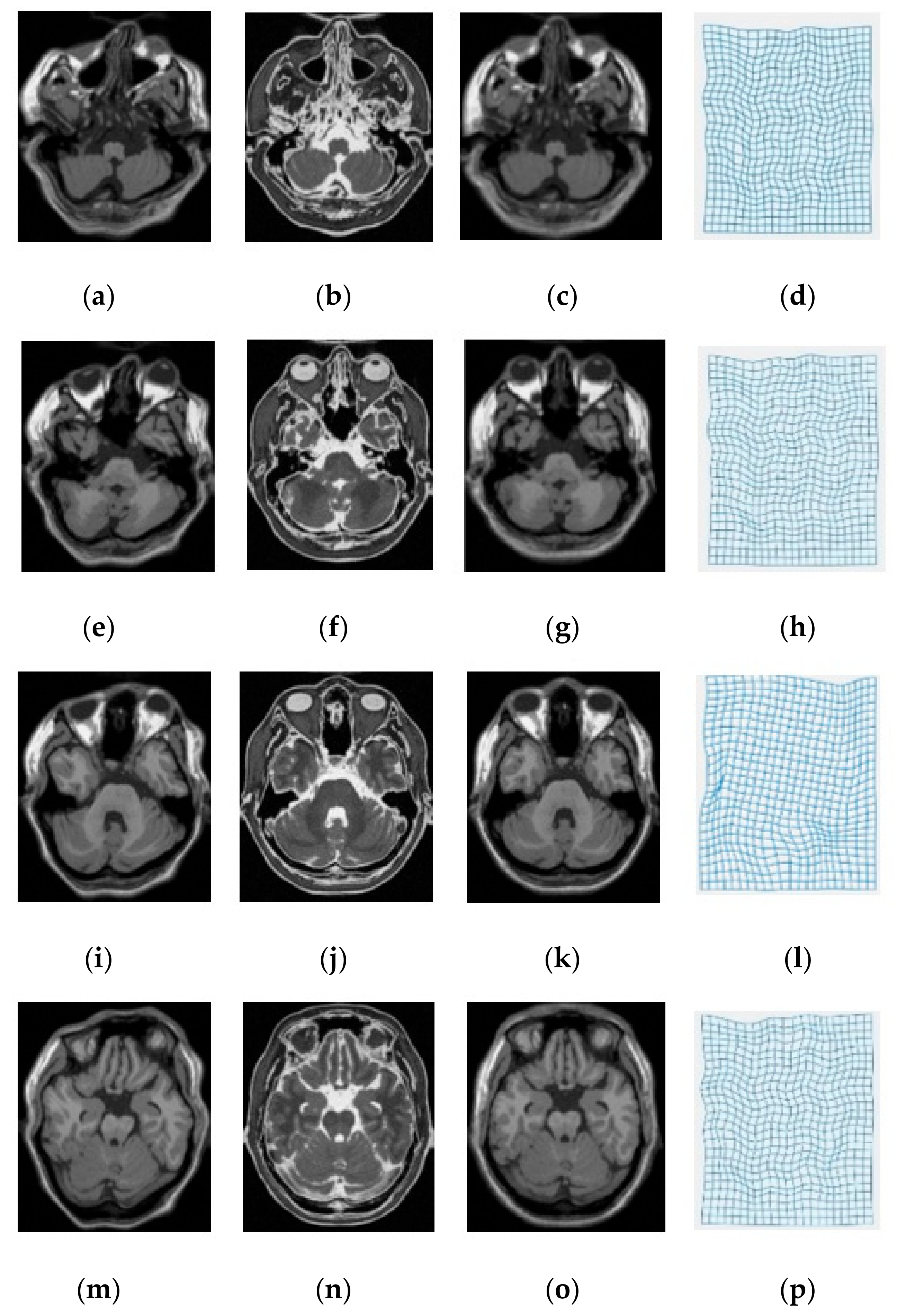
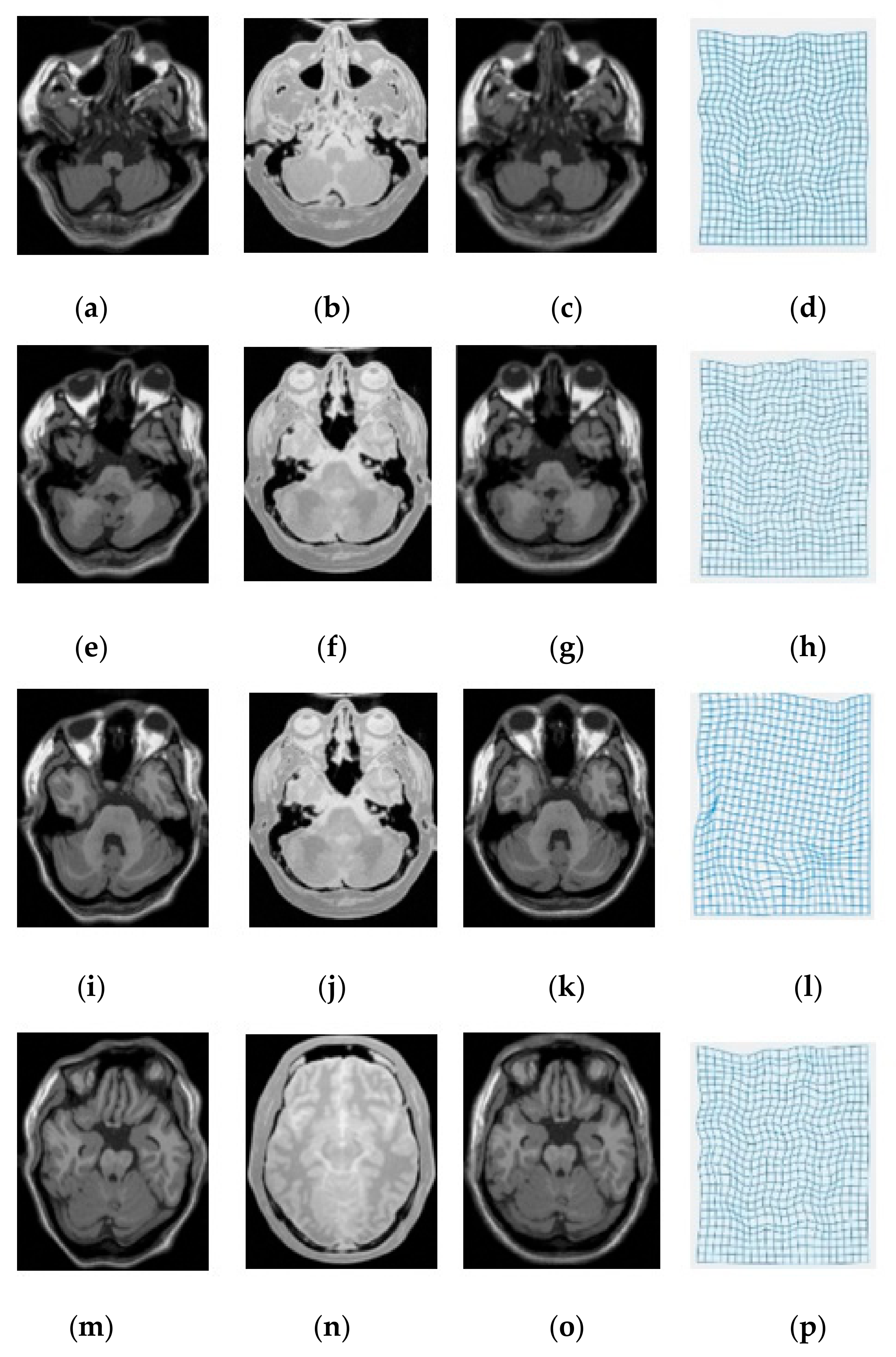
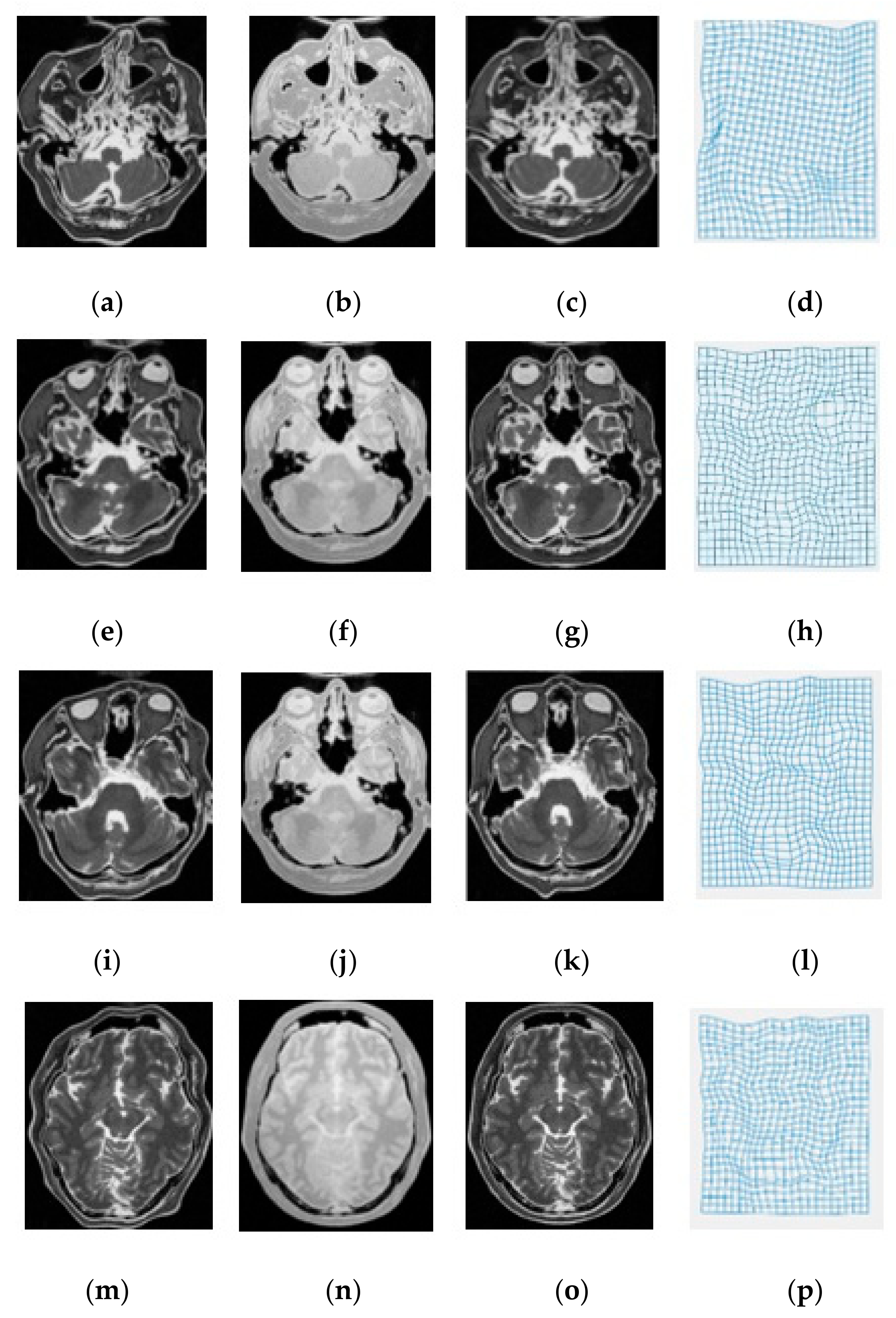
| Modality | MI [6] | SSC [21] | miLBP [25] | Ssesi [23] | miRID |
|---|---|---|---|---|---|
| T1-T2 | 2.92 | 2.86 | 2.16 | 2.09 | 1.86 |
| T1-PD | 2.68 | 2.43 | 2.23 | 1.53 | 1.62 |
| T2-PD | 2.94 | 2.86 | 2.47 | 2.05 | 1.98 |
| Average TRE | 2.85 | 2.72 | 2.29 | 1.89 | 1.82 |
| Average Time | 35.2 s | 34.1 s | 24.9 s | 31.7 s | 26.1 s |
| Modality | MI [6] | SSC [21] | miLBP [25] | Ssesi [23] | miRID |
|---|---|---|---|---|---|
| T1-T2 | 2.63 | 2.35 | 2.42 | 2.45 | 2.04 |
| T1-PD | 2.88 | 2.16 | 2.26 | 2.42 | 2.13 |
| T2-PD | 3.01 | 2.47 | 2.36 | 2.47 | 2.01 |
| Average TRE | 2.84 | 2.33 | 2.35 | 2.45 | 2.03 |
| Average Time | 42.8 s | 39.6 s | 26.2 s | 35.4 s | 27.4 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borvornvitchotikarn, T.; Kurutach, W. miRID: Multi-Modal Image Registration Using Modality-Independent and Rotation-Invariant Descriptor. Symmetry 2020, 12, 2078. https://doi.org/10.3390/sym12122078
Borvornvitchotikarn T, Kurutach W. miRID: Multi-Modal Image Registration Using Modality-Independent and Rotation-Invariant Descriptor. Symmetry. 2020; 12(12):2078. https://doi.org/10.3390/sym12122078
Chicago/Turabian StyleBorvornvitchotikarn, Thuvanan, and Werasak Kurutach. 2020. "miRID: Multi-Modal Image Registration Using Modality-Independent and Rotation-Invariant Descriptor" Symmetry 12, no. 12: 2078. https://doi.org/10.3390/sym12122078
APA StyleBorvornvitchotikarn, T., & Kurutach, W. (2020). miRID: Multi-Modal Image Registration Using Modality-Independent and Rotation-Invariant Descriptor. Symmetry, 12(12), 2078. https://doi.org/10.3390/sym12122078





