Transitivity on Minimum Dominating Sets of Paths and Cycles

Abstract

Transitivity on graphs is a concept widely investigated. This suggest to analyze the action of automorphisms on other sets. In this paper, we study the action on the family of $\gamma$-sets (minimum dominating sets), the graph is called $\gamma$-transitive if given two $\gamma$-sets there exists an automorphism which maps one onto the other. We deal with two families: paths ${\mathrm{P}}_n$ and cycles ${\mathrm{C}}_n$. Their $\gamma$-sets are fully characterized and the action of the automorphism group on the family of $\gamma$-sets is fully analyzed.

1. Introduction

In graph theory there are several families of graphs that have been studied from different points of view, for example, in [1], infinite sequences of graphs determined by its generalized spectrum from certain small starter graphs are constructed. In [2], the chromatic number of sunlet and bistar families is found and in [3], the transversal domination number for some families, such as: bipartites, multipartites, paths, cycles, wheels and sunlets, is computed.

Domination in graphs and its variations are topics comprehensively studied and many papers have been written about it, since $\gamma$-sets (dominating sets of minimum cardinality) or the domination number is an NP-complete problem for arbitrary graphs [4], most of them focus on finding and describing bounds for the domination number, for example in terms of the order [5], minimum or maximum degree [6] or size [7], to name a few. The study of dominant sets, $\gamma$-sets and the domination number has attracted the attention of mathematicians due to the applications these concepts have in areas as diverse as social networks, chemical compounds, optimization problems, among others [8]. Moreover, there have been new treatments developed around these concepts, for example k-domination and distance k-dominating sets, see [9,10].

In this paper, we deal with paths and cycles, emphasizing on characterization of minimum dominating sets and the action of the automorphism group on these sets. In addition to being important by themselves, because of their graph-theoretic properties, these families belong to a widely studied class of graphs called “chemical graphs”, broadly speaking they are graphs associated to a molecular structure of chemical compounds. For example, the molecular structure of butane ($C_4{H}_{10}$) can be identified with the path $P_4$ and that of the cyclopentane ($C_5{H}_{10}$) with the cycle $C_5$.

By graph, we mean a simple graph with no loops and it is denoted by $\mathsf{\Gamma }=(V,E)$, where V and E are the vertices and edges sets, respectively. We use the following concepts, notation and results of graph theory. Let $\mathsf{\Gamma }=(V,E)$ be a graph:

• for $v\in V$, $N\left(v\right)$ denotes its neighborhood; that is, $N\left(v\right)=\{x\in V:xv\in E\}$ and $N\left[v\right]=N\left(v\right)\cup \left\{v\right\}$;
• for $v\in V$, $degv$ denotes its degree; that is, $degv=\left|N\right(v\left)\right|$;
• for $S\subseteq V$, $N\left(S\right)={\bigcup }_{v\in S}N\left(v\right)$ and $N\left[S\right]=N\left(S\right)\cup S$;
• $D\subseteq V$ is a dominating set if $N\left[D\right]=V$;
• the domination number of $\mathsf{\Gamma }$ is:

  $$\gamma \left(\mathsf{\Gamma }\right)=min\left\{\right|D|:D\subseteq V\mathrm{is}\mathrm{dominating}\};$$
• $D\subseteq V$ is a $\gamma$-set if D is a dominating set of cardinality $\gamma$; that is, a minimum dominating set;
• ${\mathcal{D}}_{\gamma }=\{D\subseteq V:D\mathrm{is}\mathrm{a}\gamma -\mathrm{set}\}$;
• for $\mathsf{\Gamma }$ connected and $u,v\in V$, the distance between u and v is:

  $$d(u,v)=min\left\{\mathrm{length}\mathrm{of}u-v\mathrm{walks}\right\}.$$

An automorphism of $\mathsf{\Gamma }$ is an element $\sigma \in {\mathbf{S}}_V$; that is, a permutation of V, which satisfies

$$uv\in E\mathrm{if}\mathrm{and}\mathrm{only}\mathrm{if}\sigma \left(u\right)\sigma \left(v\right)\in E,$$

we denote the set of all automorphisms of $\mathsf{\Gamma }$ by $Aut\mathsf{\Gamma }$, which is, in fact, a subgroup of ${\mathbf{S}}_V$. In what follows, ${\mathbf{S}}_n$ denotes the symmetric group on n letters. We use freely the following facts about the automorphism groups we are interested in:

• $Aut{\mathrm{P}}_n\cong {\mathbf{S}}_2$, with ${\mathrm{P}}_n$ the path graph;
• $Aut{\mathrm{C}}_n\cong {\mathbf{D}}_n$, with ${\mathrm{C}}_n$ the cycle graph and ${\mathbf{D}}_n$ the dihedral group (the rigid motions taking a regular n-gon back to itself, with the composition) which has the presentation $\langle \rho ,\mu :{\rho }^n=1={\mu }^2,\rho \mu =\mu {\rho }^{-1}\rangle$.

An action of a group G on a set X is a function $A:G\times X\to X$ such that

• $A(g_1,A(g_2,x))=A(g_1{g}_2,x)$, for all $g_1,g_2\in G$ and $x\in X$;
• $A(1,x)=x$, for all $x\in X$, where $1\in G$ is the identity.

If $x\in X$, the orbit of x is the set

$$\mathcal{O}\left(x\right)=\left\{A\right(g,x):g\in G\}\subseteq X,$$

and the collection of all orbits give a partition of X. The action is called transitive if there is only one orbit; that is, given $x_1,x_2\in X$, there exists $g\in G$ such that $A(g,x_1)=x_2$.

It is clear that any subgroup $G<{\mathbf{S}}_X$ acts on X in a natural way as follows

$$A(\sigma ,x)=\sigma \left(x\right).$$

2. Results

It is known that if $\mathsf{\Gamma }=(V,E)$ then $Aut\mathsf{\Gamma }$ acts naturally on V and on E, when this action is transitive on V, $\mathsf{\Gamma }$ is called vertex-transitive, and edge-transitive if it is on E. In [11], $\gamma$-transitive graphs are defined, they are those where the action of $Aut\mathsf{\Gamma }$ on minimum dominating sets is transitive; that is, given $D_1,D_2\in {\mathcal{D}}_{\gamma }$, there is $\sigma \in Aut\mathsf{\Gamma }$ such that $\sigma \left(D_1\right)=D_2$. We may observe easily the following facts:

• any graph with just one minimum dominating set is trivially $\gamma$-transitive;
• if the cardinality of ${\mathcal{D}}_{\gamma }$ is greater than the order of $Aut\mathsf{\Gamma }$, then $\mathsf{\Gamma }$ is not $\gamma$-transitive.

In this section we fully characterize $\gamma$-sets and analyze in detail the action of $Aut\mathsf{\Gamma }$ on ${\mathcal{D}}_{\gamma }$ for path and cycle graphs to decide if they are $\gamma$-transitive. If they are not, then we compute all the orbits.

2.1. Minimum Dominating Sets and Transitivity on Paths and Cycles

2.1.1. Path Graphs

Let n be a positive integer and consider the path graph ${\mathrm{P}}_n=(V,E)$ which is defined as follows:

$$V=\{v_1,\dots ,v_n\}\mathrm{and}E=\{v_1{v}_2,\dots ,v_{n-1}{v}_n\}.$$

Figure 1, Figure 2 and Figure 3 show the ${\mathrm{P}}_{21}$, ${\mathrm{P}}_{20}$ and ${\mathrm{P}}_{19}$ graphs, respectively. We may observe that

$$deg{v}_i=\left\{\begin{array}{cc}1,\hfill & \mathrm{for}i=1,n;\hfill \\ 2,\hfill & \mathrm{for}i=2,\dots ,n-1.\hfill \end{array}\right.$$

A well known fact is that $\gamma \left({\mathrm{P}}_n\right)=k$, for $n=3k,3k-1$ and $3k-2$.The following lemmas characterize $\gamma$-sets for these graphs, they are properly counted and the action of the automorphism group on ${\mathcal{D}}_{\gamma }$ is analyzed.

Lemma 1.

For $n=3k$, $D=\{x_1,\dots ,x_k\}$ is a minimum dominating set if and only if $deg{x}_i=2$, for $i=1,\dots ,k$, and $N\left(x_i\right)\cap N\left(x_j\right)=\varnothing$, for $i\ne j$.

Proof. 

Suppose that there is $x_i\in D$ with $deg{x}_i=1$ or that there are $u,v\in D$ such that $N\left(u\right)\cap N\left(v\right)\ne \varnothing$, then

$$\left|N\left[D\right]\right|=|N\left[x_1\right]\cup \cdots \cup N\left[x_k\right]|<|N\left[x_1\right]|+\cdots +|N\left[x_k\right]|=3k,$$

thus, D is not a dominating set.

Conversely, if $deg{x}_i=2$, for $i=1,\dots ,k$ and no pair of vertices share neighbors, we have

$$\left|N\left[D\right]\right|=|N\left[x_1\right]\cup \cdots \cup N\left[x_k\right]|=|N\left[x_1\right]|+\cdots +|N\left[x_k\right]|=3k,$$

which implies, $N\left[D\right]=V$; that is, D is a $\gamma$-set. □

Observe that Lemma 1 implies that

$$D=\{v_2,v_5,\dots ,v_{n-1}\}$$

is the unique $\gamma$-set for ${\mathrm{P}}_{3k}$. Figure 1 shows this set for ${\mathrm{P}}_{21}$.

Lemma 2.

For $n=3k-1$, $D=\{x_1,\dots ,x_k\}$ is a minimum dominating set if and only if one of the following conditions hold:

i. 

$N\left(x_i\right)\cap N\left(x_j\right)=\varnothing$, for $i\ne j$, and $degx=2$ for all but one vertex;

ii. 

there exists a unique pair of vertices $x_r,x_s\in D$ such that $|N\left(x_r\right)\cap N\left(x_s\right)|=1$, $N\left(x_i\right)\cap N\left(x_j\right)=\varnothing$, for $i,j\ne r,s$, and $deg{x}_i=2$, for $i=1,\dots ,k$.

Proof. 

Suppose that D is a dominating set and let t denote the number of unordered pairs of distinct vertices $x,y\in D$ such that $N\left(x\right)\cap N\left(y\right)\ne \varnothing$; that is, $\left|N\right(x)\cap N(y\left)\right|=1$. We proceed by cases.

• If $v_1,v_n\in D$, then

  $$\left|N\right(D\left)\right|=2+(k-2)2-t=2k-2-t<2k-1,$$

  which contradicts D being dominating.
• If D contains just one vertex of degree 1, then

  $$\left|N\right(D\left)\right|=1+(k-1)2-t=2k-1-t,$$

  so $t=0$, that is, D satisfies (i).
• Finally, suppose that all vertices in D have degree 2, then

  $$\left|N\right(D\left)\right|=2k-t.$$
  Note that $3k-1=\left|N\right[D\left]\right|=\left|N\right(D\left)\right|+\left|D\right|-\left|N\right(D)\cap D|$. If $t=0$, then necessarily $\left|N\right(D)\cap D|=1$, but this is not possible. Supposing $t>1$ contradicts D being a dominating set. Thus, $t=1$ and D satisfies condition (ii).

Conversely, if $N\left(x_i\right)\cap N\left(x_j\right)=\varnothing$, for $i\ne j$, and every vertex but one has degree 2, then

$$\left|N\right[D\left]\right|=(k-1)3+2=3k-1$$

and D is a dominating set. Now suppose that there is exactly one pair of vertices $x_r,x_s\in D$ such that $|N\left(x_r\right)\cap N\left(x_s\right)|=1$ and $N\left(x_i\right)\cap N\left(x_j\right)=\varnothing$, for $i,j\ne r,s$, and $deg{x}_i=2$, for $i=1,\dots ,k$, as before, we obtain $\left|N\right[D\left]\right|=3k-1$ and, therefore, D is dominating. □

Remark 1.

By Lemma 2 we may deduce that there are exactly two minimum dominating sets satisfying the first condition

$$D_1=\{v_1,v_4,\dots ,v_{3k-2}\}\mathrm{and}{D}_2=\{v_2,v_5,\dots ,v_{3k-1}\}$$

and $k-1$ satisfying the second one

$$\begin{array}{cc}\hfill D_{2,4}& =\{v_2,v_4,v_7,v_{10},\dots ,v_{3k-5},v_{3k-2}\}\hfill \\ \hfill D_{5,7}& =\{v_2,v_5,v_7,v_{10},\dots ,v_{3k-5},v_{3k-2}\}\hfill \\ \hfill D_{8,10}& =\{v_2,v_5,v_8,v_{10},\dots ,v_{3k-5},v_{3k-2}\}\hfill \\ \hfill & ⋮\hfill \\ \hfill D_{3k-4,3k-2}& =\{v_2,v_5,v_8,v_{11},\dots ,v_{3k-4},v_{3k-2}\}.\hfill \end{array}$$

In fact, if $D\subseteq V$ is a γ-set and we consider

$$\begin{array}{cc}\hfill a& =\left|\right\{v_i\in D:i\equiv 2mod3\left\}\right|\hfill \\ \hfill b& =\left|\right\{v_i\in D:i\equiv 1mod3\left\}\right|\hfill \\ \hfill c& =\left|\right\{v_i\in D:i\equiv 0mod3\left\}\right|,\hfill \end{array}$$

there is a one-to-one correspondence between these γ-sets and triplets $(a,b,c)$ such that $a+b+c=k$, $a,b>0$ and $c=0$. Indeed, we may observe that the correspondence is given by

$$D_{3a-1,3a+1}⟷(a,k-a,0).$$

Figure 2a shows the $\gamma$-set $D_1$ and Figure 2b the $\gamma$-set $D_{8,10}$, respectively, for ${\mathrm{P}}_{20}$.

Lemma 3.

For $n=3k-2$, $D=\{x_1,\dots ,x_k\}$ is a minimum dominating set if and only if one of the following conditions hold:

i. 

$N\left[x_i\right]\cap N\left[x_j\right]=\varnothing$, for $i\ne j$, and $v_1,v_n\in D$;

ii. 

there are exactly two distinct vertices $x_r,x_s\in D$ sharing a neighbor, $N\left[x_i\right]\cap N\left[x_j\right]=\varnothing$, for $i,j\ne r,s$, and every vertex in D has degree 2, but one;

iii. 

$degx=2$ for all $x\in D$ and there are exactly two distinct vertices $x_r,x_s\in D$ such that $x_r{x}_s\in E$ and $N\left[x_i\right]\cap N\left[x_j\right]=\varnothing$, for $i,j\ne r,s$; or

iv. 

$degx=2$ for all $x\in D$ and there exist $x_r,x_s,x_a,x_b\in D$ such that $|N\left[x_r\right]\cap N\left[x_s\right]|=1$, $|N\left[x_a\right]\cap N\left[x_b\right]|=1$ and $N\left[x_i\right]\cap N\left[x_j\right]=\varnothing$, for $i,j\ne r,s,a,b$.

Proof. 

Suppose that D is a dominating set and, as in the proof of Lemma 2, let t denote the number of unordered pairs of distinct vertices $x,y\in D$ which share neighbors.

• Suppose that D contains vertices of degree 1.
  If $v_1,v_n\in D$, since D is dominating and

  $$\left|N\right(D\left)\right|=2+2(k-2)-t=2k-2-t$$

  necessarily $t=0$ and condition (i) is satisfied.
  If D contains just one vertex of degree one, then

  $$\left|N\right(D\left)\right|=1+2(k-1)-t=2k-1-t$$

  implies $t=1$, which is condition (ii).
• Suppose $degx=2$ for all $x\in D$.
  If $t=0$ then $\left|N\right(D\left)\right|=2k$ and, since $\left|N\right[D\left]\right|=3k-2$, necessarily $|D\cap N(D\left)\right|=2$ and the two vertices in this intersection form an edge, moreover, no other vertices share neighbors, thus, D satisfies (iii).
  If $t\ge 1$, we get $\left|N\right(D\left)\right|=2k-t$, obtaining $t=2$ and D satisfies (iv).

Conversely, if D satisfies (i), then

$$\left|N\left[D\right]\right|=\sum _{i=1}^k\left|N\left[x_i\right]\right|=\left(2\right)2+(k-2)3=3k-2.$$

If D satisfies condition (ii), we get

$$\begin{array}{cc}\hfill \left|N\right[D\left]\right|& =|\left(\bigcup _{i\ne r,s}N\left[x_i\right]\right)\cup N\left[x_r\right]\cup N\left[x_s\right]|=\left|\bigcup _{i}N\left[x_i\right]\right|-|N\left[x_r\right]\cap N\left[x_s\right]|\hfill \\ \hfill & =2+(k-1)3-1=3k-2.\hfill \end{array}$$

Analogously the other cases. Therefore, in any case, D is a dominating set. □

It is important to note that condition (iv) is true for $k\ge 3$. Considering the triplets $(a,b,c)$ of nonnegative integers such that $a+b+c=k$, as above, this lemma implies the following facts.

There is just one $\gamma$-set satisfying condition (i), namely,

$$\{v_1,v_4,\dots ,v_{3k-5},v_{3k-2}\},$$

which corresponds to $(0,k,0)$.

Proposition 1.

There is a one-to-one correspondence between minimum dominating sets that satisfies condition (ii) and triplets $(a,b,c)$ such that $a,b>0$ and $c=0$ or $b,c>0$ and $a=0$. Thus, the number of γ-sets of this kind is $2(k-1)$.

Proof. 

If D satisfies (ii), it contains a vertex of degree 1, say $v_1$, since there are exactly two vertices sharing a neighbor they must be of the form $v_r$ and $v_{r+2}$; moreover, preceding vertices to $v_r$ have disjoint closed neighborhoods, so that the first vertices should be $v_1,v_4,\dots ,v_{3b-2}=v_r$ and, by the same argument, the vertices after $v_{r+2}=v_{3b}$ must be $v_{3(b+1)},v_{3(b+2)},\dots ,v_{3(k-1)}$. Thus, the triplet corresponding to D is $(0,b,3k-b)$. Analogously, if $v_n\in D$, the triplet corresponding to D is $(3k-b,b,0)$.

Conversely, given a triplet $(a,b,c)$ such that $a+b+c=k$ and $a=0$ or $c=0$, we may construct easily the corresponding set as follows

$$D=\left\{\begin{array}{cc}\{v_1,v_4,\dots ,v_{3b-2},v_{3b},v_{3b+3},\dots ,v_{3k-3}\},\hfill & \mathrm{if} a=0 \mathrm{and} c=3k-b;\hfill \\ \{v_2,v_5,\dots ,v_{3b-1},v_{3b+1},v_{3b+4},\dots ,v_{3k-2}\},\hfill & \mathrm{if} c=0 \mathrm{and} a=3k-b.\hfill \end{array}\right.$$

Therefore, there are $2(k-1)$ $\gamma$-sets satisfying condition (ii). □

Proposition 2.

There is a one-to-one correspondence between minimum dominating sets that satisfy condition (iii) and triplets of natural numbers $(a,b,c)$ such that $b=0$ and $a,c>0$. Thus, the number of γ-sets corresponding to these triplets is $k-1$.

Proof. 

Let D be a $\gamma$-set satisfying condition (iii), thus every vertex has degree 2. It contains two vertices forming an edge, say $v_r,v_{r+1}$, and $N\left[x_i\right]\cap N\left[x_j\right]=\varnothing$, for $i,j\ne r,r+1$. Since every vertex has degree 2 and preceding vertices to $v_r$ have disjoint closed neighborhoods, the first vertices should be $v_2,v_5,\dots ,v_{3a-1}=v_r$, which implies $v_{r+1}=v_{3a}$ and the same argument shows that the following vertices are $v_{3(a+1)},v_{3(a+2)},\dots ,v_{3(k-1)}$. Thus, the triplet corresponding to D is $(a,0,k-a)$.

Conversely, given a triplet $(a,0,c)$ such that $a+c=k$ and $a,c>0$ we may construct the $\gamma$-set

$$\{v_2,v_5,\dots ,v_{3a-1},v_{3a},v_{3a+3},v_{3a+6},\dots ,v_{3k-3}\},$$

which clearly satisfies condition (iii).

Therefore, there are $k-1$ $\gamma$-sets satisfying this condition. □

Proposition 3.

There is a one-to-one correspondence between minimum dominating sets that satisfy condition (iv) and triplets of natural numbers $(a,b,c)$ such that $a,b,c>0$. Moreover, the number of γ-sets satisfying this condition is $\frac{(k-2)(k-1)}{2}$.

Proof. 

Let D be a $\gamma$-set satisfying condition (iv); that is, every vertex has degree 2, it contains four vertices (not necessarily different) sharing a neighbor, say $v_r,v_{r+2},v_s,v_{s+2}$, and $N\left[x_i\right]\cap N\left[x_j\right]=\varnothing$, for i or $j\ne r,r+2,s,s+2$. Applying an analogous argument as in the previous cases, we may infer that the first vertices are $v_2,v_5,\dots ,v_{3a-1}=v_r$, the vertices after $v_{r+2}=v_{3a+1}$ must be $v_{3(a+1)+1},v_{3(a+2)+1},\dots ,v_{3(a+b)+1}=v_s$ and the vertices following $v_{s+2}=v_{3(a+b+1)}$ are $v_{3(a+b+2)},v_{3(a+b+3)},\dots ,v_{3(k-1)}$. Thus, the triplet corresponding to D is $(a,b,k-(a+b\left)\right)$.

Conversely, given a triplet $(a,b,c)$ such that $a+b+c=k$ and $a,b,c>0$, we get the following $\gamma$-set

$$\{v_2,v_5,\cdots ,v_{3a-1},v_{3a+1},v_{3(a+1)+1},\cdots ,v_{3(a+b)+1},v_{3(a+b+1)},\cdots ,v_{3(k-1)}\},$$

which fulfills condition (iv).

Observe that there are $(k-2)$ triplets having $a=1$, $(k-3)$ with $a=2$ and so on. When $a=k-2$, there is just one triplet, namely, $(k-2,1,1)$. Thus, there are $1+2+\cdots +(k-2)=\frac{(k-2)(k-1)}{2}$ $\gamma$-sets satisfying condition (iv). □

Figure 3a shows the $\gamma$-set which satisfies condition (i), Figure 3b shows the one that satisfies condition (ii) corresponding to $(0,4,3)$, Figure 3c the one satisfying condition (iii) corresponding to $(4,0,3)$ and Figure 3d the set of the fourth kind which corresponds to $(2,3,2)$, respectively, for ${\mathrm{P}}_{19}$.

Recall that $Aut{\mathrm{P}}_n=\{1,\sigma \}\cong S_2$, for $n\ge 2$, where 1 is the identity and $\sigma$ is the automorphism given (on subindices) by

$$i⟼n+1-i,$$

and note that

$$\begin{array}{ccc}\hfill n=3k& \Rightarrow & n+1-i\equiv 2i+1mod3\hfill \\ \hfill n=3k-1& \Rightarrow & n+1-i\equiv 2i\phantom{+21}mod3\hfill \\ \hfill n=3k-2& \Rightarrow & n+1-i\equiv 2i+2mod3.\hfill \end{array}$$

Theorem 1.

Let n be a positive integer, considering the action of $Aut{\mathrm{P}}_n$ on ${\mathcal{D}}_{\gamma }$, we have:

i. 

${\mathrm{P}}_{3k}$ is γ-transitive;

ii. 

for $n=3k-1$ there are $⌈\frac{k-1}{2}⌉+1$ orbits;

iii. 

for $n=3k-2$ and $k\ge 3$, there are $⌈\frac{k-2}{2}⌉+\frac{1}{2}\left(\frac{(k-1)(k-2)}{2}-⌈\frac{k-2}{2}⌉\right)$ orbits.

Proof. 

By the comment made after Lemma 1, we know that there is just one $\gamma$-set for ${\mathrm{P}}_{3k}$, so that ${\mathrm{P}}_{3k}$ is trivially $\gamma$-transitive.

If $n=3k-1$, by Lemma 2 we know that there are $\gamma$-sets of two kinds: those which contain a vertex of degree 1, denoted by $D_1$ and $D_2$, and those which are in correspondence with triplets $(a,k-a,0)$; moreover, $\sigma \left(i\right)\equiv 2imod3$. Clearly, $\sigma \left(D_1\right)=D_2$ and the image under $\sigma$ of the $\gamma$-set corresponding to $(a,k-a,0)$ is the one corresponding to $(k-a,a,0)$; that is,

$$\mathcal{O}\left(D_1\right)=\{D_1,D_2\}\mathrm{and}\mathcal{O}\left(D_{3a-1,3a+1}\right)=\{D_{3a-1,3a+1},D_{3(k-a)-1,3(k-a)+1}\}.$$

Thus, there are $1+⌈\frac{k-1}{2}⌉$ orbits.

If $n=3k-2$, Lemma 3 implies that there are four kinds of $\gamma$-sets and $\sigma \left(i\right)\equiv 2i+2mod3$. We proceed by cases.

In the first case there is just one $\gamma$-set which corresponds to $(0,k,0)$ and its image under $\sigma$ is itself; thus, $\mathcal{O}(0,k,0)=\left\{\right(0,k,0\left)\right\}$.

In the second case, $\gamma$-sets are in correspondence with triplets $(a,b,c)$ such that $a,b>0$ and $c=0$ or $b,c>0$ and $a=0$. If D corresponds to $(0,b,c)$, then $\sigma \left(D\right)$ corresponds to $(c,b,0)$, and viceversa. A $\gamma$-set corresponding to $(a,b,0)$ is mapped to that corresponding to $(0,b,a)$. This implies that the orbit of one of these sets contains exactly two of them. Thus, there are $k-1$ orbits.

In the third one, the correspondence is with triplets $(a,b,c)$ such that $b=0$ and $a,c>0$. The image of the set corresponding to $(a,0,c)$ is the one that corresponds to $(c,0,a)$. Note that the orbit is a singleton if and only if $a=c$, which happens when k is even and $2a=k$, so there are $⌈\frac{k-1}{2}⌉$ orbits.

Finally, in the last case the correspondence is with triplets $(a,b,c)$ such that $a,b,c>0$. We may observe that if D corresponds to $(a,b,c)$, then $\sigma \left(D\right)$ corresponds to $(c,b,a)$, and, as in the last case, the orbit is a singleton if and only if $a=c$. In this sub-case the triplets are $(a,k-2a,a)$ and, since $k-2a>0$, there are $⌈\frac{k-2}{2}⌉$ of these sets. Thus, there are $\frac{1}{2}\left(\frac{(k-1)(k-2)}{2}-⌈\frac{k-2}{2}⌉\right)$ orbits with two elements. □

The remaining cases $n=3k-2$ for $k=1,2$ are as follows: ${\mathrm{P}}_1$ is trivially $\gamma$-transitive and we may observe easily that ${\mathrm{P}}_4$ has four $\gamma$-sets

$$\begin{array}{cccc}\hfill D_1=\{v_1,v_4\}& ⟷(0,2,0),\hfill & \hfill D_2=\{v_1,v_3\}& ⟷(1,1,0),\hfill \\ \hfill D_3=\{v_2,v_4\}& ⟷(0,1,1),\hfill & \hfill D_4=\{v_2,v_3\}& ⟷(1,0,1);\hfill \end{array}$$

and three orbits

$$\mathcal{O}\left(D_1\right)=\left\{D_1\right\},\mathcal{O}\left(D_2\right)=\{D_2,D_3\}\mathrm{and}\mathcal{O}\left(D_4\right)=\left\{D_4\right\}.$$

2.1.2. Cycle Graphs

For an integer $n\ge 3$, consider the cycle graph ${\mathrm{C}}_n=(V,E)$, where $V=\{v_1,\dots ,v_n\}$ and $E=\{v_1{v}_2,\dots ,v_{n-1}{v}_n,v_n{v}_1\}$, Figure 4, Figure 5 and Figure 6 show the ${\mathrm{C}}_{21}$, ${\mathrm{C}}_{20}$ and ${\mathrm{C}}_{19}$ graphs, respectively. In this section, we use freely that the domination number of ${\mathrm{C}}_n$ is k, for $n=3k,3k-1$ and $3k-2$.

The proof of the following lemma is completely analogous to that of Lemma 1 and it is omitted.

Lemma 4.

For $n=3k$, $D=\{x_1,\dots ,x_k\}$ is a minimum dominating set if and only if $N\left[x_i\right]\cap N\left[x_j\right]=\varnothing$, for $i\ne j$.

This lemma implies that there are exactly three $\gamma$-sets for ${\mathrm{C}}_{3k}$, namely,

$$D_1=\{v_1,v_4,\dots ,v_{3k-2}\},D_2=\{v_2,v_5,\dots ,v_{3k-1}\}\mathrm{and}{D}_3=\{v_3,v_6,\dots ,v_{3k}\}.$$

Figure 4 shows the set $D_1$ for ${\mathrm{C}}_{21}$.

Lemma 5.

For $n=3k-1$, $D=\{x_1,\dots ,x_k\}$ is a minimum dominating set if and only if there is exactly one pair of vertices $x_r,x_s$ such that $|N\left[x_r\right]\cap N\left[x_s\right]|=1$ and $N\left[x_i\right]\cap N\left[x_j\right]=\varnothing$, for $i\ne j$ and $\{i,j\}\ne \{r,s\}$.

Proof. 

Suppose that D is a $\gamma$-set and, as in the previous section, let t denote the number of unordered pairs of distinct vertices $x,y\in D$ which share neighbors. D dominating implies $\left|N\right(D\left)\right|=2k-1$ and since, in general, $\left|N\right(D\left)\right|=2k-t$, we have $t=1$. Thus, there is exactly one pair of vertices sharing a neighbor.

Now, if there are exactly two vertices sharing a neighbor, then

$$\left|N\left[D\right]\right|=|N\left[x_1\right]\cup \cdots \cup N\left[x_k\right]|=|N\left[x_1\right]|+\dots +|N\left[x_k\right]|-1=3k-1,$$

thus, D is a $\gamma$-set. □

By Lemma 5, we may observe that there is a one-to-one correspondence between ${\mathcal{D}}_{\gamma }$ and V given by

$$D_i⟷v_i,\mathrm{with}{v}_i\mathrm{the}\mathrm{unique}\mathrm{neighbor}\mathrm{shared}\mathrm{by}\mathrm{two}\mathrm{vertices}\mathrm{of}{D}_i,$$

thus, there are n sets of this kind:

$$D_i=\{v_{i+1},v_{i+4},\dots ,v_{i+3k-4}\},i=1,\dots ,n,$$

where subindices are taken modulo $n=3k-1$. In Figure 5 is shown the set $D_1$ for ${\mathrm{C}}_{20}$.

Lemma 6.

For $n=3k-2$ and $k\ge 3$, $D=\{x_1,\dots ,x_k\}$ is a minimum dominating set if and only if one of the following conditions hold:

i. 

there exists a unique pair of vertices $x_r,x_s\in D$ such that $x_r{x}_s\in E$ and $N\left[x_i\right]\cap N\left[x_j\right]=\varnothing$, for $i,j\ne r,s$; or

ii. 

there are exactly two pairs of vertices $x_r,x_s$ and $x_a,x_b$ in D sharing a neighbor and no other vertices share neighbors.

Proof. 

Let $D\subseteq V$ be a $\gamma$-set, as above, t denotes the number of unordered pairs of vertices that shares a neighbor. Since D is a $\gamma$-set, we have

$$3k-2=|D\cup N(D\left)\right|=\left|D\right|+\left|N\right(D\left)\right|-|D\cap N(D\left)\right|$$

which implies $|D\cap N(D\left)\right|=2-t$. We proceed by cases.

• If $t=0$, $|D\cap N(D\left)\right|=2$ and these vertices form an edge, which is condition (i).
• $t=1$ is not possible, as we noted in introduction.
• If $t=2$, $|D\cap N(D\left)\right|=0$ and there are two pairs of distinct vertices $x_r,x_s$ and $x_a,x_b$ sharing a neighbor, satisfying condition (ii).

Conversely, if $D=\{x_1,\dots ,x_k\}$ is a set satisfying condition (i), we get

$$\begin{array}{cc}\hfill \left|N\right[D\left]\right|& =|\left(\bigcup _{i\ne r,s}N\left[x_i\right]\right)\cup N\left[x_r\right]\cup N\left[x_s\right]|\hfill \\ \hfill & =\left|\bigcup _{i\ne r,s}N\left[x_i\right]\right|+|N\left[x_r\right]\cup N\left[x_s\right]|\hfill \\ \hfill & =3k-2,\hfill \end{array}$$

which implies that D is a $\gamma$-set. Analogously if D satisfies condition (ii). □

There is a one-to-one correspondence between $\gamma$-sets satisfying the first condition and E. This correspondence is given by

$$D_i⟷e_i,\mathrm{where}{e}_i\mathrm{is}\mathrm{the}\mathrm{edge}{x}_i{x}_{i+1}.$$

Figure 6a shows the set $D_1$ corresponding to $e_1$ for ${\mathrm{C}}_{19}$.

Proposition 4.

For those γ-sets that satisfy (ii), we have two cases:

• $x_b=x_r$, obtaining nγ-sets of this kind; or
• $x_r,x_s,x_a$ and $x_b$ are all different, getting $⌊\frac{k-2}{2}⌋n$ γ-sets of this kind for k odd and $\left(\frac{n+k-2}{2}\right)$ for k even.

Proof. 

In the first case, there is a one-to-one correspondence between these $\gamma$-sets and V as follows

$$D_i⟷x_r,\mathrm{where}{x}_r\mathrm{is}\mathrm{the}\mathrm{vertex}\mathrm{that}\mathrm{shares}\mathrm{a}\mathrm{neighbor}\mathrm{with}\mathrm{other}\mathrm{two},$$

thus, there are $n=3k-2$ sets of this kind.

In the second one, we may obtain a one-to-one correspondence between these $\gamma$-sets and pairs of vertices $u,v$ such that $d(u,v)=3l+2$, for $l=1,2,\dots ,⌊\frac{k-2}{2}⌋$, namely,

$$D_{u,v}⟷\{u,v\},\mathrm{where}u=N\left[x_r\right]\cap N\left[x_s\right]\mathrm{and}v=N\left[x_a\right]\cap N\left[x_b\right].$$

Note that if $3l+2<\frac{n}{2}$, there are exactly n pairs of vertices verifying this condition: $v_i$ and $v_{i+3l+2}$, for $1=1,\dots ,n$ and $i+3l+2$ taken modulo n. When $3l+2=\frac{n}{2}$, which happens if and only if $k=2d$ and $l=d-1$, there are just $\frac{n}{2}$ pairs of these vertices: $v_i$ and $v_{i+3d-1}$, for $i=1,\dots ,3d-1$. Thus, there are $⌊\frac{k-2}{2}⌋n$ $\gamma$-sets of this kind for k odd and $\left(\frac{n+k-2}{2}\right)$ for k even. □

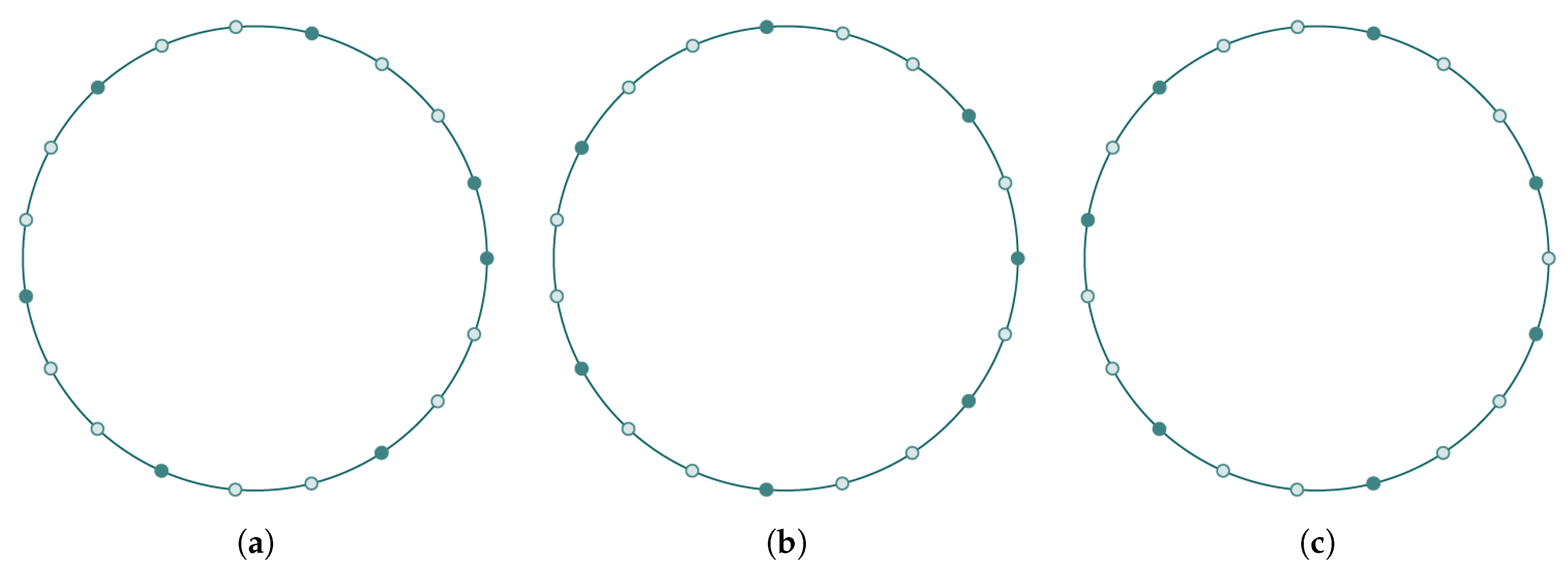
Figure 6b shows the set $D_1$, corresponding to $v_1$, and in Figure 6c is shown the set $D_{1,9}$, corresponding to the pair $\{v_1,v_9\}$, for ${\mathrm{C}}_{19}$.

It is known that $Aut{\mathrm{C}}_n\cong {\mathbf{D}}_n=\langle \rho ,\mu :ord\rho =n,ord\mu =2,\mu \rho =\mu {\rho }^{-1}\rangle$, where $\rho$ may be considered as a rotation by ${360}^{\circ }/n$ and $\mu$ the reflection across the symmetry line that fixes $v_1$ of the regular n-gon, thus,

$$\begin{array}{cccc}\hfill \rho \left(v_i\right)& =v_{i+1}\hfill & \hfill \rho \left(e_i\right)& =e_{i+1}\hfill \\ \hfill \mu \left(v_i\right)& =v_{n+2-i}\hfill & \hfill \mu \left(e_i\right)& =e_{n+1-i}.\hfill \end{array}$$

Theorem 2.

Let n be a positive integer, considering the action of $Aut{\mathrm{C}}_n$ on ${\mathcal{D}}_{\gamma }$, we have:

i. 

${\mathrm{C}}_{3k}$ is γ-transitive;

ii. 

${\mathrm{C}}_{3k-1}$ is γ-transitive;

iii. 

for ${\mathrm{C}}_{3k-2}$ there are $2+⌊\frac{k-2}{2}⌋$ orbits.

Proof. 

By Lemma 4, we know that $D_1,D_2$ and $D_3$ are the three $\gamma$-sets for ${\mathrm{C}}_{3k}$, and clearly $\rho \left(D_1\right)=D_2$ and ${\rho }^2\left(D_1\right)=D_3$; thus, ${\mathrm{C}}_{3k}$ is $\gamma$-transitive.

If $n=3k-1$, the correspondence between ${\mathcal{D}}_{\gamma }$ and V ensures that ${\rho }^i\left(D_1\right)=D_{i+1}$, for $i=1,\dots ,n-1$, so that ${\mathrm{C}}_{3k-1}$ is $\gamma$-transitive.

For $n=3k-2$, Lemma 6 implies that there are two kinds of $\gamma$-sets by cases.

In the first case, the correspondence between $\gamma$-sets and E implies that ${\rho }^i\left(D_1\right)=D_{i+1}$, for $i=1,\dots ,n-1$ and $\mu \left(D_i\right)=D_{n+1-i}$; thus, this orbit has n elements.

In the second case, there are two subcases. In the first one, $\gamma$-sets are in correspondence with the vertex set and clearly the orbit has n elements. In the second, the correspondence is between $\gamma$-sets and unordered pairs of vertices whose distance is $3l+2$, for $l=1,2,\dots ,⌊\frac{k-2}{2}⌋$. Let $D_i$ be the $\gamma$-set corresponding to the pair of vertices $v_i,v_{i+3l+2}$, thus ${\rho }^{j-1}\left(D_1\right)=D_j$ and $\mu \left(D_i\right)=D_{n-(i+3l)}$. Therefore, $\mathcal{O}\left(D_i\right)$ comprises all $\gamma$-sets of this kind, n if $3l+2<\frac{n}{2}$ and $\frac{n}{2}$ if $3l+2=\frac{n}{2}$. □

3. Concluding Remarks

In this work we have studied $\gamma$-transitivity for paths and cycles observing that our main tool is to characterize completely minimum dominating sets for each family and when a graph is not $\gamma$-transitive the orbits are computed. We have already observed that when the characterization has at least two kinds of $\gamma$-sets, the graph does not satisfy the property and has as many orbits as these kinds. As we noted above, this work was motivated by a previous research on Platonic graphs [11], in which is shown which of them are $\gamma$-transitive and why some are not. The main difference with this is that, when a graph does not have this feature, the orbits are exhibited.

There are several questions to be answered; for example, what families happen to have this attribute or are there any necessary or sufficient conditions for ensuring this property is fulfilled?