A New Ensemble Learning Algorithm Combined with Causal Analysis for Bayesian Network Structural Learning
Abstract
:1. Instruction
2. Basic Theory
2.1. Bayesian Network
- represents a directed acyclic graph. is a set of nodes representing variables in the problem domain. is a set of arcs, and a directed arc represents the causal dependency between two variables.
- is the network parameter, that is, the probability distribution of each node. expresses the degree of mutual influence among nodes and presents quantitative characteristics in the knowledge domain.
2.2. Search-Score Based Method
3. Analysis of Search-Score Based Methods
- BIC criteria:
- MDL criteria:
- BDe criteria:
4. Causality-Based Ensemble Learning Algorithm for BN Structure
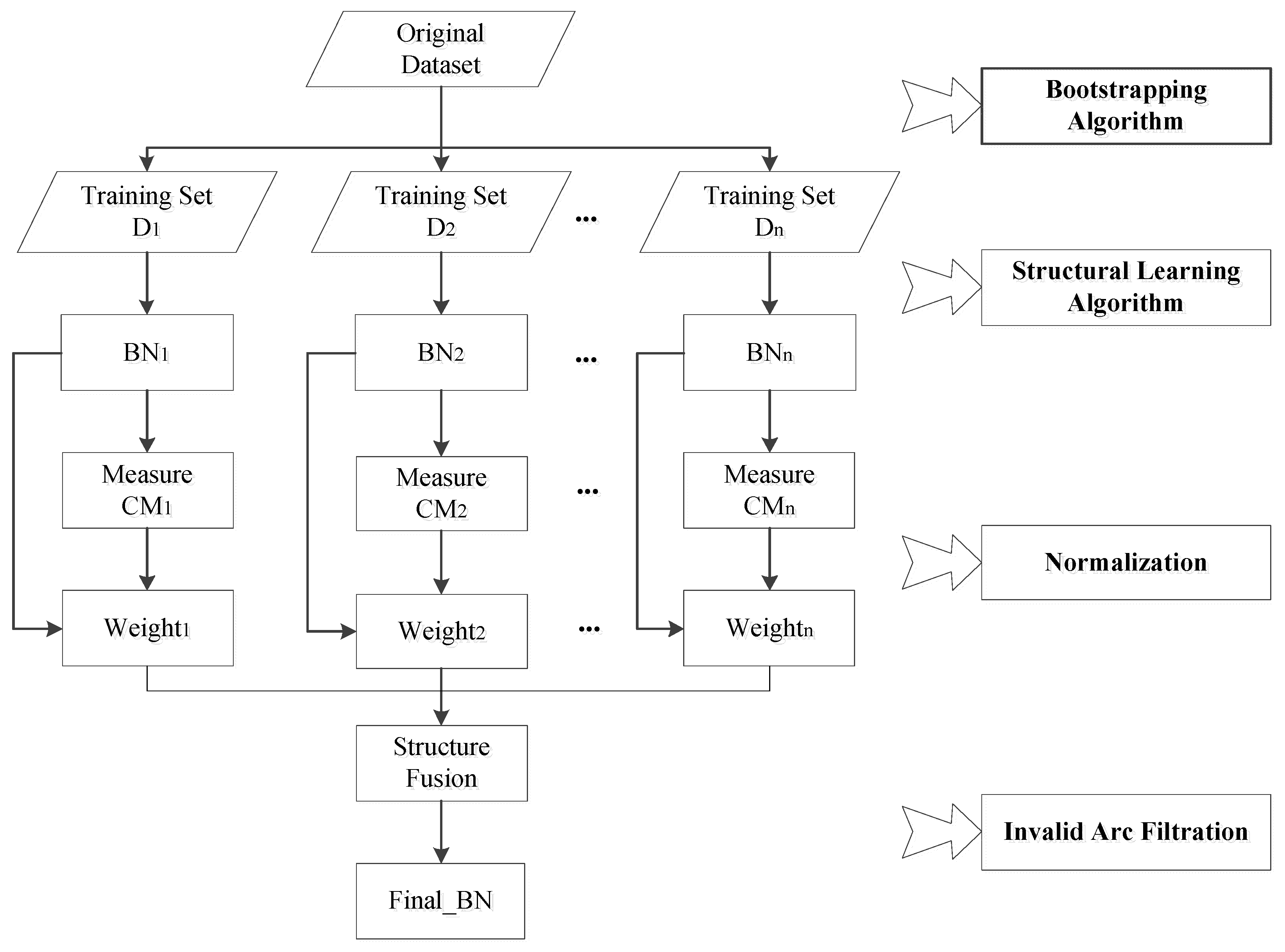
4.1. Ensemble Learning
| Algorithm 1 EL with the Bagging method |
| Input: Original data ; Base leaner Output: Integrating model Step 1: Sampling Training sets are extracted from with Bootstrapping; A total of rounds are taken, and samples are extracted in each round. Step 2: Training Each time one training set is used to train a model, and training sets can generate models. Step 3: Integration For classification: the final result is obtained by voting with the models obtained in the previous step; For regression, the mean value of the above model is calculated as the final result. |
4.2. Information Flow-Based Integration Mechanism
4.2.1. Causal Information Flow
4.2.2. Global Causality Measure
4.3. Causality-Based Ensemble Learning Algorithm
5. Experiments and Analysis
5.1. Experimental Data
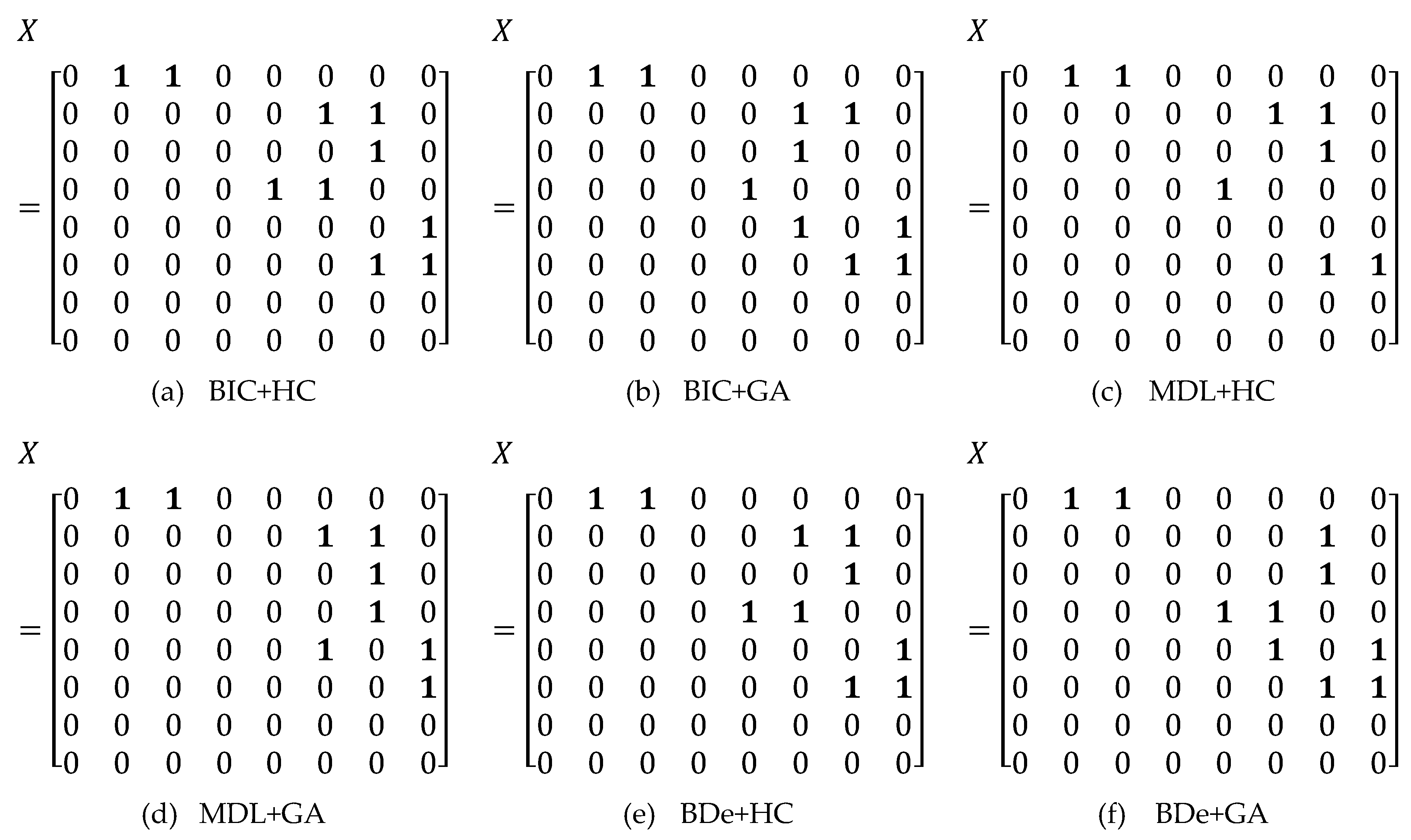
5.2. Structual Learning with C-EL
5.3. Analysis and Discussion of Results
6. Conclusions
- (1)
- Compared with individual algorithms, the network structure learned by C-EL is more accurate. With respect to the three BNs, the accuracy of the proposed algorithm has improved by 48.38% (Asia), 42.22% (Child) and 28.51% (Alarm), respectively, in terms of the optimal individual algorithm.
- (2)
- Compared with individual algorithms, C-EL has a far stronger generalization ability. As for existing SS algorithms, the accuracy of one algorithm varies greatly when dealing with different BNs. In other words, one algorithm has great performance for one BN but may not have as good performance for another BN. By contrast, the performance of C-EL is stable and it maintains high accuracy for different BNs.
- (3)
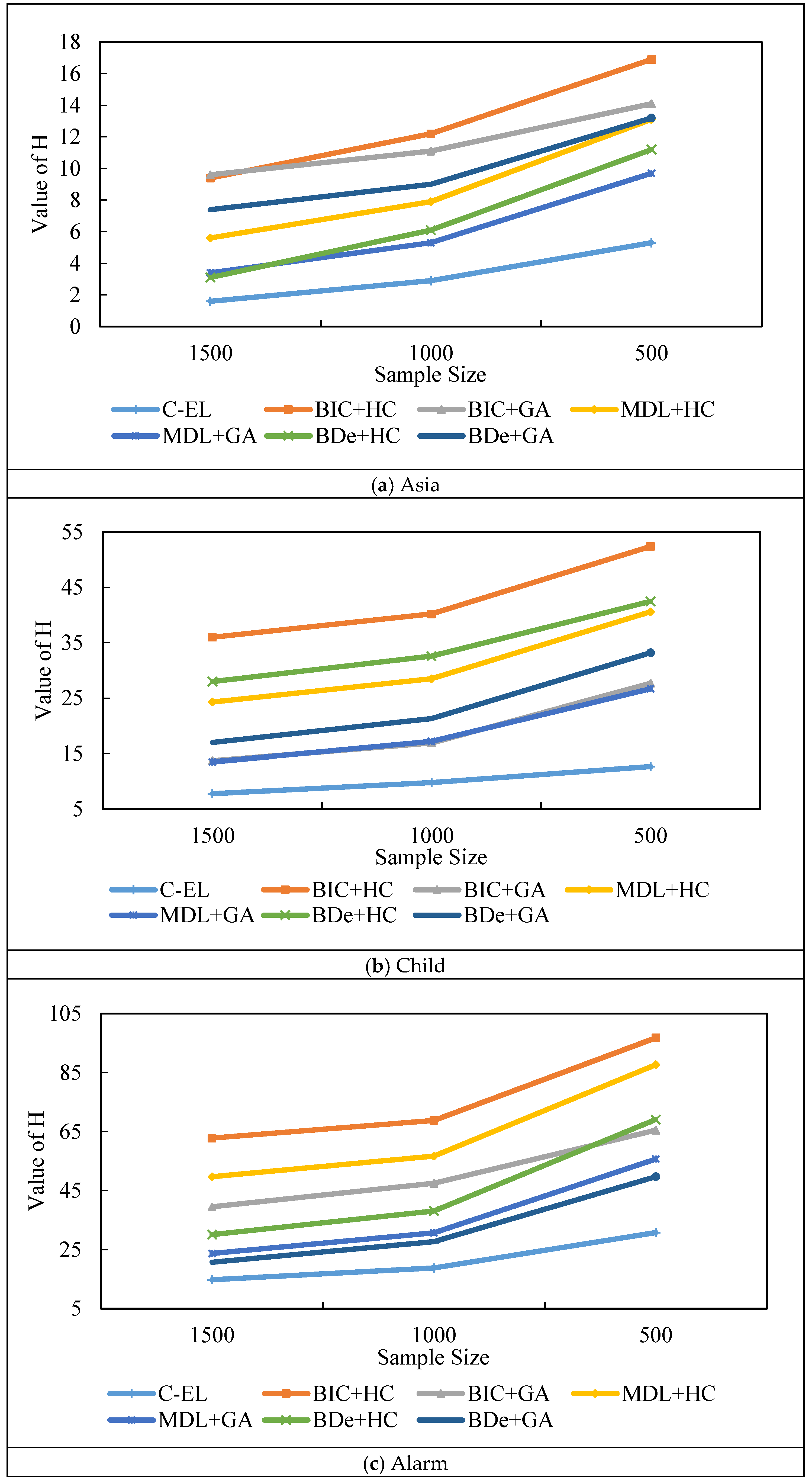
- Compared with individual algorithms, C-EL is less affected by sample size. It is capable of learning structures under the small training sample condition, especially for the structural learning of big-scale network.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pearl, J. Causality: Models, Reasoning, and Inference; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Greenland, S.; Pearl, J. Causal Diagrams. Wiley StatsRef: Statistics Reference Online; American Cancer Society: Atlanta, GA, USA, 2014. [Google Scholar]
- Peter, S.; Clark, G.; Scheines, R. Causation, Prediction, and Search, 2nd ed.; MIT Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Li, S.; Zhang, J. Review of Bayesian Networks Structure Learning. Appl. Res. Comput. 2015, 32, 642–646. [Google Scholar]
- Sahin, F.; Bay, J. Structural Bayesian network learning in a biological decision-theoretic intelligent agent and its application to a herding problem in the context of distributed multi-agent systems. In Proceedings of the 2001 IEEE International Conference on Systems, Tucson, AZ, USA, 7–10 October 2001. [Google Scholar]
- Cooper, G.F.; Herskovits, E. A Bayesian method for the induction of probabilistic networks from data. Mach. Learn. 1992, 9, 309–347. [Google Scholar] [CrossRef]
- Lam, W.; Bacchus, F. Learning Bayesian belief networks: An approach based on the MDL principle. Comput. Intell. 1994, 10, 269–293. [Google Scholar] [CrossRef] [Green Version]
- Heckerman, D.; Geiger, D.; Chickering, D.M. Learning Bayesian networks: The combination of knowledge and statistical data. Mach. Learn. 1995, 20, 197–243. [Google Scholar] [CrossRef] [Green Version]
- Zhu, M.M.; Liu, S.Y.; Yang, Y.L. Structural Learning Bayesian Network Equivalence Classes Based on a Hybrid Method. Acta Electron. Sin. 2013, 41, 98–104. [Google Scholar]
- Guo, W.; Xiao, Q.; Hou, Y. Bayesian network learning based on relationship prediction PSO and its application in agricultural expert system. In Proceedings of the 25th Chinese Control and Decision Conference (CCDC), Guiyang, China, 25–27 May 2013; pp. 1818–1822. [Google Scholar]
- Carvalho, A. A cooperative coevolutionary genetic algorithm for learning bayesian network structures. In Proceedings of the 2011 Conference on Genetic & Evolutionary Computation, Dublin, Ireland, 12–16 July 2011; ACM: New York, NY, USA, 2011. [Google Scholar]
- Ji, J.Z.; Wei, H.K.; Liu, C.N. An artificial bee colony algorithm for learning Bayesian networks. Soft Comput. 2013, 17, 983–994. [Google Scholar] [CrossRef]
- He, W.; Pan, Q.; Zhang, H.C. The Development and Prospect of the Study of Bayesian Network Structure. Inf. Control 2004, 33, 185–190. [Google Scholar]
- Campos, L.M.D. A Scoring Function for Learning Bayesian Networks based on Mutual Information and Conditional Independence Tests. J. Mach. Learn. Res. 2006, 7, 2149–2187. [Google Scholar]
- Rebai, G.A. Improving algorithms for structure learning in Bayesian Networks using a new implicit score. Expert Syst. Appl. 2010, 37, 5470–5475. [Google Scholar]
- Fan, M.; Huang, X.Y.; Shi, W.R. An Improved Learning Algorithm of Bayesian Network Structure. J. Syst. Simul. 2008, 82, 4613–4617. [Google Scholar]
- Wang, C.H.F.; Zhang, Y.H. Bayesian network structure learning method based on unconstrained optimization and genetic algorithm. Control Decis. 2013, 28, 618–622. [Google Scholar]
- Li, M.; Zhang, R.; Hong, M.; Bai, C. Improved Structural Learning Algorithm of Bayesian Network based on Information Flow. Syst. Eng. Electron. 2018, 465, 202–207. [Google Scholar]
- Li, M.; Liu, K.F. Causality-based Attribute Weighting via Information Flow and Genetic Algorithm for Naive Bayes Classifier. IEEE Access 2019, 7, 150630–150641. [Google Scholar] [CrossRef]
- Kojima, K.; Perrier, E.; Imoto, S. Optimal Search on Clustered Structural Constraint for Learning Bayesian Network Structure. J. Mach. Learn. Res. 2010, 11, 285–310. [Google Scholar]
- Liu, Y.; Yao, X. Ensemble Learning via Negative Correlation; Elsevier Science Ltd.: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Okun, O.; Valentini, G.; Re, M. Ensembles in Machine Learning Applications; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Loris, N.; Stefano, G.; Sheryl, B. Ensemble of Convolutional Neural Networks for Bioimage Classification. Appl. Comput. Inform. 2018, 6, 143–175. [Google Scholar]
- Wang, X.Z.; Xing, H.J.; Li, Y. A study on relationship between generalization abilities and fuzziness of base classifiers in ensemble learning. IEEE Trans. Fuzzy Syst. 2015, 23, 1638–1654. [Google Scholar] [CrossRef]
- Liang, X.S. Unraveling the Cause-Effect Relation between Time Series. Phys. Rev. E 2014, 90, 052150. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hu, C.L. Overview of Bayesian Network Research. J. Hefei Univ. (Nat. Sci. Ed.) 2013, 23, 33–40. [Google Scholar]
- Li, M.; Liu, K.F. Probabilistic Prediction of Significant Wave Height Using Dynamic Bayesian Network and Information Flow. Water 2020, 12, 2075. [Google Scholar] [CrossRef]
- Schwarz, G.E. Estimating the Dimension of a Model. Ann. Stats 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Chickering, D.M.; Meek, C.; Heckerman, D. Large-Sample Learning of Bayesian Networks is NP-Hard. J. Mach. Learn. Res. 2004, 5, 1287–1330. [Google Scholar]
- Tsamardinos, I. The Max-Min Hill-Climbing Bayesian Network Structure Learning Algorithm. Mach. Learn. 2006, 65, 31–78. [Google Scholar] [CrossRef] [Green Version]
- Package for Bayesian Network Learning and Inference. Available online: https://www.bnlearn.com/ (accessed on 1 January 2007).
- Jongh, M.D.; Druzdzel, M.J. A Comparison of Structural Distance Measures for Causal Bayesian Network Models. Recent Advances in Intelligent Information Systems. 2009. Available online: https://www.researchgate.net/publication/254430204 (accessed on 1 January 2020).
- Wang, Q. Research on Several Key Issues in Integrated Learning; Fudan University: Shanghai, China, 2011. [Google Scholar]
- Dietterich, T.G. Ensemble learning. In The Handbook of Brain Theory and Neural Networks, 2nd ed.; MIT Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Breiman, L. Bagging Predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.J. Flight Delay and Spread Prediction Based on Bayesian Network; Tianjin University: Tianjin, China, 2009. [Google Scholar]
- Liang, X.S. Normalizing the causality between time series. Phys. Rev. E 2015, 92, 022126. [Google Scholar] [CrossRef] [PubMed] [Green Version]
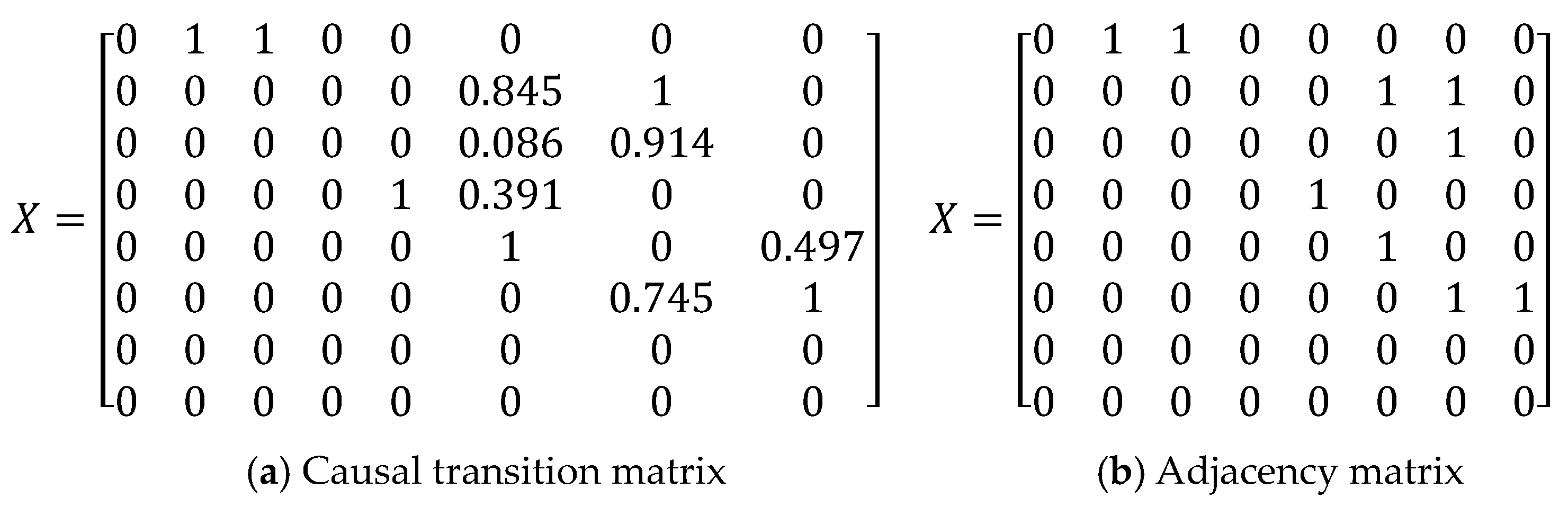
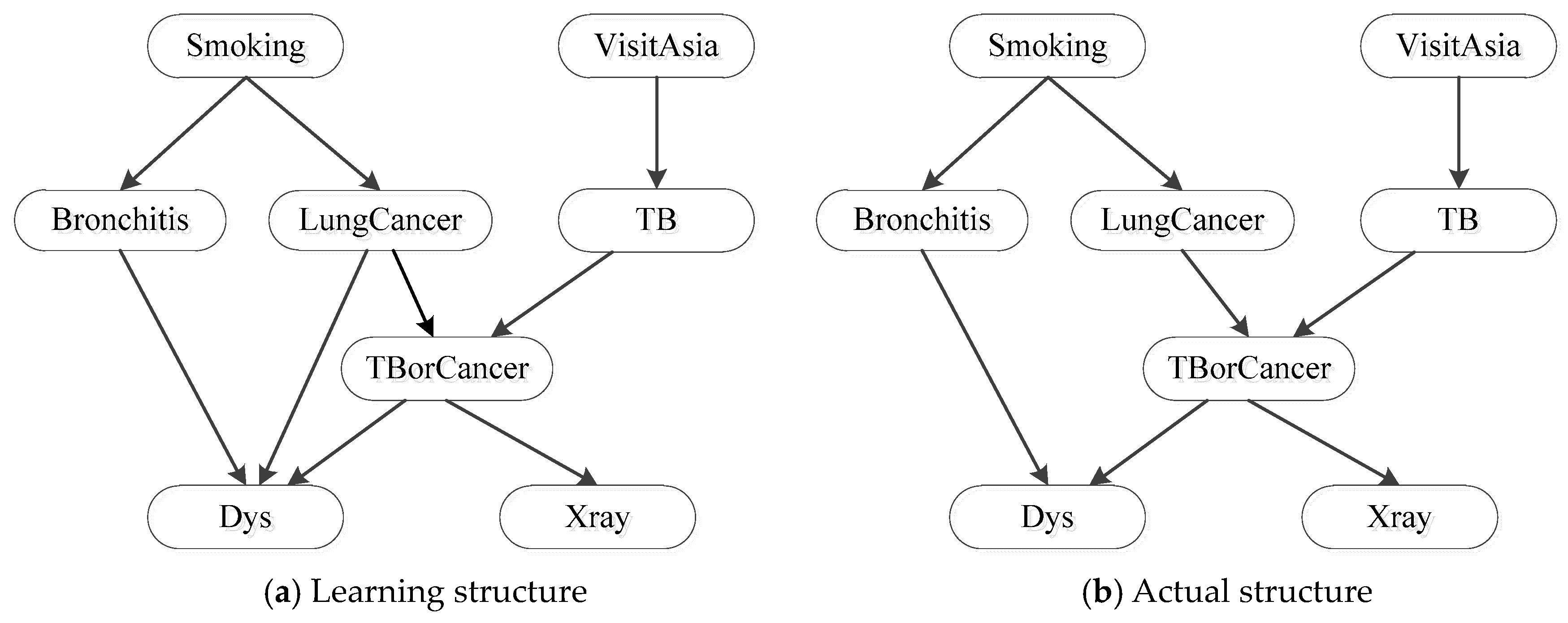

| Node | Smoking | Bronchitis | LungCancer | VisitAsia | TB | TBorCancer | Dys | Xray |
|---|---|---|---|---|---|---|---|---|
| Sample 1 | 2 | 2 | 1 | 1 | 1 | 1 | 2 | 1 |
| Sample 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Sample 3 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Sample 4 | 2 | 2 | 1 | 1 | 1 | 1 | 1 | 2 |
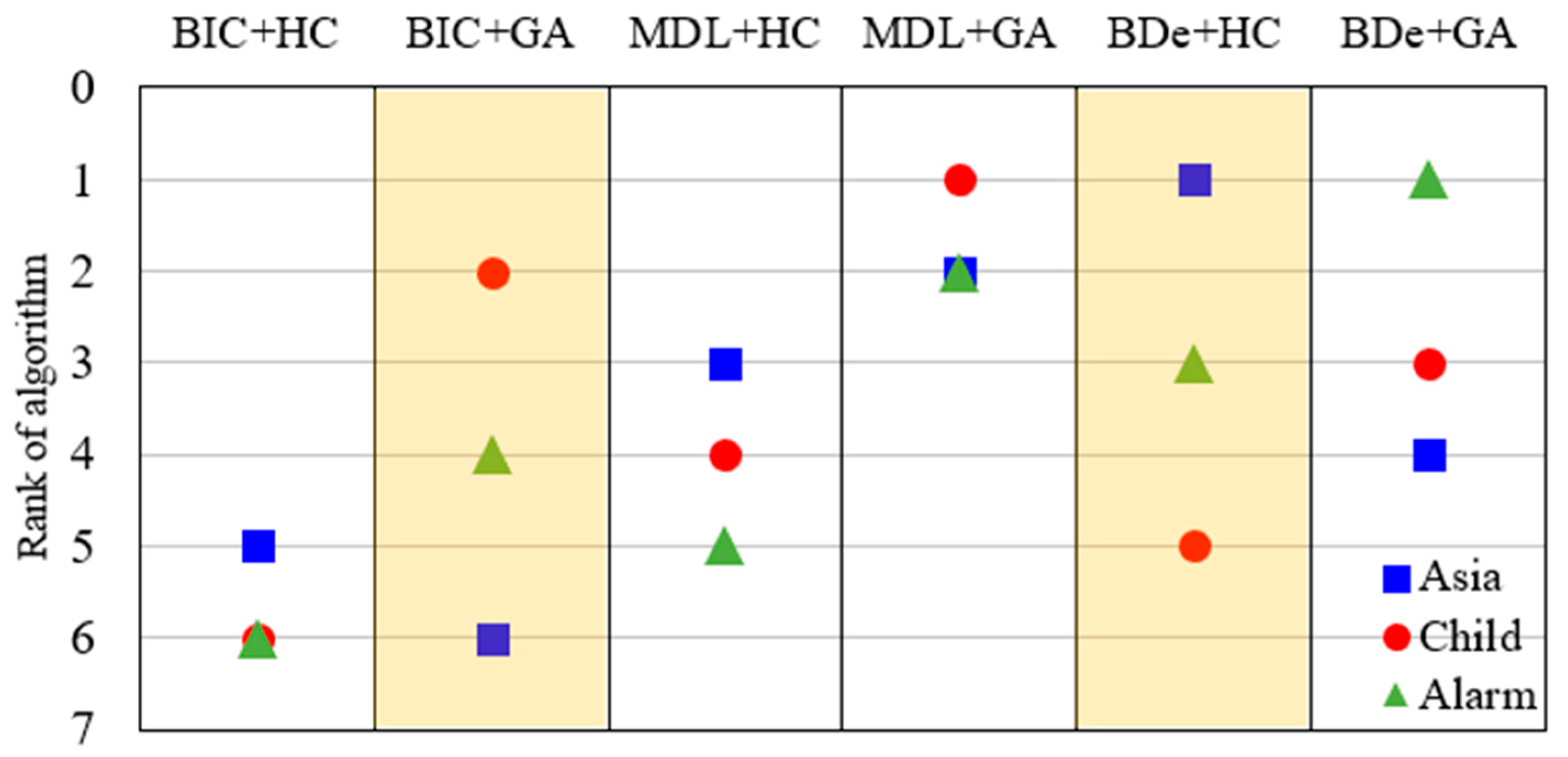
| SS Algorithm | Asia | Child | Alarm |
|---|---|---|---|
| BIC + HC | 8.3 (5) | 14.7 (6) | 68.2 (6) |
| BIC + GA | 10.4 (6) | 8.1 (2) | 39.1 (4) |
| MDL + HC | 5.9 (3) | 11.2 (4) | 52.7 (5) |
| MDL + GA | 5.1 (2) | 6.8 (1) | 25.4 (2) |
| BDe + HC | 3.2 (1) | 12.9 (5) | 31.2 (3) |
| BDe + GA | 7.6 (4) | 10.4 (3) | 17.6 (1) |
| Smoking | Bronchitis | LungCancer | VisitAsia | TB | TBorCancer | Dys | Xray | |
|---|---|---|---|---|---|---|---|---|
| Smoking | \ | 0.0109 | 0.0154 | −0.0021 | 0.0002 | 0.0152 | 0.0216 | 0.0042 |
| Bronchitis | −0.0131 | \ | 0.0030 | 0.0003 | 0.0037 | 0.0028 | 0.0332 | 0.0009 |
| LungCancer | 0.0076 | 0.0062 | \ | 0.0008 | 0.0001 | −0.6909 | 0.0152 | 0.0312 |
| VisitAsia | 0.0026 | 0.0018 | 0.0012 | \ | 0.0243 | 0.0014 | −0.0127 | 0.0025 |
| TB | −0.0087 | −0.0059 | 0.0010 | 0.0001 | \ | 0.0008 | −0.0060 | 0.0014 |
| TBorCancer | 0.0274 | 0.0056 | −0.6909 | 0.0015 | 0.0026 | \ | 0.0160 | 0.0321 |
| Dys | 0.0087 | −0.0320 | 0.0044 | 0.0029 | 0.0009 | 0.0041 | \ | 0.0078 |
| Xray | 0.0323 | 0.0011 | −0.0530 | 0.0019 | 0.0014 | −0.0537 | 0.0211 | \ |
| BN | Index | BIC + HC | BIC + GA | MDL + HC | MDL + GA | BDe + HC | BDe + GA |
|---|---|---|---|---|---|---|---|
| Asia | Causality Measure | 0.3557 | 0.3028 | 0.6332 | 0.8925 | 0.7723 | 0.5446 |
| Weight | 0.1016 | 0.0865 | 0.1809 | 0.2549 | 0.2206 | 0.1556 | |
| Child | Causality Measure | 2.0977 | 2.7955 | 2.6274 | 2.9059 | 2.4600 | 2.6893 |
| Weight | 0.1347 | 0.1795 | 0.1687 | 0.1866 | 0.1579 | 0.1727 | |
| Alarm | Causality Measure | 4.1490 | 4.4804 | 4.2021 | 4.8115 | 4.7294 | 5.0627 |
| Weight | 0.1512 | 0.1633 | 0.1532 | 0.1754 | 0.1724 | 0.1845 |
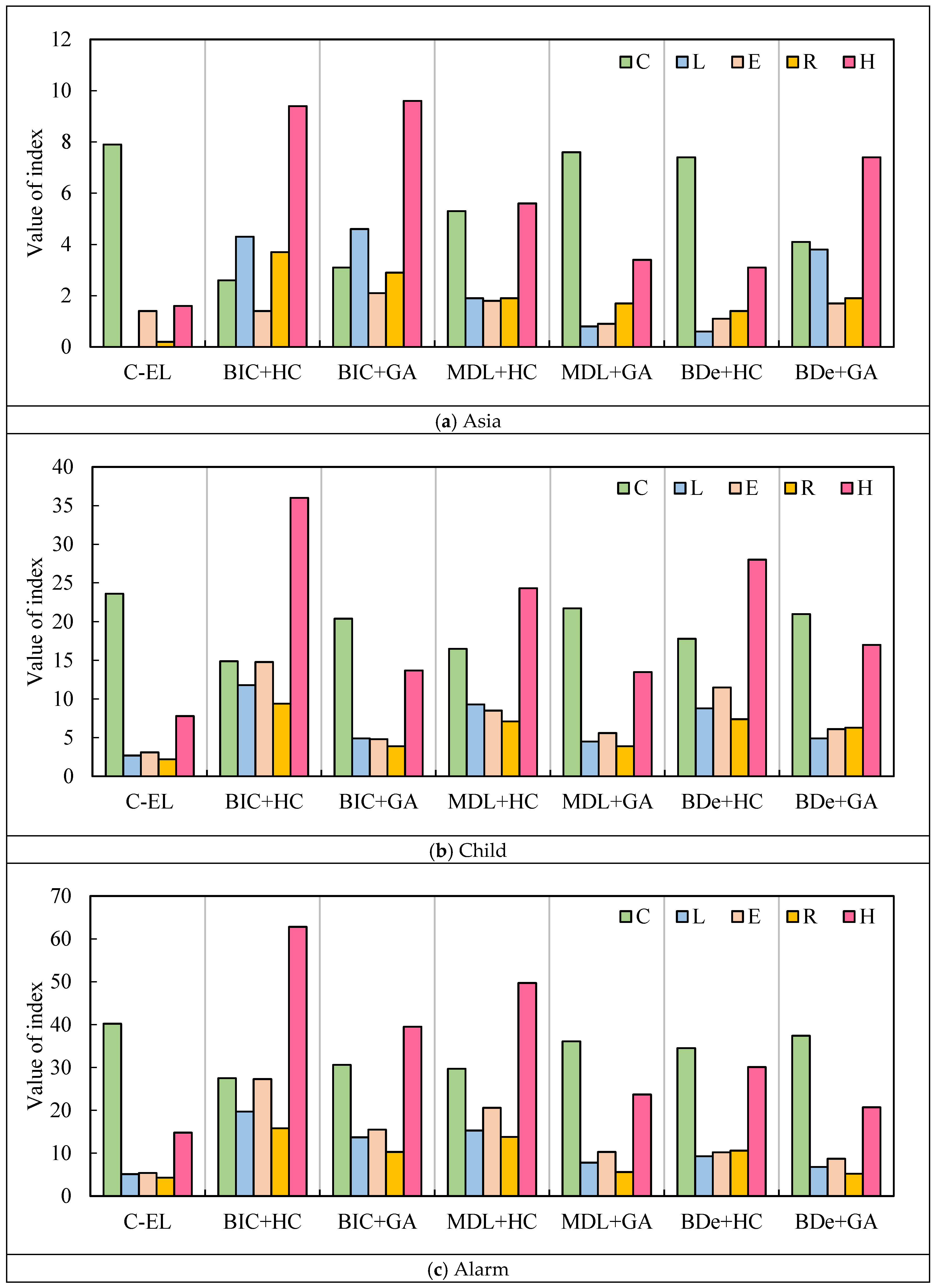
| Criteria | BN | C-EL | BIC + HC | BIC + GA | MDL + HC | MDL + GA | BDe + HC | BDe + GA |
|---|---|---|---|---|---|---|---|---|
| Asia | 7.9 | 2.6 | 3.1 | 5.3 | 7.6 | 7.4 | 4.1 | |
| Child | 23.6 | 14.9 | 20.4 | 16.5 | 21.7 | 17.8 | 21.0 | |
| Alarm | 40.2 | 27.5 | 30.6 | 29.7 | 36.1 | 34.5 | 37.4 | |
| Asia | 1.6 | 9.4 | 9.6 | 5.6 | 3.4 | 3.1 | 7.4 | |
| Child | 7.8 | 36.0 | 13.7 | 24.3 | 13.5 | 28.0 | 17.0 | |
| Alarm | 14.8 | 62.8 | 39.5 | 49.7 | 23.7 | 30.1 | 20.7 |
| Algorithm | ΔH1500→1000 | ΔH1000→500 | ||||
|---|---|---|---|---|---|---|
| Asia | Child | Alarm | Asia | Child | Alarm | |
| C-EL | 1.3 | 2.0 | 4.0 | 2.4 | 2.9 | 12.1 |
| BIC + HC | 2.8 | 4.2 | 6.2 | 4.7 | 12.2 | 26.8 |
| BIC + GA | 1.5 | 3.2 | 7.9 | 3.0 | 10.8 | 28.4 |
| MDL + HC | 2.3 | 4.2 | 7.2 | 5.2 | 12.1 | 31.2 |
| MDL + GA | 1.9 | 3.7 | 7.4 | 4.4 | 9.5 | 24.7 |
| BDe + HC | 3.0 | 4.6 | 8.2 | 5.1 | 9.9 | 31.3 |
| BDe + GA | 1.6 | 4.3 | 6.9 | 4.2 | 11.9 | 21.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Zhang, R.; Liu, K. A New Ensemble Learning Algorithm Combined with Causal Analysis for Bayesian Network Structural Learning. Symmetry 2020, 12, 2054. https://doi.org/10.3390/sym12122054
Li M, Zhang R, Liu K. A New Ensemble Learning Algorithm Combined with Causal Analysis for Bayesian Network Structural Learning. Symmetry. 2020; 12(12):2054. https://doi.org/10.3390/sym12122054
Chicago/Turabian StyleLi, Ming, Ren Zhang, and Kefeng Liu. 2020. "A New Ensemble Learning Algorithm Combined with Causal Analysis for Bayesian Network Structural Learning" Symmetry 12, no. 12: 2054. https://doi.org/10.3390/sym12122054
APA StyleLi, M., Zhang, R., & Liu, K. (2020). A New Ensemble Learning Algorithm Combined with Causal Analysis for Bayesian Network Structural Learning. Symmetry, 12(12), 2054. https://doi.org/10.3390/sym12122054




