Extended Exponential Regression Model: Diagnostics and Application to Mineral Data
Abstract
1. Introduction
- EE = E.
- EE = L.
- EE = G.
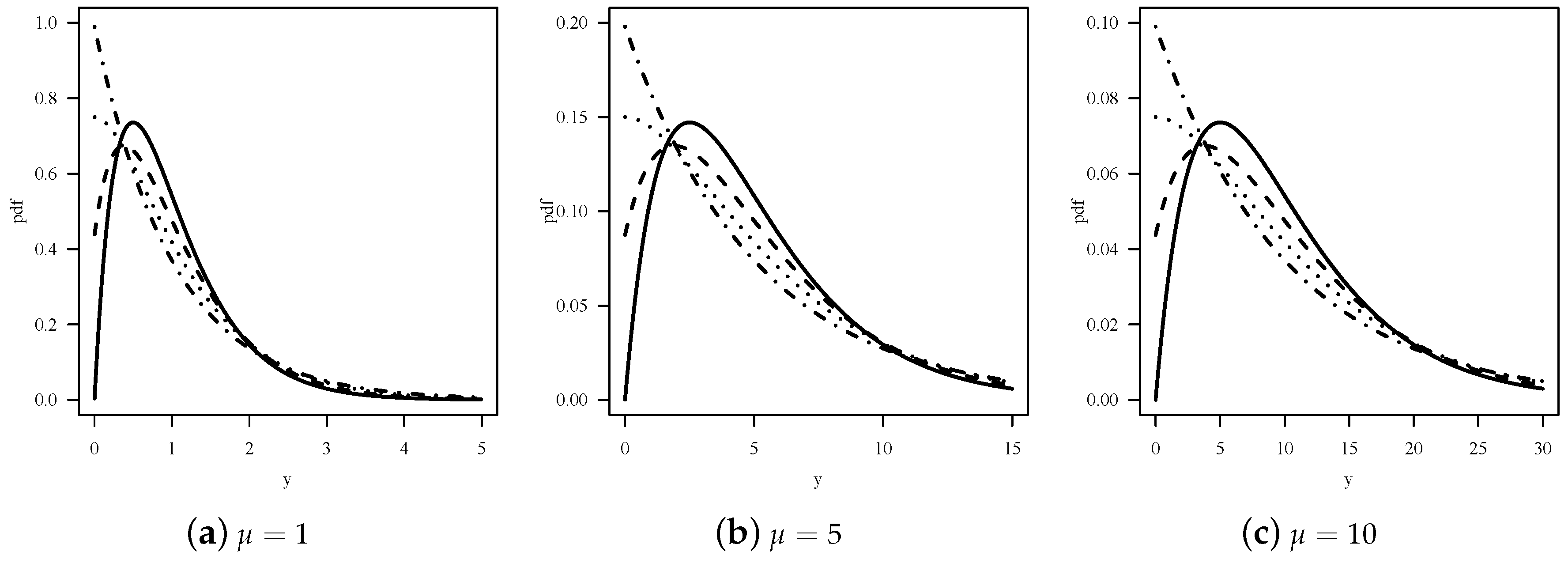
2. A EE Distribution Parameterized by Its Mean and Mixture Parameters
3. REE Regression Model
3.1. EM Algorithm
- , .
| Algorithm 1 EM algorithm for REE regression model |
|
3.2. Diagnostic Analysis
Case Deletion Measures
The Hessian Matrix
3.3. Perturbation Schemes
3.3.1. Case Weights Perturbation
3.3.2. Response Perturbation
3.3.3. Covariate Perturbation
3.4. Residual Analysis
4. Simulation Study
5. Applications
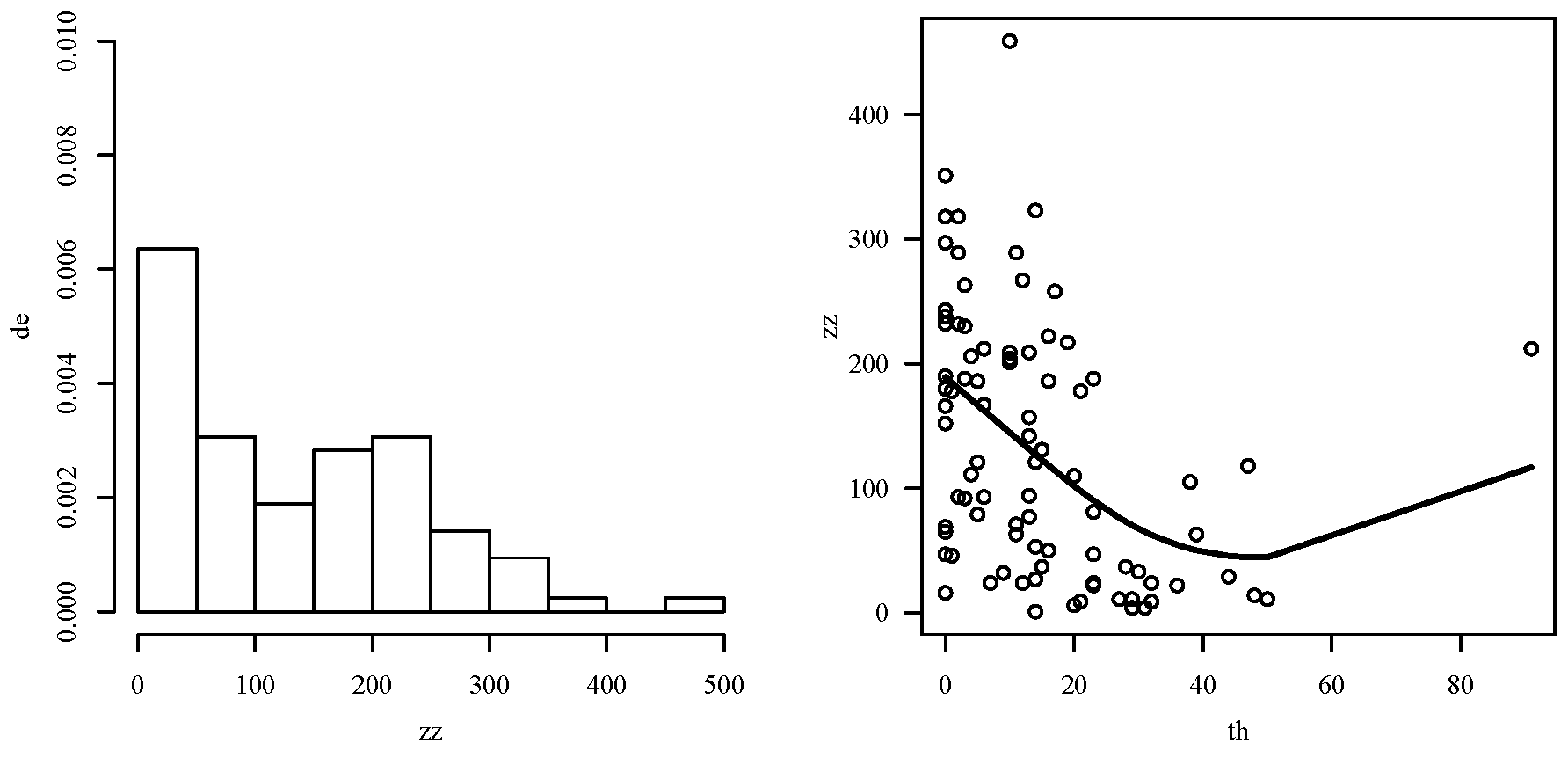
5.1. Exploratory Data Analysis to the Mineral Data Set
5.2. Estimation and Model Checking
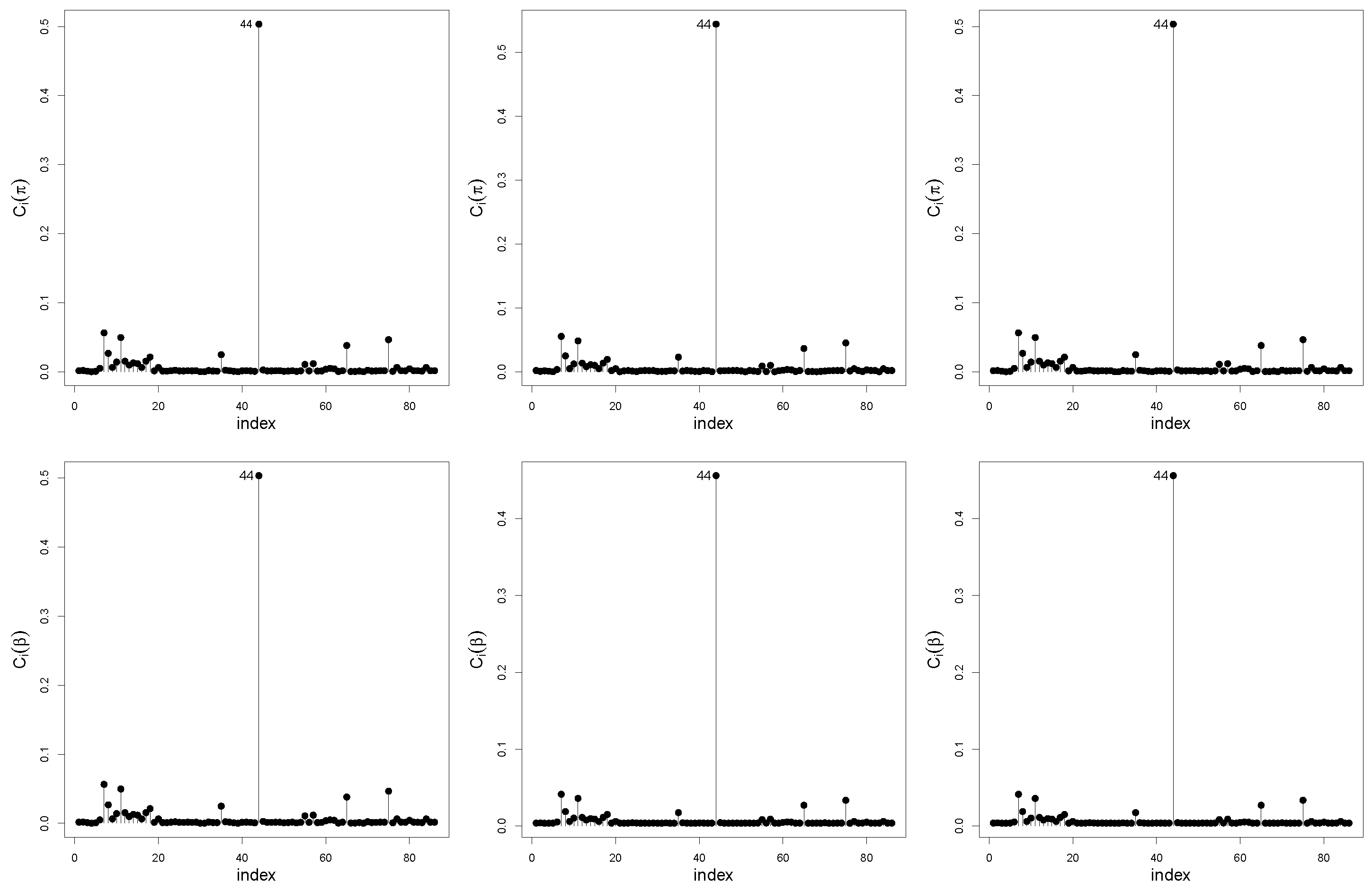
5.3. Diagnostic Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Fisher, R.A.; Tippett, L.H.C. Limiting forms of the frequency distribution of the largest and smallest member of a sample. Proc. Camb. Philos. Soc. 1928, 24, 180–190. [Google Scholar] [CrossRef]
- Gómez, Y.M.; Bolfarine, H.; Gómez, H.W. A New Extension of the Exponential Distribution. Colomb. J. Stat. 2014, 37, 25–34. [Google Scholar] [CrossRef]
- Ghitany, M.E.; Atieh, B.; Nadarajah, S. Lindley distribution and its application. Math. Comput. Simul. 2008, 78, 493–506. [Google Scholar] [CrossRef]
- Andrade, T.A.N.; Bourguignon, M.; Cordeiro, G.M. The exponentiated generalized extended exponential distribution. J. Data Sci. 2016, 14, 393–414. [Google Scholar]
- Rasekhi, M.; Alizadeh, M.; Altun, E.; Hamedani, G.G.; Afify, A.Z.; Ahmad, M. The Modified Exponential Distribution with Applications. Pak. J. Stat. 2017, 33, 383–398. [Google Scholar]
- Rasekhi, M.; Chatrabgoun, O.; Daneshkhah, A. Discrete Weighted Exponential Distribution: Properties and Applications. Filomat 2018, 32, 3043–3056. [Google Scholar] [CrossRef]
- Santos-Neto, M.; Cysneiros, F.J.; Leiva, V.; Barros, M. Reparameterized Birnbaum–Saunders regression models with varying precision. Electron. J. Stat. 2016, 10, 2825–2855. [Google Scholar] [CrossRef]
- Bourguignon, M.; Santos-Neto, M.; de Castro, M. A new regression model for positive data. arXiv 2018, arXiv:1804.07734. [Google Scholar]
- Bourguignon, M.; Leão, J.; Gallardo, D.I. Parametric modal regression with varying precision. Biom. J. 2020, 62, 2002–2020. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm (with discussion). J. R. Stat. Soc. Ser. B 1977, 39, 1–38. [Google Scholar]
- Cook, R.D. Detection of influential observation in linear regression. Technometrics 1977, 19, 15–18. [Google Scholar]
- Cook, R.D. Assessment of local influence. J. R. Stat. Soc. Ser. B 1986, 48, 133–155. [Google Scholar] [CrossRef]
- Zhu, H.-T.; Lee, S.-Y. Local influence for incomplete data models. J. R. Stat. Soc. Ser. B 2001, 63, 111–126. [Google Scholar] [CrossRef]
- Bolboaca, S.D.; Jantschi, L. The Effect of Leverage and/or Influential on Structure-Activity Relationships. Comb. Chem. High Throughput Screen. 2013, 16, 288–297. [Google Scholar] [CrossRef]
- Jantschi, L. A Test Detecting the Outliers for Continuous Distributions Based on the Cumulative Distribution Function of the Data Being Tested. Symmetry 2019, 11, 835. [Google Scholar] [CrossRef]
- Lee, S.-Y.; Xu, L. Influence analyses of nonlinear mixed-effects models. Comput. Statist. Data Anal. 2004, 45, 321–341. [Google Scholar] [CrossRef]
- Dunn, P.K.; Smyth, G.K. Randomized quantile residuals. J. Comput. Graph. Stat. 1996, 5, 236–244. [Google Scholar]
- Cox, D.R.; Snell, E.J. A general definition of residuals. J. R. Stat. Soc. Ser. B 1968, 30, 248–265. [Google Scholar] [CrossRef]
- R Development Core Team. A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- Gómez, H.W.; Venegas, O.; Bolfarine, H. Skew-symmetric distributions generated by the distribution function of the normal distribution. Envirometrics 2006, 18, 395–407. [Google Scholar] [CrossRef]
- Bolfarine, H.; Gómez, H.W.; Rivas, L.I. The log-bimodal-skew-normal model. A geochemical application. J. Chemom. 2011, 25, 329–332. [Google Scholar] [CrossRef]
- Olmos, N.M.; Varela, H.; Gómez, H.W.; Bolfarine, H. An extension of the half-normal distribution. Stat. Pap. 2012, 53, 875–886. [Google Scholar] [CrossRef]
- Reyes, J.; Barranco-Chamorro, I.; Gallardo, D.I.; Gómez, H.W. Generalized Modified Slash Birnbaum–Saunders Distribution. Symmetry 2018, 10, 724. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]


| Skewness | Kurtosis | |
|---|---|---|
| RGA | ||
| RBS | ||
| REE |
| True Values | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Estimator | Bias | SE | RMSE | CP | Bias | SE | RMSE | CP | ||||
| 0.2 | 1 | 0.5 | 0.01 | −0.018 | 0.200 | 0.165 | 0.992 | −0.012 | 0.125 | 0.124 | 0.946 | |
| −0.018 | 0.158 | 0.161 | 0.943 | −0.010 | 0.111 | 0.112 | 0.950 | |||||
| −0.007 | 0.224 | 0.226 | 0.949 | 0.001 | 0.156 | 0.155 | 0.951 | |||||
| −0.002 | 0.116 | 0.119 | 0.946 | −0.001 | 0.079 | 0.080 | 0.949 | |||||
| 1 | −1 | −0.01 | −0.018 | 0.197 | 0.167 | 0.992 | −0.011 | 0.125 | 0.122 | 0.951 | ||
| −0.017 | 0.158 | 0.164 | 0.941 | −0.009 | 0.111 | 0.111 | 0.951 | |||||
| 0.001 | 0.224 | 0.228 | 0.945 | 0.001 | 0.157 | 0.155 | 0.952 | |||||
| −0.002 | 0.115 | 0.117 | 0.949 | −0.001 | 0.080 | 0.081 | 0.944 | |||||
| 2 | −0.5 | 0.02 | −0.021 | 0.197 | 0.164 | 0.989 | −0.010 | 0.125 | 0.123 | 0.949 | ||
| −0.019 | 0.158 | 0.162 | 0.940 | −0.009 | 0.110 | 0.113 | 0.945 | |||||
| 0.003 | 0.224 | 0.228 | 0.945 | 0.000 | 0.157 | 0.158 | 0.944 | |||||
| −0.001 | 0.115 | 0.117 | 0.948 | 0.000 | 0.079 | 0.079 | 0.948 | |||||
| 0.5 | 1 | 0.5 | 0.01 | −0.060 | 0.265 | 0.245 | 0.881 | −0.025 | 0.198 | 0.190 | 0.908 | |
| −0.026 | 0.175 | 0.186 | 0.933 | −0.010 | 0.124 | 0.127 | 0.943 | |||||
| 0.004 | 0.250 | 0.258 | 0.938 | −0.002 | 0.176 | 0.178 | 0.945 | |||||
| 0.001 | 0.129 | 0.135 | 0.936 | 0.000 | 0.090 | 0.091 | 0.943 | |||||
| 1 | −1 | −0.01 | −0.062 | 0.267 | 0.247 | 0.882 | −0.024 | 0.198 | 0.189 | 0.912 | ||
| −0.025 | 0.175 | 0.184 | 0.934 | −0.013 | 0.124 | 0.126 | 0.945 | |||||
| 0.002 | 0.249 | 0.260 | 0.932 | 0.003 | 0.176 | 0.178 | 0.946 | |||||
| 0.000 | 0.129 | 0.136 | 0.937 | 0.002 | 0.090 | 0.091 | 0.947 | |||||
| 2 | −0.5 | 0.02 | −0.062 | 0.267 | 0.248 | 0.883 | −0.027 | 0.198 | 0.189 | 0.913 | ||
| −0.024 | 0.175 | 0.186 | 0.932 | −0.011 | 0.124 | 0.127 | 0.943 | |||||
| 0.002 | 0.249 | 0.258 | 0.938 | 0.001 | 0.176 | 0.179 | 0.945 | |||||
| 0.000 | 0.129 | 0.135 | 0.938 | −0.001 | 0.090 | 0.093 | 0.941 | |||||
| 0.75 | 1 | 0.5 | 0.01 | −0.136 | 0.330 | 0.287 | 0.857 | −0.075 | 0.267 | 0.218 | 0.893 | |
| −0.031 | 0.187 | 0.203 | 0.928 | −0.017 | 0.133 | 0.140 | 0.939 | |||||
| 0.002 | 0.266 | 0.281 | 0.934 | 0.002 | 0.189 | 0.199 | 0.938 | |||||
| 0.001 | 0.138 | 0.148 | 0.935 | −0.001 | 0.096 | 0.098 | 0.946 | |||||
| 1 | −1 | −0.01 | −0.138 | 0.331 | 0.288 | 0.853 | −0.078 | 0.266 | 0.220 | 0.886 | ||
| −0.028 | 0.186 | 0.202 | 0.927 | −0.013 | 0.133 | 0.138 | 0.941 | |||||
| −0.002 | 0.265 | 0.283 | 0.928 | −0.002 | 0.189 | 0.195 | 0.939 | |||||
| 0.001 | 0.138 | 0.147 | 0.936 | 0.000 | 0.096 | 0.099 | 0.944 | |||||
| 2 | −0.5 | 0.02 | −0.140 | 0.328 | 0.290 | 0.849 | −0.071 | 0.269 | 0.216 | 0.892 | ||
| −0.031 | 0.186 | 0.203 | 0.928 | −0.015 | 0.133 | 0.140 | 0.935 | |||||
| 0.007 | 0.265 | 0.284 | 0.931 | 0.006 | 0.189 | 0.198 | 0.938 | |||||
| 0.001 | 0.138 | 0.146 | 0.935 | −0.001 | 0.096 | 0.100 | 0.943 | |||||
| True Values | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Estimator | Bias | SE | RMSE | CP | Bias | SE | RMSE | CP | ||||
| 0.2 | 1 | 0.5 | 0.01 | −0.005 | 0.087 | 0.088 | 0.928 | −0.001 | 0.056 | 0.056 | 0.943 | |
| −0.004 | 0.078 | 0.079 | 0.949 | −0.001 | 0.049 | 0.049 | 0.949 | |||||
| 0.000 | 0.110 | 0.111 | 0.949 | −0.001 | 0.069 | 0.070 | 0.951 | |||||
| 0.001 | 0.056 | 0.055 | 0.953 | −0.001 | 0.035 | 0.035 | 0.949 | |||||
| 1 | −1 | −0.01 | −0.005 | 0.087 | 0.088 | 0.929 | −0.002 | 0.056 | 0.056 | 0.941 | ||
| −0.004 | 0.078 | 0.078 | 0.951 | −0.002 | 0.049 | 0.049 | 0.947 | |||||
| 0.000 | 0.110 | 0.110 | 0.950 | 0.000 | 0.069 | 0.069 | 0.950 | |||||
| 0.001 | 0.055 | 0.055 | 0.946 | 0.001 | 0.035 | 0.035 | 0.947 | |||||
| 2 | −0.5 | 0.02 | −0.007 | 0.087 | 0.088 | 0.928 | −0.002 | 0.056 | 0.055 | 0.943 | ||
| −0.005 | 0.078 | 0.079 | 0.947 | −0.002 | 0.049 | 0.049 | 0.951 | |||||
| 0.000 | 0.110 | 0.111 | 0.950 | −0.001 | 0.069 | 0.069 | 0.949 | |||||
| 0.000 | 0.056 | 0.056 | 0.949 | 0.000 | 0.035 | 0.035 | 0.949 | |||||
| 0.5 | 1 | 0.5 | 0.01 | −0.012 | 0.141 | 0.140 | 0.934 | −0.004 | 0.087 | 0.086 | 0.953 | |
| −0.006 | 0.088 | 0.089 | 0.946 | −0.003 | 0.056 | 0.057 | 0.946 | |||||
| 0.000 | 0.124 | 0.125 | 0.951 | 0.001 | 0.079 | 0.079 | 0.950 | |||||
| 0.001 | 0.063 | 0.064 | 0.944 | 0.001 | 0.039 | 0.040 | 0.945 | |||||
| 1 | −1 | −0.01 | −0.009 | 0.142 | 0.139 | 0.933 | −0.004 | 0.087 | 0.088 | 0.950 | ||
| −0.005 | 0.088 | 0.088 | 0.948 | −0.003 | 0.056 | 0.056 | 0.948 | |||||
| −0.001 | 0.125 | 0.125 | 0.949 | 0.001 | 0.079 | 0.079 | 0.948 | |||||
| 0.000 | 0.063 | 0.062 | 0.947 | 0.000 | 0.040 | 0.040 | 0.947 | |||||
| 2 | −0.5 | 0.02 | −0.012 | 0.140 | 0.137 | 0.934 | −0.004 | 0.087 | 0.087 | 0.950 | ||
| −0.006 | 0.088 | 0.089 | 0.946 | −0.003 | 0.056 | 0.056 | 0.947 | |||||
| −0.001 | 0.124 | 0.126 | 0.946 | 0.001 | 0.079 | 0.078 | 0.950 | |||||
| −0.001 | 0.063 | 0.063 | 0.948 | 0.000 | 0.040 | 0.040 | 0.950 | |||||
| 0.75 | 1 | 0.5 | 0.01 | −0.041 | 0.208 | 0.169 | 0.913 | −0.016 | 0.141 | 0.123 | 0.927 | |
| −0.007 | 0.095 | 0.097 | 0.941 | −0.003 | 0.060 | 0.062 | 0.944 | |||||
| 0.001 | 0.134 | 0.138 | 0.941 | 0.001 | 0.085 | 0.086 | 0.945 | |||||
| 0.000 | 0.068 | 0.069 | 0.945 | −0.001 | 0.043 | 0.043 | 0.946 | |||||
| 1 | −1 | −0.01 | −0.039 | 0.207 | 0.169 | 0.914 | −0.013 | 0.142 | 0.121 | 0.928 | ||
| −0.008 | 0.095 | 0.097 | 0.942 | −0.003 | 0.060 | 0.061 | 0.951 | |||||
| 0.002 | 0.134 | 0.138 | 0.940 | 0.001 | 0.085 | 0.085 | 0.953 | |||||
| −0.001 | 0.068 | 0.069 | 0.945 | 0.000 | 0.043 | 0.044 | 0.947 | |||||
| 2 | −0.5 | 0.02 | −0.038 | 0.209 | 0.168 | 0.916 | −0.014 | 0.144 | 0.121 | 0.931 | ||
| −0.007 | 0.095 | 0.097 | 0.943 | −0.003 | 0.060 | 0.061 | 0.948 | |||||
| 0.000 | 0.134 | 0.137 | 0.945 | −0.001 | 0.085 | 0.087 | 0.946 | |||||
| 0.001 | 0.068 | 0.070 | 0.941 | 0.000 | 0.043 | 0.044 | 0.945 | |||||
| MD | SD | CV | CS | CK | ||||
| 1.00 | 114.50 | 133.79 | 104.46 | 78.82 | 0.61 | 2.58 | 459.00 | 86 |
| Fitted Models | |||
|---|---|---|---|
| Parameter | RGA | RBS | REE |
| 5.0734 (0.1252) | 5.0271 (0.1767) | 5.0440 (0.1122) | |
| −0.0145 (0.0060) | −0.0172 (0.0063) | −0.0125 (0.0044) | |
| p-value | [0.0148] | [0.0068] | [0.0049] |
| 1.1955 (0.1630) | - | - | |
| - | 0.8888 (0.1376) | - | |
| - | - | 0.4650 (0.1713) | |
| log-likelihood | −503.3155 | −520.3540 | −502.5457 |
| AIC | 1012.6311 | 1046.7080 | 1011.0914 |
| BIC | 1019.9941 | 1054.0711 | 1018.4544 |
| Fitted Models | |||
|---|---|---|---|
| Parameter | RGA | RBS | REE |
| 5.3248 (0.1240) | 5.3260 (0.2020) | 5.3008 (0.1276) | |
| −0.0399 (0.0066) | −0.0453 (0.0101) | −0.0381 (0.0069) | |
| p-value | [<0.0001] | [<0.0001] | [<0.0001] |
| 1.3865 (0.1925) | - | - | |
| - | 1.0595 (0.1640) | - | |
| - | - | 0.3056 (0.1548) | |
| log-likelihood | −488.7114 | −508.1733 | −488.1657 |
| AIC | 983.4229 | 1022.3466 | 982.3314 |
| BIC | 990.7508 | 1029.6746 | 989.6594 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gómez, Y.M.; Gallardo, D.I.; Leão, J.; Gómez, H.W. Extended Exponential Regression Model: Diagnostics and Application to Mineral Data. Symmetry 2020, 12, 2042. https://doi.org/10.3390/sym12122042
Gómez YM, Gallardo DI, Leão J, Gómez HW. Extended Exponential Regression Model: Diagnostics and Application to Mineral Data. Symmetry. 2020; 12(12):2042. https://doi.org/10.3390/sym12122042
Chicago/Turabian StyleGómez, Yolanda M., Diego I. Gallardo, Jeremias Leão, and Héctor W. Gómez. 2020. "Extended Exponential Regression Model: Diagnostics and Application to Mineral Data" Symmetry 12, no. 12: 2042. https://doi.org/10.3390/sym12122042
APA StyleGómez, Y. M., Gallardo, D. I., Leão, J., & Gómez, H. W. (2020). Extended Exponential Regression Model: Diagnostics and Application to Mineral Data. Symmetry, 12(12), 2042. https://doi.org/10.3390/sym12122042








