Numerical Solution of Nonlinear Fredholm and Volterra Integrals by Newton–Kantorovich and Haar Wavelets Methods
Abstract
:1. Introduction
2. Preliminaries
3. Establishing Haar Wavelets
4. Nonlinear Fredholm Integral of the Second Kind
5. Nonlinear Volterra Integral of the Second Kind
6. Error Analysis
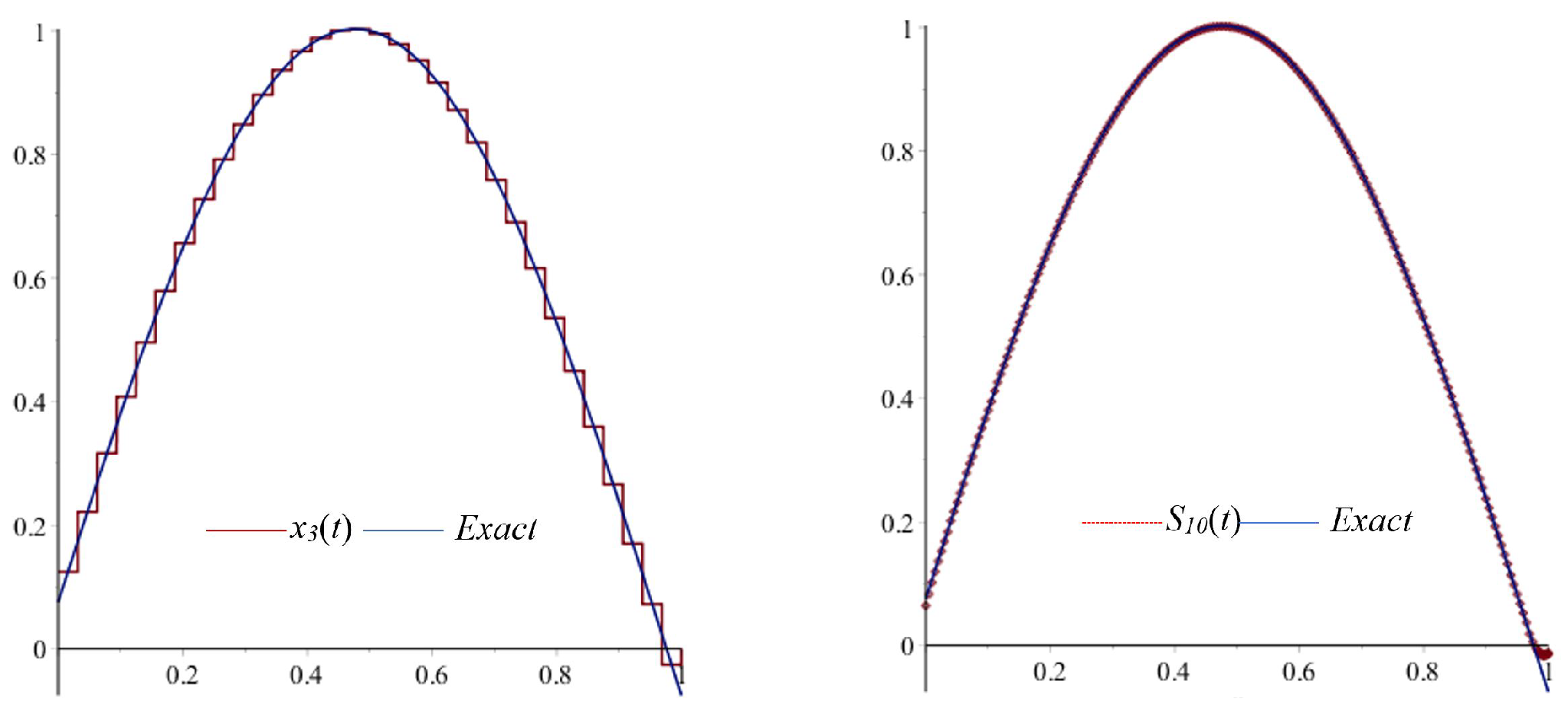
7. Numerical Examples
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Liu, Y. Application of the Chebyshev polynomial in solving Fredholm integral equations. Math. Comput. Model. 2009, 50, 465–469. [Google Scholar] [CrossRef]
- Babaaghaie, A.; Maleknejad, K. A new approach for numerical solution of two-dimensional nonlinear Fredholm integral equations in the most general kind of kernel, based on Bernstein polynomials and its convergence analysis. J. Comput. Appl. Math. 2018, 344, 482–494. [Google Scholar] [CrossRef]
- Capobianco, G.; Conte, D.; Del Prete, I. High performance parallel numerical methods for Volterra equations with weakly singular kernels. J. Comput. Appl. Math. 2009, 228, 571–579. [Google Scholar] [CrossRef] [Green Version]
- Golbabai, A.; Keramati, B. Solution of non-linear Fredholm integral equations of the first kind using modified homotopy perturbation method. Chaos Solitons Fractals 2009, 39, 2316–2321. [Google Scholar] [CrossRef]
- Yousefi, S.; Razzaghi, M. Legendre wavelets method for the nonlinear Volterra–Fredholm integral equations. Math. Comput. Simul. 2005, 70, 1–8. [Google Scholar] [CrossRef]
- Aziz, I. New algorithms for the numerical solution of nonlinear Fredholm and Volterra integral equations using Haar wavelets. J. Comput. Appl. Math. 2013, 239, 333–345. [Google Scholar] [CrossRef]
- Mohammadi, F.A. Chebyshev wavelet operational method for solving stochastic Volterra-Fredholm integral equations. Int. J. Appl. Math. Res. 2015, 4, 217. [Google Scholar] [CrossRef] [Green Version]
- Aziz, I.; Al-Fhaid, A.S. An improved method based on Haar wavelets for numerical solution of nonlinear integral and integro-differential equations of first and higher orders. J. Comput. Appl. Math. 2014, 260, 449–469. [Google Scholar]
- Babolian, E.; Shahsavaran, A. Numerical solution of nonlinear Fredholm integral equations of the second kind using Haar wavelets. J. Comput. Appl. Math. 2009, 225, 87–95. [Google Scholar] [CrossRef] [Green Version]
- Maleknejad, K.; Almasieh, H.; Roodaki, M. Triangular functions (TF) method for the solution of nonlinear Volterra–Fredholm integral equations. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 3293–3298. [Google Scholar] [CrossRef]
- Saberi-Nadjafi, J.; Heidari, M. Solving nonlinear integral equations in the Urysohn form by Newton–Kantorovich–quadrature method. Comput. Math. Appl. 2010, 60, 2058–2065. [Google Scholar] [CrossRef] [Green Version]
- Appell, J.; De Pascale, E.; Zabrejko, P.P. On the application of the Newton-Kantorovich method to nonlinear integral equations of Uryson type. Numer. Funct. Anal. Optim. 1991, 12, 271–283. [Google Scholar] [CrossRef]
- Appell, J.; De Pascale, E.; Lysenko, J.V.; Zabrejko, P.P. New results on Newton-Kantorovich approximations with applications to nonlinear integral equations. Numer. Funct. Anal. Optim. 1997, 18, 1–17. [Google Scholar] [CrossRef]
- Boikov, I.V.; Tynda, A.N. Approximate Solution of Nonlinear Integral Equations of the Theory of Developing Systems. Differ. Equ. 2003, 39, 1277–1288. [Google Scholar] [CrossRef]
- Aziz, I.; Haq, F. A comparative study of numerical integration based on Haar wavelets and hybrid functions. Comput. Math. Appl. 2010, 59, 2026–2036. [Google Scholar]
- Uko, L.U.; Argyros, I.K. A weak Kantorovich existence theorem for the solution of nonlinear equations. J. Math. Anal. Appl. 2008, 342, 909–914. [Google Scholar] [CrossRef] [Green Version]
- Kantorovich, L.V. On Newton’s method for functional equations. Dokl. Akad. Nauk SSSR 1948, 59, 1237–1240. [Google Scholar]
- Shen, W.; Li, C. Kantorovich-type convergence criterion for in exact Newton methods. Appl. Numer. 2009, 59, 1599–1611. [Google Scholar] [CrossRef]
- Argyros, I.K. On Newton’s method for solving equations containing Fr’echet-differentiable operators of order at least two. Appl. Math. Comput. 2009, 215, 1553–1560. [Google Scholar]
- Anvarjon, A. Ahmedov and Mohammad Hasan Abdul Sathar and Ahmad Fadly Nurullah Rasedee and Nor Fadzilah Binti Mokhtar. Approximating of functions from Holder classes Hα[0, 1]. by Haar wavelets. J. Phys. Conf. Ser. 2017, 890, 012073. [Google Scholar]
- Sabzevari, M. A review on “Numerical solution of nonlinear Volterra-Fredholm integral equations using hybrid of.” 52 (2013) 551–555. Alex. Eng. J. 2019, 58, 1099–1102. [Google Scholar] [CrossRef]

| t | [11] | Presented Method | Presented Method |
|---|---|---|---|
| 0 | 4.98 × 10 | 1.38 × 10 | 1.13 × 10 |
| 0.05 | 4.92 × 10 | 1.41 × 10 | 5.85 × 10 |
| 0.1 | 4.74 × 10 | 2.75 × 10 | 1.96 × 10 |
| 0.15 | 4.44 × 10 | 4.15 × 10 | 9.23 × 10 |
| 0.2 | 4.03 × 10 | 2.70 × 10 | 21.51 × 10 |
| 0.25 | 3.52 × 10 | 1.75 × 10 | 6.49 × 10 |
| 0.3 | 2.93 × 10 | 4.53 × 10 | 5.63 × 10 |
| 0.35 | 2.26 × 10 | 3.80 × 10 | 1.01 × 10 |
| 0.4 | 1.54 × 10 | 5.14 × 10 | 1.26 × 10 |
| 0.45 | 7.80 × 10 | 4.77 × 10 | 1.28 × 10 |
| 0.5 | 0 | 5.05 × 10 | 1.32 × 10 |
| 0.55 | 0.780 × 10 | 4.52 × 10 | 1.38 × 10 |
| 0.6 | 1.54 × 10 | 5.10 × 10 | 1.23 × 10 |
| 0.65 | 2.26 × 10 | 3.12 × 10 | 8.53 × 10 |
| 0.7 | 2.93 × 10 | 4.04 × 10 | 3.08 × 10 |
| 0.75 | 3.52 × 10 | 5.39 × 10 | 1.93 × 10 |
| 0.8 | 4.03 × 10 | 1.86 × 10 | 1.39 × 10 |
| 0.85 | 4.44 × 10 | 3.41 × 10 | 7.29 × 10 |
| 0.9 | 4.74 × 10 | 7.29 × 10 | 4.96 × 10 |
| 0.95 | 4.92 × 10 | 2.60 × 10 | 8.46 × 10 |
| 1 | 4.98 × 10 | 8.66 × 10 | 6.27 × 10 |
| Nodes t | [11] | Presented Method | Presented Method |
|---|---|---|---|
| 0 | 0 | 1.61 × 10 | 8.29 × 10 |
| 4.16 × 10 | 4.52 × 10 | 7.31 × 10 | |
| 3.33 × 10 | 5.98 × 10 | 4.40 × 10 | |
| 7.90 × 10 | 5.55 × 10 | 7.66 × 10 | |
| 1.54 × 10 | 2.26 × 10 | 2.79 × 10 | |
| 3.93 × 10 | 9.88 × 10 | 3.78 × 10 | |
| 6.65 × 10 | 1.37 × 10 | 4.69 × 10 | |
| 8.87 × 10 | 6.11 × 10 | 3.00 × 10 | |
| 1.39 × 10 | 4.67 × 10 | 7.69 × 10 | |
| 1.97 × 10 | 2.60 × 10 | 7.84 × 10 | |
| 0 | 9.34 × 10 | 7.31 × 10 | |
| 3.53 × 10 | 1.08 × 10 | 5.60 × 10 | |
| 4.70 × 10 | 5.30 × 10 | 7.68 × 10 | |
| 5.47 × 10 | 4.15 × 10 | 8.85 × 10 | |
| 6.90 × 10 | 2.17 × 10 | 1.84 × 10 | |
| 8.45 × 10 | 7.98 × 10 | 3.56 × 10 | |
| 9.59 × 10 | 3.31 × 10 | 6.48 × 10 | |
| 1.19 × 10 | 5.23 × 10 | 1.47 × 10 | |
| 1.43 × 10 | 1.80 × 10 | 6.48 × 10 | |
| 1.60 × 10 | 1.73 × 10 | 3.22 × 10 | |
| 1 | 1.85 × 10 | 4.42 × 10 | 4.51 × 10 |
| Nodes t | [9], | Presented Method | Presented Method | Presented Method |
|---|---|---|---|---|
| 2.05 × 10 | 3.53 × 10 | 1.94 × 10 | 4.31 × 10 | |
| 3.30 × 10 | 4.44 × 10 | 1.67 × 10 | 3.32 × 10 | |
| 8.69 × 10 | 1.71 × 10 | 1.32 × 10 | 7.91 × 10 | |
| 1.69 × 10 | 4.23 × 10 | 8.69 × 10 | 2.92 × 10 | |
| 1.87 × 10 | 7.27 × 10 | 3.54 × 10 | 1.29 × 10 | |
| 1.17 × 10 | 3.78 × 10 | 3.20 × 10 | 7.11 × 10 | |
| 2.93 × 10 | 7.32 × 10 | 2.75 × 10 | 5.49 × 10 | |
| 8.08 × 10 | 2.82 × 10 | 2.17 × 10 | 1.30 × 10 | |
| 2.16 × 10 | 3.19 × 10 | 1.43 × 10 | 4.81 × 10 |
| Nodes t | [9], | Presented Method | Presented Method | Presented Method |
|---|---|---|---|---|
| 9.46 × 10 | 3.05 × 10 | 9.42 × 10 | 1.96 × 10 | |
| 5.36 × 10 | 4.56 × 10 | 1.31 × 10 | 2.53 × 10 | |
| 4.40 × 10 | 5.03 × 10 | 1.61 × 10 | 5.22 × 10 | |
| 1.16 × 10 | 6.86 × 10 | 1.79 × 10 | 4.73 × 10 | |
| 2.30 × 10 | 9.23 × 10 | 3.13 × 10 | 9.42 × 10 | |
| 1.67 × 10 | 8.92 × 10 | 3.40 × 10 | 8.11 × 10 | |
| 8.37 × 10 | 1.18 × 10 | 3.54 × 10 | 5.42 × 10 | |
| 2.40 × 10 | 1.04 × 10 | 3.55 × 10 | 1.31 × 10 | |
| 1.59 × 10 | 3.41 × 10 | 3.38 × 10 | 8.46 × 10 |
| Nodes t | [21] | Presented Method | Presented Method | Presented Method |
|---|---|---|---|---|
| 0 | 0 | 2.87 × 10 | 1.54 × 10 | 7.90 × 10 |
| 8.33 × 10 | 3.73 × 10 | 4.79 × 10 | 2.33 × 10 | |
| 3.75 × 10 | 1.41 × 10 | 5.52 × 10 | 1.28 × 10 | |
| 1.11 × 10 | 5.86 × 10 | 5.54 × 10 | 4.25 × 10 | |
| 3.51 × 10 | 2.06 × 10 | 3.27 × 10 | 3.64 × 10 | |
| 5.80 × 10 | 2.73 × 10 | 8.20 × 10 | 1.19 × 10 | |
| 1.32 × 10 | 2.27 × 10 | 2.84 × 10 | 7.97 × 10 | |
| 4.95 × 10 | 9.48 × 10 | 3.19 × 10 | 2.41 × 10 | |
| 1.73 × 10 | 3.00 × 10 | 3.67 × 10 | 2.74 × 10 | |
| 3.68 × 10 | 1.41 × 10 | 1.68 × 10 | 2.56 × 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sathar, M.H.A.; Rasedee, A.F.N.; Ahmedov, A.A.; Bachok, N. Numerical Solution of Nonlinear Fredholm and Volterra Integrals by Newton–Kantorovich and Haar Wavelets Methods. Symmetry 2020, 12, 2034. https://doi.org/10.3390/sym12122034
Sathar MHA, Rasedee AFN, Ahmedov AA, Bachok N. Numerical Solution of Nonlinear Fredholm and Volterra Integrals by Newton–Kantorovich and Haar Wavelets Methods. Symmetry. 2020; 12(12):2034. https://doi.org/10.3390/sym12122034
Chicago/Turabian StyleSathar, Mohammad Hasan Abdul, Ahmad Fadly Nurullah Rasedee, Anvarjon A. Ahmedov, and Norfifah Bachok. 2020. "Numerical Solution of Nonlinear Fredholm and Volterra Integrals by Newton–Kantorovich and Haar Wavelets Methods" Symmetry 12, no. 12: 2034. https://doi.org/10.3390/sym12122034
APA StyleSathar, M. H. A., Rasedee, A. F. N., Ahmedov, A. A., & Bachok, N. (2020). Numerical Solution of Nonlinear Fredholm and Volterra Integrals by Newton–Kantorovich and Haar Wavelets Methods. Symmetry, 12(12), 2034. https://doi.org/10.3390/sym12122034





