1. Introduction
Nowadays, inorganic–organic hybrid materials attract special interest because of their versatile application possibilities, including their use in solar cells, multi-ferroic properties and low-dimensional magnetism [
1,
2,
3,
4]. To understand interlayer-length effects on their magnetic behavior, many systems have been suggested. Although such trials have taken place, results have not been successful, because inorganic–organic hybrid systems generally show a high insolubility, and it is difficult to obtain a high-quality crystal suitable for a crystallographic investigation. To overcome this hurdle, we have conducted many experiments and finally we have been able to synthesize a series of layered inorganic–organic hybrid perovskite crystals using phenylethylammonium cations. Among others, the crystal structures of (C
6H
5CH
2CH
2NH
3)
2CoCl
4 (Co-PEA), (C
6H
5CH
2CH
2NH
3)
2MnCl
4 (Mn-PEA) and (C
6H
5CH
2CH
2NH
3)
2CuCl
4 (Cu-PEA) have been solved by the X-ray single crystal diffraction technique [
5,
6,
7]. Co-PEA crystallizes in a monoclinic space group P12
1/c1 (No. 14), and shows no magnetic ordering at all at low temperature. Co builds an isolated tetrahedron with Cl and between inorganic and organic parts various hydrogen bonds exist. Unlike Co-PEA, Mn-PEA and Cu-PEA show an orthorhombic space group Pbca (No.61) and magnetic ordering process occurs at T
C = 10 K for Cu-PEA and at T
N = 44 K for Mn-PEA. Cu-PEA and Mn-PEA belong to the 2-dimensional layered inorganic–organic K
2NiF
4 perovskite type of general formula A
2MX
4, where A = organic cation, M = divalent metal and X = halide. Perovskite is the mineral name for CaTiO
3. However, in general, ABX
3 or A
2BX
4 type compounds are known as perovskite type. The ABX
3 type is 3-dimensional and A
2BX
4 is a double layered type. The K
2NiF
4-type materials are also known as Ruddlesden–Popper-type compounds [
8]. Although both of the abovementioned Cu-PEA and Mn-PEA are of a magnetically ordered phase below a certain temperature, we prefer Mn-PEA, because Mn-PEA is antiferromagnetic and an antiferromagnetic system is more suitable for handling with neutron diffraction techniques. Additionally, in general, an antiferromagnetic system shows forbidden half-integer peaks below a magnetic transition temperature. However, in the case of Mn-PEA, no half-integer forbidden peaks are observed below the Neel temperature. Instead, integer forbidden peaks that have originated from the magnetic phase transition are present. Based on a theoretical study [
9], if weak-ferromagnetism or ferrimagnetism by spin canting due to DM (Dzyaloshinsky-Moriya) interactions is present, the antiferromagnetic cell should be same as the chemical cell. Mn-PEA shows antiferromagnetic phase transition at around 44 K and, in addition, spin canting due to DM interactions causes a weak-ferromagnetism or ferrimagnetism [
6]. Thus, this compound should be the ideal candidate material with which the theoretical prediction could be proven. In the previous study, we reported not only X-ray single-crystal structure, but also magnetic properties using magnetic susceptibility and neutron diffraction methods combined with irreducible representation techniques. However, a new approach using a magnetic space group has recently been developed. To check and confirm our previous result using a representation method, in this study, we used a magnetic space group concept, and from this analysis, we will show that the magnetic cell in Mn-PEA is the same as a chemical cell.
3. Results and Discussion
To analyze the magnetic structure using a magnetic space group concept, we first need information such as space group, lattice parameters and the existence of any phase transitions including structural and magnetic. Mn-PEA has a space group Pbca with lattice parameters a = 7.207 Å, b = 7.301 Å, c = 39.413 Å and Z = 4, and shows two structural and one magnetic phase transitions at 367 K, 417 K and 43 K, respectively [
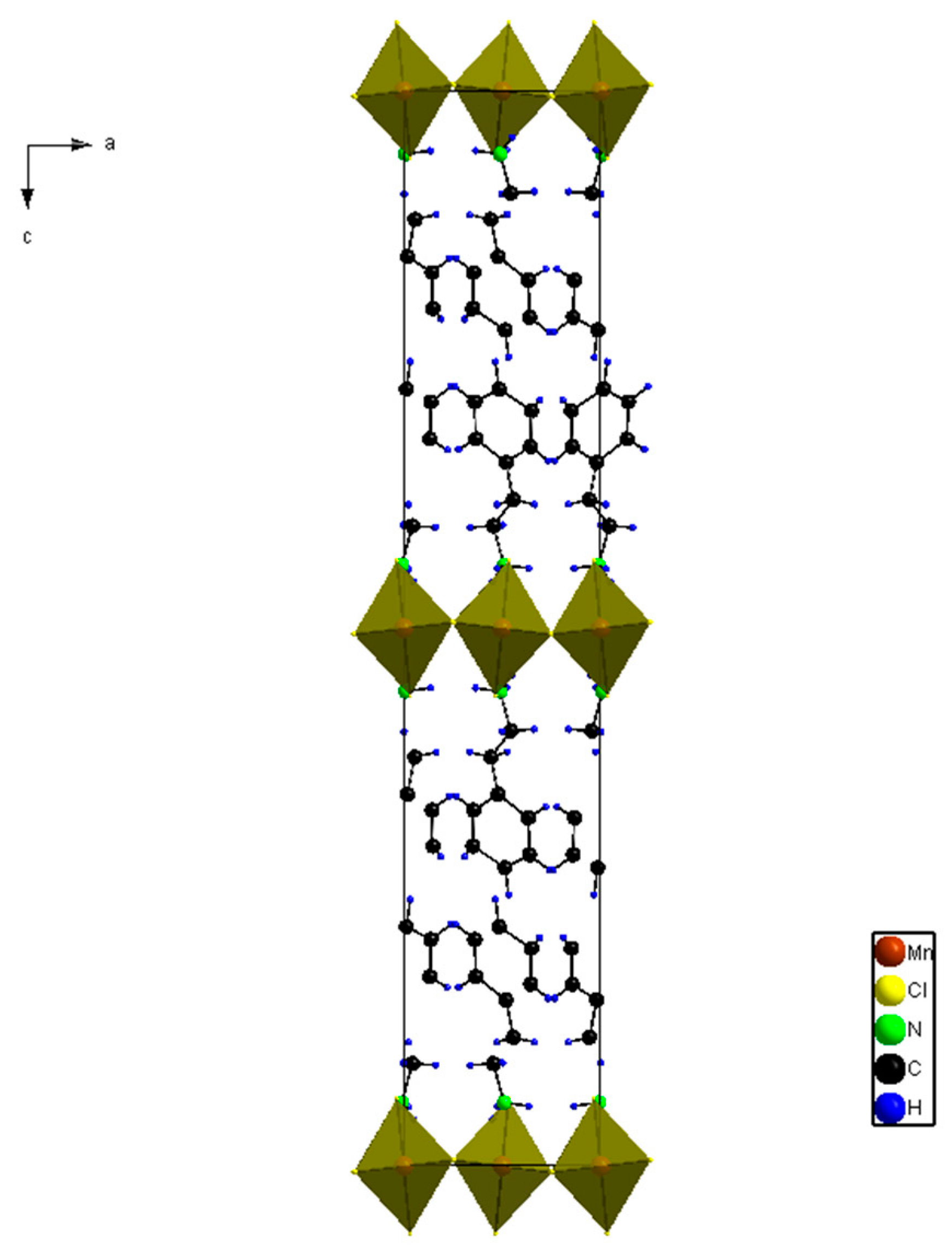
6]. The crystal structure is shown in
Figure 3. The point group of the space group Pbca is 2/m2/m2/m. If we look at the maximal subgroups and minimal super-groups of the point group [
11], there are three subgroups with an index 2 of 2/m2/m2/m, namely, 222, mm2 and 2/m. In this case, the crystallographic group G is mmm and we can describe the group G as G
mmm = {1, i, 2, m, 2
x, 2
y, m
x, m
y}, where i is inversion symmetry, 2
x is a 2-fold symmetry operation along the
x-axis and m
x is a mirror-symmetry operation perpendicular to the
x-axis. The possible subgroups of the mmm point group with index 2 are 222, mm2 and 2/m, as already mentioned above. If we denote one subgroup as H, the first subgroup can be written for example as H1 = 222 = {1, 2, 2
x, 2
y}. Analogously, we can denote H2 = mm2 = {1, m
x, m
y, 2} and H3 = 2/m = {1, i, 2, m}. In the first case, the magnetic point group M
m’m’m’ can be obtained from {1, 2, 2
x, 2
y} + {i, m, m
x, m
y}1′ (see
Table 1). This is described as {1, 2, 2
x, 2
y, i’, m’, m’
x, m’
y} = 2/m’2/m’2/m’ = m’m’m’ [
10]. This magnetic point group is not compatible with ferromagnetism, because if we look at
Table 1, half of the spins have the same sign and the rest of the spins have an opposite sign. This means an antiferromagnetic ordering. Thus, ferromagnetic ordering is impossible in this magnetic point group. This argument is valid for the rest of magnetic point groups. The second one is {1, 2, m
x, m
y} + {i, m, 2
x, 2
y}1′ = {1, 2, 2′
x, 2′
y, i, m’, m
x, m
y} = 2′/m2′/m2/m’ = mmm’ (see
Table 1). This magnetic point group is also not compatible with ferromagnetism. In the third case, the corresponding magnetic point group M
m’m’2 can be obtained from {1, 2, i, m} + {2
y, m
y, m
x, 2
x}1′ (see
Table 1). This can be rewritten as {1, 2, i, m, 2′
y, m’
y, m’
x, 2′x} = 2′/m2′/m2/m = m’m’2. This point group is compatible with ferromagnetism. The magnetic point group m’m’2 is similar to the previous two magnetic point groups. However, if we consider the magnetic moment along the c-axis, all magnetic components along the c-axis show a positive sign. This means that the ferromagnetic ordering in this point group is only possible along the c-axis. Along another two directions, namely the a- and b-axes, antiferromagnetic ordering is possible. The above results are summarized in
Table 1. If the determinant value of the matrix of a symmetry operation is +1, it is known as proper rotation, and if this value is −1, then this is an improper rotation.
To determine the sign in (x, y, z) form, we have to multiply the determinant of a corresponding symmetry operation by −1 for a primed operation. A primed operation means a symmetry operation combined with the time reversal operation 1′ [
10].
Now we will check our neutron diffraction experiment data, to find out the most suitable magnetic structure. For neutron diffraction, a large enough single crystal of Mn-PEA was measured on a four-circle diffractometer (Version, Company/Manufacturer, City, State abbrev if USA or Canada, Country) at HANARO, KAERI, Korea. By using a Ge (311) monochromator, a 1.3 Å wavelength was obtained [
12,
13]. The measurement at low temperature was carried out with closed cycle refrigerator (CCR) (DE-202, ARS, Macungie, PA, USA) and the lowest reachable temperature using CCR was 10 K. In general, the interaction between the neutrons and the nuclei of atoms is isotropic. However, for magnetic scattering, neutrons interact with the electrons in the incompletely filled shells and the intensity from the magnetic scattering shows a strong angle dependency. Besides, neutrons can detect a magnetic moment only if the scattering vector is not parallel to the spin direction. For example, when a magnetic peak is found during a scan process along the a-axis, this indicates that the spin direction is not along the a-axis. To search for magnetic peaks, we used a Q-scan and a radial scan. A propagation vector was obtained through these scans. Down to 10 K, we observed no extra phase transition except magnetic phase transition at around 43 K, which is consistent with previous results from magnetic susceptibility measurements [
6]. At room temperature, the space group of Mn-PEA is Pbca and the reflection conditions for Pbca are as follows: 0kl: k = 2n, h0l: l = 2n, hk0: h = 2n, h00: h = 2n, 0k0: k = 2n, 00l: l = 2n, hkl: h + k, h + l, k + l = 2n and hkl: h + k, h + l, k + l = 2n [
11]. This means that above the magnetic phase transition temperature, for example, such as for (1 0 0), (0 1 0) or (0 0 1), reflections are forbidden. If the forbidden peaks are present and also if the intensities of the so-called nuclear peaks remain unchanged, the appearance of a new reflection indicates the beginning of a magnetic phase transition. In addition, if we further cool down the temperature, intensities of magnetic peaks will increase due to the ordering process of a magnetic moment. As shown in
Figure 4, below 43 K, new forbidden reflections were observed and based on the nuclear cell, the new reflections were indexed as (−1 0 0), (0 1 0), (1 −2 0) and (3 −3 0) [
12]. To check if these peaks were magnetic in origin, we conducted temperature dependence measurements. As shown in
Figure 5, (−1 0 0) shows a temperature dependency but the intensity of (2 0 0) is almost constant within an error. To determine the propagation vector, we examined whether we had any half-integer reflections. If any half-integer reflections were observed, it obviously indicated an antiferromagnetic ordering. If not, there are two cases. The first one is a simple ferromagnetic ordering and the second one is an antiferromagnetic ordering. In the antiferromagnetic case, forbidden peaks have to occur. In the title compound, the transition metal Mn, which has a magnetic moment, occupies a special position 4a in the space group Pbca and the former magnetic susceptibility measurement and neutron diffraction experiment indicate that the magnetic moment should be arranged along the c-axis [
6,
12]. If we look at International Tables for Crystallography A [
11], there are three different kinds of maximal non-isomorphic subgroup, namely, I, IIa and IIb, but IIa and IIb are empty. This means that we have to consider only the subgroups belonging to I. All subgroups in I are of index 2 and are composed of seven space groups: Pbc2
1, Pb2
1a, P2
1ca, P2
12
12
1, P112
1/a, P12
1/c1 and P2
1/b11. Based on the magnetic space group approach, the magnetic cell must coincide with the nuclear cell, because only the Black–White1 group (type 3, which corresponds to the translationengleich group–maximal non-isomorphic subgroup I) is possible. This means that the propagation vector should be (0 0 0) and this has already been observed in our previous neutron diffraction experiment [
12]. To denote a magnetic space group, two notations are used: Opechowski–Guccione (OG) and Belov–Neronova–Smirnova (BNS). The only difference can be found in the magnetic lattice description and Black–White 2 groups. While BNS notation does not use the primed element in the group symbol, the primed element can be obtained from the magnetic lattice type [
14]. Based on the parent space group, we can obtain five possible magnetic space groups: Pbca, Pbca1′, Pb’ca, Pb’c’a and Pb’c’a’. The general positions of each magnetic space group are shown in
Table 2.
As already mentioned, the magnetic ion locates on a special position (0 0 0). If we apply all symmetry operations belonging to the magnetic space group Pbca, the final atomic positions are described as follows: (0, 0, 0 | m
x, m
y, m
z), (1/2, 1/2, 0 | m
x, −m
y, −m
z), (0, 1/2, 1/2 | −m
x, m
y, −m
z) and (1/2, 0, 1/2 | −m
x, −m
y, m
z). This magnetic group corresponds to antiferromagnetic ordering. This is shown in
Figure 6.
The group Pbca1′in
Table 2 is a gray group, which is either paramagnetic or diamagnetic. Therefore, this magnetic group is excluded. This magnetic space group is represented in
Figure 7. Because this is para- or diamagnetic, no arrows indicating spins are shown.
In
Table 2, the symmetry operations of the magnetic space group Pb’ca are shown. The transition-metal atom Mn locates on 4a, (0 0 0). If we apply the magnetic symmetry operations to the Mn atom, we can obtain {0, 0, 0 | m
x, m
y, m
z}, {1/2, 1/2, 0 | m
x, −m
y, −m
z}, {0, 1/2, 1/2 | −m
z, m
y, −m
z}, {1/2, 0, 1/2 | −m
z, −m
y, m
z}, {0, 0, 0 | −m
x, −m
y, −m
z}, {1/2, 1/2, 0 | −m
x, m
y, m
z}, {0, 1/2, 1/2 | m
z, −m
y, m
z} and {1/2, 0, 1/2 | m
z, m
y, −m
z}. For example, the expressions of {0, 0, 0 | m
x, m
y, m
z} and {0, 0, 0 | −m
x, −m
y, −m
z} must be same, i.e., m
x = −m
x, m
y = −m
y and m
z = −m
z. This is also valid for another expression. This means that all magnetic moments must be zero. With this magnetic space group, it is impossible to describe an antiferromagnetic ordering. In
Figure 8, the possible spin arrangements are shown.
Table 2 shows symmetry operations of the magnetic space group Pb’c’a. Analogous to the above cases, if we apply all symmetry operations to the Mn atom at (0 0 0), we obtain {0, 0, 0 | m
x, m
y, m
z}, {1/2, 0, 1/2 | −m
x, −m
y, m
z}, {0, 1/2, 1/2 | m
x, −m
y, m
z}, {1/2, 1/2, 0 | −m
z, m
y, m
z}, {0, 0, 0 | m
x, m
y, m
z}, {1/2, 0, 1/2 | −m
x, −m
y, m
z}, {0, 1/2, 1/2 | m
x, −m
y, m
z} and {1/2, 1/2, 0 | −m
x, m
y, m
z}. Among a total eight expressions, only four expressions (namely {0, 0, 0 | m
x, m
y, m
z}, {1/2, 0, 1/2 | −mx, −m
y, m
z}, {0, 1/2, 1/2 | m
x, −m
y, m
z} and {1/2, 1/2, 0 | −m
x, m
y, m
z}) are unique. Based on this magnetic space group, in the xy-plane, an antiferromagnetic ordering is allowed and along the c-axis, a ferromagnetic ordering is possible. In
Figure 9, the spin arrangements of magnetic space group Pb’c’a are shown.
In
Table 2, the symmetry operations of the magnetic space group Pb’c’a’ are presented. The transition metal Mn occupies 4a (0, 0, 0). As already mentioned, if we apply the magnetic symmetry operations in the magnetic space group Pb’c’a’ to Mn, we obtain {0, 0, 0 | m
x, m
y, m
z}, {1/2, 1/2, 0 | m
x, m
y, −m
z}, {0, 1/2, 1/2 | −m
x, m
y, −m
z}, {1/2, 0, 1/2 | −m
x, −m
y, m
z}, {0, 0, 0 | −m
x, −m
y, −m
z}, {1/2, 1/2, 0 | −m
x, m
y, m
z}, {0, 1/2, 1/2 | m
x, −m
y, m
z} and {1/2, 0, 1/2 | m
x, m
y, −m
z}. For example, the expression {0, 0, 0 | m
x, m
y, m
z} must be equal to {0, 0, 0 | −m
x, m
y, −m
z} and this means that m
x = −m
x, m
y = −m
y and m
z = −m
z. To satisfy these conditions, m
x = m
y = m
z = 0, i.e., no magnetic ordering is possible if an atom occupies a 4a position. In
Figure 10, the magnetic space group of Pb’c’a’ is shown. Among the above five magnetic space groups derived from the crystallographic space group Pbca, the magnetic ordering is only possible in the two magnetic space groups Pbca and Pb’c’a. Compared to the parent crystallographic space group Pbca, two magnetic space groups Pbca and Pb’c’a show the same translational symmetry, i.e., two magnetic space groups have same lattice parameters of the parent crystallographic space group Pbca. This means that the propagation vector must be (0 0 0). According to the previous research using magnetic susceptibility measurements [
6], antiferromagnetic ordering is observed along the c-axis. However, as already discussed in the text, in the case of the magnetic space group Pb’c’a, along the c-axis, only ferromagnetic ordering is possible. Thus, the magnetic space group Pb’c’a can be ruled out and the only possible magnetic space group is Pbca.