Suitability Study of Structure-from-Motion for the Digitisation of Architectural (Heritage) Spaces to Apply Divergent Photograph Collection
Abstract
:1. Introduction
1.1. General Framework
1.2. Related Work
| Study | Largest Dimension of Object (m) | Accuracy (mm) | Relative Accuracy | Subject | Software | Point Comparison |
|---|---|---|---|---|---|---|
| Reinoso et al., 2014 * [52] | 10_20 | 10_26 | <1:1000 | Façade of Buildings | Photomodeler | Total Station and SfM |
| Remondino et al., 2012 * [8] Remondino et al., 2012 * [8] | 15 | 35 | 1:500 | Railway Buildings | Diverse software | Total Station and SfM |
| Green et al., 2014 * [16] Green et al., 2014 * [16] | 5_15 | 19_39 | <1:400 | Church Buildings | Diverse software | Total Station and SfM |
| Koutsoudis et al., 2014 * [64] Koutsoudis et al., 2014 * [64] | 10 | 14 | 1:700 | Church Building | PhotoScan | Total Station and SfM |
| Riveiro et al., 2011 * [13] Riveiro et al., 2011 * [13] | <10 | 12 | 1:800 | Bridge | Photomodeler | TLS and SfM |
| Fassi et al., 2013 [13] Fassi et al., 2013 [13] | 5 | 5 | 1:1000 | Façade of Church | PhotoScan | TLS and SfM |
| Verdiani and Braghiroli, 2012 [14] Verdiani and Braghiroli, 2012 [14] | 1_2 | 5 | 1:400 | Detached Temple | PhotoScan, 123D Catch | TLS and SfM |
| Teza et al., 2016 [11] Teza et al., 2016 [11] | 4 | 4 | 1:1000 | Tower | PhotoScan | TLS and SfM |
| Roncella et al., 2012 [15] Roncella et al., 2012 [15] | 25 | 25 | 1:1000 | Façade of Church | Photomodeler | Total Station and SfM |
| Remondino et al., 2008 * [65] Remondino et al., 2008 * [65] | 1_2 | 1.4 | 1:1500 | Façade of Temple | Photomodeler | TLS and SfM |
| Remondino et al., 2009 * [66] Remondino et al., 2009 * [66] | <1.2 | <0.4 | 1:3000 | Façade of Basilica | Photomodeler | Total Station and SfM |
| Sapirstein, 2016 [52] | 55 | 3 | 1:16,000 | Façade of Temple | PhotoScan | Total Station and SfM |
2. Methodology
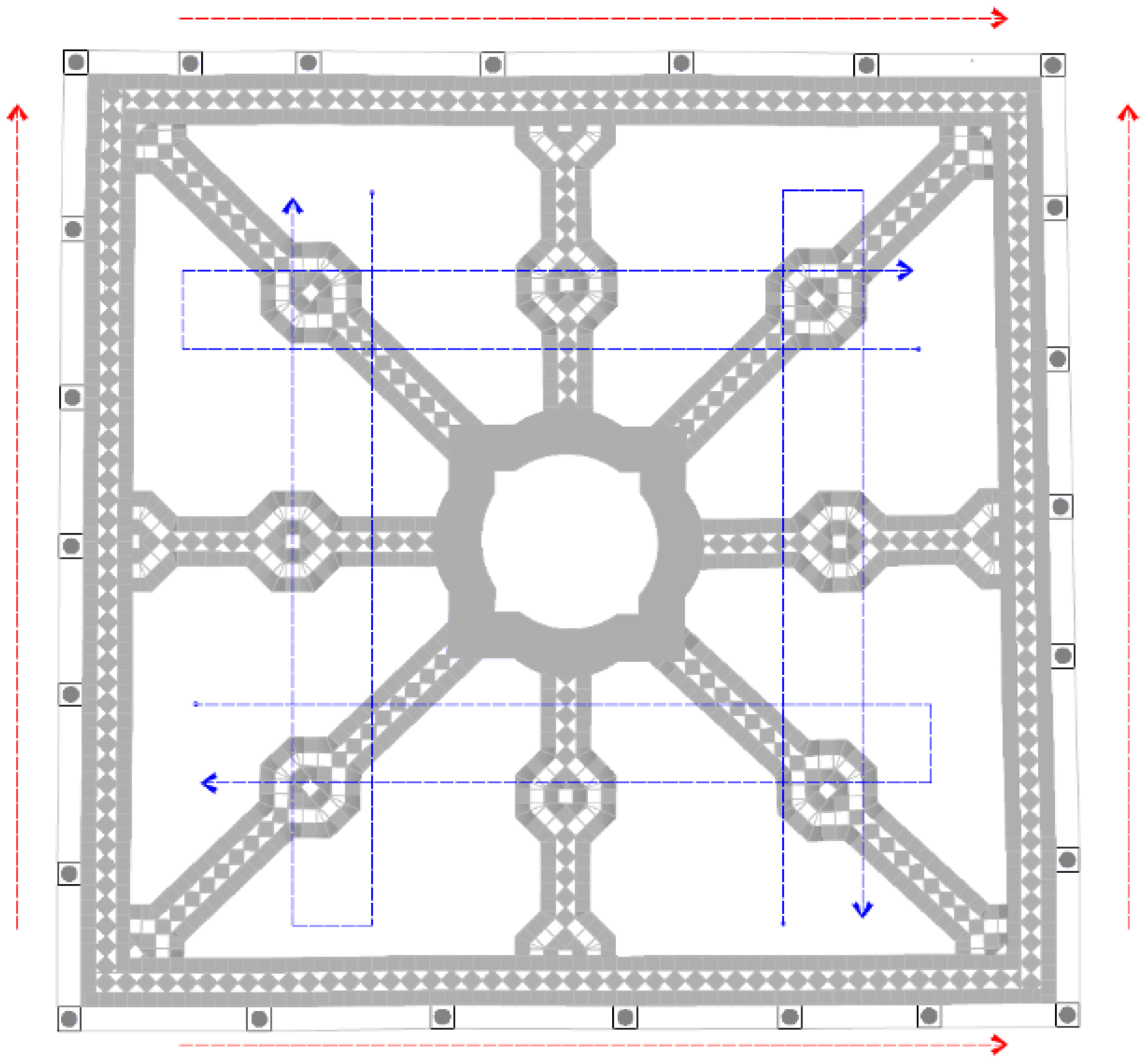
2.1. Case Study: The Main Patio of the Casa de Pilatos
2.2. Data Collection
2.2.1. Structure-from-Motion Survey
2.2.2. Terrestrial Laser Scanning Survey
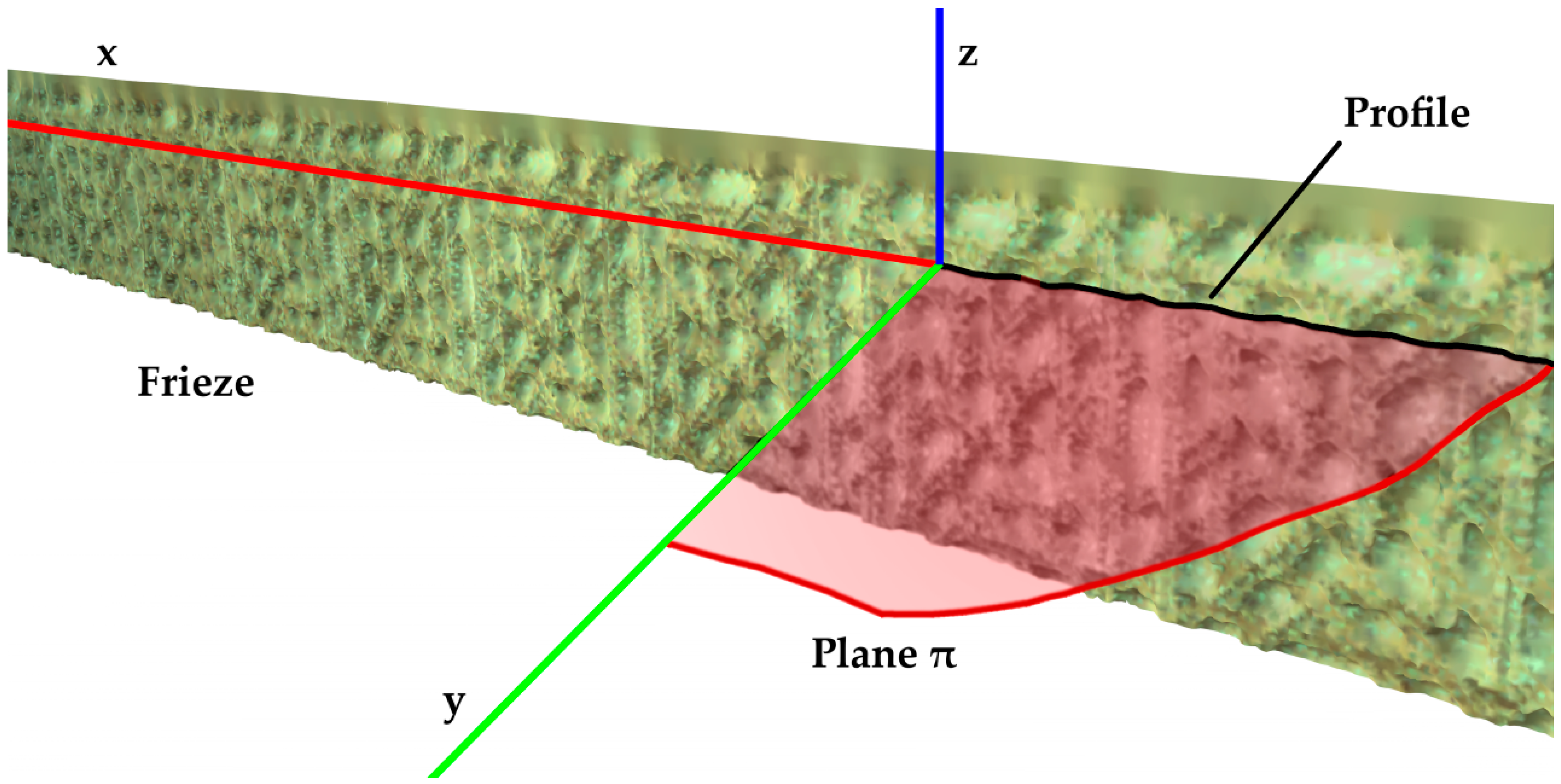
2.3. Data Processing and Analysis
3. Results
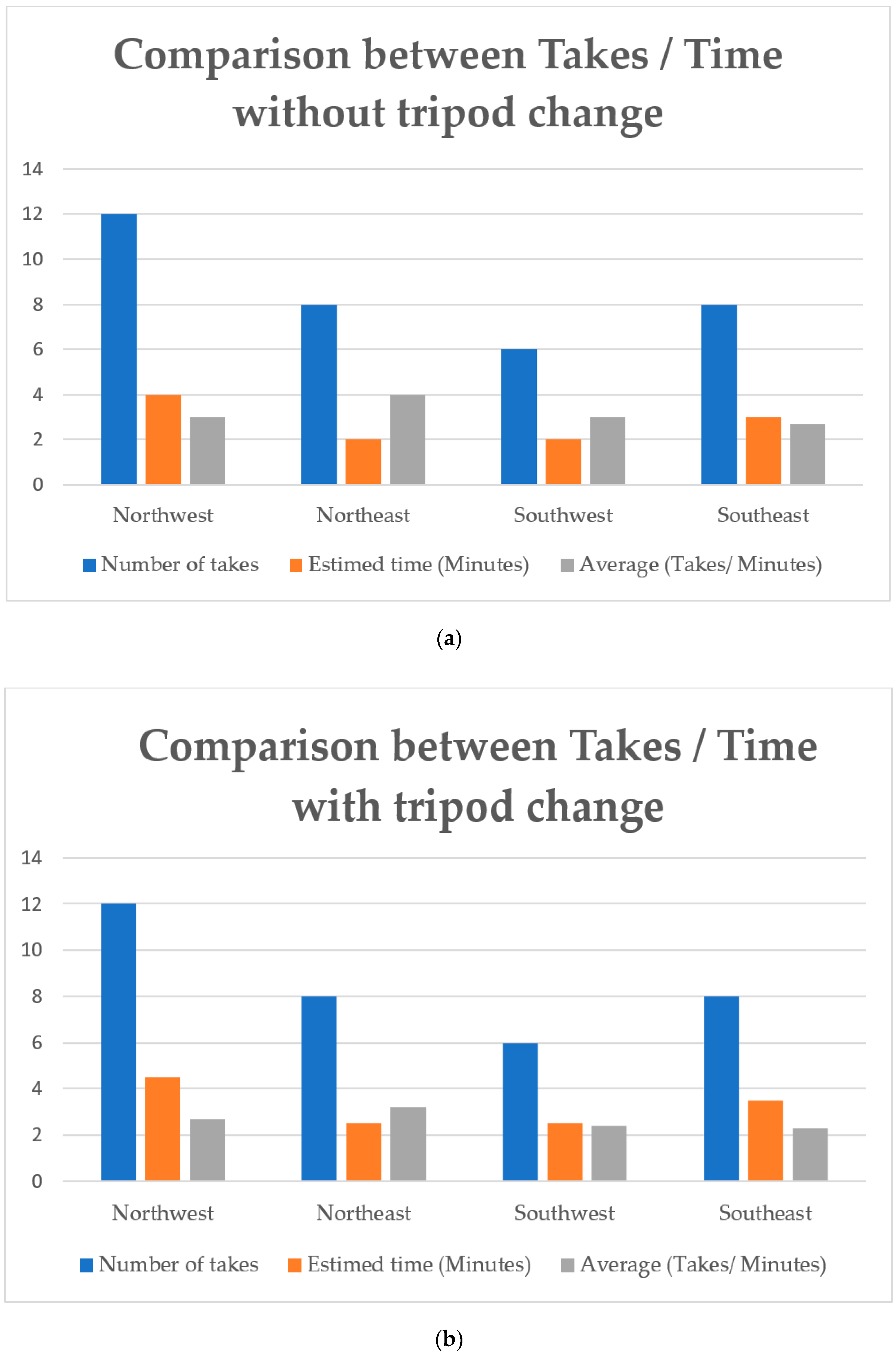
3.1. Survey A
3.2. Survey B
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Data Availability Statement
Abbreviations
| TLS | Terrestrial Laser Scanning |
| SfM | Structure-from-Motion |
| CIPA | International Committee of Architectural Photogrammetry |
| ICOMOS | International Council on Monuments and Sites |
| ISPRS | International Society of Photogrammetry and Remote Sensing |
| BIM | Building Information Modelling |
| HBIM | Historical Building Information Modelling |
| UAV | Unmanned Aerial Vehicle |
| HDR | High Dynamic Range |
| RMS | Root-Mean-Square |
| MVS | Multi-view Stereo |
| GSDs | Ground Sampling Distance |
| GCPs | Ground Control Points |
| Symbols | |
| The following symbols are used in this manuscript: | |
| f | Focal distance |
| w | Sensor width |
| W | Width of the view at distance H |
| H | Distance from camera to object |
| σ | Standard deviation |
| n | Sample size |
| x, y | Observed values |
| Mean value | |
References
- Remondino, F. Heritage recording and 3D modeling with photogrammetry and 3D scanning. Remote Sens. 2011, 3, 1104–1138. [Google Scholar] [CrossRef] [Green Version]
- Poux, F.; Neuville, R.; Van Wersch, L.; Nys, G.-A.; Billen, R.; Poux, F.; Neuville, R.; Van Wersch, L.; Nys, G.-A.; Billen, R. 3D Point Clouds in Archaeology: Advances in Acquisition, Processing and Knowledge Integration Applied to Quasi-Planar Objects. Geosciences 2017, 7, 96. [Google Scholar] [CrossRef] [Green Version]
- Guarnieri, A.; Remondino, F.; Vettore, A. Digital Photogrammetry and Tls Data Fusion Applied To Cultural Heritage 3D Modeling. Int. Arch. Photogramm. Remote Sens. Spat. Inform. Sci. 2006, 36, 1–6. [Google Scholar]
- Lambers, K.; Remondino, F. Optical 3D measurement techniques in archaeology: Recent developments and applications. In Proceedings of the Computer Applications and Quantitative Methods in Archaeology (CAA), Berlin, Germany, 2–6 April 2007; pp. 27–35. [Google Scholar]
- Castellano Román, M. Generación de un modelo de información del patrimonio inmueble en el momento de su protección jurídica. EGA. Rev. Expresión Gráfica Arquit 2015, 20, 266. [Google Scholar] [CrossRef] [Green Version]
- Bienvenido-Huertas, D.; Nieto-Julián, J.E.; Moyano, J.J.; Macías-Bernal, J.M.; Castro, J. Implementing Artificial Intelligence in H-BIM Using the J48 Algorithm to Manage Historic Buildings. Int. J. Archit. Herit. 2019, 14, 1148–1160. [Google Scholar] [CrossRef]
- Antón, D.; Pineda, P.; Medjdoub, B.; Iranzo, A. As-built 3D heritage city modelling to support numerical structural analysis: Application to the assessment of an archaeological remain. Remote Sens. 2019, 11, 1276. [Google Scholar] [CrossRef] [Green Version]
- Remondino, F.; Del Pizzo, S.; Kerten, T.; Troisi, S. Low-Cost and Open-Source Solutions for Automated Image Orientation—A Critical Overview. In Progress in Cultural Heritage Preservation; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Fassi, F.; Fregonese, L.; Ackermann, S.; De Troia, V. Comparison between laser scanning and automated 3D modelling techniques to reconstruct complex and extensive cultural heritage areas. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, XL-5/W1, 73–80. [Google Scholar] [CrossRef] [Green Version]
- Remondino, F.; Spera, M.G.; Nocerino, E.; Menna, F.; Nex, F.; Gonizzi-Barsanti, S. Dense image matching: Comparisons and analyses. In Proceedings of the 2013 Digital Heritage International Congress (DigitalHeritage), Marseille, France, 28 October–1 November 2013; pp. 47–54. [Google Scholar]
- Teza, G.; Pesci, A.; Ninfo, A. Morphological Analysis for Architectural Applications: Comparison between Laser Scanning and Structure-from-Motion Photogrammetry. J. Surv. Eng. 2016, 142, 04016004. [Google Scholar] [CrossRef]
- Koutsoudis, A.; Vidmar, B.; Arnaoutoglou, F. Performance evaluation of a multi-image 3D reconstruction software on a low-feature artefact. J. Archaeol. Sci. 2013, 40, 4450–4456. [Google Scholar] [CrossRef]
- Riveiro, B.; Caamaño, J.C.; Arias, P.; Sanz, E. Photogrammetric 3D modelling and mechanical analysis of masonry arches: An approach based on a discontinuous model of voussoirs. Autom. Constr. 2011, 20, 380–388. [Google Scholar] [CrossRef]
- Verdiani, G.; Braghiroli, A. The Ancient Fragment Collection at the Museo Archeologico in Florence, Italy, a Digital Proposal to Allow Its Acces. In Progress in Cultural Heritage Preservation; Springer: Berlin/Heidelberg, Germany, 2012; pp. 461–468. [Google Scholar]
- Roncella, R.; Re, C.; Forlani, G. Performance Evaluation of a Structure and Motion Strategy in Architecture and Cultural Heritage. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, XXXVIII-5/W16, 285–292. [Google Scholar] [CrossRef] [Green Version]
- Green, S.; Bevan, A.; Shapland, M. A comparative assessment of structure from motion methods for archaeological research. J. Archaeol. Sci. 2014, 46, 173–181. [Google Scholar] [CrossRef]
- Abbas, M.A.; Setan, H.; Majid, Z.; Chong, A.K.; Idris, K.M.; Aspuri, A. Calibration and Accuracy Assessment of Leica ScanStation C10 Terrestrial Laser Scanner. In Lecture Notes in Geoinformation and Cartography; Springer: Berlin/Heidelberg, Germany, 2013; pp. 33–47. [Google Scholar]
- Abbas, M.A.; Setan, H.; Majid, Z.; Lichti, D.D.; Chong, A.K. A self-calibration of the Leica ScanStation C10 scanner. In Proceedings of the 2013 IEEE Business Engineering and Industrial Applications Colloquium (BEIAC), Kuala Lumpur. Malaysia, 22–25 September 2013; pp. 262–266. [Google Scholar]
- Genta, G.; Minetola, P.; Barbato, G. Calibration procedure for a laser triangulation scanner with uncertainty evaluation. Opt. Lasers Eng. 2016, 86, 11–19. [Google Scholar] [CrossRef]
- Son, S.; Park, H.; Lee, K.H. Automated laser scanning system for reverse engineering and inspection. Int. J. Mach. Tools Manuf. 2002, 42, 889–897. [Google Scholar] [CrossRef]
- Gong, Z.; Wen, C.; Wang, C.; Li, J. A Target-Free Automatic Self-Calibration Approach for Multibeam Laser Scanners. IEEE Trans. Instrum. Meas. 2018, 67, 238–240. [Google Scholar] [CrossRef]
- Gašparović, M.; Malarić, I. Increase of readability and accuracy of 3D models using fusion of close range photogrammetry and laser scanning. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, XXXIX-B5, 93–98. [Google Scholar] [CrossRef] [Green Version]
- Yu, C.; Chen, X.; Xi, J. Modeling and Calibration of a Novel One-Mirror Galvanometric Laser Scanner. Sensors 2017, 17, 164. [Google Scholar] [CrossRef] [Green Version]
- Mukupa, W.; Roberts, G.W.; Hancock, C.M.; Al-Manasir, K. A review of the use of terrestrial laser scanning application for change detection and deformation monitoring of structures. Surv. Rev. 2017, 49, 99–116. [Google Scholar] [CrossRef]
- Baraccani, S.; Silvestri, S.; Gasparini, G.; Palermo, M.; Trombetti, T.; Silvestri, E.; Lancellotta, R.; Capra, A. A Structural Analysis of the Modena Cathedral. Int. J. Archit. Herit. 2016, 10, 235–253. [Google Scholar] [CrossRef]
- Pesci, A.; Teza, G.; Bonali, E.; Casula, G.; Boschi, E. A laser scanning-based method for fast estimation of seismic-induced building deformations. ISPRS J. Photogramm. Remote Sens. 2013, 79, 185–198. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, J.; Lindenbergh, R.; Hofland, B.G.; Ferreira, V. Range Image Technique for Change Analysis of Rock Slopes Using Dense Point Cloud Data. Remote Sens. 2018, 10, 1792. [Google Scholar] [CrossRef] [Green Version]
- Xu, H.; Li, H.; Yang, X.; Qi, S.; Zhou, J. Integration of Terrestrial Laser Scanning and NURBS Modeling for the Deformation Monitoring of an Earth-Rock Dam. Sensors 2018, 19, 22. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vezočnik, R.; Ambrožič, T.; Sterle, O.; Bilban, G.; Pfeifer, N.; Stopar, B. Use of Terrestrial Laser Scanning Technology for Long Term High Precision Deformation Monitoring. Sensors 2009, 9, 9873–9895. [Google Scholar] [CrossRef] [PubMed]
- Cortés-Sánchez, M.; Riquelme-Cantal, J.A.; Simón-Vallejo, M.D.; Parrilla Giráldez, R.; Odriozola, C.P.; Calle Román, L.; Carrión, J.S.; Monge Gómez, G.; Rodríguez Vidal, J.; Moyano Campos, J.J.; et al. Pre-Solutrean rock art in southernmost Europe: Evidence from Las Ventanas Cave (Andalusia, Spain). PLoS ONE 2018, 13, e0204651. [Google Scholar] [CrossRef] [Green Version]
- Lerma, J.L.; Navarro, S.; Cabrelles, M.; Villaverde, V. Terrestrial laser scanning and close range photogrammetry for 3D archaeological documentation: The Upper Palaeolithic Cave of Parpalló as a case study. J. Archaeol. Sci. 2010, 37, 499–507. [Google Scholar] [CrossRef]
- Pérez Zapata, C. Estudio Comparativo de Sistemas para la Adquisición de Datos Métricos en Rehabilitación. In Proceedings of the CD-ROM Libro de Actas I Jornada Nacional de Investigación en la Edificación, Madrid, Spain, 5 October–5 November 2007; pp. 1–12. [Google Scholar]
- Ding, Y.; Zheng, X.; Zhou, Y.; Xiong, H.; Gong, J. Low-Cost and Efficient Indoor 3D Reconstruction Through Annotated Hierarchical Structure-from-Motion. Remote Sens. 2018, 11, 58. [Google Scholar] [CrossRef] [Green Version]
- Furukawa, Y.; Curless, B.; Seitz, S.M.; Szeliski, R. Reconstructing building interiors from images. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 27 September–4 October 2009; pp. 80–87. [Google Scholar]
- Molero Alonso, B.; Barba, S.; Álvaro Tordesillas, A. Documentación del patrimonio cultural. Método basado en la fusión de técnicas fotogramétricas y de escaneado óptico de triangulación. EGA. Rev. expresión gráfica Arquit. 2016, 21, 236. [Google Scholar] [CrossRef] [Green Version]
- Kersten, T.P.; Lindstaedt, M. Image-Based Low-Cost Systems for Automatic 3D Recording and Modelling of Archaeological Finds and Objects. In Progress in Cultural Heritage Preservation; Springer: Berlin/Heidelberg, Germany, 2012; pp. 1–10. [Google Scholar]
- Chiabrando, F.; Nex, F.; Piatti, D.; Rinaudo, F. UAV and RPV systems for photogrammetric surveys in archaelogical areas: Two tests in the Piedmont region (Italy). J. Archaeol. Sci. 2011, 38, 697–710. [Google Scholar] [CrossRef]
- Colomina, I.; Molina, P. Unmanned aerial systems for photogrammetry and remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2014, 92, 79–97. [Google Scholar] [CrossRef] [Green Version]
- Haala, N. The Landscape of Dense Image Matching Algorithms. Photogramm. Week 2013 2013, 271–284. [Google Scholar]
- Nex, F.; Remondino, F. UAV for 3D mapping applications: A review. Appl. Geomatics 2014, 6, 1–15. [Google Scholar] [CrossRef]
- Nikolakopoulos, K.G.; Soura, K.; Koukouvelas, I.K.; Argyropoulos, N.G. UAV vs. classical aerial photogrammetry for archaeological studies. J. Archaeol. Sci. Reports 2017, 14, 758–773. [Google Scholar] [CrossRef]
- Barba, S.; Barbarella, M.; Di Benedetto, A.; Fiani, M.; Gujski, L.; Limongiello, M. Accuracy Assessment of 3D Photogrammetric Models from an Unmanned Aerial Vehicle. Drones 2019, 3, 79. [Google Scholar] [CrossRef] [Green Version]
- Kraus, K. Photogrammetry: Geometry from Images and Laser Scans, 2nd ed.; De Gruyter: Vienna, Austria, 2007. [Google Scholar]
- Agüera-Vega, F.; Carvajal-Ramírez, F.; Martínez-Carricondo, P. Accuracy of digital surface models and orthophotos derived from unmanned aerial vehicle photogrammetry. J. Surv. Eng. 2017, 143, 04016025. [Google Scholar] [CrossRef]
- Harwin, S.; Lucieer, A. Assessing the Accuracy of Georeferenced Point Clouds Produced via Multi-View Stereopsis from Unmanned Aerial Vehicle (UAV) Imagery. Remote Sens. 2012, 4, 1573–1599. [Google Scholar] [CrossRef] [Green Version]
- Pádua, L.; Adão, T.; Hruška, J.; Marques, P.; Sousa, A.; Morais, R.; Lourenço, J.M.; Sousa, J.J.; Peres, E. UAS-based photogrammetry of cultural heritage sites: A case study addressing Chapel of Espírito Santo and photogrammetric software comparison. In Proceedings of the ACM International Conference Proceeding Series, Osaka, Japan, 6–8 January 2018; pp. 72–76. [Google Scholar]
- Snavely, N.; Seitz, S.M.; Szeliski, R. Modeling the world from Internet photo collections. Int. J. Comput. Vis. 2008, 80, 189–210. [Google Scholar] [CrossRef] [Green Version]
- Pollefeys, M.R.K.; Gool, L.V. Realistic Surface Reconstruction of 3{D} Scenes from Uncalibrated Image Sequences. J. Vis. Comput. Animat. 2000, 11, 115–127. [Google Scholar] [CrossRef]
- Reu, J.; Plets, G.; Verhoeven, G.; Smedt, P.; Bats, M.; Cherretté, B.; Maeyer, W.; Deconynck, J.; Herremans, D.; Laloo, P.; et al. Towards a three-dimensional cost-effective registration of the archaeological heritage. J. Archaeol. Sci. 2013, 40, 1108–1121. [Google Scholar] [CrossRef]
- Doneus, M.; Verhoeven, G.; Fera, M.; Briese, C.; Kucera, M.; Neubauer, W. From Deposit to Point Cloud—A Study of Low-Cost Computer Vision Approaches for the Straightforward Documentation of Archaeological Excavations. Geoinformatics FCE CTU 2011, 6, 81–88. [Google Scholar] [CrossRef] [Green Version]
- Ippoliti, E.; Meschini, A.; Sicuranza, F. Structure from motion systems for architectural heritage. A survey of the internal loggia courtyard of palazzo dei capitani, ascoli piceno, italy. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. ISPRS Arch. 2015, 40, 53–60. [Google Scholar] [CrossRef] [Green Version]
- Sapirstein, P. Accurate measurement with photogrammetry at large sites. J. Archaeol. Sci. 2016, 66, 137–145. [Google Scholar] [CrossRef]
- Fraser, C.S.; Brown, D.C. Industrial Photogrammetry: New developments and recent applications. Photogramm. Rec. 2006, 12, 197–217. [Google Scholar] [CrossRef]
- Remondino, F.; Nocerino, E.; Toschi, I.; Menna, F. A critical review of automated photogrammetric processing of large datasets. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences—ISPRS, Ottawa, ON, Canada, 28 August–1 September 2017; Volume XLII-2-W5, pp. 591–599. [Google Scholar]
- Dai, S.-L.; Lin, H.; Ge, S.S. Scheduling-and-Control Codesign for a Collection of Networked Control Systems With Uncertain Delays. IEEE Trans. Control Syst. Technol. 2010, 18, 66–78. [Google Scholar] [CrossRef]
- De Reu, J.; De Clercq, W.; De Smedt, P.; Laloo, P.; Van Meirvenne, M.; Herremans, D. On introducing an image-based 3D reconstruction method in archaeological excavation practice. J. Archaeol. Sci. 2013, 41, 251–262. [Google Scholar] [CrossRef]
- Olson, B.R.; Placchetti, R.A.; Quartermaine, J.; Killebrew, A.E. The Tel Akko Total Archaeology Project (Akko, Israel): Assessing the suitability of multi-scale 3D field recording in archaeology. J. Field Archaeol. 2013, 38, 244–262. [Google Scholar] [CrossRef]
- Dellepiane, M.; Lindgren, S.; Callieri, M.; Scopigno, R.; Dellepiane, M. Archeological excavation monitoring using dense stereo matching techniques. J. Cult. Herit. 2012, 14, 201–210. [Google Scholar] [CrossRef]
- Martínez, S.; Ortiz, J.; Gil, M.L. Geometric documentation of historical pavements using automated digital photogrammetry and high-density reconstruction algorithms. J. Archaeol. Sci. 2015, 53, 1–11. [Google Scholar] [CrossRef]
- Lerma, J.L.; Muir, C. Evaluating the 3D documentation of an early Christian upright stone with carvings from Scotland with multiples images. J. Archaeol. Sci. 2014, 46, 311–318. [Google Scholar] [CrossRef]
- Jennings, A.; Black, J. Texture-Based Photogrammetry Accuracy on Curved Surfaces. AIAA J. 2012, 50, 1060–1071. [Google Scholar] [CrossRef]
- Barazzetti, L.; Mussio, L.; Remondino, F.; Scaioni, M. Targetless Camera Calibration. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, XXXVIII-5/W16, 335–342. [Google Scholar] [CrossRef] [Green Version]
- Fraser, C.S.; Woods, A.; Brizzi, D. Hyper redundancy for accuracy enhancement in automated close range photogrammetry. Photogramm. Rec. 2005, 20, 205–217. [Google Scholar] [CrossRef]
- Koutsoudis, A.; Vidmar, B.; Ioannakis, G.; Arnaoutoglou, F.; Pavlidis, G.; Chamzas, C. Multi-image 3D reconstruction data evaluation. J. Cult. Herit. 2014, 15, 73–79. [Google Scholar] [CrossRef]
- Remondino, F.; Baltsavias, E.; El-Hakim, S.; Picard, M.; Grammatikopoulos, L. Image-Based 3D Modeling of the Erechteion, Acropolis of Athens. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 1083–1092. [Google Scholar]
- Remondino, F.; Girardi, S.; Rizzi, A.; Gonzo, L. 3D modeling of complex and detailed cultural heritage using multi-resolution data. J. Comput. Cult. Herit. 2009, 2, 1–20. [Google Scholar] [CrossRef]
- Bernal, A.A. El origen de la Casa de Pilatos de Sevilla. 1483–1505. Atrio. Rev. Hist. Arte 2011, 17, 133–172. [Google Scholar]
- Lleó Cañal, V. La Casa de Pilatos. Actes Colloquie Tenue Tours 1994, 6, 181–192. [Google Scholar]
- Geosystems Leica Geosystems. Leica FlexLine TS02/TS06/TS09 User Manual. 2008. Available online: https://leica-geosystems.com/ (accessed on 16 March 2020).
- Krishnan, J.V.G.; Manoharan, N.; Rani, B.S. Estimation of Distance to Texture Surface Using Complex Log Mapping. J. Comput. Appl. 2010, 3, 16. [Google Scholar]
- Campos, M.; Tommaselli, A.; Ivánová, I.; Billen, R. Data Product Specification Proposal for Architectural Heritage Documentation with Photogrammetric Techniques: A Case Study in Brazil. Remote Sens. 2015, 7, 13337–13363. [Google Scholar] [CrossRef] [Green Version]
- Sanz-Ablanedo, E.; Chandler, J.; Rodríguez-Pérez, J.; Ordóñez, C. Accuracy of Unmanned Aerial Vehicle (UAV) and SfM Photogrammetry Survey as a Function of the Number and Location of Ground Control Points Used. Remote Sens. 2018, 10, 1606. [Google Scholar] [CrossRef] [Green Version]
- Agisoft LLC. 11 Degtyarniy per., St. Petersburg, Russia, 191144. 2006. Available online: https://www.agisoft.com/about/ (accessed on 18 March 2020).
- Leachtenauer, J.C.; Driggers, R.G. Surveillance and Reconnaissance Imaging Systems: Modeling and Performance Prediction; Artech House: Norwood, MA, USA, 2001. [Google Scholar]
- Gonçalves, J.A.; Henriques, R. UAV photogrammetry for topographic monitoring of coastal areas. ISPRS J. Photogramm. Remote Sens. 2015, 104, 101–111. [Google Scholar] [CrossRef]
- Szeliski, R. Computer Vision: Algorithms and Applications; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Wang, H.; Li, J.; Wang, L.; Guan, H.; Geng, Z. Automated mosaicking of UAV images based on SFM method. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Quebec, QC, Canada, 13–18 July 2014; pp. 2633–2636. [Google Scholar]
- Sanz-Ablanedo, E.; Rodríguez-Pérez, J.R.; Armesto, J.; Taboada, M.F.Á. Geometric Stability and Lens Decentering in Compact Digital Cameras. Sensors 2010, 10, 1553–1572. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Geosystems, L. Leica ScanStation C10. Available online: http://w3.leica-geosystems.com/downloads123/hds/hds/scanstation c10/brochures-datasheet/leica_scanstation_c10_ds_en.pdf (accessed on 16 March 2020).
- Moon, D.; Chung, S.; Kwon, S.; Seo, J.; Shin, J. Comparison and utilization of point cloud generated from photogrammetry and laser scanning: 3D world model for smart heavy equipment planning. Autom. Constr. 2019, 98, 322–331. [Google Scholar] [CrossRef]
- Geosystems, L. Leica Cyclone REGISTER 360-3D Laser Scanning Point Cloud Registration Software; Leica Geosystems AG: Heerbrugg, Switzerland, 2018. [Google Scholar]
- Daniel Girardeau-Montaut, D. CloudCompare: 3D Point Cloud and Mesh Processing Software. Open Source Project 2016. Available online: https://www.danielgm.net/index.php (accessed on 9 May 2019).
- Kazhdan, M.; Hoppe, H. Screened poisson surface reconstruction. ACM Trans. Graph. 2013, 32, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Robert McNeel & Associates Rhinoceros. Available online: https://www.rhino3d.com/ (accessed on 27 March 2020).
- Stamatopoulos, C.; Fraser, C.S. Automated target-free network orientation and camera calibration. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 2, 339–346. [Google Scholar] [CrossRef] [Green Version]
- Rajendra, Y.D.; Mehrotra, S.C.; Kale, K.V.; Manza, R.R.; Dhumal, R.K.; Nagne, A.D.; Vibhute, D.; Ramanujan, S.; Chair, G. Evaluation of Partially Overlapping 3D Point Cloud’s Registration by using ICP variant and CloudCompare. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, XL-8, 891–897. [Google Scholar] [CrossRef] [Green Version]
- Antón, D.; Medjdoub, B.; Shrahily, R.; Moyano, J. Accuracy evaluation of the semi-automatic 3D modeling for historical building information models. Int. J. Archit. Herit. 2018, 12, 790–805. [Google Scholar] [CrossRef] [Green Version]
- Arias, P.; Ordóñez, C.; Lorenzo, H.; Herraez, J. Methods for documenting historical agro-industrial buildings: A comparative study and a simple photogrammetric method. J. Cult. Herit. 2006, 7, 350–354. [Google Scholar] [CrossRef]
- Jalandoni, A.; Domingo, I.; Taçon, P.S.C. Testing the value of low-cost Structure-from-Motion (SfM) photogrammetry for metric and visual analysis of rock art. J. Archaeol. Sci. Reports 2018, 17, 605–616. [Google Scholar] [CrossRef]
- Barazzetti, L.; Fangi, G.; Remondino, F.; Scaioni, M. Automation in multi-image spherical photogrammetry for 3D architectural reconstructions. In VAST: International Symposium on Virtual Reality, Archaeology and Intelligent Cultural Heritage—Short and Project Papers; The Eurographics Association: Goslar, Germany, 2010. [Google Scholar]
- Barazzetti, L.; Previtali, M.; Roncoroni, F. Can we use low-cost 360 degree cameras to create accurate 3D models? Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, XLII-2, 69–75. [Google Scholar] [CrossRef] [Green Version]
- Burns, J.H.R.; Delparte, D. Comparison of commercial structure-from-motion photogrammety software used for underwater three-dimensional modeling of coral reef environments. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences—ISPRS Archives, Wuhan, China, 18–22 September 2017; Volume 42, pp. 127–131. [Google Scholar]
- Tagle, X.; Zabala, S. Workflow Agisoft Photoscan for Micasense Rededge Images. 2017. Available online: https://www.researchgate.net/profile/Ximena_Tagle/publication/320134833_Workflow_Agisoft_Photoscan_for_Micasense_Rededge_images/links/59cfe795a6fdcc181ace0866/Workflow-Agisoft-Photoscan-for-Micasense-Rededge-images.pdf (accessed on 27 March 2020).
- McCarthy, J. Multi-image photogrammetry as a practical tool for cultural heritage survey and community engagement. J. Archaeol. Sci. 2014, 43, 175–185. [Google Scholar] [CrossRef]
- Garagnani, S.; Manferdini, A.M. Parametric accuracy: Building information modeling process applied to the cultural heritage preservation. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, 40, 87–92. [Google Scholar] [CrossRef] [Green Version]


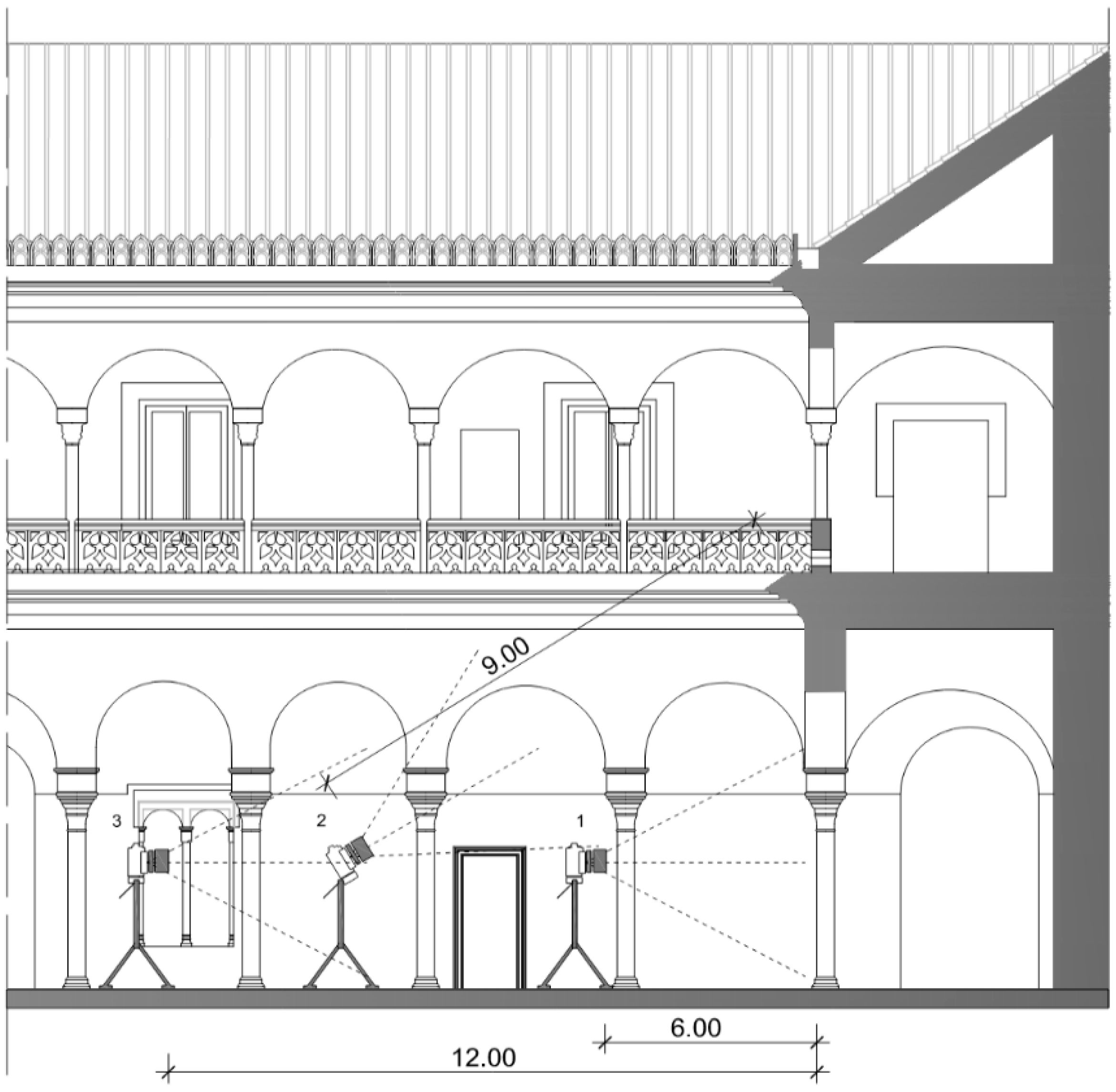







| Shooting Series | 0.20 W | GSDs (mm) | ||
|---|---|---|---|---|
| Series 1 | 6.00 | 7.86 | 1.57 | 2.71 |
| Series 2 | 9.00 | 11.80 | 2.36 | 4.07 |
| Series 3 | 12.00 | 15.73 | 3.14 | 5.42 |
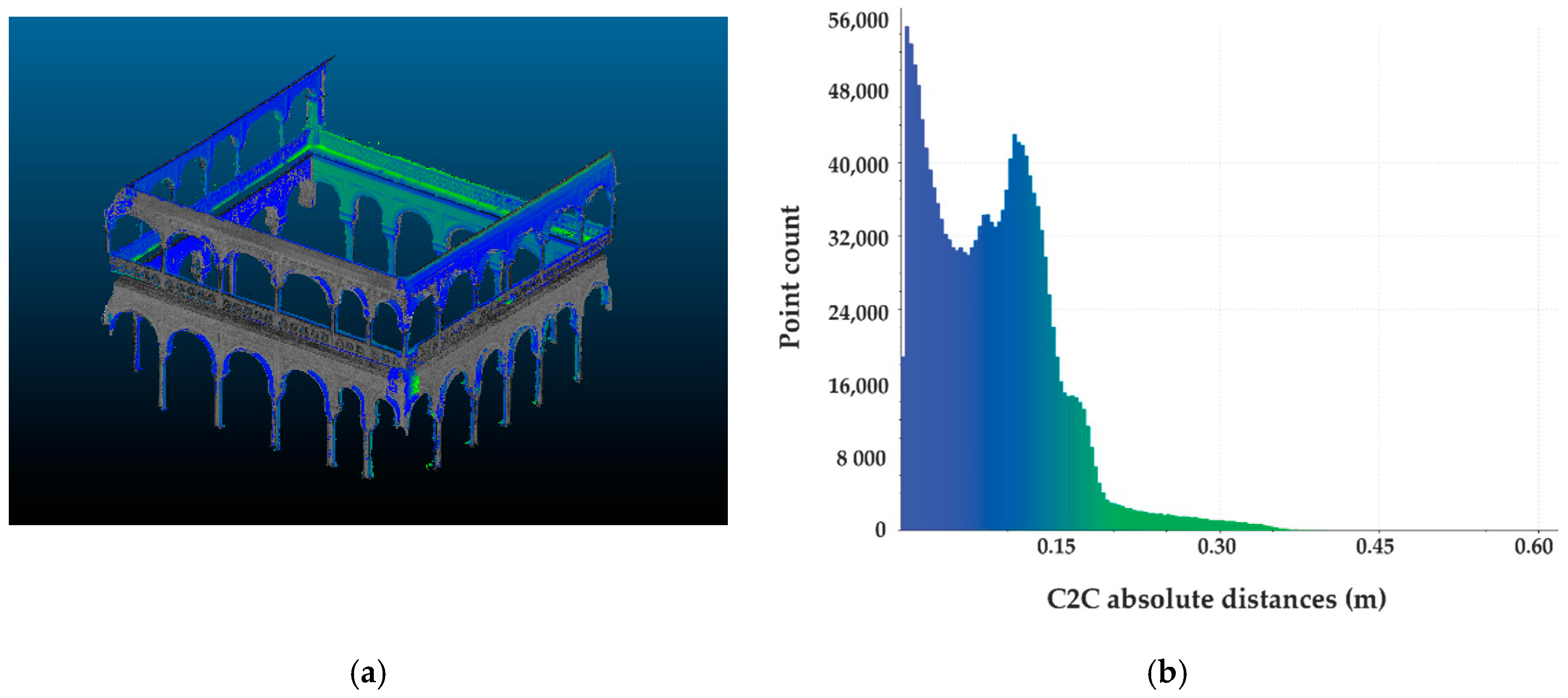
| Survey A | Standard Deviation (σ) | RMS | Minimum Distance (m) | Maximum Distance (m) | Average Distance (m) | Estimated Standard Error (m) |
|---|---|---|---|---|---|---|
| Northeast | 0.0581 | 0.1104 | 0 | 0.4044 | 0.0939 | 0.0450 |
| Northwest | 0.0576 | 0.1016 | 0 | 0.4056 | 0.0838 | 0.0485 |
| Southeast | 0.0422 | 0.0638 | 0 | 0.3191 | 0.0479 | 0.0412 |
| Southwest | 0.0539 | 0.1350 | 0 | 0.3650 | 0.1238 | 0.0521 |
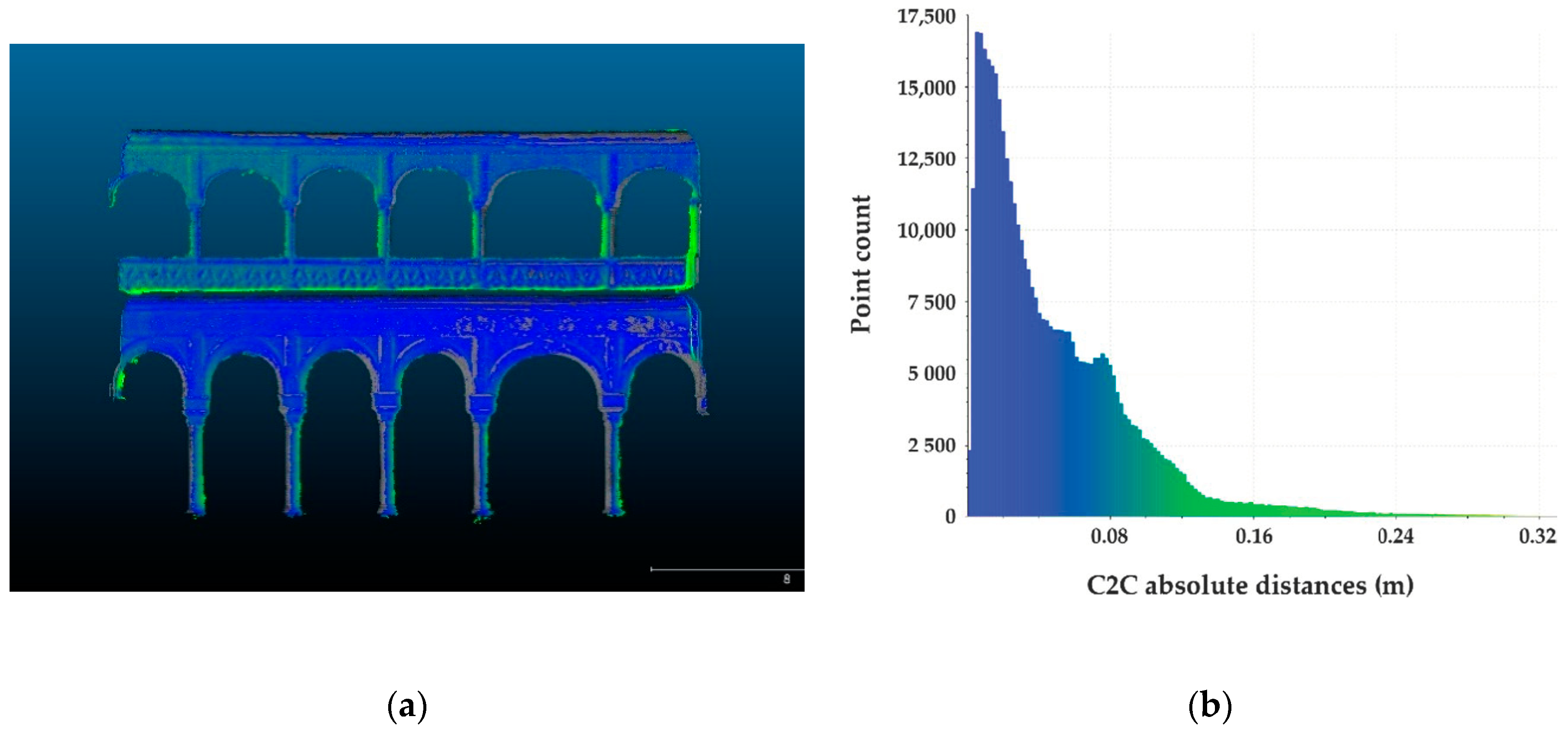
| Survey B | Standard Deviation (σ) (m) | RMS (m) | Minimum Distance (m) | Maximum Distance (m) | Average Distance (m) | Estimated Standard Error (m) |
|---|---|---|---|---|---|---|
| Northeast | 0.0104 | 0.0314 | 0.0000 | 0.2190 | 0.0009 | 0.0551 |
| Northwest | 0.0013 | 0.0453 | 0.0000 | 0.2635 | 0.0013 | 0.0537 |
| Southeast | 0.0094 | 0.0540 | 0.0000 | 0.3542 | 0.0008 | 0.0541 |
| Southwest | 0.0010 | 0.0559 | 0.0000 | 0.4600 | 0.0010 | 0.0565 |
| Resolution | Points | Nº Images | Error (m) | |
|---|---|---|---|---|
| Survey A | 2896 × 1944 | 21,973,146 | 99 | 0.21339 |
| Survey B | 2896 × 1944 | 1,658,794 | 167 | 0.00345 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moyano, J.; Nieto-Julián, J.E.; Antón, D.; Cabrera, E.; Bienvenido-Huertas, D.; Sánchez, N. Suitability Study of Structure-from-Motion for the Digitisation of Architectural (Heritage) Spaces to Apply Divergent Photograph Collection. Symmetry 2020, 12, 1981. https://doi.org/10.3390/sym12121981
Moyano J, Nieto-Julián JE, Antón D, Cabrera E, Bienvenido-Huertas D, Sánchez N. Suitability Study of Structure-from-Motion for the Digitisation of Architectural (Heritage) Spaces to Apply Divergent Photograph Collection. Symmetry. 2020; 12(12):1981. https://doi.org/10.3390/sym12121981
Chicago/Turabian StyleMoyano, Juan, Juan E. Nieto-Julián, Daniel Antón, Elena Cabrera, David Bienvenido-Huertas, and Nazareth Sánchez. 2020. "Suitability Study of Structure-from-Motion for the Digitisation of Architectural (Heritage) Spaces to Apply Divergent Photograph Collection" Symmetry 12, no. 12: 1981. https://doi.org/10.3390/sym12121981
APA StyleMoyano, J., Nieto-Julián, J. E., Antón, D., Cabrera, E., Bienvenido-Huertas, D., & Sánchez, N. (2020). Suitability Study of Structure-from-Motion for the Digitisation of Architectural (Heritage) Spaces to Apply Divergent Photograph Collection. Symmetry, 12(12), 1981. https://doi.org/10.3390/sym12121981









