Secure w-Domination in Graphs

Abstract

This paper introduces a general approach to the idea of protection of graphs, which encompasses the known variants of secure domination and introduces new ones. Specifically, we introduce the study of secure w-domination in graphs, where $w=(w_0,w_1,\dots ,w_l)$ is a vector of nonnegative integers such that $w_0\ge 1$. The secure w-domination number is defined as follows. Let G be a graph and $N\left(v\right)$ the open neighborhood of $v\in V\left(G\right)$. We say that a function $f:V\left(G\right)⟶\{0,1,\dots ,l\}$ is a w-dominating function if $f\left(N\left(v\right)\right)={\sum }_{u\in N\left(v\right)}f\left(u\right)\ge w_i$ for every vertex v with $f\left(v\right)=i$. The weight of f is defined to be $\omega \left(f\right)={\sum }_{v\in V\left(G\right)}f\left(v\right)$. Given a w-dominating function f and any pair of adjacent vertices $v,u\in V\left(G\right)$ with $f\left(v\right)=0$ and $f\left(u\right)>0$, the function $f_{u\to v}$ is defined by $f_{u\to v}\left(v\right)=1$, $f_{u\to v}\left(u\right)=f\left(u\right)-1$ and $f_{u\to v}\left(x\right)=f\left(x\right)$ for every $x\in V\left(G\right)\backslash \{u,v\}$. We say that a w-dominating function f is a secure w-dominating function if for every v with $f\left(v\right)=0$, there exists $u\in N\left(v\right)$ such that $f\left(u\right)>0$ and $f_{u\to v}$ is a w-dominating function as well. The secure w-domination number of G, denoted by ${\gamma }_w^s\left(G\right)$, is the minimum weight among all secure w-dominating functions. This paper provides fundamental results on ${\gamma }_w^s\left(G\right)$ and raises the challenge of conducting a detailed study of the topic.

1. Introduction

Let ${\mathbb{Z}}^{+}=\{1,2,3,\dots \}$ and $\mathbb{N}={\mathbb{Z}}^{+}\cup \left\{0\right\}$ be the sets of positive and nonnegative integers, respectively. Let G be a graph, $l\in {\mathbb{Z}}^{+}$ and $f:V\left(G\right)⟶\{0,\dots ,l\}$ a function. Let $V_i=\{v\in V\left(G\right):f\left(v\right)=i\}$ for every $i\in \{0,\dots ,l\}$. We identify f with the subsets $V_0,\dots ,V_l$ associated with it, and thus we use the unified notation $f(V_0,\dots ,V_l)$ for the function and these associated subsets. The weight of f is defined to be

$$\omega \left(f\right)=f\left(V\left(G\right)\right)=\sum _{i=1}^{l}i\left|V_i\right|.$$

Let $w=(w_0,\dots ,w_l)\in {\mathbb{Z}}^{+}\times {\mathbb{N}}^l$ such that $w_0\ge 1$. As defined in [1], a function $f(V_0,\dots ,V_l)$ is a w-dominating function if $f\left(N\left(v\right)\right)\ge w_i$ for every $v\in V_i$. The w-domination number of G, denoted by ${\gamma }_w\left(G\right)$, is the minimum weight among all w-dominating functions. For simplicity, a w-dominating function f of weight $\omega \left(f\right)={\gamma }_w\left(G\right)$ is called a ${\gamma }_w\left(G\right)$-function. For fundamental results on the w-domination number of a graph, we refer the interested readers to the paper by Cabrera et al. [1], where the theory of w-domination in graphs is introduced.

The definition of w-domination number encompasses the definition of several well-known domination parameters and introduces new ones. For instance, we highlight the following particular cases of known domination parameters that we define here in terms of w-domination: the domination number $\gamma \left(G\right)={\gamma }_{(1,0)}\left(G\right)={\gamma }_{(1,0,\dots ,0)}\left(G\right)$, the total domination number ${\gamma }_t\left(G\right)={\gamma }_{(1,1)}\left(G\right)={\gamma }_{(1,\dots ,1)}\left(G\right)$, the k-domination number ${\gamma }_k\left(G\right)={\gamma }_{(k,0)}\left(G\right)$, the k-tuple domination number ${\gamma }_{\times k}\left(G\right)={\gamma }_{(k,k-1)}\left(G\right)$, the k-tuple total domination number ${\gamma }_{\times k,t}\left(G\right)={\gamma }_{(k,k)}\left(G\right)$, the Italian domination number ${\gamma }_I\left(G\right)={\gamma }_{(2,0,0)}\left(G\right)$, the total Italian domination number ${\gamma }_{tI}\left(G\right)={\gamma }_{(2,1,1)}\left(G\right)$, and the $\left\{k\right\}$-domination number ${\gamma }_{\left\{k\right\}}\left(G\right)={\gamma }_{(k,k-1,\dots ,0)}\left(G\right)$. In these definitions, the appropriate restrictions on the minimum degree of G are assumed, when needed.

For any function $f(V_0,\dots ,V_l)$ and any pair of adjacent vertices $v\in V_0$ and $u\in V\left(G\right)\backslash V_0$, the function $f_{u\to v}$ is defined by $f_{u\to v}\left(v\right)=1$, $f_{u\to v}\left(u\right)=f\left(u\right)-1$ and $f_{u\to v}\left(x\right)=f\left(x\right)$ whenever $x\in V\left(G\right)\backslash \{u,v\}$.

We say that a w-dominating function $f(V_0,\dots ,V_l)$ is a securew-dominating function if for every $v\in V_0$ there exists $u\in N\left(v\right)\backslash V_0$ such that $f_{u\to v}$ is a w-dominating function as well. The securew-domination number of G, denoted by ${\gamma }_w^s\left(G\right)$, is the minimum weight among all secure w-dominating functions. For simplicity, a secure w-dominating function f of weight $\omega \left(f\right)={\gamma }_w^s\left(G\right)$ is called a ${\gamma }_w^s\left(G\right)$-function. This approach to the theory of secure domination covers the different versions of secure domination known so far. For instance, we emphasize the following cases of known parameters that we define here in terms of secure w-domination.

• The secure domination number of G is defined to be ${\gamma }_s\left(G\right)={\gamma }_{(1,0)}^s\left(G\right)$. In this case, for any secure $(1,0)$-dominating function $f(V_0,V_1)$, the set $V_1$ is known as a secure dominating set. This concept was introduced by Cockayne et al. [2] and studied further in several papers (e.g., [3,4,5,6,7,8,9]).
• The secure total domination number of a graph G of minimum degree at least one is defined to be ${\gamma }_{st}\left(G\right)={\gamma }_{(1,1)}^s\left(G\right)$. In this case, for any secure $(1,1)$-dominating function $f(V_0,V_1)$, the set $V_1$ is known as a secure total dominating set of G. This concept was introduced by Benecke et al. [10] and studied further in several papers (e.g., [7,11,12,13,14]).
• The weak Roman domination number of a graph G is defined to be ${\gamma }_r\left(G\right)={\gamma }_{(1,0,0)}^s\left(G\right)$. This concept was introduced by Henning and Hedetniemi [15] and studied further in several papers (e.g., [5,6,16,17]).
• The total weak Roman domination number of a graph G of minimum degree at least one is defined to be ${\gamma }_{tr}\left(G\right)={\gamma }_{(1,1,1)}^s\left(G\right)$. This concept was introduced by Cabrera et al. in [12] and studied further in [18].
• The secure Italian domination number of G is defined to be ${\gamma }_{{}_I}^s\left(G\right)={\gamma }_{(2,0,0)}^s\left(G\right)$. This parameter was introduced by Dettlaff et al. [19].

For the graphs shown in Figure 1, we have the following:

• $$\begin{gathered} {\gamma }_{(1,1)}^s\left(G_1\right)={\gamma }_{(2,0)}^s\left(G_1\right)={\gamma }_{(2,1)}^s\left(G_1\right)={\gamma }_{(2,0)}\left(G_1\right)={\gamma }_{(2,1)}{G}_1)={\gamma }_{(1,1,0)}^s\left(G_1\right)={\gamma }_{(1,1,1)}^s\left(G_1\right)= \\ {\gamma }_{(2,0,0)}^s\left(G_1\right)={\gamma }_{(2,1,0)}^s\left(G_1\right)={\gamma }_{(2,0,0)}\left(G_1\right)={\gamma }_{(2,1,0)}\left(G_1\right)={\gamma }_{(2,2,0)}\left(G_1\right)={\gamma }_{(2,2,1)}\left(G_1\right)= \\ {\gamma }_{(2,2,2)}\left(G_1\right)=4\mathrm{and}{\gamma }_{(2,2)}^s\left(G_1\right)={\gamma }_{(2,2)}\left(G_1\right)={\gamma }_{(2,2,0)}^s\left(G_1\right)={\gamma }_{(2,2,1)}^s\left(G_1\right)={\gamma }_{(2,2,2)}^s\left(G_1\right)= \\ {\gamma }_{(3,0,0)}^s\left(G_1\right)={\gamma }_{(3,1,0)}^s\left(G_1\right)={\gamma }_{(3,1,1)}^s\left(G_1\right)={\gamma }_{(3,2,0)}^s\left(G_1\right)={\gamma }_{(3,2,1)}^s\left(G_1\right)={\gamma }_{(3,2,2)}^s\left(G_1\right)= \\ {\gamma }_{(3,0,0)}\left(G_1\right)={\gamma }_{(3,1,0)}\left(G_1\right)={\gamma }_{(3,1,1)}\left(G_1\right)={\gamma }_{(3,2,0)}\left(G_1\right)={\gamma }_{(3,2,1)}\left(G_1\right)={\gamma }_{(3,2,2)}\left(G_1\right)=6. \end{gathered}$$
• ${\gamma }_{(1,1)}^s\left(G_2\right)={\gamma }_{(1,1,0)}^s\left(G_2\right)={\gamma }_{(1,1,1)}^s\left(G_2\right)={\gamma }_{(2,2,0)}\left(G_2\right)={\gamma }_{(2,2,1)}\left(G_2\right)={\gamma }_{(2,2,2)}\left(G_2\right)=3.$
• $$\begin{gathered} {\gamma }_{(1,1)}^s\left(G_3\right)={\gamma }_{(1,1,0)}^s\left(G_3\right)={\gamma }_{(1,1,1)}^s\left(G_3\right)={\gamma }_{(2,1,0)}\left(G_3\right)={\gamma }_{(3,0,0)}\left(G_3\right)=3<4={\gamma }_{(2,0,0)}^s\left(G_3\right)= \\ {\gamma }_{(2,1,0)}^s\left(G_3\right)={\gamma }_{(3,1,0)}^s\left(G_3\right)={\gamma }_{(2,2,0)}\left(G_3\right)={\gamma }_{(2,2,1)}\left(G_3\right)={\gamma }_{(2,2,2)}\left(G_3\right)={\gamma }_{(3,2,0)}\left(G_3\right)< \\ 5={\gamma }_{(2,2,0)}^s\left(G_3\right)={\gamma }_{(3,2,0)}^s\left(G_3\right)={\gamma }_{(2,2,1)}^s\left(G_3\right)={\gamma }_{(2,2,2)}^s\left(G_3\right)={\gamma }_{(3,1,1)}^s\left(G_3\right)={\gamma }_{(3,2,1)}^s\left(G_3\right)= \\ {\gamma }_{(3,2,1)}\left(G_3\right)={\gamma }_{(3,2,2)}\left(G_3\right)<6={\gamma }_{(3,2,2)}^s\left(G_3\right). \end{gathered}$$

This paper is devoted to providing general results on secure w-domination. We assume that the reader is familiar with the basic concepts, notation, and terminology of domination in graph. If this is not the case, we suggest the textbooks [20,21]. For the remainder of the paper, definitions are introduced whenever a concept is needed.

2. General Results on Secure $\mathit{w}$-Domination

Given a w-dominating function $f(V_0,\dots ,V_l)$, we introduce the following notation.

• Given $v\in V_0$, we define $M_f\left(v\right)=\{u\in V\left(G\right)\backslash V_0:f_{u\to v}\mathrm{as}\mathrm{a}w\text{-}\mathrm{dominating}\mathrm{function}\}$.
• ${\displaystyle {\mathcal{M}}_f\left(G\right)=\bigcup _{v\in V_0}{M}_f\left(v\right)}$.
• Given $u\in {\mathcal{M}}_f\left(G\right)$, we define $D_f\left(u\right)=\{v\in V_0:u\in M_f\left(v\right)\}$.
• Given $u\in {\mathcal{M}}_f\left(G\right)$, we define $T_f\left(u\right)=\{v\in V_0:u\in M_f\left(v\right)\mathrm{and}f\left(N\left(v\right)\right)=w_0\}$.

Obviously, if f is a secure w-dominating function, then $M_f\left(v\right)\ne ⌀$ for every $v\in V_0$.

Lemma 1.

Let f be a secure w-dominating function on a graph G, and let $u\in {\mathcal{M}}_f\left(G\right)$. If $T_f\left(u\right)\ne ⌀$, then each vertex belonging to $T_f\left(u\right)$ is adjacent to every vertex in $D_f\left(u\right)$ and, in particular, $G\left[T_f\left(u\right)\right]$ is a clique.

Proof. 

Since $T_f\left(u\right)\subseteq D_f\left(u\right)$, we only need to suppose the existence of two non-adjacent vertices $v\in T_f\left(u\right)$ and $v^{\prime }\in D_f\left(u\right)$ with $v\ne v^{\prime }$. In such a case, $f_{u\to v^{\prime }}\left(N\left(v\right)\right)<w_0$, which is a contradiction. Therefore, the result follows. □

Remark 1

([1]). Let G be a graph of minimum degree δ and let $w=(w_0,w_1,\dots ,w_l)\in {\mathbb{Z}}^{+}\times {\mathbb{N}}^l$. If $w_0\ge w_1\ge \cdots \ge w_l$, then there exists a w-dominating function on G if and only if $w_l\le l\delta .$

Throughout this section, we repeatedly apply, without explicit mention, the following necessary and sufficient condition for the existence of a secure w-dominating function on G.

Remark 2.

Let G be a graph of minimum degree δ and let $w=(w_0,w_1,\dots ,w_l)\in {\mathbb{Z}}^{+}\times {\mathbb{N}}^l$. If $w_0\ge w_1\ge \cdots \ge w_l$, then there exists a secure w-dominating function on G if and only if $w_l\le l\delta .$

Proof. 

If f is a secure w-dominating function on G, then f is a w-dominating function, and by Remark 1 we conclude that $w_l\le l\delta .$

Conversely, if $w_l\le l\delta$, then the function f, defined by $f\left(v\right)=l$ for every $v\in V\left(G\right)$, is a secure w-dominating function. Therefore, the result follows. □

It was shown by Cabrera et al. [1] that the w-domination numbers satisfy a certain monotonicity. Given two integer vectors $w=(w_0,\dots ,w_l)$ and $w^{\prime }=(w_0^{\prime },\dots ,w_l^{\prime })$, we say that $w^{\prime }\prec w$ if $w_i^{\prime }\le w_i$ for every $i\in \{0,\dots ,l\}$. With this notation in mind, we can state the next remark which is a direct consequence of the definition of w-dominating function.

Remark 3.

[1] Let G be a graph of minimum degree δ and let $w=(w_0,\dots ,w_l),w^{\prime }=(w_0^{\prime },\dots ,w_l^{\prime })\in {\mathbb{Z}}^{+}\times {\mathbb{N}}^l$ such that $w_i\ge w_{i+1}$ and $w_i^{\prime }\ge w_{i+1}^{\prime }$ for every $i\in \{0,\dots ,l-1\}$. If $w^{\prime }\prec w$ and $w_l\le l\delta$, then every w-dominating function is a $w^{\prime }$-dominating function and, as a consequence,

$${\gamma }_{w^{\prime }}\left(G\right)\le {\gamma }_w\left(G\right).$$

The monotonicity also holds for the case of secure w-domination.

Remark 4.

Let G be a graph of minimum degree δ and let $w=(w_0,\dots ,w_l),w^{\prime }=(w_0^{\prime },\dots ,w_l^{\prime })\in {\mathbb{Z}}^{+}\times {\mathbb{N}}^l$ such that $w_i\ge w_{i+1}$ and $w_i^{\prime }\ge w_{i+1}^{\prime }$ for every $i\in \{0,\dots ,l-1\}$. If $w^{\prime }\prec w$ and $w_l\le l\delta$, then every secure w-dominating function is a secure $w^{\prime }$-dominating function and, as a consequence,

$${\gamma }_{w^{\prime }}^s\left(G\right)\le {\gamma }_w^s\left(G\right).$$

Proof. 

For any ${\gamma }_w^s\left(G\right)$-function f and any $v\in V\left(G\right)$ with $f\left(v\right)=0$, there exists $u\in M_f\left(v\right)$. Since f and $f_{u\to v}$ are w-dominating functions, by Remark 3, we conclude that, if $w^{\prime }\prec w$ and $w_l\le l\delta$, then both f and $f_{u\to v}$ are $w^{\prime }$-dominating functions. Therefore, f is a secure $w^{\prime }$-dominating function and, as a consequence, ${\gamma }_{w^{\prime }}^s\left(G\right)\le \omega \left(f\right)={\gamma }_w^s\left(G\right).$ □

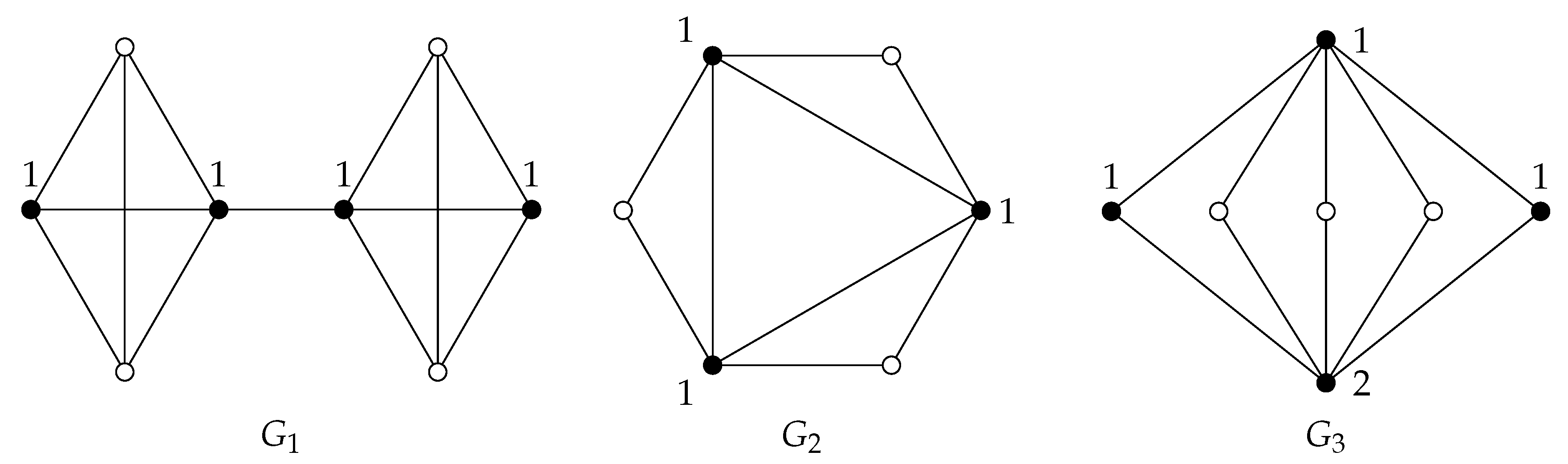
From the following equality chain, we obtain examples of equalities in Remark 4. Graph $G_1$ is illustrated in Figure 1.

$${\gamma }_{(3,0,0)}^s\left(G_1\right)={\gamma }_{(3,1,0)}^s\left(G_1\right)={\gamma }_{(3,2,0)}^s\left(G_1\right)={\gamma }_{(3,2,1)}^s\left(G_1\right)={\gamma }_{(3,2,2)}^s\left(G_1\right).$$

Theorem 1.

Let G be a graph of minimum degree δ, and let $w=(w_0,\dots ,w_l)\in {\mathbb{Z}}^{+}\times {\mathbb{N}}^l$ such that $w_i\ge w_{i+1}$ for every $i\in \{0,\dots ,l-1\}$. If $l\delta \ge w_l$, then the following statements hold.

(i) 

${\gamma }_w\left(G\right)\le {\gamma }_w^s\left(G\right).$

(ii)

If $k\in {\mathbb{Z}}^{+}$, then ${\gamma }_{(k+1,k=w_1,\dots ,w_l)}\left(G\right)\le {\gamma }_{(k,k=w_1,\dots ,w_l)}^s\left(G\right)$.

Proof. 

Since every secure w-dominating function on G is a w-dominating function on G, (i) follows.

Let $f(V_0,\dots ,V_l)$ be a ${\gamma }_{(k,k=w_1,\dots ,w_l)}^s\left(G\right)$-function. Since f is a $(k,k=w_1,\dots ,w_l)$-dominating function, $f\left(N\left(v\right)\right)\ge w_i$ for every $v\in V_i$ with $i\in \{1,\dots ,l\}$ and $w_1=k$. If $V_0=⌀$, then f is a $(k+1,k=w_1,\dots ,w_l)$-dominating function, which implies that ${\gamma }_{(k+1,k=w_1,\dots ,w_l)}\left(G\right)\le \omega \left(f\right)={\gamma }_{(k,k=w_1,\dots ,w_l)}^s\left(G\right)$. Assume $V_0\ne ⌀$. Let $v\in V_0$ and $u\in M_f\left(v\right)$. If $f\left(N\right(v\left)\right)=k$, then $f_{u\to v}\left(N\left(v\right)\right)=f\left(N\left(v\right)\right)-1=k-1$, which is a contradiction. Thus, $f\left(N\right(v\left)\right)\ge k+1$, which implies that f is a $(k+1,k=w_1,\dots ,w_l)$-dominating function. Therefore, ${\gamma }_{(k+1,k=w_1,\dots ,w_l)}\left(G\right)\le \omega \left(f\right)={\gamma }_{(k,k=w_1,\dots ,w_l)}^s\left(G\right)$, and (ii) follows. □

The inequalities above are tight. For instance, for any integers $n,n^{\prime }\ge 4$, we have that ${\gamma }_{(2,2,2)}(K_n+N_{n^{\prime }})={\gamma }_{(2,2,2)}^s(K_n+N_{n^{\prime }})=3$ and ${\gamma }_{(3,2,2)}\left(K_{2,n}\right)={\gamma }_{(2,2,2)}^s\left(K_{2,n}\right)=5$.

Corollary 1.

Let G be a graph of minimum degree δ and order n. Let $w=(w_0,\dots ,w_l)\in {\mathbb{Z}}^{+}\times {\mathbb{N}}^l$ such that $w_i\ge w_{i+1}$ for every $i\in \{0,\dots ,l-1\}$ and $l\delta \ge w_l$. The following statements hold.

(i)

If $n>w_0$, then ${\gamma }_w^s\left(G\right)\ge w_0$.

(ii)

If $n>w_0=w_1$, then ${\gamma }_w^s\left(G\right)\ge w_0+1$.

Proof. 

Assume $n>w_0$. By Theorem 1, we have that ${\gamma }_w^s\left(G\right)\ge {\gamma }_w\left(G\right)$. Now, if ${\gamma }_w\left(G\right)\le w_0-1<n-1$, then for any ${\gamma }_w\left(G\right)$-function f there exists at least one vertex $x\in V\left(G\right)$ such that $f\left(x\right)=0$ and $f\left(N\left(x\right)\right)\le \omega \left(f\right)<w_0$, which is a contradiction. Thus, ${\gamma }_w^s\left(G\right)\ge {\gamma }_w\left(G\right)\ge w_0$.

Analogously, if $w_0=w_1$, then Theorem 1 leads to ${\gamma }_w^s\left(G\right)\ge {\gamma }_{(w_0+1,w_1,\dots ,w_l)}\left(G\right)$. In this case, if ${\gamma }_{(w_0+1,w_1,\dots ,w_l)}\left(G\right)\le w_0<n$, then for any ${\gamma }_{(w_0+1,w_1,\dots ,w_l)}\left(G\right)$-function f there exists at least one vertex $x\in V\left(G\right)$ such that $f\left(x\right)=0$ and $f\left(N\left(x\right)\right)\le \omega \left(f\right)<w_0+1$, which is a contradiction. Therefore, ${\gamma }_w^s\left(G\right)\ge {\gamma }_{(w_0+1,w_1,\dots ,w_l)}\left(G\right)\ge w_0+1$. □

As the following result shows, the bounds above are tight.

Proposition 1.

For any integer n and any $w=(w_0,\dots ,w_l)\in {\mathbb{Z}}^{+}\times {\mathbb{N}}^l$ such that $w_l\le \cdots \le w_0<n$,

$${\gamma }_w^s\left(K_n\right)=\left\{\begin{array}{cc}{w}_0+1\hfill & if{w}_0=w_1,\hfill \\ w_0\hfill & otherwise.\hfill \end{array}\right.$$

Proof. 

Assume $n>w_0$. Let $S\subseteq V\left(K_n\right)$ such that $\left|S\right|=w_0+1$ if $w_0=w_1$ and $\left|S\right|=w_0$ otherwise. In both cases, the function $f(V_0,\dots ,V_l)$, defined by $V_1=S$, $V_0=V\left(G\right)\backslash V_1$ and $V_j=⌀$ whenever $j\notin \{0,1\}$, is a secure w-dominating function. Hence, ${\gamma }_w^s\left(K_n\right)\le \omega \left(f\right)=\left|S\right|$. Therefore, by Corollary 1 the result follows. □

Theorem 2.

Let G be a graph of minimum degree δ, and let $w=(w_0,\dots ,w_l),w^{\prime }=(w_0^{\prime },\dots ,w_l^{\prime })\in {\mathbb{Z}}^{+}\times {\mathbb{N}}^l$ such that $l\delta \ge w_l$, $w_i\ge w_{i+1}$ and $w_i^{\prime }\ge w_{i+1}^{\prime }$ for every $i\in \{0,\dots ,l-1\}$. If $w_i\ge w_{i-1}^{\prime }-1$ for every $i\in \{1,\dots ,l\}$, and $\max \{w_j-1,0\}\ge w_j^{\prime }$ for every $j\in \{0,\dots ,l\}$, then

$${\gamma }_{w^{\prime }}^s\left(G\right)\le {\gamma }_w\left(G\right).$$

Proof. 

Assume that $w_i\ge w_{i-1}^{\prime }-1$ for every $i\in \{1,\dots ,l\}$ and $\max \{w_j-1,0\}\ge w_j^{\prime }$ for every $j\in \{0,\dots ,l\}$. Let $f(V_0,\dots ,V_l)$ be a ${\gamma }_w\left(G\right)$-function. We claim that f is a secure $w^{\prime }$-dominating function. Since $f\left(N\left(x\right)\right)\ge w_i\ge w_i^{\prime }$ for every $x\in V_i$ with $i\in \{0,\dots ,l\}$, we deduce that f is a $w^{\prime }$-dominating function. Now, let $v\in V_0$ and $u\in N\left(v\right)\cap V_i$ with $i\in \{1,\dots ,l\}$. We differentiate the following cases for $x\in V\left(G\right)$.

• Case 1. $x=v$. In this case, $f_{u\to v}\left(v\right)=1$ and $f_{u\to v}\left(N\left(v\right)\right)=f\left(N\left(v\right)\right)-1\ge w_0-1\ge \max \{w_1-1,0\}\ge w_1^{\prime }$.
• Case 2. $x=u$. In this case, $f_{u\to v}\left(u\right)=f\left(u\right)-1=i-1$ and $f_{u\to v}\left(N\left(u\right)\right)=f\left(N\left(u\right)\right)+1\ge w_i+1\ge w_{i-1}^{\prime }$.
• Case 3. $x\in V\left(G\right)\backslash \{u,v\}.$ Assume $x\in V_j$. Notice that $f_{u\to v}\left(x\right)=f\left(x\right)=j$. Now, if $x\notin N\left(u\right)$ or $x\in N\left(u\right)\cap N\left(v\right)$, then $f_{u\to v}\left(N\left(x\right)\right)=f\left(N\left(x\right)\right)\ge w_j\ge w_j^{\prime }$, while if $x\in N\left(u\right)\backslash N\left[v\right]$, then $f_{u\to v}\left(N\left(x\right)\right)=f\left(N\left(x\right)\right)-1\ge \max \{w_j-1,0\}\ge w_j^{\prime }$.

According to the three cases above, $f_{u\to v}$ is a $w^{\prime }$-dominating function. Therefore, f is a secure $w^{\prime }$-dominating function, and so ${\gamma }_{w^{\prime }}^s\left(G\right)\le \omega \left(f\right)={\gamma }_w\left(G\right).$ □

The inequality above is tight. For instance, ${\gamma }_{(1,1,1)}^s\left(K_{n,n^{\prime }}\right)={\gamma }_{(2,2,2)}\left(K_{n,n^{\prime }}\right)=4$ for $n,n^{\prime }\ge 4$.

From Theorems 1 and 2, we derive the next known inequality chain, where G has minimum degree $\delta \ge 1$, except in the last inequality in which $\delta \ge 2$.

$${\gamma }_s\left(G\right)\le {\gamma }_2\left(G\right)\le {\gamma }_{\times 2}\left(G\right)\le {\gamma }_{st}\left(G\right)\le {\gamma }_{\times 2,t}\left(G\right).$$

The following result is a particular case of Theorem 2.

Corollary 2.

Let G be a graph of minimum degree δ, and let $w=(w_0,\dots ,w_l)\in {\mathbb{Z}}^{+}\times {\mathbb{N}}^l$ and 1 $=(1,\dots ,1)$. If $0\le w_{j-1}-w_j\le 2$ for every $j\in \{1,\dots ,i\}$, where $1\le i\le l$ and $l\delta \ge w_l+1$, then

$${\gamma }_{(w_0,\dots ,w_i,0,\dots ,0)}^s\left(G\right)\le {\gamma }_{(w_0+1,\dots ,w_i+1,0,\dots ,0)}\left(G\right)\le {\gamma }_{w+\mathbf{1}}\left(G\right).$$

For Graph $G_2$ illustrated in Figure 1, we have that ${\gamma }_{(1,1)}^s\left(G_2\right)={\gamma }_{(1,1,0)}^s\left(G_2\right)={\gamma }_{(2,2,0)}\left(G_2\right)={\gamma }_{(1,1,1)}^s\left(G_2\right)={\gamma }_{(2,2,2)}\left(G_2\right)=3$. Notice that ${\gamma }_w^s\left(G_2\right)={\gamma }_{w+\mathbf{1}}\left(G_2\right)$ for $w=\mathbf{1}=(1,1,1)$.

Next, we show a class of graphs where ${\gamma }_w\left(G\right)={\gamma }_{w+\mathbf{1}}\left(G\right)$. To this end, we need to introduce some additional notation and terminology. Given the two Graphs $G_1$ and $G_2$, the corona product graph$G_1\odot G_2$ is the graph obtained from $G_1$ and $G_2$, by taking one copy of $G_1$ and $\left|V\right(G_1\left)\right|$ copies of $G_2$ and joining by an edge every vertex from the ith copy of $G_2$ with the ith vertex of $G_1$. For every $x\in V\left(G_1\right)$, the copy of $G_2$ in $G_1\odot G_2$ associated to x is denoted by $G_{2,x}$.

Theorem 3

([1]). Let $G_1\odot G_2$ be a corona graph where $G_1$ does not have isolated vertices, and let $w=(w_0,\dots ,w_l)\in {\mathbb{Z}}^{+}\times {\mathbb{N}}^l$. If $l\ge w_0\ge \cdots \ge w_l$ and $|V\left(G_2\right)|\ge w_0$, then

$${\gamma }_w(G_1\odot G_2)=w_0\left|V\left(G_1\right)\right|.$$

From the result above, we deduce that under certain additional restrictions on $G_2$ and w we can obtain ${\gamma }_w^s(G_1\odot G_2)={\gamma }_{w+\mathbf{1}}(G_1\odot G_2)$.

Theorem 4.

Let $G_1\odot G_2$ be a corona graph, where $G_1$ does not have isolated vertices and $G_2$ is a triangle-free graph. Let $w=(w_0,\dots ,w_l)\in {\mathbb{Z}}^{+}\times {\mathbb{N}}^l$ such that $l-1\ge w_0\ge \cdots \ge w_l$. If $|V\left(G_2\right)|\ge w_0+2$, then

$${\gamma }_w^s(G_1\odot G_2)=(w_0+1)\left|V\left(G_1\right)\right|={\gamma }_{w+\mathbf{1}}(G_1\odot G_2).$$

Proof. 

Since $G_1$ does not have isolated vertices, the upper bound ${\gamma }_w^s(G_1\odot G_2)\le (w_0+1)\left|V\left(G_1\right)\right|$ is straightforward, as the function f, defined by $f\left(x\right)=w_0+1$ for every $x\in V\left(G_1\right)$ and $f\left(x\right)=0$ for the remaining vertices of $G_1\odot G_2$, is a secure w-dominating function.

On the other hand, let $f(V_0,\dots ,V_l)$ be a ${\gamma }_w^s(G_1\odot G_2)$-function and suppose that there exists $x\in V\left(G_1\right)$ such that $f\left(V\left(G_{2,x}\right)\right)+f\left(x\right)\le w_0$. Since $|V\left(G_{2,x}\right)|\ge w_0+2$, there exist at least two different vertices $u,v\in V\left(G_{2,x}\right)\cap V_0$. Hence, $f\left(N\left(u\right)\right)=f\left(N\left(v\right)\right)=w_0$, which implies that u and v are adjacent and, since $G_2$ is a triangle-free graph, $f\left(x\right)=w_0$ and $f\left(y\right)=0$ for every $y\in V\left(G_{2,x}\right)$. Thus, by Lemma 1, we conclude that $G_{2,x}$ is a clique, which is a contradiction as $\left|V\right(G_2\left)\right|\ge 3$ and $G_2$ is a triangle-free graph. This implies that $f\left(V\left(G_{2,x}\right)\right)+f\left(x\right)\ge w_0+1$ for every $x\in V\left(G_1\right)$, and so ${\gamma }_w^s(G_1\odot G_2)=\omega \left(f\right)\ge (w_0+1)\left|V\left(G_1\right)\right|$.

Therefore, ${\gamma }_w^s(G_1\odot G_2)=(w_0+1)\left|V\left(G_1\right)\right|$, and by Theorem 3 we conclude that ${\gamma }_{w+\mathbf{1}}(G_1\odot G_2)=(w_0+1)\left|V\left(G_1\right)\right|,$ which completes the proof. □

Theorem 5.

Let G be a graph of minimum degree δ and $l\ge 2$ an integer. For any $(w_0,\dots ,w_{l-1})\in {\mathbb{Z}}^{+}\times {\mathbb{N}}^{l-1}$ with $w_0\ge \cdots \ge w_{l-1}$ and $l\delta \ge w_{l-1}$,

$${\gamma }_{(w_0,\dots ,w_{l-1},w_l=w_{l-1})}^s\left(G\right)\le {\gamma }_{(w_0,\dots ,w_{l-1})}\left(G\right)+\gamma \left(G\right).$$

Proof. 

Let $f(V_0,\dots ,V_{l-1})$ be a ${\gamma }_{(w_0,\dots ,w_{l-1})}\left(G\right)$-function and S a $\gamma \left(G\right)$-set. We define a function $g(W_0,\dots ,W_l)$ as follows. Let $W_l=V_{l-1}\cap S$, $W_0=V_0\backslash S$, and $W_i=(V_{i-1}\cap S)\cup (V_i\backslash S)$ for every $i\in \{1,\dots ,l-1\}$.

We claim that g is a secure $(w_0,\dots ,w_{l-1},w_l=w_{l-1})$-dominating function. First, we observe that, if $x\in W_i\cap S$ with $i\in \{1,\dots ,l\}$, then $x\in V_{i-1}$ and $g\left(N\left(x\right)\right)\ge f\left(N\left(x\right)\right)\ge w_{i-1}\ge w_i$. Moreover, if $x\in W_i\backslash S$ with $i\in \{0,\dots ,l-1\}$, then $x\in V_i$ and $g\left(N\left(x\right)\right)\ge f\left(N\left(x\right)\right)\ge w_i$. Hence, g is a $(w_0,\dots ,w_{l-1},w_l=w_{l-1})$-dominating function.

Now, let $v\in W_0=V_0\backslash S$. Notice that there exists a vertex $u\in N\left(v\right)\cap V_{i-1}\cap S$ with $i\in \{1,\dots ,l\}$. Hence, $u\in N\left(v\right)\cap W_i$. We differentiate the following cases for $x\in V\left(G\right)$.

• Case 1. $x=v$. In this case, $g_{u\to v}\left(v\right)=1$ and, as $N\left(v\right)\cap S\ne \varnothing$, we obtain that $g_{u\to v}\left(N\left(v\right)\right)=g\left(N\left(v\right)\right)-1\ge f\left(N\left(v\right)\right)\ge w_0\ge w_1$.
• Case 2. $x=u$. In this case, $g_{u\to v}\left(u\right)=g\left(u\right)-1=i-1$ and $g_{u\to v}\left(N\left(u\right)\right)=g\left(N\left(u\right)\right)+1\ge f\left(N\left(u\right)\right)+1\ge w_{i-1}+1>w_{i-1}$.
• Case 3. $x\in V\left(G\right)\backslash \{u,v\}.$ Assume $x\in W_j$. Notice that $g_{u\to v}\left(x\right)=g\left(x\right)=j$. If $x\notin N\left(u\right)$ or $x\in N\left(u\right)\cap N\left(v\right)$, then $g_{u\to v}\left(N\left(x\right)\right)=g\left(N\left(x\right)\right)\ge f\left(N\left(x\right)\right)\ge w_j$.

Moreover, if $x\in \left(N\right(u)\backslash N[v\left]\right)\cap S$, then $x\in V_{j-1}$ and so $g_{u\to v}\left(N\left(x\right)\right)=g\left(N\left(x\right)\right)-1\ge f\left(N\left(x\right)\right)\ge w_{j-1}\ge w_j$. Finally, if $x\in \left(N\right(u)\backslash N[v\left]\right)\backslash S$, then $x\in V_j$ and therefore $g_{u\to v}\left(N\left(x\right)\right)=g\left(N\left(x\right)\right)-1\ge f\left(N\left(x\right)\right)\ge w_j$.

According to the three cases above, $g_{u\to v}$ is a $(w_0,\dots ,w_{l-1},w_l=w_{l-1})$-dominating function. Therefore, f is a secure $(w_0,\dots ,w_{l-1},w_l=w_{l-1})$-dominating function, and so ${\gamma }_{(w_0,\dots ,w_{l-1},w_l=w_{l-1})}^s\left(G\right)\le \omega \left(g\right)\le \omega \left(f\right)+\left|S\right|={\gamma }_{(w_0,\dots ,w_{l-1})}\left(G\right)+\gamma \left(G\right).$ □

From Theorem 5, we derive the next known inequalities, which are tight.

Corollary 3.

For a graph G, the following statements hold.

• Ref. [15]${\gamma }_r\left(G\right)\le 2\gamma \left(G\right)$.
• Ref. [12]${\gamma }_{tr}\left(G\right)\le {\gamma }_t\left(G\right)+\gamma \left(G\right)$, where G has minimum degree at least one.
• Ref. [19]${\gamma }_I^s\left(G\right)\le {\gamma }_2\left(G\right)+\gamma \left(G\right)$.

To establish the following result, we need to define the following parameter.

$${\nu }_{(w_0,\dots ,w_l)}^s\left(G\right)=\max \left\{\right|V_0|:f(V_0,\dots ,V_l)\mathrm{is}\mathrm{a}{\gamma }_{(w_0,\dots ,w_l)}^s\left(G\right)\text{-}\mathrm{function}.\}$$

In particular, for $l=1$ and a graph G of order n, we have that ${\nu }_{(w_0,w_1)}^s\left(G\right)=n-{\gamma }_{(w_0,w_1)}^s\left(G\right)$.

Theorem 6.

Let G be a graph of minimum degree δ and order n. The following statements hold for any $(w_0,\dots ,w_l)\in {\mathbb{Z}}^{+}\times {\mathbb{N}}^l$ with $w_0\ge \cdots \ge w_l$.

(i)

If there exists $i\in \{1,\dots ,l-1\}$ such that $i\delta \ge w_i$, then ${\gamma }_{(w_0,\dots ,w_l)}^s\left(G\right)\le {\gamma }_{(w_0,\dots ,w_i)}^s\left(G\right).$

(ii)

If $l\ge i+1>w_0$, then ${\gamma }_{(w_0,\dots ,w_i,0,\dots ,0)}^s\left(G\right)\le (i+1)\gamma \left(G\right).$

(iii)

Let $k,i\in {\mathbb{Z}}^{+}$ such that $l\ge ki$, and let $(w_0^{\prime },w_1^{\prime },\dots ,w_i^{\prime })\in {\mathbb{Z}}^{+}\times {\mathbb{N}}^l$. If $i\delta \ge w_i^{\prime }$ and $w_{kj}=k{w}_j^{\prime }$ for every $j\in \{0,1,\dots ,i\}$, then ${\gamma }_{(w_0,\dots ,w_l)}^s\left(G\right)\le k{\gamma }_{(w_0^{\prime },\dots ,w_i^{\prime })}^s\left(G\right).$

(iv)

Let $k\in {\mathbb{Z}}^{+}$ and ${\beta }_1,\dots ,{\beta }_k\in {\mathbb{Z}}^{+}$. If $l\delta \ge k+w_l>k$ and $w_0+k\ge {\beta }_1\ge \cdots \ge {\beta }_k\ge w_1+k$, then ${\gamma }_{(w_0+k,{\beta }_1,\dots ,{\beta }_k,w_1+k,\dots ,w_l+k)}^s\left(G\right)\le {\gamma }_{(w_0,\dots ,w_l)}^s\left(G\right)+k(n-{\nu }_{(w_0,\dots ,w_l)}^s\left(G\right))$.

(v)

If $l\delta \ge w_l\ge l\ge 2$, then ${\gamma }_{(w_0,\dots ,w_l)}^s\left(G\right)\le l{\gamma }_{(w_0-l+1,w_l-l+1)}^s\left(G\right).$

Proof. 

If there exists $i\in \{1,\dots ,l-1\}$ such that $i\delta \ge w_i$, then for any ${\gamma }_{(w_0,\dots ,w_i)}^s\left(G\right)$-function $f(V_0,\dots ,V_i)$ we define a secure $(w_0,\dots ,w_l)$-dominating function $g(W_0,\dots ,W_l)$ by $W_j=V_j$ for every $j\in \{0,\dots ,i\}$ and $W_j=⌀$ for every $j\in \{i+1,\dots ,l\}$. Hence, ${\gamma }_{(w_0,\dots ,w_l)}^s\left(G\right)\le \omega \left(g\right)=\omega \left(f\right)={\gamma }_{(w_0,\dots ,w_i)}^s\left(G\right)$. Therefore, (i) follows.

Now, assume $l\ge i+1>w_0$. Let S be a $\gamma \left(G\right)$-set. Let f be the function defined by $f\left(v\right)=i+1$ for every $v\in S$ and $f\left(v\right)=0$ for the remaining vertices. Since $i+1>w_0$, we can conclude that f is a secure $(w_0,\dots ,w_i,0\dots ,0)$-dominating function. Therefore, ${\gamma }_{(w_0,\dots ,w_i,0\dots ,0)}^s\left(G\right)\le \omega \left(f\right)=(i+1)\left|S\right|=(i+1)\gamma \left(G\right)$, which implies that (ii) follows.

To prove (iii), assume that $l\ge ki$, $i\delta \ge w_i^{\prime }$ and $w_{kj}=k{w}_j^{\prime }$ for every $j\in \{0,\dots ,i\}$. Let $f^{\prime }(V_0^{\prime },\dots ,V_i^{\prime })$ be a ${\gamma }_{(w_0^{\prime },\dots ,w_i^{\prime })}^s\left(G\right)$-function. We construct a function $f(V_0,\dots ,V_l)$ as $f\left(v\right)=k{f}^{\prime }\left(v\right)$ for every $v\in V\left(G\right)$. Hence, $V_{kj}=V_j^{\prime }$ for every $j\in \{0,\dots ,i\}$, while $V_j=⌀$ for the remaining cases. Thus, for every $v\in V_{kj}$ with $j\in \{0,\dots ,i\}$ we have that $f\left(N\left(v\right)\right)=k{f}^{\prime }\left(N\left(v\right)\right)\ge k{w}_j^{\prime }=w_{kj}$, which implies that f is a $(w_0,\dots ,w_l)$-dominating function. Now, for every $x\in V_0$, there exists $y\in M_{f^{\prime }}\left(x\right)$. Hence, for every $v\in V_{kj}$ with $j\in \{0,\dots ,i\}$, we have that $f_{y\to x}\left(N\left(v\right)\right)=k{f}_{y\to x}^{\prime }\left(N\left(v\right)\right)\ge k{w}_j^{\prime }=w_{kj}$, which implies that $f_{y\to x}$ is a $(w_0,\dots ,w_l)$-dominating function. Therefore, f is a secure $(w_0,\dots ,w_l)$-dominating function, and so ${\gamma }_{(w_0,\dots ,w_l)}^s\left(G\right)\le \omega \left(f\right)=k\omega \left(f^{\prime }\right)=k{\gamma }_{(w_0^{\prime },\dots ,w_i^{\prime })}^s\left(G\right)$. Therefore, (iii) follows.

Now, assume that $l\delta \ge k+w_l>k$ and $w_0+k\ge {\beta }_1\ge \cdots \ge {\beta }_k\ge w_1+k$. Let $g(W_0,\dots ,W_l)$ be a ${\gamma }_{(w_0,\dots ,w_l)}^s\left(G\right)$-function. We construct a function $f(V_0,\dots ,V_{l+k})$ as $f\left(v\right)=g\left(v\right)+k$ for every $v\in V\left(G\right)\backslash W_0$ and $f\left(v\right)=0$ for every $v\in W_0$. Hence, $V_{j+k}=W_j$ for every $j\in \{1,\dots ,l\}$, $V_0=W_0$ and $V_j=⌀$ for the remaining cases. Thus, if $v\in V_{j+k}$ and $j\in \{1,\dots ,l\}$, then $f\left(N\left(v\right)\right)\ge g\left(N\left(v\right)\right)+k\ge w_j+k$, and if $v\in V_0$, then $f\left(N\left(v\right)\right)\ge g\left(N\left(v\right)\right)+k\ge w_0+k$. This implies that f is a $(w_0+k,{\beta }_1,\dots ,{\beta }_k,w_1+k,\dots ,w_l+k)$-dominating function. Now, for every $x\in V_0=W_0$, there exists $y\in M_g\left(x\right)$. Hence, if $v\in V_{j+k}$ and $j\in \{1,\dots ,l\}$, then $f_{y\to x}\left(N\left(v\right)\right)\ge g_{y\to x}\left(N\left(v\right)\right)+k\ge w_j+k$, and if $v\in V_0$, then $f_{y\to x}\left(N\left(v\right)\right)\ge g_{y\to x}\left(N\left(v\right)\right)+k\ge w_0+k$. This implies that $f_{y\to x}$ is a $(w_0+k,{\beta }_1,\dots ,{\beta }_k,w_1+k,\dots ,w_l+k)$-dominating function, and so f is a secure $(w_0+k,{\beta }_1,\dots ,{\beta }_k,w_1+k,\dots ,w_l+k)$-dominating function. Therefore, ${\gamma }_{(w_0+k,{\beta }_1,\dots ,{\beta }_k,w_1+k,\dots ,w_l+k)}^s\left(G\right)\le \omega \left(f\right)=\omega \left(g\right)+k{\sum }_{j=1}^l|W_j|={\gamma }_{(w_0,\dots ,w_l)}^s\left(G\right)+k(n-|W_0\left|\right)\le {\gamma }_{(w_0,\dots ,w_l)}^s\left(G\right)+k(n-{\nu }_{(w_0,\dots ,w_l)}^s\left(G\right))$, concluding that (iv) follows.

Furthermore, if $l\delta \ge w_l\ge l\ge 2$, then, by applying (iv) for $k=l-1$, we deduce that

$${\gamma }_{(w_0,\dots ,w_l)}^s\left(G\right)\le {\gamma }_{(w_0-l+1,w_l-l+1)}^s\left(G\right)+(l-1)(n-{\nu }_{(w_0-l+1,w_l-l+1)}^s\left(G\right))=l{\gamma }_{(w_0-l+1,w_l-l+1)}^s\left(G\right).$$

Therefore, (v) follows. □

In the next subsections, we consider several applications of Theorem 6 where we show that the bounds are tight. For instance, the following particular cases is of interest.

Corollary 4.

Let G be a graph of minimum degree δ, and let $k,l,w_2,\dots ,w_l\in {\mathbb{Z}}^{+}$ with $k\ge w_2\ge \cdots \ge w_l$.

(i’)

If $\delta \ge k$, then ${\gamma }_{(k+1,k,w_2,\dots ,w_l)}^s\left(G\right)\le {\gamma }_{(k+1,k)}^s\left(G\right)$.

(ii’)

If $\delta \ge k$, then ${\gamma }_{(k,k,w_2,\dots ,w_l)}^s\left(G\right)\le {\gamma }_{(k,k)}^s\left(G\right)$.

(iii’)

If $l\delta \ge k\ge l\ge 2$, then ${\gamma }_{\left(\underset{l+1}{{\displaystyle \underbrace{k,k,\dots ,k}}}\right)}^s\left(G\right)\le l{\gamma }_{(k-l+1,k-l+1)}^s\left(G\right)$.

(iv’)

Let $i\in {\mathbb{Z}}^{+}$. If $l\ge ki$ and $\delta \ge 1$, then ${\gamma }_{\left(\underset{l+1}{{\displaystyle \underbrace{k,\dots ,k}}}\right)}^s\left(G\right)\le k{\gamma }_{\left(\underset{i+1}{\underbrace{1,\dots ,1}}\right)}^s\left(G\right)$.

Proof. 

If $\delta \ge k$, then by Theorem 6 (i) we conclude that (i’) and (ii’) follow. If $l\delta \ge k\ge l\ge 2$, then by Theorem 6 (v) we deduce (iii’). Finally, if $l\ge k$ and $\delta \ge 1$, then by Theorem 6 (iii) we deduce that (iv’) follows. □

To show that the inequalities above are tight, we consider the following examples. For (i’), we have ${\gamma }_{(2,1,1)}^s(K_1+(K_2\cup K_2))={\gamma }_{(2,1)}^s(K_1+(K_2\cup K_2))=3$. For (ii’) we have ${\gamma }_{(k,k,w_2,\dots ,w_l)}^s\left(G\right)={\gamma }_{(k,k)}^s\left(G\right)=k+1$ for every graph G with $k+1$ universal vertices. Finally, for (iii’) and (iv’), we take $l=k=2$ and ${\gamma }_{(2,2,2)}^s(K_2+N_n)=2{\gamma }_{(1,1)}^s(K_2+N_n)=4$ for every $n\ge 2$.

We already know that ${\gamma }_t\left(G\right)={\gamma }_{(1,1)}\left(G\right)={\gamma }_{(1,1,w_2,\dots ,w_l)}\left(G\right)$, for every $w_2,\dots ,w_l\in \{0,1\}$. In contrast, the picture is quite different for the case of secure $(1,1)$-domination, as there are graphs where the gap ${\gamma }_{(1,1)}^s\left(G\right)-{\gamma }_{(1,\dots ,1)}^s\left(G\right)$ is arbitrarily large. For instance, ${\displaystyle \underset{n\to \infty }{lim}{\gamma }_{(1,1)}^s\left(K_{1,n-1}\right)=+\infty }$, while, if $l\ge 2$, then ${\displaystyle \underset{n\to +\infty }{lim}{\gamma }_{\left(\underset{l+1}{{\displaystyle \underbrace{1,\dots ,1}}}\right)}^s\left(K_{1,n-1}\right)=3}$.

Proposition 2.

Let G be a graph of order n. Let $w=(w_0,\dots ,w_l)\in {\mathbb{Z}}^{+}\times {\mathbb{N}}^l$ such that $w_0\ge \cdots \ge w_l$. If $G^{\prime }$ is a spanning subgraph of G with minimum degree ${\delta }^{\prime }\ge \frac{w_l}{l}$, then

$${\gamma }_w^s\left(G\right)\le {\gamma }_w^s\left(G^{\prime }\right).$$

Proof. 

Let $E^{-}=\{e_1,\dots ,e_k\}$ be the set of all edges of G not belonging to the edge set of $G^{\prime }$. Let $G_0^{\prime }=G$ and, for every $i\in \{1,\dots ,k\}$, let $X_i=\{e_1,\dots ,e_i\}$ and $G_i^{\prime }=G-X_i$, the edge-deletion subgraph of G induced by $E\left(G\right)\backslash X_i$.

For any ${\gamma }_w^s\left(G_i^{\prime }\right)$-function f and any $v\in V\left(G_i^{\prime }\right)=V\left(G\right)$ with $f\left(v\right)=0$, there exists $u\in M_f\left(v\right)$. Since f and $f_{u\to v}$ are w-dominating functions on $G_i^{\prime }$, both are w-dominating functions on $G_{i-1}^{\prime }$, and so we can conclude that f is a secure w-dominating function on $G_{i-1}^{\prime }$, which implies that ${\gamma }_w^s\left(G_{i-1}^{\prime }\right)\le {\gamma }_w^s\left(G_i^{\prime }\right)$. Hence, ${\gamma }_w^s\left(G\right)={\gamma }_w^s\left(G_0^{\prime }\right)\le {\gamma }_w^s\left(G_1^{\prime }\right)\le \cdots \le {\gamma }_w^s\left(G_k^{\prime }\right)={\gamma }_w^s\left(G^{\prime }\right)$. □

As a simple example of equality in Proposition 2 we can take any graph G of order n, having $n^{\prime }+1\ge 2$ universal vertices. In such a case, for $n^{\prime }=w_1\ge \cdots \ge w_l$ we have that

$${\gamma }_{(n^{\prime },n^{\prime }=w_1,\dots ,w_l)}^s\left(K_n\right)={\gamma }_{(n^{\prime },n^{\prime }=w_1,\dots ,w_l)}^s\left(G\right)={\gamma }_{(n^{\prime },n^{\prime })}^s\left(K_n\right)={\gamma }_{(n^{\prime },n^{\prime })}^s\left(G\right)=n^{\prime }+1.$$

From Proposition 2, we obtain the following result.

Corollary 5.

Let G be a graph of order n and $w=(w_0,\dots ,w_l)\in {\mathbb{Z}}^{+}\times {\mathbb{N}}^l$ such that $w_0\ge \cdots \ge w_l$.

• If G is a Hamiltonian graph and $w_l\le 2l$, then ${\gamma }_w^s\left(G\right)\le {\gamma }_w^s\left(C_n\right)$.
• If G has a Hamiltonian path and $w_l\le l$, then ${\gamma }_w^s\left(G\right)\le {\gamma }_w^s\left(P_n\right)$.

To derive some lower bounds on ${\gamma }_w^s\left(G\right)$, we need to establish the following lemma.

Lemma 2

([1]). Let G be a graph with no isolated vertex, maximum degree Δ and order n. For any w-dominating function $f(V_0,\dots ,V_l)$ on G such that $w_0\ge \cdots \ge w_l$,

$$\Delta \omega \left(f\right)\ge w_{0}n+\sum _{i=1}^l(w_i-w_0)\left|V_i\right|.$$

Theorem 7.

Let G be a graph with no isolated vertex, maximum degree Δ and order n. Let $w=(w_0,\dots ,w_l)\in {\mathbb{Z}}^{+}\times {\mathbb{N}}^l$ such that $w_0\ge \cdots \ge w_l$ and $l\delta \ge w_l$. The following statements hold.

• If $w_0=w_1$ and $w_0-w_i\le i$ for every $i\in \{2,\dots ,l\}$, then ${\gamma }_w^s\left(G\right)\ge ⌈\frac{(w_0+1)n}{\Delta +1}⌉.$
• If $w_0=w_1$, then ${\gamma }_w^s\left(G\right)\ge ⌈\frac{(w_0+1)n}{\Delta +w_0}⌉.$
• If $w_0=w_1+1$ and $w_0-w_i\le i$ for every $i\in \{2,\dots l\}$, then ${\gamma }_w^s\left(G\right)\ge ⌈\frac{w_{0}n}{\Delta +1}⌉.$
• ${\gamma }_w^s\left(G\right)\ge ⌈\frac{w_{0}n}{\Delta +w_0}⌉.$

Proof. 

Let $w_0=w_1$ and $w_0-w_i\le i$ for every $i\in \{2,\dots ,l\}$. Let $f(V_0,\dots ,V_l)$ be a ${\gamma }_{(w_0+1,w_1,\dots ,w_l)}\left(G\right)$-function. By Lemma 2, we deduce the following.

$$\begin{array}{cc}\hfill \Delta \omega \left(f\right)& \ge (w_0+1)n+\sum _{i=1}^l(w_i-w_0)\left|V_i\right|\hfill \\ \hfill & \ge (w_0+1)n-\sum _{i=1}^{l}i\left|V_i\right|\hfill \\ \hfill & =(w_0+1)n-\omega \left(f\right).\hfill \end{array}$$

Therefore, Theorem 1 (ii) leads to ${\gamma }_w^s\left(G\right)\ge \omega \left(f\right)\ge ⌈\frac{(w_0+1)n}{\Delta +1}⌉.$

The proof of the remaining items is completely analogous. In the last two cases, we consider that $f(V_0,\dots ,V_l)$ is a ${\gamma }_w\left(G\right)$-function, and we apply Theorem 1 (i) instead of (ii). □

The bounds above are sharp. For instance, ${\gamma }_{(1,1,0)}^s\left(G\right)\ge ⌈\frac{2n}{\Delta +1}⌉$ is achieved by Graph $G_2$ shown in Figure 1, the bound ${\gamma }_{(k,k,0)}^s\left(G\right)\ge ⌈\frac{(k+1)n}{\Delta +k}⌉$ is achieved by $G\cong K_n$ for every $n>k(k-1)>0$, the bound ${\gamma }_{(2,1,1)}^s\left(G\right)\ge ⌈\frac{2n}{\Delta +1}⌉$ is achieved by the corona graph $K_2\odot K_{n^{\prime }}$ with $n^{\prime }\ge 4$, while ${\gamma }_{(2,0,0)}^s\left(G\right)\ge ⌈\frac{2n}{\Delta +2}⌉$ is achieved by $G\cong C_5$, $G\cong K_n$ and $G\cong K_{n^{\prime }}\cup K_{n^{\prime }}$ with $n\ge 2$ and $n^{\prime }\ge 4$.

To conclude the paper, we consider the problem of characterizing the graphs G and the vectors w for which ${\gamma }_w^s\left(G\right)$ takes small values. It is readily seen that ${\gamma }_{(w_0,\dots ,w_l)}^s\left(G\right)=1$ if and only if $w_0=1$, $w_1=0$ and $G\cong K_n$. Next, we consider the case ${\gamma }_w^s\left(G\right)=2.$

Theorem 8.

Let $w=(w_0,\dots ,w_l)\in {\mathbb{Z}}^{+}\times {\mathbb{N}}^l$ such that $w_0\ge \cdots \ge w_l$. For a graph G of order at least three, ${\gamma }_{(w_0,\dots ,w_l)}^s\left(G\right)=2$ if and only if one of the following conditions holds.

(i)

$w_2=0$, $\gamma \left(G\right)=1$ and one of the following conditions holds.

• $w_0=w_1=1$.
• $w_0=1$, $w_1=0$, and $G\ncong K_n$.
• $w_0=2$, $w_1\in \{0,1\}$ and $G\cong K_n$.

(ii)

$w_0=1$, $w_1=0$, and ${\gamma }_{(1,0)}^s\left(G\right)=2$.

(iii)

$w_0=w_1=1$ and ${\gamma }_{(1,1)}^s\left(G\right)=2$.

(iv)

$w_0=2$, $w_1\in \{0,1\}$, and $G\cong K_n$.

Proof. 

Assume first that ${\gamma }_{(w_0,\dots ,w_l)}^s\left(G\right)=2$ and let $f(V_0,\dots ,V_l)$ be a ${\gamma }_{(w_0,\dots ,w_l)}^s\left(G\right)$-function. Notice that $(w_0,w_1)\in \{(1,0),(1,1),(2,0),(2,1)\}$ and $|V_2|\in \{0,1\}$.

Firstly, we consider that $|V_2|=1$, i.e., $V_2=\left\{u\right\}$ for some universal vertex $u\in V\left(G\right)$. In this case, $w_2=0$, $\gamma \left(G\right)=1$, and $V_i=⌀$ for every $i\ne 0,2$. By Lemma 1, if $w_0=2$, then $G\left[T_f\left(u\right)\right]=G[V\left(G\right)\backslash \left\{u\right\}]$ is a clique, which implies that $G\cong K_n$. Obviously, in such a case, $w_1<2$. Finally, the case, $w_0=1$ and $w_1=0$ leads to $G\ncong K_n$, as ${\gamma }_{(1,0\dots ,0)}^s\left(K_n\right)=1$. Therefore, (i) follows.

From now on, assume that $V_2=⌀$. Hence, $V_i=⌀$ for every $i\ne 0,1$. If $w_0=1$ and $w_1=0$, then $G\ncong K_n$ and $V_1$ is a secure dominating set. Therefore, (ii) follows. If $w_0=w_1=1$, then $V_1$ is a secure total dominating set of cardinality two, and so ${\gamma }_{(1,1)}^s\left(G\right)=2$. Therefore, (iii) follows. Finally, assume $w_0=2$. In this case, $V_1$ is a double dominating set of cardinality two, and by Lemma 1 we know that $G\left[T_f\left(x\right)\right]=G[V\left(G\right)\backslash V_1]$ is a clique for any $x\in V_1$. Hence, $G\cong K_n$ and, in such a case, $w_1<2$. Therefore, (iv) follows.

Conversely, if one of the four conditions holds, then it is easy to check that ${\gamma }_{(w_0,\dots ,w_l)}^s\left(G\right)=2$, which completes the proof. □