A New Sum of Squares Exponentially Weighted Moving Average Control Chart Using Auxiliary Information

Abstract

The concept of control charts is based on mathematics and statistics to process forecast; which applications are widely used in industrial management. The sum of squares exponentially weighted moving average (SSEWMA) chart is a well-known tool for effectively monitoring both the increase and decrease in the process mean and/or variability. In this paper, we propose a novel SSEWMA chart using auxiliary information, called the AIB-SSEWMA chart, for jointly monitoring the process mean and/or variability. With our proposed chart, the attempt is to enhance the performance of the classical SSEWMA chart. Numerical simulation studies indicate that the AIB-SSEWMA chart has better detection ability than the existing SSEWMA and its competitive maximum EWMA based on auxiliary information (AIB-MaxEWMA) charts in view of average run lengths (ARLs). An illustrated example is used to demonstrate the efficiency of the proposed AIB-SSEWMA chart in detecting small process shifts.

1. Introduction

Statistical process control (SPC) is a statistical method application, which implies not only monitoring the status of a process, but also the ability to maintain process stabilization by distinguishing between common causes and assignable causes of variation in a process (Montgomery [1]). The control chart was first introduced by Walter A. Shewhart in the 1920s and widely used graphical tools in SPC, for monitoring production processes and improvement of process quality. For sophisticated production processes, the Shewhart control chart is insensitive in detecting small process shifts. To cope with this problem, Roberts [2] introduced the exponentially weighted moving average (EWMA) chart to improve the poor detection ability of the Shewhart control chart when small process shifts are of interest. Subsequently, various and extended EWMA charts are developed to deal shifts in process mean, process variability, and both. Such as:

(I)

Crowder [3], Ng and Case [4], Lucas and Saccucci [5], Steiner [6], and Sheu and Lin [7] developed extended EWMA charts to improve the performance of detecting small process mean shifts.

(II)

Crowder and Hamilton [8], Castagliola [9], Shu and Jiang [10], Huwang et al. [11], and Sheu and Lu [12] designed various EWMA charts to monitor small process variability shifts.

(III)

Sweet [13] and Gan [14] developed two EWMA charts, one to detect mean shifts and the other to detect changes in variability.

The two EWMA charts are applicable when there is insufficient information regarding the effect of assignable causes on the process. However, the use of such charts is time-consuming, and may cause increased costs. A single EWMA chart has therefore been developed for easy use, and reduced time and costs. Domangue and Patch [15] developed an omnibus EWMA chart to jointly monitor changes in location and spread. Chao and Cheng [16] proposed the semicircle (SC) chart for detecting changes in the process mean and variability. Chen and Cheng [17] utilized maximum absolute values of the standardized mean and standard deviation to construct a single Max chart to monitor both the process mean and dispersion. Xie [18] presented various types of single EWMA charts such as EWMA-Max, MaxEWMA, EWMA semicircle (EWMA-SC), and sum of squares EWMA (SSEWMA) charts. Chen et al. [19,20] extended the work of Xie [18] on the MaxEWMA and EWMA-SC charts, respectively. Teh et al. [21] proposed a sum of squares double EWMA (SS-DEWMA) chart to improve the performance of the SSEWMA chart in terms of the average run length ($ARL$) and standard deviation of the run length ($SDRL$) criteria.

In recent years, there is a wave of interest in developing auxiliary information-based (AIB) charts in the SPC field. AIB charts are mainly based on accurate estimators, which are estimated through auxiliary information (auxiliary variables) along with the quality characteristic (study variable), and attempts to enhance the detection ability of those not using the auxiliary information. Riaz [22], Ahmad et al. [23], and Riaz [24] developed AIB-Shewhart mean charts using regression estimators, ratio-type, and location estimators, respectively, for monitoring process mean shifts. Similarly, Riaz and Does [25] developed the AIB-Shewhart dispersion chart by using a ratio-type variance estimator. Like as the AIB-Shewhart charts have increased the performance of the original Shewhart chart. As for EWMA-type charts for monitoring small process shifts, Abbas et al. [26] proposed the AIB-EWMA chart, and showed that the proposed chart is more sensitive than both, the classical EWMA chart and the AIB-Shewhart chart in detecting small process mean shifts. Haq [27] utilized regression estimators to develop an AIB-EWMA chart to monitor increases and/or decreases in the process dispersion. For more work on the AIB charts, we refer to Haq and Khoo [28], Abbasi and Riaz [29], Riaz et al. [30], Haq and Abidin [31], Haq et al. [32], and Chen and Lu [33]. Most AIB charts mentioned are designed for separately monitoring the process mean or variability shifts. Haq [34] first introduced the AIB-MaxEWMA chart for simultaneously detecting both increases and decreases in the mean and/or dispersion of a process. Simulations revealed that the AIB-MaxEWMA chart performs uniformly better than the MaxEWMA chart in detecting all kinds of shifts in both, the process mean and dispersion.

In this paper, a single correlated auxiliary variable is used to develop a novel SSEWMA chart, namely the AIB-SSEWMA chart, for simultaneously monitoring the process mean and/or variability of a normally distributed process. Numerical simulations are evaluated by run length profiles in terms of $ARLs$ and $SDRLs$. As expected, the AIB-SSWMA chart not only improves the detection ability of the SSEWMA chart, but also outperforms the competitive AIB-MaxEWMA chart.

The rest of the paper is organized as follows: The SSEWMA chart is reviewed in Section 2. The AIB-SSEWMA chart is proposed in Section 3. Section 4 evaluates the performance of the AIB-SSEWMA charts in terms of their initial-state $ARL$ and $SDRL$ values. Section 5 compares the proposed chart with the competitive AIB-MaxEWMA chart. A numerical simulation example is presented in Section 6. Finally, significant conclusions are presented in Section 7.

2. A Review of the Sum of Squares EWMA Chart

Xie [18] proposed a sum of squares EWMA chart, called the SSEWMA chart, which not only combines two EWMA statistics into a single variable chart to jointly monitor process mean and/or variability shifts, but also identifies the sources and direction of the shift. Herein, the SSEWMA chart is applied, as described by Xie [18].

Let $X$ be a quality characteristic of interest. It is assumed that $X$ has a normal distribution with mean ${\mu }_X+\delta {\sigma }_X$ and standard deviation $\tau {\sigma }_X$, that is, $X~N({\mu }_X+\delta {\sigma }_X,{\tau }^2{\sigma }_X^2)$, where $\delta =0$ and $\tau =1$ indicate that the process is in control; otherwise, the process has changed or drifted.

Suppose $X_{tj}$,$t=1,2,\dots$, and $j=1,2,\dots ,n$ is the measurements of the variable $X$ arranged in groups of size $n$ at time $t$. Let ${\overline{X}}_t$ and $S_{X,t}^2$ denote the sample mean and sample variance, respectively. Then ${\overline{X}}_t$, $t=1,2,\dots$ are independent normal random variables with mean ${\mu }_X+\delta {\sigma }_X$ and variance ${\tau }^2{\sigma }_X^2/n$; $(n-1)S_{X,t}^2/{\tau }^2{\sigma }_X^2$ and $t=1,2,\dots$, are independent chi-square random variables with $n-1$ degrees of freedom, and ${\overline{X}}_t$ and $S_{X,t}^2$ are mutually independent random variables for an in-control process. Defining the following two transformed statistics:

$$U_{X,t}=\frac{{\overline{X}}_t-{\mu }_X}{{\sigma }_X/\sqrt{n}}$$

(1)

and

$$V_{X,t}={\mathrm{\Phi }}^{-1}\left[F\left(\frac{(n-1)S_{X,t}^2}{{\sigma }_X^2};n-1\right)\right]$$

(2)

where ${\mathrm{\Phi }}^{-1}(\cdot )$ and $F(\cdot )$ represent the inverse standard normal distribution function and the chi-square distribution function with $n-1$ degrees of freedom, respectively.

Both $U_{X,t}$ and $V_{X,t}$ are independent standard normal random variables when the process is in control, and the distributions of $U_{X,t}$ and $V_{X,t}$ are both independent of the sample size $n$. Two EWMA statistics each for the mean and variance can be defined as:

$$M_{X,t}^{}=\lambda U_{X,t}+(1-\lambda )M_{X,t-1}^{},0<\lambda \le 1, t=1,2\dots ,$$

(3)

and

$$N_{X,t}^{}=\lambda V_{X,t}+(1-\lambda )N_{X,t-1}^{},0<\lambda \le 1, t=1,2\dots ,$$

(4)

where $M_{X,0}^{}=N_{X,0}^{}=0$ are the starting values of $M_{X,t}$ and $N_{X,t}$, respectively. It is known that $M_{X,t}^{}$ and $N_{X,t}^{}$ are independent because $U_{X,t}$ and $V_{X,t}$ are independent, and when the process is in control and $M_{X,0}^{}=N_{X,0}^{}=0$, $M_{X,t}^{}~N(0,{\sigma }_{M_t^{}}^2)$ and $N_{X,t}^{}~N(0,{\sigma }_{N_t^{}}^2)$, where ${\sigma }_{M_t^{}}^2={\sigma }_{N_t^{}}^2=\frac{\lambda [1-{(1-\lambda )}^{2t}]}{2-\lambda }$.

The statistic of the SSEWMA chart, say $S{E}_t^{}$, is defined as:

$$S{E}_t=M_{X,t}^2+N_{X,t}^2,\hspace{1em}t=1,2,3,\dots$$

(5)

Since $S{E}_t^{}$ is nonnegative, the initial state of the SSEWMA chart requires only an upper control limit $(UC{L}_t)$, which is given by:

$$UC{L}_t=E(S{E}_t)+K\sqrt{ Var(S{E}_t)}$$

(6)

where $E(S{E}_t)$ and $Var(S{E}_t)$ are the mean and variance of $S{E}_t^{}$, respectively. To achieve the desired in control $ARL$, the corresponding control limit constant $K$ and the smoothing parameters $\lambda$ are determined. The process is considered to be out of control whenever $S{E}_t^{}$ exceeds $UC{L}_t$ and some action should be taken to identify and eliminate the assignable cause of the process. Xie [18] provides a simple and quick computation formula for $UC{L}_t$, given as follows:

$$UC{L}_t=2(1+K)\cdot \frac{\lambda [1-{(1-\lambda )}^{2t}]}{2-\lambda }$$

(7)

The process is considered to be out of control when the statistic $S{E}_t^{}$ exceeds $UC{L}_t$, i.e., when the pair $(M_{X,t},N_{X,t})$ plots outside the circular control region centered at (0, 0) with a radius of $\sqrt{UC{L}_t}$. To avoid the problem of concentric circles, Xie [18] plots $({\tilde{M}}_{X,t}^{},\hspace{0.17em}{\tilde{N}}_{X,t}^{})$ on a circular control region centered at (0, 0) with a radius $r$ of $\sqrt{2(1+K)}$, where ${\tilde{M}}_{X,t}^{}=M_{X,t}\sqrt{\frac{2-\lambda }{\lambda [1-{(1-\lambda )}^{2t}]}}$, ${\tilde{N}}_{X,t}^{}=N_{X,t}\sqrt{\frac{2-\lambda }{\lambda [1-{(1-\lambda )}^{2t}]}}$, and $S{\tilde{E}}_t={\tilde{M}}_{X,t}^2+{\tilde{N}}_{X,t}^2$.

3. The Proposed AIB-SSEWMA Chart

Assume that there exists a corresponding auxiliary variable $Y$ that accompanies quality characteristic $X$ of interest. Let $(X,Y)$ follow a bivariate normally distributed process with means $({\mu }_X+\delta {\sigma }_X,{\mu }_Y)$ and variances $({\tau }^2{\sigma }_X^2,{\sigma }_Y^2)$. Let $\rho$ be the correlation between $X$ and $Y$, that is, $(X,Y)~N_2({\mu }_X+\delta {\sigma }_X,{\mu }_Y,{\tau }^2{\sigma }_X^2,{\sigma }_Y^2,\rho )$, where $\delta$ and $\tau$ are magnitudes of process mean and variability shifts, respectively. Suppose $(X_{tj},Y_{tj})$, $j=1,2,\dots ,n$, is a random sample of size $n$ taken from the process at time $t$, for $t=1,2,\dots$. It is assumed that the underlying process parameters are known for phase II monitoring. The sample means and variances based on $(X_{t1},X_{t2},\dots ,X_{tn})$ and $(Y_{t1},Y_{t2},\dots ,Y_{tn})$, respectively, are:

• ${\overline{X}}_t={\displaystyle {\sum }_{j=1}^n{X}_{tj}/n}$, and ${\overline{Y}}_t={\displaystyle {\sum }_{j=1}^n{Y}_{tj}/n}$,
• $S_{X,t}^2={\displaystyle {\sum }_{j=1}^n(X_{tj}-{\overline{X}}_t}{)}^2/(n-1)$, and
• $S_{Y,t}^2={\displaystyle {\sum }_{j=1}^n(Y_{tj}-{\overline{Y}}_t}{)}^2/(n-1)$.

Assume that the underlying process is in-control ($\delta =0$ and $\tau =1$); then, following Haq and Khoo [28], the regression estimator of ${\mu }_X$ is:

$$D_{X,t}^1={\overline{X}}_t+\rho \left(\frac{{\sigma }_X}{{\sigma }_Y}\right)({\mu }_Y-{\overline{Y}}_t)$$

(8)

with its mean and variance given by

$$E(D_{X,t}^1)={\mu }_X \mathrm{and} Var(D_{X,t}^1)=\frac{1}{n}{\sigma }_X^2(1-{\rho }^2)$$

(9)

We defined the following statistic for estimator $D_{X,t}^1$:

$$A_{X,t}=\frac{D_{X,t}^1-{\mu }_X}{{\sigma }_X\sqrt{(1-{\rho }^2)/n}}$$

(10)

where $A_{X,t}$ is a standard normal random variable, that is, $A_{X,t}~N(0,1)$ when the process is in-control.

Moreover, it is known that ${\chi }_X^2=(n-1)S_{X,t}^2/{\sigma }_X^2$ and ${\chi }_Y^2=(n-1)S_{Y,t}^2/{\sigma }_Y^2$ follow a chi-squared distribution with $n-1$ degrees of freedom when the process is in-control. Then, for an in-control process, $V_{X,t}={\mathrm{\Phi }}^{-1}\left[F\left((n-1)S_{X,t}^2/{\sigma }_X^2;n-1\right)\right]$ and $V_{Y,t}={\mathrm{\Phi }}^{-1}\left[F\left((n-1)S_{Y,t}^2/{\sigma }_Y^2;n-1\right)\right]$ have a standard normal distribution, where $\mathrm{\Phi }(\cdot )$ is the distribution function of the standard normal distribution. Following Haq [34], the difference estimator of ${\sigma }_X^2$ is defined by:

$$D_{X,t}^2=V_{X,t}-{\rho }^{\ast }\cdot V_{Y,t}$$

(11)

where ${\rho }^{*}$ is the correlation coefficient between $V_{X,t}$ and $V_{X,t}$. Hence, the mean and variance of $D_{X,t}^2$ are:

$$E(D_{X,t}^2)=0 \mathrm{and} Var(D_{X,t}^2)=1-{\rho }^{\ast 2}$$

(12)

We defined the following statistic for estimator $D_{X,t}^2$:

$$B_{X,t}=\frac{D_{X,t}^2-0}{\sqrt{1-{\rho }^{\ast }{}^2}}$$

(13)

where $B_{X,t}$ is also a standard normal random variable, that is, $B_{X,t}~N(0,1)$, when the process is in-control.

Both $A_{X,t}$ and $B_{X,t}$ are independent standard normal random variables when the process is in control. Two EWMA statistics, $A_{X,t}^{*}$ and $B_{X,t}^{*}$, can be defined from $A_{X,t}$ and $B_{X,t}$, as follows:

$$A_{X,t}^{*}=\lambda A_{X,t}+(1-\lambda )A_{X,t-1}^{*},\hspace{1em}t=1,2,3,\dots ,$$

(14)

and

$$B_{X,t}^{*}=\lambda B_{X,t}+(1-\lambda )B_{X,t-1}^{*},\hspace{1em}t=1,2,3,\dots ,$$

(15)

where $A_{X,0}^{*}$ and $B_{X,0}^{*}$ are the respective starting values, and $0<\lambda \le 1$ is a smoothing constant. Note that $A_{X,t}^{*}$ and $B_{X,t}^{*}$ are also independent because of the independence of $A_{X,t}$ and $B_{X,t}$. When the process is in control and $A_{X,0}^{*}=B_{X,0}^{*}=0$, we had both $A_{X,t}^{*}~N(0,{\sigma }_{A_t^{*}}^2)$ and $B_{X,t}^{*}~N(0,{\sigma }_{B_t^{*}}^2)$, where ${\sigma }_{A_t^{*}}^2={\sigma }_{B_t^{*}}^2=\frac{\lambda [1-{(1-\lambda )}^{2t}]}{2-\lambda }$.

The AIB-SSEWMA statistic based on $A_{X,t}^{*}$ and $B_{X,t}^{*}$ is defined as:

$$S{E}_t^{*}=A_{X,t}^{*2}+B_{X,t}^{*2} ,\hspace{1em}t=1,2,3,\dots$$

(16)

Since $S{E}_t^{*}$ is a nonnegative quantity, the initial state of the AIB-SSEWMA chart only requires an upper control limit $(UC{L}_t^{*})$, which is given by:

$$UC{L}_t^{*}=E(S{E}_t^{*})+L\sqrt{Var(S{E}_t^{*})}$$

(17)

where $E(S{E}_t^{*})$ and $Var(S{E}_t^{*})$ are the in-control mean and variance of $S{E}_t^{*}$, respectively. The control limit constant $L$ and the smoothing parameter $\lambda$ are determined by the desired in control $ARL$. In order to speed up the computation of the control limit $UC{L}_t^{*}$ for the initial state AIB-SSEWMA chart, the derivation of $E(S{E}_t^{*})$ and $Var(S{E}_t^{*})$ are shown in the Appendix A, and represented as follows:

$$UC{L}_t^{*}=2(1+L)\cdot {\sigma }_{A_t^{*}}^2$$

(18)

The computation of $UC{L}_t^{*}$ for the AIB-SSEWMA chart is similar to that of the SSEWMA chart by Xie [18]. It is noted that when correlation coefficient $\rho =0$, there does not exist a single correlated auxiliary variable $Y$, that is, the estimators of the mean and variance are only estimated by the study variable $X$. Then, the AIB-SSEWMA chart reduces to the SSEWMA chart, that is, they are identical when $\rho =0$.

The AIB-SSEWMA chart initiates an out-of-control signal when the statistic $S{E}_t^{*}$ is above the $UC{L}_t^{*}$ as if when the pair $(A_{X,t}^{*},\hspace{0.17em}{B}_{X,t}^{*})$ plots outside the circular control region centered at (0, 0) with a radius of $\sqrt{UC{L}_t^{*}}$. One advantage of using the consecutive pairs of $(A_{X,t}^{*},\hspace{0.17em}{B}_{X,t}^{*})$ plotted on a chart instead of the corresponding statistic $S{E}_t^{*}$ is that it can clearly indicate the source and direction of a process shift. To avoid drawing concentric circles, let

$${\tilde{A}}_{X,t}^{*}=A_{X,t}^{*}\sqrt{\frac{2-\lambda }{\lambda [1-{(1-\lambda )}^{2t}]}}$$

(19)

$${\tilde{B}}_{X,t}^{*}=B_{X,t}^{*}\sqrt{\frac{2-\lambda }{\lambda [1-{(1-\lambda )}^{2t}]}}$$

(20)

$$S{\tilde{E}}_t^{*}={\tilde{A}}_{X,t}^{*2}+{\tilde{B}}_{X,t}^{*2}$$

(21)

Each sample point $({\tilde{A}}_{X,t}^{*},\hspace{0.17em}{\tilde{B}}_{X,t}^{*})$ is plotted on coordinates $({\tilde{A}}_{}^{*},\hspace{0.17em}{\tilde{B}}_{}^{*})$ with circular control region centered at (0, 0) and radius $r^{*}=\sqrt{2(1+L)}$. When a sample point deviates sufficiently from the ${\tilde{A}}^{*}$-axis, it indicates that the shift is due to the process mean. Similarly, a sample point that deviates sufficiently from the ${\tilde{B}}^{*}$-axis shows a shift in process variance. A sample point that is close to either the line ${\tilde{A}}^{*}={\tilde{B}}^{*}$ or ${\tilde{A}}^{*}=-{\tilde{B}}^{*}$, indicates that the change is likely caused by a shift in both, the process mean and variance.

The steps involved in constructing the AIB-SSEWMA chart for simultaneous monitoring of the process mean and variability are summarized as follows:

(1)

Choose a suitable $(\lambda ,L)$ combination based on the values of sample size $n$ and desired in-control $ARL$.

(2)

Use Equation (18) to compute the control limit, $UC{L}_t^{*}$.

(3)

Compute the values of $A_{X,t}$, $B_{X,t}$, $A_{X,t}^{*}$, $B_{X,t}^{*}$, and $S{E}_t^{*}$ for each sample by using $A_{X,0}^{}=B_{X,0}^{}=A_{X,0}^{*}=B_{X,0}^{*}=0$ as the starting values.

(4)

The consecutive pairs of $({\tilde{A}}_{X,t}^{*},\hspace{0.17em}{\tilde{B}}_{X,t}^{*})$ are computed by Equations (19) and (20), and plotted with coordinates $({\tilde{A}}_{}^{*},\hspace{0.17em}{\tilde{B}}_{}^{*})$. The circular control region is centered at (0, 0) and the radius is $r^{*}=\sqrt{2(1+L)}$.

(5)

Check if any point $({\tilde{A}}_{X,t}^{*},\hspace{0.17em}{\tilde{B}}_{X,t}^{*})$ falls outside the circular control region given in Step (4). If an out-of-control point is detected, identify the source and direction of the shift corresponding to the position on the chart. Simple criteria and symbols are described in Table 1, and also depicted in Figure 1 for easy identification of the source and direction of an out-of-control signal. The symbols in Table 1 are defined as follows: “$m+$” and “$m-$” indicate an increase and a decrease in the process mean, respectively; “$v+$” and “$v-$” indicate an increase and a decrease in the process variance, respectively; “$++$” indicates a simultaneous increase in the process mean and variance. Similar interpretations apply to the other three cases: “$-+$”, “$--$”, and “$+-$”.

Table 1. Symbols representing the source and direction of an out-of-control signal.

		${\tilde{A}}_{X,t}^{*\mathbf{2}}+{\tilde{B}}_{X,t}^{*\mathbf{2}}>r^{*\mathbf{2}}$, $r^{*}=\sqrt{\mathbf{2}(\mathbf{1}+L)}>\mathbf{0}$
(1)	$m+$	$({\tilde{A}}_{X,t}^{*}>{\tilde{B}}_{X,t}^{*})\cap ({\tilde{A}}_{X,t}^{*}>-{\tilde{B}}_{X,t}^{*})\cap (-r^{*}\le {\tilde{B}}_{X,t}^{*}\le r^{*})$
(2)	$m-$	$({\tilde{A}}_{X,t}^{*}<{\tilde{B}}_{X,t}^{*})\cap ({\tilde{A}}_{X,t}^{*}<-{\tilde{B}}_{X,t}^{*})\cap (-r^{*}\le {\tilde{B}}_{X,t}^{*}\le r^{*})$
(3)	$v+$	$({\tilde{A}}_{X,t}^{*}<{\tilde{B}}_{X,t}^{*})\cap ({\tilde{A}}_{X,t}^{*}>-{\tilde{B}}_{X,t}^{*})\cap (-r^{*}\le {\tilde{A}}_{X,t}^{*}\le r^{*})$
(4)	$v-$	$({\tilde{A}}_{X,t}^{*}>{\tilde{B}}_{X,t}^{*})\cap ({\tilde{A}}_{X,t}^{*}<-{\tilde{B}}_{X,t}^{*})\cap (-r^{*}\le {\tilde{A}}_{X,t}^{*}\le r^{*})$
(5)	$++$	$({\tilde{A}}_{X,t}^{*}={\tilde{B}}_{X,t}^{*}>r^{*}/\sqrt{2})\cup ({\tilde{A}}_{X,t}^{*}>r^{*},{\tilde{B}}_{X,t}^{*}>r^{*})$
(6)	$-+$	$({\tilde{A}}_{X,t}^{*}=-{\tilde{B}}_{X,t}^{*}<-r^{*}/\sqrt{2})\cup ({\tilde{A}}_{X,t}^{*}<-r^{*},{\tilde{B}}_{X,t}^{*}>r^{*})$
(7)	$--$	$({\tilde{A}}_{X,t}^{*}={\tilde{B}}_{X,t}^{*}<-r^{*}/\sqrt{2})\cup ({\tilde{A}}_{X,t}^{*}<-r^{*},{\tilde{B}}_{X,t}^{*}<-r^{*})$
(8)	$+-$	$({\tilde{A}}_{X,t}^{*}=-{\tilde{B}}_{X,t}^{*}>r^{*}/\sqrt{2})\cup ({\tilde{A}}_{X,t}^{*}>r^{*},{\tilde{B}}_{X,t}^{*}<-r^{*})$

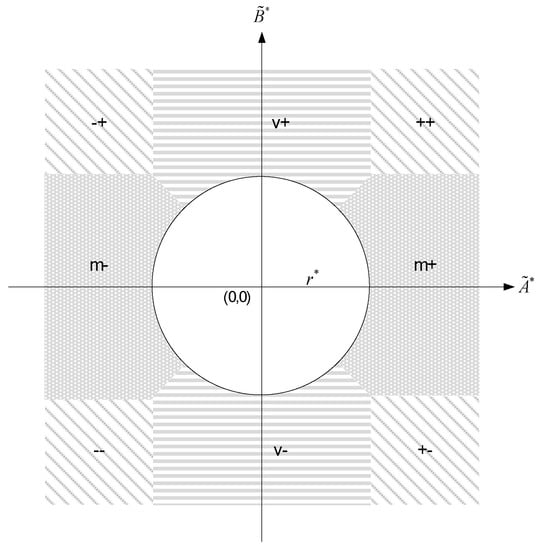Figure 1. Identification of the source and direction of an out of control signal for the auxiliary information-based (AIB)-sum of squares exponentially weighted moving average (SSEWMA) chart.

(6)

Examine each of the out-of-control points.

4. Evaluation and Performance Comparison

The performance of a control chart is generally measured in terms of its $ARL$ and $SDRL$. An in-control $ARL$ is expected to be sufficiently large to avoid frequent false alarms. However, when a present assignable cause displaces the process parameters, it results in an out-of-control process. Meanwhile, the out-of-control $ARL$ and $SDRL$ need to be sufficiently small to rapidly detect the process mean and/or variability shifts. A control chart with a smaller out-of-control $ARL$ and $SDRL$ for a given shift is generally indicated to have superior performance.

The $ARL$ and $SDRL$ values of the initial state SSEWMA and AIB-SSEWMA charts are computed through Monte Carlo simulations. In this study, the use of exact limits, instead of asymptotic limits, enables the initial state charts to quickly detect initial out-of-control signals effectively. An algorithm in R is developed to calculate $ARL$ and $SDRL$ values, which are an average of 50,000 run lengths. Without the loss of generality, the random samples $(X_{tj},Y_{tj})$, $j=1,2,\dots ,n$, for $t=1,2,\dots$, are drawn from a bivariate normal distribution, that is, $(X,Y)~N_2({\mu }_X+\delta {\sigma }_X,{\mu }_Y,{\tau }^2{\sigma }_X^2,{\sigma }_Y^2,\rho )$, where $\delta$ and $\tau$ are magnitudes of process mean and variability shifts, respectively.

Suppose ${\mu }_X={\mu }_Y=0$ and ${\sigma }_X={\sigma }_Y=1$, when $\delta =0$ and $\tau =1$ indicate that the underlying process is in-control. Subsequently the charting multiplier $L$ and charting parameter $\lambda$ are adjusted to achieve the desired in-control $ARL$. Table 2 presents the $L$ values for the initial state AIB-SSEWMA chart. The specific charting parameter of $\lambda$ = {0.05, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0}, correlation coefficient values of $\rho$ = {0.00, 0.25, 0.50, 0.75, 0.95}, and sample size $n$ = {5, 10} are considered in Table 2 to achieve an in-control $ARL$ of approximately 370. Note that ${\rho }^{*}$ is the correlation coefficient value between $V_{X,t}$ and $V_{Y,t}$ in Equation (11), which is determined by n and $\rho$ Haq [27] computes the values of ${\rho }^{*}$ for different choices of $n$ and $\rho$ through Monte Carlo simulations. The partial pair values of $(\rho ,{\rho }^{*})$ from Haq [27] are (0.25,0.05639), (0.50,0.22933), (0.75,0.53136), and (0.95,0.88808) for $n=5$; they are (0.25,0.05980), (0.50,0.24084), (0.75,0.54947), and (0.95,0.89736) for $n=10$.

Table 2. $\rho$ values for the AIB-SSEWMA charts when in-control $ARL\approx 370$.

		$\mathit{\lambda }$
$\mathit{n}$	$\mathit{\rho }$	0.05	0.1	0.2	0.3	0.4	0.5	0.7	0.8	0.9	1.0
5	0.00	3.533	4.082	4.522	4.714	4.813	4.869	4.893	4.901	4.909	4.909
	0.25	3.532	4.081	4.528	4.719	4.816	4.861	4.885	4.897	4.907	4.909
	0.50	3.528	4.083	4.516	4.719	4.812	4.861	4.888	4.907	4.911	4.921
	0.75	3.534	4.097	4.552	4.768	4.887	4.957	5.012	5.048	5.067	5.076
	0.95	3.544	4.120	4.640	4.913	5.084	5.220	5.325	5.411	5.466	5.503
10	0.00	3.526	4.076	4.522	4.708	4.799	4.849	4.881	4.899	4.912	4.919
	0.25	3.519	4.080	4.526	4.710	4.804	4.860	4.884	4.896	4.909	4.919
	0.50	3.513	4.058	4.516	4.705	4.793	4.851	4.878	4.890	4.906	4.911
	0.75	3.470	4.019	4.471	4.658	4.760	4.823	4.861	4.890	4.906	4.911
	0.95	3.356	3.896	4.349	4.543	4.658	4.732	4.778	4.810	4.833	4.848

From Table 2, we observed that a small sample size $n$ needs a large charting multiplier $L$ to achieve the desired in-control $ARL$, which was obviously larger for $\rho >0.5$. For a fixed value of $\rho$, the values of $L$ increased as the smoothing parameter $\lambda$ increased. For a fixed value of $\lambda$, the values of $L$ increased when $\rho >0.5$ at $n=5$; however, they decreased when $\rho >0.5$ at $n=10$. Moreover, the difference between $L’s$ was large for a larger $\rho$ value. For example, when $n=5$, the value of $L$ at $\rho =0$ for $\lambda$ = 0.05 and 1.0 were 3.533 and 4.909, respectively; however, those at $\rho =0.95$ are 3.544 and 5.503, respectively. Similar results were found regarding the large sample size $n=10$ in Table 2.

When $\delta \ne 0$ and/or $\tau =1$, the underlying process containing assignable causes results in an out-of-control process. The initial state AIB-SSEWMA charts are maintained at the desired in-control $ARL$, and the out-of-control $ARLs$, and $SDRLs$ were evaluated for specific process shifts. In this study, we considered the process mean shifts $\delta$ = {0.00, 0.25, 0.50, 1.00, 1.50, 3.00}, and the process standard deviation shifts $\tau$ = {0.50, 1.00, 1.25, 1.50}. For each shift combination of $(\delta ,\tau )$ under different scenarios $\rho$, the out-of-control $ARLs$ and $SDRLs$ of the initial state AIB-SSEWMA chart with sample size $n=5$ were calculated under the corresponding parameter combination of $(\lambda ,L)$, where the smoothing constant $\lambda$ = {0.05, 0.10, 0.25} and correlation coefficient $\rho$ = {0.00, 0.25, 0.50, 0.75, 0.95} were investigated to match the desired in-control $ARL$ value by adjusting the control limit constant $L$.

Table 3 and Table 4 show the $(\lambda ,L)$ combinations and the corresponding out-of-control $ARLs$ and $SDRLs$ of the AIB-SSEWMA charts with in-control $ARL$ at approximately 185 and 370, respectively. In particular, the AIB-SSEWMA chart with $\rho =0$ was identical to the SSEWMA chart proposed by Xie [18]. That is, the SSEWMA chart is a special case of the AIB-SSEWMA chart when $\rho =0$.

Table 3. The run length profiles of the AIB-SSEWMA charts when in-control $ARL\approx 185$.

			$\mathit{\delta }=\mathbf{0.00}$		$\mathit{\delta }=\mathbf{0.25}$		$\mathit{\delta }=\mathbf{0.50}$		$\mathit{\delta }=\mathbf{1.00}$		$\mathit{\delta }=\mathbf{1.50}$		$\mathit{\delta }=\mathbf{3.00}$
			ARL	SDRL	ARL	SDRL	ARL	SDRL	ARL	SDRL	ARL	SDRL	ARL	SDRL
$\mathit{\tau }$	$\mathit{\rho }$	$\mathit{L}(\mathit{K})$	$\mathit{\lambda }=0.05$
0.50	0.00	2.764	3.79	1.59	3.39	1.38	2.63	0.99	1.51	0.54	1.03	0.17	1.00	0.00
	0.25	2.763	3.77	1.59	3.36	1.37	2.57	0.97	1.46	0.53	1.02	0.15	1.00	0.00
	0.50	2.776	3.60	1.53	3.15	1.29	2.34	0.90	1.29	0.47	1.01	0.08	1.00	0.00
	0.75	2.779	2.81	1.21	2.40	1.01	1.75	0.71	1.06	0.24	1.00	0.02	1.00	0.00
	0.95	2.777	1.18	0.41	1.11	0.33	1.03	0.17	1.00	0.02	1.00	0.00	1.00	0.00
1.00	0.00	2.764	185.12	201.76	17.04	13.51	5.62	3.74	1.99	1.04	1.24	0.46	1.00	0.00
	0.25	2.763	185.04	202.23	16.14	12.64	5.35	3.52	1.91	0.98	1.20	0.43	1.00	0.00
	0.50	2.776	185.07	202.70	13.59	10.41	4.49	2.87	1.66	0.80	1.10	0.31	1.00	0.00
	0.75	2.779	184.98	201.46	8.81	6.28	2.97	1.74	1.23	0.45	1.01	0.09	1.00	0.00
	0.95	2.777	185.06	202.19	2.73	1.56	1.17	0.39	1.00	0.00	1.00	0.00	1.00	0.00
1.25	0.00	2.764	10.81	9.85	7.45	6.45	4.22	3.18	1.91	1.12	1.27	0.52	1.00	0.02
	0.25	2.763	10.77	9.85	7.29	6.24	4.07	3.05	1.85	1.06	1.24	0.49	1.00	0.02
	0.50	2.776	10.39	9.43	6.66	5.58	3.57	2.59	1.64	0.87	1.14	0.37	1.00	0.01
	0.75	2.779	8.40	7.42	4.92	3.90	2.55	1.68	1.26	0.51	1.02	0.15	1.00	0.00
	0.95	2.777	3.31	2.51	1.93	1.19	1.19	0.44	1.00	0.02	1.00	0.00	1.00	0.00
1.50	0.00	2.764	3.84	3.21	3.46	2.80	2.75	2.07	1.72	1.02	1.26	0.53	1.00	0.05
	0.25	2.763	3.81	3.19	3.42	2.76	2.70	2.01	1.68	0.98	1.24	0.50	1.00	0.04
	0.50	2.776	3.67	3.07	3.23	2.57	2.49	1.81	1.53	0.83	1.16	0.40	1.00	0.02
	0.75	2.779	2.97	2.35	2.59	1.94	1.94	1.27	1.24	0.52	1.04	0.20	1.00	0.00
	0.95	2.777	1.42	0.75	1.30	0.61	1.12	0.37	1.01	0.07	1.00	0.01	1.00	0.00
$\tau$	$\rho$	$L(K)$	$\lambda =0.10$
0.50	0.00	3.313	4.27	1.73	3.83	1.50	2.94	1.06	1.67	0.56	1.07	0.25	1.00	0.00
	0.25	3.317	4.26	1.74	3.79	1.49	2.88	1.04	1.61	0.56	1.05	0.22	1.00	0.00
	0.50	3.323	4.06	1.67	3.54	1.40	2.61	0.96	1.42	0.52	1.01	0.12	1.00	0.00
	0.75	3.326	3.15	1.31	2.67	1.08	1.92	0.76	1.10	0.30	1.00	0.02	1.00	0.00
	0.95	3.338	1.24	0.47	1.15	0.38	1.04	0.21	1.00	0.02	1.00	0.00	1.00	0.00
1.00	0.00	3.313	185.03	190.50	20.29	16.22	6.38	4.06	2.19	1.13	1.31	0.52	1.00	0.01
	0.25	3.317	184.96	189.62	19.15	15.13	6.06	3.83	2.10	1.06	1.27	0.48	1.00	0.00
	0.50	3.323	184.99	189.58	15.89	12.12	5.08	3.11	1.80	0.87	1.14	0.36	1.00	0.00
	0.75	3.326	185.09	190.38	10.11	7.01	3.31	1.87	1.30	0.51	1.01	0.11	1.00	0.00
	0.95	3.338	184.92	190.55	3.04	1.69	1.23	0.45	1.00	0.01	1.00	0.00	1.00	0.00
1.25	0.00	3.313	12.23	10.67	8.39	6.89	4.69	3.40	2.08	1.20	1.34	0.58	1.00	0.03
	0.25	3.317	12.20	10.61	8.24	6.73	4.53	3.25	2.00	1.14	1.30	0.54	1.00	0.02
	0.50	3.323	11.71	10.14	7.48	5.99	3.96	2.76	1.76	0.94	1.19	0.42	1.00	0.01
	0.75	3.326	9.49	7.91	5.52	4.16	2.81	1.80	1.33	0.57	1.03	0.18	1.00	0.00
	0.95	3.338	3.72	2.70	2.11	1.28	1.24	0.49	1.00	0.03	1.00	0.00	1.00	0.00
1.50	0.00	3.313	4.26	3.42	3.83	2.97	3.02	2.19	1.85	1.10	1.32	0.59	1.00	0.06
	0.25	3.317	4.25	3.42	3.80	2.95	2.96	2.14	1.80	1.05	1.29	0.56	1.00	0.05
	0.50	3.323	4.08	3.25	3.58	2.74	2.73	1.93	1.63	0.89	1.19	0.45	1.00	0.02
	0.75	3.326	3.30	2.53	2.84	2.07	2.11	1.36	1.30	0.57	1.05	0.22	1.00	0.00
	0.95	3.338	1.50	0.82	1.37	0.67	1.15	0.41	1.01	0.08	1.00	0.01	1.00	0.00
$\tau$	$\rho$	$L(K)$	$\lambda =0.25$
0.50	0.00	3.889	5.20	2.38	4.56	1.95	3.39	1.27	1.84	0.59	1.13	0.33	1.00	0.00
	0.25	3.900	5.18	2.39	4.51	1.93	3.31	1.23	1.78	0.58	1.10	0.30	1.00	0.00
	0.50	3.905	4.89	2.22	4.17	1.76	2.97	1.11	1.56	0.55	1.03	0.17	1.00	0.00
	0.75	3.926	3.65	1.57	3.06	1.26	2.14	0.83	1.16	0.37	1.00	0.04	1.00	0.00
	0.95	3.996	1.32	0.53	1.21	0.44	1.06	0.24	1.00	0.02	1.00	0.00	1.00	0.00
1.00	0.00	3.889	185.03	186.63	29.87	27.03	7.75	5.38	2.42	1.24	1.40	0.57	1.00	0.01
	0.25	3.900	184.98	185.26	28.10	25.09	7.34	5.01	2.31	1.17	1.35	0.54	1.00	0.01
	0.50	3.905	184.93	185.80	22.72	19.77	5.99	3.89	1.97	0.95	1.20	0.41	1.00	0.00
	0.75	3.926	184.96	185.88	13.42	10.70	3.77	2.16	1.39	0.57	1.02	0.14	1.00	0.00
	0.95	3.996	185.09	186.67	3.47	1.94	1.31	0.51	1.00	0.01	1.00	0.00	1.00	0.00
1.25	0.00	3.889	14.29	12.88	9.66	8.08	5.26	3.83	2.26	1.29	1.42	0.63	1.00	0.04
	0.25	3.900	14.32	12.88	9.50	7.89	5.07	3.67	2.17	1.22	1.37	0.59	1.00	0.03
	0.50	3.905	13.75	12.26	8.63	7.06	4.43	3.08	1.90	1.02	1.23	0.47	1.00	0.01
	0.75	3.926	11.21	9.62	6.31	4.81	3.10	1.97	1.40	0.63	1.05	0.21	1.00	0.00
	0.95	3.996	4.21	2.99	2.31	1.39	1.30	0.54	1.00	0.04	1.00	0.00	1.00	0.00
1.50	0.00	3.889	4.64	3.63	4.19	3.20	3.28	2.32	1.97	1.16	1.38	0.63	1.01	0.07
	0.25	3.900	4.64	3.64	4.15	3.14	3.22	2.26	1.92	1.11	1.35	0.60	1.00	0.06
	0.50	3.905	4.46	3.47	3.90	2.91	2.95	2.03	1.73	0.96	1.24	0.49	1.00	0.03
	0.75	3.926	3.61	2.68	3.10	2.19	2.27	1.44	1.36	0.62	1.07	0.26	1.00	0.00
	0.95	3.996	1.61	0.89	1.44	0.73	1.19	0.45	1.01	0.10	1.00	0.01	1.00	0.00

Table 4. The run length profiles of the AIB-SSEWMA charts when in-control $ARL\approx 370$.

			$\mathit{\delta }=\mathbf{0.00}$		$\mathit{\delta }=\mathbf{0.25}$		$\mathit{\delta }=\mathbf{0.50}$		$\mathit{\delta }=\mathbf{1.00}$		$\mathit{\delta }=\mathbf{1.50}$		$\mathit{\delta }=\mathbf{3.00}$
			ARL	SDRL	ARL	SDRL	ARL	SDRL	ARL	SDRL	ARL	SDRL	ARL	SDRL
$\mathit{\tau }$	$\mathit{\rho }$	$\mathit{L}(\mathit{K})$	$\mathit{\lambda }=0.05$
0.50	0.00	3.533	4.45	1.76	3.98	1.52	3.06	1.08	1.73	0.57	1.09	0.28	1.00	0.00
	0.25	3.532	4.43	1.76	3.94	1.51	2.99	1.06	1.67	0.56	1.06	0.24	1.00	0.00
	0.50	3.528	4.21	1.68	3.67	1.42	2.71	0.98	1.47	0.53	1.02	0.14	1.00	0.00
	0.75	3.534	3.27	1.33	2.78	1.11	1.99	0.77	1.12	0.32	1.00	0.03	1.00	0.00
	0.95	3.544	1.26	0.49	1.17	0.40	1.05	0.22	1.00	0.02	1.00	0.00	1.00	0.00
1.00	0.00	3.533	370.01	384.51	21.81	16.11	6.80	4.23	2.28	1.16	1.34	0.54	1.00	0.01
	0.25	3.532	370.08	386.17	20.61	15.14	6.44	3.98	2.17	1.09	1.29	0.50	1.00	0.00
	0.50	3.528	370.05	386.60	16.99	12.09	5.36	3.23	1.86	0.89	1.16	0.38	1.00	0.00
	0.75	3.534	370.25	387.45	10.80	7.20	3.47	1.94	1.33	0.53	1.01	0.12	1.00	0.00
	0.95	3.544	370.32	386.42	3.17	1.75	1.25	0.47	1.00	0.01	1.00	0.00	1.00	0.00
1.25	0.00	3.533	13.88	11.76	9.28	7.49	5.02	3.61	2.16	1.25	1.37	0.60	1.00	0.03
	0.25	3.532	13.84	11.74	9.08	7.30	4.84	3.48	2.07	1.18	1.33	0.56	1.00	0.02
	0.50	3.528	13.23	11.15	8.21	6.49	4.20	2.92	1.81	0.98	1.20	0.44	1.00	0.01
	0.75	3.534	10.61	8.72	5.97	4.49	2.94	1.90	1.35	0.59	1.04	0.19	1.00	0.00
	0.95	3.544	3.97	2.90	2.19	1.35	1.26	0.51	1.00	0.03	1.00	0.00	1.00	0.00
1.50	0.00	3.533	4.61	3.73	4.11	3.23	3.21	2.36	1.91	1.15	1.35	0.61	1.00	0.06
	0.25	3.532	4.60	3.74	4.08	3.19	3.14	2.28	1.85	1.10	1.31	0.58	1.00	0.05
	0.50	3.528	4.40	3.56	3.82	2.97	2.87	2.05	1.67	0.93	1.21	0.46	1.00	0.02
	0.75	3.534	3.52	2.74	3.00	2.21	2.19	1.44	1.32	0.60	1.06	0.23	1.00	0.00
	0.95	3.544	1.55	0.87	1.40	0.71	1.17	0.43	1.01	0.09	1.00	0.01	1.00	0.00
$\tau$	$\rho$	$L(K)$	$\lambda =0.10$
0.50	0.00	4.082	4.96	1.92	4.42	1.65	3.38	1.16	1.89	0.58	1.15	0.36	1.00	0.00
	0.25	4.081	4.94	1.92	4.37	1.63	3.30	1.14	1.82	0.57	1.12	0.32	1.00	0.00
	0.50	4.083	4.69	1.83	4.08	1.53	2.98	1.04	1.60	0.55	1.04	0.19	1.00	0.00
	0.75	4.097	3.62	1.43	3.07	1.19	2.18	0.82	1.17	0.38	1.00	0.04	1.00	0.00
	0.95	4.120	1.34	0.54	1.23	0.45	1.07	0.25	1.00	0.03	1.00	0.00	1.00	0.00
1.00	0.00	4.082	370.21	375.39	26.42	20.76	7.62	4.65	2.49	1.24	1.42	0.59	1.00	0.01
	0.25	4.081	370.13	374.52	24.85	19.30	7.21	4.35	2.37	1.17	1.37	0.55	1.00	0.01
	0.50	4.083	370.03	376.65	20.12	15.04	5.95	3.46	2.01	0.95	1.22	0.43	1.00	0.00
	0.75	4.097	370.16	374.74	12.40	8.28	3.83	2.08	1.41	0.58	1.02	0.15	1.00	0.00
	0.95	4.120	370.13	377.67	3.50	1.86	1.32	0.52	1.00	0.01	1.00	0.00	1.00	0.00
1.25	0.00	4.082	15.57	13.10	10.28	8.02	5.51	3.82	2.33	1.32	1.44	0.65	1.00	0.04
	0.25	4.081	15.53	13.10	10.04	7.80	5.31	3.67	2.24	1.25	1.39	0.61	1.00	0.03
	0.50	4.083	14.86	12.35	9.11	6.96	4.61	3.10	1.95	1.05	1.25	0.48	1.00	0.01
	0.75	4.097	11.87	9.46	6.61	4.78	3.21	2.01	1.43	0.64	1.05	0.22	1.00	0.00
	0.95	4.120	4.39	3.07	2.37	1.43	1.31	0.56	1.00	0.04	1.00	0.00	1.00	0.00
1.50	0.00	4.082	5.05	3.93	4.49	3.37	3.49	2.47	2.04	1.22	1.41	0.66	1.01	0.08
	0.25	4.081	5.03	3.91	4.45	3.35	3.41	2.41	1.98	1.17	1.37	0.62	1.00	0.06
	0.50	4.083	4.81	3.73	4.17	3.11	3.11	2.15	1.77	1.00	1.25	0.50	1.00	0.03
	0.75	4.097	3.86	2.88	3.27	2.34	2.36	1.52	1.38	0.64	1.07	0.27	1.00	0.00
	0.95	4.120	1.64	0.94	1.47	0.76	1.20	0.47	1.01	0.10	1.00	0.01	1.00	0.00
$\tau$	$\rho$	$L(K)$	$\lambda =0.25$
0.50	0.00	4.639	6.15	2.85	5.34	2.29	3.89	1.43	2.06	0.61	1.24	0.43	1.00	0.00
	0.25	4.631	6.10	2.83	5.25	2.24	3.78	1.39	1.99	0.60	1.19	0.39	1.00	0.00
	0.50	4.634	5.71	2.59	4.83	2.03	3.38	1.22	1.74	0.57	1.07	0.26	1.00	0.00
	0.75	4.675	4.21	1.77	3.49	1.40	2.40	0.90	1.24	0.44	1.00	0.05	1.00	0.00
	0.95	4.792	1.44	0.60	1.30	0.50	1.09	0.30	1.00	0.03	1.00	0.00	1.00	0.00
1.00	0.00	4.639	369.88	368.13	43.86	40.01	9.54	6.69	2.72	1.35	1.51	0.64	1.00	0.02
	0.25	4.631	369.98	369.94	40.65	36.78	8.89	6.10	2.59	1.27	1.45	0.60	1.00	0.01
	0.50	4.634	370.18	374.28	31.77	28.19	7.14	4.62	2.18	1.03	1.27	0.47	1.00	0.00
	0.75	4.675	370.08	373.69	17.54	14.21	4.35	2.44	1.50	0.63	1.04	0.18	1.00	0.00
	0.95	4.792	369.80	371.44	4.02	2.20	1.41	0.57	1.00	0.01	1.00	0.00	1.00	0.00
1.25	0.00	4.639	18.99	17.16	12.22	10.20	6.23	4.50	2.53	1.43	1.52	0.70	1.00	0.05
	0.25	4.631	18.89	17.17	11.85	9.85	5.96	4.26	2.41	1.34	1.47	0.66	1.00	0.04
	0.50	4.634	18.15	16.39	10.62	8.58	5.14	3.53	2.08	1.11	1.30	0.53	1.00	0.01
	0.75	4.675	14.47	12.49	7.60	5.77	3.52	2.21	1.50	0.69	1.07	0.25	1.00	0.00
	0.95	4.792	4.99	3.48	2.59	1.54	1.38	0.61	1.00	0.05	1.00	0.00	1.00	0.00
1.50	0.00	4.639	5.50	4.26	4.88	3.68	3.75	2.62	2.17	1.28	1.47	0.70	1.01	0.09
	0.25	4.631	5.46	4.22	4.82	3.63	3.66	2.55	2.10	1.22	1.43	0.67	1.01	0.07
	0.50	4.634	5.21	4.01	4.52	3.36	3.33	2.27	1.87	1.05	1.30	0.55	1.00	0.03
	0.75	4.675	4.20	3.10	3.53	2.47	2.53	1.60	1.44	0.69	1.09	0.30	1.00	0.00
	0.95	4.792	1.76	1.00	1.55	0.82	1.24	0.50	1.01	0.11	1.00	0.01	1.00	0.00

To ensure the accuracy of the simulation algorithm, the following example where $\rho =0$ was used to compare our numerical results of the AIB-SSEWMA chart with those of the SSEWMA chart by Xie [18]. For $\lambda =0.05$, the control limit constants $L(K)$ of both charts at in-control $ARL$ of 370 were 3.533. This parameter combination gives the out-of-control $ARL$ and $SDRL$ of the initial state AIB-SSEWMA chart at $\delta =0.25$ and $\tau =1.25$ of 9.28 and 7.49, respectively (cf. Table 4). Meanwhile, the out-of-control $ARL$ and $SDRL$ for the same parameter combination from Xie [18] were 9.28 and 7.49, respectively, which were similar to our simulated results.

From Table 3 and Table 4, it was observed that the performance of both the SSEWMA chart and the AIB-SSEWMA chart was better when detecting different shifts with smaller $\lambda$. Moreover, the AIB-SSEWMA chart performed uniformly better than the SSEWMA chart, which was obvious in detecting the small process mean and/or variability shifts. However, they performed almost equally in detecting large process shifts. As the value of $\rho$ increased, the effectiveness of the AIB-SSEWMA chart in detecting different kinds of shifts increased. For example, considering the small process shifts $\delta =0.25$ and $\tau =1.25$ maintained at in-control $ARL\approx 370$; then, the out-of-control $ARL$ values at $\lambda =0.05$ for $\rho$ = 0.00, 0.25, 0.50, 0.75, and 0.95 were 9.28, 9.08, 8.21, 5.97, and 2.19, respectively.

This section investigated the diagnostic abilities of the proposed AIB-SSEWMA chart against the existing SSEWMA chart. For each shift combination of $\delta$ = {0.00, 0.25, 0.50, 1.00, 1.50, 2.00, 3.00} and $\tau$ = {0.50, 0.75, 1.00, 1.25, 1.50, 3.00}, 1000 out-of-control signals were simulated for both charts. The guidelines to count the number of out-of-control signals triggered by both charts have been reported by Haq [34]. According to Table 4, we considered the sample size $n=5$ at in-control $ARL\approx 370$; the parameter combinations of $(\lambda ,L)$ were (0.05, 3.533) and (0.05, 3.534) used for the SSEWMA chart when $\rho =0$ and AIB-SSEWMA chart when $\rho =0.75$, respectively. Table 5 presents the number of out-of-control signals, which shows that the AIB-SSEWMA chart had better diagnostic abilities than that the SSEWMA chart. For example, in the case of an upward shift, there existed both process mean shift $\delta =0.25$ and variability shift $\tau =1.25$. The SSEWMA and AIB-SSEWMA charts triggered 323 and 421 out-of-control “$++$” signals out of 1000 signals, respectively.

Table 5. Comparison of the detection abilities of the SSEWMA and AIB-SSEWMA charts.

		SSEWMA Chart							AIB-SSEWMA Chart
$\mathit{\tau }$	$\mathit{\delta }$	0.00	0.25	0.50	1.00	1.50	2.00	3.00	0.00	0.25	0.50	1.00	1.50	2.00	3.00
0.50	$m+$	0	0	0	8	41	47	47	0	0	2	20	30	30	30
	$m-$	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	$v+$	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	$v-$	877	296	5	0	0	0	0	643	155	4	0	0	0	0
	$++$	0	4	176	808	931	953	953	0	61	433	923	967	970	970
	$+-$	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	$-+$	0	0	0	0	0	0	0	1	0	0	0	0	0	0
	$--$	123	700	819	184	28	0	0	356	784	561	57	3	0	0
0.75	$m+$	0	27	144	292	299	310	315	0	42	169	252	269	269	269
	$m-$	1	0	0	0	0	0	0	0	0	0	0	0	0	0
	$v+$	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	$v-$	835	130	5	0	0	0	0	783	37	1	0	0	0	0
	$++$	4	296	643	671	694	690	685	3	460	711	735	730	731	731
	$+-$	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	$-+$	1	0	0	0	0	0	0	1	0	0	0	0	0	0
	$--$	159	547	208	37	7	0	0	213	461	119	13	1	0	0
1.00	$m+$	158	654	585	443	385	365	351	140	639	489	387	358	356	356
	$m-$	154	0	0	0	0	0	0	169	0	0	0	0	0	0
	$v+$	153	3	2	0	0	0	0	111	1	1	0	0	0	0
	$v-$	139	5	0	0	0	0	0	159	3	0	0	0	0	0
	$++$	108	272	367	529	606	633	649	119	310	476	602	642	644	644
	$+-$	103	31	22	16	5	2	0	90	15	16	3	0	0	0
	$-+$	104	2	1	0	0	0	0	95	1	0	0	0	0	0
	$--$	81	33	23	12	4	0	0	117	31	18	8	0	0	0
1.25	$m+$	12	138	232	258	247	246	258	14	149	210	233	229	226	225
	$m-$	16	1	1	0	0	0	0	9	0	0	0	0	0	0
	$v+$	476	163	28	4	0	0	0	462	76	14	0	0	0	0
	$v-$	0	0	0	0	0	0	0	1	1	0	0	0	0	0
	$++$	75	323	516	654	720	746	742	72	421	619	730	763	774	775
	$+-$	341	362	216	79	31	8	0	357	342	152	34	8	0	0
	$-+$	75	7	1	1	0	0	0	82	8	2	0	0	0	0
	$--$	5	6	6	4	2	0	0	3	3	3	3	0	0	0
1.50	$m+$	12	26	60	125	150	167	174	8	30	79	110	137	146	147
	$m-$	12	3	1	0	0	0	0	14	2	2	0	0	0	0
	$v+$	310	242	74	11	3	0	0	286	158	43	6	0	0	0
	$v-$	0	0	0	0	0	0	0	0	1	0	0	0	0	0
	$++$	76	235	410	639	750	786	821	102	280	480	757	822	848	853
	$+-$	506	465	445	223	95	47	5	496	507	391	124	41	6	0
	$-+$	83	27	7	2	1	0	0	93	21	2	1	0	0	0
	$--$	1	2	3	0	1	0	0	1	1	3	2	0	0	0
3.00	$m+$	11	11	15	16	18	22	25	3	5	5	9	13	15	16
	$m-$	3	3	0	0	0	0	0	2	1	1	0	0	0	0
	$v+$	120	106	89	85	47	35	6	88	82	69	52	39	22	3
	$v-$	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	$++$	70	101	142	234	338	461	693	95	131	188	302	435	591	809
	$+-$	675	687	685	629	586	476	274	684	688	673	610	504	368	172
	$-+$	121	92	69	36	11	6	2	128	93	64	27	9	4	0
	$--$	0	0	0	0	0	0	0	0	0	0	0	0	0	0

5. Comparative Study

Haq [34] proposed the auxiliary information based (AIB) maximum EWMA chart, called the AIB-MaxEWMA chart. The effectiveness of the AIB-MaxEWMA chart in simultaneously detecting shifts in the process mean and variability encompasses the existing MaxEWMA chart. Haq [34] defines the plotting statistic of the AIB-MaxEWMA chart, say $H_t$, based on $A_{X,t}^{*}$ and $B_{X,t}^{*}$, and is given by:

$$H_t^{}=Max\left(\left|A_{X,t}^{*}\right|,\left|B_{X,t}^{*}\right|\right),\hspace{1em}t=1,2,3,\dots$$

(22)

Since $H_t$ is a nonnegative quantity, the initial state of the AIB-MaxEWMA chart only requires an upper control limit $(UC{L}_t)$, which is given by:

$$UC{L}_t=E(H_t)+L\sqrt{Var(H_t)}=(1.12838+L\times 0.60281){\sigma }_{A_t^{*}}$$

(23)

where the value of control limit constant $L$ helps in fixing the in-control $ARL$ of the AIB-MaxEWMA chart to a desired level. Interested readers can refer to Haq [34] for further details.

Below is a comprehensive comparison of the proposed AIB-SSEWMA and AIB-MaxEWMA charts for simultaneously detecting a small process mean and variability shifts. Haq [34] recommended using a smaller $\lambda$ for effectively monitoring small process shifts. Accordingly, Table 6 lists the $AR{L}_1$ values of the AIB-MaxEWMA and AIB-SSEWMA charts with $\lambda =0.05$ when $n=5$ and $n=10$ at in-control $ARL$ of around 370. The partial $AR{L}_1$ values of the AIB-MaxEWMA chart with $\lambda =0.05$ and $n=5$ were extracted from Haq [34]. Comparing the AIB-MaxEWMA chart with the proposed AIB-SSEWMA chart, an interesting finding was that the AIB-MaxEWMA chart performed better than AIB-SSEWMA chart when detecting either only process mean shifts, or decreased in the process variance. However, the AIB-SSEWMA chart was more sensitive than the AIB-MaxEWMA chart in simultaneously detecting a small process mean and variability shifts.

Table 6. ARLs of the AIB-MaxEWMA and AIB-SSEWMA charts when $n=5$ and $n=10$ at in-control $ARL\approx 370$.

		$\mathit{n}=5$
		AIB-MaxEWMA Chart						AIB-SSEWMA Chart
$\mathit{\tau }$	$\mathit{\rho }\backslash \mathit{\delta }$	0.00	0.25	0.50	1.00	2.00	3.00	0.00	0.25	0.50	1.00	2.00	3.00
0.50	0.00	4.00	4.00	3.81	2.03	1.00	1.00	4.45	3.98	3.06	1.73	1.00	1.00
	0.25	3.99	3.99	3.75	1.95	1.00	1.00	4.43	3.94	2.99	1.67	1.00	1.00
	0.50	3.83	3.82	3.43	1.67	1.00	1.00	4.21	3.67	2.71	1.47	1.00	1.00
	0.75	3.06	3.01	2.46	1.21	1.00	1.00	3.27	2.78	1.99	1.12	1.00	1.00
	0.95	1.28	1.22	1.09	1.00	1.00	1.00	1.26	1.17	1.05	1.00	1.00	1.00
0.75	0.00	15.41	12.86	6.22	2.14	1.01	1.00	16.75	10.70	5.41	2.12	1.02	1.00
	0.25	15.35	12.58	5.92	2.04	1.01	1.00	16.70	10.43	5.19	2.03	1.01	1.00
	0.50	14.67	11.35	4.96	1.74	1.00	1.00	15.87	9.30	4.44	1.74	1.00	1.00
	0.75	11.47	7.95	3.23	1.24	1.00	1.00	12.20	6.50	2.99	1.24	1.00	1.00
	0.95	3.91	2.46	1.23	1.00	1.00	1.00	3.97	2.12	1.17	1.00	1.00	1.00
1.00	0.00	369.83	21.36	6.59	2.22	1.05	1.00	370.01	21.81	6.80	2.28	1.06	1.00
	0.25	370.17	20.21	6.24	2.12	1.04	1.00	370.08	20.61	6.44	2.17	1.04	1.00
	0.50	370.39	16.68	5.20	1.81	1.01	1.00	370.05	16.99	5.36	1.86	1.01	1.00
	0.75	370.14	10.58	3.38	1.30	1.00	1.00	370.25	10.80	3.47	1.33	1.00	1.00
	0.95	370.10	3.08	1.23	1.00	1.00	1.00	370.32	3.17	1.25	1.00	1.00	1.00
1.25	0.00	14.31	10.15	5.41	2.22	1.09	1.00	13.88	9.28	5.02	2.16	1.09	1.00
	0.25	14.23	9.94	5.20	2.13	1.07	1.00	13.84	9.08	4.84	2.07	1.07	1.00
	0.50	13.63	9.02	4.51	1.86	1.03	1.00	13.23	8.21	4.20	1.81	1.03	1.00
	0.75	10.91	6.59	3.14	1.37	1.00	1.00	10.61	5.97	2.94	1.35	1.00	1.00
	0.95	4.10	2.41	1.31	1.00	1.00	1.00	3.97	2.19	1.26	1.00	1.00	1.00
1.50	0.00	4.78	4.37	3.47	2.03	1.12	1.00	4.61	4.11	3.21	1.91	1.11	1.00
	0.25	4.77	4.34	3.41	1.98	1.10	1.00	4.60	4.08	3.14	1.85	1.09	1.00
	0.50	4.57	4.09	3.11	1.77	1.05	1.00	4.40	3.82	2.87	1.67	1.05	1.00
	0.75	3.68	3.22	2.39	1.38	1.01	1.00	3.52	3.00	2.19	1.32	1.01	1.00
	0.95	1.61	1.46	1.21	1.01	1.00	1.00	1.55	1.40	1.17	1.01	1.00	1.00
		$n=10$
$\tau$	$\rho \backslash \delta$	0.00	0.25	0.50	1.00	2.00	3.00	0.00	0.25	0.50	1.00	2.00	3.00
0.50	0.00	2.01	2.00	1.96	1.17	1.00	1.00	2.18	2.01	1.64	1.04	1.00	1.00
	0.25	1.99	1.99	1.93	1.13	1.00	1.00	2.17	1.99	1.61	1.03	1.00	1.00
	0.50	1.92	1.92	1.80	1.05	1.00	1.00	2.08	1.88	1.48	1.01	1.00	1.00
	0.75	1.56	1.55	1.37	1.00	1.00	1.00	1.65	1.47	1.15	1.00	1.00	1.00
	0.95	1.01	1.00	1.00	1.00	1.00	1.00	1.01	1.00	1.00	1.00	1.00	1.00
0.75	0.00	7.13	6.31	3.39	1.32	1.00	1.00	7.64	5.25	2.90	1.29	1.00	1.00
	0.25	7.10	6.19	3.24	1.27	1.00	1.00	7.63	5.13	2.79	1.25	1.00	1.00
	0.50	6.78	5.66	2.77	1.13	1.00	1.00	7.26	4.65	2.43	1.12	1.00	1.00
	0.75	5.31	4.06	1.87	1.01	1.00	1.00	5.60	3.31	1.71	1.01	1.00	1.00
	0.95	1.94	1.43	1.01	1.00	1.00	1.00	1.97	1.27	1.00	1.00	1.00	1.00
1.00	0.00	370.43	11.81	3.75	1.40	1.00	1.00	370.17	12.07	3.85	1.43	1.00	1.00
	0.25	370.34	11.16	3.55	1.35	1.00	1.00	370.18	11.42	3.66	1.38	1.00	1.00
	0.50	369.99	9.25	2.99	1.20	1.00	1.00	370.14	9.45	3.07	1.23	1.00	1.00
	0.75	370.32	5.82	1.99	1.02	1.00	1.00	369.90	6.01	2.05	1.03	1.00	1.00
	0.95	369.84	1.81	1.01	1.00	1.00	1.00	370.00	1.87	1.01	1.00	1.00	1.00
1.25	0.00	7.39	5.60	3.17	1.44	1.00	1.00	7.24	5.05	2.89	1.40	1.00	1.00
	0.25	7.35	5.49	3.06	1.40	1.00	1.00	7.21	4.95	2.79	1.36	1.00	1.00
	0.50	7.01	5.00	2.67	1.26	1.00	1.00	6.90	4.51	2.47	1.24	1.00	1.00
	0.75	5.56	3.68	1.91	1.06	1.00	1.00	5.47	3.31	1.80	1.05	1.00	1.00
	0.95	2.17	1.49	1.04	1.00	1.00	1.00	2.12	1.38	1.03	1.00	1.00	1.00
1.50	0.00	2.65	2.49	2.09	1.36	1.01	1.00	2.57	2.35	1.92	1.29	1.01	1.00
	0.25	2.64	2.46	2.05	1.34	1.00	1.00	2.56	2.33	1.88	1.27	1.00	1.00
	0.50	2.54	2.35	1.90	1.24	1.00	1.00	2.46	2.21	1.76	1.18	1.00	1.00
	0.75	2.07	1.89	1.51	1.07	1.00	1.00	2.01	1.79	1.42	1.05	1.00	1.00
	0.95	1.13	1.08	1.02	1.00	1.00	1.00	1.11	1.07	1.01	1.00	1.00	1.00

6. Illustrated Example

A simulated dataset was used to illustrate the implementation of the existing SSEWMA and proposed AIB-SSEWMA charts. The monitored quality characteristics and the auxiliary variable of the underlying process, $(X_{tj},Y_{tj})$, $t=1,2,3,\dots$, and $j=1,2,\dots ,n$, followed a bivariate normal distribution with ${\mu }_X={\mu }_Y=0$, ${\sigma }_X={\sigma }_Y=1$, and specific $\rho$. In this study, $\rho =0$ was designed for the SSEWMA chart, and $\rho =0.75$ was considered for the AIB-SSEWMA chart. Then, we generated 30 bivariate samples of five observations each, from a bivariate normal distribution. The first 10 samples were from $N_2(0,0,1,1,0)$ and $N_2(0,0,1,1,0.75)$, referred to as in-control for the SSEWMA chart and AIB-SSEWMA chart, respectively. Assume that the underlying process mean shifts from ${\mu }_X$ to ${\mu }_X+\delta {\sigma }_X$, and the process standard deviation changes from ${\sigma }_X$ to $\tau {\sigma }_X$ due to some assignable causes. Shifts of $\delta =0.25$ in the process mean and $\tau =1.25$ in the process variability were considered for the last 20 samples. Table 7 lists the 30 successive pairs of $({\tilde{M}}_{X,t}^{},\hspace{0.17em}{\tilde{N}}_{X,t}^{})$ representing the SSEWMA statistics when $\rho =0$; similarly, the pairs of $({\tilde{A}}_{X,t}^{*},\hspace{0.17em}{\tilde{B}}_{X,t}^{*})$ represent the AIB-SSEWMA statistics when $\rho =0.75$.

Table 7. Simulation dataset of the SSEWMA and AIB-SSEWMA charts at process mean shift $\delta =0.25$ and variability shift $\tau =1.25$.

	SSEWMA						AIB-SSEWMA
No.	${\mathit{M}}_{\mathit{X},\mathit{t}}^{}$	${\mathit{N}}_{\mathit{X},\mathit{t}}^{}$	${\tilde{\mathit{M}}}_{\mathit{X},\mathit{t}}^{}$	${\tilde{\mathit{N}}}_{\mathit{X},\mathit{t}}^{}$	$\sqrt{\mathit{S}{\tilde{\mathit{E}}}_{\mathit{t}}^{}}$	$\mathit{r}$	${\mathit{A}}_{\mathit{X},\mathit{t}}^{*}$	${\mathit{B}}_{\mathit{X},\mathit{t}}^{*}$	${\tilde{\mathit{A}}}_{\mathit{X},\mathit{t}}^{*}$	${\tilde{\mathit{B}}}_{\mathit{X},\mathit{t}}^{*}$	$\sqrt{\mathit{S}{\tilde{\mathit{E}}}_{\mathit{t}}^{*}}$	${\mathit{r}}^{*}$
1	−0.027	0.012	−0.531	0.233	0.580	2.951	−0.015	−0.046	−0.295	−0.918	0.964	2.951
2	−0.016	0.032	−0.232	0.466	0.521	2.951	0.014	−0.054	0.204	−0.777	0.803	2.951
3	−0.047	0.018	−0.568	0.220	0.609	2.951	0.037	−0.063	0.449	−0.762	0.884	2.951
4	−0.055	0.078	−0.590	0.837	1.024	2.951	0.032	−0.039	0.348	−0.421	0.546	2.951
5	−0.017	0.070	−0.169	0.694	0.714	2.951	0.016	−0.002	0.162	−0.018	0.163	2.951
6	−0.047	0.097	−0.436	0.892	0.993	2.951	0.009	0.013	0.086	0.120	0.147	2.951
7	−0.095	0.165	−0.831	1.442	1.664	2.951	0.016	0.051	0.143	0.445	0.468	2.951
8	−0.049	0.055	−0.413	0.459	0.617	2.951	0.001	0.073	0.004	0.605	0.605	2.951
9	−0.112	0.058	−0.897	0.468	1.012	2.951	−0.028	0.049	−0.223	0.391	0.450	2.951
10	−0.118	0.128	−0.922	0.998	1.359	2.951	0.028	−0.027	0.219	−0.211	0.305	2.951
11	−0.076	0.236	−0.581	1.789	1.881	2.951	0.077	−0.045	0.585	−0.340	0.677	2.951
12	−0.020	0.354	−0.147	2.630	2.635	2.951	0.110	−0.015	0.816	−0.112	0.823	2.951
13	0.050	0.347	0.367	2.526	2.553	2.951	0.167	0.012	1.212	0.089	1.215	2.951
14	−0.044	0.297	−0.311	2.127	2.150	2.951	0.172	0.041	1.233	0.293	1.267	2.951
15	0.097	0.263	0.685	1.854	1.977	2.951	0.189	0.049	1.330	0.344	1.374	2.951
16	0.185	0.331	1.288	2.300	2.636	2.951	0.280	0.196	1.950	1.362	2.379	2.951
17	0.143	0.291	0.984	2.004	2.232	2.951	0.289	0.250	1.986	1.722	2.628	2.951
18	0.216	0.339	1.472	2.309	2.739	2.951	0.328	0.335	2.235	2.281	3.193	2.951
19	0.201	0.290	1.353	1.955	2.377	2.951	0.371	0.390	2.501	2.633	3.631	2.951
20	0.292	0.239	1.951	1.598	2.522	2.951	0.342	0.367	2.290	2.452	3.355	2.951
21	0.308	0.260	2.049	1.726	2.679	2.951	0.482	0.349	3.200	2.316	3.950	2.951
22	0.261	0.444	1.725	2.932	3.402	2.951	0.559	0.398	3.686	2.627	4.527	2.951
23	0.285	0.495	1.867	3.248	3.746	2.951	0.597	0.325	3.915	2.134	4.459	2.951
24	0.349	0.461	2.280	3.007	3.773	2.951	0.565	0.283	3.689	1.849	4.127	2.951
25	0.401	0.524	2.604	3.405	4.286	2.951	0.571	0.171	3.714	1.110	3.877	2.951
26	0.364	0.683	2.359	4.423	5.013	2.951	0.662	0.187	4.289	1.208	4.456	2.951
27	0.364	0.705	2.346	4.548	5.117	2.951	0.649	0.338	4.187	2.181	4.721	2.951
28	0.516	0.611	3.316	3.931	5.143	2.951	0.589	0.369	3.785	2.373	4.467	2.951
29	0.557	0.662	3.569	4.247	5.547	2.951	0.570	0.367	3.651	2.354	4.344	2.951
30	0.475	0.765	3.038	4.893	5.760	2.951	0.557	0.285	3.558	1.820	3.997	2.951

To compare the performance of the sum of squares EWMA chart with and without the use of an auxiliary variable, the in-control $ARL$ of the two charts were maintained as 370. According to Table 4, the parameter combination $(\lambda ,K)$ of the SSEWMA chart with time-varying control limits was selected as (0.05, 3.533) when the specific shift combination $(\delta ,\tau )$ was (0.25, 1.25). When the auxiliary variable was available, the parameter combination $(\lambda ,L)$ of the AIB-SSEWMA chart with time-varying control limits was selected at (0.05, 3.534) using the same shift combination for a fair comparison. The corresponding radius $r=\sqrt{2(1+K)}$ of the SSEWMA chart and $r^{*}=\sqrt{2(1+L)}$ of the AIB-SSEWMA chart are also listed in Table 7 and illustrated in Figure 2.

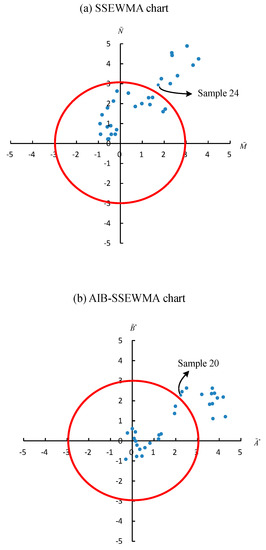
Figure 2. (a) The SSEWMA chart ($\lambda =0.05$, $K=3.533$ ) and (b) the AIB-SSEWMA chart ($\lambda =0.05$,$L=3.534$ ) for the example data in Table 7, respectively.

Figure 2a,b plots the SSEWMA and AIB-SSEWMA charts, respectively, with the 30 samples from Table 7. The two charts show that the process remained in control for the first 10 samples. However, when an assignable cause produced small shifts in both the process mean and variability, the first out-of-control signal was detected with the SSEWMA chart on sample 24, while 20 samples were only required to enable the AIB-SSEWMA chart to signal the out-of-control. The remaining out-of-control samples of the AIB-SSEWMA chart in Figure 2b deviated far from the upper part of the ${\tilde{A}}^{*}$-axis and the right side of the ${\tilde{B}}^{*}$-axis, as they were shifted due to a joint increase in the process mean and variability. Similar results also occurred in the SSEWMA chart. Moreover, if the deviation of an out-of-control sample from the ${\tilde{A}}^{*}$ or ${\tilde{B}}^{*}$ axes was not obvious, Figure 1 provides a guide to identify the direction and source of a shift in the AIB-SSEWMA chart. For shifts in the process mean $(\delta =0.25)$ and variability $(\tau =1.25)$, the illustration results indicate that the AIB-SSEWMA chart was more sensitive than the SSEWMA chart in detecting small process shifts.

7. Conclusions

As a single auxiliary quality characteristic (auxiliary variable) is available and accompanied with the quality characteristic (study variable), the performance of control charts is improved by the precision of process parameter estimators. In this article, we proposed a novel sum of squares exponentially weighted moving average chart, named as the AIB-SSEWMA chart, for effectively monitoring the small process mean and/or variability shifts. The study of the numerical simulations indicates that the AIB-SSEWMA chart performed uniformly better than the existing SSEWMA chart in detecting various kinds of process shifts. Additionally, the proposed chart was sensitive to small shifts in both the process mean and variability compared to its counterpart, the AIB-MaxEWMA chart. On the basis of the run length profiles, the study recommended that the AIB-SSEWMA chart with $\lambda =0.05$ was more helpful in detecting the small process mean and variability shifts in an industrial production process. Future work was recommended to extend the AIB-SSEWMA chart by adding an adjustment parameter, a sum of squares generally weighted moving average (SSGWMA) chart using auxiliary information, namely the AIB-SSGWMA chart. Furthermore, the double technique could be adopted to develop the AIB-SSDGWMA chart to simultaneously monitor the process mean and variability shifts in a single chart.