1. Introduction
Recent advances of experimental capabilities reached such precision that simultaneous detection of many ultracold atoms in a trap is possible [
1,
2]. This development paved the way to study positions of many trapped atoms subjected to the Fermi or the Bose statistics. What is even more important, simultaneous measurements of positions allow for the study of mutual correlations between particle positions. This is of particular interest for fermionic atoms, since the Pauli exclusion principle leads to nontrivial correlations between the position of atoms even if interactions between them are negligible. In this case, the Pauli crystals is the name coined for the spatial distribution of identical non-interacting fermions in a confined area. Such systems can be realized by e.g., optical traps. Particles with the Fermi statistics cannot be close to each other, because of the exclusion principle. Relative positions of particles, therefore, are determined by the joined action of the attractive trapping potential and the exclusion principle. These two mechanisms lead to nontrivial correlations of relative positions.
In the context of the Pauli crystals, most attention was devoted to the study of a small number of fermions in a two-dimensional harmonic trap. The system was at zero temperature, hence in the quantum many-body ground state. For simplicity, it was assumed that the number of atoms matches the number of the quantum states in the lowest energy shells. It was determined by numerical modeling [
3,
4,
5,
6,
7,
8] and also in experiments with
Li atoms [
9] that indeed the atoms tend to take positions in the vicinity of vertices of non-trivial polygons, forming the so-called geometrical shells. Importantly, these shells do not have much in common with the energy shells.
Relative positions of particles, hence the shape of the Pauli crystal, are directly related to inter-particle correlations present in a particular many-body quantum state. The standard approach to many-body correlations with the help of the high order correlation functions has, however, serious shortcomings. The correlation functions depend on many arguments, as many as the number of particles, so their presentation and analysis is complicated. On the contrary, as argued in [
3], the shape of the Pauli crystal gives a natural way of the study and visualization of the many-body correlations between particle positions.
The Pauli crystals exhibit unexpected symmetries. Some of them are simple and follow from the symmetry of the trapping potential. Some others can be linked to the closest packing principle. In most cases, however, none of the crystal symmetry can be explained in such way. Typically, the Pauli crystals show structures that do not have simple relations with the close packing nor with the shape of the potential, but rather follow from an interplay of many symmetries that leads to new geometric structures.
The Pauli crystals are not the only structures formed by trapped particles. A lot of attention has been paid to the Coulomb crystals formed by classical charged particles confined in a trap [
10,
11,
12] or the Wigner crystals formed by charged particles in a uniform oppositely charged background [
13,
14,
15,
16,
17]. In both cases the equilibrium is determined by the mutual action of the attractive trapping forced by the potential or background and the repulsive Coulomb interaction between the particles; these structures were observed in many laboratories (see e.g., [
15,
18] and references therein). When comparing these classical structures to the Pauli crystals, it should be noted that the electrostatic interaction between singly charged ions leads to much larger distances between the particles than the exclusion principle in the case of the Pauli crystals. Thus, the requirements for the observation of the Pauli crystal, temperature and spatial resolution, are much more strict than in the case of Coulomb crystals. Classical mechanics is sufficient for a theoretical description of ions forming a Coulomb crystal in a trap since they are separated by a high potential barrier and their wave functions do not overlap. This should be opposed to the Pauli crystal, where the overlap of wave functions of individual particles is the leading factor that determines the structure.
In the present paper, we discuss the geometric structures of the Pauli crystals in case of a two-dimensional isotropic harmonic trap and also in a spherically symmetric harmonic trap in three spatial dimensions. Similarities and differences between the Pauli crystals and Coulomb crystals are discussed. In addition, we discuss cases when the particles do not form closed shells, hence the symmetry of the trap is broken by the quantum state. Finally, we discuss the case of particles in a two-dimensional square trap. Here the natural symmetry of space is broken by the potential. The symmetry of the trap influences in a significant way the shape of Pauli crystals and leads to an interesting interplay of the symmetry of the square and the natural symmetry of fermions.
2. Pauli Crystals
In this section, we will recapitulate basic properties of the Pauli crystals, the way they are simulated numerically, and measured in real experiments. For this purpose, let us consider a relatively small number
N of fermions, i.e., half-integer-spin particles with all their spins permanently polarized. For simplicity we will consider here a two dimensional harmonic isotropic trap. The Hamiltonian of the system in the second quantization formalism reads
where
m and
denote the mass of the particles and the oscillation frequency of these particles in the trap, respectively. Fermionic field operators
fulfill the standard fermionic anti-commutation relations
and can be decomposed in the basis formed by eigenstates of the single-particle Hamiltonian as
Here, the wavefuntion denotes the energy eigenstate with excitation n and m in the x and y spatial direction, respectively. The corresponding single-particle energy is equal to , thus states with the same sum belong to the same single-particle energy shell. The state denotes the single-particle ground-state.
In principle, simultaneous measurement of
N-particle positions is possible. According to the rules of the quantum mechanics the results are random, i.e., repeated measurements give different locations of the particles after each measurement. The measured positions are, however, strongly correlated and the probability of finding a given set of positions is determined by the state dependent probability density
where
is the single-particle density operator, and
denotes the quantum state of the system. In this work we focus only on pure many-body states of the system. Generalization to mixed states, described by density matrix operators, is straightforward [
4].
A natural way to discuss correlations between the particle positions is to use the hierarchy of correlation functions. The lowest of these functions give the one-particle density function — the probability density of finding a particle at a given position. The second correlation function determines joined probability density of finding two particles at given positions, etc. Higher correlation functions, as functions of many arguments, are difficult to visualize and to discuss. Particularly, this is the case when the highest correlation function is considered.
The study of the correlation functions is not the only way to discuss the particle positions and correlations between them. An alternative procedure was suggested recently [
3,
4], it allows capturing and visualizing geometrical correlations between particle positions encoded in the total probability density
. The procedure bypasses difficulties caused by the correlation functions. It begins with the study of the many-particle distribution function and finds the location of particles with the largest probability. These positions form a unique pattern. Next, one performs a sequence of measurements of particle positions in repeated experiments. In the numerical simulation, these measurements are replaced by a random choice of positions, with the probability distribution given by the modulus square of the wave function. After each such measurement, the particle positions are shifted so that the measured center of mass is moved to the center of the trap, and rotated by such an angle that the particles come as close as possible to the pattern. These are symmetry transformations that do not change the measured relative positions of particles. After many measurements and transformations described above one obtains a specific configuration density function
formed by all registered positions. The resulting geometrical structure is called the Pauli crystal. Details of this procedure in the theoretical framework can be found in [
3,
4] and in the experimental realization in [
8].
It should be noted that the geometric structures shown explicitly here are also hidden in the standard correlation functions. The applied procedure of handling the data obtained from many measurements of particle positions allows for a simple visualization of the resulting shapes.
3. Few Particles in One Dimension
Let us first look at the one-dimensional case of non-interacting particles in a harmonic trap. In this case the wave function of the ground state of the system
is a simple Slater determinant of
N lowest one-particle orbitals
. Each orbital is given by the standard harmonic-oscillator wave function:
where
is the norm and
is
n-th Hermite polynomial. The position
x is expressed in the normal harmonic oscillator units
, where
m is the particle mass, and
is the frequency of the trap. Please note that there is no other length scale in this system, this length scale determines the system geometry. In a non-interacting many-particle state each fermion occupies one state, and therefore we have
N-particle probability density function in the form:
The function above describes the probability density that positions of
N particles measured simultaneously in one measurement will be given by
. Please note that the same function describes Bose particles in 1D with infinitely large, delta-like repulsion, the Girardeau model [
19]. It means that the results for such system will be the same as these for Fermion system.
To analyze the probability distribution (
6) first we will find the particle pattern. Configurations that correspond to the maximal value of the probability density function (
6) for small number of particles are relatively easy to find. For two particles the maximum of function (
6) is for
, three particles will most probably be found at
and four particles at points
. All values are given in the normal harmonic oscillator unit
a. In such a way we have found the unique pattern for each of these systems. It consist particle positions for which the function (
6) has the maximum. This pattern will be the basis, all measured sets of positions will be compared to this basic set. The question is if such procedure leads to distinguishable spots in the general case. In other words if, according to the probability distribution (
6), the dispersion around the well-defined maximum is small of large. We estimated this quantity for each of the examples listed above by the dispersion of position of one particle, assuming that all other particles occupy positions given by the pattern of maximal probability. We calculated this dispersion using conditional probability
. It turned out that in each calculated case the dispersion of the particle position
was the same, equal to
in the oscillator units. Interestingly, this value was the same for each position for each system, so it seems to be some universal value. The most important result is that this value is equal to one half of the distance between the particles in two particle system and a little more than one half for systems with more particles. It means that the spots around the main particle position should be well separated from each other. This is illustrated in
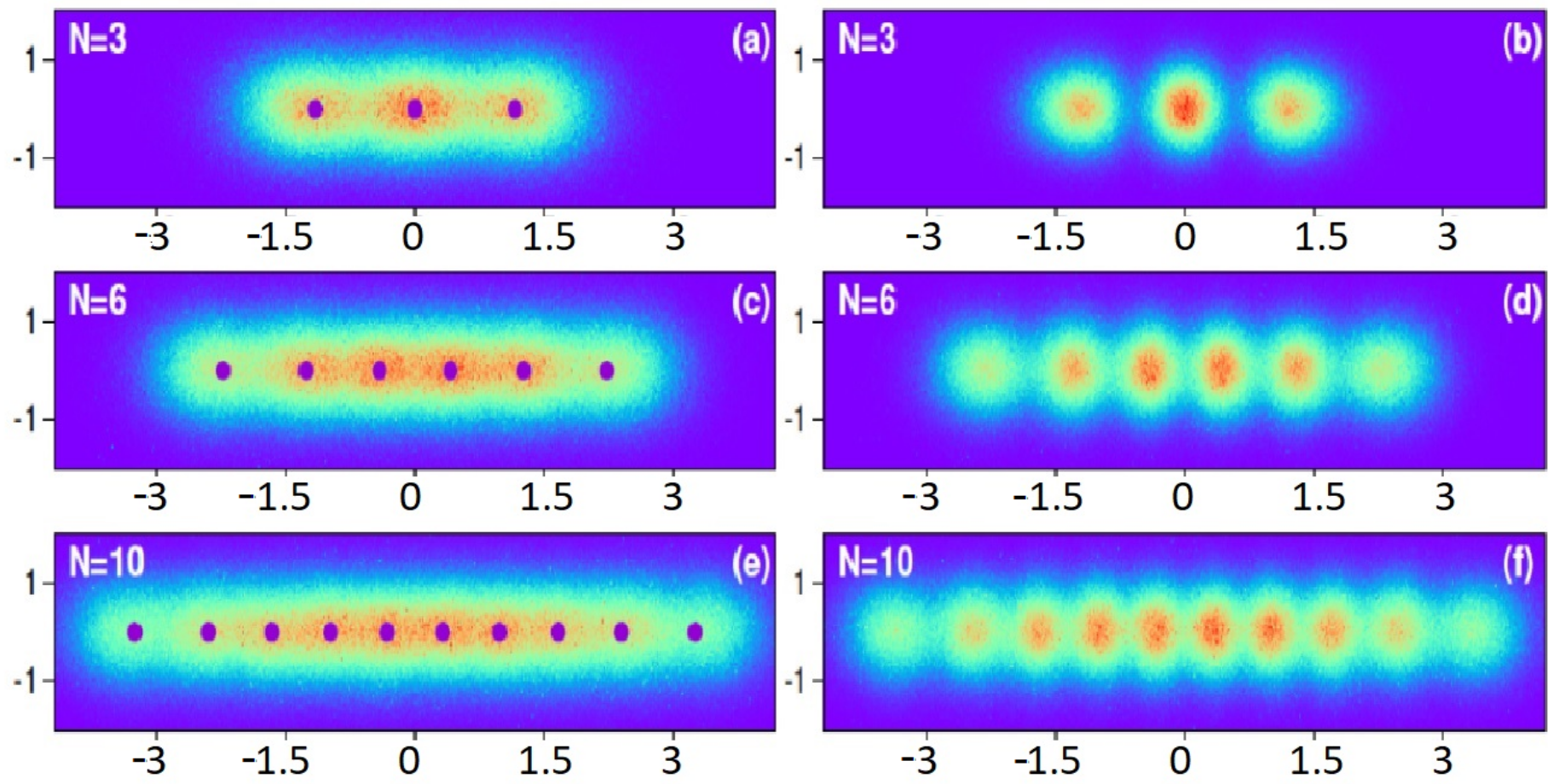
Figure 1, where the single particle density at the left side is compared with the results of the numerical analysis of many-particle density function, for systems of a few particles in a quasi-one dimensional trap (harmonic trap elongated along one direction with aspect ratio 1 to 10). It can be seen that the distances between particles decrease with number of particles, but the individual spots around each particle position can be clearly seen.
4. Closed Shells
The many-body wave function of the state in the two dimensional trap is a simple Slater determinant of N lowest one-particle orbitals , dependent on two quantum numbers n and m. In this case, due to the degeneracy of orbitals with the same total number of excitations , one distinguishes two different scenario: (i) the number of particles can be such that all one-particle states of the same energy are occupied (closed energy shell scenario) and the ground state is non-degenerate, or (ii) the number of one-particle states of given energy does not fit the number of particles and then the many-body ground state is not unique (energy shells are not closed).
In this section, we will discuss the closed energy shells scenario. In this case, the wave function is uniquely determined by the total energy and in two dimensions and is realized whenever
etc. particles are considered. These numbers originate from the
n-fold degeneracy (
) of each energy state. As an instructive example, let us examine the case of
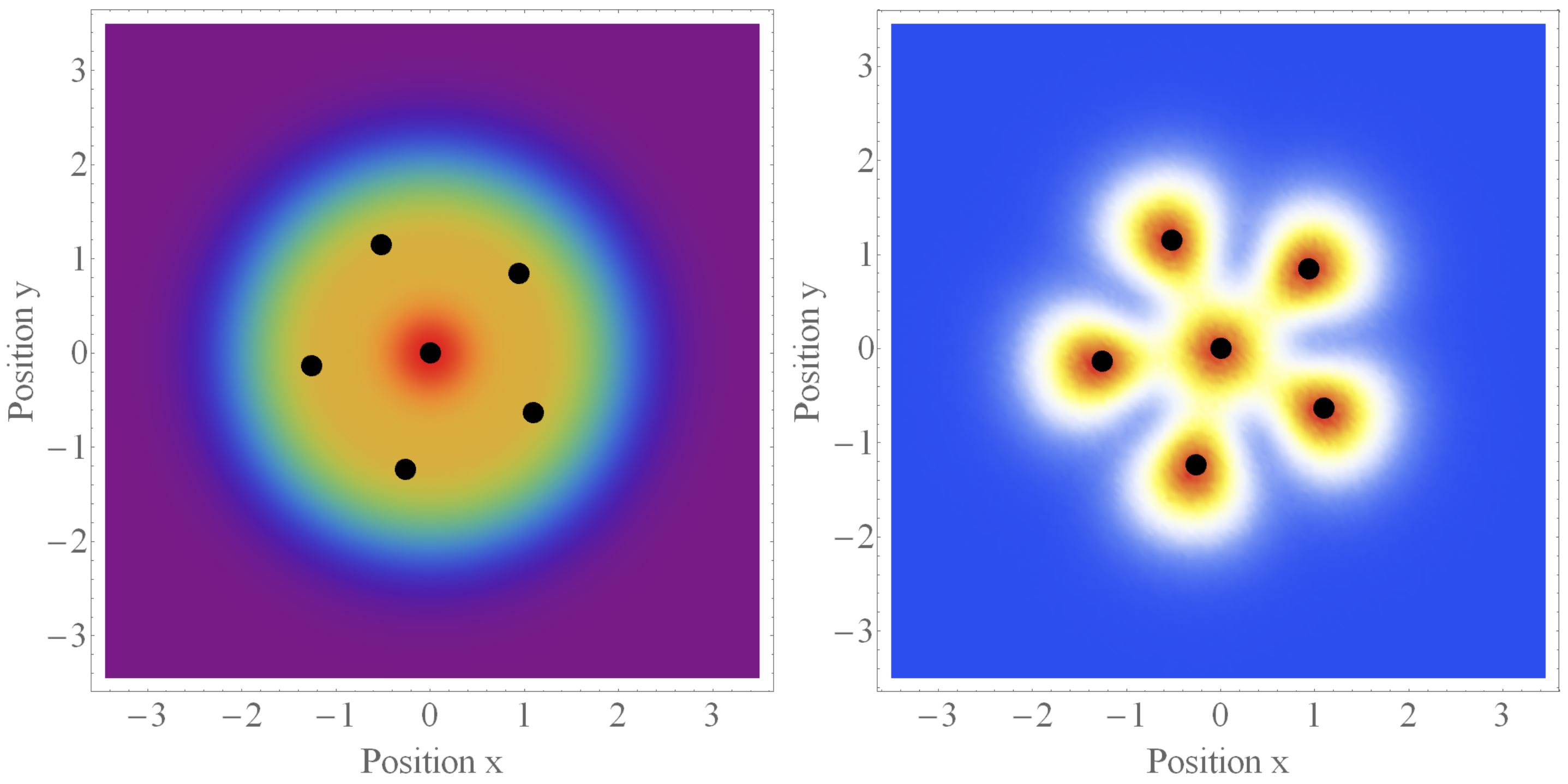
particles which occupy the three lowest energy shells. After performing extraction of the Pauli crystal and obtaining the configuration density function
one finds that the number of geometrical shells differs from the number of energy shells (see
Figure 2 reproduced from [
3]). As opposed to the energetic structure of the state, only two geometric shells are clearly seen. The inner shell consists of one particle, while five particles form the outer shell. It is very important to note that, although the quantum state describing particles in the case of closed shells is rotationally invariant, the Pauli crystal violates the rotational symmetry of the trap. The rotational symmetry is broken by the measurement and an arbitrary choice of the pattern orientation during the data analysis. Equally well the whole shape could be rotated by an arbitrary angle.
A naive intuition may suggest that the particles should have a tendency to be located at vertices of a regular hexagon. This is not the case, the probability density function does not distinguish such configuration. One can also look at the fivefold symmetry of the outer shell from another perspective and consider it as something natural. For example, it is well-known that the Coulomb crystals (electrically charged particles in an external harmonic trap) exhibit the same shape. In fact, the Coulomb interactions are not specific for the fivefold symmetry and any repulsive two-body interactions depending on the relative distances only lead to the same shape of the particle positions. This is because such systems realize the principle of the closest packing regardless of the details of interactions. The Pauli crystal formed by six particles exhibits the same behavior even though there are no two-body interactions between the particles.
Inspection of
particles case may suggest that the Pauli exclusion principle can be considered to be a specific two-body repulsive interaction. This however is not true and the result obtained for
is not universal. To see this let us consider the case of
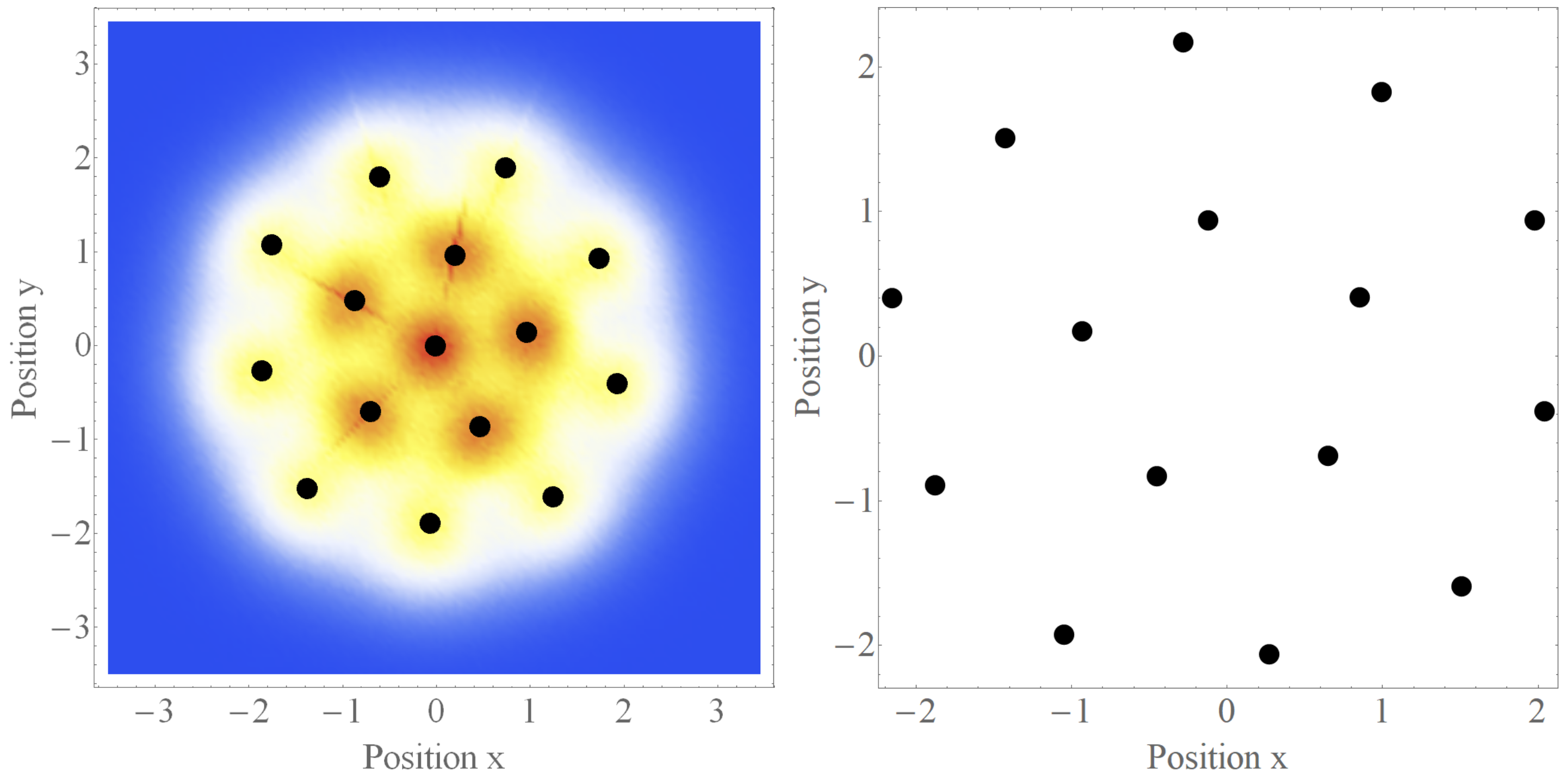
particles (
Figure 3). Here the configuration of the Pauli crystal consists of three geometric shells, containing respectively 1, 5, and 9 particles. The geometry of the inner shell exhibits fivefold symmetry imposed by the closest packing, the outer shell does not have this symmetry. The structure of the Coulomb crystal with the same number of particles, also shown in
Figure 3 for comparison, is essentially different. The Coulomb crystal contains only two geometrical shells, with 5 and 10 particles.
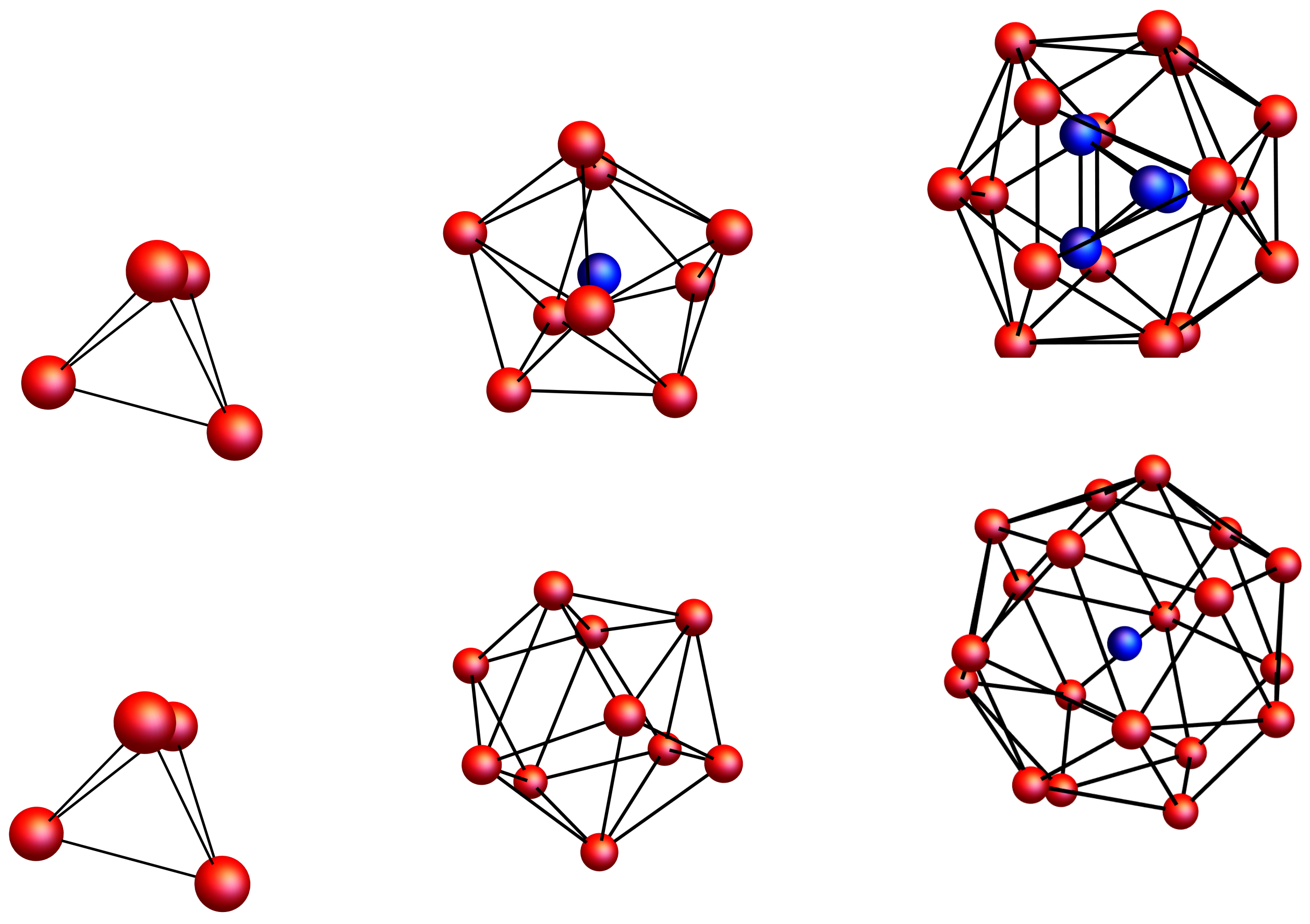
The difference between the Pauli and Coulomb crystals can also be seen in three dimensions. To clarify this, in
Figure 4 we compare shapes of Coulomb crystals with the corresponding Pauli crystals for
, 10, and 20 particles (for clearness we present the most probable configuration only). Both crystals have the same geometry in the case of
particles. For
particles, however, the Coulomb crystal contains two geometric shells— the inner shell with one particle and the outer shell with 9 particles. For
particles, both structures contain two geometric shells, but the inner shell of the Pauli crystal contains 4 particles, while of the Coulomb crystal only 1 particle. These examples clearly show that Pauli crystals are not governed by the closest packing principle. Thus, the exclusion principle cannot be considered to be a kind of two-body repulsive interactions.
There is one more difference between the Pauli crystals and structures formed by atoms interacting by two-body forces. The probability distribution function for atomic positions, given by Equation (
4), exhibits one global maximum (defined up to symmetry transformations) regardless of the number of particles. This should be opposed to the energy function, which leads to equilibrium positions of charged particles. The latter has many local minima even for a relatively small number of particles [
20]. This is one more evidence that the Pauli exclusion principle should not be considered to be a kind of mutual interaction of particles.
An open question remains as to whether the exclusion principle can be modelled by repulsive many body interactions. It is clear that it cannot be true as a general statement. However, in some cases such modelling can lead to correct results, especially when more sophisticated approaches such as statistical interaction potential are considered [
5,
6].
5. Open Energy Shells
In this section, we will extend our analysis to the open energy shells scenario. In these cases, the ground-state energy does not determine the state uniquely since the most excited particles may occupy different orbitals. Obviously, the one-particle density as well as the configuration density function (the shape of the Pauli crystal) depend on the whole state and not only on the energy. Thus, there is no unique structure of Pauli crystals for a given energy of the system. We will now discuss some examples.
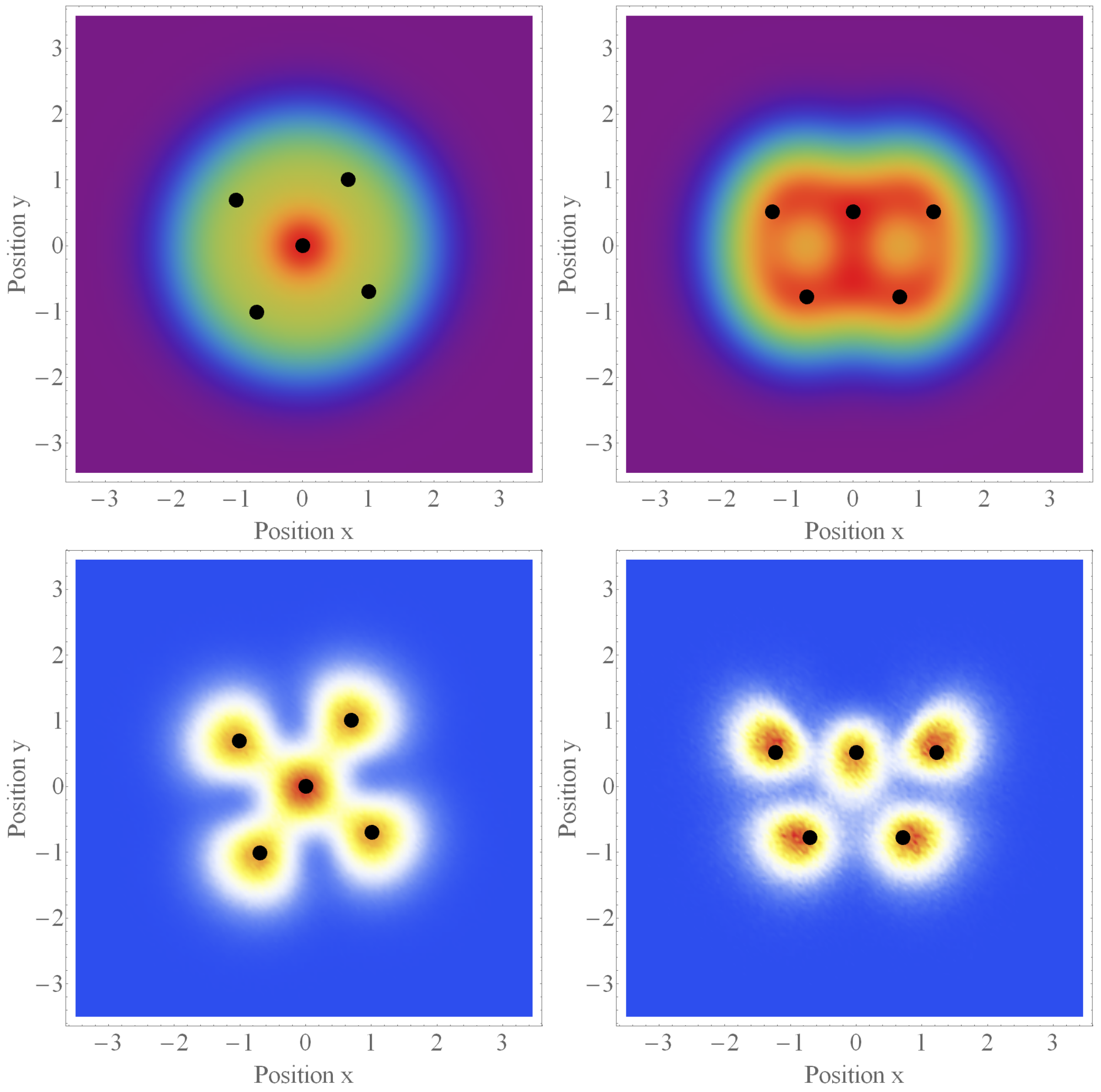
First, let us consider the case of
atoms (
Figure 5). The first two energy shells (containing one and two particles, respectively) are fully occupied but the remaining two atoms may be distributed among three possible states. Among all possibilities, we will consider two specific examples. The first uses the one-particle states with a given angular momentum to build the many particle state. We assume that the levels with magnetic quantum numbers
and
in the highest energy shell are occupied. The state, called the ”circular state”, is thus
where lower indices denote the radial and angular momentum excitation respectively. This state can be reached by introducing a small nonzero magnetic field in the trap, the field does not affect energies of the inner energy shells but removes the degeneracy of the one-particle states in the outer energy shell. In the ground state of the system, the one-particle states with the lowest energies are occupied. Finally, the magnetic field is set to zero, energies become degenerate but the wavefunction remains unchanged. In this way, we have selected a possible many-particle state. The shape of the Pauli crystal in such a case is shown in the top panel in
Figure 5.
In the second example, we use the cartesian basis, namely the states in the outer energy shell are chosen as double excitation along the
x axis, single excitation along both
x and
y axes, and double excitation along the
y axis. We assume that the excitations in the
y direction have slightly higher energy than in the
x direction. Now, occupied one particle states have double excitation along the
x axis and single excitation along both axes. Finally, as before, the states are made degenerate, but the wave function remains unchanged. The many-particle state, called the “cartesian state” is
The Pauli crystal corresponding to this state is shown in the bottom panel in
Figure 5, which differs from the previous shape. Other states describing an open shell exist and can be easily formulated.
An important feature of the last case is that the maxima of the one-particle density functions do not coincide with the positions of particles forming the Pauli crystal. This is an illustration of a more general feature— the one-particle density function does not give reliable information about positions of individual particles measured in a single measurement. One particle density gives averages of positions rather than information about the single measurements.
Let us note that the Pauli crystals do not have the symmetry of the trap, in the case of closed energy shells the symmetry is broken by the process of measurement. The Pauli crystals corresponding to open energy shells break the trap symmetry in a much stronger way, measurements are additional factors leading to an even stronger violation. The two examples described above show clearly that the symmetry of the Pauli crystal is lower than the symmetry of the trap. In the first case considered above the crystal has the rotational symmetry, while in the second case the Pauli crystal is not rotationally symmetric.
At this point, it should be emphasized that the mentioned degeneracy of open-shell ground states cannot be captured by any semi-classical method which treats quantum particles obeying the Pauli exclusion principle as a kind of classical system with appropriately tailored mutual interactions. All features caused by the degeneracy of the many-body ground state are solely reserved for a fully quantum description of the system.
6. Particles in a Square Potential Well
In this section, we will discuss the case when the particles are bound by a two-dimensional square well potential. Thus, the external potential has a lower symmetry, the natural fivefold symmetry of the particles competes with the lower symmetry of the potential. Denoting the size of the well by
a, normalized one-particle wave functions have a form:
where
n and
m are natural numbers denoting spatial excitations in
x and
y direction, respectively. The operators creating a particle in the state with wave function
are denoted by
. As before, first we find maxima of the many-particle probability distribution function
in the many-body ground-state. Then we simulate single-shot measurements of positions of all particles and generate the configuration density function
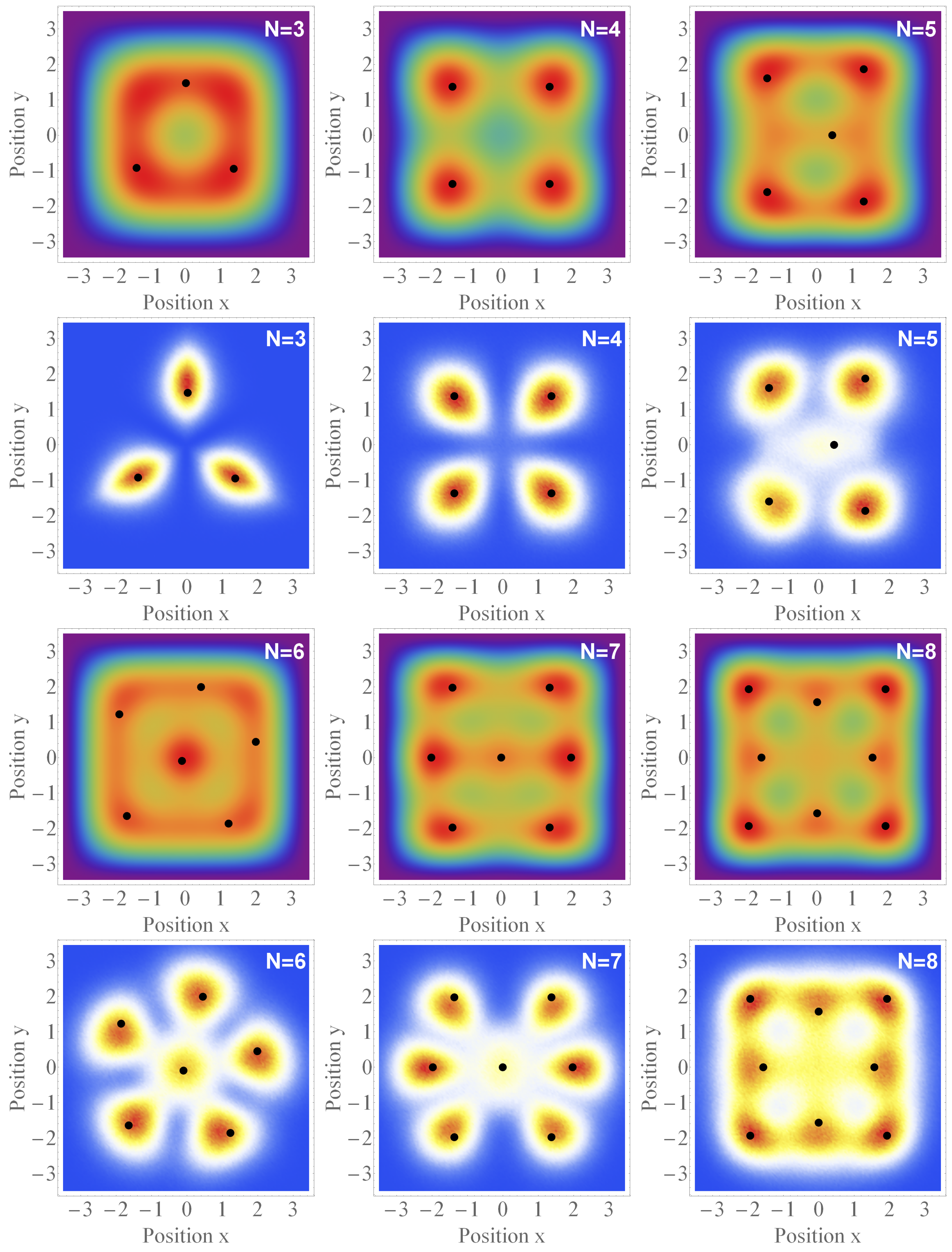
. Since the symmetry of the potential is now lower than in the previous examples, therefore the distillation has to be restricted to transformations that do not violate the symmetry of the potential. The results are shown in
Figure 6. The top row shows the one-particle density function
for
particles, while in the lower row, the corresponding configuration density function
is displayed. The simple case of
particles is very interesting. Let us note that in this case, the particles occupy the first two energy shells and that these shells are closed. While the particles themselves prefer the triangular symmetry, the external potential has the symmetry of a square. As a result, the one-particle density distribution
has the symmetry of the potential and exhibits no sign of three maxima. On the contrary, the configuration density function
has purely triangular symmetry and the positions of three particles are clearly distinguished. In this case, the exclusion principle dominates over the symmetry of the potential and consequently leads to the triangular configuration of the Pauli crystal.
The situation is essentially different in the case of
particles. The next energy shell is not fully occupied and the fourth particle is doubly excited. Assuming that this double excitation is along the
x axis the many-body ground state of the system is
As clearly seen in
Figure 6 (the second column), in this case the maxima of the one-particle density function
mirror the shape of the most probable configuration and the shape of the Pauli crystal. The whole system has the symmetry of the square— the symmetry of the potential. This is, however, an exceptional case, as illustrated by the state with
particles. For example, if one considers a five-particle state of the form
then the resulting single-particle density
and the configuration density function
have rectangular rather than square shape (the third column in
Figure 6). Closer inspection of the results shows that the one-particle density function only vaguely resembles the configuration density. However, the configuration density does not have the symmetry of the potential.
The third energy shell is finally closed in the case of
particles and the Pauli crystal forms two geometric shells (the fourth column in
Figure 6). The inner geometric shell contains one particle, the outer one contains the remaining five particles, such as in the case of a harmonic isotropic trap. Observe, however, that the one-particle density function
exhibits only four maxima in the outer geometric shell (roughly in the corners of the trap). In contrast, the configuration density
shows clearly that the outer geometric shell contains five particles. Similar features are seen in the case of
particles. These effects illustrate a general statement that the shape of the one-particle density profile
does not always give proper positions of the particles if they are measured simultaneously. An exactly opposite mismatch between the number of particles and the number of maxima in the one-particle density is seen in the case of
particles. Namely, the one-particle density function
has nine maxima on the outer geometric shell, while the Pauli crystal contains only eight particles there. A clear local maximum of the one-particle density function located in the center of the potential does not correspond to the presence of a particle.
These examples show clearly the interplay between the symmetry of the external potential with the symmetry imposed by the quantum statistics. While the fermionic nature of particles supports rather fivefold symmetry, the potential supports the symmetry of the square. While the shape of the one-particle density function is rather dominated by the symmetry of the potential, the shape of the configuration density function is quite difficult to predict and emerges as a result of non-trivial competition between the quantum statistics and the external confinement.
7. Conclusions
We discussed possible configurations of particles with the fermi statistics in a confining potential. The Pauli exclusion principle prevents particles from being close to each other even if the particles do not interact. Thus, the exclusion principle leads to correlations between particle positions. We pointed out that the particles tend to take positions in vertexes of non-trivial polygons, called the Pauli crystals. We compared positions of these vertexes with maxima of the one-particle density functions and showed that in many cases they do not coincide. Thus the maxima of the one density distribution function cannot be identified with the most probable positions of particles.
Positions of particles form geometrical structures, we compared symmetries of these structures with the symmetries of the confining potential. It turned out that there is no simple relation between these two symmetries. Rather the shape of the Pauli crystals results from an interplay between the symmetry of the potential and the natural symmetry of fermions.
We compared the Pauli crystals with analogous structures formed by interacting particles, namely electrically charged particles in a trap (Coulomb crystals). We showed that although the shapes are the same for a small number of particles they become different for a larger (larger than 8) particle number. This is a clear indication that the Pauli principle cannot be considered to be a kind of interaction. Rather it provides a mechanism leading to high order correlations between the particles that in general cannot be modeled by two-body interactions.