A New Hyperchaotic Map for a Secure Communication Scheme with an Experimental Realization
Abstract
1. Introduction
- We introduce an analytical framework to understand the dynamical behavior of the 2D-ICSM including stability of its fixed points, bifurcation diagram, and Lyapunov Exponents.
- We experimentally evaluate the complexity, sensitivity, and randomness of the 2D-ICSM using Sample Entropy, cross-correlation coefficient, and NIST-800-22 statistical test, respectively.
- To demonstrate the efficiency and simplicity of the 2D-ICSM in practical applications, we design a secure communication system, and then experimented tested it on an optical channel with Arduino microcontrollers.
2. The 2D Infinite-Collapse-Sine Model
2.1. Definition of 2D-ICSM
2.2. Stability Analysis
3. Dynamical Behaviors
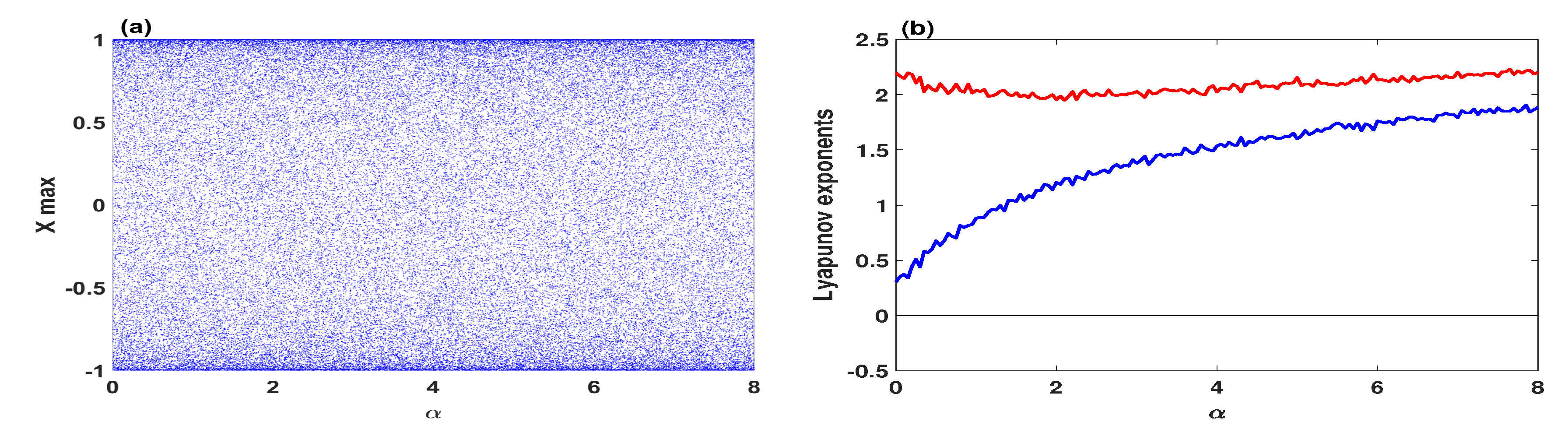
3.1. Bifurcation Diagram and Lyapunov Exponents
3.2. Hyperchaotic Attractor
4. Performance Evaluations
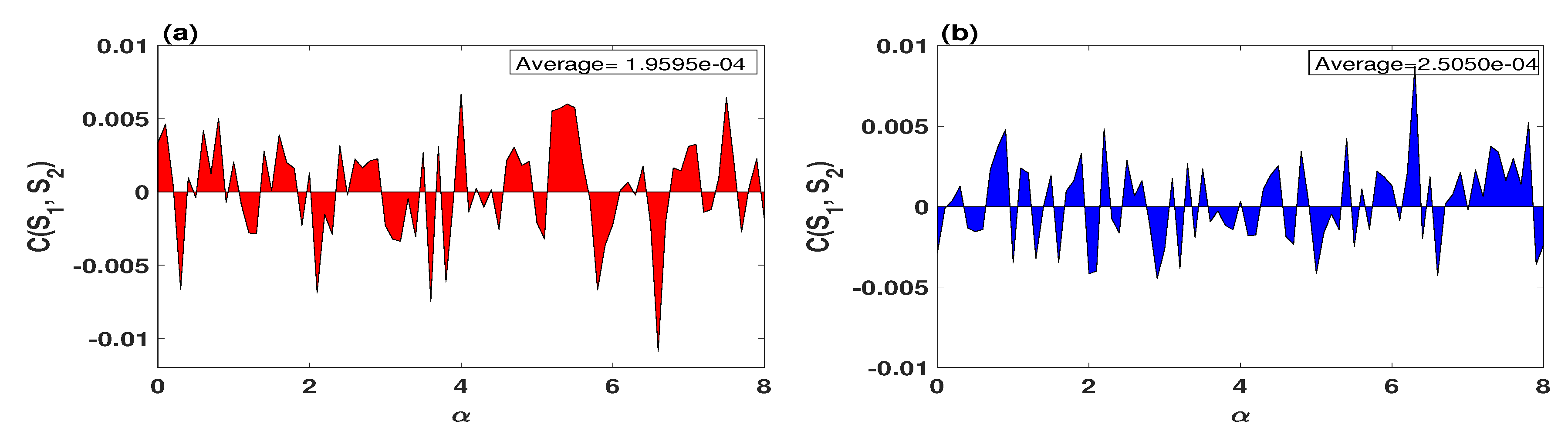
4.1. Cross-Correlation Coefficient
4.2. Chaos-Based Pseudorandom Number Generator
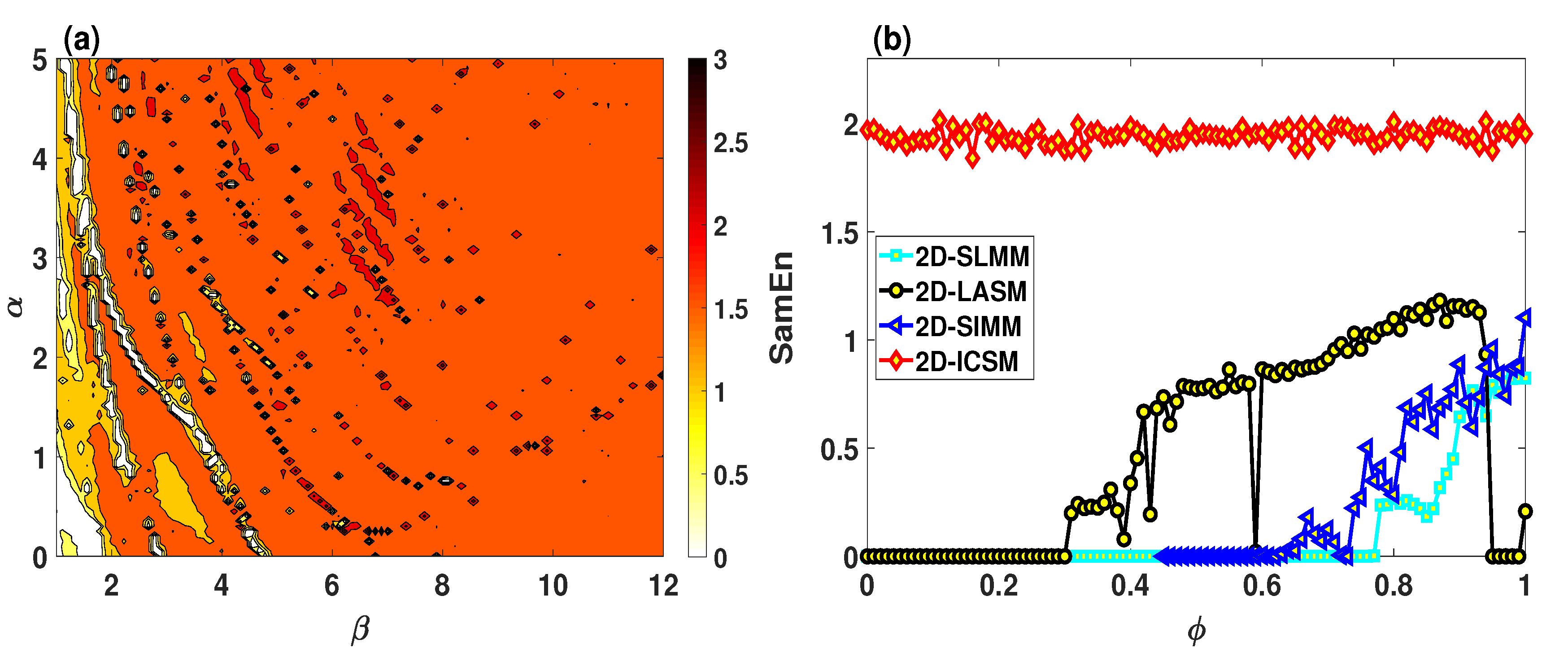
5. Complexity-Based Sample Entropy
- Reconstruction: the time series can be reconstructed as follows,where m is embedding dimension and is time delay.
- Counting the vector pairs: For a given tolerance parameter r, let be the number of vectors such thathere, is the distance between and , which is defined as
- Calculating : According to the obtained number of vector pairs, we can getthen calculate by
- Calculating SamEn: Repeating the above steps we can get , then SamEn is given by
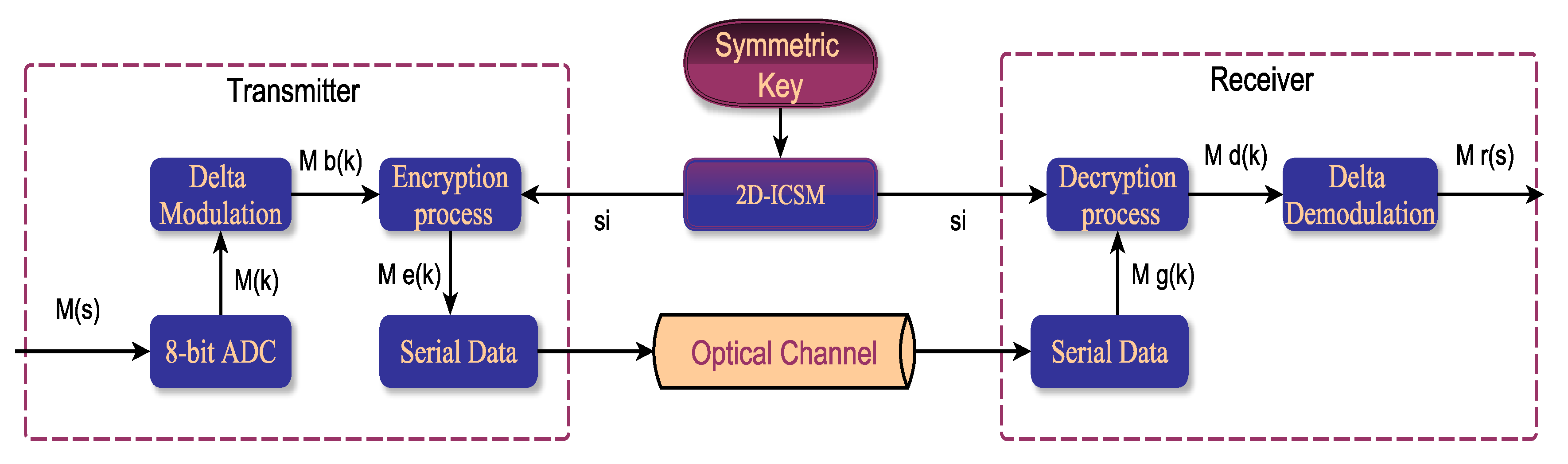
6. Chaos Based Cryptography
6.1. Arduino Transmitter
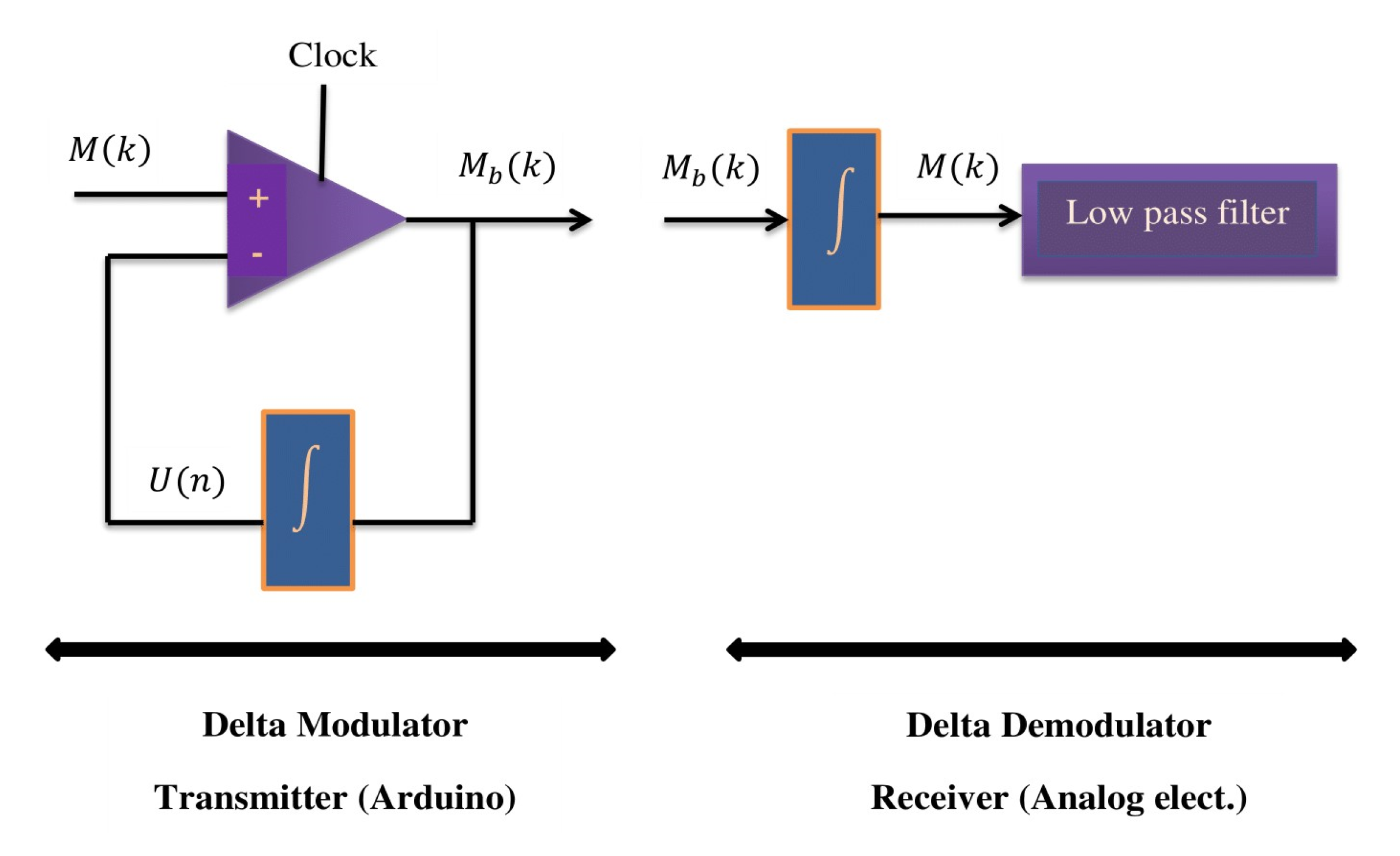
6.2. Delta Modulation
| Algorithm 1: Delta Modulation |
 |
6.3. Encryption Process
| Algorithm 2: The encryption process. |
 |
6.4. Decryption Process
7. Experimental Implementation
7.1. Simulation Implementation
Key Sensitivity Analysis
7.2. Hardware Implementation
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Casdagli, M. Nonlinear prediction of chaotic time series. Phys. Nonlinear Phenom. 1989, 35, 335–356. [Google Scholar] [CrossRef]
- Cho, K.; Takaya, M. Chaotic cryptography using augmented Lorenz equations aided by quantum key distribution. IEEE Trans. Circuits Syst. Regul. Pap. 2014, 62, 478–487. [Google Scholar] [CrossRef]
- Natiq, H.; Banerjee, S.; He, S.; Said, M.R.M.; Kilicman, A. Designing an M-dimensional nonlinear model for producing hyperchaos. Chaos Solitons Fractals 2018, 114, 506–515. [Google Scholar] [CrossRef]
- Natiq, H.; Banerjee, S.; Ariffin, M.R.K.; Said, M.R.M. Can hyperchaotic maps with high complexity produce multistability? Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 011103. [Google Scholar] [CrossRef]
- Berry, H.; Daniel, G.P.; Olivier, T. Chaos in computer performance. Chaos Interdiscip. J. Nonlinear Sci. 2006, 16, 013110. [Google Scholar] [CrossRef] [PubMed]
- Argyris, A.; Syvridis, D.; Larger, L.; Annovazzi-Lodi, V.; Colet, P.; Fischer, I.; Garcia-Ojalvo, J.; Mirasso, C.R.; Pesquera, L.; Shore, K.A. Chaos-based communications at high bit rates using commercial fibre-optic links. Nature 2005, 438, 343–346. [Google Scholar] [CrossRef] [PubMed]
- Natiq, H.; Said, M.R.M.; Al-Saidi, N.M.; Kilicman, A. Dynamics and complexity of a new 4d chaotic laser system. Entropy 2019, 21, 34. [Google Scholar] [CrossRef]
- Akgul, A.; Calgan, H.; Koyuncu, I.; Pehlivan, I.; Istanbullu, A. Chaos-based engineering applications with a 3D chaotic system without equilibrium points. Nonlinear Dyn. 2016, 84, 481–495. [Google Scholar] [CrossRef]
- Farhan, A.K.; Ali, R.S.; Natiq, H.; Al-Saidi, N.M. A new S-box generation algorithm based on multistability behavior of a plasma perturbation model. IEEE Access 2019, 7, 124914–124924. [Google Scholar] [CrossRef]
- Viet-Thanh, P.H.A.M.; Ali, D.S.; Al-Saidi, N.M.; Rajagopal, K.; Alsaadi, F.E.; Jafari, S. A Novel Mega-stable Chaotic Circuit. Radioengineering 2020, 29, 141. [Google Scholar]
- Alvarez, G.; Li, S. Some basic cryptographic requirements for chaos-based cryptosystems. Int. J. Bifurc. Chaos 2006, 16, 2129–2151. [Google Scholar] [CrossRef]
- Hua, Z.; Zhou, Y.; Pun, C.M.; Chen, C.P. 2D Sine Logistic modulation map for image encryption. Inf. Sci. 2015, 297, 80–94. [Google Scholar] [CrossRef]
- Liu, W.; Sun, K.; Zhu, C. A fast image encryption algorithm based on chaotic map. Opt. Lasers Eng. 2016, 84, 26–36. [Google Scholar] [CrossRef]
- Hua, Z.; Zhou, Y. Image encryption using 2D Logistic-adjusted-Sine map. Inf. Sci. 2016, 339, 237–253. [Google Scholar] [CrossRef]
- Cao, C.; Sun, K.; Liu, W. A novel bit-level image encryption algorithm based on 2D-LICM hyperchaotic map. Signal Process. 2018, 143, 122–133. [Google Scholar] [CrossRef]
- Natiq, H.; Al-Saidi, N.M.G.; Said, M.R.M.; Kilicman, A. A new hyperchaotic map and its application for image encryption. Eur. Phys. J. Plus 2018, 133, 1–14. [Google Scholar] [CrossRef]
- Moysis, L.; Tutueva, A.; Volos, C.; Butusov, D.; Munoz-Pacheco, J.M.; Nistazakis, H. A Two-Parameter Modified Logistic Map and Its Application to Random Bit Generation. Symmetry 2020, 12, 829. [Google Scholar] [CrossRef]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Rössler, O.E. An equation for continuous chaos. Phys. Lett. 1976, 57, 397–398. [Google Scholar] [CrossRef]
- Sprott, J.C. Some simple chaotic flows. Phys. Rev. 1994, 50, R647. [Google Scholar] [CrossRef]
- Chen, G.; Ueta, T. Yet another chaotic attractor. Int. J. Bifurc. Chaos 1999, 9, 1465–1466. [Google Scholar] [CrossRef]
- Chen, A.; Lu, J.; Lü, J.; Yu, S. Generating hyperchaotic Lü attractor via state feedback control. Phys. Stat. Mech. Appl. 2006, 364, 103–110. [Google Scholar] [CrossRef]
- May, R.M. Simple mathematical models with very complicated dynamics. Nature 1976, 261, 459–467. [Google Scholar] [CrossRef] [PubMed]
- Baier, G.; Klein, M. Maximum hyperchaos in generalized Hénon maps. Phys. Lett. 1990, 151, 281–284. [Google Scholar] [CrossRef]
- Natiq, H.; Al-Saidi, M.N.; Said, M.R.M. Complexity and dynamic characteristics of a new discrete-time hyperchaotic model. In Proceedings of the 2017 Second Al-Sadiq International Conference on Multidisciplinary in IT and Communication Science and Applications (AIC-MITCSA), Baghdad, Iraq, 30–31 December 2017. [Google Scholar]
- Hussein, W.A.; Al-Saidi, N.M.; Natiq, H. A New 2D Hénon-Logistic Map for Producing Hyperchaotic Behavior. In Proceedings of the 2018 Third Scientific Conference of Electrical Engineering (SCEE), Baghdad, Iraq, 19–20 December 2018. [Google Scholar]
- Natiq, H.; Ariffin, M.R.K.; Said, M.R.M.; Banerjee, S. Enhancing the sensitivity of a chaos sensor for internet of things. Internet Things 2019, 7, 100083. [Google Scholar] [CrossRef]
- Chen, C.; Sun, K.; He, S. A class of higher-dimensional hyperchaotic maps. Eur. Phys. J. Plus 2019, 134, 410. [Google Scholar] [CrossRef]
- Hua, Z.; Zhou, B.; Zhou, Y. Sine-transform-based chaotic system with FPGA implementation. IEEE Trans. Ind. Electron. 2017, 65, 2557–2566. [Google Scholar] [CrossRef]
- Zhu, Z.; Leung, H. Identification of linear systems driven by chaotic signals using nonlinear prediction. IEEE Trans. Circuits Syst. Fundam. Theory Appl. 2002, 49, 170–180. [Google Scholar]
- Skrobek, A. Cryptanalysis of chaotic stream cipher. Phys. Lett. 2007, 363, 84–90. [Google Scholar] [CrossRef]
- Natiq, H.; Banerjee, S.; Said, M.R.M. Cosine chaotification technique to enhance chaos and complexity of discrete systems. Eur. Phys. J. Spec. Top. 2019, 228, 185–194. [Google Scholar] [CrossRef]
- Farhan, A.K.; Al-Saidi, N.M.; Maolood, A.T.; Nazarimehr, F.; Hussain, I. Entropy analysis and image encryption application based on a new chaotic system crossing a cylinder. Entropy 2019, 21, 958. [Google Scholar] [CrossRef]
- Liu, C.; Li, K.; Zhao, L.; Liu, F.; Zheng, D.; Liu, C.; Liu, S. Analysis of heart rate variability using fuzzy measure entropy. Comput. Biol. Med. 2013, 43, 100–108. [Google Scholar] [CrossRef] [PubMed]
- Bian, C.; Qin, C.; Ma, Q.D.; Shen, Q. Modified permutation-entropy analysis of heartbeat dynamics. Phys. Rev. 2012, 85, 021906. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol.-Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [PubMed]
- Hua, Z.; Zhou, B.; Zhou, Y. Sine chaotification model for enhancing chaos and its hardware implementation. IEEE Trans. Ind. Electron. 2018, 66, 1273–1284. [Google Scholar] [CrossRef]
- He, D.; He, C.; Jiang, L.G.; Zhu, H.W.; Hu, G.R. Chaotic characteristics of a one-dimensional iterative map with infinite collapses. IEEE Trans. Circuits Syst. Fundam. Theory Appl. 2001, 48, 900–906. [Google Scholar]
- Gao, Y.; Liu, B. Study on the dynamical behaviors of a two-dimensional discrete system. Nonlinear Anal. Theory Methods Appl. 2009, 70, 4209–4216. [Google Scholar] [CrossRef]
- Rukhin, A.; Soto, J.; Nechvatal, J.; Smid, M.; Barker, E. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications, Tech. rep., Booz-allen and hamilton inc mclean va 2001. Available online: https://www.nist.gov/publications/statistical-test-suite-random-and-pseudorandom-number-generators-cryptographic (accessed on 2 November 2020).
- Zapateiro De la Hoz, M.; Acho, L.; Vidal, Y. An experimental realization of a chaos-based secure communication using arduino microcontrollers. Sci. World J. 2015, 2015, 123080. [Google Scholar] [CrossRef]
- Taylor, D.S. Design of Continuously Variable Slope Delta Modulation Communication Systems. Motorola Technical Document AN1544. 1996. Available online: http://gamearchive.askey.org/General/DataSheets/cvsdspeechinfo/an1544cvsd.pdf (accessed on 2 November 2020).

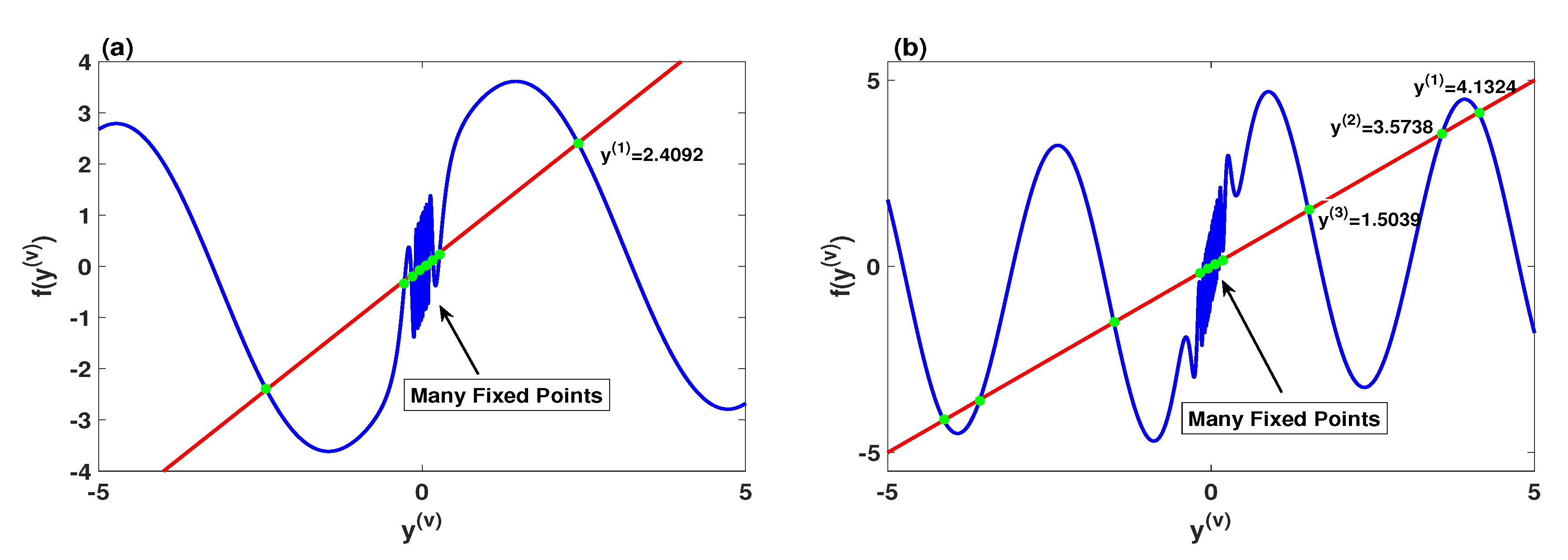










| Parameters | Fixed Points | Stability Analysis | ||
|---|---|---|---|---|
| , | unstable | |||
| unstable | ||||
| , | unstable | |||
| unstable |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Saidi, N.M.G.; Younus, D.; Natiq, H.; K. Ariffin, M.R.; Asbullah, M.A.; Mahad, Z. A New Hyperchaotic Map for a Secure Communication Scheme with an Experimental Realization. Symmetry 2020, 12, 1881. https://doi.org/10.3390/sym12111881
Al-Saidi NMG, Younus D, Natiq H, K. Ariffin MR, Asbullah MA, Mahad Z. A New Hyperchaotic Map for a Secure Communication Scheme with an Experimental Realization. Symmetry. 2020; 12(11):1881. https://doi.org/10.3390/sym12111881
Chicago/Turabian StyleAl-Saidi, Nadia M. G., Dhurgham Younus, Hayder Natiq, M. R. K. Ariffin, M. A. Asbullah, and Z. Mahad. 2020. "A New Hyperchaotic Map for a Secure Communication Scheme with an Experimental Realization" Symmetry 12, no. 11: 1881. https://doi.org/10.3390/sym12111881
APA StyleAl-Saidi, N. M. G., Younus, D., Natiq, H., K. Ariffin, M. R., Asbullah, M. A., & Mahad, Z. (2020). A New Hyperchaotic Map for a Secure Communication Scheme with an Experimental Realization. Symmetry, 12(11), 1881. https://doi.org/10.3390/sym12111881





