Spatial-Temporal-DBSCAN-Based User Clustering and Power Allocation for Sum Rate Maximization in Millimeter-Wave NOMA Systems
Abstract
1. Introduction
- mmWave can strongly correlate the channels of different users through its highly directional transmissions; thus, the necessary combination between NOMA and mmWave can be achieved; and,
- with the higher connectivity and the high capacity provided by NOMA, the benefits of mmWave-NOMA systems can be multiplied based on the aforementioned characteristics.
- The optimization problem was investigated to maximize the sum-rate of a downlink mmWave- NOMA-based system by jointly optimizing user clustering, PA, and HBF strategies. It is challenging to solve this problem, because it involves combinatorial complexity. Thus, we separated the underlying problem into sub-problems of the user clustering, PA, and HBF problems.
- To solve the user clustering problem, we propose a novel spatial–temporal density-based spatial clustering of applications with noise (ST-DBSCAN)-based algorithm for user clustering in downlink mmWave-NOMA systems. Our proposed ST-DBSCAN algorithm exploits the similarity between the position of users and the correlation between the channel gains of users to group users into clusters. Recent research has only focused on the correlations between user channel gains and has not considered the spatial distribution of users. In this study, we consider both user positions and channel gains to maximize the system sum-rate. When the users are in close proximity to each other, the BS can form a narrower beam in order to achieve a higher beam gain than that achievable with a wider beam [9]. By exploiting this characteristic, our ST-DBSCAN-based user clustering algorithm can enhance the performance of mmWave-NOMA systems.
- We obtain a sub-optimal inter-cluster PA under fixed and arbitrary HBF. To deal with the non-convexity of the PA problem, we separate this problem into two sub-problems, intra-cluster PA, and inter-cluster PA. Based on the intra-cluster PA that was solved in [10], we propose an inter-cluster PA algorithm. Moreover, we apply the boundary-compressed particle swarm optimization (BC-PSO) algorithm to eliminate inter-cluster interference, to boost the performance of the system.
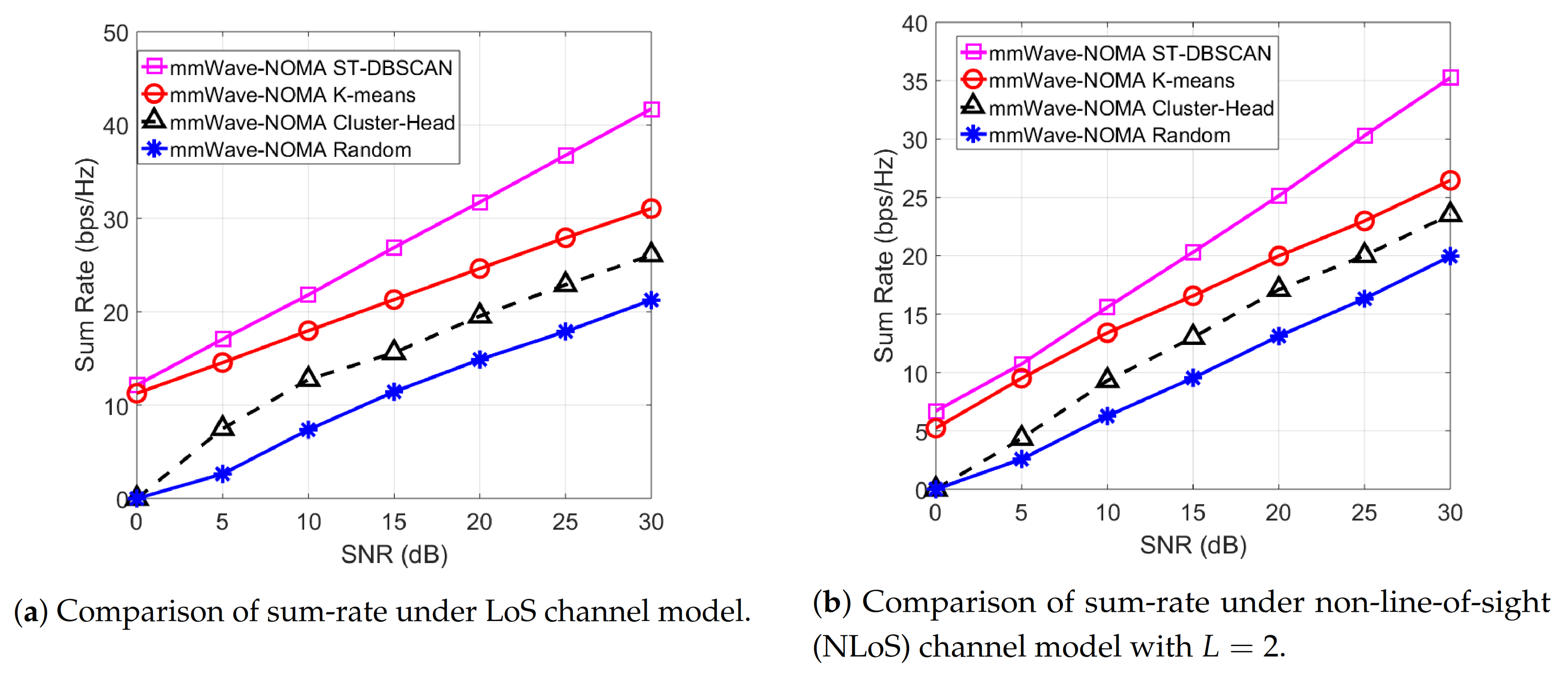
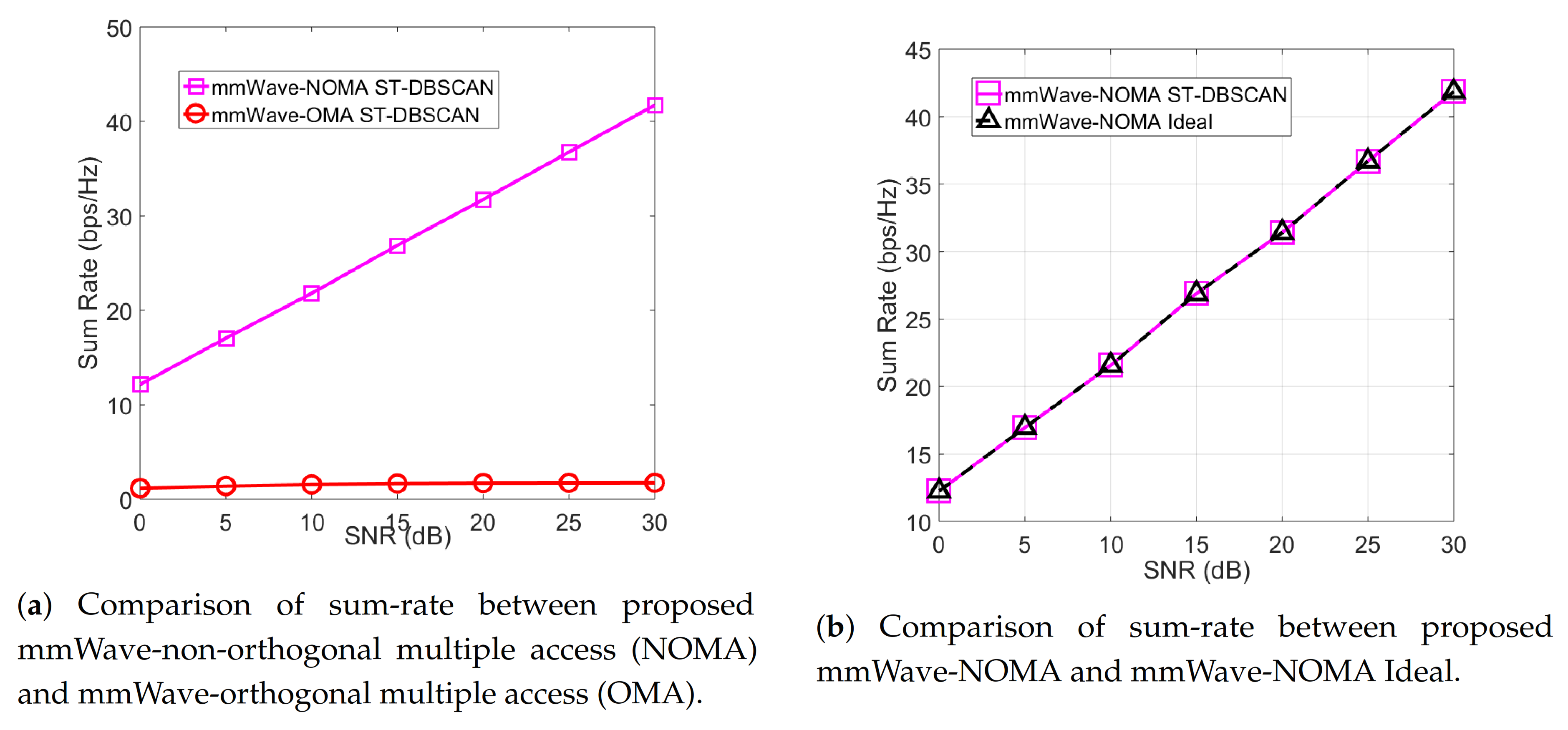
- Simulation results show that the proposed ST-DBSCAN-based user clustering algorithm outperforms other user clustering algorithms. The simulation results also show that our PA and HBF solutions can improve the performance of mmWave-NOMA systems.
2. Related Work
2.1. User Pairing
2.2. User Clustering
3. System Model
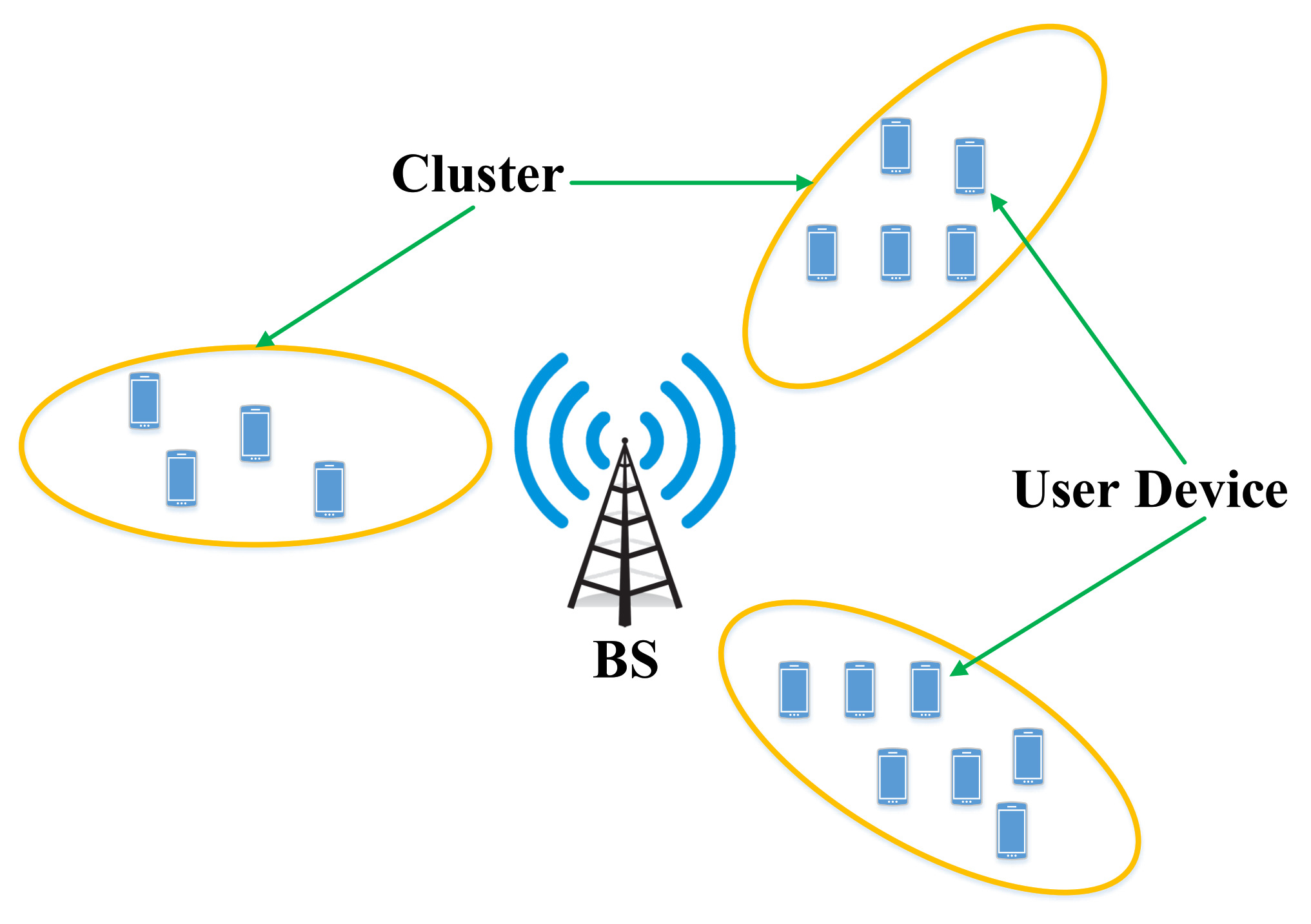
3.1. Network Model
3.2. User Spatial Distribution Model
3.3. Channel Model
3.4. Signal Model
4. Problem Formulation
5. ST-DBSCAN-Based User Clustering for mmWave-NOMA Systems
5.1. Overview and Preliminaries of ST-DBSCAN
- 1.
- : (Maximality) If and b is density-reachable from a with regard to minPts and Eps, then .
- 2.
- : (Connectivity) A point a is density-connected to point b with regard to minPts and Eps.
5.2. ST-DBSCAN Based User Clustering
| Algorithm 1 ST-DBSCAN-based user clustering algorithm |
| Input: Set of user information . Input: Eps1 (): Radius between users in geographical coordinates. Input: Eps2 (): Maximum channel gain between users. Input: minPts: Density threshold (minimum number of users within and distance). Input: : Threshold value of a cluster.
Output: Set of clusters and set of users in cluster . |
6. Solution of Power Allocation and Hybrid Beamforming
6.1. Power Allocation with Fixed Beamforming
6.1.1. Intra-Cluster Power Allocation
6.1.2. Inter-Cluster Power Allocation
| Algorithm 2 Inter-cluster power allocation algorithm |
Input:
|
6.2. HBF with BC-PSO
6.2.1. DBF Using AZF
6.2.2. BC-PSO Based ABF
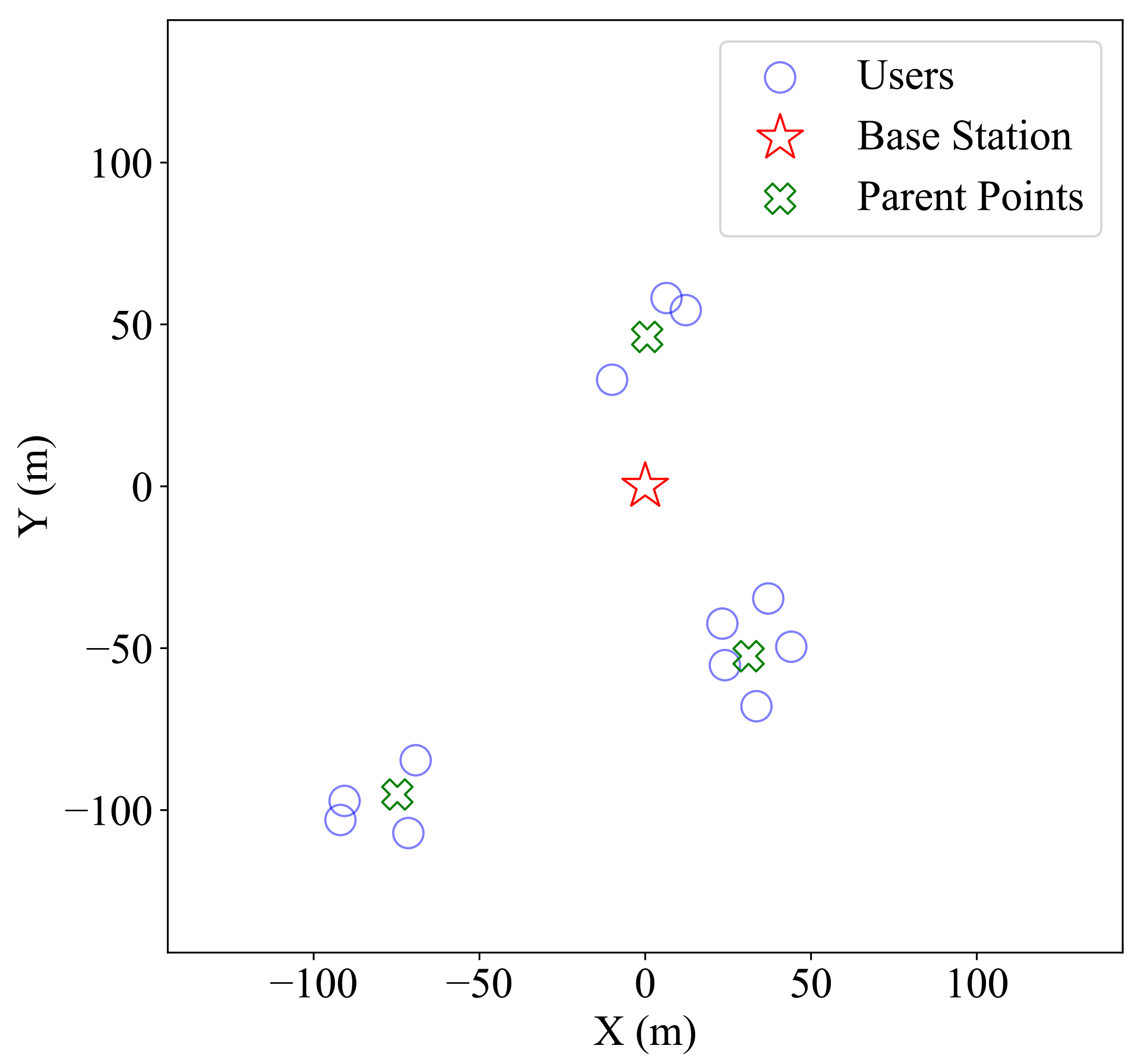
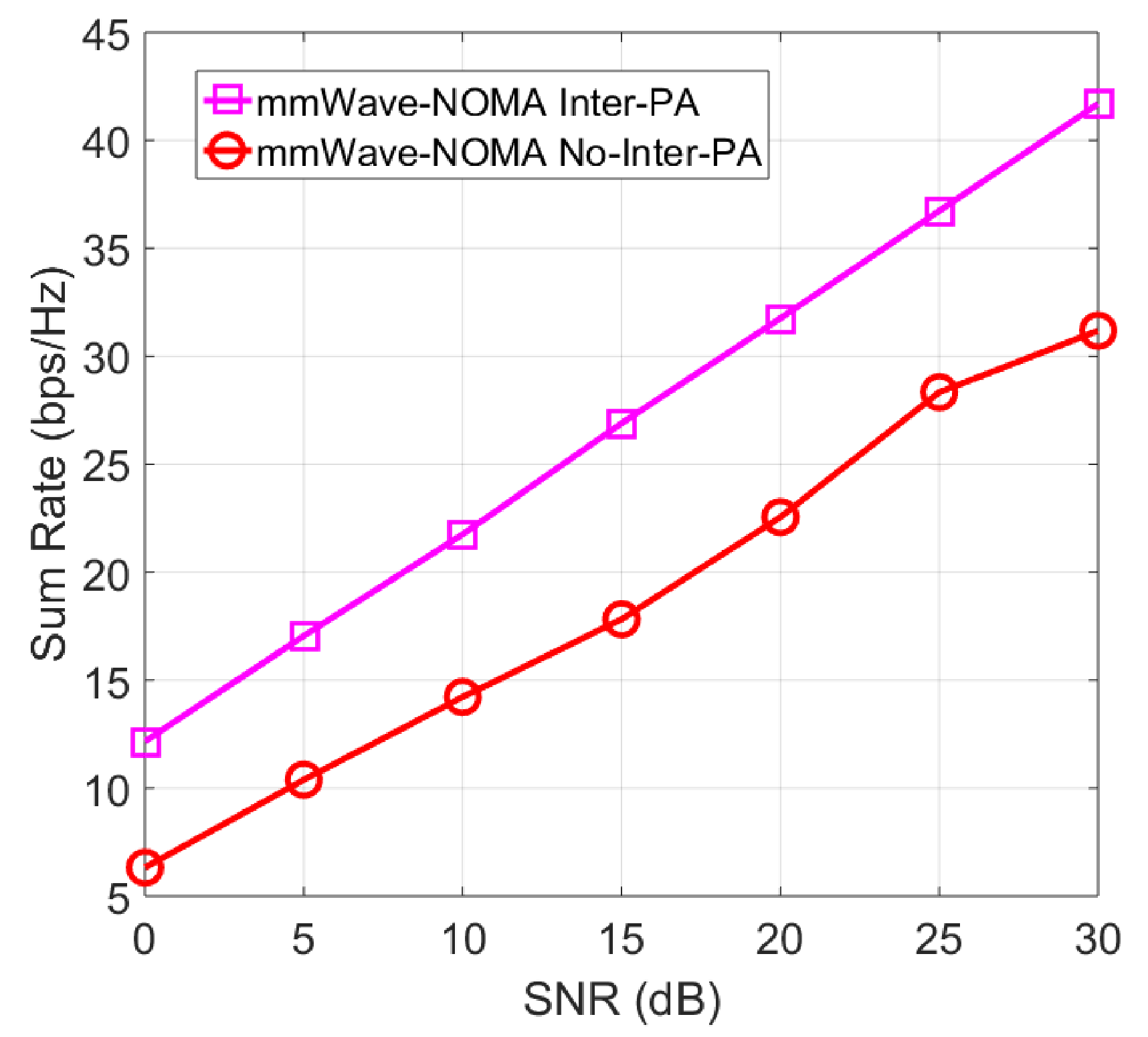
7. Simulation Results
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Proof of Proposition 1
References
- Forecast, G.M.D.T. Cisco Visual Networking Index: Global Mobile Data Traffic Forecast Update, 2017–2022. Update 2019, 2017, 1–36. [Google Scholar]
- Saito, Y.; Kishiyama, Y.; Benjebbour, A.; Nakamura, T.; Li, A.; Higuchi, K. Non-orthogonal multiple access (NOMA) for cellular future radio access. In Proceedings of the 2013 IEEE 77th Vehicular Technology Conference (VTC Spring), Dresden, Germany, 2–5 June 2013; pp. 1–5. [Google Scholar]
- Yue, X.; Qin, Z.; Liu, Y.; Kang, S.; Chen, Y. A unified framework for non-orthogonal multiple access. IEEE Trans. Commun. 2018, 66, 5346–5359. [Google Scholar] [CrossRef]
- Huynh, T.P.; Ngoc Son, P.; Voznak, M. Secrecy performance of underlay cooperative cognitive network using non-orthogonal multiple access with opportunistic relay selection. Symmetry 2019, 11, 385. [Google Scholar] [CrossRef]
- Ly, T.T.H.; Nguyen, H.S.; Nguyen, T.S.; Huynh, V.V.; Nguyen, T.L.; Voznak, M. Outage probability analysis in relaying cooperative systems with NOMA considering power splitting. Symmetry 2019, 11, 72. [Google Scholar] [CrossRef]
- Kim, J.; Koh, J.; Kang, J.; Lee, K.; Kang, J. Design of user clustering and precoding for downlink non-orthogonal multiple access (NOMA). In Proceedings of the MILCOM 2015—2015 IEEE Military Communications Conference, Tampa, FL, USA, 26–28 October 2015; pp. 1170–1175. [Google Scholar]
- Cui, J.; Liu, Y.; Ding, Z.; Fan, P.; Nallanathan, A. Optimal user scheduling and power allocation for millimeter wave NOMA systems. IEEE Trans. Wirel. Commun. 2017, 17, 1502–1517. [Google Scholar] [CrossRef]
- Fang, F.; Zhang, H.; Cheng, J.; Leung, V.C. Energy-efficient resource allocation for downlink non-orthogonal multiple access network. IEEE Trans. Commun. 2016, 64, 3722–3732. [Google Scholar] [CrossRef]
- Zhu, L.; Xiao, Z.; Xia, X.G.; Wu, D.O. Millimeter-wave communications with non-orthogonal multiple access for B5G/6G. IEEE Access 2019, 7, 116123–116132. [Google Scholar] [CrossRef]
- Cui, J.; Ding, Z.; Fan, P.; Al-Dhahir, N. Unsupervised machine learning-based user clustering in millimeter-wave-NOMA systems. IEEE Trans. Wirel. Commun. 2018, 17, 7425–7440. [Google Scholar] [CrossRef]
- Liang, W.; Ding, Z.; Li, Y.; Song, L. User pairing for downlink non-orthogonal multiple access networks using matching algorithm. IEEE Trans. Commun. 2017, 65, 5319–5332. [Google Scholar] [CrossRef]
- Chen, Z.; Ding, Z.; Dai, X.; Zhang, R. An optimization perspective of the superiority of NOMA compared to conventional OMA. IEEE Trans. Signal Process. 2017, 65, 5191–5202. [Google Scholar] [CrossRef]
- Xu, P.; Ding, Z.; Dai, X.; Poor, H.V. A new evaluation criterion for non-orthogonal multiple access in 5G software defined networks. IEEE Access 2015, 3, 1633–1639. [Google Scholar] [CrossRef]
- Zheng, B.; Wu, Q.; Zhang, R. Intelligent reflecting surface-assisted multiple access with user pairing: NOMA or OMA? IEEE Commun. Lett. 2020, 24, 753–757. [Google Scholar] [CrossRef]
- Janjua, M.B.; da Costa, D.B.; Arslan, H. User Pairing and Power Allocation Strategies for 3D VLC-NOMA Systems. IEEE Wirel. Commun. Lett. 2020, 9, 866–870. [Google Scholar] [CrossRef]
- Ding, Z.; Fan, P.; Poor, H.V. Impact of user pairing on 5G nonorthogonal multiple-access downlink transmissions. IEEE Trans. Veh. Technol. 2015, 65, 6010–6023. [Google Scholar] [CrossRef]
- Timotheou, S.; Krikidis, I. Fairness for non-orthogonal multiple access in 5G systems. IEEE Signal Process. Lett. 2015, 22, 1647–1651. [Google Scholar] [CrossRef]
- Ding, Z.; Peng, M.; Poor, H.V. Cooperative non-orthogonal multiple access in 5G systems. IEEE Commun. Lett. 2015, 19, 1462–1465. [Google Scholar] [CrossRef]
- Benjebbour, A.; Saito, K.; Li, A.; Kishiyama, Y.; Nakamura, T. Non-orthogonal multiple access (NOMA): Concept, performance evaluation and experimental trials. In Proceedings of the 2015 International Conference on Wireless Networks and Mobile Communications (WINCOM), Marrakech, Morocco, 20–23 October 2015; pp. 1–6. [Google Scholar]
- Shahab, M.B.; Irfan, M.; Kader, M.F.; Young Shin, S. User pairing schemes for capacity maximization in non-orthogonal multiple access systems. Wirel. Commun. Mob. Comput. 2016, 16, 2884–2894. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, D.K.; Meng, W.X.; Li, C. User pairing algorithm with SIC in non-orthogonal multiple access system. In Proceedings of the 2016 IEEE International Conference on Communications (ICC), Kuala Lumpur, Malaysia, 22–27 May 2016; pp. 1–6. [Google Scholar]
- Wan, D.; Wen, M.; Cheng, X.; Mumtaz, S.; Guizani, M. A promising non-orthogonal multiple access based networking architecture: Motivation, conception, and evolution. IEEE Wirel. Commun. 2019, 26, 152–159. [Google Scholar] [CrossRef]
- Shi, L.; Li, B.; Chen, H. Pairing and power allocation for downlink nonorthogonal multiple access systems. IEEE Trans. Veh. Technol. 2017, 66, 10084–10091. [Google Scholar] [CrossRef]
- Di, B.; Song, L.; Li, Y. Sub-channel assignment, power allocation, and user scheduling for non-orthogonal multiple access networks. IEEE Trans. Wirel. Commun. 2016, 15, 7686–7698. [Google Scholar] [CrossRef]
- Marcano, A.S.; Christiansen, H.L. Impact of NOMA on network capacity dimensioning for 5G HetNets. IEEE Access 2018, 6, 13587–13603. [Google Scholar] [CrossRef]
- Ding, Z.; Schober, R.; Poor, H.V. A general MIMO framework for NOMA downlink and uplink transmission based on signal alignment. IEEE Trans. Wirel. Commun. 2016, 15, 4438–4454. [Google Scholar] [CrossRef]
- Kimy, B.; Lim, S.; Kim, H.; Suh, S.; Kwun, J.; Choi, S.; Lee, C.; Lee, S.; Hong, D. Non-orthogonal multiple access in a downlink multiuser beamforming system. In Proceedings of the MILCOM 2013—2013 IEEE Military Communications Conference, San Diego, CA, USA, 18–20 November 2013; pp. 1278–1283. [Google Scholar]
- Wang, B.; Dai, L.; Wang, Z.; Ge, N.; Zhou, S. Spectrum and energy-efficient beamspace MIMO-NOMA for millimeter-wave communications using lens antenna array. IEEE J. Sel. Areas Commun. 2017, 35, 2370–2382. [Google Scholar] [CrossRef]
- Ding, Z.; Fan, P.; Poor, H.V. Random beamforming in millimeter-wave NOMA networks. IEEE Access 2017, 5, 7667–7681. [Google Scholar] [CrossRef]
- Zhang, D.; Zhou, Z.; Xu, C.; Zhang, Y.; Rodriguez, J.; Sato, T. Capacity analysis of NOMA with mmWave massive MIMO systems. IEEE J. Sel. Areas Commun. 2017, 35, 1606–1618. [Google Scholar] [CrossRef]
- Fang, F.; Zhang, H.; Cheng, J.; Roy, S.; Leung, V.C. Joint user scheduling and power allocation optimization for energy-efficient NOMA systems with imperfect CSI. IEEE J. Sel. Areas Commun. 2017, 35, 2874–2885. [Google Scholar] [CrossRef]
- Adhikary, A.; Nam, J.; Ahn, J.Y.; Caire, G. Joint spatial division and multiplexing—The large-scale array regime. IEEE Trans. Inf. Theory 2013, 59, 6441–6463. [Google Scholar] [CrossRef]
- Nam, J.; Adhikary, A.; Ahn, J.Y.; Caire, G. Joint spatial division and multiplexing: Opportunistic beamforming, user grouping and simplified downlink scheduling. IEEE J. Sel. Top. Signal Process. 2014, 8, 876–890. [Google Scholar] [CrossRef]
- You, H.; Pan, Z.; Liu, N.; You, X. User Clustering Scheme for Downlink Hybrid NOMA Systems Based on Genetic Algorithm. IEEE Access 2020, 8, 129461–129468. [Google Scholar] [CrossRef]
- Ren, J.; Wang, Z.; Xu, M.; Fang, F.; Ding, Z. An EM-Based User Clustering Method in Non-Orthogonal Multiple Access. IEEE Trans. Commun. 2019, 67, 8422–8434. [Google Scholar] [CrossRef]
- Marasinghe, D.; Jayaweera, N.; Rajatheva, N.; Latva-Aho, M. Hierarchical User Clustering for mmWave-NOMA Systems. In Proceedings of the 2020 2nd 6G Wireless Summit (6G SUMMIT), Levi, Finland, 17–20 March 2020; pp. 1–5. [Google Scholar]
- Saha, C.; Afshang, M.; Dhillon, H.S. Enriched K-tier HetNet model to enable the analysis of user-centric small cell deployments. IEEE Trans. Wirel. Commun. 2017, 16, 1593–1608. [Google Scholar] [CrossRef]
- Chiu, S.N.; Stoyan, D.; Kendall, W.S.; Mecke, J. Stochastic Geometry and Its Applications; John Wiley & Sons: Chichester, West Sussex, UK, 2013. [Google Scholar]
- Kulkarni, M.N.; Ghosh, A.; Andrews, J.G. A comparison of MIMO techniques in downlink millimeter wave cellular networks with hybrid beamforming. IEEE Trans. Commun. 2016, 64, 1952–1967. [Google Scholar] [CrossRef]
- El Ayach, O.; Rajagopal, S.; Abu-Surra, S.; Pi, Z.; Heath, R.W. Spatially sparse precoding in millimeter wave MIMO systems. IEEE Trans. Wirel. Commun. 2014, 13, 1499–1513. [Google Scholar] [CrossRef]
- Alkhateeb, A.; Leus, G.; Heath, R.W. Limited feedback hybrid precoding for multi-user millimeter wave systems. IEEE Trans. Wirel. Commun. 2015, 14, 6481–6494. [Google Scholar] [CrossRef]
- Rappaport, T.S.; Sun, S.; Mayzus, R.; Zhao, H.; Azar, Y.; Wang, K.; Wong, G.N.; Schulz, J.K.; Samimi, M.; Gutierrez, F. Millimeter wave mobile communications for 5G cellular: It will work! IEEE Access 2013, 1, 335–349. [Google Scholar] [CrossRef]
- Lee, G.; Sung, Y.; Seo, J. Randomly-directional beamforming in millimeter-wave multiuser MISO downlink. IEEE Trans. Wirel. Commun. 2015, 15, 1086–1100. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. KDD 1996, 96, 226–231. [Google Scholar]
- Birant, D.; Kut, A. ST-DBSCAN: An algorithm for clustering spatial–temporal data. Data Knowl. Eng. 2007, 60, 208–221. [Google Scholar] [CrossRef]
- Lemic, F.; Martin, J.; Yarp, C.; Chan, D.; Handziski, V.; Brodersen, R.; Fettweis, G.; Wolisz, A.; Wawrzynek, J. Localization as a feature of mmWave communication. In Proceedings of the 2016 International Wireless Communications and Mobile Computing Conference (IWCMC), Paphos, Cyprus, 5–9 September 2016; pp. 1033–1038. [Google Scholar]
- Maletic, N.; Sark, V.; Gutiérrez, J.; Grass, E. Device localization using mmWave ranging with sub-6-assisted angle of arrival estimation. In Proceedings of the 2018 IEEE International Symposium on Broadband Multimedia Systems and Broadcasting (BMSB), Valencia, Spain, 6–8 June 2018; pp. 1–6. [Google Scholar]
- Mohammed, S.L.; Alsharif, M.H.; Gharghan, S.K.; Khan, I.; Albreem, M. Robust Hybrid Beamforming Scheme for Millimeter-Wave Massive-MIMO 5G Wireless Networks. Symmetry 2019, 11, 1424. [Google Scholar] [CrossRef]
- Zhu, L.; Zhang, J.; Xiao, Z.; Cao, X.; Wu, D.O.; Xia, X.G. Joint Tx-Rx beamforming and power allocation for 5G millimeter-wave non-orthogonal multiple access networks. IEEE Trans. Commun. 2019, 67, 5114–5125. [Google Scholar] [CrossRef]
- Ali, S.; Hossain, E.; Kim, D.I. Non-orthogonal multiple access (NOMA) for downlink multiuser MIMO systems: User clustering, beamforming, and power allocation. IEEE Access 2016, 5, 565–577. [Google Scholar] [CrossRef]
- Pham, Q.V.; Dao, N.N.; Huynh-The, T.; Zhao, J.; Hwang, W.J. Clustering and Power Allocation for UAV-assisted NOMA-VLC Systems: A Swarm Intelligence Approach. arXiv 2020, arXiv:2007.15430. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hoang, H.-T.; Pham, Q.-V.; Hwang, W.-J. Spatial-Temporal-DBSCAN-Based User Clustering and Power Allocation for Sum Rate Maximization in Millimeter-Wave NOMA Systems. Symmetry 2020, 12, 1854. https://doi.org/10.3390/sym12111854
Hoang H-T, Pham Q-V, Hwang W-J. Spatial-Temporal-DBSCAN-Based User Clustering and Power Allocation for Sum Rate Maximization in Millimeter-Wave NOMA Systems. Symmetry. 2020; 12(11):1854. https://doi.org/10.3390/sym12111854
Chicago/Turabian StyleHoang, Huu-Trung, Quoc-Viet Pham, and Won-Joo Hwang. 2020. "Spatial-Temporal-DBSCAN-Based User Clustering and Power Allocation for Sum Rate Maximization in Millimeter-Wave NOMA Systems" Symmetry 12, no. 11: 1854. https://doi.org/10.3390/sym12111854
APA StyleHoang, H.-T., Pham, Q.-V., & Hwang, W.-J. (2020). Spatial-Temporal-DBSCAN-Based User Clustering and Power Allocation for Sum Rate Maximization in Millimeter-Wave NOMA Systems. Symmetry, 12(11), 1854. https://doi.org/10.3390/sym12111854




