Abstract
Accurate memory resource prediction can achieve optimal performance for complex system simulation (CSS) using optimistic parallel execution in the cloud computing environment. However, because of the varying memory resource demands of CSS applications caused by the simulation entity scale and frequent optimistic synchronization, the existing approaches are unable to predict the memory resource required by a CSS application accurately, which cannot take full advantage of the elasticity and symmetry of cloud computing. In this paper, a probabilistic prediction approach based on ensemble learning, which regards the entity scale and frequent optimistic synchronization as the important features, is proposed. The approach using stacking strategy consists of a two-layer architecture. The first-layer architecture includes two kinds of base models, namely, back-propagation neural network (BPNN) and random forest (RF). The root mean squared error-based pruning algorithm is designed to choose the optimal subset of the base models. The second-layer is the Gaussian process regression (GPR) model, which is applied to quantify the uncertainty information in the probabilistic prediction for memory resources. A series of experiments are presented to prove that the proposed approach can achieve higher accuracy and performance compared to RF, BPNN, GPR, Bagging ensemble approach, and Regressive Ensemble Approach for Prediction.
1. Introduction
Large-scale complex systems contain a large number of components with complex interactions, such as combat system, economic system, and disease spread system [1]. Complex system simulation (CSS) has played an important role in the study of complex systems. With the increase in the scale of CSS applications and the complexity of interactions between the simulation entities, the demand for simulation performance has also increased. Optimistic parallel execution can improve the simulation efficiency, which is widely used in CSS [2]. On the other hand, the uncertainty of the interaction between simulation entities in CSS applications has led to different memory resource requirements [3]. Traditional high-performance computing environments cannot support the efficient operation of CSS applications [2]. The cloud computing provides a symmetric network architecture for the operation of CSS applications. The symmetry in the cloud computing means that the simulation applications can access the equal sharing of resources, which can make it easier to expand the resources compared to traditional high-performance computing environments [4]. The scalability and flexibility of cloud computing can provide dynamic and matched resources for CSS applications, which can meet the elastic resource requirements of simulation applications [5]. Therefore, this paper focuses on large-scale CSS using optimistic parallel execution in the cloud computing environment (hereinafter referred to as CSS).
In the cloud environment, the simulation entities in CSS applications will be distributed to different groups. The interactions between the simulation entities will produce frequent communication operations, which will lead to a large number of memory allocation and recycling operations [6]. Memory has become one of the main factors which limit the performance of CSS applications. It is normal that the processors will spend about 60% time waiting for the completion of memory operations [7]. If too few memory resources are allocated to CSS applications, it is difficult to support the efficient operation of the simulation applications. If a CSS application is allocated more memory resources than it actually needs, the excess resources will be wasted. On the other hand, the execution efficiency of the CSS applications with excess memory resources will decrease [8]. The limited memory resources can avoid the excessively optimistic execution of the simulation applications, thereby avoiding the excessive rollback operations and simulation performance degradation. Memory allocation for CSS applications in the cloud environment is a challenging and open issue. Accurate allocation of memory resources is significant to improve the simulation performance and make use of the elasticity and symmetry of cloud computing. For efficient memory allocation, it is critical to predict the memory resources required by the simulation applications [9].
At present, many models have been proposed in the research of resource prediction, that are mainly divided into two kinds: application resource prediction and host load prediction [10]. Application resource prediction is mainly to predict the resource requirements of applications (parallel tasks, video, etc.). Parallel tasks are decomposed into independent subtasks [11]. The resource requirements of parallel tasks can be obtained by predicting the resource requirements of subtasks. The resources requirements of video applications can be predicted based on the characteristics of video applications (frames, time, etc.). Host load prediction is to predict the workload in the high-performance computing systems [12]. However, to the best of the authors’ knowledge, the existing models, which do not take into account simulation entity scale and frequent time synchronization, make it difficult to accurately predict the memory resources required by the simulation applications.
To solve the above problems, a probabilistic approach based on ensemble learning is proposed to predict memory resources of CSS applications. The proposed approach using stacking strategy consists of a two-layer architecture. Gaussian process regression (GPR) [13] is a probabilistic prediction approach in the Bayesian context, which can quantify the uncertainty in memory resource prediction. Uncertainty information can help make the best decision [14]. Random forest (RF) [15] is an ensemble algorithm based on decision trees. RF can achieve good performance with few hyper-parameters to be adjusted. Back-propagation neural network (BPNN) [16] can present the nonlinear relationship effectively and it is resistant to noise. The diversity between the base models is the key factor which affects the performance of ensemble models. Considering the different features of RF, BPNN, and GPR, RF and BPNN are used as the first-layer base models, and GPR is used as the second-layer meta model. The predictions of the base models are applied as the input of the meta model for probabilistic prediction. The contributions of the article are as follows:
- As the memory prediction dataset is not available, the dataset is conducted by collecting static and dynamic information (entity scale, rollback events, simulation end time, etc.) of CSS applications which are deployed in the cloud environment.
- A probabilistic approach is proposed to predict memory resources required by CSS applications based on ensemble learning. A root mean squared error-based pruning (RMSEP) algorithm is proposed to select the optimal subset of the base models, which can improve the performance of the probabilistic approach.
- The experiments verified the effectiveness of the proposed approach for memory resource prediction.
The remainder of this paper is as follows: Section 2 introduces the related work. In Section 3, we briefly introduce RF, BPNN, and GPR. Section 4 describes the memory prediction framework and the memory probabilistic prediction approach. Section 5 depicts the data which are used to evaluate the proposed model. In Section 6, the experiments and results are described in detail, and the conclusions and future work of this paper are presented in Section 7.
2. Related Works
2.1. Resource Prediction in Cloud Environment
2.1.1. Application Resource Prediction
Application resource prediction mainly aims at predicting future resource demand based on the characteristics of the application. The proposed method in the paper belongs to the application resource prediction category. Al-Rawahi et al. [17] collected the features of video applications based on Hadoop and proposed four machine learning methods to predict the execution time of the application. This method, which conducted bridges a gap in video prediction, is based on video applications with important features (video resolution, file size, etc.), but prediction accuracy needs to be improved in future work. Mukhtaj et al. [18] proposed a Local Weighted Linear Regression approach to predict the execution time of the job based on the historical execution of the Hadoop job, and the resources would be allocated to the job before a deadline. The accuracy rate is improved, but the method cannot adapt to the changes of the applications. Gurleen et al. [19] deployed the scientific application Cybershake in a cloud environment and proposed a Regressive Ensemble Approach for Prediction (REAP) to predict the CPU utilization of Cybershake. REAP is the ensemble learning approach, which can achieve good performance. But REAP ignores the prior knowledge of resource information. Ganapathi et al. [20] proposed a statistical method to predict the resource requirements of data-intensive applications in the cloud environment. The method can extract the correlation between resource and performance, and the weakness of the method is the sensitivity to outliers. Gopal et al. [21] considered the long/short-term resource requirements of CPU/memory-intensive applications and proposed a Bayesian method to predict the resources required by the applications. The Bayesian method is simple, but it cannot capture the features of the applications.
2.1.2. Host Load Prediction
Host load prediction is mainly to predict the resource demand in the next period through the trajectory history information of the high-performance computing system. Hisham [22] considered the seasonal and trend characteristics in time series and proposed the Swarm Intelligence Based Prediction Approach to predict cloud resource demand. The study solves the resource prediction problem from the perspective of the cloud consumer, but it is difficult to adapt to the changes of the workloads. Some researchers are mainly to test the resource prediction algorithms on real workloads. For example, Mehiar et al. [23] proposed a resource prediction algorithm to reduce energy consumption, and the effectiveness of the algorithm is verified on the Google traces, Ali et al. [24] proposed an ensemble algorithm based on learning automata to predict CPU load. The algorithm can dynamically adjust weights according to the performance of the constituent models. The experiments on the COMON dataset proved the effectiveness of the ensemble algorithm, and Mostafa et al. [25] proposed a resource prediction method for cloud services, which combined automated computing and reinforcement learning. ClarkNet and NASA traces were used to evaluate the effectiveness of the prediction model. These methods study the problem from the perspective of the cloud data center, which ignores the resource requirements of the applications.
2.2. Ensemble Model
Recently, the ensemble model has been widely applied in many fields. Jinping et al. [26] proposed an ensemble model of kernel extreme learning machines for network intrusion detection. A selective ensemble method to minimize the marginal distance is proposed to ensure the effectiveness of the ensemble model. The method integrates the homogeneous models, and the integration of the heterogeneous models may improve the accuracy. Some methods combine heterogeneous models to achieve good performance. For example, Ning et al. [27] proposed a deep ensemble learning framework which is used as the Alzheimer’s disease classification algorithm. The dataset from the National Alzheimer’s Coordinating Center proved that the algorithm can achieve better performance than the other six ensemble algorithms, Deepak et al. [28] proposed two malware detection methods based on ensemble learning. The first method is an ensemble model based on weighted voting. The second method is to select the base models with good performance to improve the performance and generalization of the malware detection method, and Tiago et al. [29] proposed three ensemble models (gradient boosted regression trees, random forest, and adapted Adaboost) to predict short-term load. The adapted Adaboost can achieve better performance on the electricity consumption dataset of office buildings. However, these methods cannot select the optimal subset of the base models.
In summary, many models have been used to predict the resources required by the applications (Parallel tasks, video, etc.). CSS applications will perform frequent synchronization and send/receive a large number of messages during the execution. It is difficult to decompose CSS applications into independent subtasks. The current resource prediction algorithms, which do not consider the simulation entity scale and frequent optimistic synchronization in CSS applications, cannot predict the memory required by the CSS applications accurately. Ensemble learning has been shown to be excellent in many fields, and can improve the performance of the single model. Therefore, this paper designed an ensemble model to predict memory resources for CSS applications, which considers the characteristics of the simulation applications. RMSEP is used to select the optimal subset of the base models to improve the performance.
3. Prerequisite
3.1. Random Forest
RF was proposed by Breiman et al. [15], and belongs to ensemble learning. RF uses bagging strategy to integrate multiple decision trees. Furthermore, the random feature selection is applied to train the decision trees. In other words, each independent decision tree is trained on randomly selected samples and features. RF increases the diversity between base models through sample disturbance and feature disturbance, which can improve the generalization of the model. Therefore, RF is widely used to solve the classification and regression problems. For regression, the average of predictions in the set of decision trees is used as the output of RF. The process of the RF regression model is shown in Figure 1.
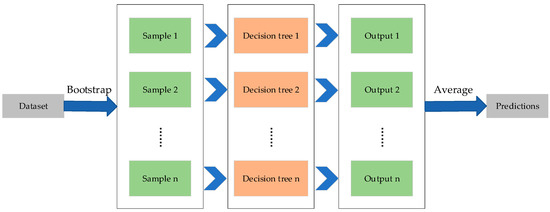
Figure 1.
The process of the random forest (RF) regression model.
3.2. Back-Propagation Neural Network
BPNN is a multi-layer feedforward neural network using a back-propagation algorithm in general, which has been widely applied to solve regression problems [30]. The structure of BPNN is shown in Figure 2.
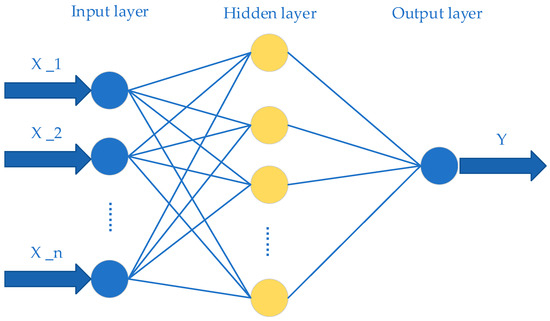
Figure 2.
The structure of a Back-Propagation Neural Network (BPNN).
A typical BPNN consists of three layers, input layer, hidden layer, and output layer [31]. For each sample, the BPNN will measure the error of the output layer, then propagate the error back to the hidden layer, and finally adjust the weight and threshold according to the error. The training error can be reduced through continuous iteration.
3.3. Gaussian Process Regression
GPR is a non-parametric model in the Bayesian context, which can be allowed for probabilistic prediction [32]. The GPR model can be represented by the mean function and the covariance function .
Noise needs to be considered in the regression problem, so the predicted value can be expressed as:
The predicted value of the test sample is , then the joint distribution of and the observation value of the training set can be represented as:
Then the posterior distribution of can be defined as:
where is the predicted value of GPR, and is the variance of the predictions.
4. Methodology
4.1. Cloud Memory Prediction Framework
At present, cloud computing provides an effective platform for studying CSS. The simulation applications need to be allocated optimal memory resources to improve simulation performance [33]. Therefore, we proposed a cloud memory prediction framework based on feedback loops. The key idea is to combine ensemble learning with feedback loops. The prediction model can learn from the feedback data, which can ensure the continuous update and iteration of the model. The model can predict the memory resources required by the simulation application accurately, and the predicted memory resources will be allocated to the CSS applications.
The cloud memory prediction framework is depicted in Figure 3, which mainly includes three modules, namely a cloud resource module, dataset module, and memory probabilistic prediction module.
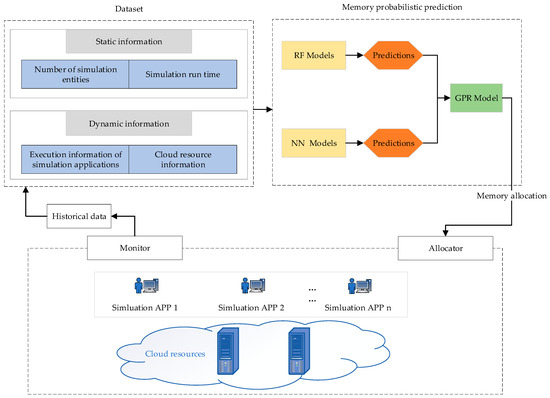
Figure 3.
Architecture of the cloud memory prediction framework.
The cloud resource module can monitor the status of the simulation applications and allocate the memory resources required by the simulation applications. The monitor will record the execution status of the simulation applications in real-time and return the monitoring information to the dataset module. The allocator will allocate predicted memory to the simulation applications.
The dataset module can collect and pre-process the static and dynamic information of the simulation applications. The static information includes the number of simulation entities and simulation run time. The dynamic information includes the execution information of simulation applications and cloud resource information. The execution information of simulation applications includes CPU utilization, memory utilization, the number of simulation event rollbacks, the execution time of the simulation applications, network delay, and the data sent/received by the network. The collected data will be standardized to eliminate dimensional inconsistencies for the training and testing of the memory probabilistic prediction model.
The memory probabilistic prediction model trains on the historical data, which can solve the problem of learning from insufficient data. The stacking strategy is applied to integrate models. The performance of the ensemble model is related to the diversity between the base models. Therefore, RF and BPNN are selected as the first-level base models, and GPR is the second-level meta model to perform the final probabilistic prediction. The proposed ensemble model can predict the memory resources required by simulation applications accurately. Finally, the predicted result will be sent to the cloud resource module.
4.2. Memory Probabilistic Prediction Model
The structure of the proposed memory probabilistic prediction model is shown in Figure 4. To predict the memory resources required by the simulation applications accurately, a large number of samples need to be generated, which can indicate the characteristics of the simulation applications. Therefore, the simulation applications are deployed in the cloud environment, and the dynamic information is collected at intervals of 10 s by the monitor. The simulation application memory dataset consists of dynamic information and static information. The dataset generated by different simulation applications needs to be cleaned. We use box plots to find outliers in the dataset, and replace the outliers with the mean of the previous sample and the next sample. At the same time, the features in the simulation application memory dataset need to be standardized. The dataset is divided into two parts: train set and test set. The train set is divided into train fold and validation fold. More specifically, 80% of the simulation application samples are used as the train set, 20% of the samples are used as the test set, 80% of the train set is used as the training fold, and 20% of the train set is used as the validation fold.
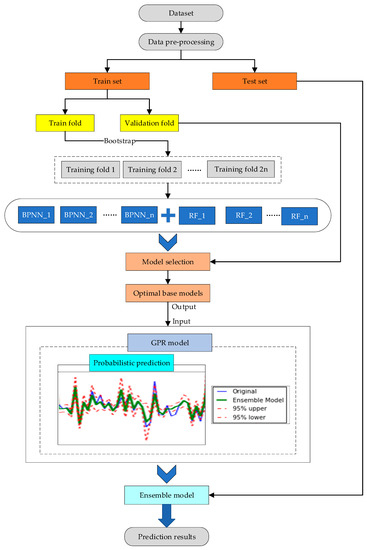
Figure 4.
Schematic diagram of the proposed memory probabilistic prediction model.
Ensemble learning has attracted the attention of many researchers. The performance of the ensemble model is mainly affected by two factors, the diversity between the base models and the performance of the base models [34]. To improve the diversity between the base models, we use bootstrap sampling to increase the disturbance of the samples. To improve the performance of the ensemble model, we need to choose the optimal base models to eliminate the negative influences of poor base models. Therefore, the root mean squared error-based pruning (RMSEP) algorithm is proposed to select the optimal subset of the base models according to the RMSE. Algorithm 1 shows the RMSEP algorithm, which can be represented by the following steps:
- (1)
- Calculate the RMSE of base models.
- (2)
- Sort the base models by RMSE in ascending order, and the base models predict the memory resources on the dataset.
- (3)
- Calculate the mean of each base model as the output of the model set, and then calculate the RMSE of the model set.
- (4)
- Select the model set with the minimum RMSE.
| Algorithm 1. RMSEP |
| Input: dataset , base models {} Output: final model set 1: for = 1 to 2: calculate of base model ; 3: end for 4: sort the base models {} by RMSE in ascending order, and the sorted model set can be represented by {}; 5: for = 1 to 6: make memory predictions on the dataset with the model set {}, the mean of the model set {} is used as the output of the ensemble model, and calculate the of the model set; 7: end for 8: the model set {} which has the min in {} is selected as the final model set ; 9: return ; |
4.3. Evaluation Metrics
Root mean squared error (RMSE), mean absolute error (MAE), and mean relative error (MRE) are used to evaluate the memory prediction performance of each model, the definitions of which are as follows:
where and , respectively, represent the true value and predicted value of sample , and n is the number of samples.
5. Case Study
5.1. Social Opinion System
Social Opinion System (SOS) [35] is a memory-intensive simulation application, which is used to evaluate the performance of the memory prediction algorithm. Simulation applications can be distinguished by adjusting different parameters. Table 1 shows the parameter configuration.

Table 1.
Parameter configuration.
SOS is a typical CSS application with a large number of simulation entities, which plays an important role in the political filed. SOS is developed to model the social opinion and study the trend and change of social opinion, which can provide support for policy formulation. Figure 5 shows the structure of SOS. SOS mainly consists of four components, namely interpersonal network, resources, cities, and media. We can study the spread of social public opinions through SOS. Resources include water, electricity, energy, and so on. When the resources are destroyed, the media can release information to influence the development of public opinion and the policies formulated by the city. Individuals can express their opinions and cities can adjust the policies according to public opinions. Public opinions can be affected by many factors, for example, individuals, media, and policies. On the other hand, because of the uncertainty of the components and frequent optimistic synchronization in the SOS, it is difficult to estimate the memory requirements accurately.
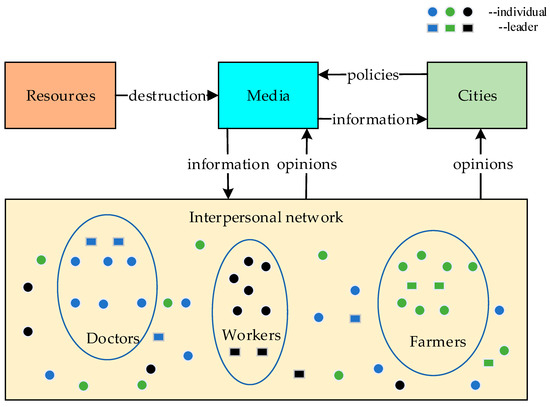
Figure 5.
Composition structure of a Social Opinion System (SOS).
5.2. Dataset
We adjust different parameter configurations of SOS to generate different simulation application samples. The simulation applications are deployed in a real cloud environment. Historical information can be collected by the monitor. The simulation memory prediction dataset was generated by the static and dynamic information. The features we mainly consider are shown in Table 2. The target of the dataset is the memory requirements.

Table 2.
Features in the dataset.
6. Experiments and Results
6.1. Experimental Environment
The simulation applications were deployed in a real cloud environment, which was built by the open container engine Docker. Docker container virtualization technology was used to build eight nodes. Each Docker container was set up with a core of 3.40 GHz Intel Core i5-7500 CPU and 2 GB memory. We used the discrete event simulation platform SUPE [36] to support the effective operation of the simulation applications. The simulation application contains many simulation entities, which were divided into multiple logical process groups, and each logical process group had the same memory requirements. The proposed memory prediction model was evaluated on a machine with Intel(R) Core (TM) i5-7500 and 16 GB memory by python 3.5 and PyCharm integrated development environment.
6.2. Experimental Results
We conducted two kinds of experiments to evaluate the memory prediction approach. (1) Parameter experiments. The performance of the approach was evaluated with different parameters. (2) Performance experiments. The effectiveness of the proposed memory prediction approach can be verified in the performance experiments.
6.2.1. Parameter Experiments
There are many parameters that can affect the performance of the proposed probabilistic approach. In this paper, RMSEP is proposed to choose the first-layer base models with good performance, and the selection of kernel function is crucial to improving the performance of GPR. Therefore, we mainly consider the ensemble size N of the first-layer base models and the kernel function of GPR.
In the experiments, multiple base models are initialized. The RMSEP algorithm is used to select the optimal subset of the base models. The algorithm needs to be tested many times to obtain statistically significant results. The standard error is used to describe the deviation of the sample mean and universal mean. When we conducted 40 experiments, the standard error was considered to be stable and declines slowly. Therefore, 40 experiments were conducted to evaluate the performance of the models objectively. Figure 6 depicts the performance of the first-layer base models with different ensemble sizes.
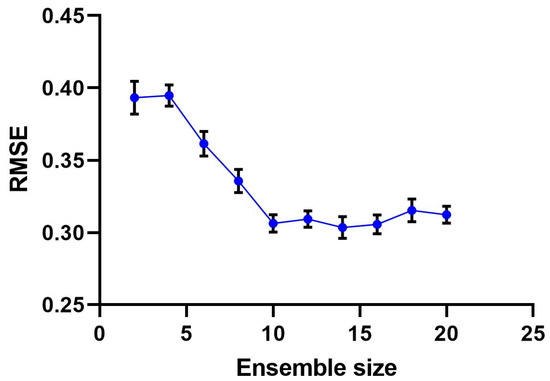
Figure 6.
The root mean squared error (RMSE) of the first-layer base models with different ensemble sizes.
As can be seen from Figure 6, as the ensemble size increases, the RMSE of the model will gradually decrease at first, and then turn to be stable. Because the RMSEP algorithm can select the base models with good performance and avoid the negative impacts of the base models with poor performance. When the ensemble size is over 10, RMSE will remain stable in a specific range. At this time, as the number of the base models increases, the performance is improved slowly. Therefore, in this article, 10 base models (5 BPNNs, 5 RFs) are used to generate the first-layer base models.
The kernel function in GPR can describe the correlation between the predicted value and the true value. The kernel function has a great influence on the performance of GPR. Therefore, we need to choose a suitable kernel function to improve the performance of the GPR model. Currently commonly used kernel functions in GPR include exponential sine square kernel (ESS), Matern kernel (MA), squared exponential kernel (SE), and rational quadratic kernel (RQ). Figure 7a–c depict the performance of the GPR model with different kernel functions.
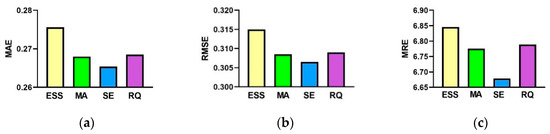
Figure 7.
The performance of Gaussian process regression (GPR) model with different kernel functions. (a) mean absolute error (MAE); (b) RMSE; (c) mean relative error (MRE).
As shown in Figure 7, the GPR using the SE kernel function can achieve the best performance. Therefore, the SE is used as the kernel function of the GPR in the ensemble model.
6.2.2. Performance Experiments
Figure 8a–c depict the probability density function (PDF) of the predicted values on different samples when the simulation end time is 1000. The PDF can be calculated by the mean and covariance of the samples. It can be seen from Figure 8 that the true values of the samples fall in the 95% confidence interval, and they are also close to the mean of the predicted values. It shows that the proposed approach can predict the memory resources required for simulation applications effectively.
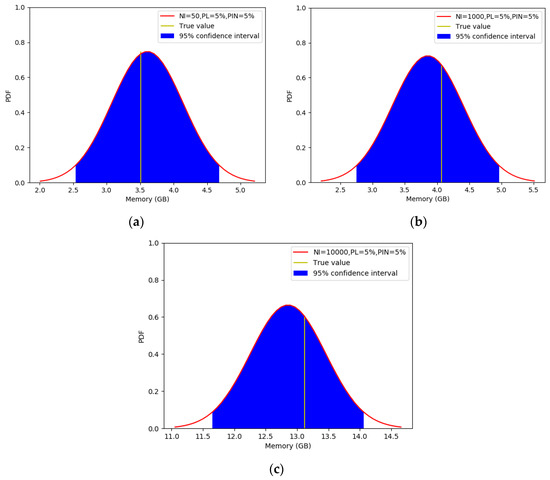
Figure 8.
Probability density function (PDF). Number of individuals (NI). Probability of leaders (PL). Probability of interpersonal network (PIN): (a) NI = 50, PL = 5%, PIN = 5%; (b) NI = 1000, PL = 5%, PIN = 5%; (c) NI = 10000, PL = 5%, PIN = 5%.
We compare the proposed probabilistic approach with RF, BPNN, GPR, bagging (RF, BPNN, and GPR are integrated with the bagging strategy), and REAP to prove the effectiveness of this approach. We performed 40 independent experiments to obtain the average of the models. The results are shown in Table 3.

Table 3.
Memory prediction results.
As can be seen from Table 3, our proposed probabilistic approach has the best performance compared with other models. RF cannot perform well in memory prediction. The ensemble model with bagging strategy and REAP can achieve performance similar to the proposed probabilistic approach. The proposed probabilistic approach achieved the lowest MAE, RMSE, and MRE. In memory prediction, the proposed probabilistic approach can achieve better results than the other models, because the RMSEP algorithm can eliminate the impacts of the base models with poor performance to improve the performance of the approach. Therefore, the proposed probabilistic approach can better meet the memory requirements of simulation applications.
7. Conclusions and Future Works
In this paper, we study the memory prediction issue in CSS applications using optimistic parallel execution. The memory prediction dataset is conducted by collecting static and dynamic information of CSS applications which are deployed in the cloud environment. A cloud memory prediction framework was proposed to allocate optimal memory resources to the simulation applications, and we proposed a probabilistic approach to predict the memory required by CSS applications in the cloud environment. RF and BPNN are used as the first-layer base models. The RMSEP algorithm is proposed to select the optimal subset of the base models, which can improve the performance of the proposed probabilistic approach. GPR is used as the second-layer meta model to perform probabilistic predictions. The outputs of RF and BPNN are applied as the input of GPR. Accurate memory prediction is critical to improve the performance of CSS applications. Experiments show that the proposed probabilistic approach can achieve better performance in comparison to RF, BPNN, GPR, bagging ensemble approach, and REAP. Therefore, the proposed approach can predict the optimal resources required by the simulation applications more accurately, which results in a great improvement in execution efficiency and resource utilization.
In future work, the plans to extend the proposed approach are as follows:
- (1)
- We hope to evaluate our approach on a large cloud platform and evaluate the proposed approach on other CSS applications.
- (2)
- Considering the limitation that the memory prediction method does not exploit the domain information of CSS applications, we plan to build the strong correlation features of CSS applications.
- (3)
- Commit to the investigate the correlation between the cloud resources, and provide more reliable results for the resource allocation.
Author Contributions
Conceptualization, S.W. and F.Z.; methodology, S.W.; software, Y.Y.; validation, S.W. and F.Z.; formal analysis, S.W. and F.Z.; investigation, S.W.; resources, W.T.; data curation, S.W. and Y.X.; writing—original draft preparation, S.W. and F.Z.; writing—review and editing, S.W. and Y.X.; visualization, S.W.; supervision, Y.Y. and F.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (no. 61903368).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jiang, Z.; Zhao, T.; Wang, S.; Ren, F. A Novel Risk Assessment and Analysis Method for Correlation in a Complex System Based on Multi-Dimensional Theory. Appl. Sci. 2020, 10, 3007. [Google Scholar] [CrossRef]
- Fujimoto, R.M. Research Challenges in Parallel and Distributed Simulation. ACM Trans. Modeling Comput. Simul. 2016, 26, 1–29. [Google Scholar] [CrossRef]
- Fujimoto, R.M.; Malik, A.W.; Park, A.J. Parallel and distributed simulation in the cloud. SCS M S Mag. 2010, 3, 1–10. [Google Scholar]
- Wang, Y.; Tang, W.; Yao, Y.; Zhu, F. DA-OCBA: Distributed Asynchronous Optimal Computing Budget Allocation Algorithm of Simulation Optimization Using Cloud Computing. Symmetry 2019, 11, 1297. [Google Scholar] [CrossRef]
- Shuai, W.; Feng, Z.; Yiping, Y.; Wenjie, T.; Yuhao, X.; Siqi, X. A Computing Resources Prediction Approach Based on Ensemble Learning for Complex System Simulation in Cloud Environment. Simul. Model. Pract. Theory 2020. [Google Scholar] [CrossRef]
- Tianlin, L.; Yiping, Y.; Wenjie, T.; Feng, Z.; Zhongwei, L. An Efficient Multi-threaded Memory Allocator for PDES Applications. Simul. Model. Pract. Theory 2020, 100, 102067. [Google Scholar]
- Zuberek, W.M. Balancing the performance of block multithreaded distributed-memory systems. Simul. Model. Pract. Theory 2011, 19, 1318–1329. [Google Scholar] [CrossRef]
- Malik, A.; Park, A.; Fujimoto, R.M. Optimistic synchronization of parallel simulations in cloud computing environments. In Proceedings of the IEEE International Conference on Cloud Computing, Bangalore, India, 21–25 September 2009; pp. 49–56. [Google Scholar]
- Kumar, K.D.; Umamaheswari, E. Prediction methods for effective resource provisioning in cloud computing: A survey. Multiagent Grid Syst. 2018, 14, 283–305. [Google Scholar] [CrossRef]
- Amiri, L.M.; Mohammad, K. Survey on prediction models of applications for resources provisioning in cloud. J. Netw. Comput. Appl. 2017, 82, 93–113. [Google Scholar] [CrossRef]
- Feng, Y.; Yiping, Y.; Lining, X.; Huangke, C. An Intelligent Scheduling Algorithm for Complex Manufacturing System Simulation with Frequent Synchronizations in Clouds. Memetic Comput. 2019, 11, 357–370. [Google Scholar] [CrossRef]
- Shaw, R.; Howley, E.; Barrett, E. An energy efficient anti-correlated virtual machine placement algorithm using resource usage predictions. Simul. Model. Pract. Theory 2019, 93, 322–342. [Google Scholar] [CrossRef]
- Alodat, M.T.; Mohammed, K.S. Gaussian process regression with skewed errors. J. Comput. Appl. Math. 2020, 370, 15. [Google Scholar] [CrossRef]
- Roman, K. Bayesian system for probabilistic river stage forecasting. J. Hydrol. 2002, 268, 16–40. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Jiao, A.; Zhang, G.; Liu, B.; Liu, W. Prediction of Manufacturing Quality of Holes Based on a BP Neural Network. Appl. Sci. 2020, 10, 2108. [Google Scholar] [CrossRef]
- Al-Rawahi, M.; Edirisinghe, A.; Jeyarajan, T. Machine Learning-Based Framework for Resource Management and Modelling for Video Analytic in Cloud-Based Hadoop Environment. In Proceedings of the 2016 Intl IEEE Conferences on Ubiquitous Intelligence & Computing, Advanced and Trusted Computing, Scalable Computing and Communications, Cloud and Big Data Computing, Internet of People, and Smart World Congress, Toulouse, France, 18–21 July 2016; pp. 801–807. [Google Scholar]
- Mukhtaj, K.; Yong, J.; Maozhen, L.; Yang, X.; Changjun, J. Hadoop Performance Modeling for Job Estimation and Resource Provisioning. IEEE Trans. Parallel Distrib. Syst. 2015, 99, 441–454. [Google Scholar]
- Gurleen, K.; Anju, B.; Inderveer, C. An intelligent regressive ensemble approach for predicting resource usage in cloud computing. J. Parallel Distrib. Comput. 2019, 123, 1–12. [Google Scholar]
- Ganapathi, A.; Chen, Y.; Fox, A.; Katz, R.; Patterson, D. Statistics-driven workload modeling for the Cloud. In Proceedings of the 26th International Conference on Data Engineering, Long Beach, CA, USA, 1–6 March 2010; pp. 87–92. [Google Scholar]
- Gopal, K.S.; Sunilkumar, S.M. Virtual Resource Prediction in Cloud Environment: A Bayesian Approach. J. Netw. Comput. Appl. 2016, 65, 144–154. [Google Scholar]
- Hisham, A.K. An Intelligent Swarm Based Prediction Approach For Predicting Cloud Computing User Resource Needs. Comput. Commun. 2020, 151, 133–144. [Google Scholar]
- Mehiar, D.; Bechir, H.; Mohsen, G.; Ammar, R. Efficient Datacenter Resource Utilization Through Cloud Resource Overcommitment. In Proceedings of the 2015 IEEE INFOCOM Workshop on Mobile Cloud and Virtualization, Hong Kong, China, 26 April–1 May 2015; pp. 330–335. [Google Scholar]
- Ali, R.; Mostafa, G.A.; Sajjad, T. A learning automata-based ensemble resource usage prediction algorithm for cloud computing environment. Future Gener. Comput. Syst. 2018, 79, 54–71. [Google Scholar]
- Mostafa, G.A.; Sam, J.; Mohammad, A.P. An autonomic resource provisioning approach for service-based cloud applications: A hybrid approach. Future Gener. Comput. Syst. 2018, 78, 191–210. [Google Scholar]
- Jinping, L.; Jiezhou, H.; Wuxia, Z.; Tianyu, M.; Zhaohui, T.; Jean, P.N.; Weihua, G. ANID-SEoKELM: Adaptive network intrusion detection based on selective ensemble of kernel ELMs with random features. Knowl.-Based Syst. 2019, 177, 104–116. [Google Scholar]
- Ning, A.; Huitong, D.; Jiaoyun, Y.; Rhoda, A.; Ting, F.A.A. Deep ensemble learning for Alzheimer’s disease classification. J. Biomed. Inform. 2020, 105, 103411. [Google Scholar]
- Deepak, G.; Rinkle, R. Improving malware detection using big data and ensemble learning. Comput. Electr. Eng. 2020, 86, 106729. [Google Scholar]
- Tiago, P.; Isabel, P.; Zita, V.; Jose, S. Ensemble learning for electricity consumption forecasting in office buildings. Neurocomputing 2020, in press. [Google Scholar]
- Robert, H.N. Theory of the Backpropagation Neural Network. In Proceedings of the International Joint Conference on Neural Networks, Honolulu, HI, USA, 12–17 May 2002; pp. 593–605. [Google Scholar]
- Liu, Y.; Li, M.; Su, P.; Ma, B.; You, Z. Porosity Prediction of Granular Materials through Discrete Element Method and Back Propagation Neural Network Algorithm. Appl. Sci. 2020, 10, 1693. [Google Scholar] [CrossRef]
- Zhenxing, L.; Xiaodan, H.; Kuangrong, H.; Lei, C.; Biao, H. Gaussian process regression with heteroscedastic noises—A machine-learning predictive variance approach. Chem. Eng. Res. Des. 2020, 157, 162–173. [Google Scholar]
- Srikanth, B.Y.; Kalyan, S.P. Efficient Parallel Discrete Event Simulation on Cloud/Virtual Machine Platforms. ACM Trans. Modeling Comput. Simul. 2015, 26, 1–26. [Google Scholar]
- Rafael, M.O.C.; Robert, S.; George, D.C.C.; Tsang, I.R. META-DES: A dynamic ensemble selection framework using meta-learning. Pattern Recognit. 2015, 48, 1925–1935. [Google Scholar] [CrossRef]
- Feng, Z.; Yiping, Y.; Wenjie, T.; Jun, T. A hierarchical composite framework of parallel discrete event simulation for modelling complex adaptive systems. Simul. Model. Pract. Theory 2017, 77, 141–156. [Google Scholar]
- Bonan, H.; Yiping, Y.; Bing, W. Modeling and simulation of large-scale social networks using parallel discrete event simulation. Simul. Trans. Soc. Modeling Simul. Int. 2013, 89, 1173–1183. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).