Multiquadrics without the Shape Parameter for Solving Partial Differential Equations
Abstract
1. Introduction
2. The Collocation Method of the Multiquadric Radial Basis Function
3. Accuracy and Convergence Analysis
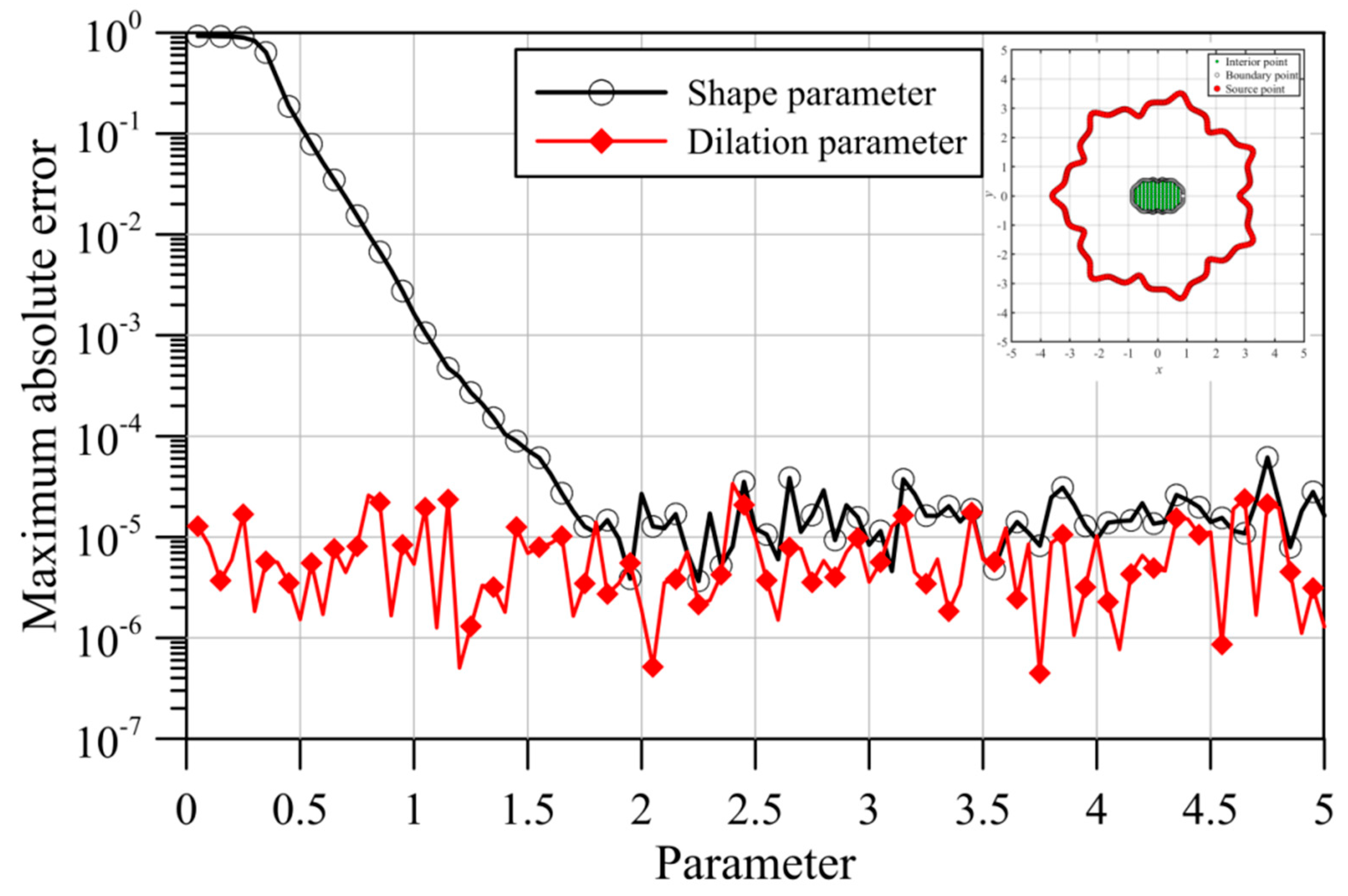
4. Numerical Examples
4.1. A Two-Dimensional Wave Problem
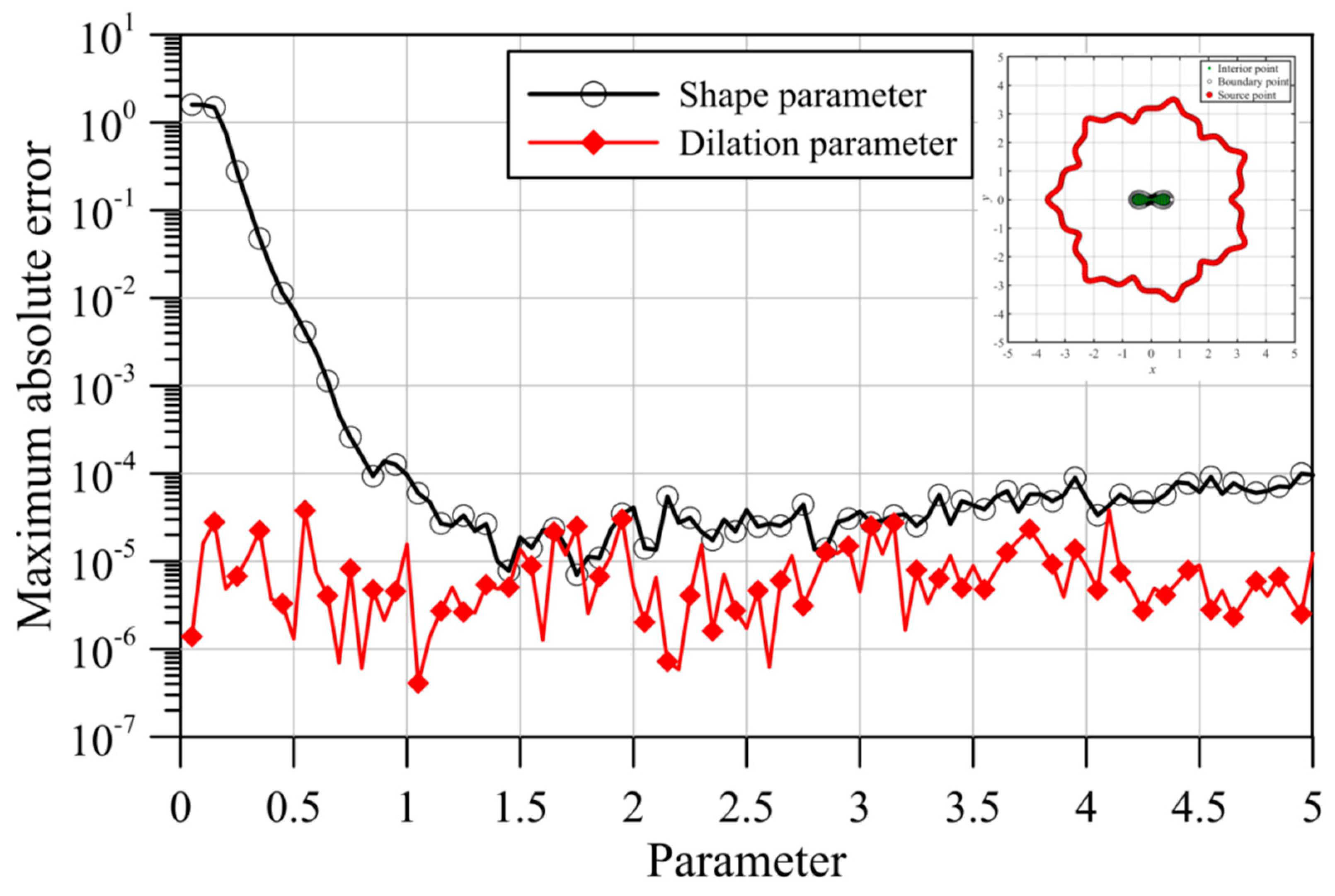
4.2. A Two-Dimensional Groundwater Flow Problem
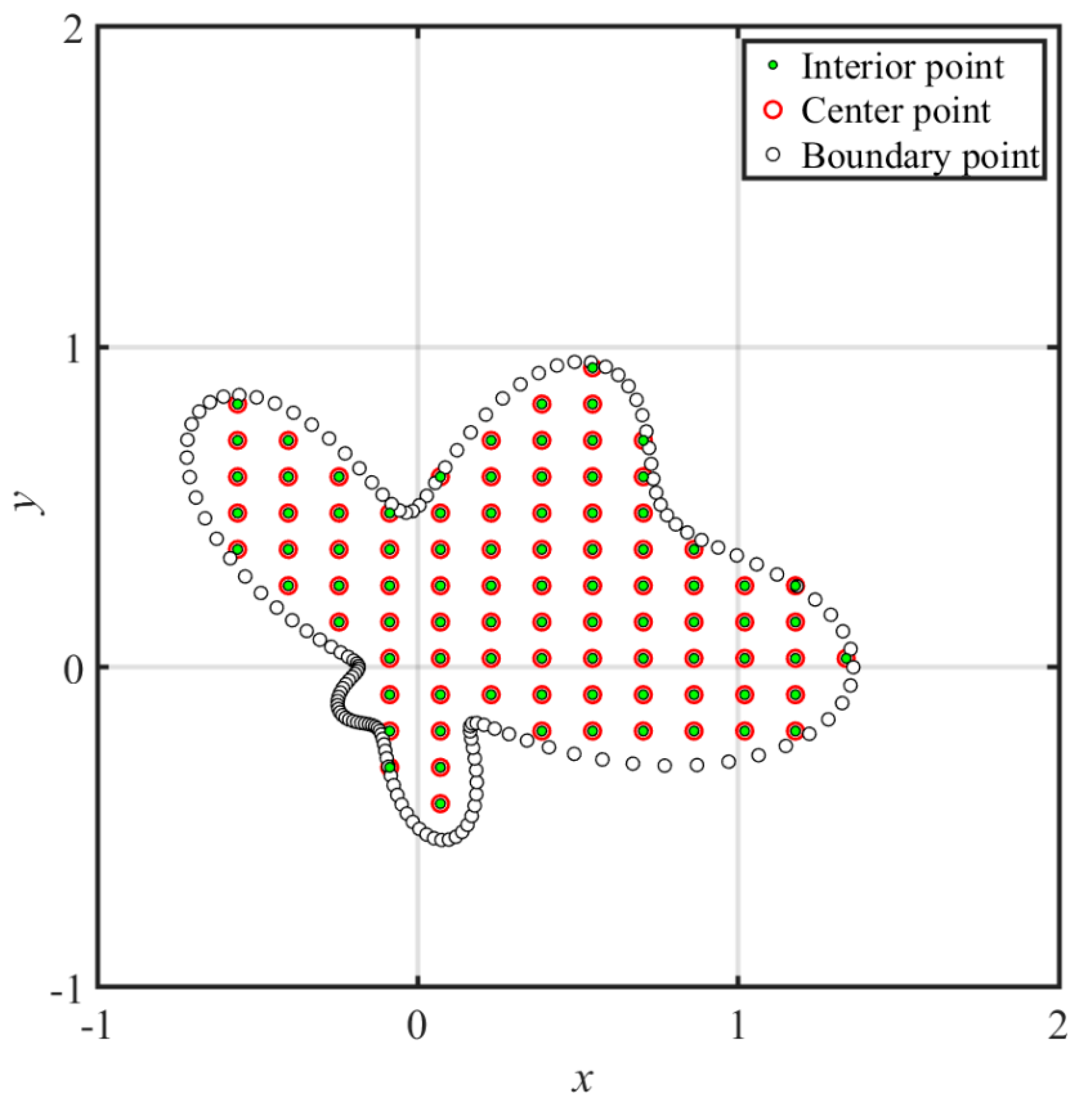
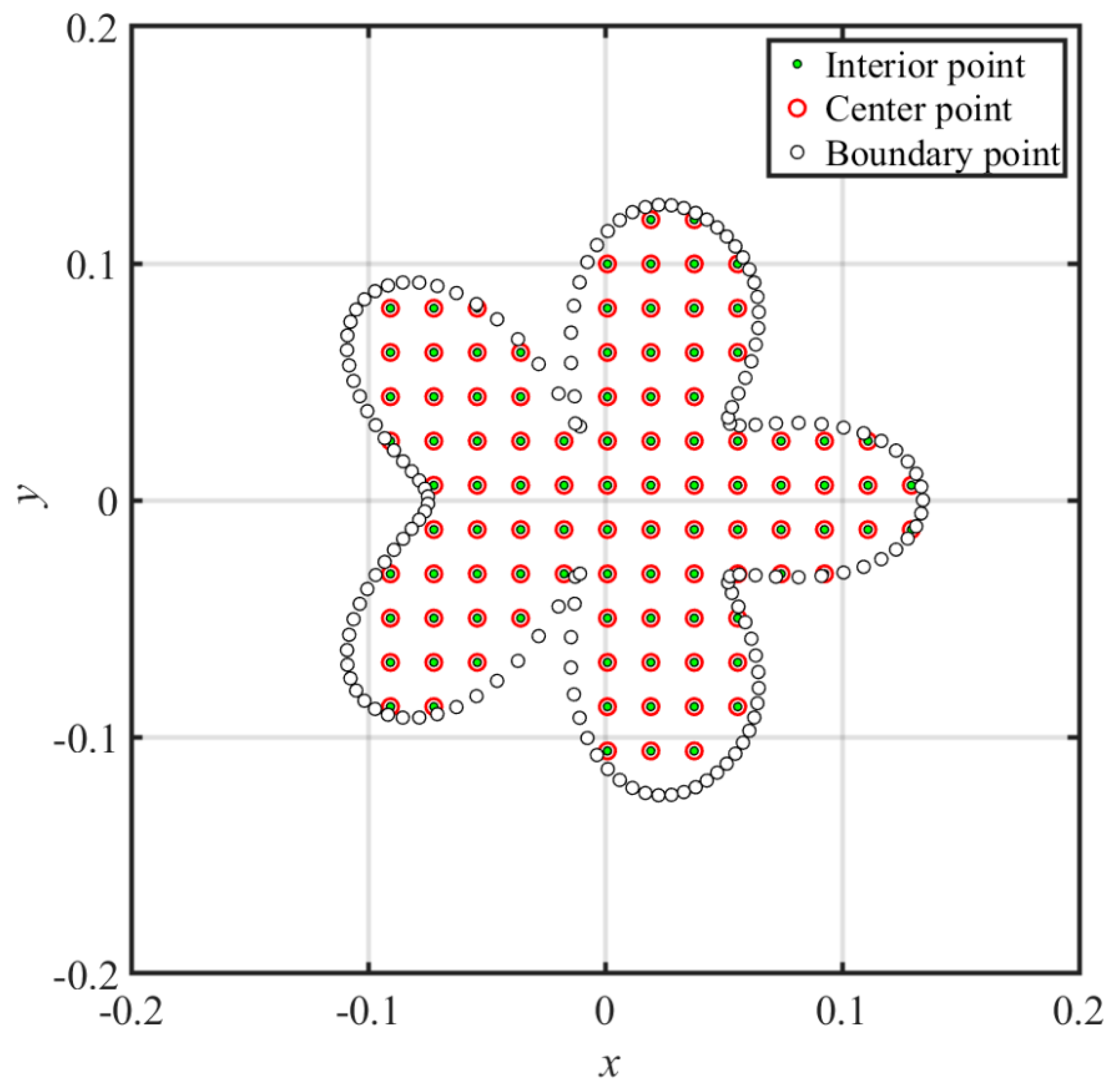
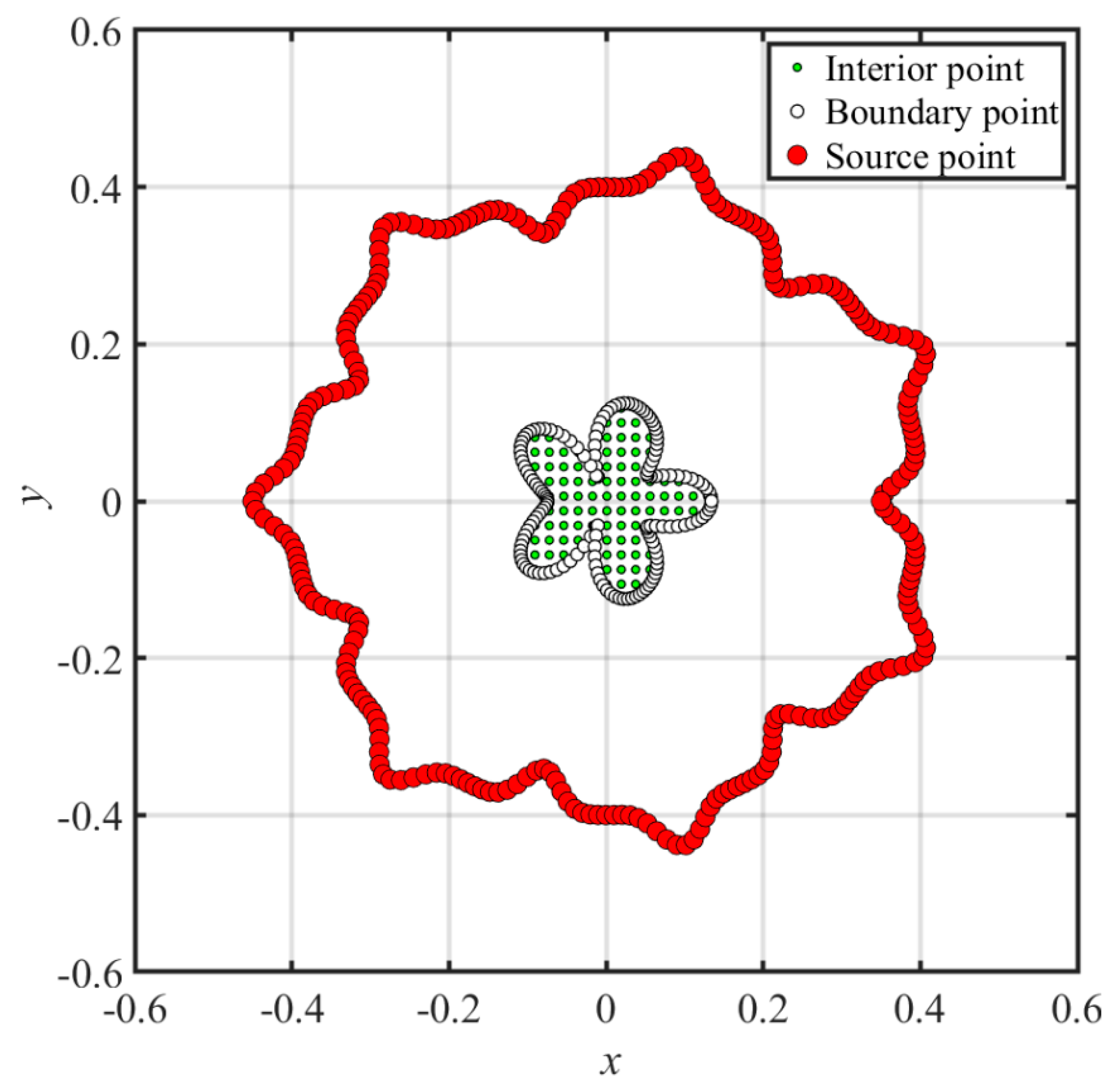
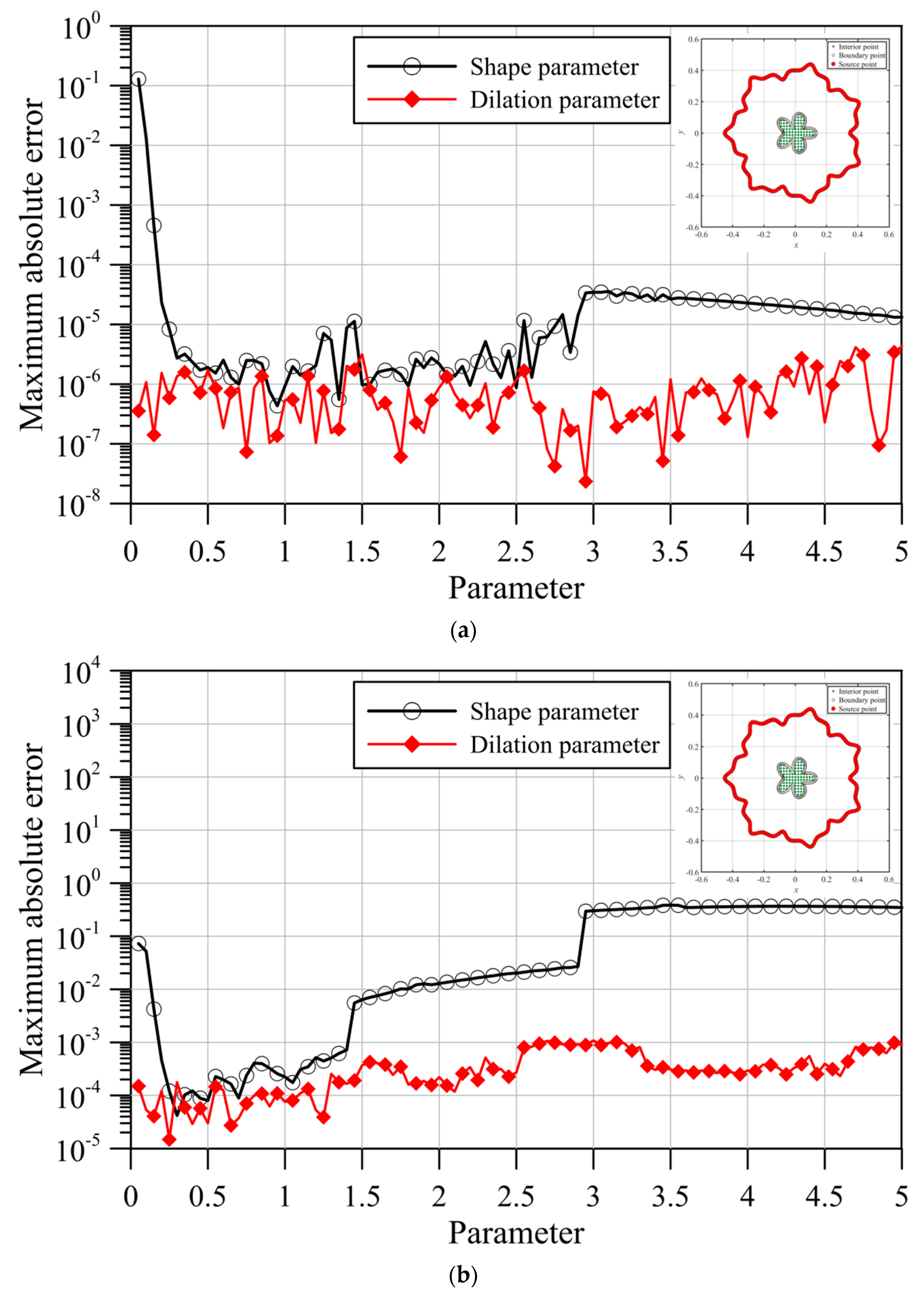
4.3. An Unsaturated Flow Problem
5. Conclusions
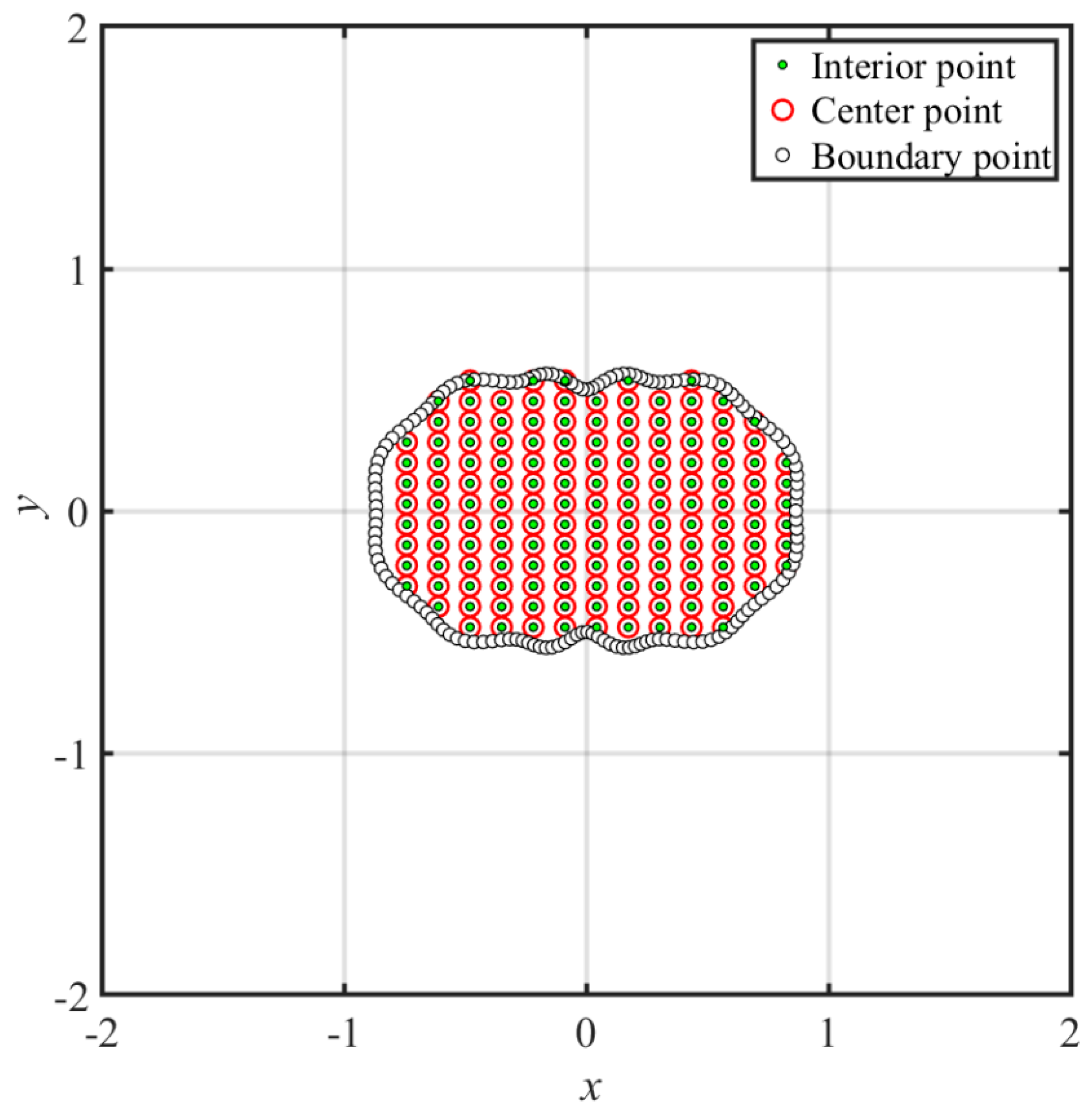
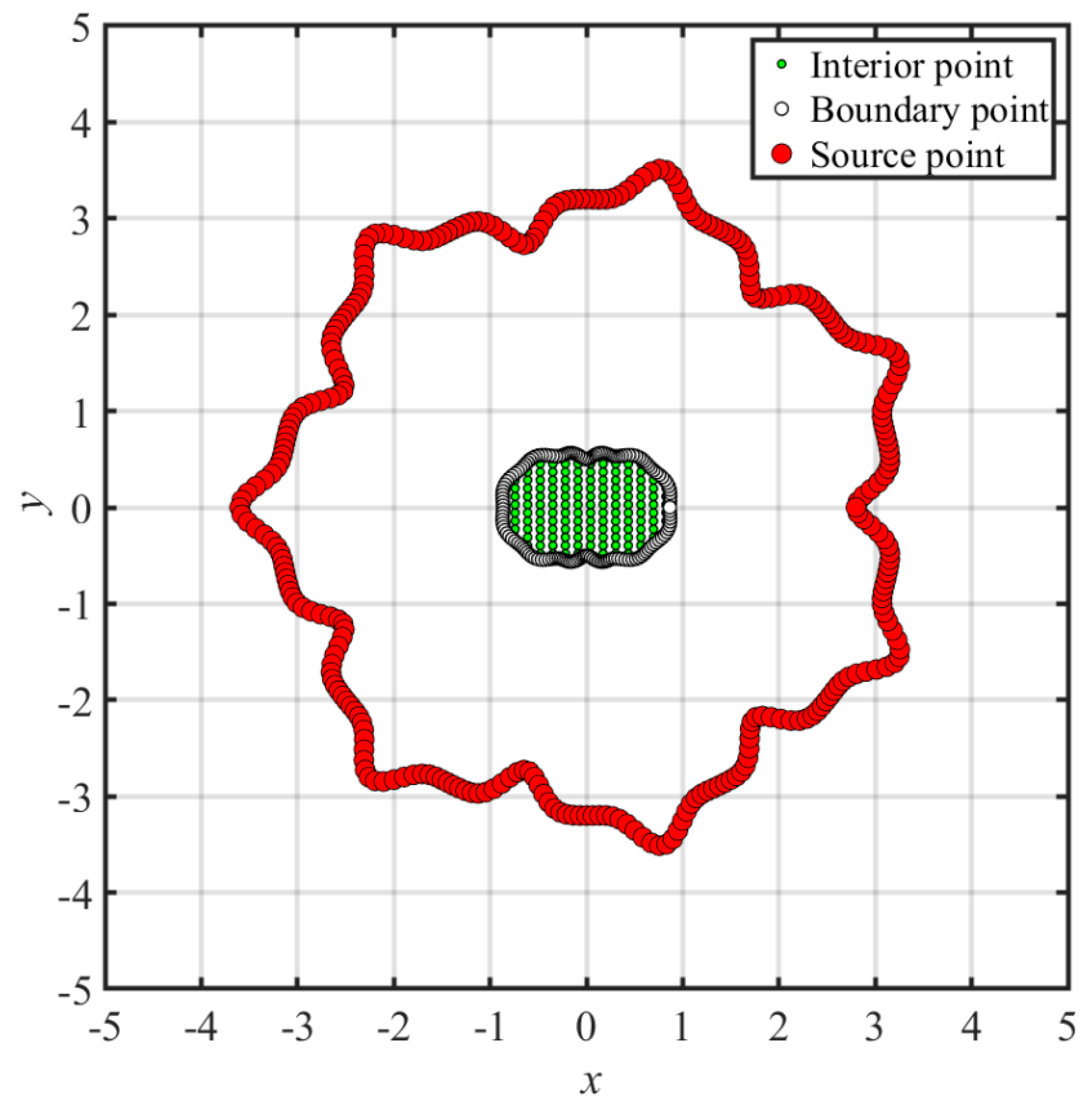
- We considered the center point as the fictitious source collocated outside the domain. The radial distance between the interior point and the source point was, therefore, always greater than zero. As a result, the MQ and IMQ RBFs and their derivatives in the governing equation were smooth and globally infinitely differentiable. Boundary value problems are solved by the proposed collocation method using MQ and IMQ RBFs without the shape parameter.
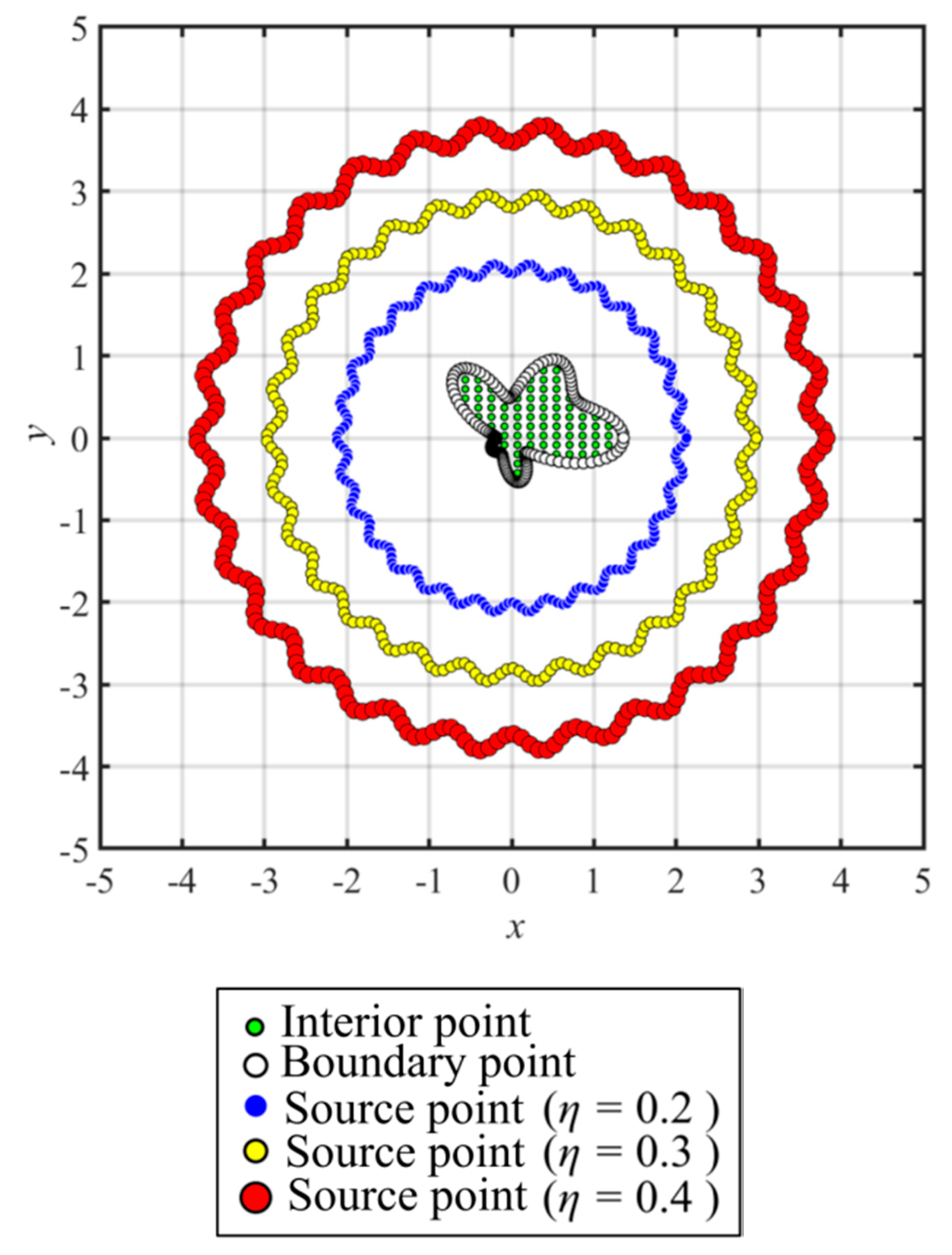
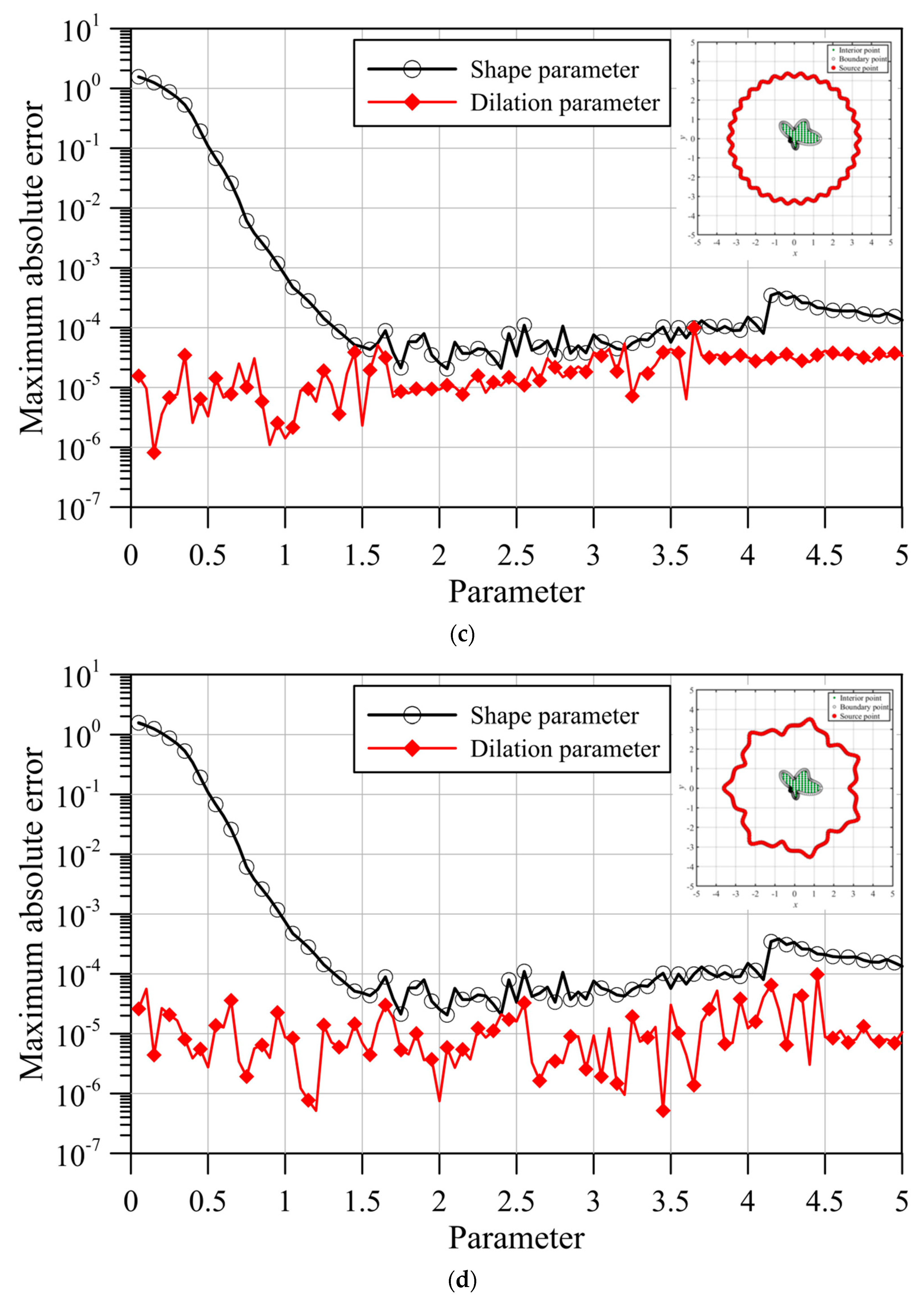
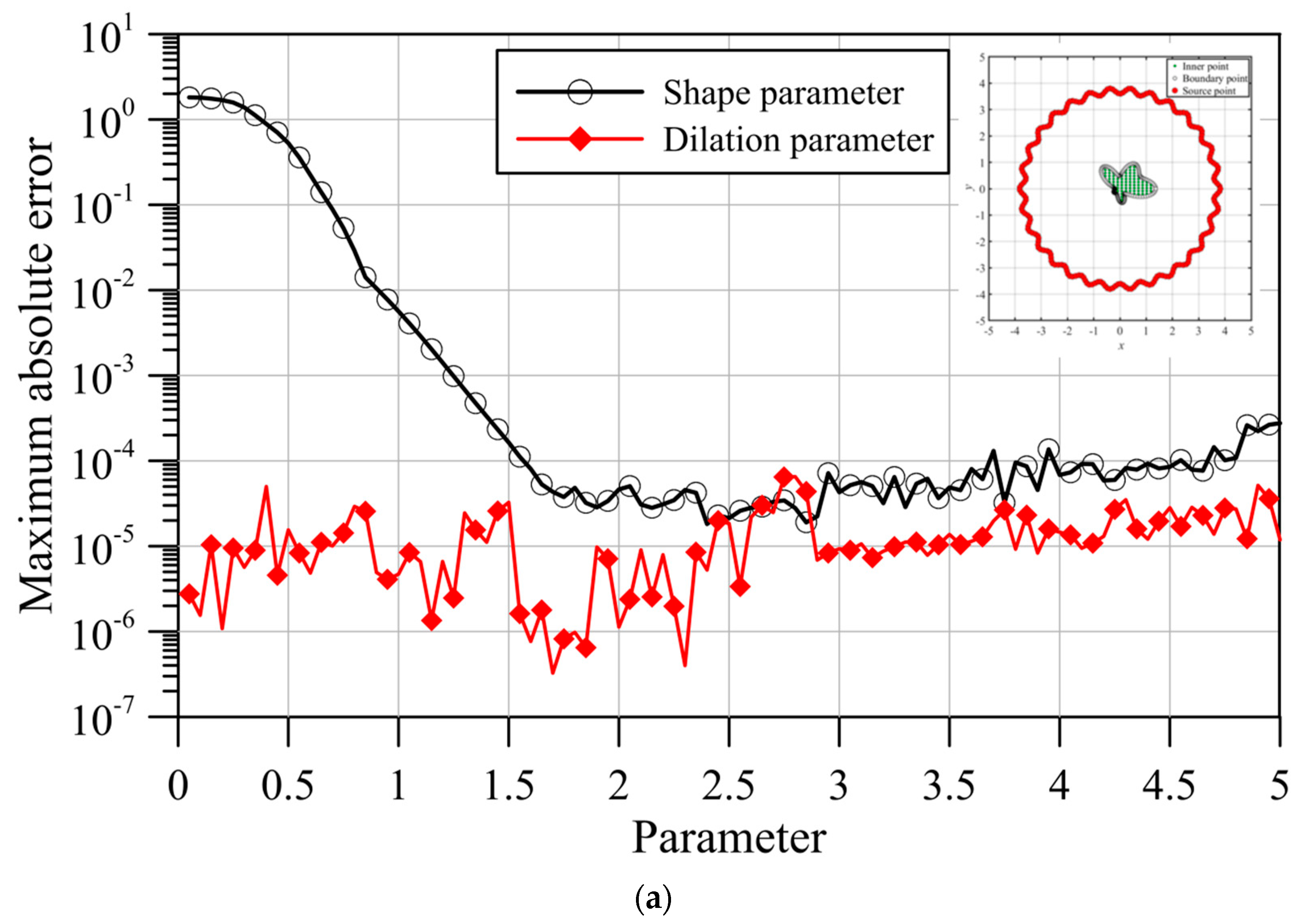
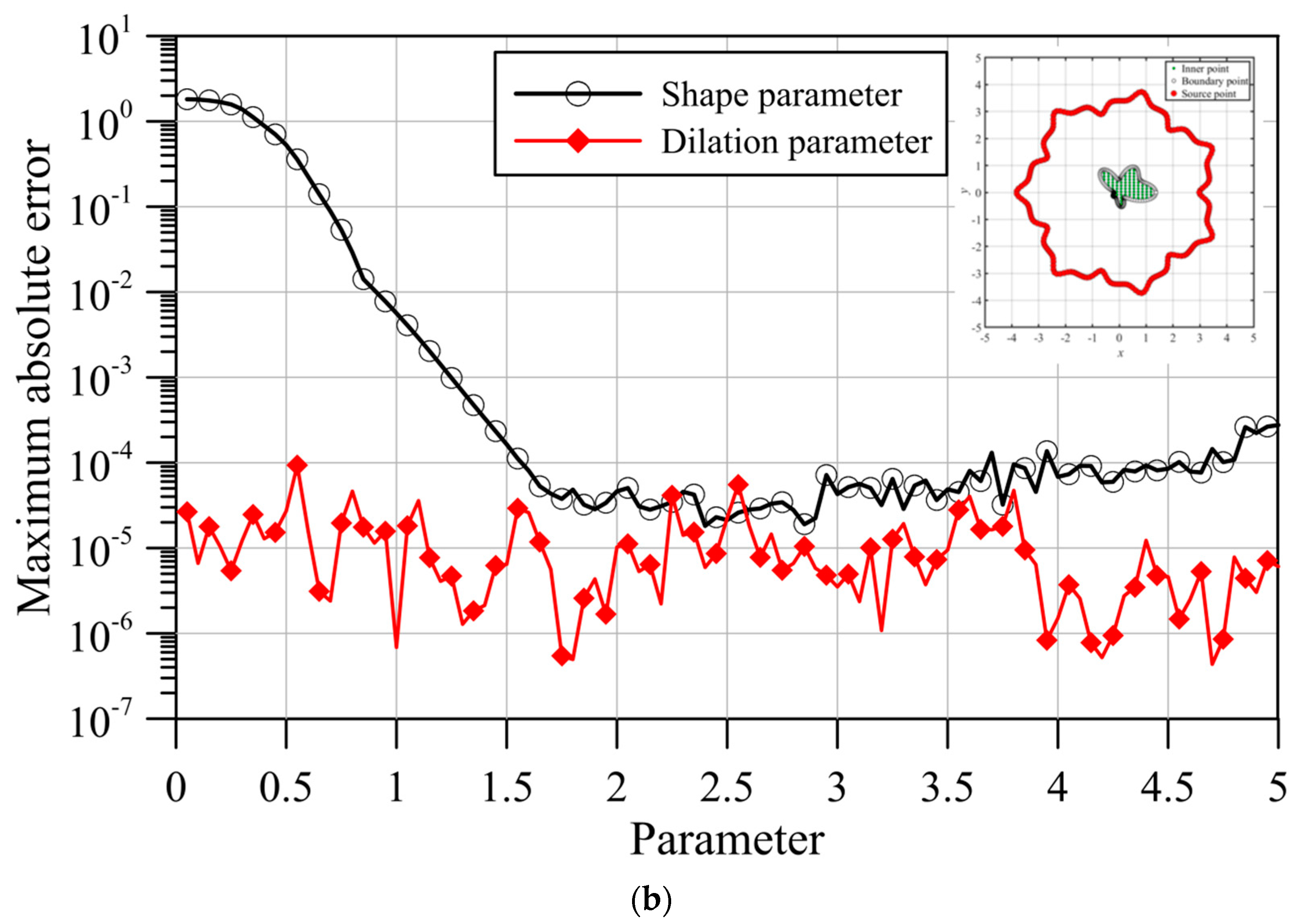
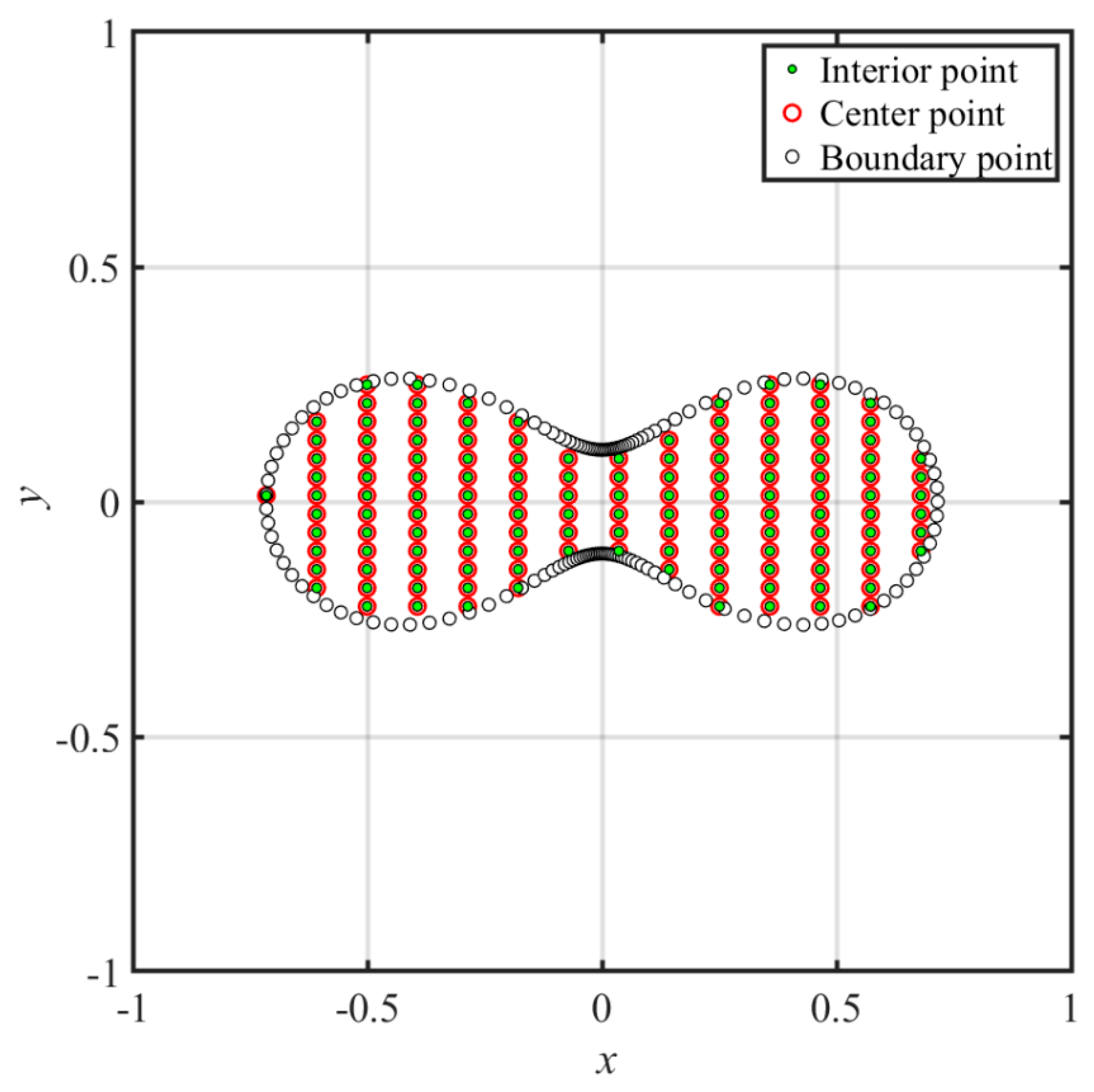
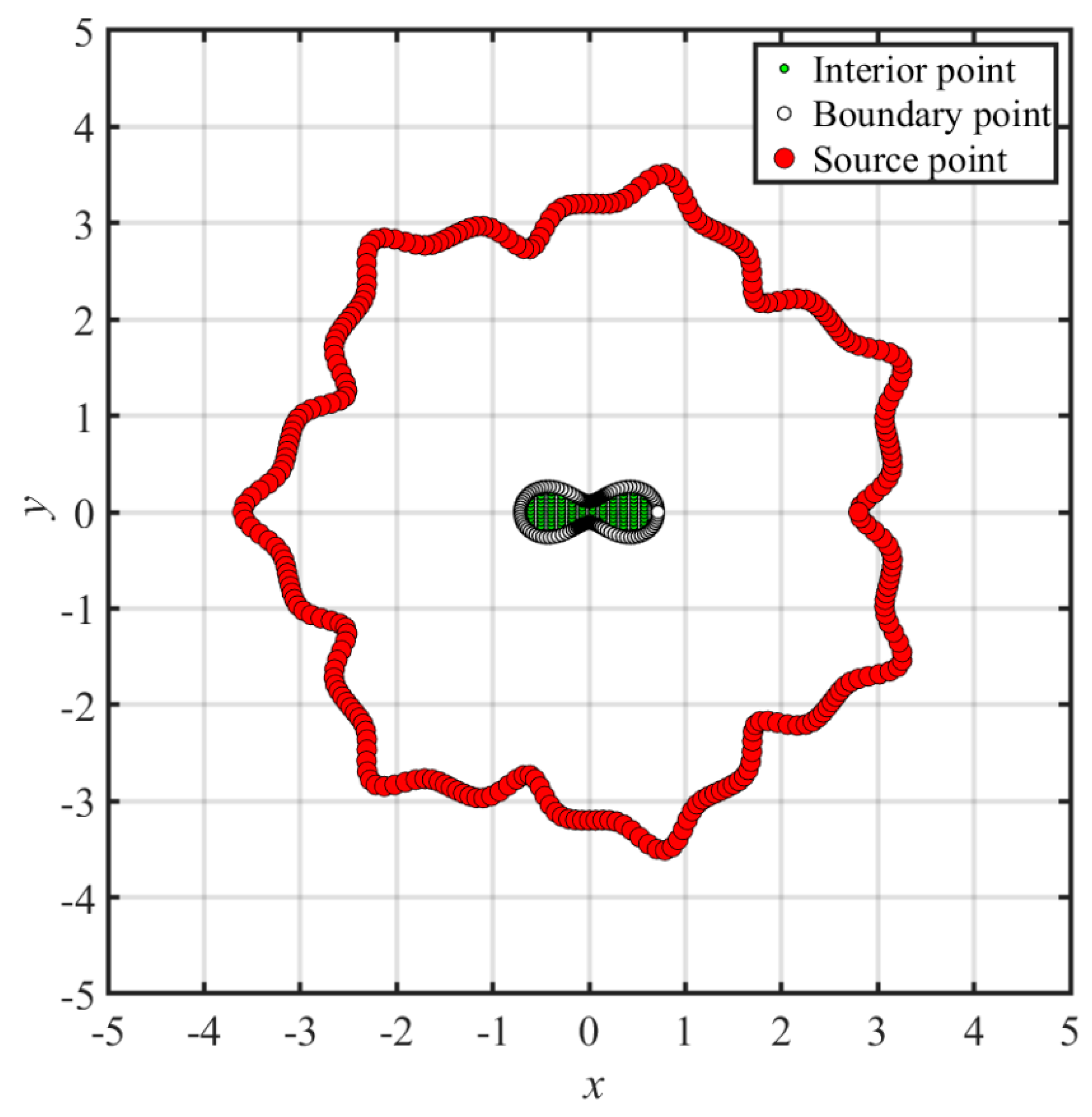
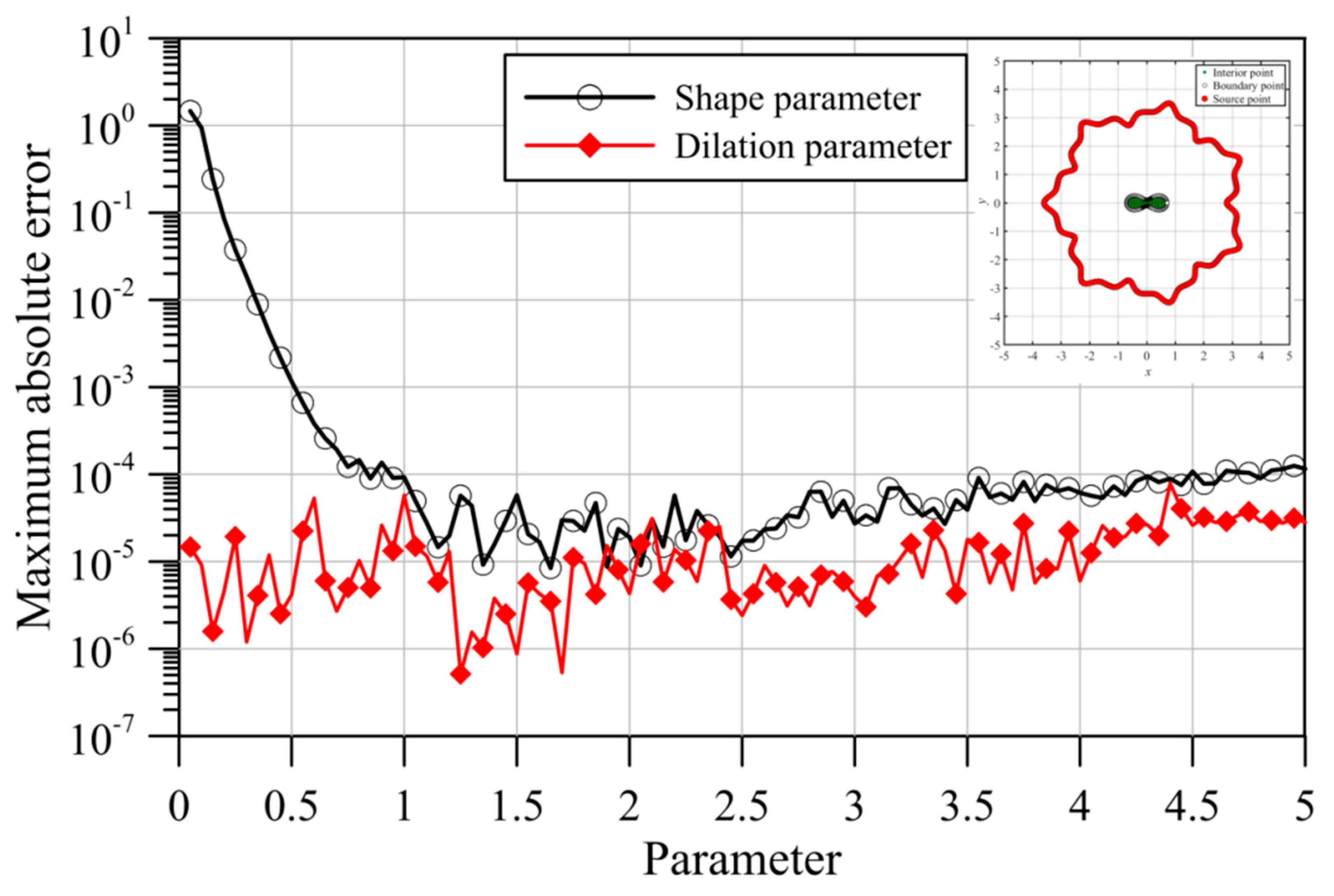
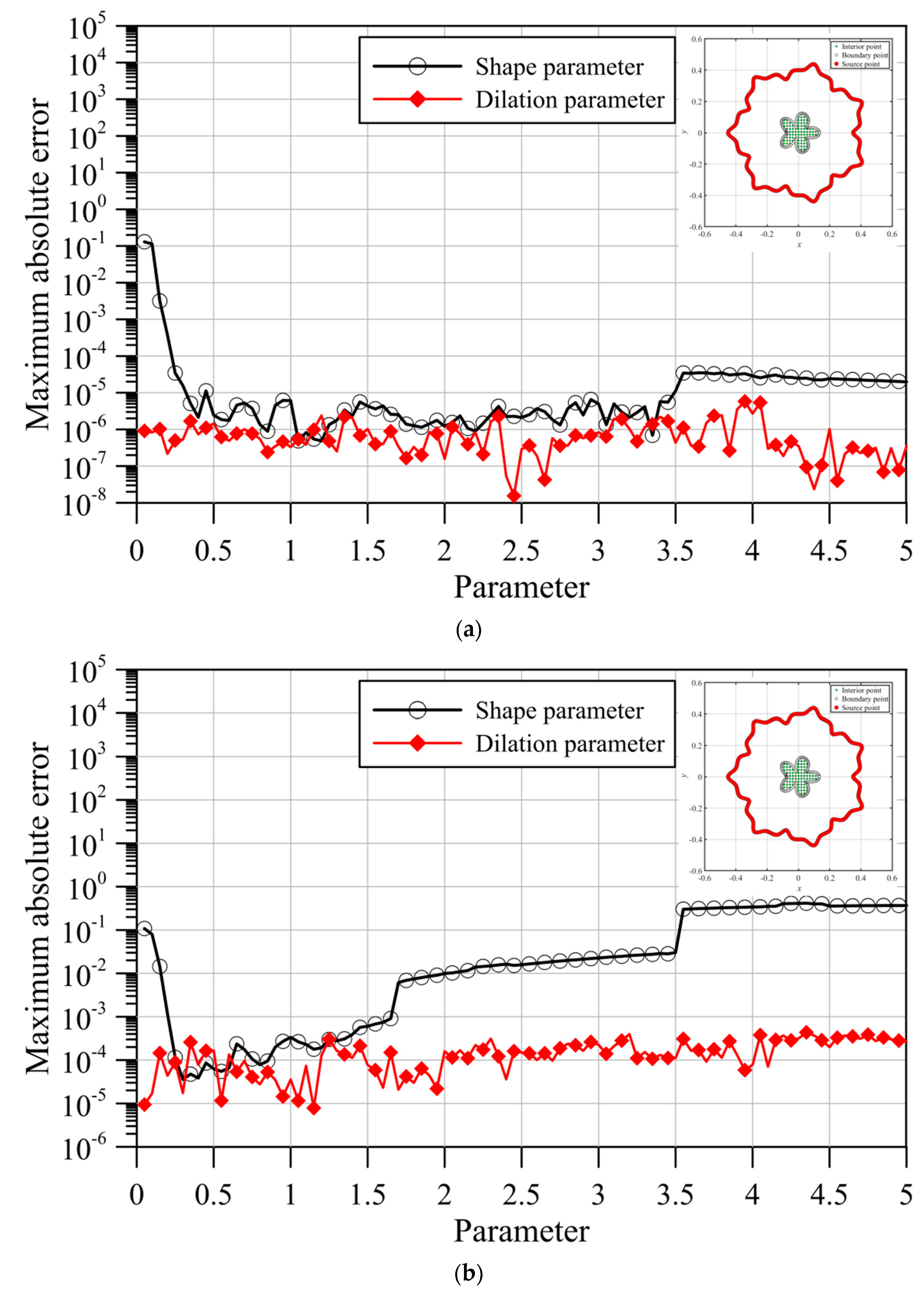
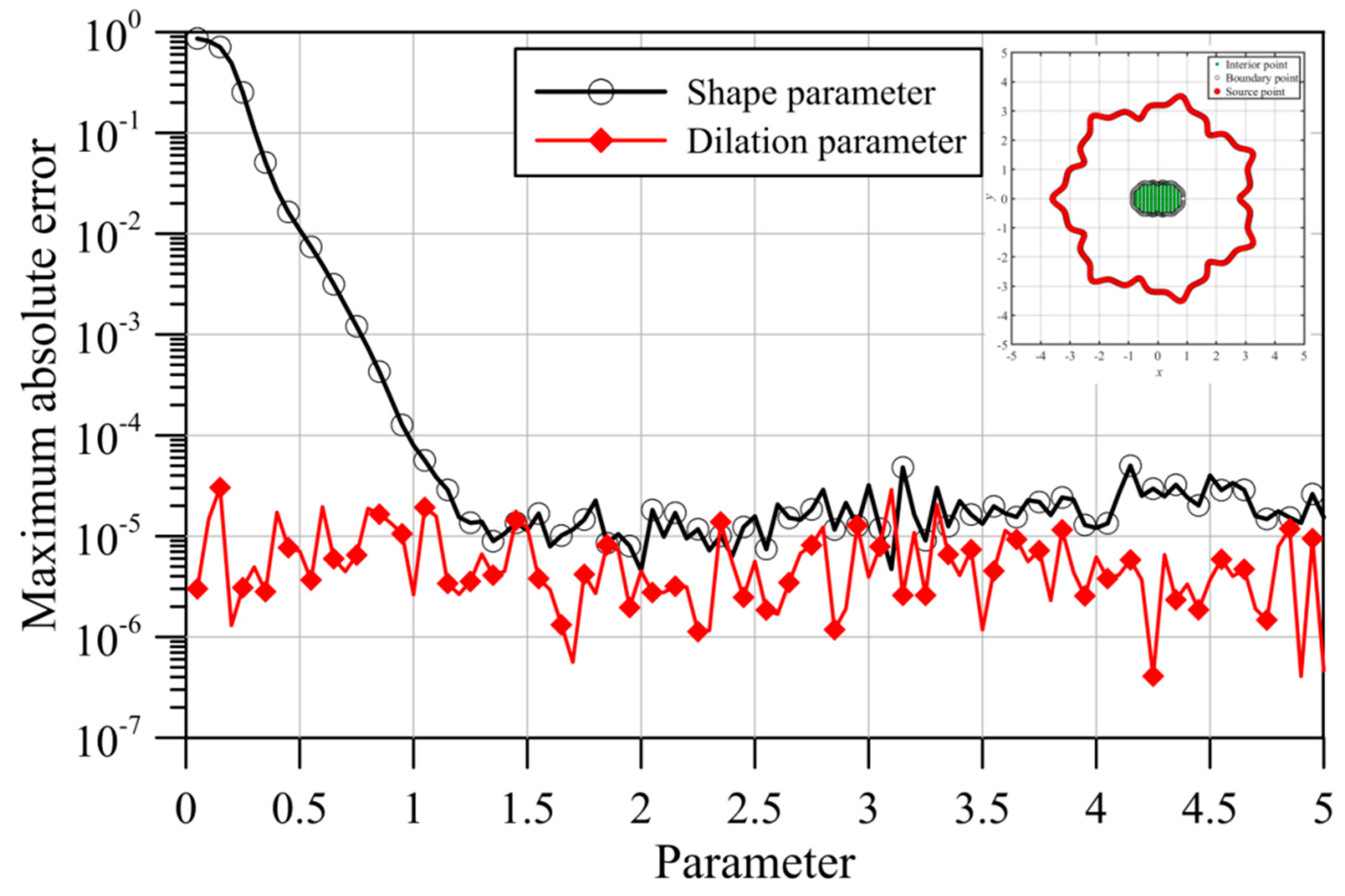
- The fictitious boundary shape surrounded by the source points and the locations of the source points may affect the accuracy. We conducted a sensitivity analysis to examine the accuracy. In the sensitivity analysis, we investigated the source points placed at different positions outside the domain. Moreover, four irregular fictitious boundary shapes surrounded by the source points were studied. Results illustrate that the locations of fictitious sources are not sensitive to the accuracy if the suggested fictitious irregular circular boundary is adopted.
- Several examples were conducted to verify the robustness and accuracy of our method. The results demonstrated that the proposed method using MQ and IMQ RBFs acquires more accurate results than the RBFCM, even with the optimum shape parameter. Additionally, it was found that the locations of fictitious sources were not sensitive to the accuracy.
Author Contributions
Funding
Conflicts of Interest
References
- Hon, Y.C.; Sarler, B.; Yun, D.F. Local radial basis function collocation method for solving thermo-driven fluid-flow problems with free surface. Eng. Anal. Bound. Elem. 2015, 57, 2–8. [Google Scholar] [CrossRef]
- Kansa, E.J.; Hon, Y.C. Circumventing the ill-conditioning problem with multi- quadric radial basis functions: Applications to elliptic partial differential equations. Comput. Math. Appl. 2000, 39, 123–137. [Google Scholar] [CrossRef]
- Kansa, E.J. Multiquadrics—A scattered data approximation scheme with applications to computational fluid-dynamics. I Surface approximations and partial derivative estimates. Comput. Math. Appl. 1990, 19, 127–145. [Google Scholar] [CrossRef]
- Mahdavi, A.; Chi, S.W.; Zhu, H. A gradient reproducing kernel collocation method for high order differential equations. Comput. Mech. 2019, 64, 1421–1454. [Google Scholar] [CrossRef]
- Ku, C.Y.; Liu, C.Y.; Xiao, J.E.; Huang, W.P.; Su, Y. A spacetime collocation Trefftz method for solving the inverse heat conduction problem. Adv. Mech. Eng. 2019, 11, 1–11. [Google Scholar] [CrossRef]
- Mahdavi, A.; Chi, S.W.; Kamali, N. Harmonic-Enriched Reproducing Kernel Approximation for Highly Oscillatory Differential Equations. J. Eng. Mech. 2020, 146, 04020014. [Google Scholar] [CrossRef]
- Ku, C.Y.; Xiao, J.E. A Collocation Method Using Radial Polynomials for Solving Partial Differential Equations. Symmetry 2020, 12, 1419. [Google Scholar] [CrossRef]
- Cheng, A.H.-D. Multiquadric and its shape parameter—A numerical investigation of error estimate, condition number, andround-off error by arbitrary precision computation. Eng. Anal. Bound. Elem. 2012, 36, 220–239. [Google Scholar] [CrossRef]
- Gutmann, H.M. A radial basis function method for global optimization. J. Glob. Optim. 2001, 19, 201–227. [Google Scholar] [CrossRef]
- Hardy, R.L. Multiquadric equations of topography and other irregular surfaces. J. Geophys. Res. 1971, 76, 1905–1915. [Google Scholar] [CrossRef]
- Kansa, E.J. Multiquadrics—A scattered data approximation scheme with applications to computational fluid-dynamics. II Solutions to parabolic, hyperbolic and elliptic partial-differential equations. Comput. Math. Appl. 1990, 19, 147–161. [Google Scholar] [CrossRef]
- Chen, W.; Tanaka, M. A meshless, integration-free, and boundary-only RBF technique. Comput. Math. Appl. 2002, 43, 379–391. [Google Scholar] [CrossRef]
- Ring, M.; Eskofier, B.M. An approximation of the Gaussian RBF kernel for efficient classification with SVMs. Pattern Recognit. Lett. 2016, 84, 107–113. [Google Scholar] [CrossRef]
- Chen, C.S.; Karageorghis, A.; Dou, F. A novel RBF collocation method using fictitious centres. Appl. Math. Lett. 2020, 101, 106069. [Google Scholar] [CrossRef]
- Soleymani, F.; Barfeie, M.; Haghani, F.K. Inverse multi-quadric RBF for computing the weights of FD method: Application to American options. Commun. Nonlinear Sci. Numer. Simul. 2018, 64, 74–88. [Google Scholar] [CrossRef]
- Keller, W.; Borkowski, A. Thin plate spline interpolation. J. Geod. 2019, 93, 1251–1269. [Google Scholar] [CrossRef]
- Fasshauer, G.E.; Zhang, J.G. On choosing “optimal” shape parameters for RBF approximation. Numer. Algorithms 2007, 45, 345–368. [Google Scholar] [CrossRef]
- Biazar, J.; Hosami, M. Selection of an interval for variable shape parameter in approximation by radial basis functions. Adv. Numer. Anal. 2016, 2016, 1–11. [Google Scholar] [CrossRef]
- Chen, W.; Hong, Y.; Lin, J. The sample solution approach for determination of the optimal shape parameter in the Multiquadric function of the Kansa method. Comput. Math. Appl. 2018, 75, 2942–2954. [Google Scholar] [CrossRef]
- Ng, Y.L.; Ng, K.C.; Sheu, T.W.H. A new higher-order RBF-FD scheme with optimal variable shape parameter for partial differential equation. Numer. Heat Transf. Part B Fundam. 2019, 75, 289–311. [Google Scholar] [CrossRef]
- Franke, R. Recent advances in the approximation of surfaces from scattered data. In Topics in Multivariate Approximation; Academic Press: Cambridge, MA, USA, 1987; pp. 79–98. [Google Scholar]
- Chen, C.-S.; Karageorghis, A.; Li, Y. On choosing the location of the sources in the MFS. Numer. Algorithms 2016, 72, 107–130. [Google Scholar] [CrossRef]
- Li, X. On solving boundary value problems of modified Helmholtz equations by plane wave functions. J. Comput. Appl. Math. 2006, 195, 66–82. [Google Scholar] [CrossRef]
- Strack, O.D.L.; Ausk, B.K. A formulation for vertically integrated groundwater flow in a stratified coastal aquifer. Water Resour. Res. 2015, 51, 6756–6775. [Google Scholar] [CrossRef]
- Ku, C.Y.; Liu, C.Y.; Su, Y.; Xiao, J.E. Modeling of transient flow in unsaturated geomaterials for rainfall-induced landslides using a novel spacetime collocation method. Geofluids 2018, 2018, 1–16. [Google Scholar] [CrossRef]



| The Kansa Method | The Proposed Method (MQ RBF) | ||||
|---|---|---|---|---|---|
| With the Optimum Shape Parameter | Without the Shape Parameter | ||||
| Case A | Case B | Case C | Case D | ||
| (c = 1.65) | |||||
| MAE | 2.06 × 10−5 | 8.58 × 10−6 | 2.98 × 10−6 | 8.11 × 10−7 | 5.15 × 10−7 |
| RMSE | 6.53 × 10−7 | 4.20 × 10−7 | 1.12 × 10−7 | 5.14 × 10−8 | 2.48 × 10−8 |
| The Conventional IMQ RBF | The Proposed Method (IMQ RBF) | ||
|---|---|---|---|
| With the Optimum Shape Parameter | Without the Shape Parameter | ||
| Case C | Case D | ||
| (c = 2.40) | |||
| MAE | 1.82 × 10−5 | 3.26 × 10−7 | 4.35 × 10−7 |
| RMSE | 3.26 × 10−7 | 9.63 × 10−9 | 2.19 × 10−8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ku, C.-Y.; Liu, C.-Y.; Xiao, J.-E.; Hsu, S.-M. Multiquadrics without the Shape Parameter for Solving Partial Differential Equations. Symmetry 2020, 12, 1813. https://doi.org/10.3390/sym12111813
Ku C-Y, Liu C-Y, Xiao J-E, Hsu S-M. Multiquadrics without the Shape Parameter for Solving Partial Differential Equations. Symmetry. 2020; 12(11):1813. https://doi.org/10.3390/sym12111813
Chicago/Turabian StyleKu, Cheng-Yu, Chih-Yu Liu, Jing-En Xiao, and Shih-Meng Hsu. 2020. "Multiquadrics without the Shape Parameter for Solving Partial Differential Equations" Symmetry 12, no. 11: 1813. https://doi.org/10.3390/sym12111813
APA StyleKu, C.-Y., Liu, C.-Y., Xiao, J.-E., & Hsu, S.-M. (2020). Multiquadrics without the Shape Parameter for Solving Partial Differential Equations. Symmetry, 12(11), 1813. https://doi.org/10.3390/sym12111813







