Cooperative Optimization Model of BRT Speed and Timing Based on Dual Station at an Intersection
Abstract
1. Introduction
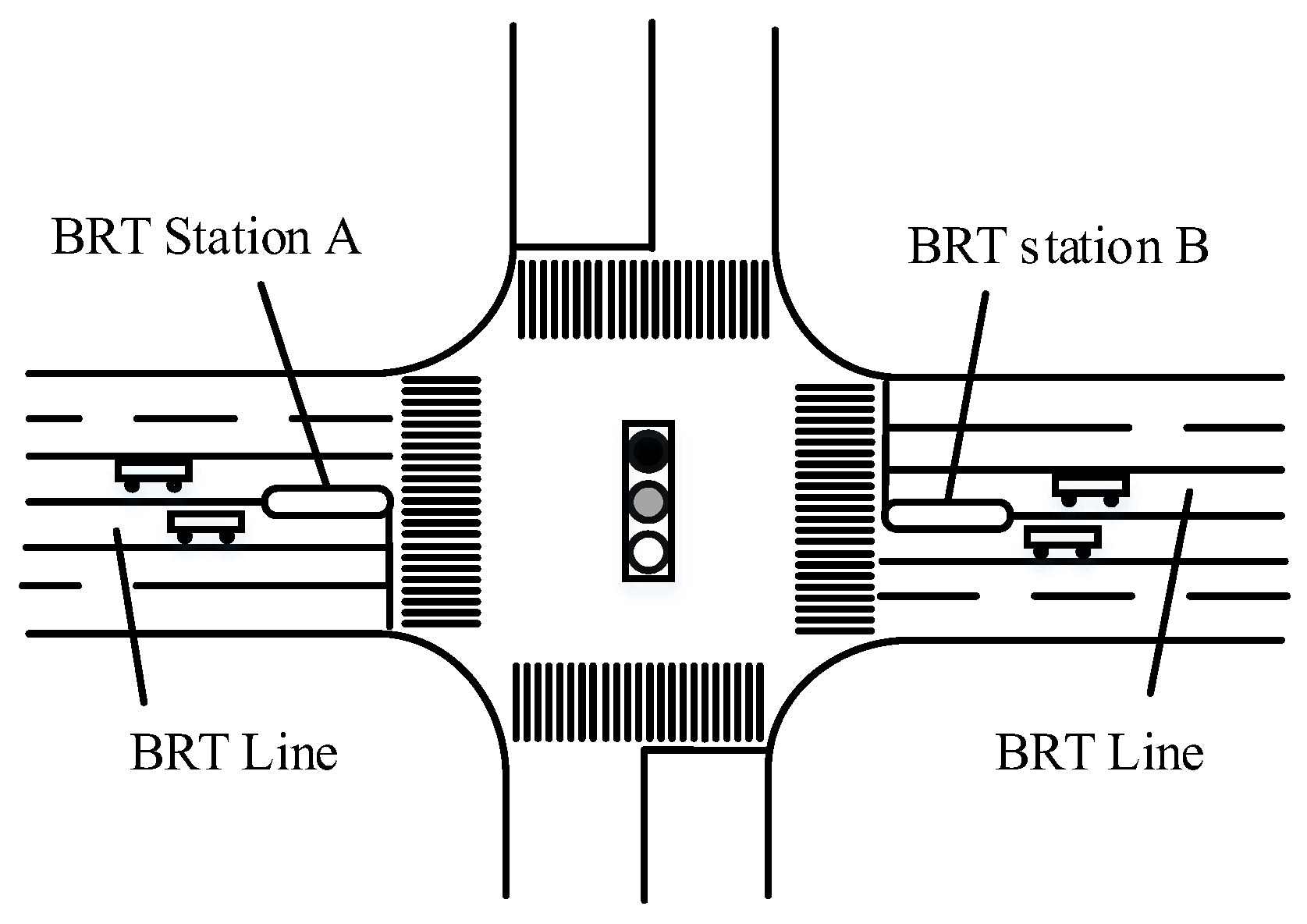
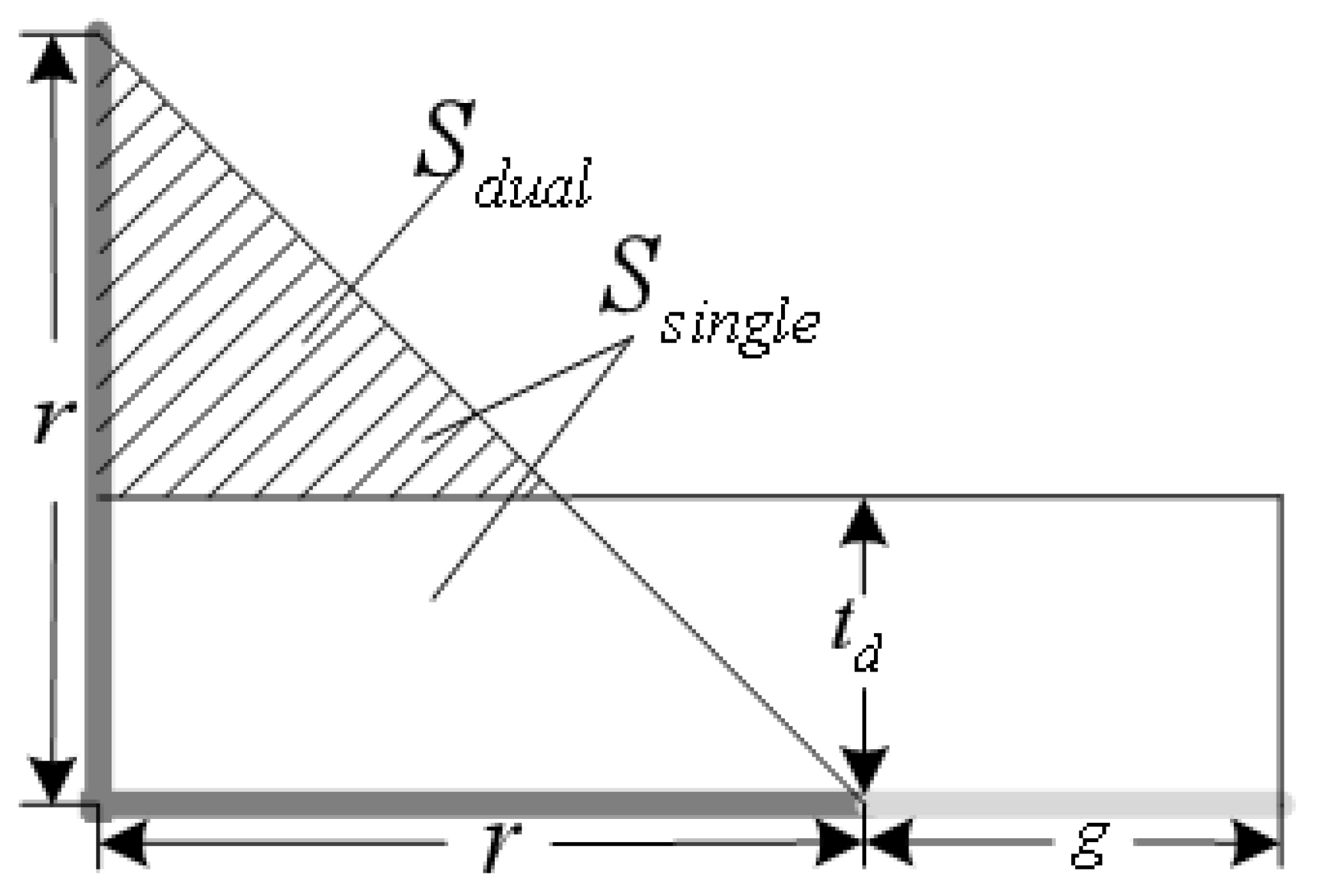
2. The Setting and Delay Analysis of BRT Dual Station
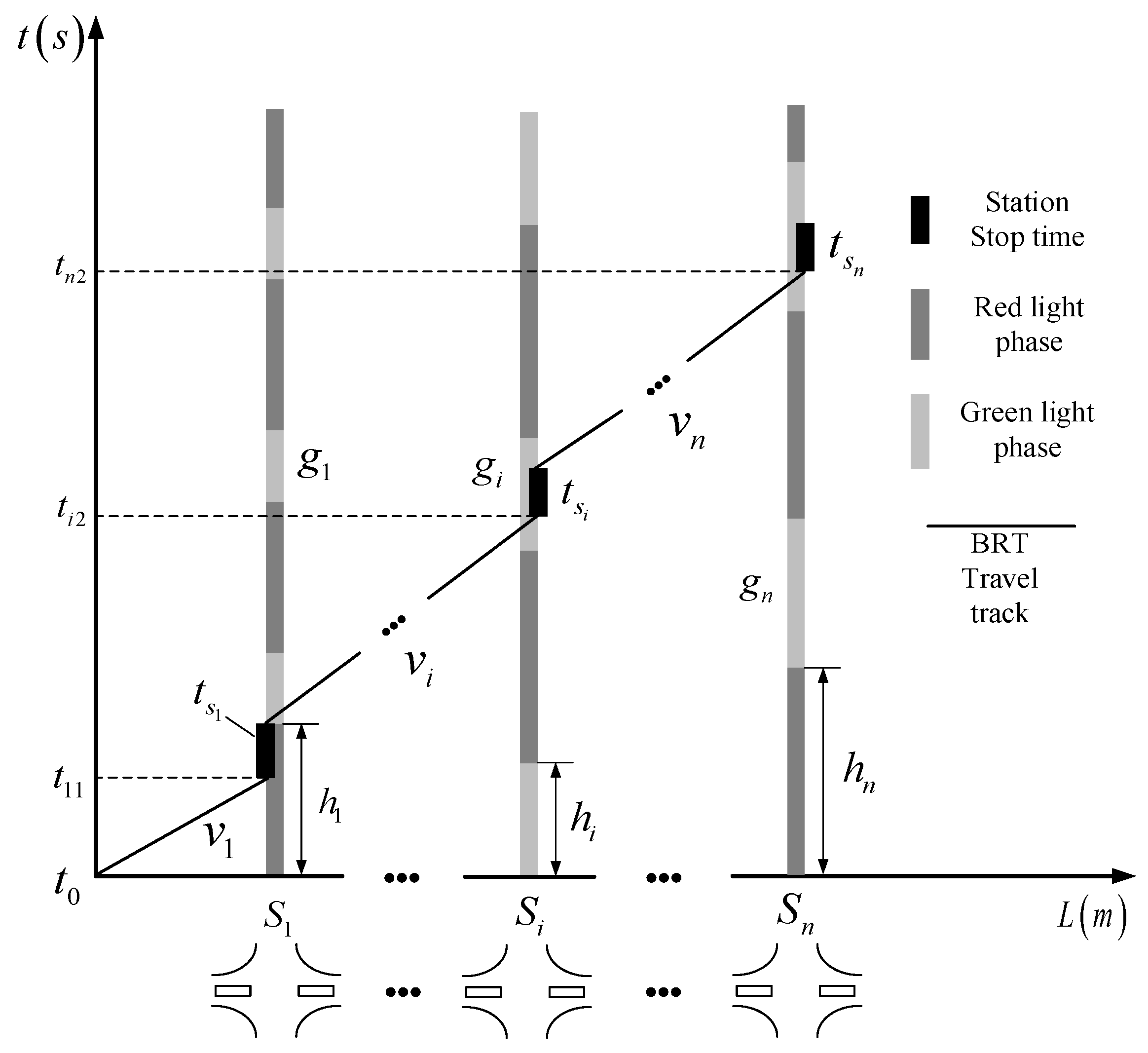
3. BRT Priority Collaborative Control Model
3.1. Model Assumptions
- (1)
- The arrival of BRT vehicles is evenly distributed, and the departure time interval is fixed, and only one BRT vehicle arrives in a short time;
- (2)
- All BRT vehicles drive on the BRT lane, the drivers strictly abide by the recommended speed and the speed range of BRT vehicles in each shift is known;
- (3)
- On the premise of not changing the basic signal control phase structure, the signal priority strategy in the model adopts two methods of green light extension and red light early breaking. Other methods (such as phase insertion, phase sequence adjustment, etc.) are not considered for the time being;
- (4)
- BRT vehicle departure time, arrival time and the remaining time of signal timing at the intersections along the way can be predicted.
3.2. Constraints
4. Data Investigation and Collection
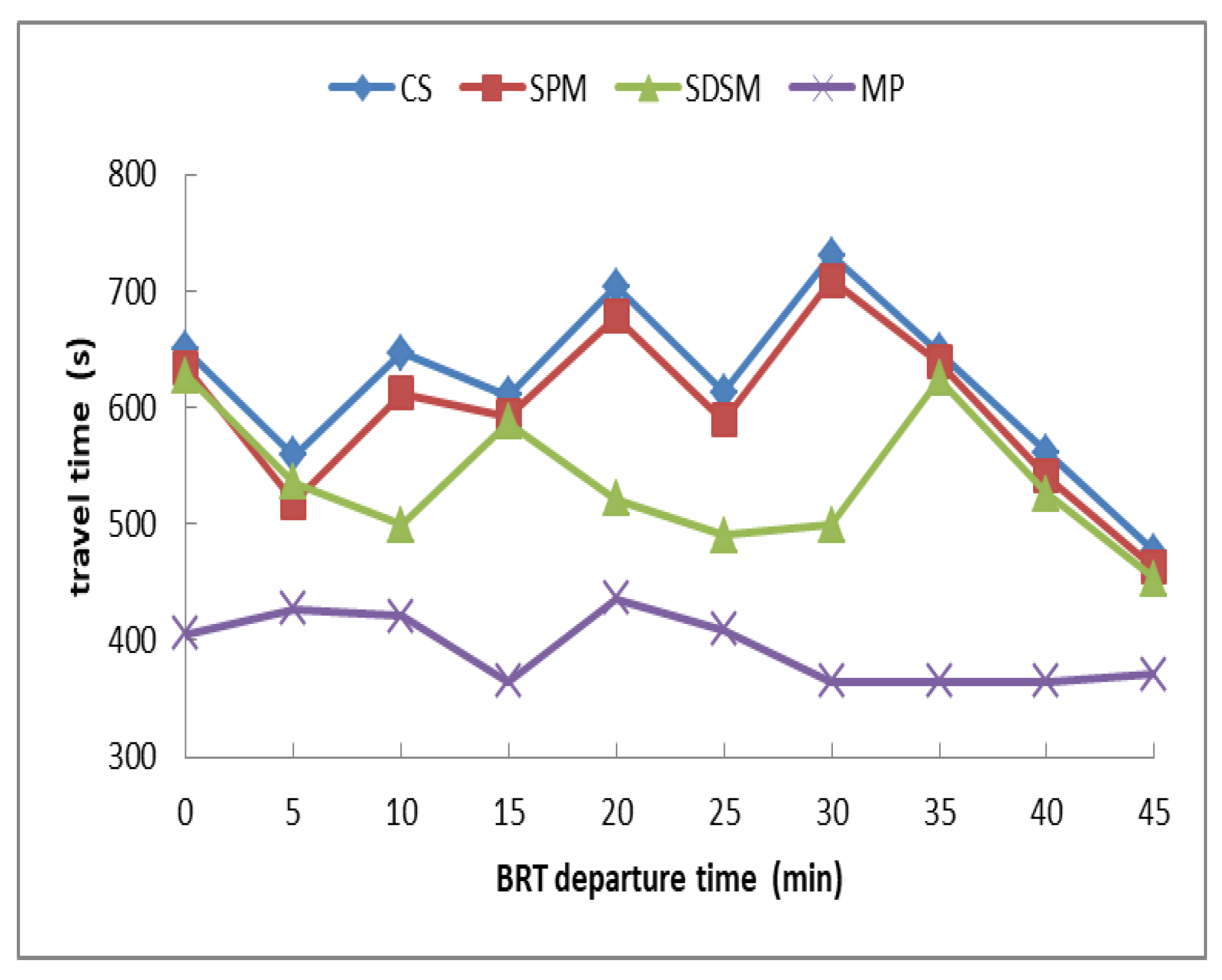
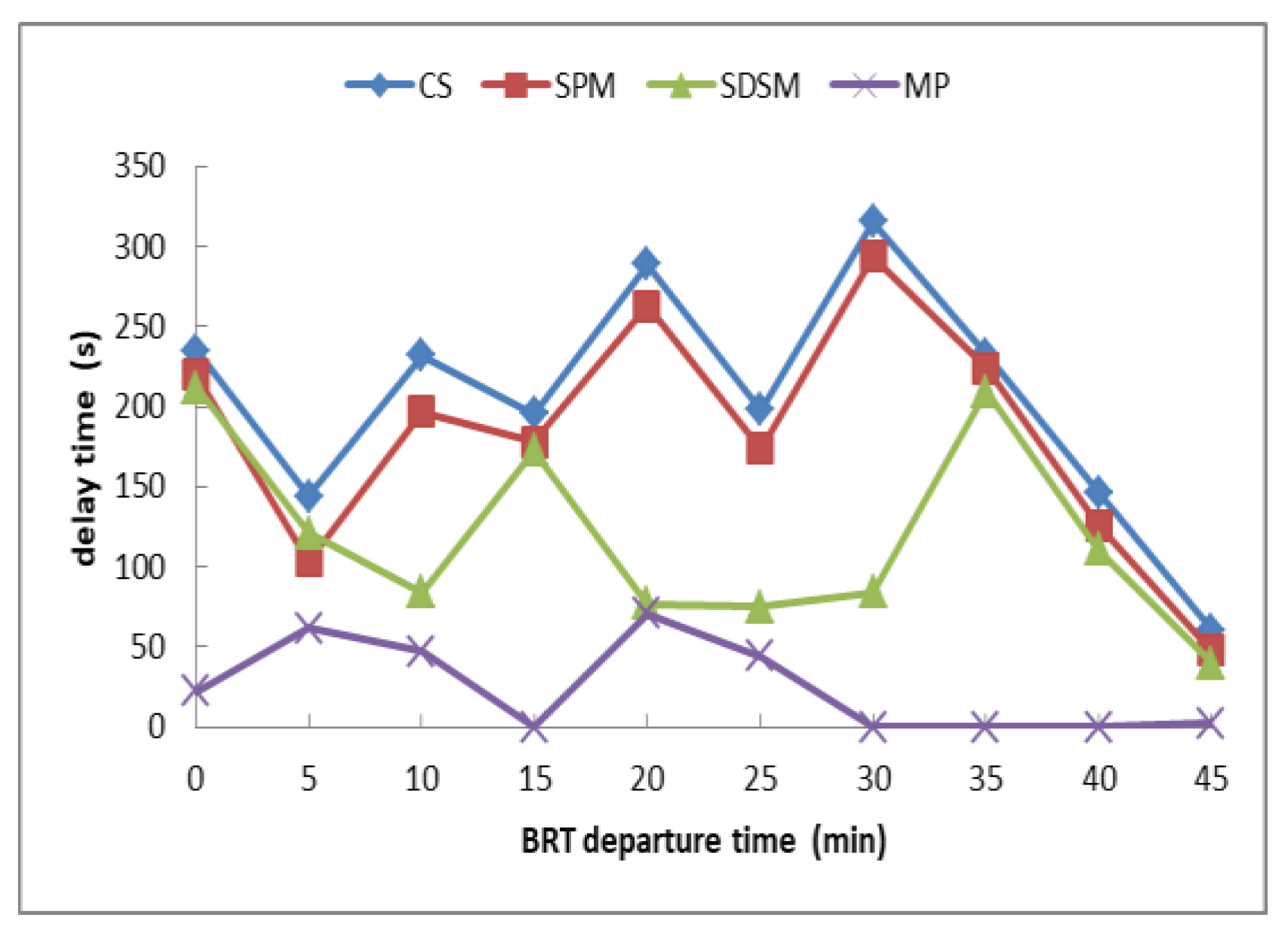
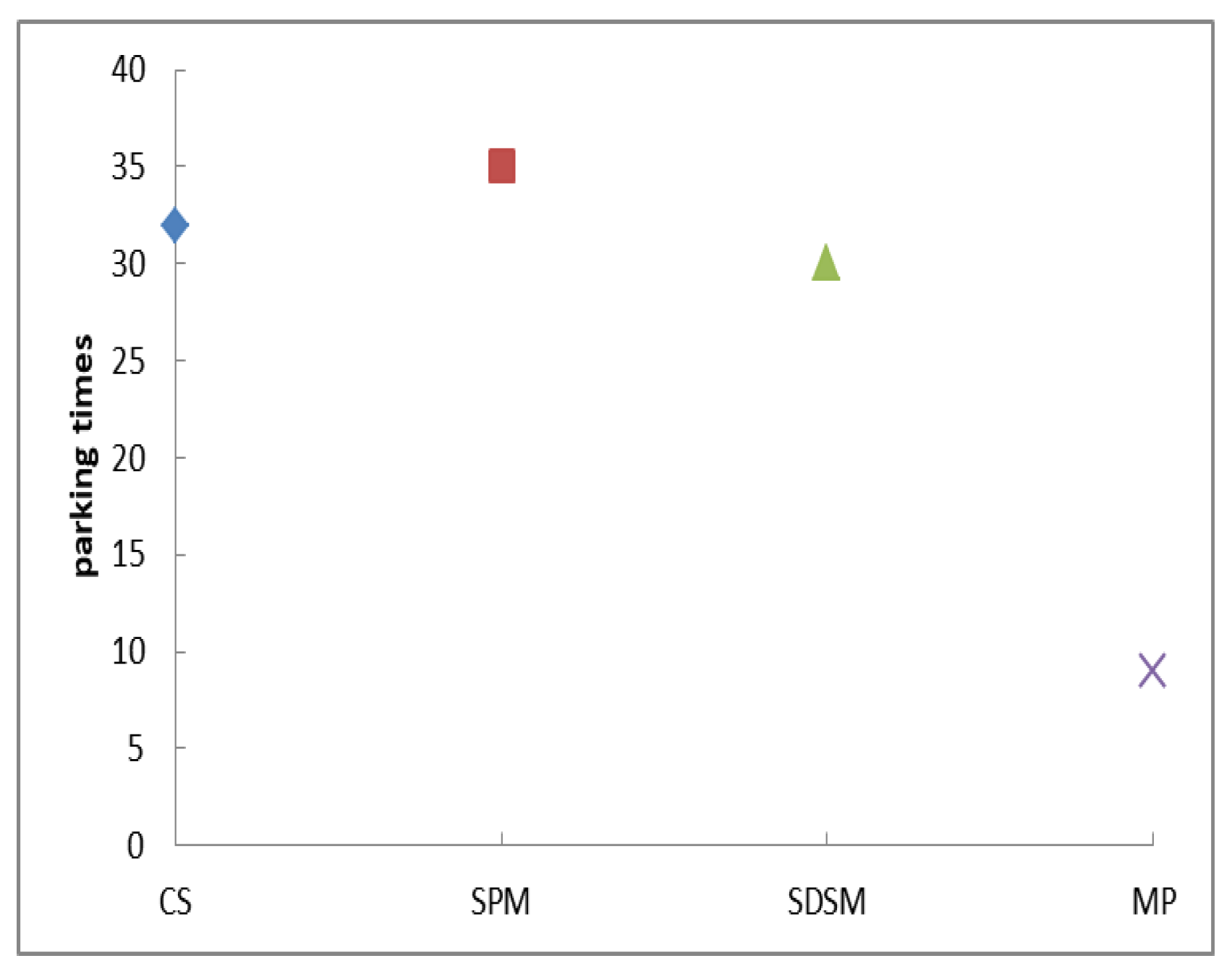
5. Case Analysis
6. Conclusions
- (1)
- Under the condition of no signal timing adjustment and no speed guidance, the setting of BRT dual station can achieve priority control of BRT.
- (2)
- This paper establishes a binary integer linear programming model based on dual stations at intersection, taking the shortest travel time of BRT as the optimization objective, and taking the selection of dual station, green light time of intersection and cycle time as optimization variables. Example calculations show that: the application of this model can greatly reduce BRT driving delays, travel time and the number of stops without disturbing social vehicles.
- (3)
- Previous studies mostly focused on BRT single point priority control. The collaborative optimization model proposed in this paper can realize a BRT trunk line priority and make BRT operation more rapid and stable.
Author Contributions
Funding
Conflicts of Interest
References
- Shah, S.A.R.; Shahzad, M.; Ahmad, N.; Zamad, A.; Hussan, S.; Aslam, M.A.; Khan, A.R.; Asif, M.A.; Shahzadi, G.; Waseem, M. Performance Evaluation of Bus Rapid Transit System: A Comparative Analysis of Alternative Approaches for Energy Efficient Eco-Friendly Public Transport System. Energies 2020, 13, 1377. [Google Scholar] [CrossRef]
- Li, Z.; Yi-Zhe, W.; Yang-Dong, L. Study on Signal Priority and Control Method of BRT Based on Vehicle Infrastructure Integration. Traffic Eng. 2017, 12, 60–64. [Google Scholar]
- Li, J.; Liu, Y.; Yang, H.; Chen, B. Bus Priority Signal Control Considering Delays of Passengers and Pedestrians of Adjacent Intersections. J. Adv. Transp. 2020, 2020, 1–12. [Google Scholar] [CrossRef]
- Zhu, W.-T.; Qian, G.-M. Bus delay model considering influence of stop at upstream of intersection. J. Zhejiang Univ. (Eng. Sci.) 2020, 54, 796–803. [Google Scholar]
- Xu, H.-F.; Zheng, Q.-M.; Zhang, K. Signal Priority Technique for Bus Rapid Transit System along an Arterial Based on Vertical Equity. China J. Highw. Transp. 2019, 32, 144–153. [Google Scholar]
- Sun, X.; Lin, K.; Jiao, P.; Lu, H. Signal Timing Optimization Model Based on Bus Priority. Information 2020, 11, 325. [Google Scholar] [CrossRef]
- Zheng, C.; Zheng, C.-J. Research and Application of Bus Speed Induction. J. Zhengzhou Univ. (Eng. Sci.) 2013, 34, 19–22. [Google Scholar]
- Teng, J.; Jin, W.-M. A Section-Speed Guiding Method for Bus Operation Control. J. Tongji Univ. (Nat. Sci.) 2015, 43, 1194–1199. [Google Scholar]
- Wu, W.; Ma, W.; Long, K.; Zhou, H.; Zhang, Y. Designing Sustainable Public Transportation: Integrated Optimization of Bus Speed and Holding Time in a Connected Vehicle Environment. Sustainability 2016, 8, 1170. [Google Scholar] [CrossRef]
- Zhang, C.B.; Ran, B.; Mei, C.; Zhang, P.L. An Optimization Method of Traffic Signal Control Based on Cooperative Vehicle Infrastructure System. J. Transp. Syst. Eng. Inf. Technol. 2013, 13, 40–45. [Google Scholar]
- Wu, Z.; Tan, G.; Shen, J.; Wang, C. A Schedule-based Strategy of transit signal priority and speed guidance in Connected Vehicle environment. In Proceedings of the International Conference on Intelligent Transportation Systems (ITSC), Rio de Janeiro, Brazil, 1–4 November 2016. [Google Scholar]
- Colombaroni, C.; Fusco, G.; Isaenko, N. A Simulation-Optimization Method for Signal Synchronization with Bus Priority and Driver Speed Advisory to Connected Vehicles. Transp. Res. Procedia 2020, 45, 890–897. [Google Scholar] [CrossRef]
- Zhang, P.; Wang, P.-F.; Sun, C. Research on BRT Priority Control Method Based on Two Stations at Intersection. J. Transp. Syst. Eng. Inf. Technol. 2020, 20, 83–88. [Google Scholar]

| Intersection Name | Intersection Spacing (m) | Signal Timing | ||
|---|---|---|---|---|
| Red Light Time (s) | Green Light Time (s) | Cycle Time (s) | ||
| Tongjiang-Huanghe | 800 | 99 | 47 | 146 |
| Tongjiang-Hanjiang | 730 | 115 | 53 | 168 |
| Tongjiang-Hehai | 1100 | 140 | 74 | 214 |
| Tongjiang-Taihu | 700 | 136 | 98 | 234 |
| Tongjiang-Longcheng | 840 | 161 | 48 | 209 |
| BRT | Control Method | DT d0 (s) | S1 | S2 | S3 | S4 | S5 | TT (s) | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Delay (s) | COP | Delay (s) | COP | Delay (s) | COP | Delay (s) | COP | Delay (s) | COP | ||||
| 1 | CS | 0 | 88.4 | 0 | 114.44 | 0 | 0 | 0 | 0 | 0 | 31.92 | 0 | 650 |
| SPM | 0 | 84.4 | 0 | 110.44 | 0 | 0 | 0 | 0 | 0 | 24.64 | 0 | 634.48 | |
| SDSM | 0 | 65.4 | 1 | 0 | 0 | 127.24 | 0 | 19.12 | 0 | 0 | 1 | 627 | |
| MP | 0 | 0 | 0 | 22.2 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 406 | |
| 2 | CS | 300 | 80.4 | 0 | 0 | 0 | 26.24 | 0 | 0 | 0 | 37.12 | 0 | 559 |
| SPM | 300 | 76.4 | 0 | 0 | 0 | 13.8 | 0 | 0 | 0 | 13.42 | 0 | 518.62 | |
| SDSM | 300 | 70.84 | 1 | 0 | 0 | 35.8 | 0 | 0 | 1 | 14.12 | 1 | 536 | |
| MP | 300 | 0 | 0 | 22.2 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 406 | |
| 3 | CS | 600 | 76.84 | 0 | 0 | 0 | 127.8 | 0 | 26.6 | 0 | 0.52 | 0 | 647 |
| SPM | 600 | 72.84 | 0 | 0 | 0 | 73.24 | 0 | 19.6 | 0 | 31.32 | 0 | 612 | |
| SDSM | 600 | 49.4 | 1 | 34.44 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 499.08 | |
| MP | 600 | 3 | 0 | 21.2 | 0 | 8 | 0 | 15 | 0 | 0 | 1 | 421 | |
| 4 | CS | 900 | 64.4 | 0 | 78.44 | 0 | 5.8 | 0 | 46.6 | 0 | 0 | 0 | 610.48 |
| SPM | 900 | 60.4 | 0 | 69.44 | 0 | 39.24 | 0 | 0 | 0 | 9 | 0 | 593.08 | |
| SDSM | 900 | 41.4 | 1 | 84.24 | 1 | 0 | 1 | 46.6 | 1 | 0 | 0 | 587.48 | |
| MP | 900 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 365.2 | |
| 5 | CS | 1200 | 56.4 | 0 | 0 | 0 | 6.24 | 0 | 66.6 | 0 | 159.52 | 0 | 704 |
| SPM | 1200 | 52.4 | 0 | 0 | 0 | 114.6 | 0 | 37 | 0 | 59.08 | 0 | 678.08 | |
| SDSM | 1200 | 33.4 | 1 | 0 | 0 | 0 | 0 | 43.6 | 1 | 0 | 0 | 521.48 | |
| MP | 1200 | 39.2 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 31.6 | 1 | 436 | |
| 6 | CS | 1500 | 48.4 | 0 | 0 | 0 | 0 | 0 | 14.84 | 0 | 134.52 | 0 | 613 |
| SPM | 1500 | 44.4 | 0 | 15.44 | 0 | 0 | 0 | 83.6 | 0 | 30.56 | 0 | 589 | |
| SDSM | 1500 | 25.4 | 1 | 0 | 1 | 0 | 0 | 37.84 | 0 | 11.52 | 1 | 490 | |
| MP | 1500 | 0 | 0 | 21.2 | 0 | 15 | 0 | 8 | 1 | 0 | 0 | 409.4 | |
| 7 | CS | 1800 | 82.84 | 0 | 0 | 0 | 21.8 | 0 | 126.6 | 0 | 84.52 | 0 | 731 |
| SPM | 1800 | 78.84 | 0 | 69.88 | 0 | 36.24 | 0 | 109.04 | 0 | 0 | 0 | 709 | |
| SDSM | 1800 | 17.4 | 1 | 42.44 | 1 | 21.8 | 1 | 0 | 0 | 2.12 | 1 | 499 | |
| MP | 1800 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 365.2 | |
| 8 | CS | 2100 | 32.4 | 0 | 86.44 | 0 | 113.8 | 0 | 0 | 0 | 0 | 0 | 647.88 |
| SPM | 2100 | 28.4 | 0 | 0 | 0 | 98.44 | 0 | 0 | 0 | 97.16 | 0 | 639 | |
| SDSM | 2100 | 9.4 | 1 | 86.44 | 1 | 113.8 | 1 | 0 | 0 | 0 | 0 | 624.88 | |
| MP | 2100 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 365.2 | |
| 9 | CS | 2400 | 24.4 | 0 | 0 | 0 | 122.24 | 0 | 0 | 0 | 0 | 0 | 561.88 |
| SPM | 2400 | 20.4 | 0 | 33.44 | 0 | 72.04 | 0 | 0 | 0 | 0 | 0 | 540.88 | |
| SDSM | 2400 | 1.4 | 1 | 0 | 0 | 0 | 0 | 109.36 | 0 | 0 | 1 | 526 | |
| MP | 2400 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 365.2 | |
| 10 | CS | 2700 | 22.84 | 0 | 0 | 0 | 37.8 | 0 | 0 | 0 | 0 | 0 | 475.88 |
| SPM | 2700 | 18.84 | 0 | 12.88 | 0 | 16.16 | 0 | 0 | 0 | 0 | 0 | 462.88 | |
| SDSM | 2700 | 16.4 | 0 | 6.44 | 0 | 14.8 | 1 | 1 | 0 | 1 | 0 | 452.88 | |
| MP | 2700 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 371 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, P.; Gao, S.; Wang, P.; Li, W. Cooperative Optimization Model of BRT Speed and Timing Based on Dual Station at an Intersection. Symmetry 2020, 12, 1814. https://doi.org/10.3390/sym12111814
Zhang P, Gao S, Wang P, Li W. Cooperative Optimization Model of BRT Speed and Timing Based on Dual Station at an Intersection. Symmetry. 2020; 12(11):1814. https://doi.org/10.3390/sym12111814
Chicago/Turabian StyleZhang, Peng, Shuangxi Gao, Pengfei Wang, and Wenquan Li. 2020. "Cooperative Optimization Model of BRT Speed and Timing Based on Dual Station at an Intersection" Symmetry 12, no. 11: 1814. https://doi.org/10.3390/sym12111814
APA StyleZhang, P., Gao, S., Wang, P., & Li, W. (2020). Cooperative Optimization Model of BRT Speed and Timing Based on Dual Station at an Intersection. Symmetry, 12(11), 1814. https://doi.org/10.3390/sym12111814




