Abstract
Eurocodes are currently under revision within a six-year program by CEN/TC 250. In this framework, concentric bracings, particularly in cross configuration, have been largely debated; indeed, several criticisms affect the seismic design procedure currently codified within Eurocode 8, entailing significant design efforts and leading to massive and non-economical structural systems, even characterized by poor seismic behavior. The efforts of SC8 have been aimed at improving the codified seismic design criteria for concentrically braced frames, by providing requirements and detailing rules conceived to simplify the design process and to improve the seismic performance. The current paper provides recent advances in the field of computational and structural engineering focusing on symmetric X concentrically bracings in seismic area, outlining the evolution of Eurocode 8 (EC8) seismic design rules, by examining the following aspects: (i) ductility class and behavior factor, (ii) analysis and modelling aspects, (iii) design of dissipative members; (iv) design of non-dissipative zones; (v) brace-to-frame connections.
1. Introduction
X concentric bracings are widely used lateral resisting systems, often opted by structural designers due to their inherent advantages in terms of lateral strength and stiffness, low constructional cost and simplicity of design. Seismic design criteria provided by Eurocode 8 (EN 1998-1 [1]) theoretically aim at restraining plastic deformation into diagonal members (responsible of dissipating seismic input energy), while beams, columns and connections should behave in the elastic range. During the last ten years, Eurocode 8 (EN 1998-1 [1]) has been widely used by structural designers and numerous researchers, deepened the seismic performance of concentrically braced frames (CBF); several authors [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56] highlighted that the design procedure currently codified Eurocode 8 (EN 1998-1 [1]) is affected by several criticisms. On the contrary, a large number of existing studies demonstrated that the seismic design and performance of steel structures in accordance with North American codes are satisfactory to guarantee high performance and ease of use [57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91].
Eurocodes are currently under revision within a six-year program by CEN/TC 250. In particular, the SC8 subcommittee of CEN/TC250, collaborating with the working group (WG2)—Steel and composite structures—which is in charge of carrying out, on behalf of the SC8, all the preliminary work concerning issues relating to the chapters “Steel structures” and “Composite steel–concrete structures”, is involved in the revision activities of seismic design of steel structures. In this framework, concentric bracings, particularly in the cross configuration (X-CBF), have been largely debated. Indeed, as also confirmed by scientific literature [6,7,8,10] that the seismic design criteria provided by current EC8 entails significant difficulties in the design process (e.g., sizing of diagonal members), and they lead to massive and non-economical structural systems whose corresponding performance is unsatisfactory and poorly efficient.
Solely for X-CBFs, Eurocode 8 allows performing a simplified design procedure and calculating the required strength of diagonal members by global elastic analysis on a tension-only (TO) diagonal scheme, in which the contribution of braces under compression is disregarded. The reason for using a TO model is related to the assumption that compression diagonals offer negligible contributions to lateral capacity due to buckling phenomena; however, such an assumption can be considered sufficiently accurate solely for slender braces in the post-buckling condition, while at the first stages of a seismic event and in cases of stockier members, both diagonals are active and both transmit axial forces to non-dissipative zones [10]. Moreover, using a TO diagonal scheme may be responsible for misleading interpretation of structural behavior: in the absence of specific provisions, the TO model may induce the designer to consider that only the diagonal under tension is mechanically active and to disregard the brace-to-brace mutual restraint, leading to inaccurate prediction of in-plane and out-of-plane buckling phenomena (i.e., diagonals stockier than expected are selected).
According to current detailing rules, the brace slenderness ratio should be kept in the range [1.3, 2]; the upper bound limit is fixed to avoid undesired buckling phenomena at the serviceability limit state, while the lower bound limit is mandated in order to avoid the overloading of columns and connections due to the axial force transmitted by compression diagonals neglected in the TO scheme, and it does not distinguish the case of continuous and discontinuous bracings.
The need to satisfy the minimum allowed brace slenderness ratio () entails significant efforts in the sizing of diagonal members, especially if few bays are equipped with X bracings, and it often forces the designer to increase the number of braced bays to withstand the design base shear, with a consequent increase in the number of members, connections and structural costs.
To prevent the soft-story mechanism and to favor uniform distribution of plastic deformation along the building height, the Eurocode 8 (EN 1998-1 [1]) mandates controlling the braces’ overstrength variation; that is, the capacity-to-demand ratio, , should be limited in the range (Ω; 1.25 Ω), where Npl,Rd,i is the plastic capacity under tension of the brace at the i-th story, and Npl,Ed,i is the relevant required strength.
Several numerical studies [2,3,6,7,10] have already shown that this requirement is not adequate to mitigate the tendency of this type of system to soft-story mechanisms; in this regard, the authors suggested in previous studies [3,10] that it may be more effective to define the i-th overstrength ratio by considering the compression axial strength of the brace at the i-th story (rather than the plastic strength), given that the buckling of the brace under compression is the actual first nonlinear event occurring at each story. Further criticisms are due to the interrelation and juxtaposition of such a requirement with the need to satisfy the maximum allowable slenderness (); indeed, the brace at the roof level is generally characterized by the largest overstrength ratio, given that the selection of the cross-section is generally ruled by the slenderness limit; to meet the requirement of the overstrength homogeneity, the designer is then forced to oversize the elements at the lower and intermediate stories, leading to cost-ineffective and massive structural systems characterized by large lateral overstrength (Ω even significantly overcomes the unit), which exhibit poor plastic engagement and energy dissipation capacity.
Another hindrance to efficient design and performance of concentrically braced frames is due to the lack of specific detailing rules and technological requirements for brace-to-frame connections; indeed the Code currently addresses conceptually the design of brace-to-frame, and no provisions are given except for the capacity design requirement, which solely accounts for the axial force transferred by braces yielded under tension, disregarding the need to accommodate the buckling of braces under compression; moreover, the flexural strength that the connection should exhibit if the braces are fixed at both ends is not accounted for [92]. It is also worth noting that the issues of seismic design of connections and members have been systematically addressed in prEN 1998-1-2:2019.3 [93], where specific rules have been drafted on the basis of the outcomes of recent European studies [94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131]. Analogous efforts can be recognized in different fields of structural engineering, e.g., the field of composite materials and structures [132,133,134,135,136,137].
The current paper provides recent advances in a key topic of structural engineering, as the main result of numerous studies about symmetric X concentric bracings in seismic areas carried out by the University of Naples “Federico II” that have been also within the current draft of prEN 1998-1-2:2019.3 [93]. In particular, the following aspects are examined: (i) ductility class and behavior factor, (ii) analysis and modelling aspects, (iii) design of dissipative members; (iv) design of non-dissipative zones; and (v) brace-to-frame connections.
For the sake of clarity it is worth specifying that in the next version of Eurocode 8 (prEN 1998-1-2:2019.3 [93]), the material independent part will be addressed in Section EN 1998-1-1 and the material dependent part in Section EN 1998-1-2.
2. Ductility Classes and Behavioral Factors
2.1. Current EN 1998-1
The current Eurocode 8 (EN 1998-1 [1]) provides different ductility classes depending on the level of plastic engagement expected in the dissipative zones, and the upper limit for the behavior factor, directly related to the ductility of the system, is assigned per each ductility class and structural typology. At current stage, the ductility classes considered are the following: (i) low ductility class (DCL); (ii) medium ductility class (DCM); (iii) high ductility class (DCH).
The q factor according to Eurocode 8 (EN 1998-1 [1]) for regular structural systems is given as follows:
where qo is the reference value of the behavior factor for regular structural systems, while au/a1 is the plastic redistribution parameter accounting for the system overstrength due to redundancy. EC8 [1] recommends au/a1 = 1 for CBFs.
In DCL, poor dissipative behavior is expected, the action effects can be calculated by simple linear-elastic analyses without accounting for material nonlinearity, and the strength of members and connection is verified according to EN 1993-1 without accounting for any capacity design requirement; the upper limit of the reference value of the behavior factor is set equal to 1.5–2. Design to DCL is limited to seismic areas up to 0.01 Sagr, S being the soil factor and agr the reference ground acceleration.
For structures designed in DCM or DCH, the capability of the specific zones of the system to resist the seismic event through inelastic behavior is accounted for, and moderate and large plastic engagement of dissipative zones is expected, respectively. At the current stage in Eurocode 8 (EN 1998-1 [1]) for X-CBFs, the upper limit for q value is identically set at 4 in DCM as well as DCH, and the reason why it coincides in both classes is unclear.
As a general remark, it should be noted that current Eurocode 8 assigns the behavior factor depending on the ductility class and thus on the expected energy dissipation capacity of the system; however, the design requirements are given practically identically for both medium and high ductility classes, except solely for the allowed cross section class (Class 1 and Class 1 or 2 according to EN 1993 [14] in DCH and DCM, respectively) and the beam-to-column joint rotational capacity.
2.2. prEN 1998-1-2:2019.3
According to the next version of Eurocode 8 (prEN 1998-1-2:2019.3 [93]), three ductility classes are considered as follows: (i) DC1, low dissipative behavior; (ii) DC2, medium dissipative behavior; (iii) DC3: high dissipative structural behavior.
The behavior factor q, which accounts for overstrength, deformation capacity and energy dissipation capacity, is given by the following formula:
where:
- qS is the behavior factor component accounting for overstrength due to all other sources;
- qR is the behavior factor component accounting for overstrength due to the redistribution of
- seismic action effects in redundant structures;
- qD is the behavior factor component accounting for the deformation capacity and energy
- dissipation capacity.
The total values of q for cross concentrically braced frames are given in Table 1 and are also compared with the current rules.

Table 1.
Ductility classes and behavior factors for X-CBFs.
Low dissipative structures (DC1) should be designed to withstand the seismic action in the elastic range; the design forces are evaluated assuming both qR = qD = 1, while q = qS = 1.5; structural members and connections are verified according to Eurocode 3 [14].
For structures designed in DC2 or DC3, the capability of the specific zones of the system to resist the seismic event through inelastic behavior is accounted for and different design requirements, more stringent in DC3 than DC2, are provided.
3. Overstrength Factors
3.1. Current EN 1998-1
The current EN 1998-1 allows simplified design procedure to be performed to calculate the internal seismic forces acting on CBFs.
Under gravity load conditions, only beams and columns should be considered to resist vertical loads without accounting for diagonal members.
As already mentioned, for X-CBF in both DCM and DCH, Eurocode 8 mandates calculating the design action effects by performing a linear elastic analysis on a tension-only diagonal scheme, in which the braces under compression are omitted.
The earthquake-induced effects in non-dissipative components (namely beams, columns and connections) are estimated by magnifying them by the overstrength factor, , the internal forces calculated by means of the former elastic analysis.
3.2. prEN 1998-1-2:2019.3
Beams and columns should be considered to resist gravity loads in the persistent and transient design situation without considering the bracing members. In addition, the buckling resistance of diagonal bracings should be verified against the axial forces due to the imposed and variable loads as given at the ultimate limit state in non-seismic design situations.
The tension-only (TO) scheme is allowed solely for DC2 frames, provided that the lateral resistance of the building in both pre-buckling and post-buckling range is lower than the resistance of the building evaluated solely considering the tension diagonals; in DC3 a tension–compression diagonal scheme (TC), in which all braces are explicitly accounted for, is requested.
The earthquake-induced effects in non-dissipative components (namely beams, columns) are differently calculated depending on the ductility class: (i) for frames designed to DC2, the required strength of non-dissipative members is evaluated by magnifying the seismic-induced effect by the overstrength factor Ω fixed a-priori in function of the structural typology; (ii) for frames designed to DC3, a plastic mechanism analysis should be performed and the internal forces are calculated on the basis of a free-body distribution of plastic forces representative of the non-linear range.
4. Design of Dissipative Members
4.1. Current EN 1998-1
According to the current EN-1998 [1], diagonals in cross configuration should be designed to guarantee , where Npl,Rd is the design plastic strength of brace cross-section, and NEd is calculated by linear-elastic analysis on the TO model. Since the braces provide poor energy dissipation in the post-buckling range, the Code states further requirements devoted to limit the global and local slenderness of the diagonal members. The global slenderness, (Ncr,br being the Eulerian critical load), of bracing members must fall in the range (1.3, 2).
To assure an uniform distribution of damage along the building height, the overstrength ratio, , should fall in the range .
Concerning the local slenderness, EC8 adopts the classification for cross sections provided in EC3, in which cross-sectional classes 1, 2 or 3 are required to correspond to behavior factors in the range (1.5, 2.0), while class 1 or 2 are required for q in a range (2.0, 4.0); only class 1 is allowed for DCH (q > 4.0).
4.2. prEN 1998-1-2:2019.3
In DC2, if a TO model is used, diagonals in cross configuration should be designed to guarantee , where Npl,Rd is the design plastic strength of brace cross-section, and NEd is calculated by linear-elastic analysis.
In DC3, the use of a tension–compression diagonal scheme is mandatory, and the diagonals should be verified against their compression capacity as , χ being the buckling reduction factor according to EN 1993.
For concentrically-braced frames in DC2, when the tension-only scheme is adopted, the brace slenderness ratio should be limited in the range ; in DC2 and DC3 frames when the TC model is used, the brace slenderness ratio should be smaller than 2.0. The global slenderness limitations can be waived for frames up to two stories with tension–compression bracings.
The next Code specifies that the length of the bracings may be taken as the theoretical node-to-node length, disregarding the size of the gusset connections at both brace ends. The buckling length should also account for the degree of restraint given by the brace end-connections, and the mutual restraint due to the mid-length brace-to-brace connection.
To mitigate the effect of rocking-like displacements in DC3 frames with at least six stories, the braces at the roof level should be designed to guarantee , NEd,G being the axial force due to gravity loads in seismic-design situations, q the behavior factor assumed at design stage and NEd,E the axial force due to the seismic action.
For concentrically braced frames in DC3, it should also be verified that the compression overstrength factor (with ) should not vary along the building height more than 25%, with the exception of the top story.
Cross-sectional classes 1 and 2, corresponding to behavior factors in the range [2.0, 4.0], can be selected for concentric bracings in DC2, while class 1 is required for DC3. In addition, for frames designed to DC3, the following requirement should be met:
- Circular hollow sections should verify , where D is the external diameter and t is the thickness of the cross section, γmr is the material randomness coefficient and .
- For rectangular hollow sections, the maximum local slenderness c/t should not be greater than , c being the side width and t the thickness of the cross section.
The evolution of design requirements for bracings is summarized in Table 2.

Table 2.
Evolution of design requirements for dissipative members.
5. Design of Non-Dissipative Members
5.1. Current EN 1998-1
According to the current EN-1998 [1], the non-dissipative members (namely beams and columns) should be designed to verify the following inequality:
where:
- Npl,Rd(MEd) is the design resistance to axial force of the beam or column calculated in accordance with EN 1993:1-1 [14], accounting for the interaction with the design value of bending moment;
- MEd, in the seismic design situation;
- NEd,G is the axial force in the beam or in the column due to the non-seismic actions in the seismic design situation;
- NEd,E is the axial force in the beam or in the column due to the design seismic action;
- γov is the material overstrength factor;
- Ω is the minimum overstrength ratio
5.2. prEN 1998-1-2:2019.3
For DC2 frames, the resistance and stability of both beams and columns should be verified in compression, bending and shear considering the most unfavorable combination of the axial force NEd, bending moments MEd and shear force VEd calculated as:
where NEd,G, MEd,G and VEd,G are the axial force, the bending moment and the shear force in the non-dissipative member due to the non-seismic actions in the seismic design situation, and NEd,E, MEd,E and VEd,E are the axial force, the bending moment and the shear force, in the non-dissipative member due to the design seismic action;
Ω is the seismic action magnification factor; for DC2 it depends on the type of plastic behavior of the dissipative zone and varies with the structural system. It should be assumed equal to 1.5 for concentric bracings.
For DC3 frames, beams and columns should be designed to resist the most severe condition between the scenario defined in the following from (i) to (iii).
- (i)
- The resistance and stability of both beams and columns should be verified in compression against the following actions:where γrm is the material randomness coefficient (depending on the steel grade); γsh is the factor accounting for hardening of the dissipative zone; and Ωd is the minimum design overstrength .
- (ii)
- The internal forces are calculated by mean of plastic mechanism analysis, namely considering a free-body distribution of axial forces in both tension and compression diagonals with values equal to their expected buckling resistance equal to ;
- (iii)
- The internal forces are calculated by mean of plastic mechanism analysis, considering a free-body distribution of axial forces in which the braces under tension transmit a force equal to and the braces under compression attain their post-buckling resistance equal to .
In addition, for frames in DC3, the resistance and stability of columns should be verified considering the combined effect of axial force (evaluated according to the most detrimental scenario between (i), (ii) or (iii)) and uniform bending moment in the direction of the braced bay set equal to the 20% of the relevant plastic strength. The evolution of design requirements for beams and columns is summarized in Table 3.

Table 3.
Evolution of design requirements for non-dissipative members.
6. Design of Brace-to-Frame Connections
6.1. Current EN 1998-1
According to the current EN 1998-1, the brace-to-frame connections should be designed to meet the following capacity design requirement:
where Nj.Rd is the joint axial strength, Npl,Rd is the brace plastic axial strength and γov is the material randomness
6.2. prEN 1998-1-2:2019.3
According to prEN 1998-1-2:2019.3, the brace connections should be designed to withstand the axial force due to the yielding and hardening of braces under tension and to restrain the rotation at the end brace or to accommodate the brace buckling.
For connections restraining brace buckling, the following inequalities occur both in-plane and out-of-plane, without considering any interaction between the axial and flexural effects:
where:
- Npl,Rd is the design plastic resistance of the brace in tension;
- Nb,Rd is the design buckling resistance of the brace in compression;
- Mpl,Rd is the design plastic moment of the cross section of the brace;
- γrm and γsh are the material randomness and the hardening factors, respectively.
For connections accommodating the buckling of braces under compression in one plane, the requirement given by Equations (7) to (9) should be met in the restrained plane. In the plane of the buckling, Equation (8) should be satisfied, and the connection should be properly designed to have enough rotational capacity to accommodate the required rotation at the design story drift. Inelastic rotation can be generally sustained by using gusset plate connections with the brace ending before a linear (Figure 1) or elliptical (Figure 2) clearance corresponding to the theoretical yielding line of the gusset plate [92].
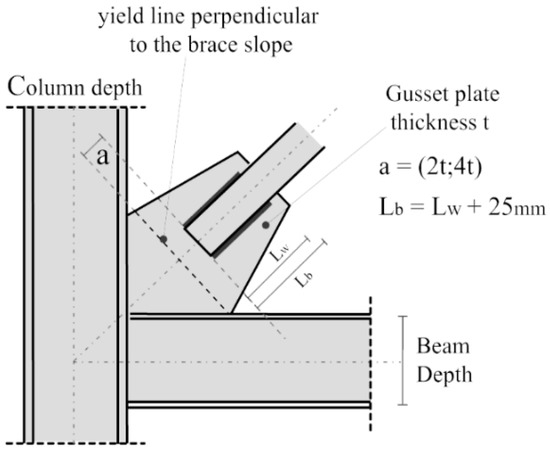
Figure 1.
Gusset plate connections accommodating brace buckling with the brace ending before a linear clearance corresponding to the theoretical yielding line of the gusset plate [92].
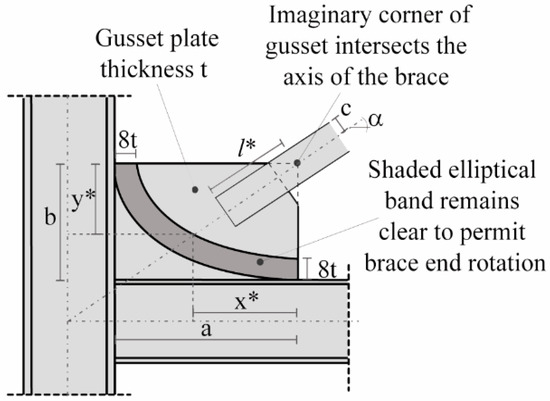
Figure 2.
Gusset plate connections accommodating brace buckling with the brace ending before an elliptical clearance corresponding to the theoretical yielding line of the gusset plate [92].
7. Conclusive Remarks
Eurocodes are currently under revision within a six-year program by CEN/TC 250. In particular, the subcommittee SC8, collaborating with the working group (WG2)—Steel and composite structures, is involved in the revision activities of seismic design of steel structures. In this framework, concentric bracings, particularly in cross configuration, have been largely debated.
Several criticisms affect the seismic design procedure currently codified within Eurocode 8, entailing significant design efforts and leading to massive and non-economical structural systems, even those characterized by poor seismic behavior.
The main criticisms are related to the following aspects:
- the use of a tension-only diagonal scheme;
- the requirement of diagonal slenderness;
- the homogeneity condition of the overstrength factor;
- the design of brace-to-frame connections.
The efforts of SC8 have been aimed at improving the codified seismic design criteria for concentrically braced frames by providing requirements and detailing rules conceived to simplify the design process and to improve the seismic performance.
The evolution of seismic design rules for X concentric bracings between the current EN 1998-1 and the draft of next standard prEN 1998-1-2:2019.3 [93] was discussed with reference to the following issues: (i) ductility class and behavior factor, (ii) analysis and modelling aspects, (iii) design of dissipative members; (iv) design of non-dissipative zones; and (v) brace-to-frame connections.
Author Contributions
Conceptualization, A.C. and S.C.; methodology, A.C. and S.C.; writing—original draft preparation, A.C. and S.C.; writing—review and editing, A.C. and S.C.; visualization, A.C. and S.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- CEN. EN 1998-1, Design of Structures for Earthquake Resistance—Part 1: General Rules, Seismic Actions and Rules for Buildings; The European Union Per Regulation: Bruxelles, Belgium, 2005. [Google Scholar]
- Costanzo, S.; D’Aniello, M.; Landolfo, R. Seismic design criteria for chevron CBFs: European vs North American codes (PART-1). J. Constr. Steel Res. 2017, 135, 83–96. [Google Scholar] [CrossRef]
- Costanzo, S.; D’Aniello, M.; Landolfo, R. Seismic design criteria for chevron CBFs: Proposals for the next EC8 (PART-2). J. Constr. Steel Res. 2017, 138C, 17–37. [Google Scholar] [CrossRef]
- Elghazouli, A.Y. Seismic design of steel framed structures to Eurocode 8. Struct. Eng. 2017, 85, 26–31. [Google Scholar]
- Tenchini, A.; D’Aniello, M.; Rebelo, C.; Landolfo, R.; da Silva, L.; Lima, L. High strength steel in chevron concentrically braced frames designed according to Eurocode 8. Eng. Struct. 2016, 124, 167–185. [Google Scholar] [CrossRef]
- Brandonisio, G.; Toreno, M.; Grande, E.; Mele, E.; De Luca, A. Seismic design of concentric braced frames. J. Constr. Steel Res. 2012, 78, 22–37. [Google Scholar] [CrossRef]
- Bosco, M.; Brandonisio, G.; Marino, E.M.; Mele, E.; De Luca, A. Ω* method: An alternative to Eurocode 8 procedure for seismic design of X-CBFs. J. Constr. Steel Res. 2017, 134, 135–147. [Google Scholar] [CrossRef]
- Marino, E.M. A unified approach for the design of high ductility steel frames with concentric braces in the framework of Eurocode. Earthq. Eng Struct. Dyn. 2013, 43, 97–118. [Google Scholar] [CrossRef]
- Marino, E.M.; Nakashima, M. Seismic performance and new design procedure for chevron-braced frames. Earthquake Eng. Struct. Dyn. 2016, 35, 433–452. [Google Scholar] [CrossRef]
- Costanzo, S.; D’Aniello, M.; Landolfo, R. Proposal of design rules for ductile X-CBFS in the framework of EUROCODE 8. Earthq. Eng. Struct. Dyn. 2019, 48, 124–151. [Google Scholar] [CrossRef]
- Longo, A.; Montuori, R.; Piluso, V. Plastic design of V-braced frames. J. Earthq. Eng. 2008, 12, 1246–1266. [Google Scholar] [CrossRef]
- Freddi, F.; Tubaldi, E.; Zona, A.; Dall’Asta, A. Seismic performance of dual systems coupling moment-resisting and buckling-restrained braced frames. Earthq. Eng. Struct. Dyn. 2020, 1–25. [Google Scholar] [CrossRef]
- Morfuni, F.; Freddi, F.; Galasso, C. Seismic performance of dual systems with BRBs under mainshock-aftershock sequences. In Proceedings of the 13th International Conference on Applications of Statistics and Probability in Civil Engineering ICASP, Seoul, Korea, 26–30 May 2019. [Google Scholar]
- Kotoky, N.; Freddi, F.; Ghosh, J.; Raghunandan, M. BRBs uncertainty propagation in seismic retrofit of RC structures. In Proceedings of the 13th International Conference on Applications of Statistics and Probability in Civil Engineering ICASP, Seoul, Korea, 26–30 May 2019. [Google Scholar]
- Qie, Y.; Barbagallo, F.; Marino, E.M.; Du, C.; Wang, T. Full-scale hybrid test for realistic verification of a seismic upgrading technique of RC frames by BRBs. Earthq. Eng. Struct. Dyn. 2020, 49, 1452–1472. [Google Scholar] [CrossRef]
- Barbagallo, F.; Bosco, M.; Marino, E.M.; Rossi, P.P. Seismic design and performance of dual structures with BRBs and semi-rigid connections. J. Constr. Steel Res. 2019, 158, 306–316. [Google Scholar] [CrossRef]
- Barbagallo, F.; Bosco, M.; Marino, E.M.; Rossi, P.P. Achieving a more effective concentric braced frame by the double-stage yield BRB. Eng. Struct. 2019, 186, 484–497. [Google Scholar] [CrossRef]
- Barbagallo, F.; Bosco, M.; Marino, E.M.; Rossi, P.P. Behavior factor of dual systems with BRBs and semi-rigid connections. Key Eng. Mater. 2018, 763, 949–956. [Google Scholar] [CrossRef]
- Bosco, M.; Ghersi, A.; Marino, E.M.; Rossi, P.P. Generalized corrective eccentricities for nonlinear static analysis of buildings with framed or braced structure. Bull. Earthq. Eng. 2017, 15, 4887–4913. [Google Scholar] [CrossRef]
- Montuori, R.; Nastri, E.; Piluso, V.; Todisco, P. A simplified performance based approach for the evaluation of seismic performances of steel frames. Eng. Struct. 2020, 224, 111222. [Google Scholar] [CrossRef]
- Dell’Aglio, G.; Montuori, R.; Nastri, E.; Piluso, V. Consideration of second-order effects on plastic design of steel moment resisting frames. Bull. Earthq. Eng. 2019, 17, 3041–3070. [Google Scholar] [CrossRef]
- Montuori, R.; Piluso, V.; Streppone, S. Design and seismic assessment of MRFS and dual CBFS equipped with friction dampers. Compdyn Proc. 2019, 3, 4213–4225. [Google Scholar]
- Wang, Y.; Nastri, E.; Tirca, L.; Montuori, R.; Piluso, V. Comparative response of earthquake resistant CBF buildings designed according to Canadian and European code provisions. Key Eng. Mater. 2018, 763, 1155–1163. [Google Scholar] [CrossRef]
- Dell’Aglio, G.; Montuori, R.; Nastri, E.; Piluso, V. A critical review of plastic design approaches for failure mode control of steel moment resisting frames. Ing. Sismica 2017, 34, 82–102. [Google Scholar]
- Montuori, R.; Nastri, E.; Piluso, V. Influence of the bracing scheme on seismic performances of MRF-EBF dual systems. J. Constr. Steel Res. 2017, 132, 179–190. [Google Scholar] [CrossRef]
- Longo, A.; Montuori, R.; Piluso, V. Moment frames—Concentrically braced frames dual systems: Analysis of different design criteria. Struct. Infrastruct. Eng. 2016, 12, 122–141. [Google Scholar] [CrossRef]
- Longo, A.; Montuori, R.; Piluso, V. Seismic design of chevron braces cupled with MRF fail safe systems. Earthq. Struct. 2015, 8, 1215–1239. [Google Scholar] [CrossRef]
- Elghazouli, A.Y.; Castro, J.M.; Izzuddin, B.A. Seismic performance of composite moment-resisting frames. Eng. Struct. 2008, 30, 1802–1819. [Google Scholar] [CrossRef]
- Araújo, M.; Castro, J.M. On the quantification of local deformation demands and adequacy of linear analysis procedures for the seismic assessment of existing steel buildings to EC8-3. Bull. Earthq. Eng. 2016, 14, 1613–1642. [Google Scholar] [CrossRef]
- Peres, R.; Castro, J.M.; Bento, R. An extension of an improved forced based design procedure for 3D steel structures. Steel Compos. Struct. 2016, 22, 1115–1140. [Google Scholar] [CrossRef]
- Araújo, M.; Castro, J.M. Simplified procedure for the estimation of local inelastic deformation demands for seismic performance assessment of buildings. Earthq. Eng. Struct. Dyn. 2017, 46, 491–514. [Google Scholar] [CrossRef]
- Silva, A.; Santos, L.; Ribeiro, T.; Castro, J.M. Improved Seismic Design of Concentrically X-Braced Steel Frames to Eurocode 8. J. Earthq. Eng. 2018. [Google Scholar] [CrossRef]
- Macedo, L.; Silva, A.; Castro, J.M. From design to earthquake loss assessment of steel moment-resisting frames. Key Eng. Mater. 2018, 763, 124–130. [Google Scholar] [CrossRef]
- Araújo, M.; Castro, J.M. A Critical Review of European and American Provisions for the Seismic Assessment of Existing Steel Moment-Resisting Frame Buildings. J. Earthq. Eng. 2018, 22, 1336–1364. [Google Scholar] [CrossRef]
- Silva, A.; Castro, J.M.; Monteiro, R. On the importance of brace connection modelling for seismic performance assessment of steel CBFs. Compdyn Proc. 2019, 3, 4907–4915. [Google Scholar]
- Macedo, L.; Silva, A.; Castro, J.M. A more rational selection of the behaviour factor for seismic design according to Eurocode 8. Eng. Struct. 2019, 188, 69–86. [Google Scholar] [CrossRef]
- Silva, A.; Castro, J.M.; Monteiro, R. Practical considerations on the design of concentrically-braced steel frames to Eurocode 8. J. Constr. Steel Res. 2019, 158, 71–85. [Google Scholar] [CrossRef]
- Macedo, L.; Castro, J.M. Earthquake loss assessment of steel moment-resisting frames designed according to Eurocode 8. Soil Dyn. Earthq. Eng. 2019, 124, 58–71. [Google Scholar] [CrossRef]
- Silva, A.; Castro, J.M.; Monteiro, R. Implications of modelling simplifications on the seismic performance of concentrically-braced steel framed buildings. In Proceedings of the 9th International Conference on Advances in Steel Structures, ICASS, Hong Kong, China, 5–7 December 2018. [Google Scholar]
- Silva, A.; Macedo, L.; Monteiro, R.; Castro, J.M. Earthquake-induced loss assessment of steel buildings designed to Eurocode 8. Eng. Struct. 2020, 208, 110244. [Google Scholar] [CrossRef]
- Silva, A.; Castro, J.M.; Monteiro, R. A rational approach to the conversion of FEMA P-58 seismic repair costs to Europe. Earthq. Spectra 2020, 36, 1607–1618. [Google Scholar] [CrossRef]
- Silva, A.; Castro, J.M.; Monteiro, R. Brace-to-frame connection modelling effects on seismic loss assessment of steel concentrically-braced frames. J. Constr. Steel Res. 2020, 172, 106230. [Google Scholar] [CrossRef]
- Di Sarno, L.; Elnashai, A.S.; Nethercot, D.A. Seismic response of stainless steel braced frames. In Proceedings of the International Colloquium on Stability and Ductility of Steel Structures, SDSS 2006, Lisbon, Portugal, 6–8 September 2006. [Google Scholar]
- Di Sarno, L.; Elnashai, A.S. Seismic performance of retrofitted steel moment resisting frames. High Performance. Struct. Mater. 2004, 7, 643–652. [Google Scholar]
- Di Sarno, L.; Elnashai, A.S.; Nethercot, D.A. Seismic performance assessment of stainless steel frames. J. Constr. Steel Res. 2003, 59, 1289–1319. [Google Scholar] [CrossRef]
- Di Sarno, L.; Elnashai, A.S.; Nethercot, D.A. Seismic retrofitting of framed structures with stainless steel. J. Constr. Steel Res. 2006, 62, 93–104. [Google Scholar] [CrossRef]
- Di Sarno, L. Bracing systems for seismic retrofitting of steel frames. In Proceedings of the 5th International Conference on Behaviour of Steel Structures in Seismic Areas—Stessa, Yokohama, Japan, 17 July 2006; pp. 821–826. [Google Scholar]
- Di Sarno, L.; Elnashai, A.S.; Nethercot, D.A. Seismic response of stainless steel braced frames. J. Constr. Steel Res. 2008, 64, 914–925. [Google Scholar] [CrossRef]
- Di Sarno, L.; Elnashai, A.S. Bracing systems for seismic retrofitting of steel frames. J. Constr. Steel Res. 2009, 65, 452–465. [Google Scholar] [CrossRef]
- Di Sarno, L. Ductile response of composite steel and concrete frames. In Proceedings of the SDSS’ Rio 2010: International Colloquium Stability and Ductility of Steel Structures, Janeiro, Brazil, 8–10 September 2010; Volume 2, pp. 831–838. [Google Scholar]
- Di Sarno, L.; Paolacci, F.; Sextos, A.G. Seismic performance assessment of existing steel buildings: A case study. Key Eng. Mater. 2018, 763, 1067–1076. [Google Scholar] [CrossRef]
- Di Sarno, L.; Wu, J.-R. Seismic assessment of existing steel frames with masonry infills. J. Constr. Steel Res. 2020, 169, 106040. [Google Scholar] [CrossRef]
- Pnevmatikos, N.G.; Papagiannopoulos, G.A.; Papavasileiou, G.S. Fragility curves for mixed concrete/steel frames subjected to seismic excitation. Soil Dyn. Earthq. Eng. 2019, 116, 709–713. [Google Scholar] [CrossRef]
- Papavasileiou, G.S.; Pnevmatikos, N.G. The seismic performance of steel buildings retrofitted with steel cables against progressive collapse. Compdyn Proc. 2019, 2, 2167–2173. [Google Scholar]
- Papavasileiou, G.S.; Charmpis, D.C. Earthquake-resistant buildings with steel or composite columns: Comparative assessment using structural optimization. J. Build. Eng. 2020, 27, 100988. [Google Scholar] [CrossRef]
- Papavasileiou, G.S.; Charmpis, D.C.; Lagaros, N.D. Optimized seismic retrofit of steel-concrete composite buildings. Eng. Struct. 2020, 213, 110573. [Google Scholar] [CrossRef]
- Balazadeh-Minouei, Y.; Tremblay, R.; Koboevic, S. Seismic Retrofit of an Existing 10-Story Chevron-Braced Steel-Frame. J. Struct. Eng. 2018, 144, 04018180. [Google Scholar] [CrossRef]
- Balazadeh-Minouei, Y.; Koboevic, S.; Tremblay, R. Seismic Assessment of Existing Steel Chevron Braced Frames. J. Struct. Eng. 2018, 144, 040180461. [Google Scholar] [CrossRef]
- Balazadeh-Minouei, Y.; Koboevic, S.; Tremblay, R. Seismic evaluation of a steel braced frame using NBCC and ASCE 41. J. Constr. Steel Res. 2017, 135, 110–124. [Google Scholar] [CrossRef]
- Toutant, G.; Minouei, Y.B.; Imanpour, A.; Koboevic, S.; Tremblay, R. Stability of steel columns in steel concentrically braced frames subjected to seismic loading. In Structures Congress 2017: Buildings and Special Structures—Selected Papers from the Structures Congress; ASCE: Denver, CO, USA, 2017; pp. 143–154. [Google Scholar]
- Imanpour, A.; Tremblay, R.; Davaran, A.; Stoakes, C.; Fahnestock, L.A. Seismic Performance Assessment of Multitiered Steel Concentrically Braced Frames Designed in Accordance with the 2010 AISC Seismic Provisions. J. Struct. Eng. 2016, 142, 04016135. [Google Scholar] [CrossRef]
- Imanpour, A.; Auger, K.; Tremblay, R. Seismic design and performance of multi-tiered steel braced frames including the contribution from gravity columns under in-plane seismic demand. Adv. Eng. Softw. 2016, 101, 106–122. [Google Scholar] [CrossRef]
- Imanpour, A.; Tremblay, R. Seismic design and response of steel multi-tiered concentrically braced frames in Canada. Can. J. Civ. Eng. 2016, 43, 908–919. [Google Scholar] [CrossRef]
- Tirca, L.; Chen, L.; Tremblay, R. Assessing collapse safety of CBF buildings subjected to crustal and subduction earthquakes. J. Constr. Steel Res. 2015, 115, 4287. [Google Scholar] [CrossRef]
- Davaran, A.; Gélinas, A.; Tremblay, R. Inelastic Buckling Analysis of Steel X-Bracing with Bolted Single Shear Lap Connections. J. Struct. Eng. 2015, 141, 04014204. [Google Scholar] [CrossRef]
- Sizemore, J.; Davaran, A.; Fahnestock, L.; Tremblay, R.; Hines, E. Seismic behavior of low-ductility concentrically-braced frames. In Proceedings of the 2014 Structures Congress, Boston, MA, USA, 3–5 April 2014; pp. 2369–2380. [Google Scholar]
- Davaran, A.; Tremblay, R.; Beland, T.; Fahnestock, L.A.; Hines, E.M. Experimental behavior of low-ductility brace connection limit states. In Proceedings of the 2014 Structures Congress, Boston, MA, USA, 3–5 April 2014; pp. 2429–2441. [Google Scholar]
- Gélinas, A.; Tremblay, R.; Davaran, A. Buckling response of bolted mid-connections in steel X-bracing. In Proceedings of the Annual Conference—Canadian Society for Civil Engineering, Montreal, QC, Canada, 29 May–1 June 2013; Volume 3, pp. 2448–2457. [Google Scholar]
- Tremblay, R.; Davaran, A.; Gélinas, A. Stability of x-bracing systems with traditional bolted connections. Structures congress 2013: Bridging your passion with your profession. In Proceedings of the 2013 Structures Congress, Pittsburgh, PA, USA, 2–4 May 2013; pp. 2662–2674. [Google Scholar]
- Gélinas, A.; Tremblay, R.; Davaran, A. Seismic behaviour of steel HSS X-bracing of the conventional construction category. In Proceedings of the 2012 Structures Congress, Chicago, IL, USA, 29–31 March 2012; pp. 1649–1660. [Google Scholar]
- Agüero, A.; Izvemari, C.; Tremblay, R. Modeling of the seismic response of concentrically braced steel frames using the Opensees analysis environment. Adv. Steel Constr. 2006, 2, 242–274. [Google Scholar]
- Lacerte, M.; Tremblay, R. Making use of brace overstrength to improve the seismic response of multistorey split-X concentrically braced steel frames. Can. J. Civ. Eng. 2006, 33, 1005–1021. [Google Scholar] [CrossRef]
- Tremblay, R.; Poncet, L. Seismic performance of concentrically braced steel frames in multistory buildings with mass irregularity. J. Struct. Eng. 2005, 131, 1363–1375. [Google Scholar] [CrossRef]
- Tremblay, R. Fundamental periods of vibration of braced steel frames for seismic design. Earthq. Spectra 2005, 21, 833–860. [Google Scholar] [CrossRef]
- Tremblay, R.; Poncet, L. Improving the seismic stability of concentrically braced steel frames. In Proceedings of the Annual Stability Conference, Structural Stability Research Council, Long Beach, CA, USA, 24–27 March 2004; pp. 19–38. [Google Scholar]
- Tremblay, R.; Archambault, M.-H.; Filiatrault, A. Seismic response of concentrically braced steel frames made with rectangular hollow bracing members. J. Struct. Eng. 2003, 129, 1626–1636. [Google Scholar] [CrossRef]
- Tremblay, R. Achieving a stable inelastic seismic response for multi-story concentrically braced steel frames. Eng. J. 2003, 40, 111–129. [Google Scholar]
- Tremblay, R. Inelastic seismic response of steel bracing members. J. Constr. Steel Res. 2002, 58, 665–701. [Google Scholar] [CrossRef]
- Tremblay, R. Seismic behavior and design of concentrically braced steel frames. Eng. J. 2001, 38, 148–166. [Google Scholar]
- Tremblay, R.; Robert, N. Seismic performance of low- and medium-rise chevron braced steel frames. Can. J. Civ. Eng. 2001, 28, 699–714. [Google Scholar] [CrossRef]
- Filiatrault, A.; Tremblay, R. Design of Tension-Only Concentrically Braced Steel Frames for seismic induced impact loading. Eng. Struct. 1998, 20, 1087–1096. [Google Scholar] [CrossRef]
- Tremblay, R.; Filiatrault, A. Seismic impact loading in inelastic tension-only concentrically braced steel frames: Myth or reality? Earthq. Eng Struct. Dyn. 1996, 25, 1373–1389. [Google Scholar] [CrossRef]
- Tirca, L.; Serban, O.; Lin, L.; Wang, M.; Lin, N. Improving the Seismic Resilience of Existing Braced-Frame Office Buildings. J. Struct. Eng. 2016, 142, 4015003. [Google Scholar] [CrossRef]
- Tirca, L.; Chen, L. Numerical simulation of inelastic cyclic response of HSS braces upon fracture. Adv. Steel Constr. 2014, 10, 442–462. [Google Scholar]
- Tirca, L.; Chen, L. The influence of lateral load patterns on the seismic design of zipper braced frames. Eng. Struct. 2012, 40, 536–555. [Google Scholar] [CrossRef]
- Sizemore, J.G.; Fahnestock, L.A.; Hines, E.M. Seismic Performance Assessment of Low-Ductility Concentrically Braced Frames. J. Struct. Eng. 2019, 145, 04019016. [Google Scholar] [CrossRef]
- Grabner, K.D.M.; Fahnestock, L.A. Seismic stability of special concentrically braced frames in a moderate seismic region. In Proceedings of the Structural Stability Research Council Annual Stability Conference, Louis, MI, USA, 2–5 April 2019; Volume 1, pp. 307–320. [Google Scholar]
- Sizemore, J.G.; Fahnestock, L.A.; Hines, E.M.; Bradley, C.R. Parametric Study of Low-Ductility Concentrically Braced Frames under Cyclic Static Loading. J. Struct. Eng. 2017, 143, 04017032. [Google Scholar] [CrossRef]
- Bradley, C.R.; Fahnestock, L.A.; Hines, E.M.; Sizemore, J.G. Full-Scale Cyclic Testing of Low-Ductility Concentrically Braced Frames. J. Struct. Eng. 2017, 143, 04017029. [Google Scholar] [CrossRef]
- Stoakes, C.D.; Fahnestock, L.A. Cyclic flexural testing of concentrically braced frame beam-column connections. J. Struct. Eng. 2011, 137, 739–747. [Google Scholar] [CrossRef]
- Landolfo, R.; Mazzolani, F.M.M.; Dubina, D.; da Silva, L.S.; D’Aniello, M. Design of Steel Structures for Buildings in Seismic Areas: Eurocode 8: Design of Structures for Earthquake Resistance. Part 1-1—General RULES, Seismic Actions and Rules for Buildings, 1st ed.; Wilhelm Ernst & Sohn Verlag für Architektur und Technische Wissenschaften GmbH & Co. KG: Berlin, Germany; WILEY: Hoboken, NJ, USA, 2017; ISBN 978-3-433-03010-3. [Google Scholar]
- CEN. CEN prEN 1998-1-2: Draft; 2019. In Eurocode 8: Design of Structures for Earthquake Resistance—Part 1-2: Rules for New Buildings; CEN: Bruxelles, Belgium; The European Union Per Regulation: Brussel, Belgium, 2019. [Google Scholar]
- CEN. EN 1993:1-1, Eurocode 3: Design of Steel Structures—Part 1-1: General Rules and Rules for Buildings; CEN: Bruxelles, Belgium; The European Union Per Regulation: Brussel, Belgium, 2005. [Google Scholar]
- Latour, M.; Rizzano, G. Design of X-shaped double split tee joints accounting for moment-shear interaction. J. Constr. Steel Res. 2015, 104, 115–126. [Google Scholar] [CrossRef]
- Francavilla, A.B.; Latour, M.; Piluso, V.; Rizzano, G. Design of full-strength full-ductility extended end-plate beam-to-column joints. J. Constr. Steel Res. 2018, 148, 77–96. [Google Scholar] [CrossRef]
- Francavilla, A.B.; Latour, M.; Piluso, V.; Rizzano, G. Design criteria for beam-to-column connections equipped with friction devices. J. Constr. Steel Res. 2020, 172, 106240. [Google Scholar] [CrossRef]
- Ferrante Cavallaro, G.; Francavilla, A.B.; Latour, M.; Piluso, V.; Rizzano, G. Cyclic response of low yielding connections using different friction materials. Soil Dyn. Earthq. Eng. 2018, 114, 404–423. [Google Scholar] [CrossRef]
- Lemos, A.; da Silva, L.S.; Latour, M.; Rizzano, G. Numerical modelling of innovative DST steel joint under cyclic loading. Arch. Civ. Mech. Eng. 2018, 18, 687–701. [Google Scholar] [CrossRef]
- Chisari, C.; Francavilla, A.B.; Latour, M.; Piluso, V.; Rizzano, G.; Amadio, C. Critical issues in parameter calibration of cyclic models for steel members. Eng. Struct. 2017, 132, 123–138. [Google Scholar] [CrossRef]
- Latour, M.; Rizzano, G. Mechanical modelling of exposed column base plate joints under cyclic loads. J. Constr. Steel Res. 2019, 162, 105726. [Google Scholar] [CrossRef]
- Iannone, F.; Latour, M.; Piluso, V.; Rizzano, G. Experimental analysis of bolted steel beam-to-column connections: Component identification. J. Earthq. Eng. 2011, 15, 214–244. [Google Scholar] [CrossRef]
- Latour, M.; Rizzano, G. Experimental behavior and mechanical modeling of dissipative T-stub connections. J. Struct. Eng. 2012, 138, 170–182. [Google Scholar] [CrossRef]
- Francavilla, A.B.; Latour, M.; Piluso, V.; Rizzano, G.; Jaspart, J.P.; Demonceau, J.F. On the Robustness of Earthquake-Resistant Moment-Resistant Frames: Influence of Innovative Beam-to-Column Joints. Open Constr. Build. Technol. J. 2018, 12, 101–111. [Google Scholar] [CrossRef]
- Di Benedetto, S.; Latour, M.; Rizzano, G. Stiffness prediction of connections between CHS tubes and externally welded I-beams: Fe analyses and analytical study. Materials 2020, 13, 3030. [Google Scholar] [CrossRef]
- Di Benedetto, S.; Latour, M.; Rizzano, G. Chord failure resistance of 3D cut welded connections with CHS columns and through I-BEAMS. Thin Walled Struct. 2020, 154, 106821. [Google Scholar] [CrossRef]
- Di Benedetto, S.; Latour, M.; Rizzano, G. Assessment of the stiffness of 3D cut welded connections with CHS columns and through I-BEAMS. Structures 2020, 27, 247–258. [Google Scholar] [CrossRef]
- Poursadrollah, A.; D’Aniello, M.; Landolfo, R.; De Martino, A. Preliminary study on the seismic performance of hybrid steel structures with truss lightweight girders and plug-and-play connections. Ing. Sismica Int. J. Earthq. Eng. 2020, 37, 103–113. [Google Scholar]
- Santos, A.F.; Santiago, A.; Latour, M.; Rizzano, G.; da Silva, L.S. Response of friction joints under different velocity rates. J. Constr. Steel Res. 2020, 168, 106004. [Google Scholar] [CrossRef]
- Di Benedetto, S.; Francavilla, A.B.; Latour, M.; Ferrante Cavallaro, G.; Piluso, V.; Rizzano, G. Pseudo-dynamic testing of a full-scale two-storey steel building with RBS connections. Eng. Struct. 2020, 212, 110494. [Google Scholar] [CrossRef]
- Di Lorenzo, G.; Formisano, A.; Landolfo, R.; Mazzolani, F.M.; Terracciano, G. On the use of cold-formed thin walled members for vertical addition of existing masonry buildings. In Proceedings of the SDSS’ Rio 2010: International Colloquium Stability and Ductility of Steel Structures, Janeiro, Brazil, 8–10 September 2010; Volume 2, pp. 945–952. [Google Scholar]
- Di Lorenzo, G.; Formisano, A.; Landolfo, R. On the origin of I beams and quick analysis on the structural efficiency of hot-rolled steel members. Open Civ. Eng. J. 2017, M3, 332–344. [Google Scholar] [CrossRef]
- Formisano, A.; Di Lorenzo, G.; Iannuzzi, I.; Landolfo, R. Seismic vulnerability and fragility of existing Italian industrial steel buildings. Open Civ. Eng. J. 2017, 11, 1122–1137. [Google Scholar] [CrossRef]
- Rizzo, F.; Di Lorenzo, G.; Formisano, A.; Landolfo, R. Time-Dependent Corrosion Wastage Model for Wrought Iron Structures. J. Mater. Civ. 2019, 31, 4019165. [Google Scholar] [CrossRef]
- Di Lorenzo, G.; Babilio, E.; Formisano, A.; Landolfo, R. Innovative steel 3D trusses for preservating archaeological sites: Design and preliminary results. J. Constr. Steel Res. 2019, 154, 250–326. [Google Scholar] [CrossRef]
- Tartaglia, R.; D’Aniello, M. Nonlinear Performance of Extended Stiffened End Plate Bolted Beam-to-column Joints Subjected to Column Removal. Open Civ. Eng. J. 2017, 11, 369–383. [Google Scholar] [CrossRef]
- Tartaglia, R.; D’Aniello, M.; De Martino, A. Ultimate performance of external end-plate bolted joints under column loss scenario accounting for the influence of the transverse beam. Open Constr. Build. Technol. J. 2017, 12, 132–139. [Google Scholar] [CrossRef]
- Tartaglia, R.; D’Aniello, M.; Rassati, G.A. Proposal of AISC-compliant seismic design criteria for ductile partially-restrained end-plate bolted joints. J. Constr. Steel Res. 2019, 159, 364–383. [Google Scholar] [CrossRef]
- Tartaglia, R.; D’Aniello, M.; Zimbru, M. Experimental and numerical study on the T-Stub behaviour with preloaded bolts under large deformations. Structures 2020, 27, 2137–2155. [Google Scholar] [CrossRef]
- D’Aniello, M.; Tartaglia, R.; Cassiano, D. Experimental investigation of the inelastic tensile behaviour of non-preloadable grade 8.8 bolts. Ing. Sismica, Int. J. Earthq. Eng. 2020, 2, 92–110. [Google Scholar]
- Tartaglia, R.; D’Aniello, M.; Landolfo, R.; Rassati, G.A.; Swanson, J. Finite element analyses on seismic response of partial strength extended stiffened joints. COMPDYN 2017. In Proceedings of the 6th International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Rhodes Island, Greece, 15–17 June 2017; Volume 2, pp. 4952–4964. [Google Scholar]
- Tartaglia, R.; D’Aniello, M. Influence of transverse beams on the ultimate behaviour of seismic resistant partial strength beam-to-column joints. Ing. Sismica Int. J. Earthq. Eng. 2020, 3, 50–66. [Google Scholar]
- Tartaglia, R.; D’Aniello, M.; Rassati, G.A.; Swanson, J.A.; Landolfo, R. Full strength extended stiffened end-plate joints: AISC vs recent European design criteria. Eng. Struct. 2018, 159, 155–171. [Google Scholar] [CrossRef]
- Tartaglia, R.; D’Aniello, M.; Landolfo, R. The influence of rib stiffeners on the response of extended end-plate joints. J. Constr. Steel Res. 2018, 148, 669–690. [Google Scholar] [CrossRef]
- Tartaglia, R.; D’Aniello, M.; Rassati, G.A.; Swanson, J.; Landolfo, R. Influence of composite slab on the nonlinear response of extended end-plate beam-to-column joints. Key Eng. Mater. 2017, 763, 818–825. [Google Scholar] [CrossRef]
- Tartaglia, R.; D’Aniello, M.; Zimbru, M.; Landolfo, R. Finite element simulations on the ultimate response of extended stiffened end-plate joints. Steel Compos Struct. 2018, 27, 727–745. [Google Scholar]
- Cassiano, D.; D’Aniello, M.; Rebelo, C. Seismic behaviour of gravity load designed flush end-plate joints. Steel Compos. Struct. 2018, 26, 621–634. [Google Scholar] [CrossRef]
- Cassiano, D.; D’Aniello, M.; Rebelo, C. Parametric finite element analyses on flush end-plate joints under column removal. J. Constr. Steel Res. 2017, 137, 77–92. [Google Scholar] [CrossRef]
- D’Aniello, M.; Güneyisi, E.M.; Landolfo, R.; Mermerdaş, K. Analytical prediction of available rotation capacity of cold-formed rectangular and square hollow section beams. Thin Walled Struct. 2014, 77, 141–152. [Google Scholar] [CrossRef]
- Güneyisi, E.M.; D’Aniello, M.; Landolfo, R.; Mermerdaş, K. Prediction of the flexural overstrength factor for steel beams using artificial neural network. Steel Compos Struct. 2014, 17, 215–236. [Google Scholar] [CrossRef]
- D’Aniello, M.; Güneyisi, E.M.; Landolfo, R.; Mermerdaş, K. Predictive models of the flexural overstrength factor for steel thin-walled circular hollow section beams. Thin Walled Struct. 2015, 94, 67–78. [Google Scholar] [CrossRef]
- Ascione, L.; Berardi, V.P.; Giordano, A.; Spadea, S. Macro-scale analysis of local and global buckling behavior of T and C composite sections. Mech. Res. Commun. 2014, 58, 105–111. [Google Scholar] [CrossRef]
- Razaqpur, A.G.; Ascione, F.; Lamberti, M.; Spadea, S.; Malagic, M. GFRP hollow column to built-up beam adhesive connection: Mechanical behaviour under quasi-static, cyclic and fatigue loading. Compos. Struct. 2019, 224, 111069. [Google Scholar] [CrossRef]
- Ascione, F.; Lamberti, M.; Razaqpur, A.G.; Spadea, S.; Malagic, M. Pseudo-ductile failure of adhesively joined GFRP beam-column connections: An experimental and numerical investigation. Compos. Struct. 2018, 200, 864–873. [Google Scholar] [CrossRef]
- Ascione, L.; Berardi, V.P.; Giordano, A.; Spadea, S. Buckling failure modes of FRP thin-walled beams. Compos. Part B Eng. 2013, 47, 357–364. [Google Scholar] [CrossRef]
- Ascione, L.; Berardi, V.P.; Giordano, A.; Spadea, S. Local buckling behavior of FRP thin-walled beams: A mechanical model. Compos. Struct. 2013, 98, 111–120. [Google Scholar] [CrossRef]
- Ascione, L.; Berardi, V.P.; Giordano, A.; Spadea, S. Pre-buckling imperfection sensitivity of pultruded FRP profiles. Compos. Part B Eng. 2015, 72, 206–212. [Google Scholar] [CrossRef]
- Ascione, L.; Giordano, A.; Spadea, S. Lateral buckling of pultruded FRP beams. Compos. Part B Eng. 2011, 42, 819–824. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).