Mathematical Modeling of Mixed Convection Boundary Layer Flows over a Stretching Sheet with Viscous Dissipation in Presence of Suction and Injection

Abstract

The variational principle, developed by Gyarmati, embodying the principles of thermodynamics of irreversible processes is employed to study the mixed convection flows near the stagnation point of an incompressible viscous fluid with suction, injection and viscous dissipation effects towards a vertical stretching sheet. The velocity and temperature of the stretching sheet are considered to vary linearly proportional to the distance from the stagnation point. In this analysis, two equal and opposite forces are applied on the stretching sheet by keeping the origin fixed in a viscous fluid with constant free-stream temperature. The velocity and temperature distributions are assumed as simple polynomial functions and then the variational principle has been formulated. The corresponding Euler–Lagrange equations of the variational principle have been transformed into coupled polynomial equations in terms of hydro-dynamical and thermal boundary layer thicknesses. These equations are solvable for any combinations of Prandtl number, suction and injection parameter, Eckert number and buoyancy parameter. The obtained results are compared with known numerical results for assisting and opposing flows, and the comparison reveals that the accuracy is quite acceptable and found to be in good agreement.

1. Introduction

The objective of the present study is to apply recent developments in thermodynamics of irreversible processes in order to obtain a rapid analytical solution to mixed convection boundary layer flows with suction, injection (blowing) and viscous dissipation over a vertical stretching sheet near the stagnation point. The problem of viscous dissipation in the fluid flow has many practical applications, such as oil product transportation through ducts and polymer processing. The physical significance of the boundary layer flow with suction and injection plays a vital role in numerous engineering applications, especially in the fields of mechanical, chemical and aerospace engineering.

The effect of viscous dissipation occurs in strong gravitational fields and also where the scale of process is very high. The amount of heat due to viscous dissipation in the energy equation is very small and it can be ignored. However, when the gravitational force is very large, the viscous dissipative effects cannot be ignored. The viscous dissipation effect plays an important role in mixed convection flows in various devices due to large deceleration and also in strong gravitational fields. The effect of suction consists in the removal of decelerated fluid particles from the interior of the boundary layer before they are given a chance to cause separation. By applying suction, greater pressure increases on the upper side of the aerofoil are obtained at large angles of incidence, and consequently, much larger maximum lift values, and it is also applied to reduce the drag. Injection is an another method to prevent separation by imparting additional energy to the fluid particles which are retarded in the boundary layer by injecting fluid from the interior region of the boundary layer with the help of a special blower.

The mixed convection boundary layer flows and heat transfer of a viscous and incompressible fluid over stretching surfaces have many applications in engineering and have attracted many researchers in recent times. The study of mixed convection fluid flow over a moving plate, and the numerical simulation of thermal transport over moving flat sheets in the field of material process, were discussed by Karwe and Jaluria [1,2]. Sakiadis [3,4] was the first who initiated the study of boundary layer flow and heat transfer over a stretching sheet. Since then, many researchers have analyzed various significant properties of fluid flows and heat transfer under several physical conditions over a stretching sheet. A combined analytical experimental study of the flow and temperature fields in the boundary layer on a continuous moving surface has been investigated by Tsou et al. [5]. Later, in 1970, Crane [6] extended this concept for the boundary layer flow, analyzed the flow pattern over a linear stretching surface and similarity solution was given for the steady two-dimensional incompressible flow. Brady and Acrivos [7] have studied the properties of flow and given similarity solutions for the steady flow inside a stretching channel and a stretching cylinder. On the other hand, Chiam [8] has studied and given analytical and numerical solutions for steady laminar two-dimensional boundary layer stagnation flow of an incompressible viscous fluid over a stretching plate with variable thermal conductivity. The effects of buoyancy forces by considering the boundary layer flow over a vertical stretching sheet within a quiescent viscous and incompressible fluid have been analyzed by Chamkha [9]. Meanwhile, Mahapatra and Gupta [10,11] have discussed heat transfer in a stagnation flow of a viscous and visco-elastic fluids over stretching sheets and obtained an exact similarity solution for the corresponding Navier–Stokes equations. At the same time, Nazar et al. [12] studied in detail and gave solutiosn for unsteady boundary layer flow of a stretching flat deformable sheet near the stagnation point. Ishak et al. [13] analyzed and discussed the features of flow and characteristics of heat transfer of a steady two dimensional stagnation flow over a stretching vertical sheet and provided numerical solutions for various non-dimensional parameters. Again, Ishak et al. [14] studied and analyzed the flow and heat transfer over a vertical stretching sheet and obtained dual solutions for opposing flow and unique solution for assisting flow. A non-similar solution to a mixed convection flow over a vertical power-law stretching sheet was provided by Patil et al. [15]. Recently, Zaimi and Ishak [16] numerically investigated and presented solutions for steady, stagnation flow over a vertical stretching sheet with slip effects.

All these research works dealt with the investigations that are restricted only on boundary layer flows and heat transfer over various stretching surfaces. Relatively speaking, to our knowledge, less studies have been carried out to analyze the properties of suction, injection and viscous dissipation when the fluid flow passes towards a stretching sheet. This motivates the authors to study the effects of suction, injection and viscous dissipation for the flow and heat transfer in mixed convection towards a stretching sheet.

As mentioned in the above published research papers, Ishak et al. [13] have considered the problem of steady mixed convection flow near the stagnation point of an incompressible viscous fluid over a vertical stretching sheet. Motivated by the applications and importance of this problem, the objective of the present study is to extend the work of Ishak et al. [13] by introducing the effects of suction, injection and viscous dissipation in mixed convection flows towards a stretching sheet near the stagnation point, additionally in the energy equation and in the boundary conditions. Indeed, in the work of [13], the system of governing partial differential equations are transformed in to ordinary differential equations subject to the boundary conditions and these equations have been solved numerically by using the Keller-box method, and solutions have been found for various non-dimensional parameters.

Now, the present analysis is emphasized to obtain an analytical solution with high order of accuracy for mixed convection flows by using the genuine variational principle developed by Gyarmati, based on the principles of non-equilibrium thermodynamics. Using Gyarmati’s variational principle, the non linear governing conservation equations are transformed into coupled polynomial equations, which are solved for various non dimensional parameters. An extensive analysis has been carried out to study the effects of skin friction, heat transfer, velocity and thermal boundary layers for various suction, injection and viscous dissipation parameters. The present results are exhibited in the form of Tables and Graphs and the obtained results are compared with the results of Ishak et al. [13]. The comparison is well acceptable and is in excellent agreement.

2. Governing Equations of the System

Using Boussinesq approximations, and assuming that the fluid properties are constants, the governing conservation equations for the system of steady, two-dimensional, laminar, mixed convection [13] with viscous dissipation effects are

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\partial u}{\partial x}}+{\displaystyle \frac{\partial v}{\partial y}}& =& 0,\hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill u{\displaystyle \frac{\partial u}{\partial x}}+v{\displaystyle \frac{\partial u}{\partial y}}& =& U_{\infty }{\displaystyle \frac{d{U}_{\infty }}{dx}}+\nu {\displaystyle \frac{{\partial }^{2}u}{\partial y^2}}\pm g\beta (T-T_{\infty }),\hfill \end{array}$$

(2)

$$\begin{array}{ccc}\hfill u{\displaystyle \frac{\partial T}{\partial x}}+v{\displaystyle \frac{\partial T}{\partial y}}& =& \alpha {\displaystyle \frac{{\partial }^{2}T}{\partial y^2}}+{\displaystyle \frac{\nu }{C_p}}{\left({\displaystyle \frac{\partial u}{\partial y}}\right)}^2.\hfill \end{array}$$

(3)

In Equations (1)–(3), u and v represent velocities along the x and y directions, respectively. $“T”$ is the temperature of the fluid and $“g”$ is acceleration due to gravity. The notations $\alpha$, $\nu$, $C_p$ and $\beta$ are thermal diffusivity, kinematic viscosity, heat capacity and thermal expansivity, respectively. In Equation (2), the symbols $“+”$ and $“-”$ represent assisting and opposing buoyancy flows, respectively. Further, the fluid flow is confined to $y>0$. It is assumed that the boundary conditions of the conservation Equations (1)–(3) are

$$\begin{array}{c}\begin{array}{cc}\hfill v=V_0,u=U_0\left(x\right)=cx,T=T_0\left(x\right)=T_{\infty }+bx& \mathrm{at}y=0,\hfill \\ \hfill u=U_{\infty }\left(x\right)=ax,T=T_{\infty }& \mathrm{at}y\to \infty \hfill \end{array}\end{array}$$

(4)

where $V_0$ is the suction/injection velocity. Here $U_0$, $U_{\infty }$, $T_0$ and $T_{\infty }$ are the velocity of the fluid at the stretching sheet, free stream velocity, temperature of the stretching surface and free stream temperature of the stretching sheet, respectively. Additionally, from Equations (4), it is assumed that a, b and c are positive constants.

3. Formulation of the Governing Principle of Dissipative Processes (GPDP)

Gyarmati [17,18] formulated the Governing Principle of Dissipative Processes, which is given in the universal form

$$\delta \underset{V}{\int }\left[\sigma -(\mathsf{\Psi }+\mathsf{\Phi })\right]dV=0.$$

(5)

The variational principle (5) is represented in energy picture [18] as

$$\delta \underset{V}{\int }\left[T\sigma -({\mathsf{\Psi }}^{*}+{\mathsf{\Phi }}^{*})\right]dV=0,$$

(6)

where the integration is taken over the entire volume V of the thermodynamic system and $\delta$ is the symbol for variation.

The balance equations of the governing system in non equilibrium thermodynamics has significant role in the formulation of Gyarmati’s principle. Hence, the governing conservation Equations (1)–(3) are rewritten in the balance form as

$$\begin{array}{ccc}\hfill \nabla ·\mathbf{V}& =& 0,(\mathbf{V}=\mathbf{i}u+\mathbf{j}v)\hfill \end{array}$$

(7)

$$\begin{array}{ccc}\hfill \rho (\mathbf{V}·\nabla )\mathbf{V}+\nabla ·\mathsf{P}& =& \rho g\beta (T-T_{\infty })\mathbf{i},\hfill \end{array}$$

(8)

$$\begin{array}{ccc}\hfill \rho c_p(\mathbf{V}·\nabla )T+\nabla ·{\mathbf{J}}_{\mathbf{q}}& =& \mu {\left(u_y\right)}^2.\hfill \end{array}$$

(9)

In Equation (8), $\mathsf{P}$ represents the pressure tensor which is decomposed [18] as

$$\mathsf{P}=p\mathbf{1}+\stackrel{\circ }{{\mathsf{P}}^{vs}},$$

(10)

where p represents the hydrostatic pressure, $\mathbf{1}$ is the unit tensor and $\stackrel{\circ }{{\mathsf{P}}^{vs}}$ is the symmetric part of the pressure tensor whose trace is zero.

The energy dissipation [18] for the variational system is denoted by,

$$T\sigma =-J_q\frac{\partial lnT}{\partial y}-P_{12}\frac{\partial u}{\partial y},$$

(11)

where $J_q$ is the thermal flux and $P_{12}$ is the momentum flux, which are satisfied by the relations [19,20]

$$J_q=-L_{\lambda }\frac{\partial lnT}{\partial y}\mathrm{and}{P}_{12}=-L_s\frac{\partial u}{\partial y}.$$

(12)

Here, $L_{\lambda }=\lambda T$ and $L_s=\mu$. Using Equation (12), the dissipation potentials of the energy picture are expressed as [19,20]

$$\begin{array}{ccc}\hfill {\mathsf{\Psi }}^{*}& =& T\mathsf{\Psi }=\left(\frac{1}{2}\right)\left[L_{\lambda }{\left(\frac{\partial lnT}{\partial y}\right)}^2+L_s{\left(\frac{\partial u}{\partial y}\right)}^2\right],\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill {\mathsf{\Phi }}^{*}& =& T\mathsf{\Phi }=\left(\frac{1}{2}\right)\left[R_{\lambda }{J}_q^2+R_s{P}_{12}^2\right]\hfill \end{array}$$

(14)

where $L_{\lambda }=R_{\lambda }^{-1}$ and $L_s=R_s^{-1}$.

Using Equations (11)–(14), the energy picture of Gyarmati’s variational principle (6) assumes the form

$${\displaystyle \delta \underset{0}{\overset{L}{\int }}\underset{0}{\overset{\infty }{\int }}\left[-J_q\left(\frac{\partial lnT}{\partial y}\right)-P_{12}\left(\frac{\partial u}{\partial y}\right)-\frac{L_{\lambda }}{2}{\left(\frac{\partial lnT}{\partial y}\right)}^2-\frac{L_s}{2}{\left(\frac{\partial u}{\partial y}\right)}^2-\frac{R_{\lambda }}{2}{J}_q^2-\frac{R_s}{2}{P}_{12}^2\right]dydx=0,}$$

(15)

where $“L”$ is the length of the stretching sheet.

This principle was already applied to various dissipation systems and proved as the most general and exact variational principle [17] of thermodynamics of irreversible processes. Additionally, many such variational principles have been already proved as partial forms of Gyarmati’s principle. Recently, Chandrasekar and Kasiviswanathan [21,22,23] have employed this variational principle to study the important significant properties of fluid flows and heat transfer problems.

4. Method of Solution

A steady, two-dimensional, laminar, incompressible and viscous flow of a fluid near the stagnation point towards a vertical stretching sheet placed on $y=0$ of a Cartesian co-ordinate system with x-axis along the stretching sheet is considered. Two equal and opposite buoyancy forces are applied along the x direction by keeping the origin fixed in a viscous fluid with constant ambient temperature.

The physical model and the co-ordinate system are as shown in Figure 1.

In the present study, the velocity and temperature of the stretching sheet is linearly proportional to the distance x from the stagnation point. The stretching sheet is held fixed at a constant temperature $T_0\left(x\right)$ which is higher than the free stream temperature $T_{\infty }\left(x\right)$. Therefore it is assumed that ${\displaystyle \frac{T_0-T_{\infty }}{T_{\infty }}}<<1$.

The velocity and temperature distributions within their respective boundary regions are assumed by the following polynomial functions

$$\begin{array}{c}\begin{array}{cc}\hfill {\displaystyle \frac{u}{U_0}}& =1-{\displaystyle \frac{2\left(1-{\displaystyle \frac{a}{c}}\right)y}{d_1}}+{\displaystyle \frac{2\left(1-{\displaystyle \frac{a}{c}}\right)y^3}{d_1^3}}-{\displaystyle \frac{\left(1-{\displaystyle \frac{a}{c}}\right)y^4}{d_1^4}},\hfill \\ \hfill {\displaystyle \frac{T-T_{\infty }}{T_0-T_{\infty }}}& =1-{\displaystyle \frac{2}{d_2}}y+{\displaystyle \frac{2}{d_2^3}}{y}^3-{\displaystyle \frac{1}{d_2^4}}{y}^4.\hfill \end{array}\end{array}$$

(16)

The velocity and temperature distributions (16) satisfy the compatibility conditions (4). The quantities $d_1$ and $d_2$ are the hydro-dynamical and thermal boundary layer thicknesses, respectively. These unknown parameters are to be determined from the variational analysis. As defined in Equation (4), the constant $“a”$ is proportional to the free stream velocity and $“c”$ is proportional to the velocity of the fluid at the stretching sheet. In the present analysis, the constant term $a/c$ plays a predominant role in analyzing the flow characteristic features.

The expression for the transverse velocity component $“v”$ is obtained from the mass balance Equation (1) as

$$\begin{array}{ccc}\hfill v& =& V_0-cy-{\displaystyle \frac{a{y}^2}{d_1}}+{\displaystyle \frac{a{y}^4}{2d_1^3}}-{\displaystyle \frac{a{y}^5}{5d_1^4}}+{\displaystyle \frac{c{y}^2}{d_1}}-{\displaystyle \frac{c{y}^4}{2d_1^3}}+{\displaystyle \frac{c{y}^5}{5d_1^4}}+{\displaystyle \frac{a{d}_1^{\prime }x{y}^2}{d_1^2}}-{\displaystyle \frac{3a{d}_1^{\prime }x{y}^4}{2d_1^4}}\hfill \\ & & +{\displaystyle \frac{4a{d}_1^{\prime }x{y}^5}{5d_1^5}}-{\displaystyle \frac{c{d}_{1}x{y}^2}{d_1^2}}+{\displaystyle \frac{3c{d}_1^{\prime }x{y}^4}{2d_1^4}}-{\displaystyle \frac{4c{d}_1^{\prime }x{y}^5}{5d_1^5}}.\hfill \end{array}$$

(17)

In Equation (17), the prime denotes the derivative with respect to x. The velocity and temperature functions (16) together with boundary conditions (4) are used in the balance Equations (7)–(9) and by performing integration with respect to y with the help of smooth-fit conditions, the fluxes $P_{12}$ and $J_q$ are obtained. Using the velocity and temperature distributions and the expressions of momentum and energy fluxes, the variational principle (15) is formulated for the cases $Pr\le 1$ and $Pr\ge 1$.

After performing the integration with respect to y, the principle (15) is simplified in the forms

$$\begin{array}{c}\begin{array}{cc}\hfill \delta \underset{0}{\overset{L}{\int }}{L}_1[d_1,d_2,d_1^{\prime },d_2^{\prime }]dx& =0(Pr\le 1),\hfill \\ \hfill \delta \underset{0}{\overset{L}{\int }}{L}_2[d_1,d_2,d_1^{\prime },d_2^{\prime }]dx& =0(Pr\ge 1).\hfill \end{array}\end{array}$$

(18)

Here, $L_1$ and $L_2$ are the Lagrangian densities. The variational principles (18) are identical in the case of $d_1=d_2(Pr=1)$. The Euler–Lagrange equations corresponding to the principles (18) are

$$\begin{array}{c}\begin{array}{cc}\hfill {\displaystyle \frac{\partial L_{1,2}}{\partial d_1}}-{\displaystyle \frac{d}{dx}}\left({\displaystyle \frac{\partial L_{1,2}}{\partial d_1^{\prime }}}\right)& =0,\hfill \\ \hfill {\displaystyle \frac{\partial L_{1,2}}{\partial d_2}}-{\displaystyle \frac{d}{dx}}\left({\displaystyle \frac{\partial L_{1,2}}{\partial d_2^{\prime }}}\right)& =0(Pr\ge 1,Pr\le 1).\hfill \end{array}\end{array}$$

(19)

Equation (19) obtains ordinary differential equations of second order in $d_1$ and $d_2$ respectively. These equations can be solved numerically by introducing the dimensionless boundary layer thicknesses $d_1^{*}$ and $d_2^{*}$ by the relations

$$d_1=d_1^{*}\sqrt{{\displaystyle \frac{\nu x}{U_0}}}\mathrm{and}{d}_2=d_2^{*}\sqrt{{\displaystyle \frac{\nu x}{U_0}}}.$$

(20)

By virtue of these transformations, the Euler–Lagrange Equations (19) is reduced to simple polynomial equations,

$${\displaystyle \frac{\partial L_{1,2}}{\partial d_1^{*}}}=0,\mathrm{and}{\displaystyle \frac{\partial L_{1,2}}{\partial d_2^{*}}}=0(Pr\ge 1,Pr\le 1).$$

(21)

Equations (21) are obtained as coupled polynomial equations in $d_1^{*}$ and $d_2^{*}$. The coefficients of these three Equations (21) depend on the independent parameters $Pr$, $\lambda$, H and $Ec$, where $Pr$ is the Prandtl number, $\left(Pr={\displaystyle \frac{\nu }{\alpha }}\right)$, $\lambda$ is the buoyancy parameter $\left(\lambda ={\displaystyle \frac{Gr}{R_x^2}}\right)$, $R_x$ denotes the Reynolds number $\left(R_x={\displaystyle \frac{U_{0}x}{\nu }}\right)$, and $Gr$ denotes Grassoff number $\left(Gr={\displaystyle \frac{g\beta (T_0-T_{\infty })x^3}{{\nu }^2}}\right)$. Here, H is the non-dimensional suction/injection speed, which is given by $H=V_0\sqrt{{\displaystyle \frac{R_x}{U_0}}}$, $Ec$ denotes Eckert number $\left(Ec={\displaystyle \frac{U_0^2}{C_p(T_0-T_{\infty })}}\right)$. In this analysis, suction represents $H<0$ and injection represents $H>0$.

These equations can be easily solved for any given combinations of $Pr$, $\lambda$, H and $Ec$. Hence, by the Gyarmati’s variational principle, the non-linear partial differential equations governing the system are transformed into coupled polynomial equations. These equations are essential to analyze important characteristics of fluids which are of much useful for engineering and technological applications.

5. Analysis of Results and Discussions

For fluid flow and heat transfer problems, most of the engineering applications depend on skin friction (shear stress) and heat transfer (Nusselt number). These two significant characteristic properties are investigated with help of the expressions (22) and (23).

$${\tau }_w=H-{\displaystyle \frac{23}{63}}{d}_1^{*}+{\displaystyle \frac{337}{630}}{d}_1^{*}{\left(\frac{a}{c}\right)}^2-{\displaystyle \frac{107}{630}}{d}_1^{*}\left(\frac{a}{c}\right)-H\left(\frac{a}{c}\right)+d_1^{*}\lambda -{\displaystyle \frac{{d_1^{*}}^2\lambda }{d_2^{*}}}+{\displaystyle \frac{1}{2}}{\displaystyle \frac{{d_1^{*}}^4\lambda }{{d_2^{*}}^3}}-{\displaystyle \frac{1}{5}}{\displaystyle \frac{{d_1^{*}}^5\lambda }{{d_2^{*}}^4}},$$

(22)

$$\begin{array}{ccc}\hfill -N{u}_l& =& HPr-{\displaystyle \frac{3d_2^{*}Pr}{5}}+{\displaystyle \frac{4{d_2^{*}}^{2}Pr}{15d_1^{*}}}-{\displaystyle \frac{3{d_2^{*}}^{4}Pr}{70{d_1^{*}}^3}}+{\displaystyle \frac{{d_2^{*}}^{5}Pr}{90{d_1^{*}}^4}}-{\displaystyle \frac{8{d_2^{*}}^{3}EcPr}{{d_1^{*}}^4}}+{\displaystyle \frac{4{d_2^{*}}^{4}EcPr}{{d_1^{*}}^5}}+{\displaystyle \frac{36{d_2^{*}}^{5}EcPr}{5{d_1^{*}}^6}}\hfill \\ \hfill & & -{\displaystyle \frac{8{d_2^{*}}^{6}EcPr}{{d_1^{*}}^7}}+{\displaystyle \frac{16{d_2^{*}}^{7}EcPr}{7{d_1^{*}}^8}}-{\displaystyle \frac{4{d_2^{*}}^2\left({\displaystyle \frac{a}{c}}\right)Pr}{15d_1^{*}}}+{\displaystyle \frac{3{d_2^{*}}^4\left({\displaystyle \frac{a}{c}}\right)Pr}{70{d_1^{*}}^3}}-{\displaystyle \frac{{d_2^{*}}^5\left({\displaystyle \frac{a}{c}}\right)Pr}{90{d_1^{*}}^4}}+{\displaystyle \frac{4d_2^{*}EcPr}{{d_1^{*}}^2}}\hfill \\ & & -{\displaystyle \frac{8d_2^{*}Ec\left({\displaystyle \frac{a}{c}}\right)Pr}{{d_1^{*}}^2}}+{\displaystyle \frac{4d_2^{*}Ec{\left({\displaystyle \frac{a}{c}}\right)}^{2}Pr}{{d_1^{*}}^2}}+{\displaystyle \frac{16{d_2^{*}}^{3}Ec\left({\displaystyle \frac{a}{c}}\right)Pr}{{d_1^{*}}^4}}-{\displaystyle \frac{8{d_2^{*}}^{4}Ec\left({\displaystyle \frac{a}{c}}\right)Pr}{{d_1^{*}}^5}}\hfill \\ \hfill & & -{\displaystyle \frac{72{d_2^{*}}^{5}Ec\left({\displaystyle \frac{a}{c}}\right)Pr}{5{d_1^{*}}^6}}+{\displaystyle \frac{16{d_2^{*}}^{6}Ec\left({\displaystyle \frac{a}{c}}\right)Pr}{{d_1^{*}}^7}}-{\displaystyle \frac{32{d_2^{*}}^{7}Ec\left({\displaystyle \frac{a}{c}}\right)Pr}{7{d_1^{*}}^8}}-{\displaystyle \frac{8{d_2^{*}}^{3}Ec{\left({\displaystyle \frac{a}{c}}\right)}^{2}Pr}{{d_1^{*}}^4}}\hfill \\ \hfill & & +{\displaystyle \frac{4{d_2^{*}}^{4}Ec{\left({\displaystyle \frac{a}{c}}\right)}^{2}Pr}{{d_1^{*}}^5}}+{\displaystyle \frac{36{d_2^{*}}^{5}Ec{\left({\displaystyle \frac{a}{c}}\right)}^{2}Pr}{5{d_1^{*}}^6}}-{\displaystyle \frac{8{d_2^{*}}^{6}Ec{\left({\displaystyle \frac{a}{c}}\right)}^{2}Pr}{{d_1^{*}}^7}}+{\displaystyle \frac{16{d_2^{*}}^{7}Ec{\left({\displaystyle \frac{a}{c}}\right)}^{2}Pr}{7{d_1^{*}}^8}}.\hfill \end{array}$$

(23)

The energy Equation (3) has been solved for $d_1^{*}\le d_2^{*}(Pr\le 1)$ and $d_1^{*}\ge d_2^{*}(Pr\ge 1)$. These two independent computations provide solutions which match at $Pr=1$ where the regions of momentum and thermal boundary layers are equal and coincide with each other. Under this circumstance, it is worth mentioning that the analysis leads to results of reasonable accuracy. It is convention that when a mathematical technique is applied to a problem, the results obtained by the present technique are compared with the available known solution in order to establish the accuracy of the present results. Accordingly, the skin friction and heat transfer values are computed with Intel Core i3 processor with 4 GB RAM and the CPU time taken between 1 min 45 s and 2 min 45 s for different values of non dimensional parameters are noted and compared with the results of Nazar [12], Mahapatra and Gupta [10], Ishak [13] and Zaimi and Ishak [16] as tabulated in

Table 1. Comparison of skin friction values (${\tau }_w$) for various values of $a/c$ when $\lambda =0$ and $H=0$ with known results.

$\mathit{a}/\mathit{c}$	Mahapatra and Gupta [10]	Nazar [12]	Ishak [13]	Present Values
0.1	$-0.9694$	$-0.9694$	$-0.9694$	$-1.0020185155$
0.2	$-0.9181$	$-0.9181$	$-0.9181$	$-0.9415583926$
0.5	$-0.6673$	$-0.6673$	$-0.6673$	$-0.6750132565$
2.0	2.0175	2.0176	2.0175	2.0030860233
3.0	4.7293	4.7296	4.7294	4.6788471978

,

Table 2. Comparison of skin friction (${\tau }_w$) and heat transfer ($N{u}_l$) for assisting flow when $a/c=1$, $\lambda =1$, $Ec=0$ and $H=0$ for various $Pr$ with known results.

$\mathit{Pr}$	Skin Friction (${\mathit{\tau }}_{\mathit{w}}$)			Heat Transfer (${\mathit{Nu}}_{\mathit{l}}$)
	Ishak [13]	Zaimi and Ishak [16]	Present Values	Ishak [13]	Zaimi and Ishak [16]	Present Values
0.72	0.3645	0.36449	0.3603630329	1.0931	1.09310	1.1465484808
6.8	0.1804	0.18041	0.2034171744	3.2902	3.28957	3.2776601900
10		0.15563	0.1677420992		3.98240	3.9747468140
20	0.1175	0.11750	0.1186115759	5.6230	5.62013	5.6211408516
30		0.09889	0.0968459461		6.87771	6.8844634292
40	0.0873	0.08724	0.0838710496	7.9463	7.93830	7.9494936288
50		0.07903	0.0750165473		8.87292	8.8878040696
60	0.0729	0.07284	0.0684804252	9.7327	9.71801	9.7361015508
70		0.06794	0.0634005541		10.49524	10.5161915945
80	0.0640	0.06394	0.0593057879	11.2413	11.21874	11.2422817008
90		0.06059	0.0559140330		11.89831	11.9242404422
100	0.0578	0.05772	0.0530447092	12.5726	12.54109	12.5692530540

and

Table 3. Comparison of skin friction (${\tau }_w$) and heat transfer ($N{u}_l$) for opposing flow when $a/c=1$, $\lambda =1$, $Ec=0$ and $H=0$ for various $Pr$ with known results.

$\mathit{Pr}$	Skin Friction (${\mathit{\tau }}_{\mathit{w}}$)			Heat Transfer (${\mathit{Nu}}_{\mathit{l}}$)
	Ishak [13]	Zaimi and Ishak [16]	Present Values	Ishak [13]	Zaimi and Ishak [16]	Present Values
0.72	$-0.3852$	$-0.38518$	$-0.3603630329$	1.0293	1.02925	1.1465484808
6.8	$-0.1832$	$-0.18323$	$-0.2034171744$	3.2466	3.24608	3.2776601900
10		$-0.15747$	$-0.1677420992$		3.94370	3.9747468140
20	$-0.1183$	$-0.11831$	$-0.1186115759$	5.5923	5.58959	5.6211408516
30		$-0.09938$	$-0.0968459461$		6.85149	6.8844634292
40	$-0.0876$	$-0.08758$	$-0.0838710496$	7.9227	7.91489	7.9494936287
50		$-0.07929$	$-0.0750165473$		8.85153	8.8878040696
60	$-0.0731$	$-0.07304$	$-0.0684804252$	9.7126	9.69818	9.7361015508
70		$-0.06810$	$-0.0634005541$		10.47665	10.5161915945
80	$-0.0642$	$-0.06407$	$-0.0593057879$	11.2235	11.20117	11.2422817008
90		$-0.06070$	$-0.0559140330$		11.88161	11.9242404422
100	$-0.0579$	$-0.05782$	$-0.0530447092$	12.5564	12.52515	12.5692530540

.

Table 1 exhibits the skin friction (${\tau }_w$) for various values of $a/c$ when $\lambda =0$, $H=0$ and the present values of skin friction are compared with the results of Mahapatra and Gupta [10], Nazar [12] and Ishak [13]. From this table, it is evident that the comparison of the present results is in good agreement with those values and the accuracy is remarkable. It is also observed that the skin friction values increase with increasing $a/c$, in the absence of buoyancy, suction and injection parameters.

The skin friction(${\tau }_w$) and heat transfer ($N{u}_l$) for different values of $Pr$ when $a/c=1$, $\lambda =1$, $Ec=0$ and $H=0$ are presented for assisting and opposing flows in Table 2 and Table 3, respectively. The obtained results are compared with Ishak [13] and Zaimi and Ishak [16] for assisting and opposing flows. The comparison of present results with available existing results establishes that the accuracy is quite acceptable and is in excellent agreement. The error involved in this analysis with known existing results hardly exceeds five percent. From these two tables, it is found that the heat transfer values are always positive and also increase with the increase in Prandtl numbers for both assisting and opposing flows. This phenomenon is true because of the basic definition of Prandtl number, which is the ratio of kinematic viscosity and thermal diffusivity. However, with regard to skin friction values, it is noted that the skin friction values decrease with increasing Prandtl numbers, for assisting flow and skin friction values increase with increasing Prandtl numbers for opposing flow. The skin friction values for the buoyancy parameter $\lambda =1$ are significant for fluids with less Prandtl numbers because the viscosity is less than the fluids with high Prandtl number. Additionally, from Table 2 and Table 3, it can be observed that, for a given specific Prandtl number, the buoyancy assisting flow and opposing flow are opposite to each other, pertaining to the corresponding skin friction values. Furthermore, the values of heat transfer increase with increase in $Pr$. Thus, this piece of research work provides confidence and assures a guarantee that Gyarmati’s principle yields an analytical solution for the mixed convection flow with high order of accuracy based on macroscopic continuum physics.

The skin friction for various values of $a/c$, H and $Ec$, when $Pr=6.8$, are graphically presented in Figure 2a–e. From these figures, it can be easily understood that the buoyancy assisting flows increase the skin friction values while the buoyancy opposing flows decrease the skin friction values. This physical phenomenon occurs when there is a increase in the buoyancy force, the velocity of the fluid increases. Simultaneously, when the velocity of the fluid increases, the values of skin friction also increase. Further, for small suction/injection and viscous dissipation parameters, the skin friction values increase rapidly for assisting flows and it decreases for opposing flows. Therefore, the assisting and opposing flows are in the opposite directions for the small values of viscous dissipation, suction and injection. In the analysis of Ishak et al. [13], the computations have been carried out for $Pr=1$. To differentiate from Ishak et al. [13], the present analysis is performed for $Pr=6.8$ to discuss the significant properties of skin friction, heat transfer, velocity and thermal boundary layers. Hence, one could expect that the solutions of Equation (21) for all the non-dimensional parameters are also in the same order of accuracy.

Figure 2f depicts the skin friction for different values of Prandtl numbers when $a/c=1$, $H=0$ and $Ec=0$. This figure demonstrates that all the assisting and opposing flows intersect at the point $\lambda =0$, where the buoyancy force is zero. Here, one can also notice that, when the buoyancy force is zero, the value of skin friction remains zero. Additionally, for assisting flow, skin friction values decrease when Prandtl numbers increase for the buoyancy parameter. Furthermore, when Prandtl numbers increase, the viscosity also increases and simultaneously the flow speed of the fluid gets decreased. Under this circumstance, for assisting flow, it reduces the skin friction and, for the opposing flow, the trend is completely opposite during $Ec=0$ and $H=0$.

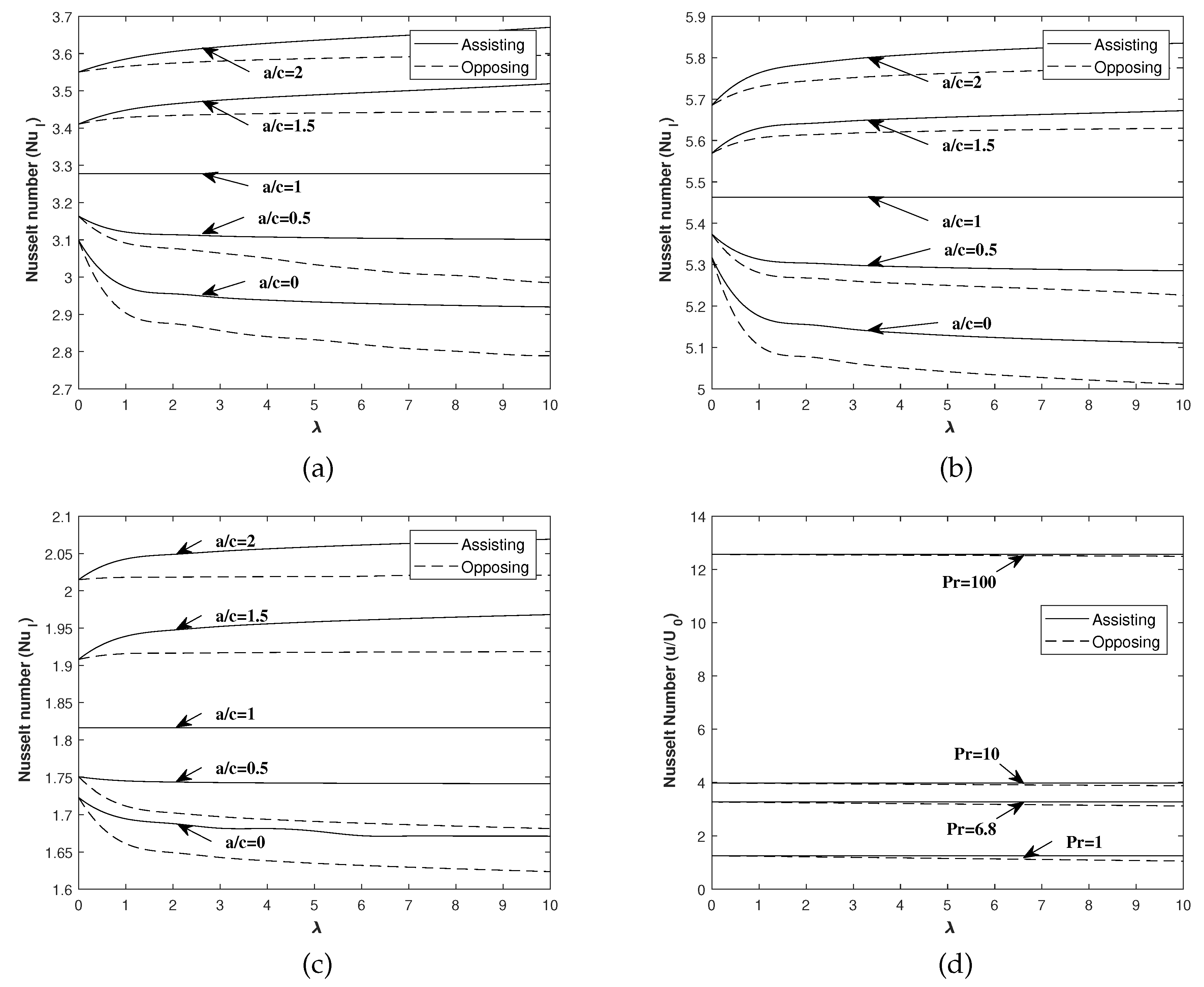
Figure 3a–c represent the values of heat transfer for various values of $a/c$ when $Pr=6.8$, $Ec=0$, $H=0$, $H=-0.5$ and $H=0.5$, respectively. Further, it is observed from these figures that, during suction/injection, the heat transfer values increase with the increase in $a/c$ for both assisting and opposing flows when the constant term $a/c>1$. When the term is $a/c=1$, the heat transfer remains stable and uniform for all the values of buoyancy parameter $\lambda$. When $a/c<1$, the heat transfer decreases with decreasing values of $a/c$ for both assisting and opposing flows.

From Figure 3d, it is found that, for a given Prandtl number, the heat transfer increases very slowly with the increasing value of buoyancy parameter $\lambda$ for the assisting and opposing flows. Additionally, it is interesting to note that, for each $Pr$, the corresponding assisting and opposing flows have very small difference in the flow pattern.

The velocity profiles for various values of $a/c$, $\lambda$, H and $Ec$ when $Pr=6.8$ are exhibited in Figure 4a–h. From Figure 4a–e, it is evident that, for small values of suction, injection and viscous dissipation, when the constant term $a/c>1$, the flow has a definite structure and the boundary layer thickness is decreasing with the increase in $a/c$. When the term $a/c<1$, the boundary layer flow has a contrary pattern and it becomes a reverse boundary layer. That means when $a/c<1$, the velocity of the fluid at the stretching sheet exceeds the free stream velocity at the edge of the boundary layer. In addition to the above facts, from Figure 4d, it is interesting to mention that, during suction, the buoyancy opposing flows dominate the assisting flows for all the values of $a/c$, except at $a/c=1$. This situation occurs as a special feature of the flow pattern in the velocity profile during the effect of suction. From Figure 4f–h, during the effects of suction/injection, it is inferred that, for assisting flows, the velocity increases suddenly from the value 1 at the beginning and it reaches a particular maximum value then it decreases gradually until the value becomes 1. The velocity profile attains its maximum value when the value of $\lambda$ is high. Hence, the large buoyancy parameter produces high buoyancy force which, in turn, produces large kinetic energy. For opposing flows, the opposite trend prevails irrespective of the buoyancy parameter $\lambda$.

Figure 5a–c represent the temperature profile for various values of $a/c$ in the boundary layer when $Pr=6.8$, $\lambda =1$, $Ec=0$, $H=0$, $H=-0.5$ and $H=0.5$ respectively. From these figures, it is demonstrated that, during suction and injection, the temperature of the fluid at a given point decreases from the value 1 as the distance from the stretching sheet increases for assisting and opposing flows until it reaches a positive value which is close to 0 for various values of $a/c$ when $Pr=6.8$, $\lambda =1$ and $Ec=0$. Further, from Figure 5b,c, one can notice that, during suction, the boundary layer thickness is very thin when compared with the thickness of the thermal boundary layer during injection. Hence, heat flows from the stretching sheet to free stream temperature for assisting and opposing flows during suction and injection.

6. Conclusions

This investigation presents an analytical solution to heat transfer in mixed convection boundary layer flows towards a stretching sheet near the stagnation point with the effects of suction, injection and viscous dissipation.

• The governing non linear partial differential equations are converted into coupled polynomial equations whose solutions are quite straight forward.
• The solutions have been computed for the non-dimensional skin friction, heat transfer, velocity and thermal boundary layers for various values of $Pr$, $\lambda$, H and $Ec$.
• The skin friction values increase with the increase in $a/c$ in the absence of buoyancy, suction and injection parameters.
• The heat transfer values increase with the increase in $Pr$ for both assisting and opposing flows.
• The skin friction values decrease with increasing $Pr$ for assisting flow and increase with the increase in $Pr$ for opposing flows during $a/c=1$, $\lambda =1$, $H=0$ and $Ec=0$.
• For small values of viscous dissipation, suction and injection, the buoyancy assisting flow increases the skin friction and opposing flow decreases the skin friction.
• During suction and injection, the heat transfer values increase with the increase in $a/c$ for both flows when $a/c>1$. When $a/c<1$, the heat transfer decreases with the decrease in $a/c$ for both flows.
• For small values of viscous dissipation, suction and injection, when $a/c>1$, the flow has a definite boundary layer structure and the flow has an inverted boundary layer when $a/c<1$.
• The advantage of the present variational principle is that the results have been arrived at directly without sacrificing the accuracy of the results.
• The comparison of the present solution with numerical solutions reveals that the accuracy of the present variational technique is acceptable for the applications of engineering and technology.
• The method of solution exhibited in this analysis has further advantage for obtaining analytic solution for the present problem.
• The amount of calculation time is also certainly less when compared with other numerical procedures.
• Hence it can be concluded that this variational principle is a unique approximate technique for solving various boundary layer flows and heat transfer problems.