Abstract
To assess the risk of project cost overrun, it is necessary to consider large amounts of symmetric and asymmetric data. This paper proposes a cost overrun risk prediction model, the structure of which is based on the fuzzy inference model of Mamdani. The model consists of numerous inputs and one output (multi-input-single-output (MISO)), based on processes running consecutively in three blocks (the fuzzy block, the interference block, and the block of sharpening the representative output value). The input variables of the model include the share of element costs in the building costs (SE), predicted changes in the number of works (WC), and expected changes in the unit price (PC). For the input variable SE, it is proposed to adjust the fuzzy set shapes to the type of building object. Single-family residential buildings, multi-family residential buildings, office buildings, highways, expressways, and sports fields were analyzed. The initial variable is the value of the risk of exceeding the costs of a given element of a construction investment project (R). In all, 27 rules were assumed in the interference block. Considering the possibility of applying sharpening methods in the cost overrun risk prediction model, the following defuzzification methods were investigated: the first of maxima, middle of maxima, and last of maxima method, the center of gravity method, and the bisector area method. Considering the advantages and disadvantages, the authors assumed that the correct and basic defuzzification method in the cost overrun risk prediction model was the center of gravity method. In order to check the correctness of the assumption made at the stage of designing the rule database, result diagrams were generated for the relationships between the variable (R) and the input variables of individual types of buildings. The results obtained confirm the correctness of the assumed assumptions and allow to consider the input variable (SE), adjusted individually to the model for each type of construction object, as crucial in the context of the impact on the output value of the output variable (R).
1. Introduction
Cost overruns in construction projects are a common phenomenon, occurring in different market and legal conditions and, unfortunately, often negatively influencing the achievement of project goals. Numerous research results indicate the scale of this problem. For instance, Love et al. [1] analyzed cost overruns from 276 construction and engineering projects. The research revealed a mean cost overrun of 12.22%. According to research performed by Andrić et al. [2] on cost overruns in infrastructure projects in Asia, the mean value of cost overrun is 26.24%. Senouci et al. [3] in their study on the increase in term cost in 122 construction contracts in Qatari showed that 54% had their costs increased and 72% their deadlines increased. Larsen et al. [4] established that more than half of Malaysian construction projects (55%) experienced cost overruns.
Different types of construction investments can be specified in various stages of their implementation, and these are characterized by different technological, organizational, and economic specificities. When determining the risk of cost overruns, this specificity and different symmetry and asymmetry data must be taken into account. However, when attempting to determine the risk of exceeding the costs of a given element of a facility, one should consider, for instance, the share of a given element in the total cost of the facility, the risk of changes in the number of works, as well as exposure of a given type of works to changes in the unit price, including the price of construction materials [5].
In the literature, various approaches have been described to estimate the real costs of construction projects, including the value of cost overrun. The novelty of the proposed methodology is the assumption of the analysis of individual works included in the project, which allows for a more detailed analysis of the cost overrun risk. The model takes into account the impact of three elements on the risk of cost overrun for a given construction work, which are input variables, namely share of element costs in the building costs (SE), predicted changes in the number of works (WC), and expected changes in the unit price (PC). For each of the variables, a fuzzy interpretation was proposed. The first variable depends on the type of the building and is therefore the most difficult to describe. The authors decided to analyze different types of buildings in the context of determining for each of the them a fuzzy interpretation of the linguistic input variable SE. This can greatly simplify the use of the model in practice.
The aim of the paper is to present a model allowing to assess the risk of exceeding the costs of individual stages of a construction project, adapted to various construction investments.
2. Literature Review
The problem often discussed in the literature are the factors influencing cost overruns in construction projects. According to [2], the main reasons of cost overruns are the increasing cost of resources (labor, materials, machinery), changes in design specifications, land acquisition and resettlement as well as changes in currency exchange. Chen and Hu [6] identified the following main reasons of cost overruns: delay in construction period, engineering quantity increase, and lack of technical skill and experience. Cantarelli et al. [7] investigated the causes of cost overruns in construction projects and categorized them into four main explanations for cost overruns, i.e., technical, economic, psychological, and political. Specific examples of factors were identified for each of these categories. The results of research performed by Phama et al. [8] show that four factors—risks, resources, incompetence of parties, and components, transportation, and machinery cost—are important. Firm policies, project policies, and poor collaboration of parties are not very important for cost overrun. Shaikh [9] identified five main factors as common in causing time and cost overrun in megaprojects in Pakistan. These main factors are financial issues, weather conditions, political approach, design changes, and owner interference. In [10], the authors concluded that the most significant cost overrun factors are schedule delay (47%), improper planning and scheduling (47%), frequent design changes (45%), frequent changes to the scope of work (43%), and inaccurate time and cost estimates of the project (42%). In [11], the authors identified 44 factors affecting cost overrun. Of these, 11 have a decisive influence. Sohu et al. [12] identified nine major causes of cost overrun from professionals working with contractors in highway projects in Pakistan. Catalão et al. [13] presented a methodology using the existing methods but taking into account political, legal, regulatory, and economic determinants. The analysis suggests that these factors have been underestimated in the literature but are of great importance in understanding cost overruns.
Many authors draw attention to the complexity of cost overruns, emphasizing that the factors causing overrun can only be understood by looking at the whole project system in which it occurs and how several variables dynamically interact with each other [14]. The relationships between the different characteristics of the project and cost overrun were studied, for example, in [15,16,17,18,19,20]. Many authors also analyze the generating process of cost overruns along the various phases of the project life cycle [21,22,23].
Another extremely important issue is the possibility of predicting the risk of cost overruns and the amount of such overruns. The risk of cost overruns is dynamic, interdependent, complex, subjective, and fuzzy, especially in large and complex projects [24]. This is the reason why many researchers have attempted to apply fuzzy set theory to solve problems related to cost overrun. Sharma and Goyal [25] proposed a fuzzy-based model to estimate the risk magnitude of the same factors influencing cost overrun. Fuzzy sets were also applied by Marzouk and Amin [26], Knight and Robinson-Fayek [27], and Plebankiewicz [5].
Ghazal and Hammad [28] proposed a Knowledge Discovery in Databases (KDD) model, which may supplement the traditional estimation methods and provide more reliable final cost forecasting to overcome the cost overrun problem. In [29], the authors developed a method for estimating the impact of project management maturity (PMM) on project performance. The proposed method uses Bayesian networks to formalize the knowledge of project management experts and to extract knowledge from a database of previous projects. The operation of the method is shown using the example of a large project in the oil and gas industry.
Other approaches used for the analysis of cost overrun problems include statistical methods, such as multiple regression analysis (MRA) [30], a regression and ANN models [31], and case-based reasoning (CBR) [32,33].
3. Concept of a Cost Overrun Risk Prediction Model
3.1. Main Assumptions of the Model
The construction of the cost overrun risk prediction model was based on the fuzzy inference model of Mamdani. This model has been frequently used in the field of construction management, for instance, to build fuzzy risk inference models, in the context of assessing:
- exceeding the time and cost of construction investments [34],
- exceeding the time, cost, and impact on quality and other technical considerations in the implementation of construction projects [35,36],
- occupational risks on construction sites [37],
- level of safety of construction workers [38],
- technological, financial, political, environmental, and legal risk factors in the life cycle of buildings [39],
- technological risk factors for old buildings [40].
A cost overrun risk prediction model is a model with multiple inputs and one output (multi-input-single-output (MISO)), based on processes that run sequentially in three blocks (the fuzzy block, the interference block, and the block of sharpening the representative output value). Share of element costs in the building costs (SE), predicted changes in the number of works (WC), and expected changes in the unit price (PC) are the input variables of the model. The database of 27 individually designed rules supports the inference process in the interference block, and the level of risk of exceeding the costs of a given element of a construction project (R) is an output variable (y).
To construct a cost overrun risk prediction model, the authors decided to choose the theory of possibilities and fuzzy logic, because the risk is related to the so-called measurable uncertainty. Its measurable character results also from the fact that the risk is quantifiable and can be directly translated into the size of parameters necessary, for example, to determine the value of the risk of cost overrun. In practice, it often happens that an expert who evaluates risk does not have a sufficient number of historical data to perform statistical research that would result in a probabilistic distribution, and thus determines subjectively the size of parameters necessary for risk assessment.
3.2. Block of Fuzzification
The input variables, namely share of element costs in the building costs (SE), predicted changes in the number of works (WC), and expected changes in the unit price (PC), are described with appropriate linguistic terms (fuzzy sets) in the consideration spaces on the so-called universes X1, X2, and X3. The domain (range of arguments) of the universes was determined as a percentage within the interval [0; 100%] for each input variable, with the model using the decimal notation corresponding to the interval [0; 1]. In defining the X consideration spaces, for all variables described by the linguistic terms “high”, “average”, and “low”, it was assumed that the adjacent fuzzy sets (representing consecutive linguistic terms) would overlap. According to Hovde and Moser [41], only this modelling of the linguistic terms for the input variables gives a favorable effect in the inference process.
Table 1 represents the fuzzy sets for the linguistic terms L(X2) and L(X3), that is, for the input variables WC and PC. For the description of linguistic terms, membership functions with line graphs were used (triangular functions and classes Γ and L). The qualitative definition of fuzzy sets was based on the selection of appropriate types of membership functions. The quantitative definition was performed on the basis of the selection of the values of parameters characterizing the functional curves, which made it possible to precisely determine the degrees of membership of individual fuzzy sets. Degrees of membership for fuzzy sets are described in Table 1 (in the last column) by means of four numbers {α1, α2, α3, α4}. These parameters indicate, respectively, the intervals of achieving the value of membership degree 1.0 {α2, α3} and the left or right width of the distribution of the membership function to the value of the membership degree 0.0 {α1, α4}. It was assumed that linguistic values for both input variables (WC and PC) would remain unchanged regardless of the type of the building object.

Table 1.
Fuzzy interpretations of the linguistic input variables “predicted changes in the number of works” (WC) or expected changes in the unit price (PC).
The data presented in Table 1 correspond to the graphic interpretation of fuzzy sets of linguistic values for WC and PC, which is illustrated in Figure 1.
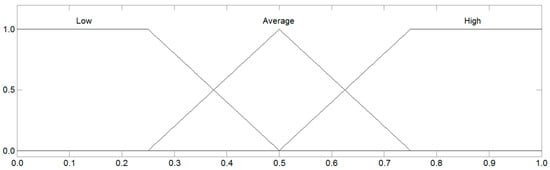
Figure 1.
Linguistic terms of the input variables WC and PC.
Input variable: share of element costs in the building costs (SE) should be subject to the process of adjusting the shapes of fuzzy sets described by the linguistic terms “high”, “average”, and “low” individually, depending on the type of the building object. The authors decided to analyze the following types of building objects in the context of determining the parameters denoting the intervals of attaining the value of the membership degree of 1.0 and the left or right width of the distribution of the membership function to the value of the membership degree 0.0. The following types of buildings were analyzed:
- single-family residential buildings,
- multi-family residential buildings,
- office buildings,
- highways and expressways,
- sports fields.
Each of the buildings was divided according to cost elements following the tables of billing elements for an average of five buildings of each type. Table 2 presents the range of cost elements for cubature facilities, highways and expressways, as well as sports fields.

Table 2.
Range of cost elements for individual buildings.
For each building object, based on the data from an average of five objects, the average percentage of each cost component was determined. Then, the values of quartiles Q1 and Q3 and the median were calculated using statistical measures. The results are presented in Table 3.

Table 3.
Values of statistical measures for cost elements of building objects.
It should be noted that the research sample (five objects) is relatively small. However, it can be concluded that for standard material and technological solutions, the deviations from the results obtained for a given type of building are small. In the case of non-standard solutions, the share of component costs should be modified, taking into account the specificity of a given building object.
On the basis of the data presented in Table 3, a fuzzy interpretation of the linguistic input variable SE for each of the buildings was proposed. It was assumed that for fuzzy sets:
- “high”—description of the variable would relate to the value “about or above quartile Q3”,
- “average”—description of the variable would relate to the value “about median”,
- “low”—description of the variable would relate to the value “about or below quartile Q1”.
Table 4 depicts a fuzzy interpretation of the linguistic input variable SE for all types of buildings.

Table 4.
Fuzzy interpretation of the linguistic input variable share of element costs in the building costs (SE).
In Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6, graphical interpretations of the input variable consideration space are presented for the subsequent types of buildings subjected to analysis. These interpretations accurately reproduce the fuzzy sets for linguistic terms “high”, “average”, and “low”, which are described in Table 4.
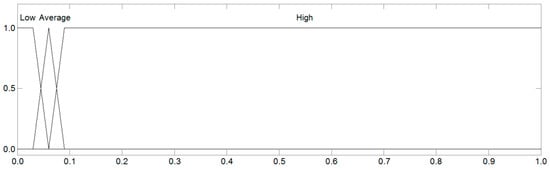
Figure 2.
Linguistic terms of the input variable SE for single-family residential buildings.
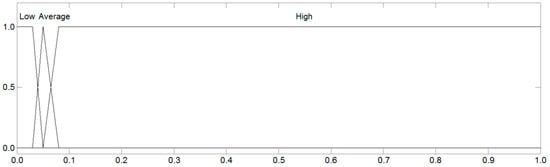
Figure 3.
Linguistic terms of the input variable SE for multi-family residential buildings.
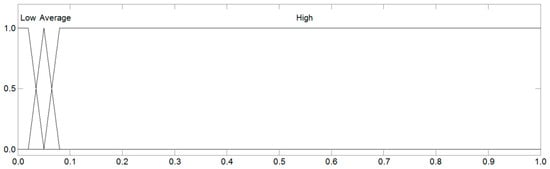
Figure 4.
Linguistic terms of the input variable SE for office buildings.
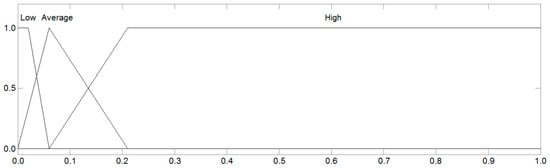
Figure 5.
Linguistic terms of the input variable SE for highways and expressways.
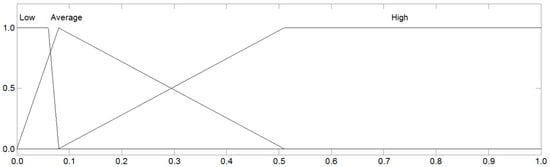
Figure 6.
Linguistic terms of the input variable SE for sports fields.
3.3. Block of Inference
In the inference block in the fuzzy inference model of Mamdani of the MISO type, the resulting membership function is calculated for the output variable μ(y). Its calculation is based on the values of the degree of membership of the sharp input variables μ(x1), μ(x2), and μ(x3) for individual fuzzy sets of linguistic values. The resulting function often has a complex shape and its calculation is done by the so-called inference (inference process). The inference block consists of two basic elements, namely the rule base and the inference mechanism, the operation of which is based on the three following consecutive mathematical operations: aggregation of simple premises, implications of fuzzy inference rules, and aggregation of conclusions of all rules.
The designed base of rules in the cost overrun risk prediction model has a conjunctive form due to the logical conjunction “and” used in conditional sentences, which combines all three simple premises. The model proposes five result conclusions that inform about the size of the calculated risk of cost overruns, i.e., “very low” (Vl), “quite low” (Ql), “average” (Av), “quite high” (Qh), and “very high” (Vh).
For the purpose of developing the rule base, the authors assumed that with an increase in the share of element costs in the building costs (SE), predicted changes in the number of works (WC), and expected changes in the unit price (PC), the value of the risk level of exceeding the costs of a given element in the construction project (R) will naturally and smoothly increase. For this purpose, it was decided to examine the quantities of the products of all combinations of input variables in a set of all 27 possible rules, and then to assign the results to five possible result conclusions on the assumption that the minimum quantities correspond to the “very low” conclusion, the maximum—to the “very high” conclusion, and the intermediate—to the “quite low”, “average”, and “quite high” conclusions, respectively and proportionally. The following weights were assumed for the linguistic input variables SE, WC, and PC: 1 for “low”, 2 for “average”, and 3 for “high”. Table 5 illustrates the rule base of the inference block consisting of 27 rules, for which equal degrees of fuzzy relationship validity are assumed to be 1.0.

Table 5.
Rule base of the inference block.
In the interference block, the processes of premise aggregation and rule conclusion aggregation are performed. Aggregation of simple premises consists in calculating the degree of belonging (truthfulness) of the fuzzy rule created by these premises. Due to the fact that in the conditional sentences the logical conjunction “and” was used, which in fuzzy logic is represented by the concept of intersection (product) of the fuzzy sets, the operation of premise aggregation was reduced to searching for the value of the degree of membership to the fuzzy relationship (FR). This value was determined by applying the Mamdani fuzzy implication rule (T-norm), calculated according to the following formula:
The final stage of the inference block is the aggregation of the conclusions of all running fuzzy rules (the so-called output aggregation). This procedure consists of summing up the conclusions of activated rules that are responsible for the shape of the resulting membership function μ(y). According to the calculation algorithm, the first step is to define separately the modified membership functions of the fuzzy sets of the output variable for the rules involved in the inference, and then sum up these fuzzy sets based on one of the formulas for S-norm. In the cost overrun risk prediction model, the basic S-norm is the following formula of Mamdani:
Output variable (y) is described in space (universe) Y. The scope of the Y universe was determined as a percentage [0; 100%]. As in the case of all input variables, the record of the argument domain in the decimal interval was adopted [0; 1]. Sets correspond to the resultant conclusions in the rule database (“very low”, “quite low”, “average”, “quite high”, and “very high”).
Fuzzy sets for the final result conclusions (“very low” and “very high”) and the intermediate internal conclusion (“average”) were attempted to be parameterized in such a way that the membership function graphs did not interpenetrate, but were continuous in the full scope of the Y universe. For internal relative conclusions (“quite low” and “quite high”), the same procedure was followed, where the fuzzy sets were entered symmetrically between the extreme (final) and internal (intermediate) conclusions. The parameterization was performed in such a way that the adjacent fuzzy sets overlapped with the membership degree for intermediate elements equal to μ(0.2) = μ(0.4) = μ(0.6) = μ(0.8) = 0.5. Table 6 presents sets of linguistic terms L(Y) for the output variable (y). The membership of all fuzzy sets was defined as in the case of the input variables, that is, using four numbers {α1, α2, α3, α4}.

Table 6.
Fuzzy interpretation of the linguistic output variable R.
Figure 7 presents a graphic interpretation of the consideration space of the output variable (y), which is represented by the fuzzy sets of all five result conclusions, described in Table 6.
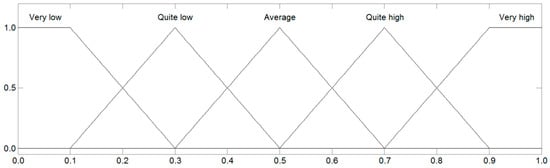
Figure 7.
Linguistic terms of the output variable R.
3.4. Block of Defuzzification
The defuzzification process is a mathematical operation performed on the resultant membership function shape (the resulting fuzzy set) obtained after aggregating the conclusions of all inference rules. This operation aims to determine one sharp value of the variable (y) that will appropriately represent the output fuzzy set and indicate unambiguously the result conclusion.
Considering the possibility of using sharpening methods in the cost overrun risk prediction model, the following defuzzification methods were investigated: the first of maxima, middle of maxima, and last of maxima method, the center of gravity method, and the bisector area method. The advantages and disadvantages, as well as the conditions for the application of individual methods, were highlighted. The suggestions and observations contained in [42] were especially taken into account, according to which the methods of maxima:
- are not able to implement the assumption adopted for the purposes of building the rule base, that with the increase in the share of element costs in the building costs (SE), predicted changes in the number of works (WC), and expected changes in the unit price (PC), the value of the risk level of exceeding the costs of a given element of the construction investment (R) will naturally and smoothly increase,
- result in sharp values, which will not in every case adequately represent the output fuzzy set, which is caused by the impact on the sharp result of only the most activated fuzzy set of the output variable.
Figure 8 confirms the observations described above with regard to the use of the last of maxima defuzzification method. On the left, there is the result surface for the output variable (R) due to the influence of the input variables PC and SE. The result surface is analogous for the set of input variables WC and SE. On the right, the same result area is shown, but in terms of the input variables PC and WC.
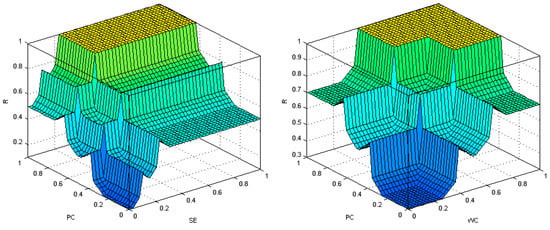
Figure 8.
Result area in terms of input variables PC and SE (left) and PC and WC (right)—last of maxima defuzzification method.
Taking into account the above observations, it was assumed that the proper and basic defuzzification method in the cost overrun risk prediction model would be the center of gravity method.
4. Discussion
A cost overrun risk prediction model was developed for each type of construction site separately using the “Fuzzy Logic Designer” application that is available in the MATLAB R2013a software package (The MathWorks, Inc., Natick, MA, USA) for scientific and engineering calculations.
In order to investigate the correctness of the assumption made at the design stage of the rule base (i.e., that as the share of element costs in the building costs (SE), predicted changes in the number of works (WC) and expected changes in the unit price (PC) increase, the value of the risk level of exceeding the costs of a given element of the construction project (R) will increase naturally and smoothly) and also to examine the impact of the change of the membership function for the input variable (i.e., share of element costs in the building costs (SE) for individual types of building objects on the value of the results obtained for the output variable (R)), the following result diagrams were generated for the relationships between the variable R and the input variables:
- diagrams of the result area for the output variable (R) due to the influence of the input variables PC and SE in the cross-section, when WC = 0.5, and WC and SE in the cross-section, when PC = 0.5,
- diagrams of the result area for the output variable (R) taking into account the set of input variables PC and WC in the cross-section, when SE = 0.5,
- flat diagrams of the resultant curves for the output variable (R) due to the influence of PC input variables in the cross-section, when WC = SE = 0.5, WC in the cross-section, when PC = SE = 0.5, and SE in the cross-section, when PC = WC = 0.5.
The following figures show flat and spatial diagrams for the relationships between the output variable (R) and the input variables (SE, WC, and PC) for all types of buildings under analysis (single- and multi-family residential buildings, office buildings, highways and expressways, and sports fields). Figure 9 shows the result area for the output variable (R) in terms of PC and WC variables (left diagram) and the relationship between the output variable (R) and the PC input variable (right diagram). It should be noted that both the result areas as well as dependencies on the output variable (R) are analogous for each type of building object because, in the cost overrun risk prediction model, it was assumed that PC and WC input variables would remain the same for all buildings.
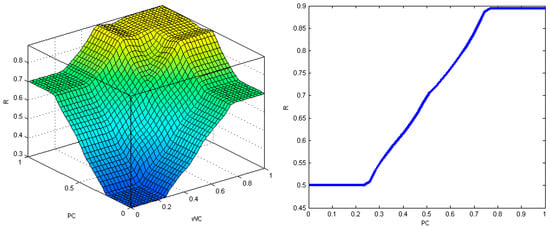
Figure 9.
The result area for the output variable (R) in terms of the PC and WC variables in the cross-section, when SE = 0.5 (left diagram), and the relationship between the output variable (R) and the input variable PC in the cross-section, when WC = SE = 0.5 (right diagram).
Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14 show the result area for the output variable (R) in terms of the variables PC and SE (diagrams on the left, respectively) and the relationships between the output variable (R) and the input variable SE (diagrams on the right, respectively). It should be noted that both the result area and the dependencies with respect to the output variable (R) are analogous for the set of input variables WC and SE.
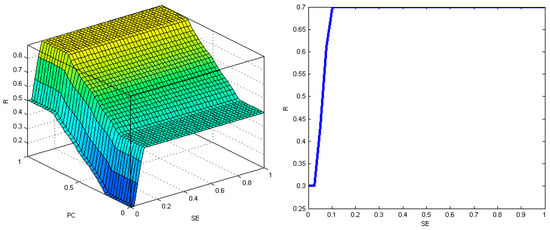
Figure 10.
The result area for the output variable (R) in terms of the PC and SE variables in the cross-section, when WC = 0.5 (left diagram), and the relationship between the output variable (R) and the input variable SE in the cross-section, when WC = PC = 0.5 (right diagram)—single-family residential buildings.
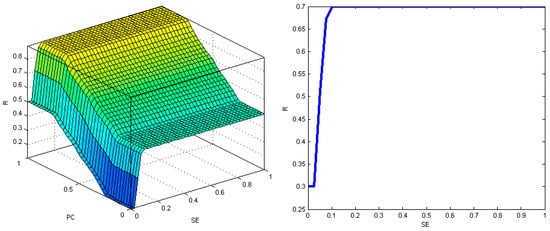
Figure 11.
The result area for the output variable (R) in terms of the PC and SE variables in the cross-section, when WC = 0.5 (left diagram), and the relationship between the output variable (R) and the input variable SE in the cross-section, when WC = PC = 0.5 (right diagram)—multi-family residential buildings.
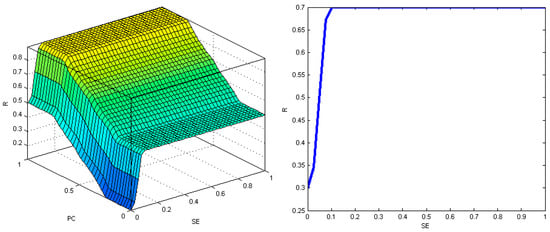
Figure 12.
The result area for the output variable (R) in terms of the PC and SE variables in the cross-section, when WC = 0.5 (left diagram), and the relationship between the output variable (R) and the input variable SE in the cross-section, when WC = PC = 0.5 (right diagram)—office buildings.
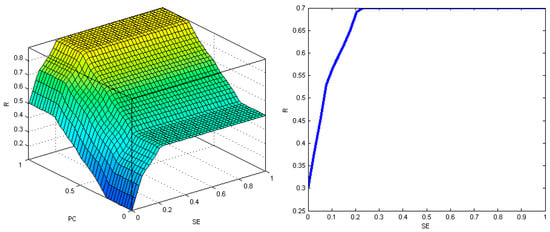
Figure 13.
The result area for the output variable (R) in terms of the PC and SE variables in the cross-section, when WC = 0.5 (left diagram), and the relationship between the output variable (R) and the input variable SE in the cross-section, when WC = PC = 0.5 (right diagram)—highways and expressways.
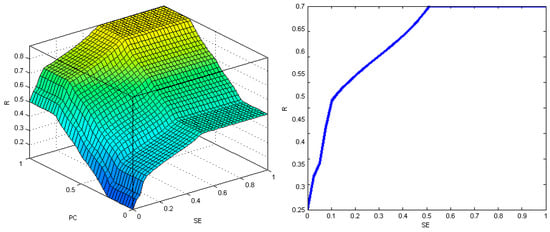
Figure 14.
The result area for the output variable (R) in terms of the PC and SE variables in the cross-section, when WC = 0.5 (left diagram), and the relationship between the output variable (R) and the input variable SE in the cross-section, when WC = PC = 0.5 (right diagram)—sports.
Diagrams of the result areas and of the relationship between the output variable (R) and the input variables confirm the correctness of the assumptions made when designing the rule base of the cost overrun risk prediction model. Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14 indicate unequivocally that with an increase in the share of element costs in the building costs (SE), predicted changes in the number of works (WC), and expected changes in the unit price (PC), the value of the risk level of exceeding the costs of a given element of a construction investment (R) increases naturally and smoothly.
In contrast, the diagrams of the dependence between the output variable (R) and the input variable SE in the cross-section were superimposed on Figure 15 when WC = PC = 0.5 for all five types of construction objects.
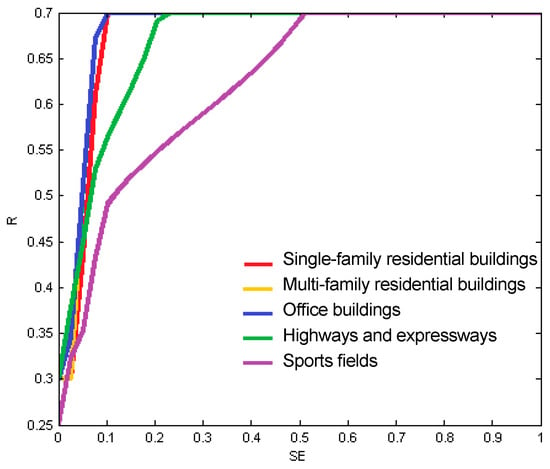
Figure 15.
The diagrams of the dependence between the output variable (R) and the input variable SE for all five types of construction objects.
From the comparison of flat dependence diagrams (Figure 15), the input variable share of element costs in the building costs (SE), adjusted individually to the model for each building type, should be considered crucial in the context of the impact on the result value of the output variable (R). The lower the membership for the values of the arguments of the X1 universe domain for the linguistic terms “average” and “high” of the SE variable, the more the resulting value of the risk of construction investment cost overrun (R) increases for the arguments of the X1 variable universe with smaller values—the SE interval approximately [0.1; 0.3]. This conclusion is confirmed in particular by the comparison of the course of the result curves for office buildings (blue line) and sports fields (purple line).
5. Conclusions
The phenomenon of exceeding planned investment costs is often encountered in the construction industry, and the determination of the risk associated with it may be of key importance for achieving the objectives of the project. This paper discusses a cost overrun risk prediction model, the development of which was based on the fuzzy inference model of Mamdani. The model input variables include the following: share of element costs in the building costs (SE), predicted changes in the number of works (WC), and expected changes in the unit price (PC). The basic problem is to adjust the shape of the fuzzy sets for a given input SE to the type of building object. The paper proposes a shape for cubature buildings (residential and office ones), highways and expressways, and sports fields.
In order to check the correctness of the assumption made of the rule database, result diagrams were generated for the relationships between the variable R and the input variables of individual types of buildings. The obtained results confirm the correctness of the assumptions. With an increase in input variables, the value of the risk level of exceeding the costs increases naturally and smoothly. The results prove that the input variable SE, adjusted individually to the model for each type of construction object, is crucial in the context of influencing the output value. The lower the membership for the values of the arguments of the X1 universe domain for the linguistic terms “average” and “high” of the SE variable, the more the resulting value of the risk of construction investment cost overrun (R) increases for the arguments of the X1 variable universe with smaller values.
The model requires further research, both in terms of the input data taken into account and the diversity of the analyzed construction projects. Further testing of the model on actual construction projects will confirm its usefulness in determining the risk of cost overruns.
Author Contributions
E.P. carried out a review of the literature concerning the introduction part. E.P. and D.W. described all assumptions of the cost overrun risk prediction model. D.W. prepared all figures and tables. E.P. and D.W. discussed the results, drew conclusions. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Love, P.E.D.; Wang, X.; Sing, C.; Tiong, R.L.K. Determining the Probability of Cost Overruns. J. Constr. Eng. Manag. 2013, 139, 321–330. [Google Scholar] [CrossRef]
- Andrić, J.M.; Mahamadu, A.; Wang, J.; Zou, P.X.W.; Zhong, R. The cost performance and causes of overruns in infrastructure development projects in Asia. J. Civ. Eng. Manag. 2019, 25, 203–214. [Google Scholar] [CrossRef]
- Senouci, A.; Ismail, A.; Eldin, N. Time Delay and Cost Overrun in Qatari Public Construction Projects. Procedia Eng. 2016, 164, 368–375. [Google Scholar] [CrossRef]
- Larsen, J.K.; Shen, G.Q.; Lindhard, S.M.; Ditlev, T. Factors Affecting Schedule Delay, Cost Overrun, and Quality Level in Public Construction Projects. J. Manag. Eng. 2016, 32, 04015032. [Google Scholar] [CrossRef]
- Plebankiewicz, E. Model of predicting cost overrun in construction projects. Sustainability 2018, 10, 4387. [Google Scholar] [CrossRef]
- Chen, Y.; Hu, Z. Exploring the properties of cost overrun risk propagation network (CORPN) for promoting cost management. J. Civ. Eng. Manag. 2019, 25, 1–18. [Google Scholar] [CrossRef]
- Cantarelli, C.C.; Flyvbjerg, B.; Molin, J.E.E.; van Wee, B. Cost Overruns in Large-Scale Transportation Infrastructure Projects: Explanations and their Theoretical Embeddedness. Eur. J. Transp. Infrastruct. Res. 2010, 10, 21. [Google Scholar]
- Phama, H.; Luub, T.-V.; Kimc, S.-Y.; Viend, D.-T. Assessing the Impact of Cost Overrun Causes in Transmission Lines Construction Projects. Ksce J. Civ. Eng. 2020, 24, 1029–1036. [Google Scholar] [CrossRef]
- Shaikh, F.A. Financial Mismanagement: A Leading Cause of Time and Cost Overrun in Mega Construction Projects in Pakistan. Eng. Technol. Appl. Sci. Res. 2020, 10, 5247–5250. [Google Scholar]
- Gunduz, M.; Maki, O.L. Assessing the risk perception of cost overrun through importance rating. Technol. Econ. Dev. Econ. 2018, 24, 1829–1844. [Google Scholar] [CrossRef]
- El-Kholy, A.M. Predicting Cost Overrun in Construction Projects. Int. J. Constr. Eng. Manag. 2015, 4, 95–105. [Google Scholar]
- Sohu, S.; Abdullah, A.H.; Nagapan, S.; Rind, T.A.; Jhatial, A.A. Controlling Measures for Cost Overrun Causes in Highway Projects of Sindh Province Engineering. Technol. Appl. Sci. Res. 2019, 9, 4276–4280. [Google Scholar]
- Catalão, F.P.; Cruz, C.O.; Sarmento, J.M. The determinants of cost deviations and overruns in transport projects, an endogenous models approach. Transp. Policy 2019, 74, 224–238. [Google Scholar] [CrossRef]
- Ahiaga-Dagbui, D.D.; Gordon, R.; Love, P.E.D.; Smith, S.D.; Ackermann, F. Toward a Systemic View to Cost Overrun Causation in Infrastructure Projects: A Review and Implications for Research. Proj. Manag. J. 2017, 48, 88–98. [Google Scholar] [CrossRef]
- Huo, T.; Ren, H.; Cai, W.; Shen, G.Q.; Liu, B.; Zhu, M.; Wu, H. Measurement and dependence analysis of cost overruns in megatransport infrastructure projects: Case study in Hong Kong. J. Constr. Eng. Manag. 2018, 144, 05018001. [Google Scholar] [CrossRef]
- França, A.; Haddad, A. Causes of Construction Projects Cost Overrun in Brazil. Int. J. Sustain. Constr. Eng. Technol. 2018, 9, 69–83. [Google Scholar] [CrossRef]
- Johnson, J. Comparing the Effects of ABC and BIM in Construction Projects and Choose the Best Solution to Minimise the Delay and Cost Overrun Using MADMA. PM World J. 2019, 8, 1–18. [Google Scholar]
- Keng, T.C.; Mansor, N.; Ching, Y.K. An Exploration of Cost Overrun in Building Construction Projects. Glob. Bus. Manag. Res. Int. J. 2018, 10, 638–646. [Google Scholar]
- Mahamid, I. Study of relationship between cost overrun and labour productivity in road construction projects. Int. J. Product. Qual. Manag. 2018, 24, 143–164. [Google Scholar] [CrossRef]
- Akinradewo, O.; Aghimien, D.; Aigbavboa, C. Comparative Analysis of Cost Overrun on Road Construction Projects Executed by Indigenous and Expatriate Contractors. In Proceedings of the International Conference on Industrial Engineering and Operations Management, Dubai, United Arab Emirates, 10–12 March 2020. [Google Scholar]
- Cavalieri, M.; Cristaudo, R.; Guccio, C. On the magnitude of cost overruns throughout the project life-cycle: An assessment for the Italian transport infrastructure projects. Transp. Policy 2019, 79, 21–36. [Google Scholar] [CrossRef]
- Derakhshanalavijeh, R.; Teixeira, J.M.C. Cost overrun in construction projects in developing countries, Gas-Oil industry of Iran as a case study. J. Civ. Eng. Manag. 2017, 23, 125–136. [Google Scholar] [CrossRef]
- Cantarelli, C.C.; Molin, E.J.E.; van Wee, B.; Flyvbjerg, B. Characteristics of cost overruns for Dutch transport infrastructure projects and the importance of the decision to build and project phases. Transp. Policy 2012, 22, 49–56. [Google Scholar] [CrossRef]
- Islam, M.S.; Nepal, M.P.; Skitmore, M.; Kabir, G. A knowledge-based expert system to assess power plant project cost overrun risks. Expert Syst. Appl. 2019, 136, 12–32. [Google Scholar]
- Sharma, S.; Goyal, P.K. Fuzzy assessment of the risk factors causing cost overrun in construction industry. Evol. Intell. 2019, 1–13. [Google Scholar] [CrossRef]
- Marzouk, M.; Amin, A. Predicting Construction materials prices using fuzzy logic and neural networks. J. Constr. Eng. Manag. 2013, 139, 1190–1198. [Google Scholar] [CrossRef]
- Knight, K.; Robinson-Fayek, A. Use of fuzzy logic of predicting design cost overruns on building projects. J. Constr. Eng. Manag. 2002, 128, 503–512. [Google Scholar] [CrossRef]
- Ghazal, M.M.; Hammad, A.M. Data Acquisition Model for Analyzing Cost Overrun in Construction Projects using KDD. In Proceedings of the International Conference on Industrial Engineering and Operations Management, Bandung, Indonesia, 6–8 March 2018; pp. 2255–2266. [Google Scholar]
- Sanchez, F.; Bonjour, E.; Micaelli, J.-P.; Monticolo, D. An Approach Based on Bayesian Network for Improving Project Management Maturity: An Application to Reduce Cost Overrun Risks in Engineering Projects. Comput. Ind. 2020, 119, 103227. [Google Scholar] [CrossRef]
- Abu Hammad, A.A.; Ali, S.M.A.; Sweis, G.J.; Basher, A. Prediction Model for Construction Cost and Duration in Jordan. Jordan J. Civ. Eng. 2008, 2, 250–266. [Google Scholar]
- Juszczyk, M.; Leśniak, A.; Zima, K. ANN based approach for estimation of construction costs of sports fields. Complexity 2018, 2018, 7952434. [Google Scholar] [CrossRef]
- Ji, S.H.; Park, M.; Lee, H.S. Cost Estimation Model for Building Projects Using Case-Based Reasoning. Can. J. Civ. Eng. 2011, 38, 570–581. [Google Scholar] [CrossRef]
- Leśniak, A.; Zima, K. Cost Calculation of Construction Projects Including Sustainability Factors Using the Case Based Reasoning (CBR) Method. Sustainability 2018, 10, 1608. [Google Scholar] [CrossRef]
- Ibadov, N.; Kulejewski, J. The assessment of construction project risks with the use of fuzzy sets theory. Tech. Trans. 2014, 1-B, 175–182. [Google Scholar]
- Nieto-Morote, A.; Ruz-Vila, F. A fuzzy approach to construction project risk assessment. Int. J. Proj. Manag. 2011, 29, 220–231. [Google Scholar] [CrossRef]
- Tavakolan, M.; Mohammadi, A. Construction risk management framework using fuzzy sets and failure mode and effect analysis. In Proceedings of the 51st ASC Annual International Conference, The Associated Schools of Construction, College Station, TX, USA, 22–25 April 2015. [Google Scholar]
- Debnath, J.; Biswas, A.; Sivan, P.; Sen, K.N.; Sahu, S. Fuzzy inference model for assessing occupational risks in construction sites. Int. J. Ind. Ergon. 2016, 55, 114–128. [Google Scholar] [CrossRef]
- Othman, M.H.H.; Arbaiy, N.; Lah, M.S.C.; Lin, P.C. Mean-Variance Model With Fuzzy Random Data. J. Crit. Rev. 2020, 7, 1347–1352. [Google Scholar]
- Plebankiewicz, E.; Wieczorek, D. Rozmyta ocena ryzyka w cyklu życia obiektów budowlanych. Mater. Bud. 2016, 6, 59–61. [Google Scholar] [CrossRef]
- Konior, J. Technical assessment of old buildings by fuzzy approach. Arch. Civil. Eng. 2019, 65, 130–141. [Google Scholar] [CrossRef]
- Hovde, P.J.; Moser, K. Performance based Methods for Service Life Prediction; State of the Art Reports; CIB Report; Trondheim Publication: Trondheim, Norway, 2004; p. 294. [Google Scholar]
- Wieczorek, D. Fuzzy risk assessment in the life cycle of building object—Selection of the right defuzzification method. In AIP Conference Proceedings; AIP Publishing: Melville, NY, USA, 2018; Volume 1978, p. 240005. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).