On the Statistical GARCH Model for Managing the Risk by Employing a Fat-Tailed Distribution in Finance
Abstract
1. Introduction
1.1. Literature Review on VaR and CVaR
1.2. Garch Model
1.3. Motivation and Article’S Plan
2. VaR Based on the EVD
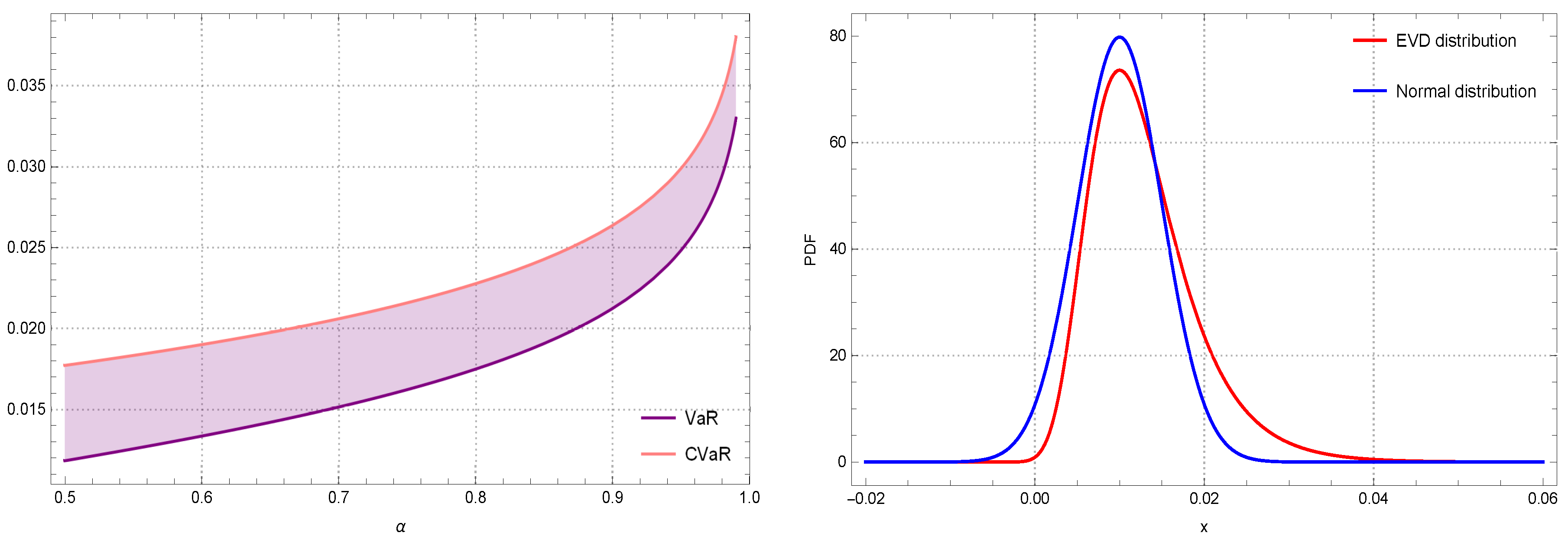
3. CVaR Based on the EVD
4. Discussion of Findings: Results and Simulations
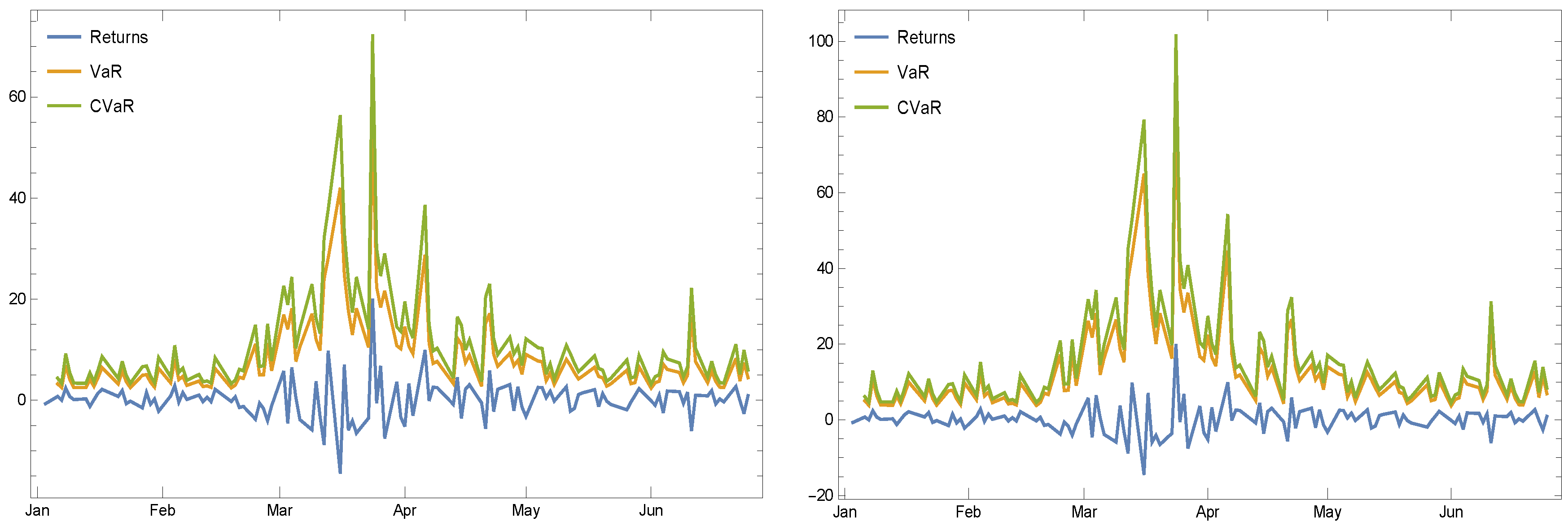
4.1. Stocks
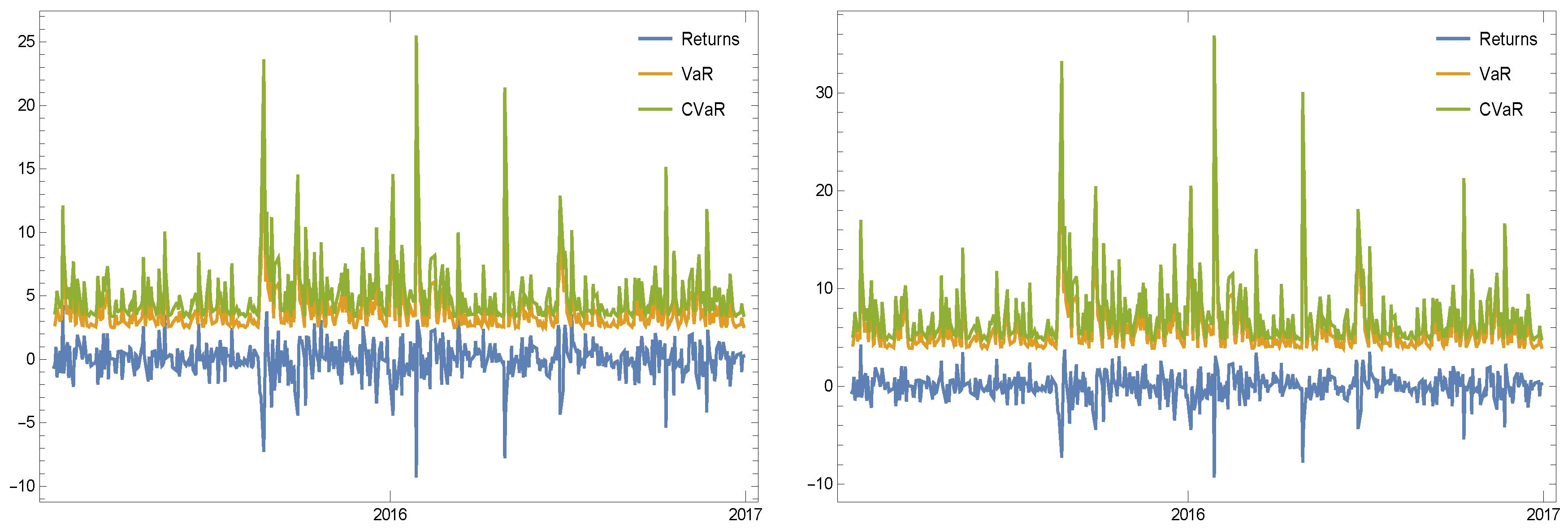
- The first experiment is based on the stock’s ticker “NYSE:ABT” which is used during a specified period of time for checking the usefulness of the discussed risk measures. The information of this considered stock is furnished clearly in Table 2 and in Figure 2 based upon its newest (as of writing this work) trading volume and its available dates.
- The second experiment is based on “NASDAQ:ZION”.
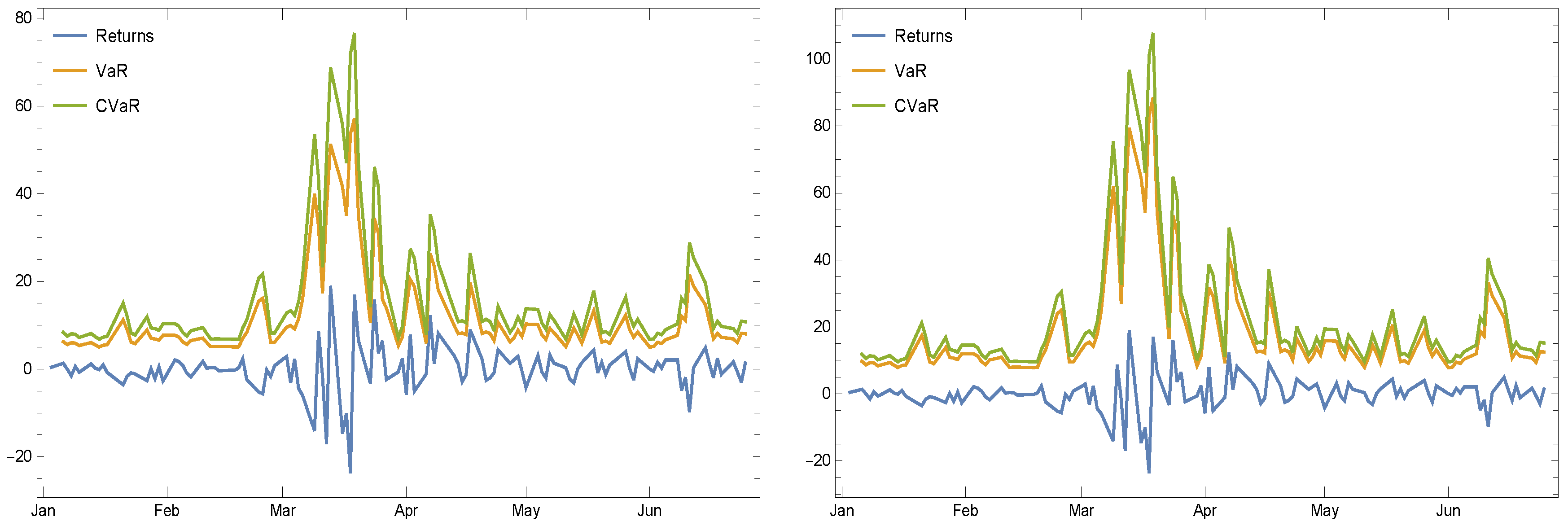
- The third experiment is based on “NYSE:WMB”.
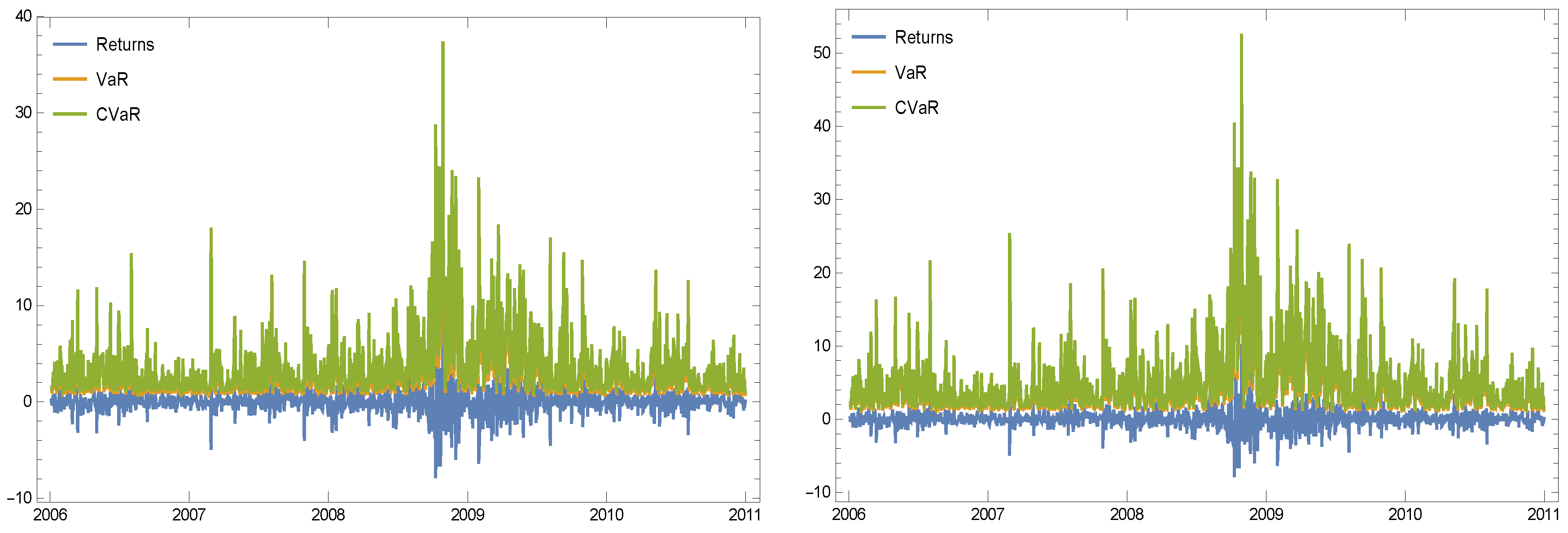
- The fourth experiment is based on “NYSE:PG”. Basically, this is a test which has been conducted during the periods of different stock market dynamics (e.g., the financial crisis of 2008–2009), while the number of 755 observations are sufficient to judge of VaR/CVaR at 99%. Here, we have at least 1250 daily observations.
- The fifth experiment is based on “NASDAQ:INTU”.
4.2. Empirical Results
- First of all, by increasing the pre-determined tail level, both measures tend to each other.
- Choosing the pre-determined confidence level sounds to be a good choice for a highly volatile stock as long as we use such risk measures under the EVD.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Albrecher, H.; Binder, A.; Lautscham, V.; Mayer, P. Introduction to Quantitative Methods for Financial Markets; Springer: Basel, Switzerland, 2013. [Google Scholar]
- Bormetti, G.; Cisana, E.; Montagna, G.; Nicrosini, O. A non-Gaussian approach to risk measures. Phys. A 2007, 376, 532–542. [Google Scholar] [CrossRef]
- Galindo, J.; Tamayo, P. Credit risk assessment using statistical and machine learning basic methodology and risk modeling applications. Comput. Econ. 2000, 15, 107–143. [Google Scholar] [CrossRef]
- Markowitz, H. Portfolio selection. J. Financ. 1952, 7, 77–91. [Google Scholar]
- Roy, A. Safety first and the holding of assets. Econometrica 1952, 20, 431–449. [Google Scholar] [CrossRef]
- Lechner, L.A.; Ovaert, T.C. Value-at-risk: Techniques to account for leptokurtosis and asymmetric behavior in returns distributions. J. Risk Fin. 2010, 11, 464–480. [Google Scholar] [CrossRef]
- Altun, E.; Tatlidil, H.; Ozel, G.; Nadaraja, S. Does the Assumption on Innovation Process Play an Important Role for Filtered Historical Simulation Model? J. Risk Financ. Manag. 2018, 11, 7. [Google Scholar] [CrossRef]
- Benninga, S.; Wiener, Z. Value-at-Risk (VaR). Math. Edu. Res. 1998, 7, 1–8. [Google Scholar]
- Braione, M.; Scholtes, N.K. Forecasting value-at-risk under different distributional assumptions. Econometrics 2016, 4, 3. [Google Scholar] [CrossRef]
- Wang, Z.-R.; Chen, X.-H.; Jin, Y.-B.; Zhou, Y.-J. Estimating risk of foreign exchange portfolio: Using VaR and CVaR based on GARCH-EVT-Copula model. Phys. A 2010, 389, 4918–4928. [Google Scholar] [CrossRef]
- Soleymani, F.; Itkin, A. Pricing foreign exchange options under stochastic volatility and interest rates using an RBF-FD method. J. Comput. Sci. 2019, 37, 101028. [Google Scholar] [CrossRef]
- Sarykalin, S.; Serraino, G.; Uryasev, S. Value-at-risk vs. conditional value-at-risk in risk management and optimization. Informs 2008, 270–294. [Google Scholar] [CrossRef]
- Schmid, K.; Belzner, L.; Kiermeier, M.; Neitz, A.; Phan, T.; Gabor, T.; Linnhoff, C. Risk-sensitivity in simulation based online planning. In Proceedings of the 41st German Conference on AI, Berlin, Germany, 24–28 September 2018. [Google Scholar]
- Basel Committee on Banking Supervision. Minimum Capital Requirements for Market Risk; Basel Committee on Banking Supervision: Basel, Switzerland, January 2019. [Google Scholar]
- Williams, B. GARCH(1,1) Models; Ruprecht-Karls-Universität: Heidelberg, Germany, 2011. [Google Scholar]
- Halkos, G.E.; Tsirivis, A.S. Value-at-risk methodologies for effective energy portfolio risk management. Econ. Anal. Policy 2019, 62, 197–212. [Google Scholar] [CrossRef]
- Bollerslev, T. Generalized autoregressive conditional heteroskedasticity. J. Econom. 1986, 31, 307–327. [Google Scholar] [CrossRef]
- Hlivka, I. VaR, CVaR and Their Time Series Applications; Research Note; Quant Solutions Group: London, UK, 2015; pp. 1–2. [Google Scholar]
- Chu, J.; Chan, S.; Nadarajah, S.; Osterrieder, J. GARCH Modelling of Cryptocurrencies. J. Risk Financ. Manag. 2017, 10, 17. [Google Scholar] [CrossRef]
- Echaust, K.; Just, M. Value at risk estimation using the GARCH-EVT approach with optimal tail selection. Mathematics 2020, 8, 114. [Google Scholar] [CrossRef]
- Davis, R.A.; Mikosch, T. Extreme value theory for garch processes. In Handbook of Financial Time Series; Springer: Berlin/Heidelberg, Germany, 2009; pp. 187–200. [Google Scholar]
- Gilli, M.; Kellezi, E. An application of extreme value theory for measuring financial risk. Comput. Econ. 2006, 27, 1–23. [Google Scholar] [CrossRef]
- Norton, M.; Khokhlov, V.; Uryasev, S. Calculating CVaR and bPOE for common probability distributions with application to portfolio optimization and density estimation. Ann. Oper. Res. 2019. [Google Scholar] [CrossRef]
- McNeil, Q.J.; Frey, R.; Embrechts, P. Quantitative Risk Management, Revised ed.; Princeton University Press: Princeton, NJ, USA, 2015. [Google Scholar]
- Goode, J.; Kim, Y.S.; Fabozzi, F.J. Full versus quasi MLE for ARMA-GARCH models with infinitely divisible innovations. Appl. Econ. 2015, 47, 5147–5158. [Google Scholar] [CrossRef]
- Owusu-Ansah, E.D.J.; Barnes, B.; Donkoh, E.K.; Appau, J.; Effah, B.; Mccall, M. Quantifying economic risk: An application of extreme value theory for measuring fire outbreaks financial loss. Finan. Math. Appl. 2019, 4, 1–12. [Google Scholar]
- Tabasi, H.; Yousefi, V.; Tamošaitienė, J.; Ghasemi, F. Estimating conditional value at risk in the Tehran stock exchange based on the extreme value theory using GARCH models. Adm. Sci. 2019, 9, 40. [Google Scholar] [CrossRef]
- He, X.; Gong, P. Measuring the coupled risks: A copula-based CVaR model. J. Comput. Appl. Math. 2009, 223, 1066–1080. [Google Scholar] [CrossRef]
- Georgakopoulos, N.L. Illustrating Finance Policy with Mathematica; Springer International Publishing: Cham, Switzerland, 2018. [Google Scholar]
- Engle, R.F. Autoregressive conditional heteroskedasticity with estimates of the variance of U.K. inflation. Econometrica 1982, 50, 987–1008. [Google Scholar] [CrossRef]
- Aliyev, F.; Ajayi, R.; Gasim, N. Modelling asymmetric market volatility with univariate GARCH models: Evidence from Nasdaq-100. J. Econ. Asymmetries 2020, 22, e00167. [Google Scholar] [CrossRef]
- Herwartz, H. Stock return prediction under GARCH–An empirical assessment. Int. J. Forecast. 2017, 33, 569–580. [Google Scholar] [CrossRef]
- Nelson, D.B. Conditional heteroskedasticity in asset returns: A new approach. Econometrica 1991, 59, 347–370. [Google Scholar] [CrossRef]
- Glosten, L.R.; Jagannathan, R.; Runkle, D.E. On the relation between the expected value and the volatility of the nominal excess return on stocks. J. Financ. 1993, 48, 1779–1801. [Google Scholar] [CrossRef]
- Christoffersen, P.F. Evaluating interval forecasts. Int. Econ. Rev. 1998, 39, 841–862. [Google Scholar] [CrossRef]
- Berkowitz, J. Testing density forecasts, with applications to risk management. J. Bus. Econ. Stat. 2001, 19, 465–474. [Google Scholar] [CrossRef]
- Acerbi, C.; Szekely, B. Back-testing expected shortfall. Risk 2014, 27, 76–81. [Google Scholar]



| VaR(Normal) | VaR(EVD) | CVaR(Normal) | CVaR(EVD) | |||
|---|---|---|---|---|---|---|
| 0.02 | 0.002 | 0.9 | 0.022 | 0.024 | 0.023 | 0.026 |
| 0.02 | 0.002 | 0.94 | 0.023 | 0.025 | 0.023 | 0.027 |
| 0.02 | 0.002 | 0.98 | 0.024 | 0.027 | 0.024 | 0.029 |
| 0.02 | 0.003 | 0.9 | 0.023 | 0.026 | 0.025 | 0.029 |
| 0.02 | 0.003 | 0.94 | 0.024 | 0.028 | 0.025 | 0.031 |
| 0.02 | 0.003 | 0.98 | 0.026 | 0.031 | 0.027 | 0.034 |
| 0.02 | 0.004 | 0.9 | 0.025 | 0.029 | 0.027 | 0.033 |
| 0.02 | 0.004 | 0.94 | 0.026 | 0.031 | 0.027 | 0.035 |
| 0.02 | 0.004 | 0.98 | 0.028 | 0.035 | 0.029 | 0.039 |
| 0.02 | 0.005 | 0.9 | 0.026 | 0.031 | 0.028 | 0.036 |
| 0.02 | 0.005 | 0.94 | 0.027 | 0.033 | 0.029 | 0.038 |
| 0.02 | 0.005 | 0.98 | 0.030 | 0.039 | 0.032 | 0.044 |
| 0.03 | 0.002 | 0.9 | 0.032 | 0.034 | 0.033 | 0.036 |
| 0.03 | 0.002 | 0.94 | 0.033 | 0.035 | 0.033 | 0.037 |
| 0.03 | 0.002 | 0.98 | 0.034 | 0.037 | 0.034 | 0.039 |
| 0.03 | 0.003 | 0.9 | 0.033 | 0.036 | 0.035 | 0.039 |
| 0.03 | 0.003 | 0.94 | 0.034 | 0.038 | 0.035 | 0.041 |
| 0.03 | 0.003 | 0.98 | 0.036 | 0.041 | 0.037 | 0.044 |
| 0.03 | 0.004 | 0.9 | 0.035 | 0.039 | 0.037 | 0.043 |
| 0.03 | 0.004 | 0.94 | 0.036 | 0.041 | 0.037 | 0.045 |
| 0.03 | 0.004 | 0.98 | 0.038 | 0.045 | 0.039 | 0.049 |
| 0.03 | 0.005 | 0.9 | 0.036 | 0.041 | 0.038 | 0.046 |
| 0.03 | 0.005 | 0.94 | 0.037 | 0.043 | 0.039 | 0.048 |
| 0.03 | 0.005 | 0.98 | 0.040 | 0.049 | 0.042 | 0.054 |
| 0.04 | 0.002 | 0.9 | 0.042 | 0.044 | 0.043 | 0.046 |
| 0.04 | 0.002 | 0.94 | 0.043 | 0.045 | 0.043 | 0.047 |
| 0.04 | 0.002 | 0.98 | 0.044 | 0.047 | 0.044 | 0.049 |
| 0.04 | 0.003 | 0.9 | 0.043 | 0.046 | 0.045 | 0.049 |
| 0.04 | 0.003 | 0.94 | 0.044 | 0.048 | 0.045 | 0.051 |
| 0.04 | 0.003 | 0.98 | 0.046 | 0.051 | 0.047 | 0.054 |
| 0.04 | 0.004 | 0.9 | 0.045 | 0.049 | 0.047 | 0.053 |
| 0.04 | 0.004 | 0.94 | 0.046 | 0.051 | 0.047 | 0.055 |
| 0.04 | 0.004 | 0.98 | 0.048 | 0.055 | 0.049 | 0.059 |
| 0.04 | 0.005 | 0.9 | 0.046 | 0.051 | 0.048 | 0.056 |
| 0.04 | 0.005 | 0.94 | 0.047 | 0.053 | 0.049 | 0.058 |
| 0.04 | 0.005 | 0.98 | 0.050 | 0.059 | 0.052 | 0.064 |
| Name | Ticker Symbol | Exchange | Sector | Float Shares | Start Time | End Time | Data Points |
|---|---|---|---|---|---|---|---|
| Abbott Laboratories | NYSE:ABT | NYSE | Medical Devices | 1767397615 | 16 Jan. 2015 | 30 Dec. 2016 | 492 |
| Zions Bancorp NA | NASDAQ:ZION | Nasdaq | Banks Regional | 176962996 | 16 Jan. 2015 | 30 Dec. 2016 | 493 |
| Williams Companies Inc. | NYSE:WMB | NYSE | Oil And Gas Midstream | 1212022398 | 01 Jan. 2020 | 26 June 2020 | 121 |
| Procter & Gamble | NYSE:PG | NYSE | Household And Personal Products | 2502633120 | 04 Jan. 2006 | 31 Dec. 2010 | 1258 |
| Intuit Inc | NASDAQ:INTU | Nasdaq | Software Application | 259243385 | 01 Jan. 2020 | 26 June 2020 | 121 |
| w | Error Variance | ||
|---|---|---|---|
| 0.722542 | 0.185968 | 0.464826 | 26.6742 |
| w | |||||
| GARCH(1,1) | 0.628876 | 0.139426 | 0.813362 | ||
| w | |||||
| ARCH(4) | 5.29924 | 0.0858145 | 0.198913 | 0.176051 | 0.14139 |
| AR(0) | w | ||||
| 0.103026 | 13.3097 |
| # | Candidate | AIC |
|---|---|---|
| 1 | GARCHProcess(1,1) | 1254.61 |
| 2 | GARCHProcess(0,1) | 1285.77 |
| 1 | ARCHProcess(4) | 1260.03 |
| 2 | ARCHProcess(3) | 1261.61 |
| 3 | ARCHProcess(5) | 1261.80 |
| 4 | ARCHProcess(2) | 1266.24 |
| 5 | ARCHProcess(1) | 1276.89 |
| 6 | ARCHProcess(0) | 1283.77 |
| 1 | ARProcess(0) | 459.57 |
| 2 | ARProcess(1) | 461.45 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Long, H.V.; Jebreen, H.B.; Dassios, I.; Baleanu, D. On the Statistical GARCH Model for Managing the Risk by Employing a Fat-Tailed Distribution in Finance. Symmetry 2020, 12, 1698. https://doi.org/10.3390/sym12101698
Long HV, Jebreen HB, Dassios I, Baleanu D. On the Statistical GARCH Model for Managing the Risk by Employing a Fat-Tailed Distribution in Finance. Symmetry. 2020; 12(10):1698. https://doi.org/10.3390/sym12101698
Chicago/Turabian StyleLong, H. Viet, H. Bin Jebreen, I. Dassios, and D. Baleanu. 2020. "On the Statistical GARCH Model for Managing the Risk by Employing a Fat-Tailed Distribution in Finance" Symmetry 12, no. 10: 1698. https://doi.org/10.3390/sym12101698
APA StyleLong, H. V., Jebreen, H. B., Dassios, I., & Baleanu, D. (2020). On the Statistical GARCH Model for Managing the Risk by Employing a Fat-Tailed Distribution in Finance. Symmetry, 12(10), 1698. https://doi.org/10.3390/sym12101698







