On the Degeneracy of the Orbit Polynomial and Related Graph Polynomials

Abstract

The orbit polynomial is a new graph counting polynomial which is defined as $O_G\left(x\right)={\sum }_{i=1}^r{x}^{|O_i|},$ where $O_1$, …, $O_r$ are all vertex orbits of the graph G. In this article, we investigate the structural properties of the automorphism group of a graph by using several novel counting polynomials. Besides, we explore the orbit polynomial of a graph operation. Indeed, we compare the degeneracy of the orbit polynomial with a new graph polynomial based on both eigenvalues of a graph and the size of orbits.

1. Introduction

In quantum chemistry, the early Hückel theory computes the levels of $\pi$-electron energy of the molecular orbitals in conjugated hydrocarbons, as roots of the characteristic/spectral polynomial which are called the eigenvalues of a molecular graph, see [1]. This concept was generalized by Hosoya [2] and the others [3,4,5] by changing the adjacency matrix with other matrices based on graph invariants. In the mathematical chemistry literature, the counting polynomials have first been introduced by Hosoya, see [6]. Other counting polynomials have later been proposed: Matching polynomial [7,8], independence [9,10], king [11,12], color [12], star or clique polynomials [13,14], etc. An overview of graph polynomials is provided in reference [15].

In the current work, we introduce a novel graph polynomial based on orbit-partitions of regarding graph, see [16,17]. It is derived from the concept of orbit polynomial. The typical terms of the orbit polynomial is of the form $c_n{x}^n$, where $c_n$ is the number of orbits of the automorphism group of size n. It should be noted that the characteristic polynomials do not characterize graphs due to several isospectral graphs, see [18].

We proceed as follows. In Section 2, the definitions used in the present work are introduced and known results needed are given. Section 3, contains the main results of this paper based on the orbit structure of a graph. Finally, in Section 4, by using the concept of graph spectra, we define a new version of orbit polynomial whose unique positive root is a measure that discriminate all graphs of order six, uniquely.

2. Preliminaries

In this research, $V\left(G\right)$ and $E\left(G\right)$ indicates the vertex and edge sets of the graph G, respectively. We assume that all graphs are simple, connected and finite.

In this paper, the automorphism group of a graph as well as the vertex-orbits are needed to infer the orbit polynomial. The automorphism group is a collection of all permutations on the set of vertices that preserves the adjacency between vertices of a graph, namely $e=xy$ is an edge of graph G if and only if $\pi \left(e\right)=\pi \left(x\right)\pi \left(y\right)$ is an edge. We denote the automorphism group of a graph G by Aut($G$).

For the vertex u, an orbit containing u is the collection of all $\alpha \left(v\right)$’s in which $\alpha$ is an automorphism element of G. The graph G is said to be vertex-transitive, if it has exactly one orbit. This means that in a vertex-transitive all vertices can be mapped to each other, namely for two elements a and b, there is at least an automorphism $\beta$ that $\beta \left(a\right)=b$. An edge-transitive graph can be defined similarly.

Let $\mathsf{\Gamma }$ be a group acting on the set X. The stabilizer of element $x\in X$ is defined as ${\mathsf{\Gamma }}_x=\{g\in \mathsf{\Gamma }:g.x=x\}.$ The orbit-stabilizer theorem implies that $|x^{\mathsf{\Gamma }}|\times |{\mathsf{\Gamma }}_x|=|\mathsf{\Gamma }|$, see [19].

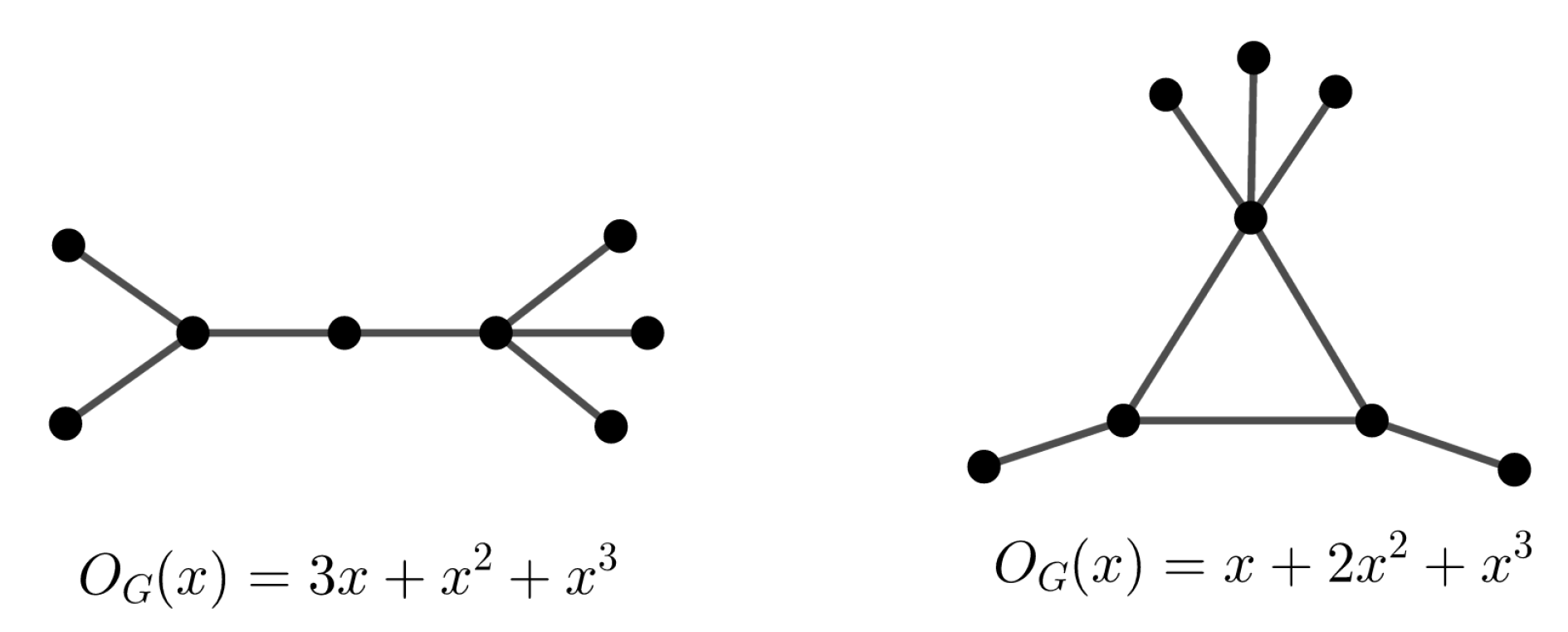
3. The Orbit and the Modified Orbit Polynomials

The orbit polynomial was defined by Dehmer et al. in [16] as

$$O_G\left(x\right)={\displaystyle \sum _{i=1}^t}{x}^{|O_i|},$$

where $O_1,\dots O_t$ are all vertex-orbits of G. Moreover, the the modified version of orbit polynomial, $O_G^{🟉}$ is defined as

$$O_G^{🟉}\left(x\right)=1-{\displaystyle \sum _{i=1}^t}{x}^{|O_i|}.$$

Many structural properties of a graph can be derived from the orbit polynomial. Let G be a graph of order n. From the definition, it is clear that if $Aut\left(G\right)\cong id$, then $O_G\left(x\right)=nx$ and thus $O_G^{🟉}\left(x\right)=1-nx$. Moreover, a graph is vertex-transitive if and only if $O_G\left(x\right)=x^n$ and consequently $O_G^{🟉}\left(x\right)=1-x^n$.

Example 1.

The cycle graph $C_n$ is vertex-transitive and by the above discussion $O_{C_n}\left(x\right)=x^n$ and $O_{C_n}^{🟉}\left(x\right)=1-x^n$.

Example 2.

For the path graph $P_n$ we obtain

$$\begin{array}{c}\hfill O_{P_n}\left(x\right)=\left\{\begin{array}{cc}\frac{n}{2}{x}^2,\hfill & 2\mid n\\ x+\frac{n-1}{2}{x}^2,\hfill & 2⩗n\end{array}\right.,\end{array}$$

and

$$\begin{array}{c}\hfill O_{P_n}^{🟉}\left(x\right)=\left\{\begin{array}{cc}1-\frac{n}{2}{x}^2,\hfill & 2\mid n\\ 1-x-\frac{n-1}{2}{x}^2,\hfill & 2⩗n\end{array}\right..\end{array}$$

From the orbit polynomial $P_n$, one can easily see that if n is even then $P_n$ has a pendant edge and if n is odd then $P_n$ has a central vertex, since each tree has a central vertex or a central edge, see [20]. We also explore that in the case that n is even (n is odd), then $P_n$ has $\frac{n}{2}$ ($\frac{n-1}{2}$) orbits of length two.

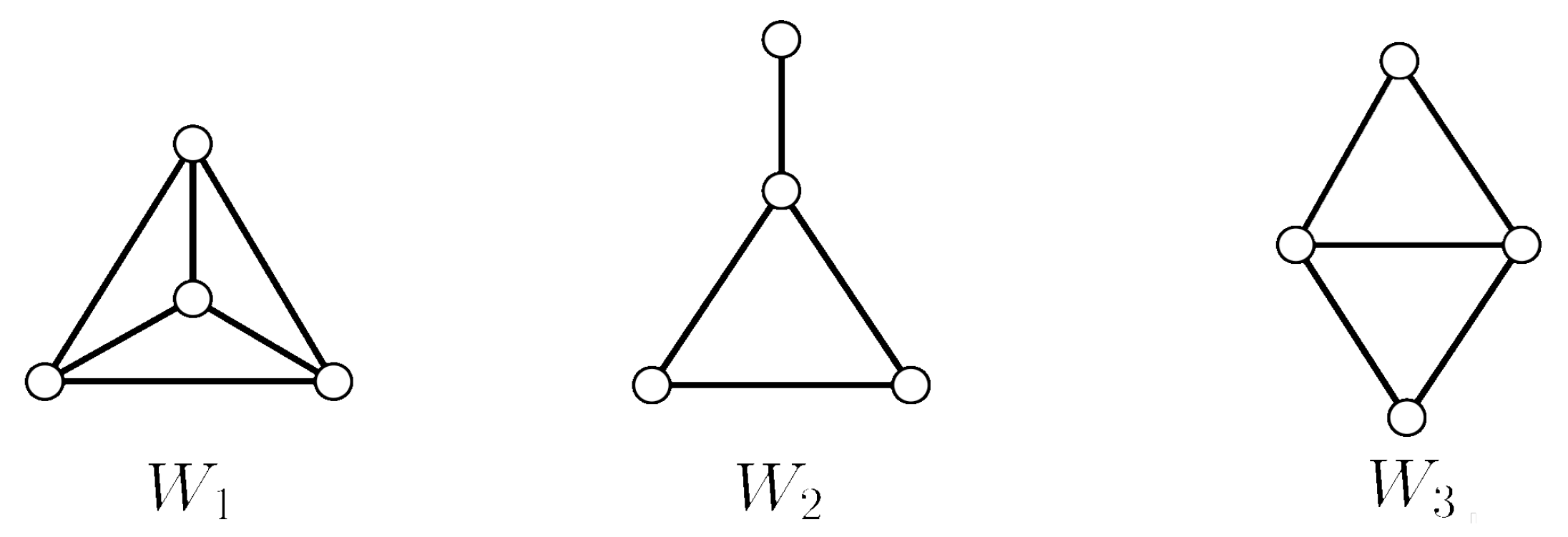
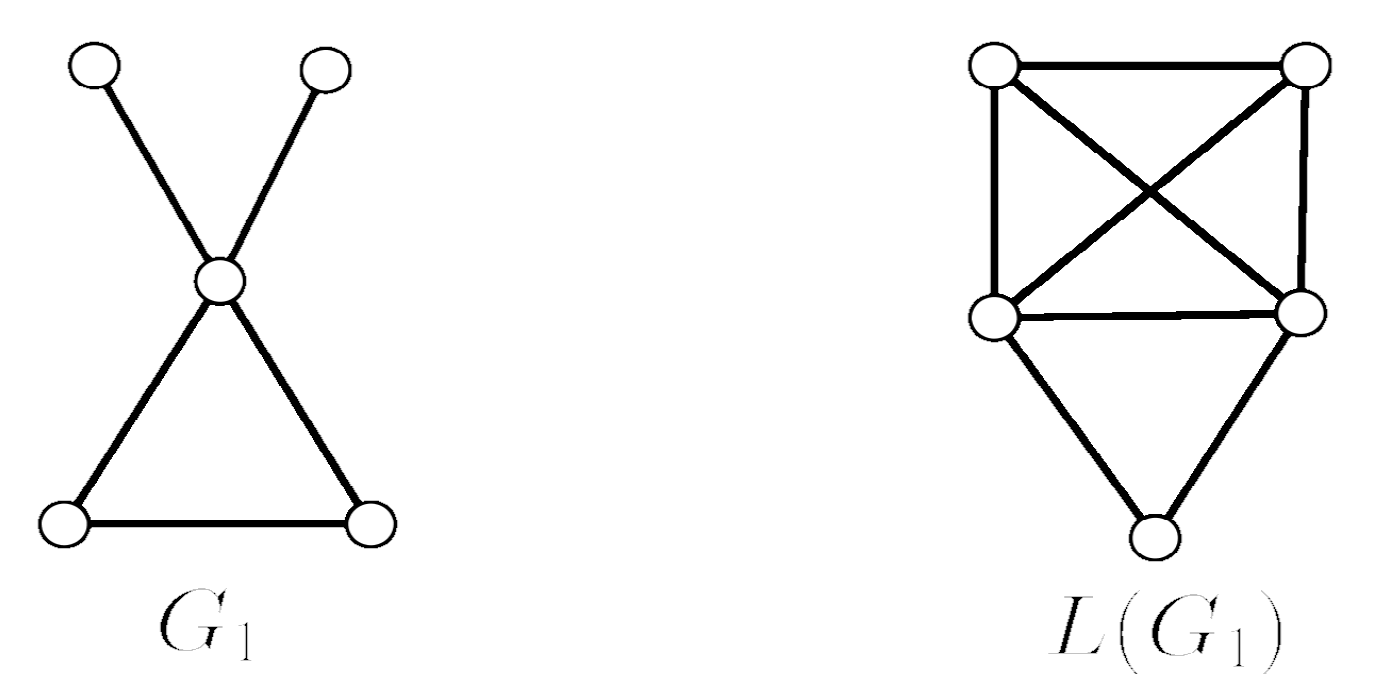
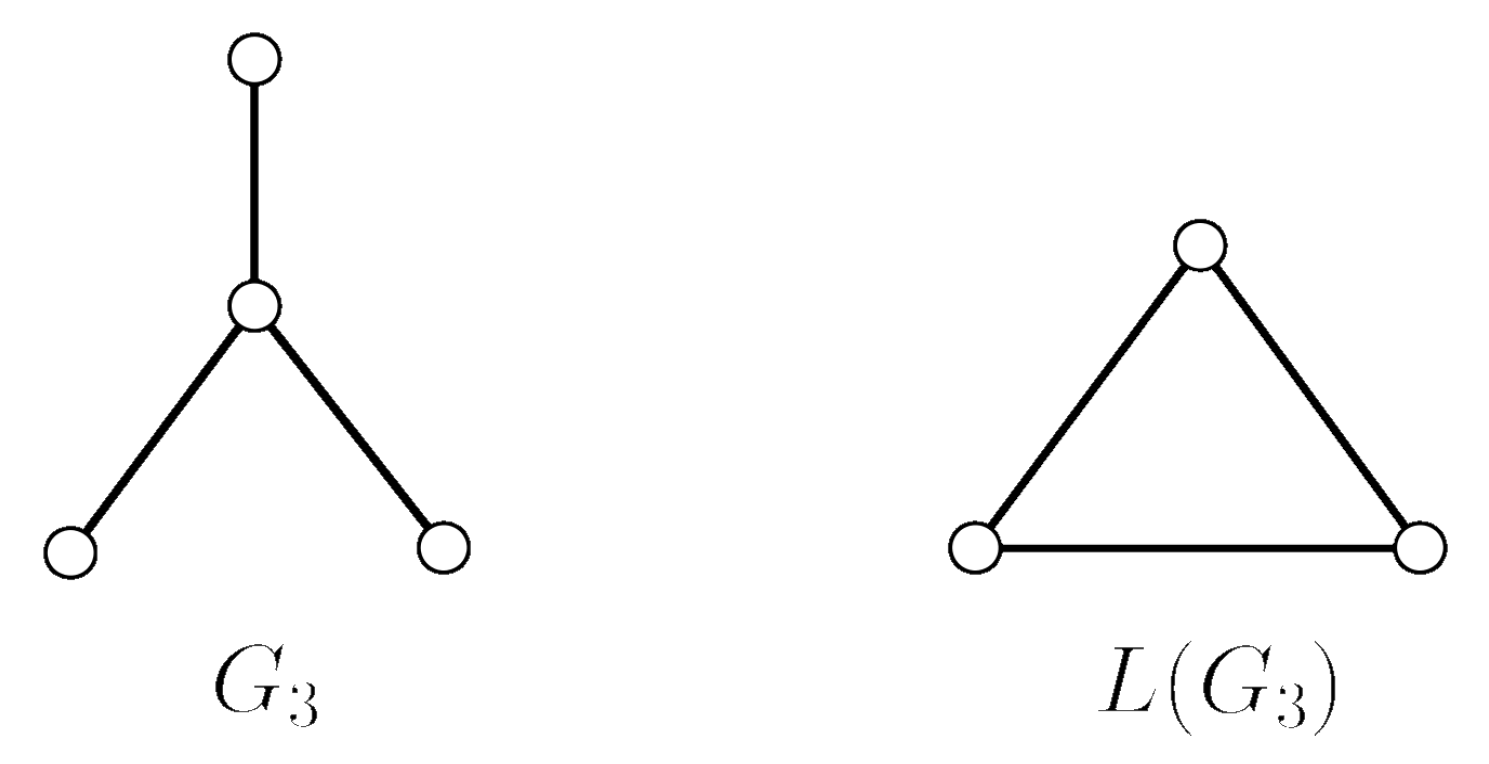
3.1. Orbit Polynomial of Line Graphs

An edge-automorphism of graph G is a bijection $\alpha$ on $E\left(G\right)$ such that two edges $e,f$ are adjacent if and only if $\alpha \left(e\right)$ and $\alpha \left(f\right)$ are adjacent in G. The set of all edge-automorphisms of graph G is also a group under the composition of functions and we denote it by $Au{t}_1\left(G\right)$.

Any automorphism $\alpha$ of G induces a bijection $\overline{\alpha }$ on $E\left(G\right)$, defined by $\overline{\alpha }\left(uv\right)=\alpha \left(u\right)\alpha \left(v\right)$. It is clear that $\overline{\alpha }$ is an edge-automorphism. The set

$$Au{t}^{🟉}\left(G\right)=\{\overline{\alpha }:\alpha \in Aut\left(G\right)\}$$

is a subgroup of $Aut\left(G\right)$ induced by edge-automorphisms of G.

Theorem 3

([20]). Assume that G is a graph of order $n\ge 3$. Then $Aut\left(G\right)\cong Au{t}^{🟉}\left(G\right)$.

For a graph G, its line graph $\mathcal{L}\left(G\right)$ is a new graph with the vertex set is $E\left(G\right)$ and two vertices are adjacent in $\mathcal{L}\left(G\right)$ if and only if the corresponding edges are adjacent in G. An automorphism of $\mathcal{L}\left(G\right)$ is an edge-automorphism of G. Suppose $\mathcal{W}=\{W_1,W_2,W_3\}$ are the set of graphs as depicted in Figure 1. Then we have the following theorem.

Theorem 4

([1]). For a connected graph G, where $G\notin \mathcal{W}$, we have

$$Aut\left(G\right)\cong Aut\left(\mathcal{L}\right(G\left)\right).$$

Consider two graphs $G_1$ and $\mathcal{L}\left(G_1\right)$ in Figure 2. Both of them have the same orbit polynomial $O_{G_1}\left(x\right)=O_{\mathcal{L}\left(G_1\right)}\left(x\right)=2x^2+x$ while for two graphs $G_2$ and $\mathcal{L}\left(G_2\right)$ in Figure 3, we have $O_{G_2}\left(x\right)=x^2+x^4$ and $O_{\mathcal{L}\left(G_2\right)}\left(x\right)=x^3+x$. Finally, consider the graph $G_3$ and its line graph as depicted in Figure 4. The automorphism group of both of them is isomorphic with symmetric group ${\mathbb{S}}_3$ but $O_{G_3}\left(x\right)=x+x^3$ and $O_{\mathcal{L}\left(G_3\right)}\left(x\right)=x^3$.

The distance between two vertices x and y a graph G is the length of the shortest path between them and we denote it by $d(x,y)$. For the vertex u of graph G, suppose ${\mathsf{\Gamma }}_i\left(u\right)$ is the number of vertices at distance i from u. If for two vertices u and v, we have ${\mathsf{\Gamma }}_i\left(u\right)={\mathsf{\Gamma }}_i\left(v\right)$ ($1\le i\le d\left(G\right)$) then they are Hosoya-equivalent or H-equivalent, see [21,22,23,24,25,26,27,28,29,30].

The set of H-equivalent vertices is called an H-partition of G. Moreover, the Hosoya polynomial is defined as ${\displaystyle P_G\left(x\right)={\displaystyle \sum _{i=1}^l}{x}^{h_i}}$, where $H_1,\dots ,H_l$ are all H-partitions of G and $h_i=\left|H_i\right|$. The modified Hosoya polynomial is also $P_G^{🟉}\left(x\right)=1-P_G\left(x\right)$.

Theorem 5.

Suppose $O_1,\dots ,O_r$ are all orbits of graph G. If for any pair of vertices $v_i\in O_i$ and $v_j\in O_j$, we have $deg\left(v_i\right)\ne deg\left(v_j\right)$$(1\le i,j\le r)$, then $O_i$’s are all H-partitions of G.

Proof. 

It is clear that two vertices in the same orbit have the same degree. Moreover, two vertices u and v in a same H-partition have the same degree, since $dds\left(u\right)=dds\left(v\right)$ yields that $s_1\left(u\right)=s_1\left(v\right)$. Thus, if vertices of different orbits have different degrees, then they are in different H-partitions. This completes the proof. □

Corollary 6.

If the degrees of orbit vertices are distinct, then the orbit and Hosoya polynomials are the same, namely

$$O_G\left(x\right)=P_G\left(x\right)and{O}_G^{🟉}\left(x\right)=P_G^{🟉}\left(x\right).$$

By considering the definition of action of automorphism group of graph G on the set of edges, the edge version of orbit polynomial can be defined as follows.

Definition 7.

Let $E_1,\dots E_h$ are all edge-orbits under the action of $Aut\left(G\right)$ on the set of edges. Then

$$\begin{array}{ccc}\hfill {\overline{O}}_G\left(x\right)& =& {\displaystyle \sum _{i=1}^h}{x}^{|E_i|},\hfill \\ \hfill {\overline{O}}_G^{🟉}\left(x\right)& =& 1-{\displaystyle \sum _{i=1}^h}{x}^{|E_i|}.\hfill \end{array}$$

For example, the star graph $S_n$ is edge-transitive; hence ${\overline{O}}_{S_n}=x^{\left|E\right|}=x^{n-1}$ and ${\overline{O}}_{S_n}^{🟉}=1-x^{n-1}$. On the other hand, if T is a tree on n vertices with ${\overline{O}}_T\left(x\right)=x^{n-1}$, then T is edge-transitive and so T is a bi-regular graph, which means that all vertices of T are of degrees r and s for some $r,s\in \mathbb{N}$. If T is regular, then $T\cong K_2$ which confirms our claim. If T is a bi-regular tree, then $T\cong S_n$, since the pendant vertices compose an orbit and the central vertex is a singleton orbit. Notice that if $n\ge 3$, then an edge-transitive tree has not a central edge. Hence, we proved the following theorem.

Theorem 8.

The edge-orbit polynomial ${\overline{O}}_T\left(x\right)=x^{n-1}$ if and only if $T\cong S_n$.

In continuing this section, we prove that the cycle graph $C_n$ can be characterized by its edge-orbit polynomial.

Theorem 9.

Let G be a graph without a pendant edge. Then $O_G\left(x\right)={\overline{O}}_G\left(x\right)$ if and only if $G\cong C_n$.

Proof. 

If $G\cong C_n$, then we are done. Conversely, by $O_G\left(x\right)={\overline{O}}_G\left(x\right)$, one can immediately conclude that the number of edges and the number of vertices of graph G are the same and thus G is a unicycle graph. If G has a vertex of degree greater than two, then G has at least two cycles, a contradiction. Hence, G is a connected regular graph of degree 2 and the assertion follows. □

Suppose G is a graph with k orbits of equal sizes. Then $O_G\left(x\right)=k{x}^{\frac{n}{k}}$ and thus zero is the only root of $O_G$. On the other hand, if $x=0$ is the only root of $O_G$, then $O_G\left(x\right)=k{x}^t$, for some $k,t\in \mathbb{N}$. However, the set of orbits of a graph is a partition of the vertex set and thus $kt=n$, which means that $t=\frac{n}{k}$. In particular, if $k=1$ then G is vertex-transitive and if $k=n$ then G is asymmetric graph. Hence, we proved the following theorem.

Theorem 10.

The integer $x=1$ is a root of $O_G^{🟉}\left(x\right)$ if and only if G is vertex-transitive.

Proof. 

If G is vertex-transitive, then $O_G^{🟉}\left(x\right)=1-x^n$ and clearly $x=1$ is a zero of it. Conversely, if $x=1$ is a zero of $O_G^{🟉}\left(x\right)=1-{\sum }_{i=1}^r{a}_i{x}^{|O_i|}$, then $O_G^{🟉}\left(1\right)=1-a_1-\dots -a_r=0$. Since, $a_i\ge 1$, necessarily $r=1$ and $a_1=1$ which yields that G is vertex-transitive as desired. □

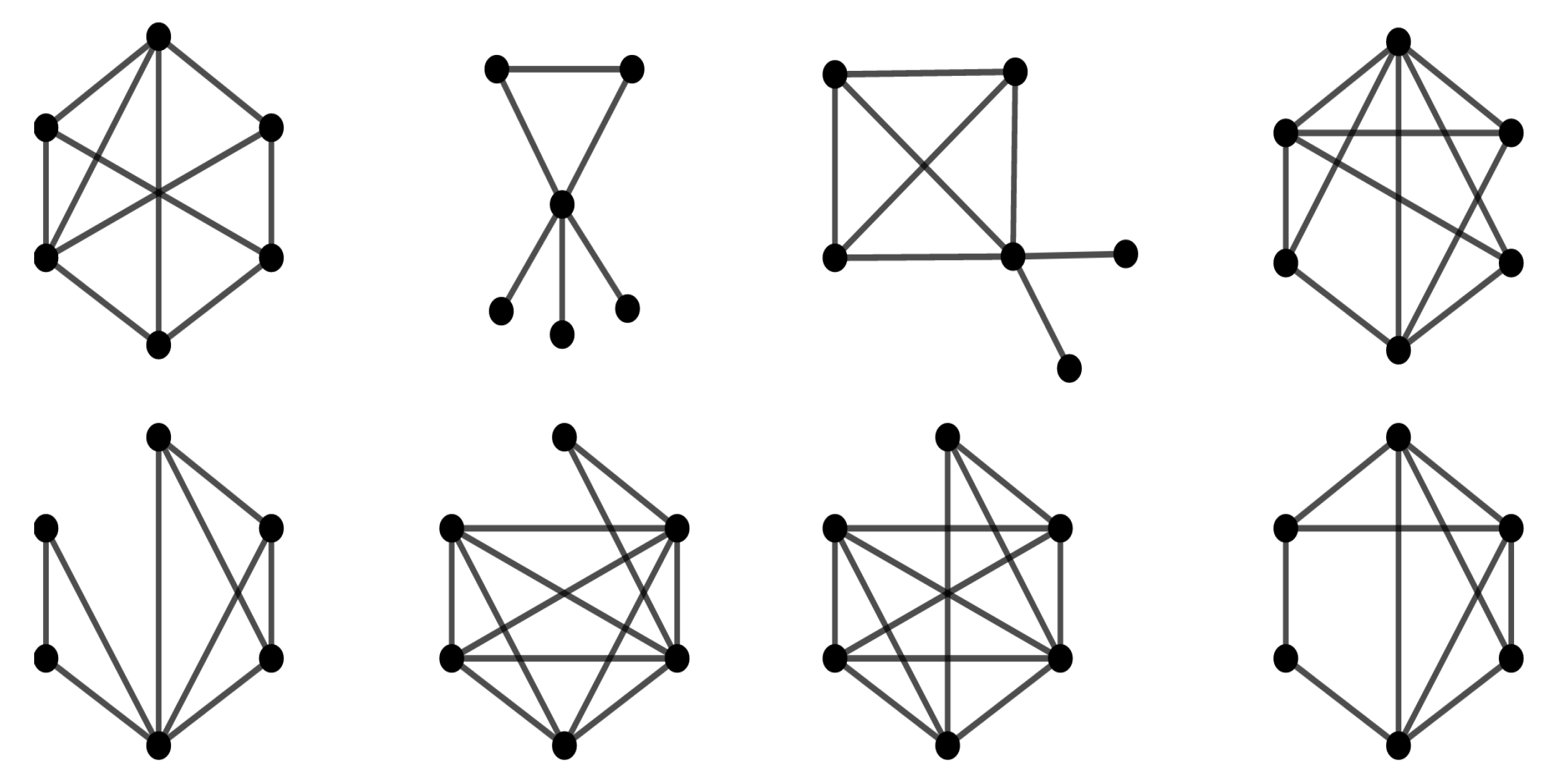
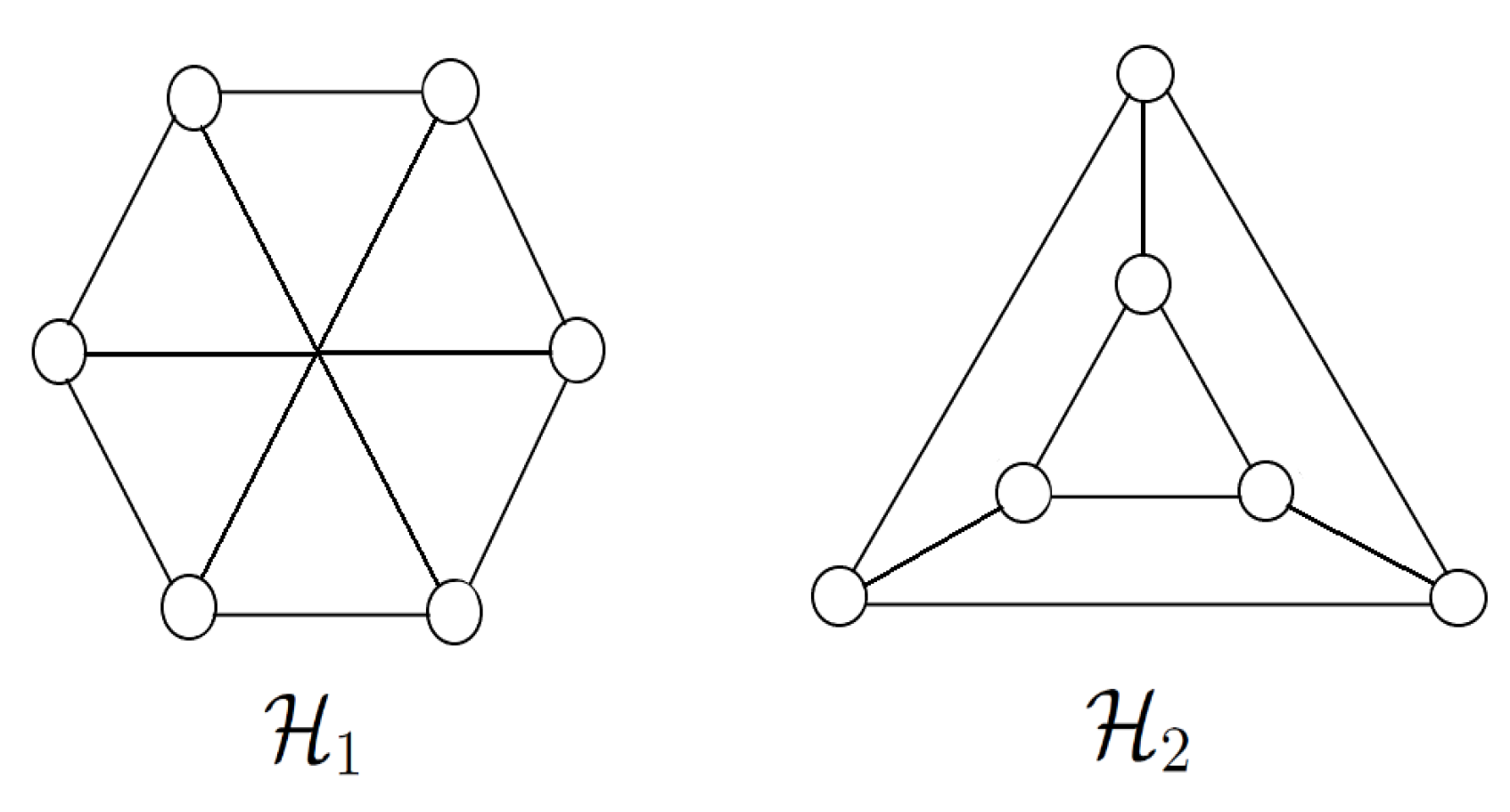
3.2. Graph Classification with Respect to Orbit Polynomial

One of the classical problem in algebraic graph theory is characterizing the graphs in terms of the graph polynomials. Here, we introduce three classes of trees that can be characterized by their orbit polynomials.

Theorem 11.

If G is a graph with orbit polynomial $x+x^2+x^3$, then G is a graph on 6 vertices. Moreover, if G has a pendant edge, then it has three pendant edges.

Proof. 

Clearly, G has 6 vertices, since the set of orbits is a partition for the vertex set. If G has only one pendant edge, then its endpoints compose two different singleton orbits, a contradiction. If G has two pendant edges, then necessarily they compose an orbit of size two. These edges share a common vertex, because in other case either we have two orbits of sizes 2 and 4 or three orbits of size two or there are two orbits of size 2, all of them are contradictions. Hence, three other vertices are in the same orbit and they have the same degree. If they are of degree 2, then $G\cong (K_3\cup {\overline{K}}_2)+K_1$ or $G\cong C_4+3e$. If $G\cong C_4+3e$, then $O_G\left(x\right)=2x+2x^2$, a contradiction. □

Example 12.

All graphs on six vertices with the orbit polynomial $O_G\left(x\right)=x+x^2+x^3$ are as depicted in Figure 5. They have different automorphism groups while their orbit polynomials are the same.

Example 13.

Suppose $O_G\left(x\right)=ax+b{x}^2+c{x}^3$. Then $O_G\left(1\right)=a+2b+3c=n$, $(1\le a,b,c\le 3)$ and thus $6\le n\le 18$. All graphs with this property have at least six and at most 18 vertices. The problem is solved completely for $n=6$. If $n=7$, then necessarily $a=2$ and $b=c=1$. Hence, $O_G\left(x\right)=2x+x^2+x^3$. This means that the related graph has two orbits of size 1, an orbit of size 2 and an orbit of size 3. There are 39 graphs of order 7 by this property. Some of them are depicted in Figure 6.

If $n=8$, then $O_G\left(x\right)=3x+x^2+x^3$ or $O_G\left(x\right)=x+2x^2+x^3$, see Figure 7. Since the orbit sizes are $1,2,3$, then by orbit-stabilizer theorem, we obtain

$$2,3\mid \left|Aut\right(G\left)\right|\mathrm{and}\gcd (2,3)=1,$$

(1)

and thus $6\mid \left|\mathrm{Aut}\right(G\left)\right|$. On the other hand, G has no a permutation of order 6, since otherwise we have a singleton orbit. Moreover, by a similar argument, we can show that there is no permutation of order 5 or 4. This means that G is a $\{2,3\}$ group and thus $\left|Aut\left(G\right)\right|=2^{\alpha }.3^{\beta }$, since all orbits are of sizes 1, 2, 3. If for example, we have only one orbit of each size 1, 2 and 3, then $\left|Aut\left(G\right)\right|=2^{\alpha }.3^{\beta }$, where $\alpha \in \{0,1\}$ and $\beta \in \{0,1\}$. This means that by applying Equation (1), $\left|\mathrm{Aut}\right(G\left)\right|=$ 6 or 12 and thus $Aut\left(G\right)\cong {\mathbb{Z}}_6$ or ${\mathbb{S}}_3$ or ${\mathbb{Z}}_2\times {\mathbb{S}}_3$. Hence, we proved the following theorem.

Theorem 14.

Let G be a graph of order 6. Then $O_G\left(x\right)=x+x^2+x^3$ if and only if $Aut\left(G\right)\cong {\mathbb{Z}}_6$ or ${\mathbb{S}}_3$ or ${\mathbb{Z}}_2\times {\mathbb{S}}_3$.

4. Orbit-Entropy Polynomial

The characteristic polynomial [1] of a graph G with adjacency matrix $A\left(G\right)$ is

$$\chi (G,\lambda )=det(\lambda I-A(G\left)\right).$$

The roots of this polynomial are eigenvalues of G and form the spectrum of G as

$$spec\left(G\right)=\left\{{\left[{\lambda }_1\right]}^{m_1},{\left[{\lambda }_2\right]}^{m_2},\dots ,{\left[{\lambda }_r\right]}^{m_r}\right\},$$

where $m_i$ ($1\le i\le r$) is the multiplicity of eigenvalue ${\lambda }_i$ and ${\lambda }_1\ge {\lambda }_2\ge \dots \ge {\lambda }_r$.

Here, consider all graphs of order six and their orbit polynomials as reported in

Table 1. All graphs of order six together with their unique positive roots of $O_G^{🟉}$ and ${\tilde{O}}_G$.

Edges	${\mathit{O}}_{\mathit{G}}\left(\mathit{x}\right)$	${\mathit{\delta }}_1$	${\mathit{\delta }}_2$
$1215162334364556$	$x^6$	1	$0.6702212$
$121416232534364556$	$x^6$	$0.1666667$	1
$121314162324253536454656$	$x^6$	1	$1.0699132$
$1213142536454656$	$x^6$	$0.1666667$	$1.113457$
$121314151623242526343536454656$	$x^6$	1	$1.1383303$
$121623344556$	$x^6$	1	$1.164993$
$12131415162326344556$	$x^5+x$	$0.7548777$	$0.4729019$
$1213141516$	$x^5+x$	$0.7548777$	$0.7548777$
$121314151626364656$	$x^4+x^2$	$0.7861514$	$0.8941061$
$1213141526364656$	$x^4+x^2$	$0.7861514$	$0.9495666$
$1213242534354656$	$x^4+x^2$	$0.7861514$	$0.9550358$
$12131415162324252634354656$	$x^4+x^2$	$0.7861514$	$0.9586942$
$1213144546$	$x^4+x^2$	$0.7861514$	$0.986161$
$1213141516232425263435364546$	$x^4+x^2$	$0.7861514$	$0.9962842$
$1213141523242634354656$	$x^4+x^2$	$0.7861514$	$1.017727$
$12131423243536454656$	$x^4+x^2$	$0.7861514$	$1.018589$
$1213232434454656$	$x^4+x^2$	$0.7861514$	$1.032434$
$12131524263456$	$x^4+x^2$	$0.7861514$	$1.043184$
$12132324253435454656$	$x^4+x^2$	$0.7861514$	$1.048236$
$1213142324343536454656$	$x^4+x^2$	$0.7861514$	$1.053093$
$12132334454656$	$x^4+x^2$	$0.7861514$	$1.064051$
$1223242526343536454656$	$x^4+2x$	$0.4746266$	$0.8519102$
$12131415162345$	$x^4+2x$	$0.4533977$	$0.866788$
$121416232425263436454656$	$2x^3$	$0.7937005$	$0.9545863$
$121314232536$	$2x^3$	$0.7937005$	$1.052146$
$121623242634454656$	$2x^3$	$0.7937005$	$1.0553004$
$1213141516242634364556$	$x^3+x^2+x$	$0.543689$	$0.6815621$
$12141516232534364556$	$x^3+x^2+x$	$0.543689$	$0.7255892$
$121314151656$	$x^3+x^2+x$	$0.543689$	$0.7655241$
$12131416232426344556$	$x^3+x^2+x$	$0.543689$	$0.8057402$
$1213141516454656$	$x^3+x^2+x$	$0.543689$	$0.8307845$
$12131423242526343536454656$	$x^3+x^2+x$	$0.543689$	$0.8466243$
$121323242526343536454656$	$x^3+x^2+x$	$0.543689$	$0.8593803$
$121314232434454656$	$x^3+x^2+x$	$0.543689$	$0.8959589$
$1213141525354556$	$x^3+3x$	$0.3221854$	$0.5236913$
$12131415364656$	$x^3+3x$	$0.3221854$	$0.5303547$
$1213141556$	$x^3+3x$	$0.3221854$	$0.5623349$
$12131423242534354556$	$x^3+3x$	$0.3221854$	$0.6598521$
$1213142324344556$	$x^3+3x$	$0.3221854$	$0.7888727$
$121314232435364546$	$3x^2$	$0.5773503$	$0.754669$
$12131415354556$	$3x^2$	$0.5773503$	$0.7832625$
$1213141525453656$	$3x^2$	$0.5773503$	$0.7906526$
$121314354556$	$3x^2$	$0.5773503$	$0.7941527$
$1213152324263435454656$	$3x^2$	$0.5773503$	$0.8132007$
$12131423243435364546$	$3x^2$	$0.5773503$	$0.8189366$
$13142324354656$	$3x^2$	$0.5773503$	$0.8463915$
$121324343536454656$	$3x^2$	$0.5773503$	$0.8475269$
$12131423242536454656$	$3x^2$	$0.5773503$	$0.8496398$
$121314151623243435454656$	$3x^2$	$0.5773503$	$0.8570451$
$1213141535344556$	$3x^2$	$0.5773503$	$0.863892$
$12131434354556$	$3x^2$	$0.5773503$	$0.8752257$
$121623263435364556$	$3x^2$	$0.5773503$	$0.8791742$
$121423343546$	$3x^2$	$0.5773503$	$0.8799624$
$1223344556$	$3x^2$	$0.5773503$	$0.8943799$
$1213142324354656$	$3x^2$	$0.5773503$	$0.8985653$

and

Table 2. (Continuation of Table 1).

Edges	${\mathit{O}}_{\mathit{G}}\left(\mathit{x}\right)$	${\mathit{\delta }}_1$	${\mathit{\delta }}_2$
$1213141516344556$	$2x^2+2x$	$0.3660254$	$0.2511261$
$1213151623344556$	$2x^2+2x$	$0.3660254$	$0.3991883$
$12141516233435364556$	$2x^2+2x$	$0.3660254$	$0.5461031$
$12131435364546$	$2x^2+2x$	$0.3660254$	$0.5707891$
$121314154656$	$2x^2+2x$	$0.3660254$	$0.5840871$
$12131434354656$	$2x^2+2x$	$0.3660254$	$0.6006301$
$121314151623263435454656$	$2x^2+2x$	$0.3660254$	$0.6079497$
$1213141516232634364656$	$2x^2+2x$	$0.3660254$	$0.6146048$
$121323242534354656$	$2x^2+2x$	$0.3660254$	$0.6146802$
$12131415163436454656$	$2x^2+2x$	$0.3660254$	$0.6220295$
$1213141516232634354556$	$2x^2+2x$	$0.3660254$	$0.6358562$
$1213141524344556$	$2x^2+2x$	$0.3660254$	$0.6387785$
$1213143536454656$	$2x^2+2x$	$0.3660254$	$0.6393063$
$12131416232634454656$	$2x^2+2x$	$0.3660254$	$0.6438021$
$1213141516234556$	$2x^2+2x$	$0.3660254$	$0.6500915$
$12131415234656$	$2x^2+2x$	$0.3660254$	$0.6508345$
$12131415162334354556$	$2x^2+2x$	$0.3660254$	$0.6566663$
$12131415164556$	$2x^2+2x$	$0.3660254$	$0.6618526$
$121314454656$	$2x^2+2x$	$0.3660254$	$0.6629316$
$121314151623344556$	$2x^2+2x$	$0.3660254$	$0.6712485$
$12131415164556$	$2x^2+2x$	$0.3660254$	$0.6736593$
$121314232434354556$	$2x^2+2x$	$0.3660254$	$0.6858483$
$121314354656$	$2x^2+2x$	$0.3660254$	$0.6927251$
$121315162326344556$	$2x^2+2x$	$0.3660254$	$0.6933868$
$1213141523454656$	$2x^2+2x$	$0.3660254$	$0.7033814$
$1213143645$	$2x^2+2x$	$0.3660254$	$0.7035179$
$12152334454656$	$2x^2+2x$	$0.3660254$	$0.7133716$
$121314162325344556$	$x^2+4x$	$0.236068$	$0.409835$
$1213141534364556$	$x^2+4x$	$0.236068$	$0.4131627$
$1213141526344656$	$x^2+4x$	$0.236068$	$0.4183624$
$121314154556$	$x^2+4x$	$0.236068$	$0.4276625$
$121314253546$	$x^2+4x$	$0.236068$	$0.4343068$
$1213144556$	$x^2+4x$	$0.236068$	$0.4411921$
$12131415162325344556$	$x^2+4x$	$0.236068$	$0.4527634$
$121314152325344556$	$x^2+4x$	$0.236068$	$0.4601455$
$121314151634254556$	$x^2+4x$	$0.236068$	$0.4609852$
$121323242534354556$	$x^2+4x$	$0.236068$	$0.4722518$
$12131415232456$	$x^2+4x$	$0.236068$	$0.4798687$
$12131415232426344556$	$x^2+4x$	$0.236068$	$0.4853394$
$121314151634364546$	$x^2+4x$	$0.236068$	$0.4879452$
$12132324344556$	$x^2+4x$	$0.236068$	$0.4913081$
$1213141536454656$	$x^2+4x$	$0.236068$	$0.4950764$
$1213141516232434354556$	$x^2+4x$	$0.236068$	$0.4981524$
$121316232634354556$	$x^2+4x$	$0.236068$	$0.4990413$
$12131424343536454656$	$x^2+4x$	$0.236068$	$0.513049$
$12131415234546$	$x^2+4x$	$0.236068$	$0.5143182$
$121314153456$	$x^2+4x$	$0.236068$	$0.5174416$
$121314234556$	$x^2+4x$	$0.236068$	$0.5219741$
$1213141523344556$	$6x$	$0.1666667$	$0.3597291$
$121314162334354556$	$6x$	$0.1666667$	$0.36443$
$1213141523344556$	$6x$	$0.1666667$	$0.3744274$
$1213141523344656$	$6x$	$0.1666667$	$0.3752572$
$12131415453656$	$6x$	$0.1666667$	$0.3787899$
$12131415353645$	$6x$	$0.1666667$	$0.3788464$
$12131435454656$	$6x$	$0.1666667$	$0.3808788$
$121314344556$	$6x$	$0.1666667$	$0.3903846$

. There are 13 graphs with the same orbit polynomial $O_G=x^2+x^4$. This means that the orbit polynomial has not a power discrimination to characterize all graphs of the same order. In [16], it is claimed that the degeneracy of roots of the modified version of orbit polynomial is less than orbit polynomial, but for the 13 mentioned graph of order 6, we obtain $O_G^{🟉}=1-x^2-x^4$ which implies that the modified orbit polynomial is not also a powerful discrimination to capture structural information for these graphs. Here, we introduce a new polynomial with more powerful discrimination than orbit polynomial, to capture structural information.

A number of measures using Shannon’s entropy function have been introduced and investigated since the fifties, see [31,32,33,34]. The discrete form of this well-known function is defined for a probability vector $p=(p_1,p_2,\dots ,p_n)$ and has the form ${\displaystyle I\left(p\right)=-{\displaystyle \sum _{i=1}^n}{p}_{i}log\left(p_i\right)}$; see [35,36].

Let ${\lambda }_1,\dots ,{\lambda }_s$ be all non-zero eigenvalues of a graph G. Then $I_{\lambda }\left(G\right)$ is called the eigenvalue-entropy based on ${\lambda }_i$’s, where

$${\displaystyle I_{\lambda }\left(G\right)=-{\displaystyle \sum _{i=1}^s}{\displaystyle \frac{c_i\left|{\lambda }_i\right|}{{\sum }_{j=1}^s{c}_j\left|{\lambda }_j\right|}}log\left({\displaystyle \frac{c_i\left|{\lambda }_i\right|}{{\sum }_{j=1}^s{c}_j\left|{\lambda }_j\right|}}\right).}$$

(2)

If $c_1=c_2=\dots =c_s$, then the Equation (2) can be reformulated as follows:

$${\displaystyle I_{\lambda }\left(G\right)=-{\displaystyle \sum _{i=1}^s}{\displaystyle \frac{|{\lambda }_i|}{\mathcal{E}\left(G\right)}}log\left({\displaystyle \frac{|{\lambda }_i|}{\mathcal{E}\left(G\right)}}\right),}$$

where $\mathcal{E}\left(G\right)={\sum }_{j=1}^s\left|{\lambda }_j\right|$ is the adjacency energy of graph G, see [5,37].

The degeneracy problem of orbit polynomial can be overcome, by constructing the so-called super polynomial which is defined by subtracting the orbit polynomial from eigenvalue entropy:

$${\tilde{O}}_G\left(x\right)=I_{\lambda }\left(G\right)-{\displaystyle \sum _{i=1}^r}{x}^{|O_i|}=I_{\lambda }\left(G\right)-O_G\left(x\right).$$

The unique positive roots ($\delta$) of the orbit-entropy polynomials ${\tilde{O}}_G$ for all graphs of order six is reported in the third column of Table 1. Comparing these quantities with the orbit polynomial roots, we obtain that $\delta$’s are distinct, for all these 13 graphs.

Bear in mind that two vertex-transitive graphs of the same order have the same orbit polynomials and thus the same modified orbit polynomials. However, in general, their orbit-entropy polynomials are not equal. For example, consider two graphs ${\mathcal{H}}_1$ and ${\mathcal{H}}_2$ in Figure 8. The spectrum of these graphs are

$$spec\left({\mathcal{H}}_1\right)=\{{[-3]}^1,{\left[0\right]}^4,{\left[3\right]}^1\},$$

and

$$spec\left({\mathcal{H}}_2\right)=\{{[-2]}^2,{\left[0\right]}^2,{\left[1\right]}^1,{\left[3\right]}^1\}.$$

Then $I_{\lambda }\left({\mathcal{H}}_1\right)=1$ and $I_{\lambda }\left({\mathcal{H}}_2\right)=1.41$. Hence, ${\tilde{O}}_{{\mathcal{H}}_1}=1-x^6,$ and ${\tilde{O}}_{{\mathcal{H}}_2}=1.41-x^6$ while the orbit polynomial of both of them is $O_{{\mathcal{H}}_i}=x^6,i=1,2$.

5. Summary and Conclusions

The Hosoya partition and the orbit polynomials of several kinds of graphs were investigated. Moreover, a relation between the orbit and Hosoya partition polynomials was explored. We also defined a new polynomial based on both orbit sizes and eigenvalues of a graph, and it was shown that the degeneracy of new polynomial relative to the orbit polynomial is quite low. Applying the theory of groups, especially the automorphism group approach used in this paper, enables one to analyze networks and we capture information about the number of interconnections of components. Finally, a characterization for all graphs with orbit polynomial $O_G\left(x\right)=x+x^2+x^3$ is given.