Exact Solutions and Conservation Laws of the (3 + 1)-Dimensional B-Type Kadomstev–Petviashvili (BKP)-Boussinesq Equation
Abstract
1. Introduction
2. Lie Point Symmetry
3. The Optimal System of One-Dimensional Subalgebras
4. Similarity Reductions of the BKP-Boussinesq Equation
5. The Explicit Solutions of Reduced Equations
5.1. Description of the Tanh Method
- Consider a general form of nonlinear partial differential equationwhere F is a polynomial of the u and its derivatives.
- Next, we introduce an independent variablewhich has the following changes
- We assume that the solution of Equation (24) is written in the following formwhere k is an integer, which is determined by balancing the highest order derivative terms with the nonlinear terms in the resulting equation. After determining k, putting Equations (26) and (27) into Equation (24), we get a polynomial concerning . Then we collect all terms of and make each of them equal to zero, which obtaina the algebraic equations containing unknown numbers and c. Solving these equations, we get the values of unknowns. Finally, plugging these values into equations, we derive exact solutions of equations.
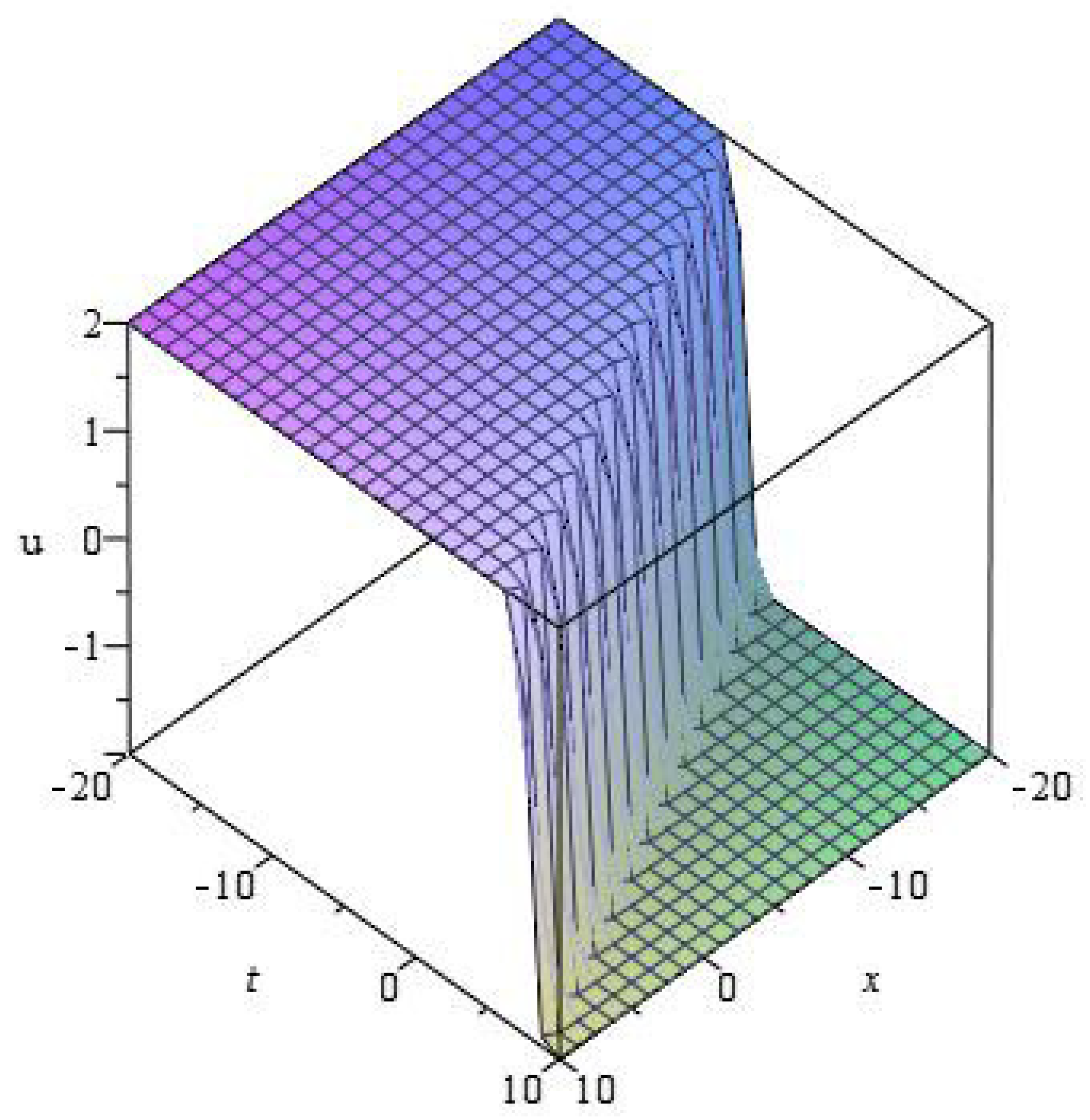
5.2. Exact Solution of Equation (12)
5.3. Exact Solution of Equation (13)
5.4. Exact Solution of Equation (14)
5.5. Exact Solution of Equation (15)
5.6. Exact Solution of Equation (16)
6. Construction of Conservation Laws
6.1. Nonlinear Self-Adjointness of Equation (2)
6.2. Construction of Conservation Laws
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wazwaz, A.M. Two B-type Kadomtsev-Petviashvili equations of (2 + 1) and (3 + 1) dimensions: Multiple soliton solutions, rational solutions and periodic solutions. Comput. Fluids 2013, 86, 357–362. [Google Scholar] [CrossRef]
- Verma, P.; Kaur, L. Integrability, bilinearization and analytic study of new form of (3 + 1)-dimensional B-type Kadomstev–Petviashvili (BKP)-Boussinesq equation. Appl. Math. Comput. 2019, 346, 879–886. [Google Scholar] [CrossRef]
- Cheng, L.; Zhang, Y. Grammian-type determinant solutions to generalized KP and BKP equations. Comput. Math. Appl. 2017, 74, 727–735. [Google Scholar] [CrossRef]
- Tu, J.M.; Tian, S.F.; Xu, M.J.; Ma, P.L.; Zhang, T.T. On periodic wave solutions with asymptotic behaviors to a (3 + 1)-dimensional generalized B-type Kadomtsev-Petviashvili equation in fluid dynamics. Comput. Math. Appl. 2016, 72, 2486–2504. [Google Scholar] [CrossRef]
- Yang, J.Y.; Ma, W.X. Lump solutions to the BKP equation by symbolic computation. Int. J. Modern Phys. B 2016, 30, 1–7. [Google Scholar] [CrossRef]
- Ma, W.X.; Zhu, Z. Solving the (3 + 1)-dimensional generalized KP and BKP equations by the multiple exp-function algorithm. Appl. Math. Comput. 2012, 218, 11871–11879. [Google Scholar] [CrossRef]
- Wazwaz, A.M.; Tantawy, S.A.E. Solving the (3 + 1)-dimensional KP-boussinesq and BKP-boussinesq equations by the simplified hirotas method. Nonlinear Dyn. 2017, 88, 3017–3021. [Google Scholar] [CrossRef]
- Yan, X.W.; Tian, S.F.; Dong, M.J.; Zou, L. Bäcklund transformation, rogue wave solutions and interaction phenomena for a (3 + 1)-dimensional B-type Kadomtsev-Petviashvili-Boussinesq equation. Nonlinear Dyn. 2018, 92, 709–720. [Google Scholar] [CrossRef]
- Hirota, R. Exact solutions of the Sine-Gordon equation for multiple collisions of solitons. J. Phys. Soc. Jpn. 1972, 33, 1459–1463. [Google Scholar] [CrossRef]
- Fan, E.; Zhang, H.Q. A note on the homogeneous balance method. Phys. Lett. A 1998, 246, 403–406. [Google Scholar] [CrossRef]
- Baskonus, H.M.; Bulut, H.; Sulaiman, T.A. New Complex Hyperbolic Structures to the Lonngren-Wave Equation by Using Sine-Gordon Expansion Method. Appl. Math. Nonlinear Sci. 2019, 4, 129–138. [Google Scholar] [CrossRef]
- Imai, K. Generlization of Kaup-Newell inverse scattering formulation and Darboux transformation. J. Phys. Soc. 1999, 68, 355–359. [Google Scholar] [CrossRef]
- Wang, M.L.; Li, X.Z.; Zhang, J.L. The (G′/G)-expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics. Phys. Lett. A 2008, 372, 417–423. [Google Scholar] [CrossRef]
- Khalique, C.M.; Mhlanga, I.E. Travelling waves and conservation laws of a (2 + 1)-dimensional coupling system with Korteweg-de Vries equation. Appl. Math. Nonlinear Sci. 2018, 3, 241–254. [Google Scholar] [CrossRef]
- Hydon, P.E. Symmetry Methods for Differential Equations; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Sophus, L. Theories der Tranformationgruppen, Dritter and Letzter Abschnitt; Teubner: Leipzig/Berlin, Germany, 1888. [Google Scholar]
- Olver, P.J. Applications of Lie Groups to Differential Equations; Springer: Heidelberg, Germany, 1986. [Google Scholar]
- Ovsiannikov, L.V. Group Analysis of Differential Equations; Academic Press: New York, NY, USA, 1982. [Google Scholar]
- Boiti, M.; Leon, J.J.; Manna, M.; Pempinelli, F. On the spectral transform of a Korteweg-de Vries equation in two spatial dimensions. Inverse Probl. 1986, 2, 271–279. [Google Scholar] [CrossRef]
- Wazwaz, A.M. The Tanh method: solitons and periodic solutions for the Dodd-Bullough-Mikhailov and the Tzitzeica-Dodd-Bullough equations. Chaos Solitons Fractals. 2015, 25, 55–63. [Google Scholar] [CrossRef]
- Malfliet, W. Solitary wave solutions of nonlinear wave equations. Am. J. Phys. 1992, 60, 650–654. [Google Scholar] [CrossRef]
- Gao, B.; Wang, Y.X. Invariant Solutions and Nonlinear Self-Adjointness of the Two-Component Chaplygin Gas Equation. Discret. Dyn. Nat. Soc. 2019, 2019, 9609357. [Google Scholar] [CrossRef]
- Silva, V.A. Lie point symmetries and conservation laws for a class of BBM-KdV systems. Commun. Nonlinear Sci. Numer. Simul. 2019, 69, 73–77. [Google Scholar] [CrossRef]
- Ibragimov, N.H. A new conservation theorem. J. Math. Anal. Appl. 2007, 333, 311–328. [Google Scholar] [CrossRef]
- Grigoriev, Y.N.; Ibragimov, N.H.; Kovalev, V.F.; Meleshko, S.V. Symmmetry of Integro-Differential Equations: With Applications in Mechanics and Plasma Physica; Springer: Berlin, Germany, 2010. [Google Scholar]
- Ibragimov, N.H. Integrating factors, adjoint equations and Lagrangians. J. Math. Anal. Appl. 2006, 318, 742–757. [Google Scholar] [CrossRef]
- Bluman, G.W.; Cheviakov, A.; Anco, S. Applications of Symmetry Methods to Partial Differential Equations; Springer: Berlin, Germany, 2010. [Google Scholar]
- Ibragimov, N.H. Nonlinear self-adjointness and conservation laws. J. Phys. A 2011, 44, 432002. [Google Scholar] [CrossRef]
- Ibragimov, N.H. Nonlinear self-adjointness in constructing conservation laws. Arch. ALGA 2011, 7, 1–99. [Google Scholar]
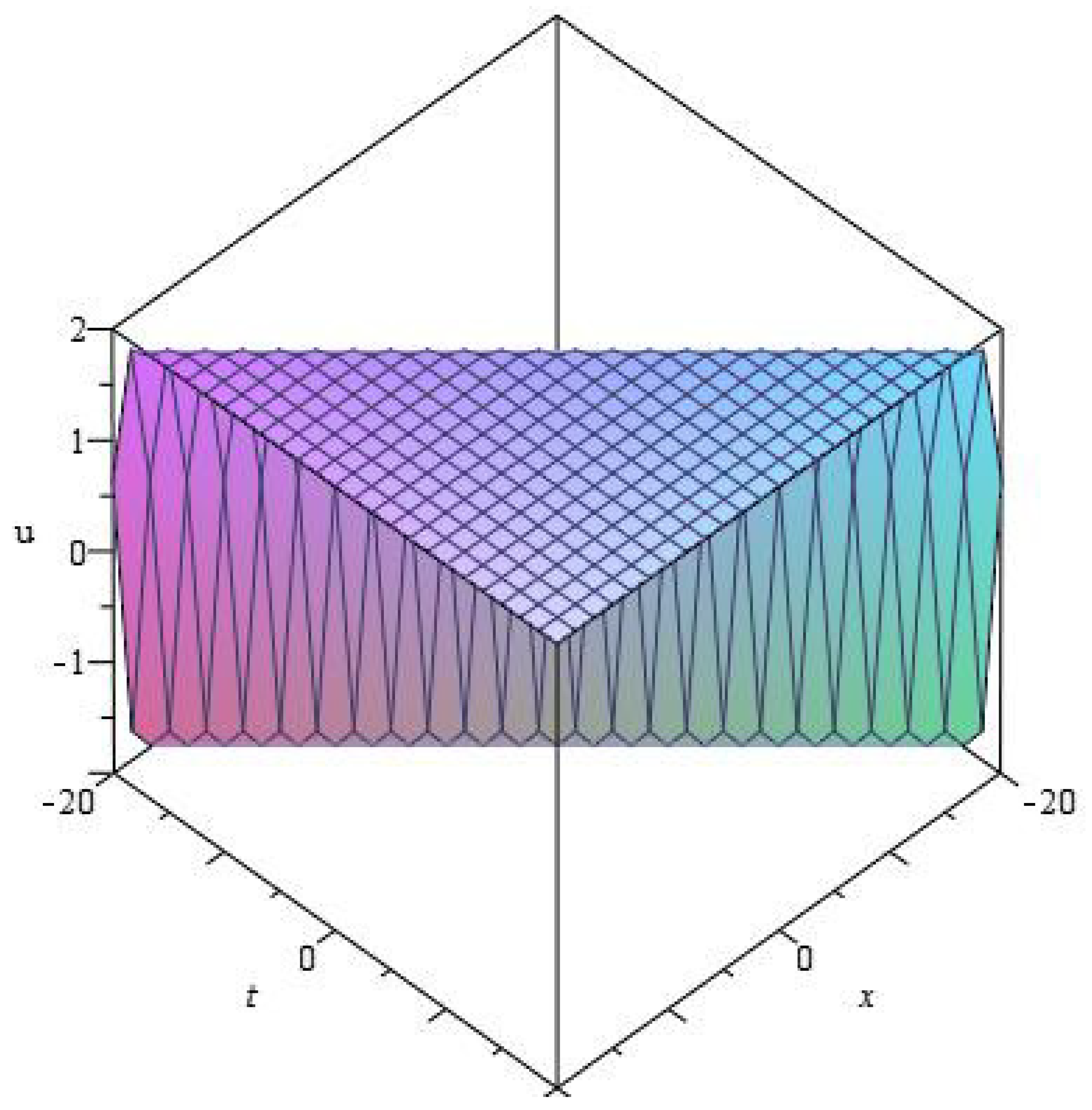
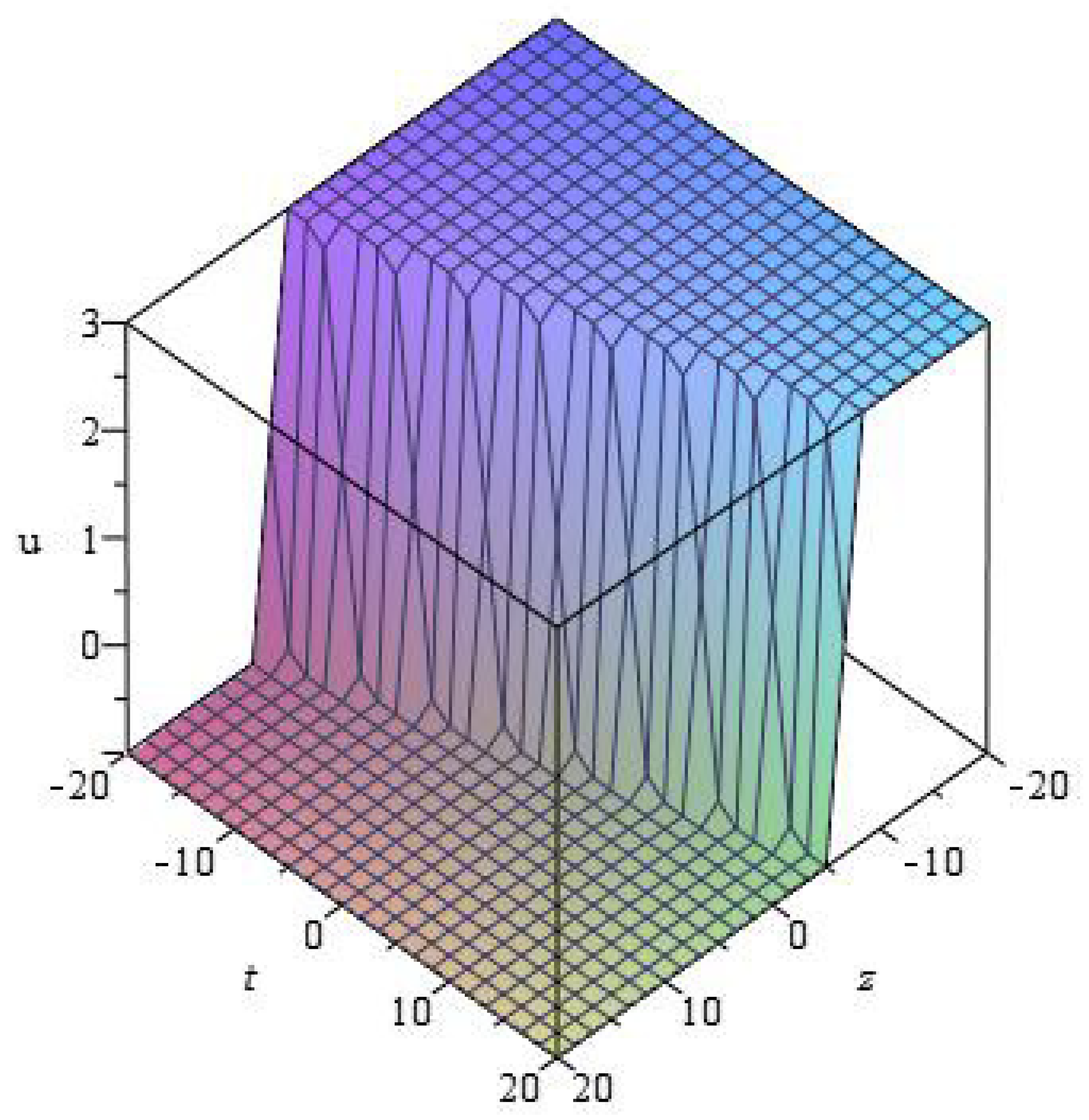
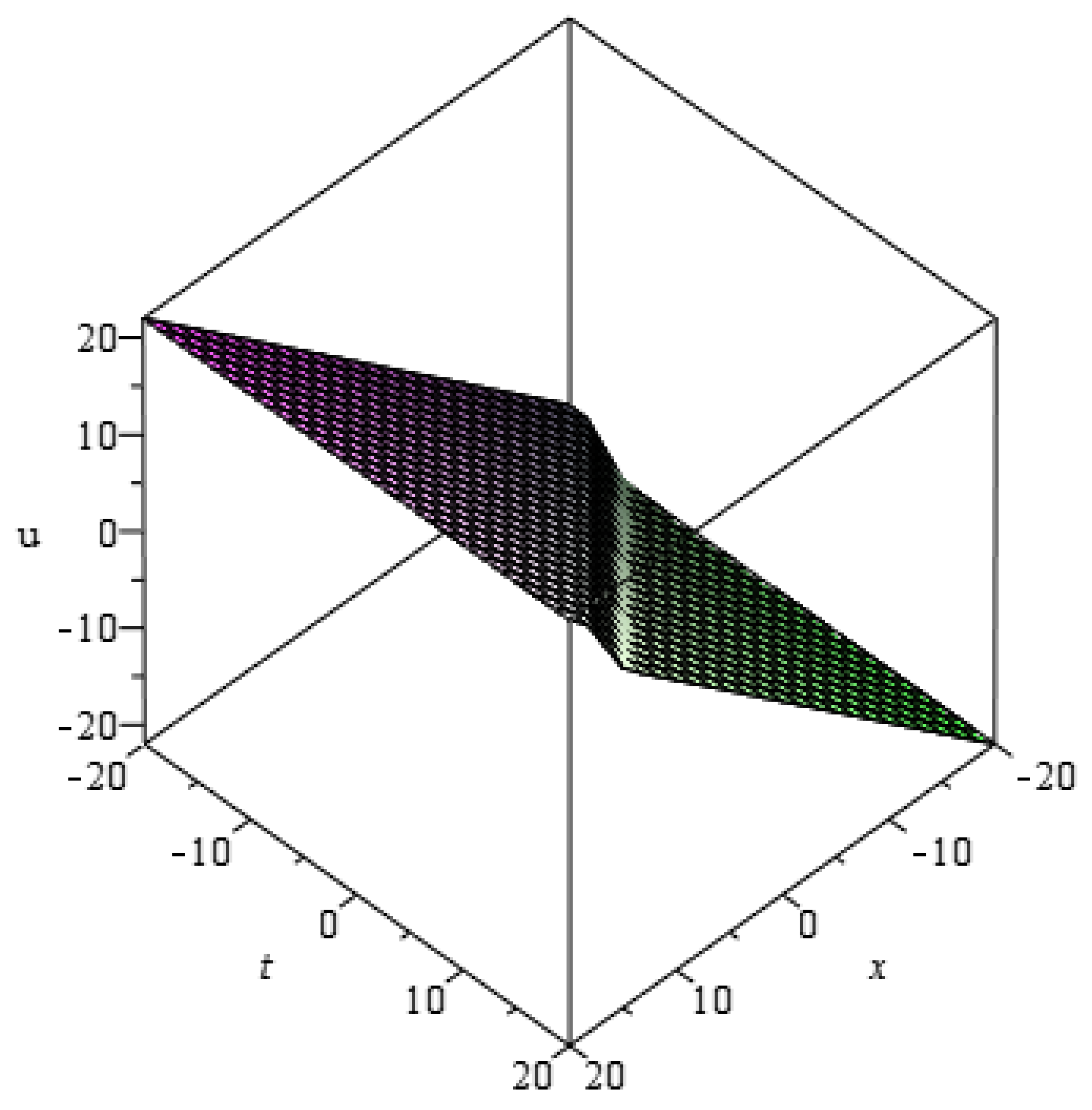
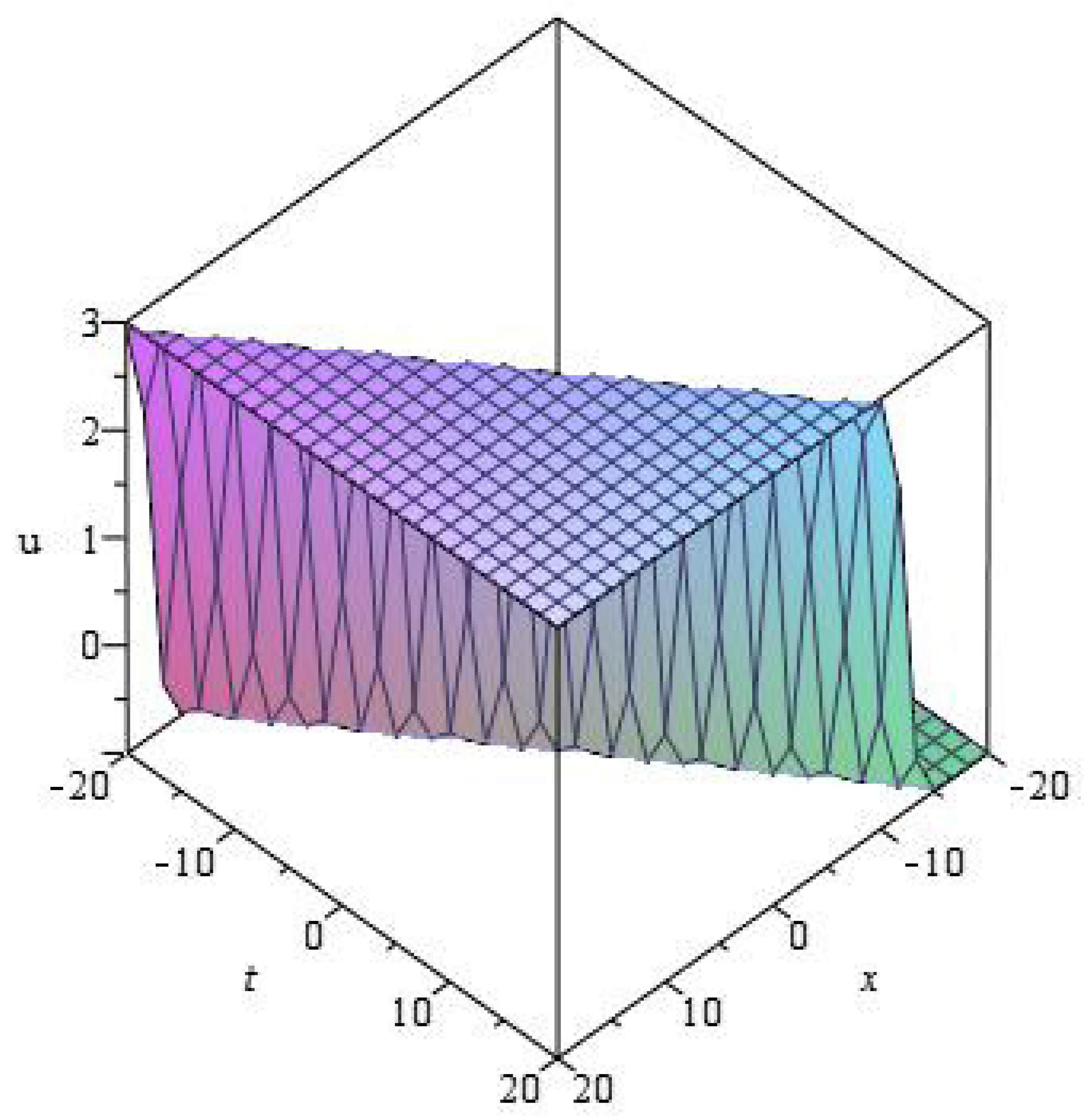
| 0 | |||||||
| 0 | 0 | 0 | 0 | 0 | 0 | ||
| 0 | 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | 0 | ||
| 0 | 0 | 0 | 0 | 0 | 0 | ||
| 0 | 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | 0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, B.; Zhang, Y. Exact Solutions and Conservation Laws of the (3 + 1)-Dimensional B-Type Kadomstev–Petviashvili (BKP)-Boussinesq Equation. Symmetry 2020, 12, 97. https://doi.org/10.3390/sym12010097
Gao B, Zhang Y. Exact Solutions and Conservation Laws of the (3 + 1)-Dimensional B-Type Kadomstev–Petviashvili (BKP)-Boussinesq Equation. Symmetry. 2020; 12(1):97. https://doi.org/10.3390/sym12010097
Chicago/Turabian StyleGao, Ben, and Yao Zhang. 2020. "Exact Solutions and Conservation Laws of the (3 + 1)-Dimensional B-Type Kadomstev–Petviashvili (BKP)-Boussinesq Equation" Symmetry 12, no. 1: 97. https://doi.org/10.3390/sym12010097
APA StyleGao, B., & Zhang, Y. (2020). Exact Solutions and Conservation Laws of the (3 + 1)-Dimensional B-Type Kadomstev–Petviashvili (BKP)-Boussinesq Equation. Symmetry, 12(1), 97. https://doi.org/10.3390/sym12010097




