Machine Learning Algorithms for Smart Data Analysis in Internet of Things Environment: Taxonomies and Research Trends
Abstract
1. Introduction
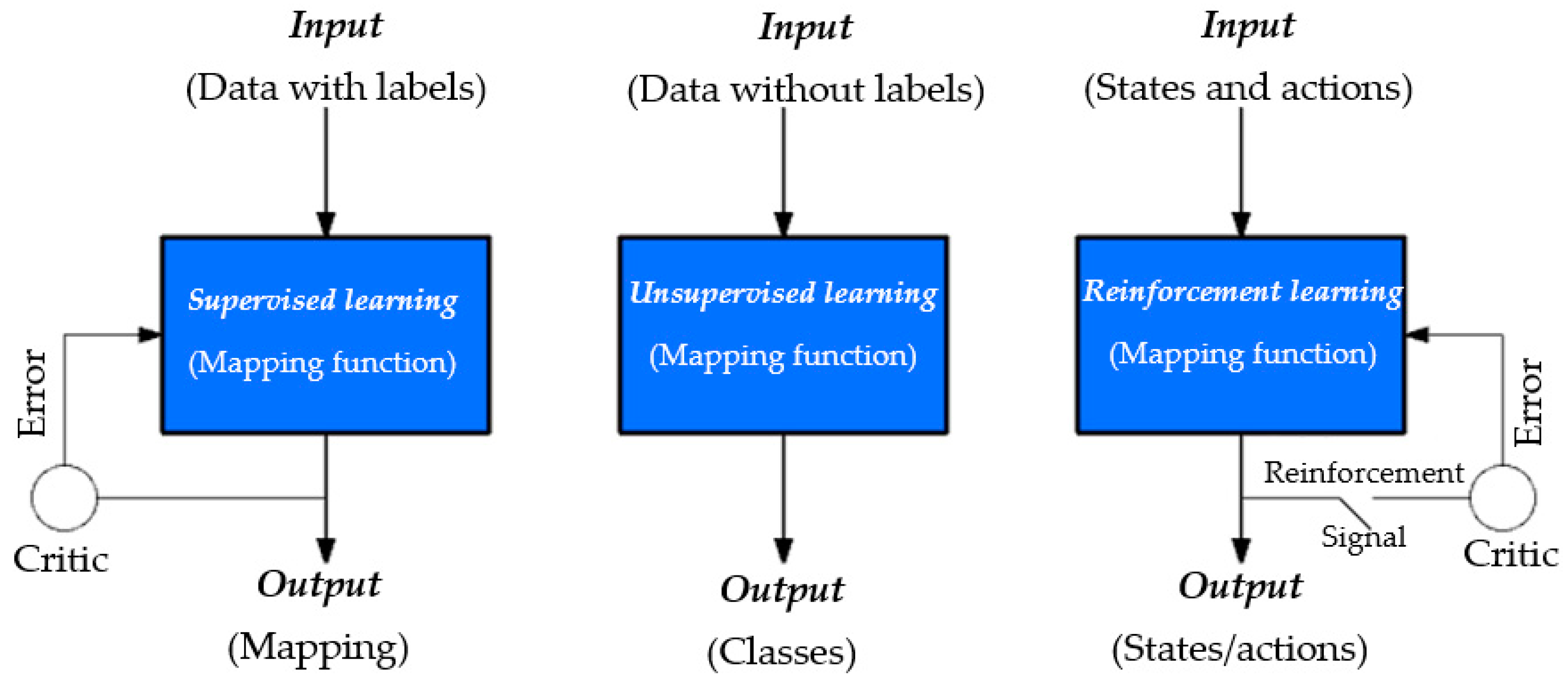
- Supervised learning. This learning algorithm uses samples of input vectors as their target vectors. The target vectors are typically referred to as labels. Supervised learning algorithm’s goal is to estimate the output vector for a specific input vector using learning algorithms. User-cases that have target identifiers are contained in a finite distinct group. This is typically referred to as classification assignment. When these targeted identifiers consists of one or more constant variables, they are called regression assignment [5].
- Unsupervised learning. This learning algorithm does not require labeling of the training set. The objective of this type of learning is to identify hidden patterns of the analogous samples in the input data. This is commonly called clustering. This learning algorithm provides suitable internal understanding of the input-source information, by preprocessing the baseline input-source, making it possible to reposition it into a different variable space of the algorithm. The preprocessing phase enhances the outcome of a successive ML algorithm. This is typically referred to as a feature extraction [7].
- Reinforcement learning. This learning algorithm involves deploying similar actions or series of actions when confronted with same problem with the aim of maximizing payoff [8]. Any outcome that does not lead to favorable expectation is dropped and conversely. Expectedly, this type of algorithm consumes lots of memory space and is predisposed in applications that are executed continuously.
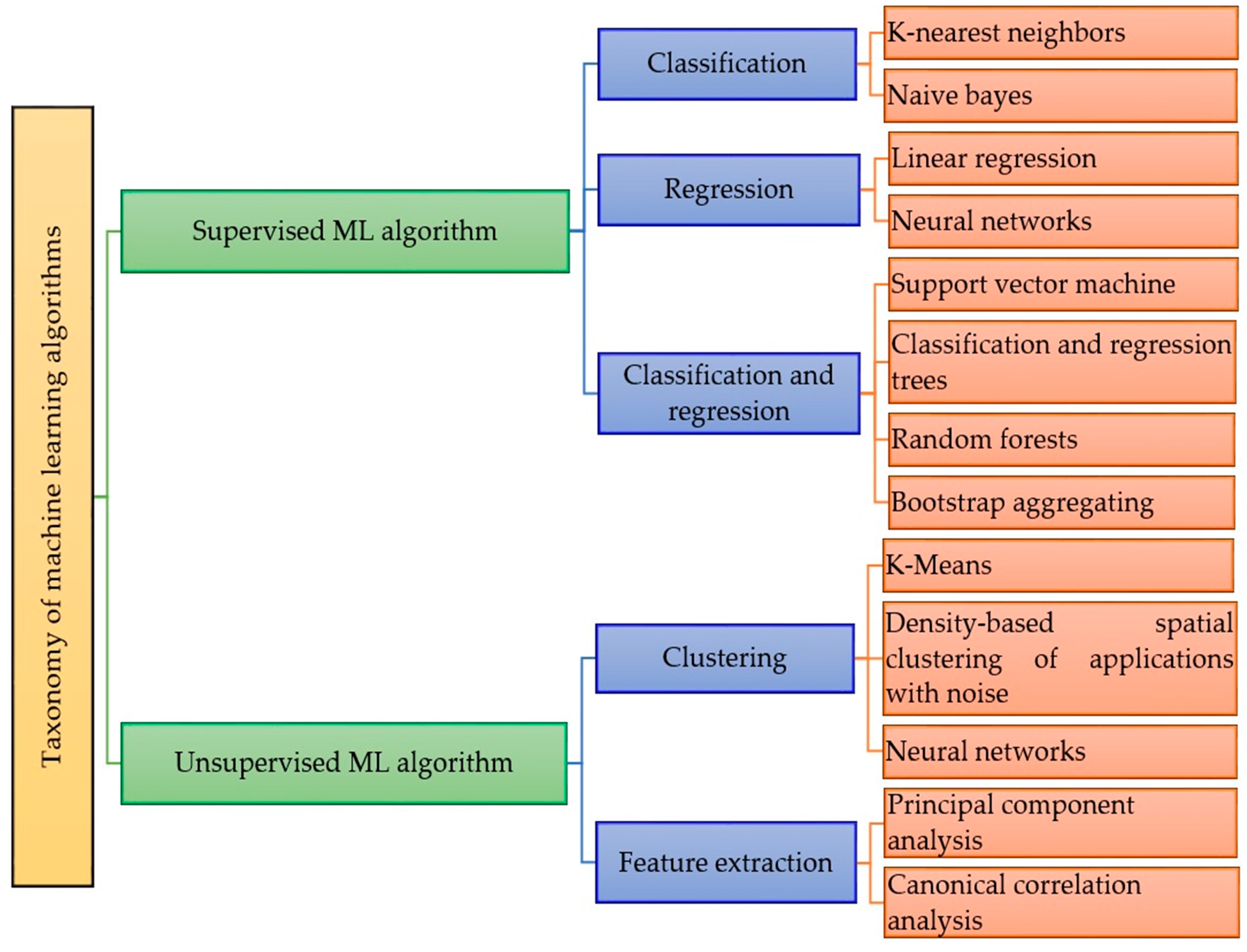
2. Taxonomies of Supervised and Unsupervised ML Algorithms
2.1. Supervised ML Algorithm
2.1.1. Classification Tasks
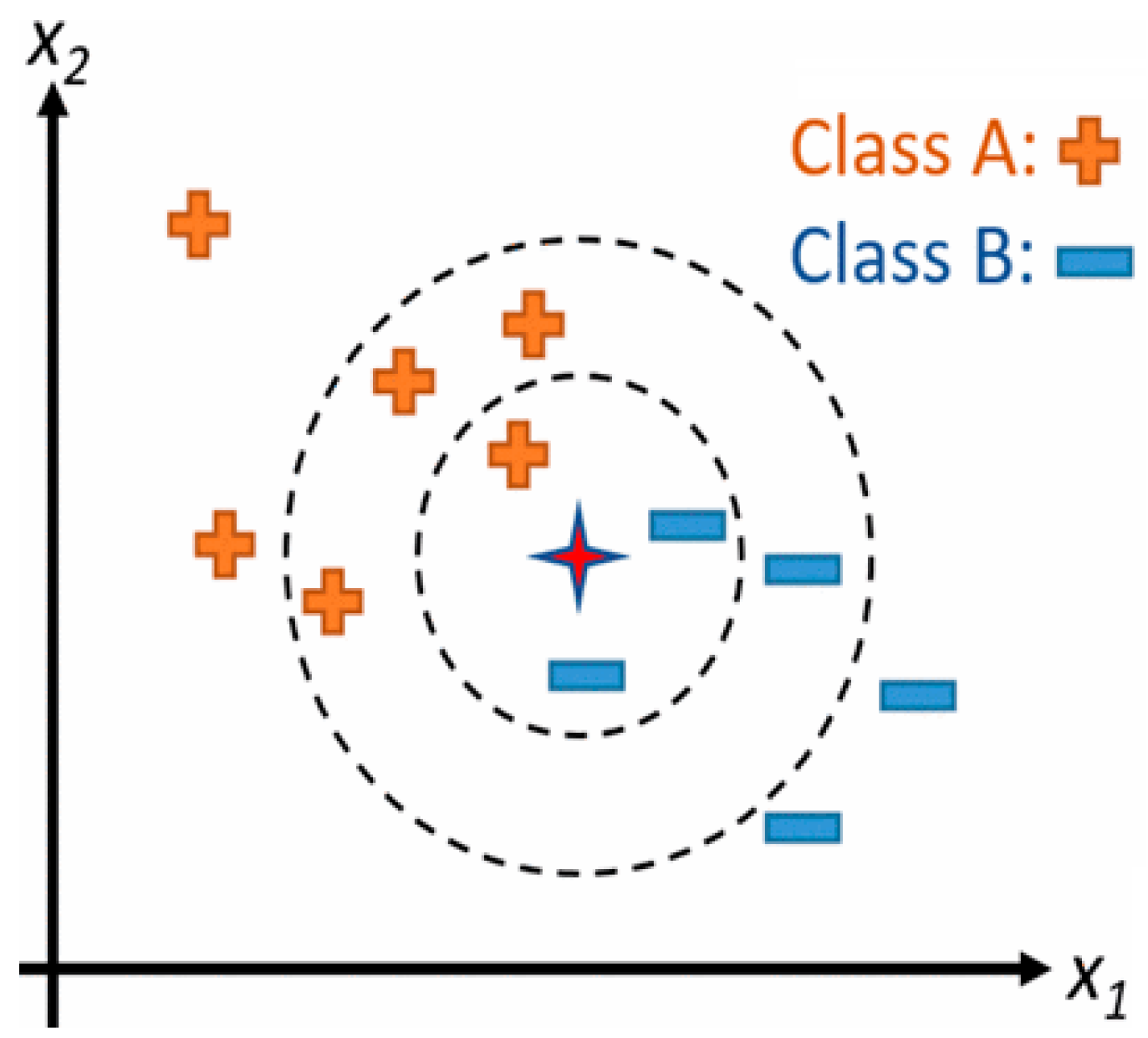
K-Nearest Neighbors (KNN)
Naive Bayes
2.1.2. Regression Tasks
Linear Regression
2.1.3. Combining Classification and Regression Tasks
Support Vector Machine (SVM)
Classification and Regression Trees (CART)
Random Forests
Bootstrap Aggregating
2.2. Unsupervised ML Algorithm
2.2.1. Clustering
K-Means
Density-Based Spatial Clustering of Applications with Noise (DBSCAN)
2.2.2. Feature Extraction
Principal Component Analysis (PCA)
Canonical Correlation Analysis (CCA)
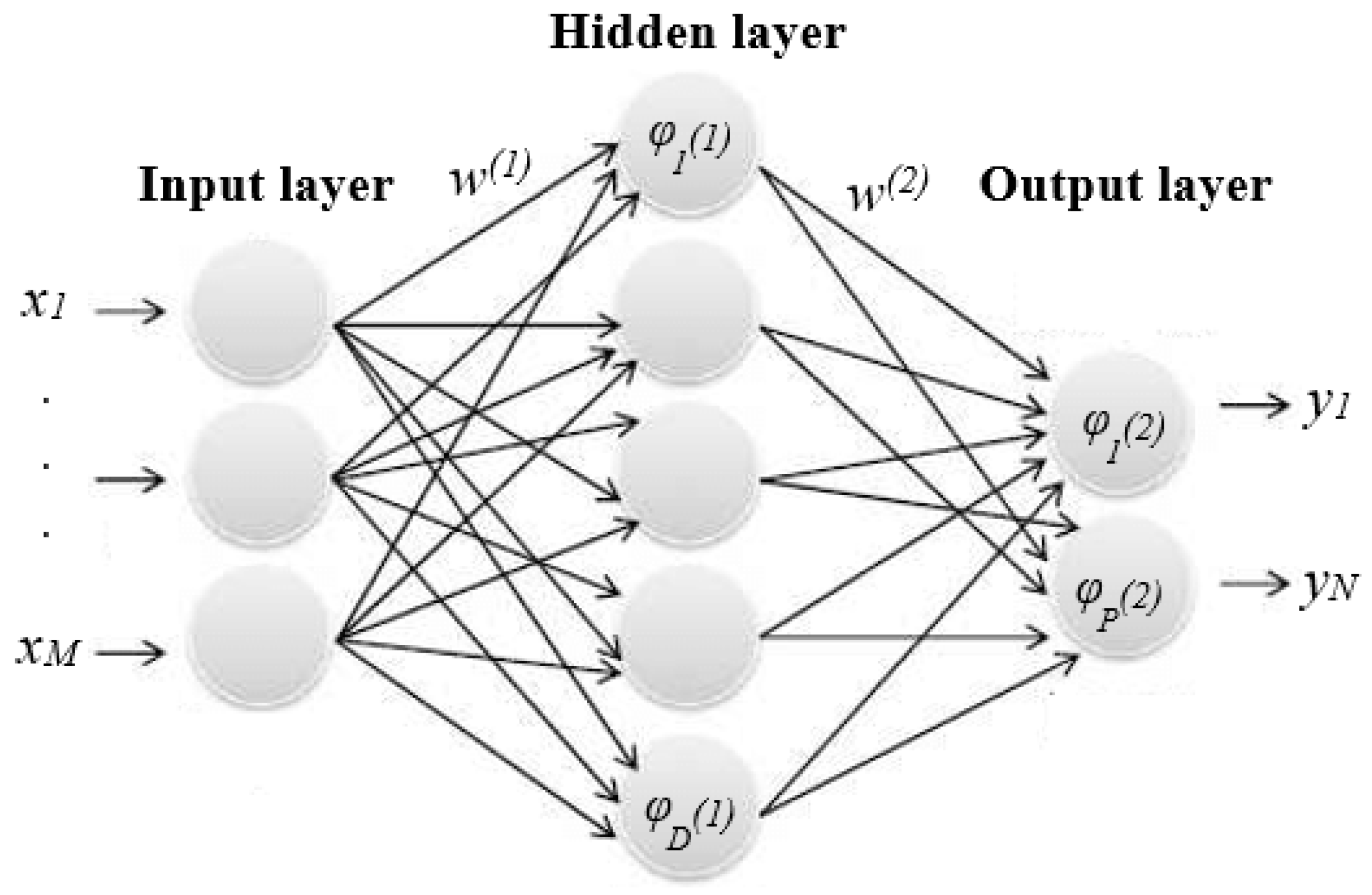
2.3. Neural Networks
3. Research Trends and Open Issues
3.1. Privacy and Security
3.2. Real-Time Data Analytics
4. Conclusions and Recommendations
Author Contributions
Funding
Conflicts of Interest
References
- Sharakhina, L.V.; Skvortsova, V. Big Data, Smart Data in Effective Communication Strategies Development. In Proceedings of the 2019 Communication Strategies in Digital Society Workshop (ComSDS), Saint Petersburg, Russia, 10 April 2019; pp. 7–10. [Google Scholar]
- Al-Fuqaha, A.; Guizani, M.; Mohammadi, M.; Aledhari, M.; Ayyash, M. Internet of things: A survey on enabling technologies, protocols, and applications. IEEE Commun. Surv. Tutor. 2015, 17, 2347–2376. [Google Scholar] [CrossRef]
- Alzubi, J.; Nayyar, A.; Kumar, A. Machine Learning from Theory to Algorithms: An Overview; Journal of Physics: Conference Series; IOP Publishing: London, UK, 2018; p. 012012. [Google Scholar]
- Jagannath, J.; Polosky, N.; Jagannath, A.; Restuccia, F.; Melodia, T. Machine learning for wireless communications in the Internet of things: A comprehensive survey. Ad Hoc Netw. 2019, 101913. [Google Scholar] [CrossRef]
- Kashyap, R. Machine Learning for Internet of Things. In Next-Generation Wireless Networks Meet Advanced Machine Learning Applications; IGI Global: Hershey, PA, USA, 2019; pp. 57–83. [Google Scholar]
- Masegosa, A.R.; Martínez, A.M.; Ramos-López, D.; Cabañas, R.; Salmerón, A.; Langseth, H.; Nielsen, T.D.; Madsen, A.L. AMIDST: A Java toolbox for scalable probabilistic machine learning. Knowl.-Based Syst. 2019, 163, 595–597. [Google Scholar] [CrossRef]
- Buskirk, T.D.; Kirchner, A.; Eck, A.; Signorino, C.S. An introduction to machine learning methods for survey researchers. Surv. Pract. 2018, 11, 2718. [Google Scholar] [CrossRef]
- Luong, N.C.; Hoang, D.T.; Gong, S.; Niyato, D.; Wang, P.; Liang, Y.-C.; Kim, D.I. Applications of deep reinforcement learning in communications and networking: A survey. IEEE Commun. Surv. Tutor. 2019, 21, 3133–3174. [Google Scholar] [CrossRef]
- Schrider, D.R.; Kern, A.D. Supervised machine learning for population genetics: A new paradigm. Trends Genet. 2018, 34, 301–312. [Google Scholar] [CrossRef]
- Lee, J.H.; Shin, J.; Realff, M.J. Machine learning: Overview of the recent progresses and implications for the process systems engineering field. Comput. Chem. Eng. 2018, 114, 111–121. [Google Scholar] [CrossRef]
- Singh, A.; Thakur, N.; Sharma, A. A review of supervised machine learning algorithms. In Proceedings of the 2016 3rd International Conference on Computing for Sustainable Global Development (INDIACom), New Delhi, India, 16–18 March 2016; pp. 1310–1315. [Google Scholar]
- Osisanwo, F.; Akinsola, J.; Awodele, O.; Hinmikaiye, J.; Olakanmi, O.; Akinjobi, J. Supervised machine learning algorithms: Classification and comparison. Int. J. Comput. Trends. Technol. 2017, 48, 128–138. [Google Scholar]
- Qu, G.; Li, N. Accelerated distributed nesterov gradient descent for smooth and strongly convex functions. In Proceedings of the 2016 54th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 27–30 September 2016; pp. 209–216. [Google Scholar]
- Lee, J.; Stanley, M.; Spanias, A.; Tepedelenlioglu, C. Integrating machine learning in embedded sensor systems for Internet-of-Things applications. In Proceedings of the 2016 IEEE International Symposium on Signal Processing and Information Technology (ISSPIT), Limassol, Cyprus, 12–14 December 2016; pp. 290–294. [Google Scholar]
- Kanj, S.; Abdallah, F.; Denoeux, T.; Tout, K. Editing training data for multi-label classification with the k-nearest neighbor rule. Pattern Anal. Appl. 2016, 19, 145–161. [Google Scholar] [CrossRef]
- Maillo, J.; Ramírez, S.; Triguero, I.; Herrera, F. kNN-IS: An Iterative Spark-based design of the k-Nearest Neighbors classifier for big data. Knowl.-Based Syst. 2017, 117, 3–15. [Google Scholar] [CrossRef]
- Chomboon, K.; Chujai, P.; Teerarassamee, P.; Kerdprasop, K.; Kerdprasop, N. An empirical study of distance metrics for k-nearest neighbor algorithm. In Proceedings of the 3rd International Conference on Industrial Application Engineering, Kitakyushu, Japan, 28–31 March 2015; pp. 1–6. [Google Scholar]
- Prasath, V.; Alfeilat, H.A.A.; Lasassmeh, O.; Hassanat, A.; Tarawneh, A.S. Distance and Similarity Measures Effect on the Performance of K-Nearest Neighbor Classifier—A Review. arXiv 2017, arXiv:1708.04321. [Google Scholar]
- Berisha, V.; Wisler, A.; Hero, A.O.; Spanias, A. Empirically estimable classification bounds based on a nonparametric divergence measure. IEEE Trans. Signal Process. 2015, 64, 580–591. [Google Scholar] [CrossRef] [PubMed]
- Azar, A.T.; Hassanien, A.E. Dimensionality reduction of medical big data using neural-fuzzy classifier. Soft Comput. 2015, 19, 1115–1127. [Google Scholar] [CrossRef]
- Ghaderi, A.; Frounchi, J.; Farnam, A. Machine learning-based signal processing using physiological signals for stress detection. In Proceedings of the 2015 22nd Iranian Conference on Biomedical Engineering (ICBME), Tehran, Iran, 25–27 November 2015; pp. 93–98. [Google Scholar]
- Sharmila, A.; Geethanjali, P. DWT based detection of epileptic seizure from EEG signals using naive Bayes and k-NN classifiers. IEEE Access 2016, 4, 7716–7727. [Google Scholar] [CrossRef]
- Garcia, L.P.; de Carvalho, A.C.; Lorena, A.C. Effect of label noise in the complexity of classification problems. Neurocomputing 2015, 160, 108–119. [Google Scholar] [CrossRef]
- Lu, W.; Du, X.; Hadjieleftheriou, M.; Ooi, B.C. Efficiently Supporting Edit Distance Based String Similarity Search Using B+ -Trees. IEEE Trans. Knowl. Data Eng. 2014, 26, 2983–2996. [Google Scholar] [CrossRef]
- Do, C.-T.; Douzal-Chouakria, A.; Marié, S.; Rombaut, M. Multiple Metric Learning for large margin kNN Classification of time series. In Proceedings of the 2015 23rd European Signal Processing Conference (EUSIPCO), Nice, France, 31 August–4 September 2015; pp. 2346–2350. [Google Scholar]
- Ma, X.; Wu, Y.-J.; Wang, Y.; Chen, F.; Liu, J. Mining smart card data for transit riders’ travel patterns. Transp. Res. Part C Emerg. Technol. 2013, 36, 1–12. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, Y.; Waytowich, N.R.; Krusienski, D.J.; Zhou, G.; Jin, J.; Wang, X.; Cichocki, A. Discriminative feature extraction via multivariate linear regression for SSVEP-based BCI. IEEE Trans. Neural Syst. Rehabil. Eng. 2016, 24, 532–541. [Google Scholar] [CrossRef]
- Hilbe, J.M. Practical Guide to Logistic Regression; Chapman and Hall/CRC: Boca Raton, FL, USA, 2016. [Google Scholar]
- Mahdavinejad, M.S.; Rezvan, M.; Barekatain, M.; Adibi, P.; Barnaghi, P.; Sheth, A.P. Machine learning for Internet of Things data analysis: A survey. Digit. Commun. Netw. 2018, 4, 161–175. [Google Scholar] [CrossRef]
- Jadhav, S.D.; Channe, H. Comparative study of K-NN, naive Bayes and decision tree classification techniques. Int. J. Sci. Res. 2016, 5, 1842–1845. [Google Scholar]
- Xu, S. Bayesian Naïve Bayes classifiers to text classification. J. Inf. Sci. 2018, 44, 48–59. [Google Scholar] [CrossRef]
- Singh, G.; Kumar, B.; Gaur, L.; Tyagi, A. Comparison between Multinomial and Bernoulli Naïve Bayes for Text Classification. In Proceedings of the 2019 International Conference on Automation, Computational and Technology Management (ICACTM), London, UK, 24–26 April 2019; pp. 593–596. [Google Scholar]
- Pham, B.T.; Prakash, I.; Jaafari, A.; Bui, D.T. Spatial prediction of rainfall-induced landslides using aggregating one-dependence estimators classifier. J. Indian Soc. Remote Sens. 2018, 46, 1457–1470. [Google Scholar] [CrossRef]
- Han, W.; Gu, Y.; Zhang, Y.; Zheng, L. Data driven quantitative trust model for the internet of agricultural things. In Proceedings of the 2014 International Conference on the Internet of Things (IOT), Cambridge, MA, USA, 6–8 October 2014; pp. 31–36. [Google Scholar]
- Cherian, V.; Bindu, M. Heart disease prediction using Naive Bayes algorithm and Laplace Smoothing technique. Int. J. Comput. Sci. Trends Technol. 2017, 5. [Google Scholar]
- Weichenthal, S.; Van Ryswyk, K.; Goldstein, A.; Bagg, S.; Shekkarizfard, M.; Hatzopoulou, M. A land use regression model for ambient ultrafine particles in Montreal, Canada: A comparison of linear regression and a machine learning approach. Environ. Res. 2016, 146, 65–72. [Google Scholar] [CrossRef]
- Hoffmann, J.P.; Shafer, K. Linear Regression Analysis; NASW Press: Washington, DC, USA, 2015. [Google Scholar]
- Montgomery, D.C.; Peck, E.A.; Vining, G.G. Introduction to Linear Regression Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2012; Volume 821. [Google Scholar]
- Robert, C. Machine Learning, a Probabilistic Perspective; Taylor & Francis: Abingdon, UK, 2014. [Google Scholar]
- Derguech, W.; Bruke, E.; Curry, E. An autonomic approach to real-time predictive analytics using open data and internet of things. In Proceedings of the 2014 IEEE 11th Intl Conf on Ubiquitous Intelligence and Computing and 2014 IEEE 11th Intl Conf on Autonomic and Trusted Computing and 2014 IEEE 14th International Conference on Scalable Computing and Communications and Its Associated Workshops, Bali, Indonesia, 9–12 December 2014; pp. 204–211. [Google Scholar]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, Sardinia, Italy, 13–15 May 2010; pp. 249–256. [Google Scholar]
- Ding, S.; Qi, B.; Tan, H. An overview on theory and algorithm of support vector machines. J. Univ. Electron. Sci. Technol. China 2011, 40, 2–10. [Google Scholar]
- Nikam, S.S. A comparative study of classification techniques in data mining algorithms. Orient. J. Comput. Sci. Technol. 2015, 8, 13–19. [Google Scholar]
- Alber, M.; Zimmert, J.; Dogan, U.; Kloft, M. Distributed optimization of multi-class SVMs. PLoS ONE 2017, 12, e0178161. [Google Scholar] [CrossRef]
- Ponte, P.; Melko, R.G. Kernel methods for interpretable machine learning of order parameters. Phys. Rev. B 2017, 96, 205146. [Google Scholar] [CrossRef]
- Utkin, L.V.; Chekh, A.I.; Zhuk, Y.A. Binary classification SVM-based algorithms with interval-valued training data using triangular and Epanechnikov kernels. Neural Netw. 2016, 80, 53–66. [Google Scholar] [CrossRef]
- Díaz-Morales, R.; Navia-Vázquez, Á. Distributed Nonlinear Semiparametric Support Vector Machine for Big Data Applications on Spark Frameworks. IEEE Trans. Syst. Man Cybern. Syst. 2018, 1–12. [Google Scholar] [CrossRef]
- Lee, C.-P.; Roth, D. Distributed box-constrained quadratic optimization for dual linear SVM. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 987–996. [Google Scholar]
- Huang, X.; Shi, L.; Suykens, J.A. Sequential minimal optimization for SVM with pinball loss. Neurocomputing 2015, 149, 1596–1603. [Google Scholar] [CrossRef]
- Azim, R.; Rahman, W.; Karim, M.F. Bangla Hand-Written Character Recognition Using Support Vector Machine. Int. J. Eng. Works 2016, 3, 36–46. [Google Scholar]
- Liu, P.; Choo, K.-K.R.; Wang, L.; Huang, F. SVM or deep learning? A comparative study on remote sensing image classification. Soft Comput. 2017, 21, 7053–7065. [Google Scholar] [CrossRef]
- Cang, Z.; Mu, L.; Wu, K.; Opron, K.; Xia, K.; Wei, G.-W. A topological approach for protein classification. Comput. Math. Biophys. 2015, 3. [Google Scholar] [CrossRef]
- Wahab, O.A.; Mourad, A.; Otrok, H.; Bentahar, J. CEAP: SVM-based intelligent detection model for clustered vehicular ad hoc networks. Expert Syst. Appl. 2016, 50, 40–54. [Google Scholar] [CrossRef]
- Khan, M.A.; Khan, A.; Khan, M.N.; Anwar, S. A novel learning method to classify data streams in the internet of things. In Proceedings of the 2014 National Software Engineering Conference, Rawalpindi, Pakistan, 11–12 November 2014; pp. 61–66. [Google Scholar]
- Nikravesh, A.Y.; Ajila, S.A.; Lung, C.-H.; Ding, W. Mobile network traffic prediction using MLP, MLPWD, and SVM. In Proceedings of the 2016 IEEE International Congress on Big Data (BigData Congress), San Francisco, CA, USA, 27 June–2 July 2016; pp. 402–409. [Google Scholar]
- Breiman, L. Classification and Regression Trees; Routledge: Abingdon, UK, 2017. [Google Scholar]
- Krzywinski, M.; Altman, N. Points of Significance: Classification and Regression Trees; Nature Publishing Group: Berlin, Germany, 2017. [Google Scholar]
- Wuest, T.; Weimer, D.; Irgens, C.; Thoben, K.-D. Machine learning in manufacturing: Advantages, challenges, and applications. Prod. Manuf. Res. 2016, 4, 23–45. [Google Scholar] [CrossRef]
- Hagenauer, J.; Helbich, M. A comparative study of machine learning classifiers for modeling travel mode choice. Expert Syst. Appl. 2017, 78, 273–282. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Biau, G.; Scornet, E. A random forest guided tour. Test 2016, 25, 197–227. [Google Scholar] [CrossRef]
- Selvi, S.T.; Karthikeyan, P.; Vincent, A.; Abinaya, V.; Neeraja, G.; Deepika, R. Text categorization using Rocchio algorithm and random forest algorithm. In Proceedings of the 2016 Eighth International Conference on Advanced Computing (ICoAC), Chennai, India, 19–21 January 2017; pp. 7–12. [Google Scholar]
- Hassan, A.R.; Bhuiyan, M.I.H. Computer-aided sleep staging using complete ensemble empirical mode decomposition with adaptive noise and bootstrap aggregating. Biomed. Signal Process. Control 2016, 24, 1–10. [Google Scholar] [CrossRef]
- Syafrudin, M.; Alfian, G.; Fitriyani, N.; Rhee, J. Performance Analysis of IoT-Based Sensor, Big Data Processing, and Machine Learning Model for Real-Time Monitoring System in Automotive Manufacturing. Sensors 2018, 18, 2946. [Google Scholar] [CrossRef] [PubMed]
- Satija, U.; Ramkumar, B.; Manikandan, M.S. Real-Time Signal Quality-Aware ECG Telemetry System for IoT-Based Health Care Monitoring. IEEE Internet Things J. 2017, 4, 815–823. [Google Scholar] [CrossRef]
| Data Analysis Tasks | ML Algorithm | Advantages | Disadvantages |
|---|---|---|---|
| Classification | KNN |
|
|
| Naive Bayes |
|
| |
| Regression | Linear Regression |
|
|
| Combining Classification and Regression | SVM |
|
|
| Random Forest |
|
| |
| Bootstrap Aggregating |
|
|
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alsharif, M.H.; Kelechi, A.H.; Yahya, K.; Chaudhry, S.A. Machine Learning Algorithms for Smart Data Analysis in Internet of Things Environment: Taxonomies and Research Trends. Symmetry 2020, 12, 88. https://doi.org/10.3390/sym12010088
Alsharif MH, Kelechi AH, Yahya K, Chaudhry SA. Machine Learning Algorithms for Smart Data Analysis in Internet of Things Environment: Taxonomies and Research Trends. Symmetry. 2020; 12(1):88. https://doi.org/10.3390/sym12010088
Chicago/Turabian StyleAlsharif, Mohammed H., Anabi Hilary Kelechi, Khalid Yahya, and Shehzad Ashraf Chaudhry. 2020. "Machine Learning Algorithms for Smart Data Analysis in Internet of Things Environment: Taxonomies and Research Trends" Symmetry 12, no. 1: 88. https://doi.org/10.3390/sym12010088
APA StyleAlsharif, M. H., Kelechi, A. H., Yahya, K., & Chaudhry, S. A. (2020). Machine Learning Algorithms for Smart Data Analysis in Internet of Things Environment: Taxonomies and Research Trends. Symmetry, 12(1), 88. https://doi.org/10.3390/sym12010088






