PointNet++ and Three Layers of Features Fusion for Occlusion Three-Dimensional Ear Recognition Based on One Sample per Person
Abstract
1. Introduction
2. Related Work and Contributions
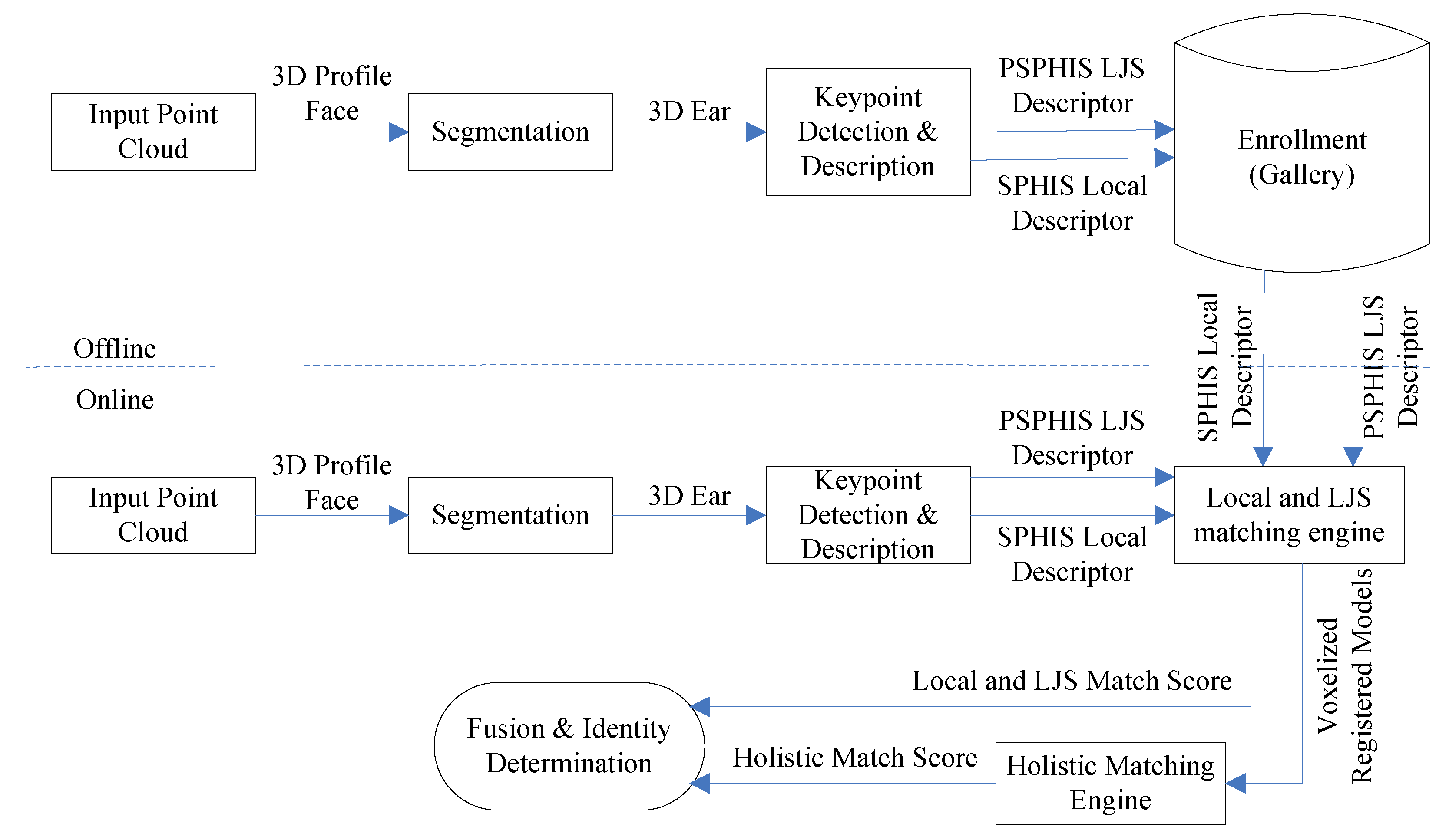
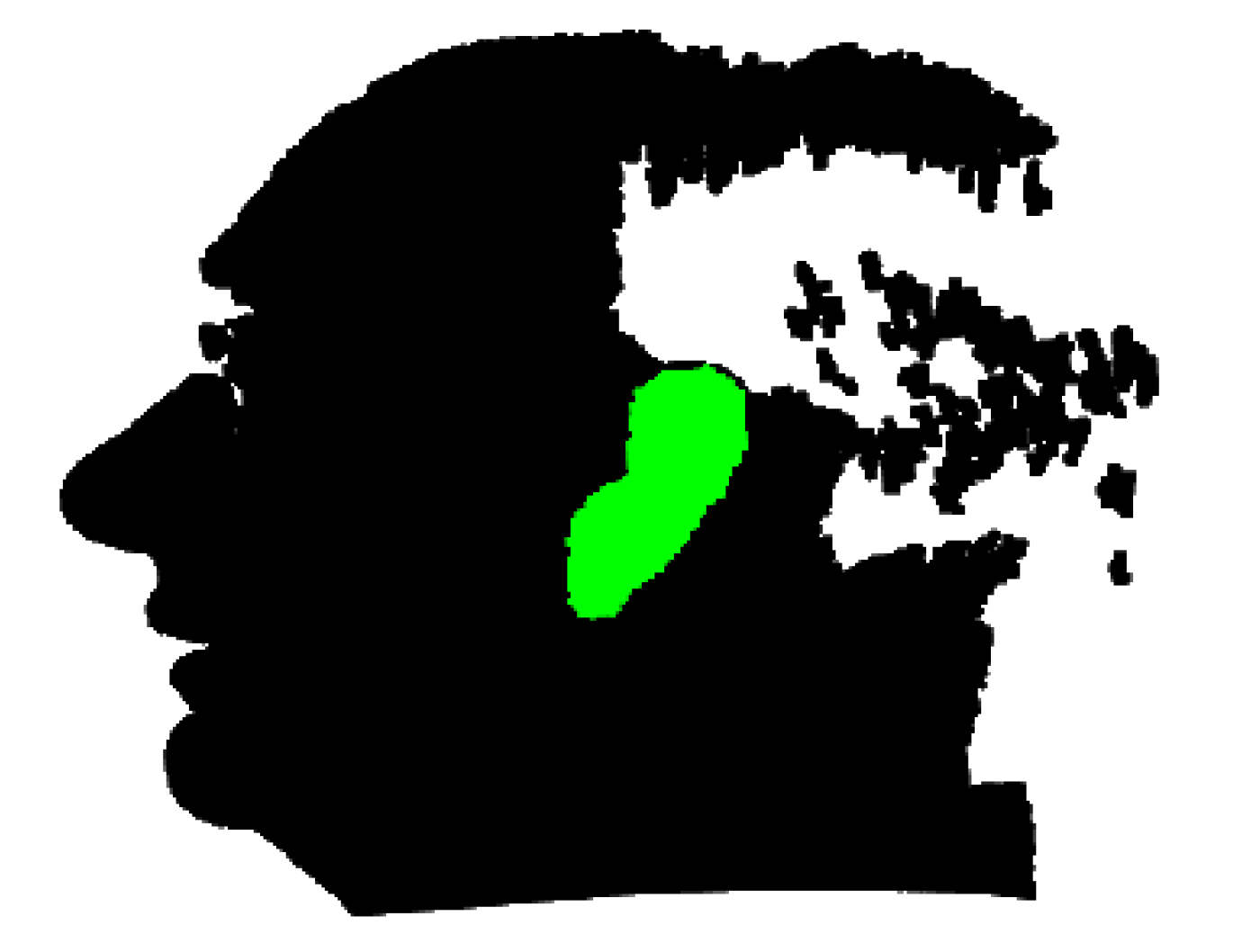
3. Segmentation
4. Local and LJS Feature Extraction
4.1. Data Preprocessing
4.2. Definition of Shape Index and Curvedness Features
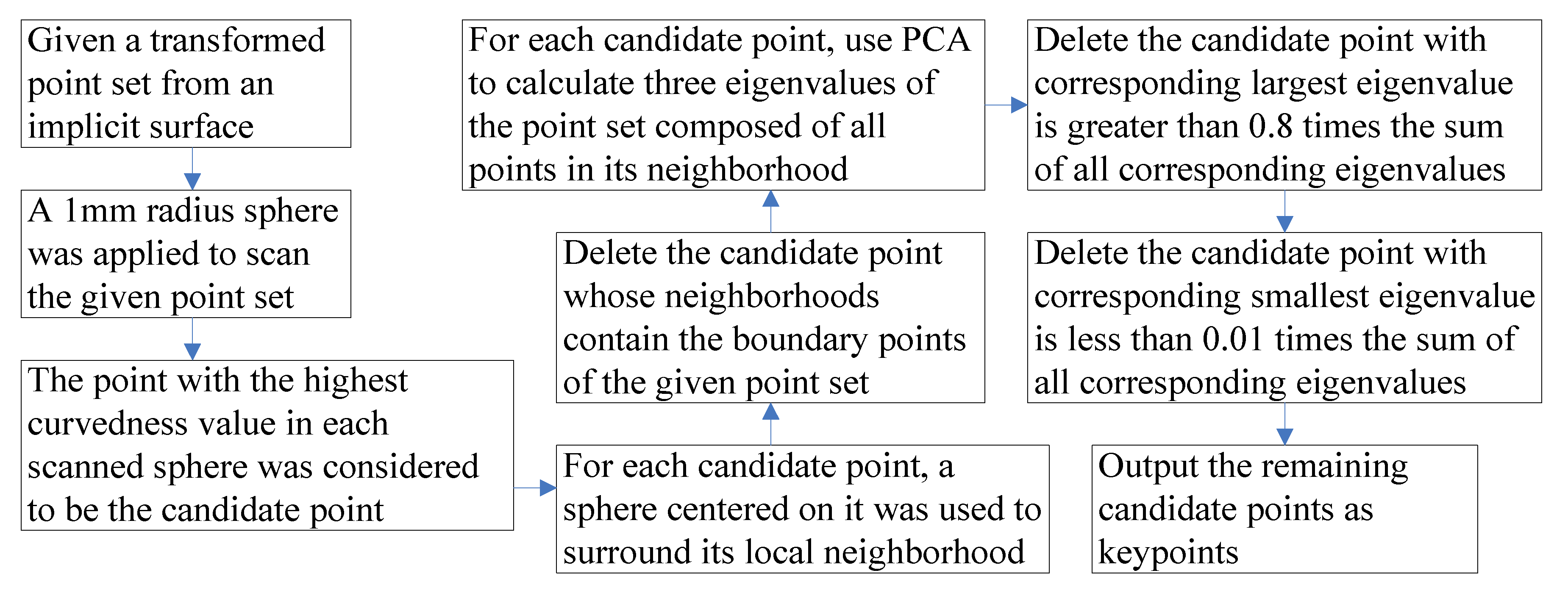
4.3. Proposed Keypoint Selection Method
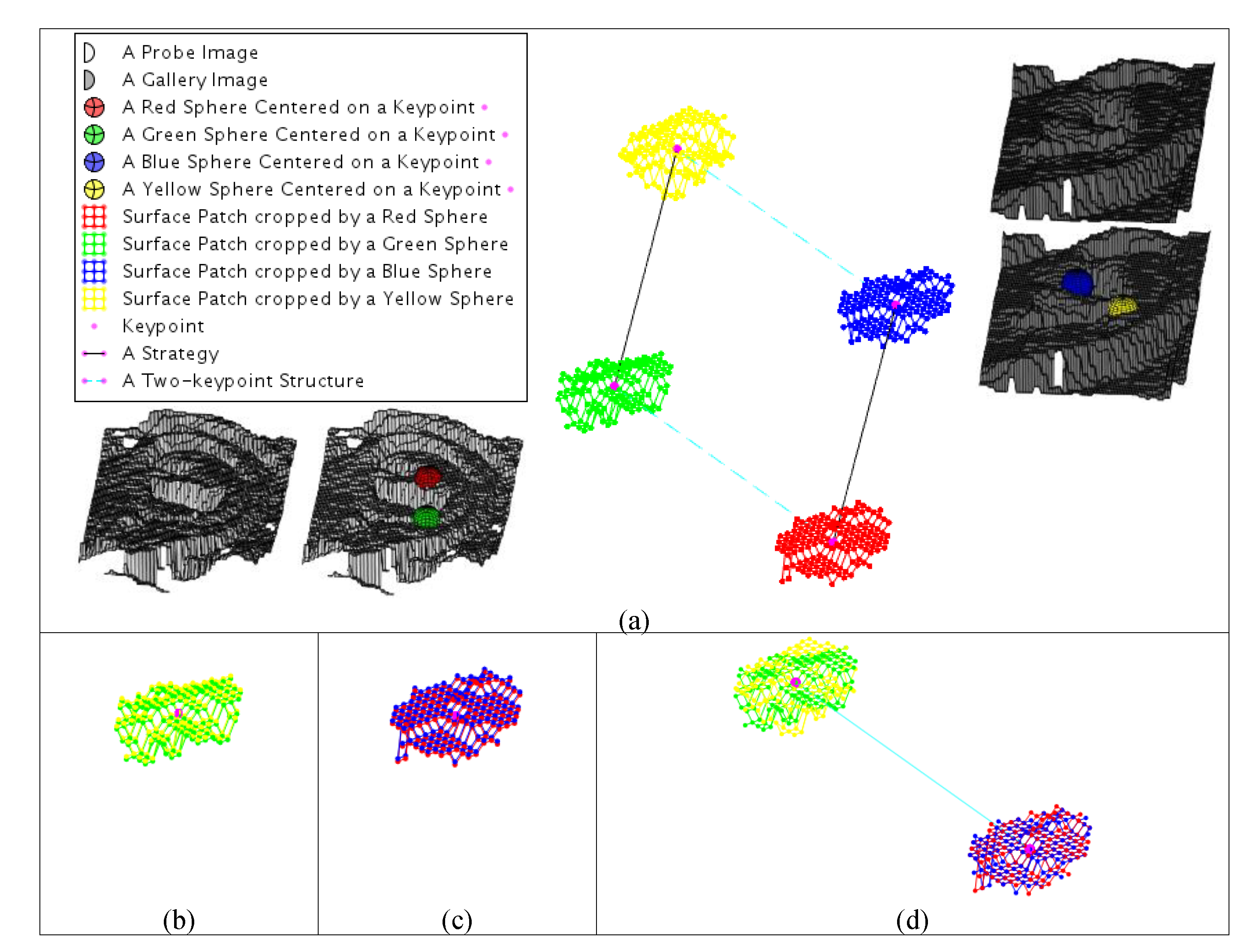
4.4. Definition of the Local Feature
4.5. Proposed LJS Feature
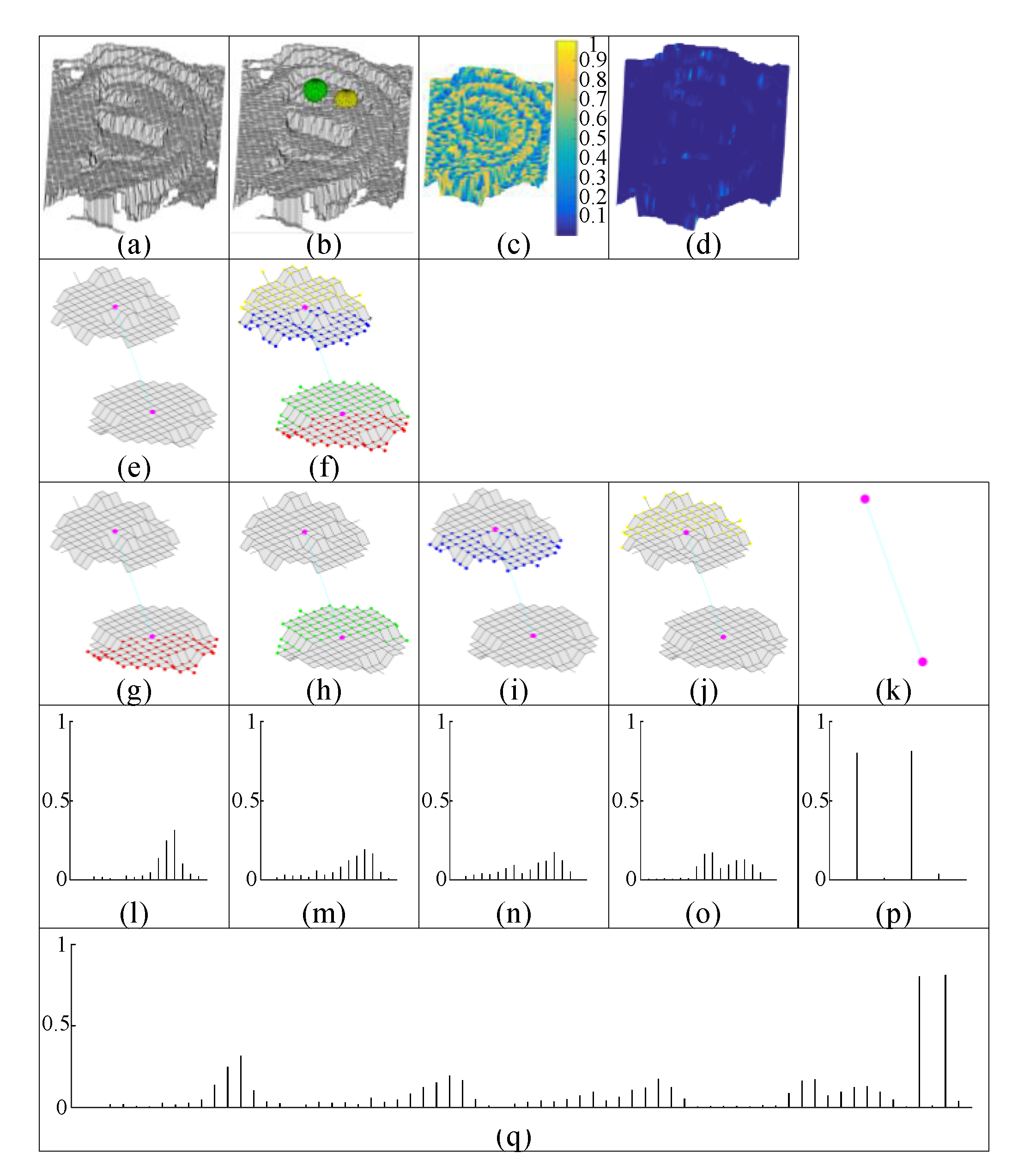
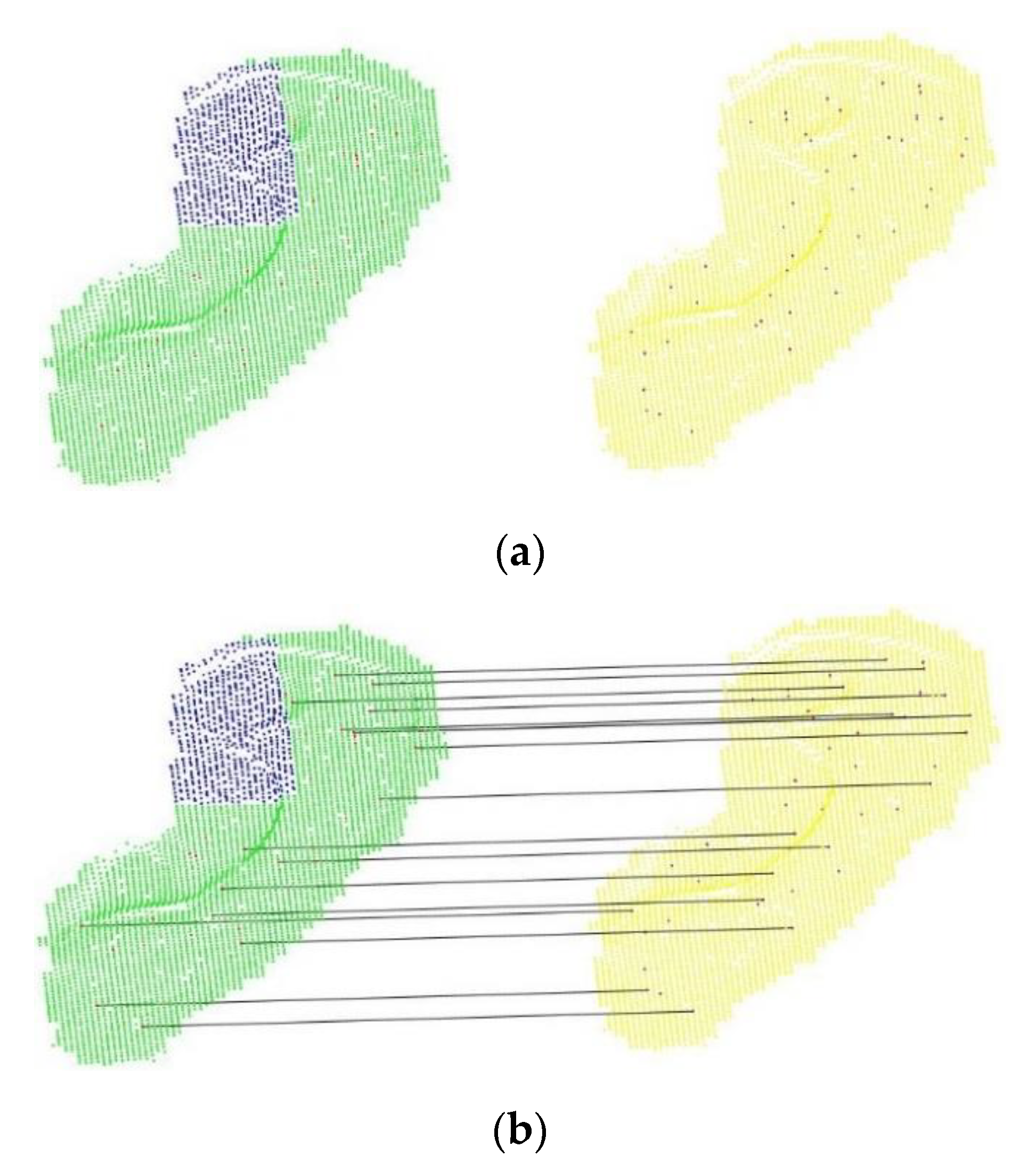
4.6. Proposed Local and LJS Matching Engine
| Algorithm 1: Local and LJS matching engine |
| 1. Given keypoint sets and , the local SPHIS feature descriptor of keypoint , the two-keypoint structure associated with a pair of keypoints , the LJS PSPHIS feature descriptor of the two-keypoint structure , where , , and . Here, . • First stage 2. Use (7) to establish a candidate strategy set . 3. Use (8–11) to construct the payoff matrix. 4. Search the optimal solution, obtain the share of every strategy in set , and concatenate the share of all the strategies to vector . 5. Extract set composed by every strategy with a share greater than in set 6. Register models and . • Second stage 7. 3D point filtering. Obtain keypoint sets and from the keypoints of the gallery and probe ear model, respectively, the local SPHIS feature descriptor of retained keypoint from the models generated by the retained point set, the two-keypoint structure associated with a pair of keypoints , the LJS PSPHIS feature descriptor of the two-keypoint structure , where , , . Here, 8. Use (12) to establish a candidate strategy set 9. Perform Steps 3–5. 10. Output as similarity match score. |
5. Brief Review of the Holistic Matching Engine
6. Fusion
7. Experiments
- Evaluation of segmentation result;
- Ear recognition with random occlusion, where occlusions are close to the probe ear surface;
- Ear recognition with random occlusion, where all points contained in the random occlusion-presented random distribution in region from the ear surface to the camera lens;
- Ear recognition with pose variation; and
- Comparison with another ear recognition method.
7.1. Evaluation of Segmentation Result
7.2. Ear Recognition with Random Occlusion Close to the Ear Surface
7.3. Ear Recognition with All Points in Random Occlusion-Presented Random Distribution in the Region from the Ear Surface to the Camera Lens
7.4. Ear Recognition with Pose Variation
7.5. Comparison with Other Recognition Methods
7.6. Training of the Data Fusion Parameters
8. Summary and Future Direction
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Emeršič, Z.; Meden, B.; Peer, P.; Struc, V. Evaluation and analysis of ear recognition models: Performance, complexity and resource requirements. In Neural Computing and Applications; Springer: Berlin, Germany, 2018; pp. 1–16. [Google Scholar]
- Iannarelli, A.V. Ear Identification (Forensic Identification Series); Paramont: Fremont, CA, USA, 1989. [Google Scholar]
- Pflug, A.; Busch, C. Ear biometrics: A survey of detection, feature extraction and recognition methods. IET Biomet. 2012, 1, 114–129. [Google Scholar] [CrossRef]
- Zhu, Q.; Mu, Z. Local and holistic feature fusion for occlusion-robust 3D ear recognition. Symmetry 2018, 10, 565. [Google Scholar] [CrossRef]
- Tian, L.; Mu, Z. Ear recognition based on deep convolutional network. In Proceedings of the International Congress on Image and Signal Processing, BioMedical Engineering and Informatics (CISP-BMEI), Datong, China, 15–17 October 2016; pp. 437–441. [Google Scholar]
- Alshazly, H.; Linse, C.; Barth, E.; Martinetz, T. Ensemble of deep learning models and transfer learning for ear recognition. Sensors 2019, 19, 4139. [Google Scholar] [CrossRef] [PubMed]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. In Advances in Neural Information Processing Systems; AbeBooks: Victoria, BC, Canada, 2017; pp. 5099–5108. [Google Scholar]
- Zhou, J.; Cadavid, S.; Abdel-Mottaleb, M. An efficient 3-D ear recognition system employing local and holistic features. IEEE Trans. Inf. Forensics Secur. 2012, 7, 978–991. [Google Scholar] [CrossRef]
- Ganapathi, I.I.; Prakash, S. 3D ear recognition using global and local features. IET Biom. 2018, 7, 232–241. [Google Scholar] [CrossRef]
- Yan, P.; Bowyer, K.W. Biometric recognition using 3D ear shape. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 1297–1308. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Bhanu, B. Human ear recognition in 3D. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 718–737. [Google Scholar] [CrossRef] [PubMed]
- Cadavid, S.; Abdel-Mottaleb, M. 3-D ear modeling and recognition from video sequences using shape from shading. IEEE Trans. Inform. Forensics Secur. 2008, 3, 709–718. [Google Scholar] [CrossRef]
- Sun, X.; Zhao, W. Parallel registration of 3D ear point clouds. In Proceedings of the 8th International Conference on Information Technology in Medicine and Education (ITME), Fuzhou, China, 23–25 December 2016; pp. 650–653. [Google Scholar]
- Prakash, S. False mapped feature removal in spin images based 3D ear recognition. In Proceedings of the 3rd International Conference on Signal Processing and Integrated Networks (SPIN), Noida, India, 11–12 February 2016; pp. 620–623. [Google Scholar]
- Tharewal, S.; Gite, H.; Kale, K.V. 3D face & 3D ear recognition: Process and techniques. In Proceedings of the International Conference on Current Trends in Computer, Electrical, Electronics and Communication (CTCEEC), Mysore, India, 8–9 September 2017; pp. 1044–1049. [Google Scholar]
- Zhang, Y.; Mu, Z.; Yuan, L.; Zeng, H.; Chen, L. 3D ear normalization and recognition based on local surface variation. Appl. Sci. 2017, 7, 104. [Google Scholar] [CrossRef]
- Albarelli, A.; Rodola, E.; Bergamasco, F.; Torsello, A. A non-cooperative game for 3D object recognition in cluttered scenes. In Proceedings of the International Conference on 3D Imaging, Modeling, Processing, Visualization and Transmission, Hangzhou, China, 16–19 May 2011; pp. 252–259. [Google Scholar]
- Albarelli, A.; Rodola, E.; Torsello, A. Fast and accurate surface alignment through an isometry-enforcing game. Pattern Recognit. 2015, 48, 2209–2226. [Google Scholar] [CrossRef]
- Goldman, R. Curvature formulas for implicit curves and surfaces. Comp. Aided Geom. Des. 2005, 22, 632–658. [Google Scholar] [CrossRef]
- Zhang, J.; Hon, J.; Wu, T.; Zhong, L.; Gong, S.; Tang, Y. Rapid surface reconstruction algorithm for 3D scattered point cloud model. J. Comput. Aided Des. Comput. Graph. 2018, 30, 235–243. [Google Scholar] [CrossRef]
- Wendland, H. Piecewise polynomial, positive definite and compactly supported radial functions of minimal degree. Adv. Comput. Math. 1995, 4, 389–396. [Google Scholar] [CrossRef]
- Xu, H.; Fang, X.; Hu, L. Computing point orthogonal projection onto implicit surfaces. J. Comput. Aided Des. Comput. Graph. 2008, 20, 1641–1646. [Google Scholar]
- Dorai, C.; Jain, A.K. COSMOS-A representation scheme for 3D free-form objects. IEEE Trans. Pattern Anal. Mach. Intell. 1997, 19, 1115–1130. [Google Scholar] [CrossRef]
- Jolliffe, I. Principal component analysis. In International Encyclopedia of Statistical Science; Springer: Berlin/Heidelberg, Germany, 2011; pp. 1094–1096. [Google Scholar]
- Bulò, S.R.; Bomze, I.M. Infection and immunization: A new class of evolutionary game dynamics. Games Econ. Behav. 2011, 71, 193–211. [Google Scholar] [CrossRef]
- Cappelli, R.; Maio, D.; Maltoni, D. Combining fingerprint classifiers. In Proceedings of the International Workshop on Multiple Classifier Systems, Cagliari, Italy, 21–23 June 2000; pp. 351–361. [Google Scholar]
- Yi, L.; Kim, V.G.; Ceylan, D.; Shen, I.-C.; Yan, M.; Su, H.; Lu, C.; Huang, Q.; Sheffer, A.; Guibas, L. A scalable active framework for region annotation in 3d shape collections. ACM Trans Graph. 2016, 35, 210. [Google Scholar] [CrossRef]
- Zhang, X.; Jiang, C. Improved SVM for learning multi-class domains with ROC evaluation. In Proceedings of the International Conference on Machine Learning and Cybernetics, Hong Kong, China, 19–22 August 2007; pp. 2891–2896. [Google Scholar]

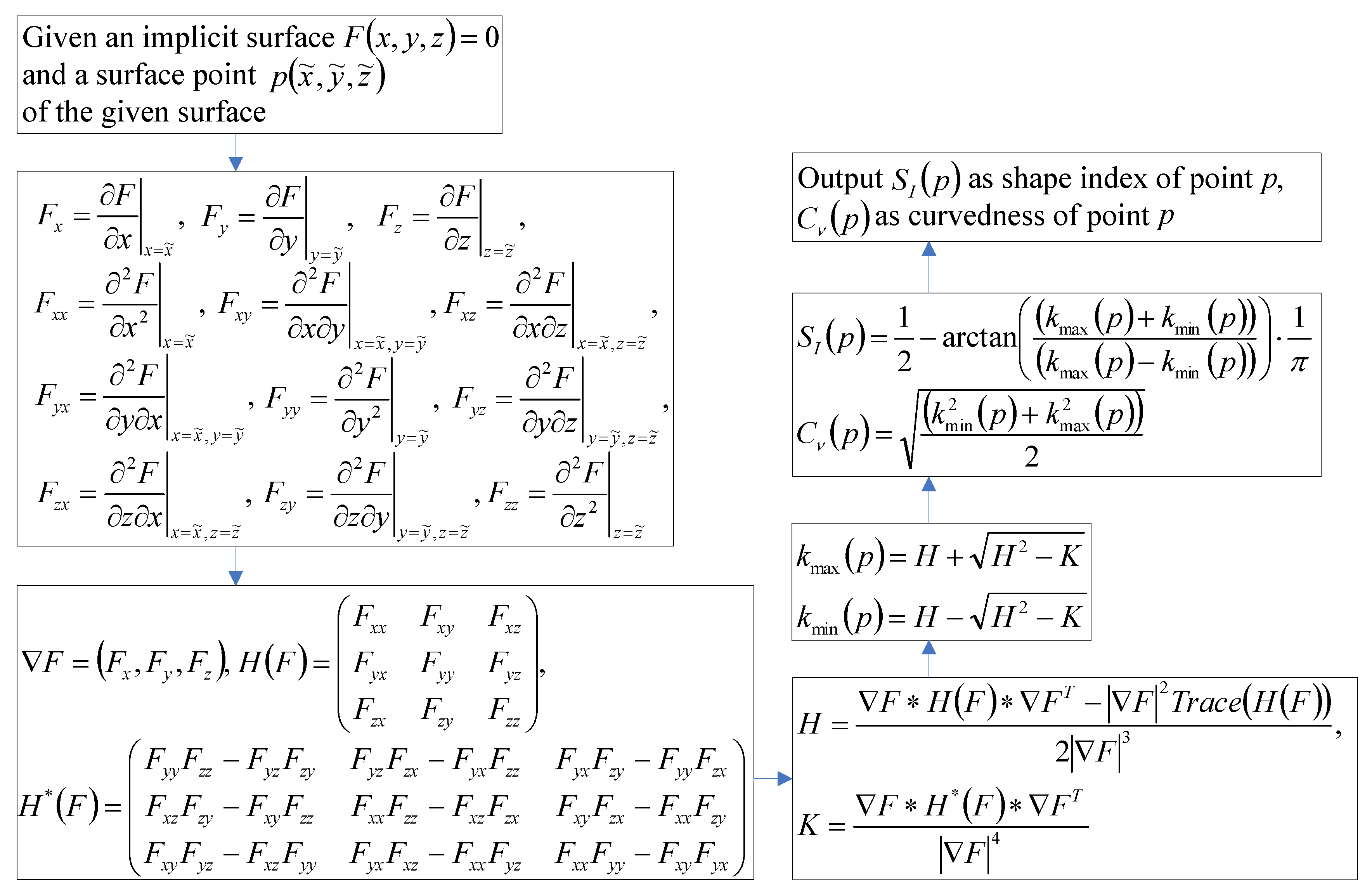





| Technique | Occlusion Percentage (%) | |||||
|---|---|---|---|---|---|---|
| 0 | 10 | 20 | 30 | 40 | 50 | |
| PointNet++ | 93.0 | 91.3 | 89.1 | 86.8 | 84.2 | 81.4 |
| Technique | Occlusion Percentage (%) | |||||
|---|---|---|---|---|---|---|
| 0 | 10 | 20 | 30 | 40 | 50 | |
| VICP | 97.80 | 73.01 | 44.33 | 24.82 | 8.67 | 1.40 |
| ICP–LSV | 98.55 | 73.73 | 45.30 | 25.83 | 9.40 | 2.17 |
| DFF | 98.30 | 95.86 | 89.16 | 63.13 | 38.31 | 17.11 |
| LHFFO | 98.80 | 97.98 | 91.81 | 69.88 | 47.95 | 25.54 |
| Proposed method | 98.82 | 98.36 | 95.08 | 83.71 | 70.84 | 55.86 |
| Technique | Occlusion Percentage (%) | |||||
|---|---|---|---|---|---|---|
| 0 | 10 | 20 | 30 | 40 | 50 | |
| VICP | 97.80 | 73.49 | 45.06 | 25.78 | 8.92 | 1.45 |
| ICP–LSV | 98.55 | 74.21 | 46.02 | 26.75 | 9.88 | 2.41 |
| DFF | 98.30 | 95.90 | 90.12 | 65.06 | 40.48 | 18.80 |
| LHFFO | 98.80 | 98.31 | 94.22 | 80.48 | 64.58 | 44.82 |
| Proposed method | 98.82 | 98.41 | 95.28 | 85.06 | 74.94 | 64.92 |
| Probe/Gallery | Straight-On | 15° Off | 30° Off | 45° Off |
|---|---|---|---|---|
| Straight-On | 100 | 95.8 | 87.5 | |
| [100,100, 100,100] | [95.8,87.5, 95.8,87.5] | [87.5,70.8, 87.5,70.8] | ||
| 15° off | 100 | 100% | 91.7% | |
| [100,100, 100,100] | [100,100, 100,100] | [91.7,83.3, 91.7,87.5] | ||
| 30° off | 100% | 100% | 95.8% | |
| [100,91.7, 100,87.5] | [100,100, 100,100] | [95.8,87.5, 91.7,95.8] | ||
| 45° off | 87.5 | 91.7 | 100 | |
| [83.3,58.3, 83.3,79.2] | [91.7,83.3, 91.7,87.5] | [100,83.3, 95.8,100] |
| Method | Number of SPG * | Ear Normalization | Rank-1 Recognition Rate (%) | Runtime (per Pair Sample) |
|---|---|---|---|---|
| VICP | 1 | Yes | 97.8 | 5–8 s |
| ICP–LSV | 1 | Yes | 98.55 | 2.72 s |
| DFF | 1 | No | 98.3 | 0.02 s |
| LHFFO | 1 | No | 98.8 | 0.019 s |
| Ganapathi and Prakash [9] | 1 | Yes | 98.69 | 0.36 s |
| Proposed method | 1 | No | 98.82 | 0.033 s |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Q.; Mu, Z. PointNet++ and Three Layers of Features Fusion for Occlusion Three-Dimensional Ear Recognition Based on One Sample per Person. Symmetry 2020, 12, 78. https://doi.org/10.3390/sym12010078
Zhu Q, Mu Z. PointNet++ and Three Layers of Features Fusion for Occlusion Three-Dimensional Ear Recognition Based on One Sample per Person. Symmetry. 2020; 12(1):78. https://doi.org/10.3390/sym12010078
Chicago/Turabian StyleZhu, Qinping, and Zhichun Mu. 2020. "PointNet++ and Three Layers of Features Fusion for Occlusion Three-Dimensional Ear Recognition Based on One Sample per Person" Symmetry 12, no. 1: 78. https://doi.org/10.3390/sym12010078
APA StyleZhu, Q., & Mu, Z. (2020). PointNet++ and Three Layers of Features Fusion for Occlusion Three-Dimensional Ear Recognition Based on One Sample per Person. Symmetry, 12(1), 78. https://doi.org/10.3390/sym12010078





