Adaptive Stabilization of a Fractional-Order System with Unknown Disturbance and Nonlinear Input via a Backstepping Control Technique
Abstract
1. Introduction
2. Preliminaries and System Description
3. Main Results
4. Simulation Results
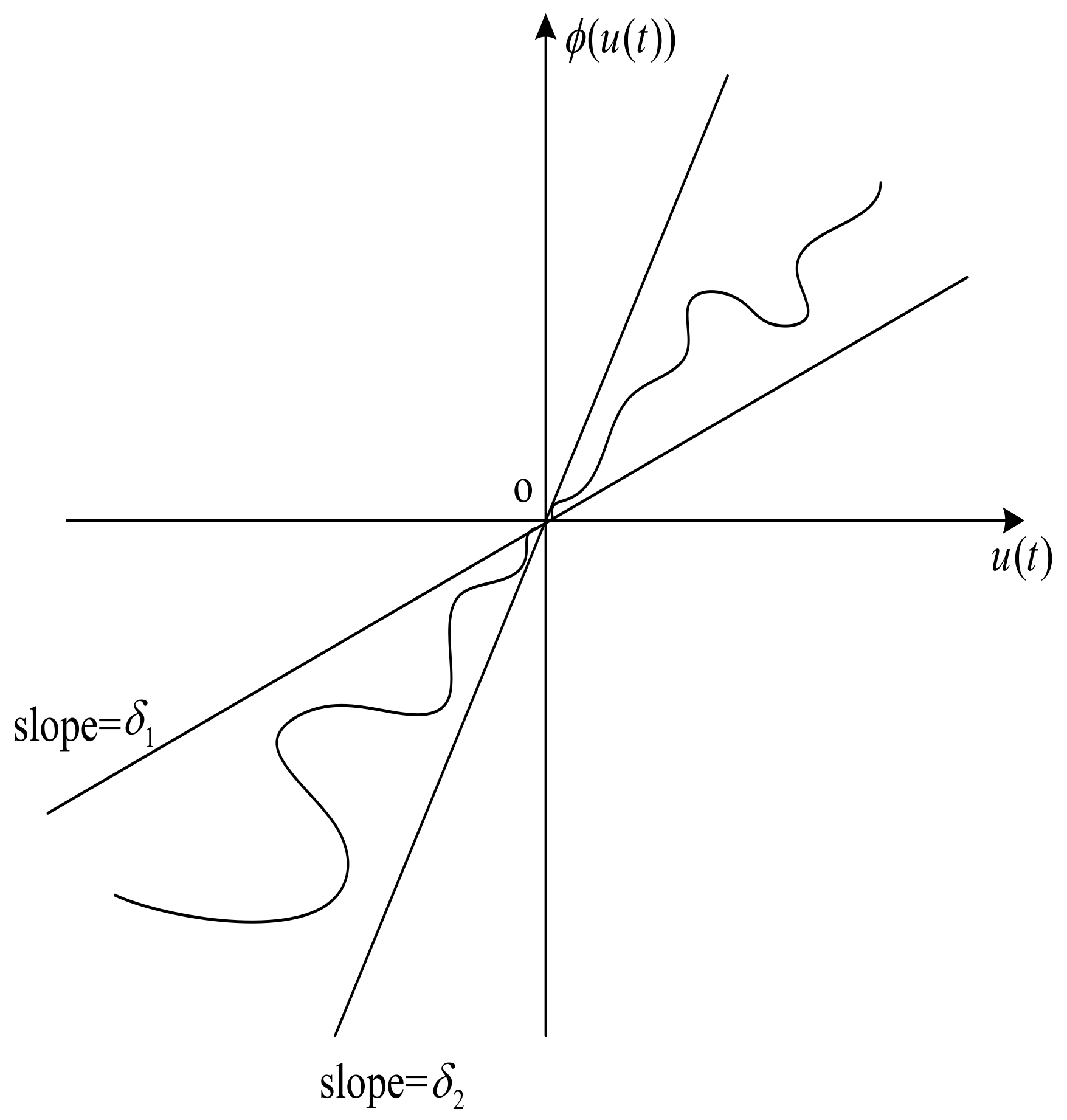
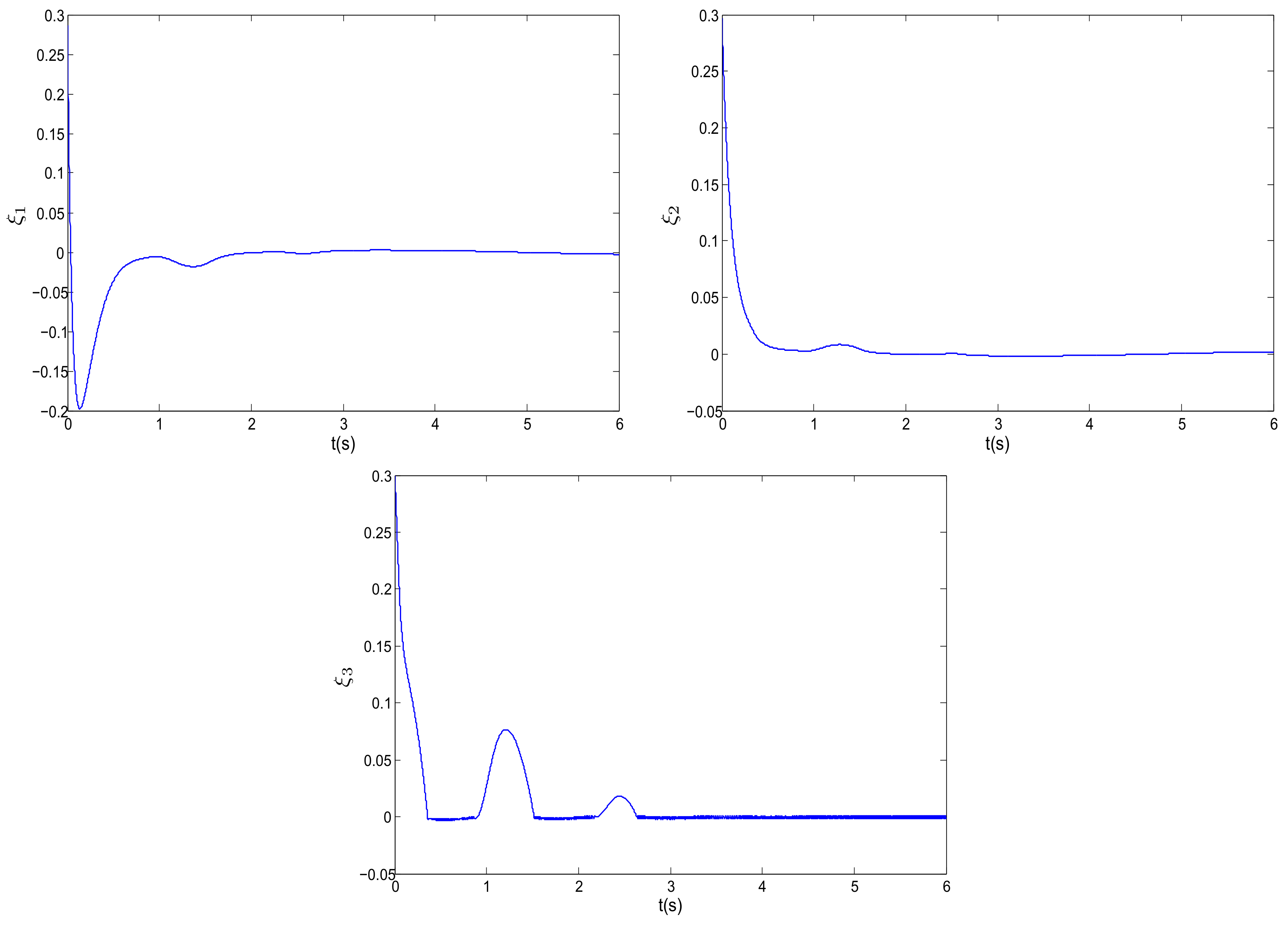
4.1. Adaptive Stabilization of Fractional-Order Chua System with Sector Nonlinear Input
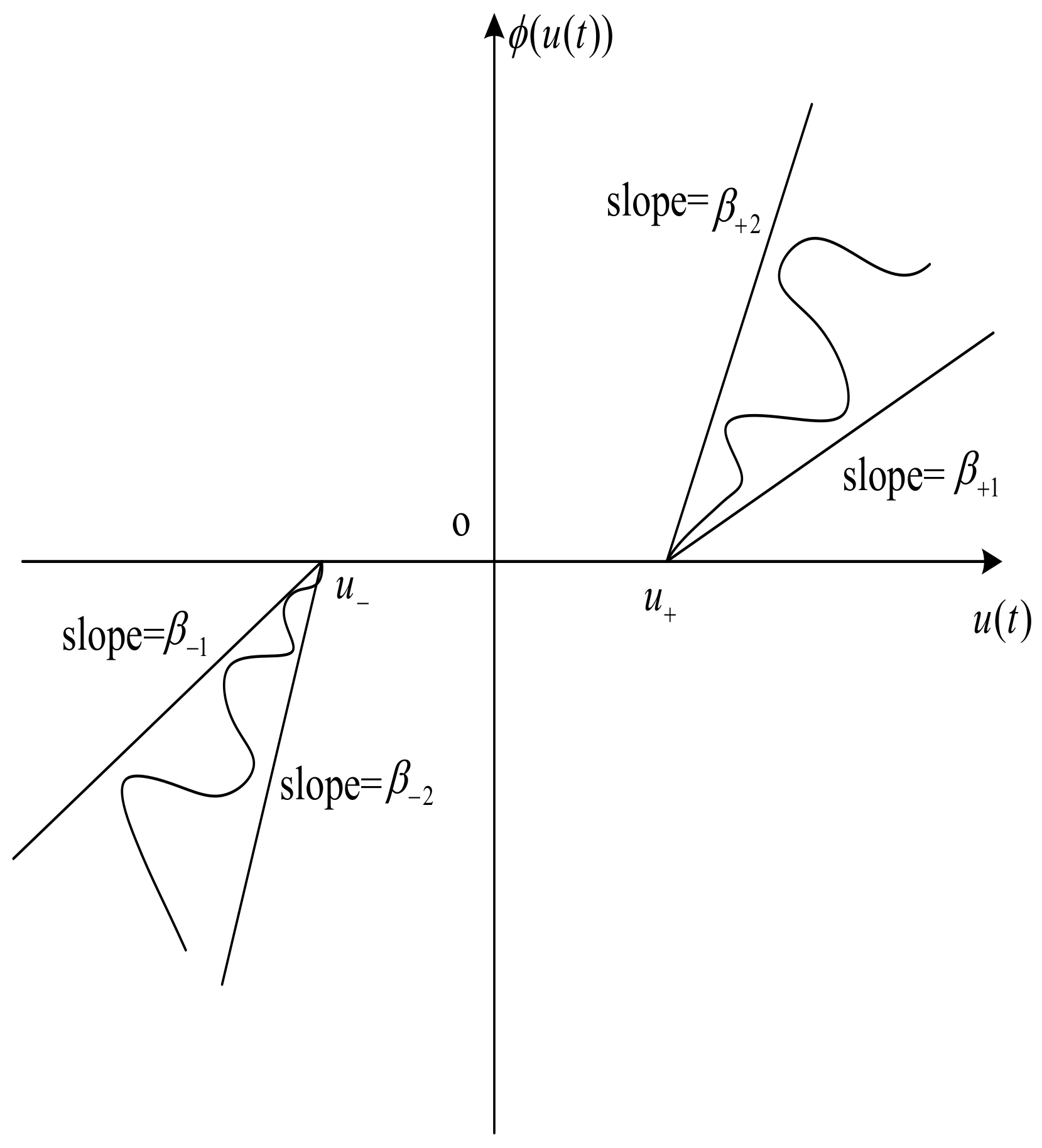
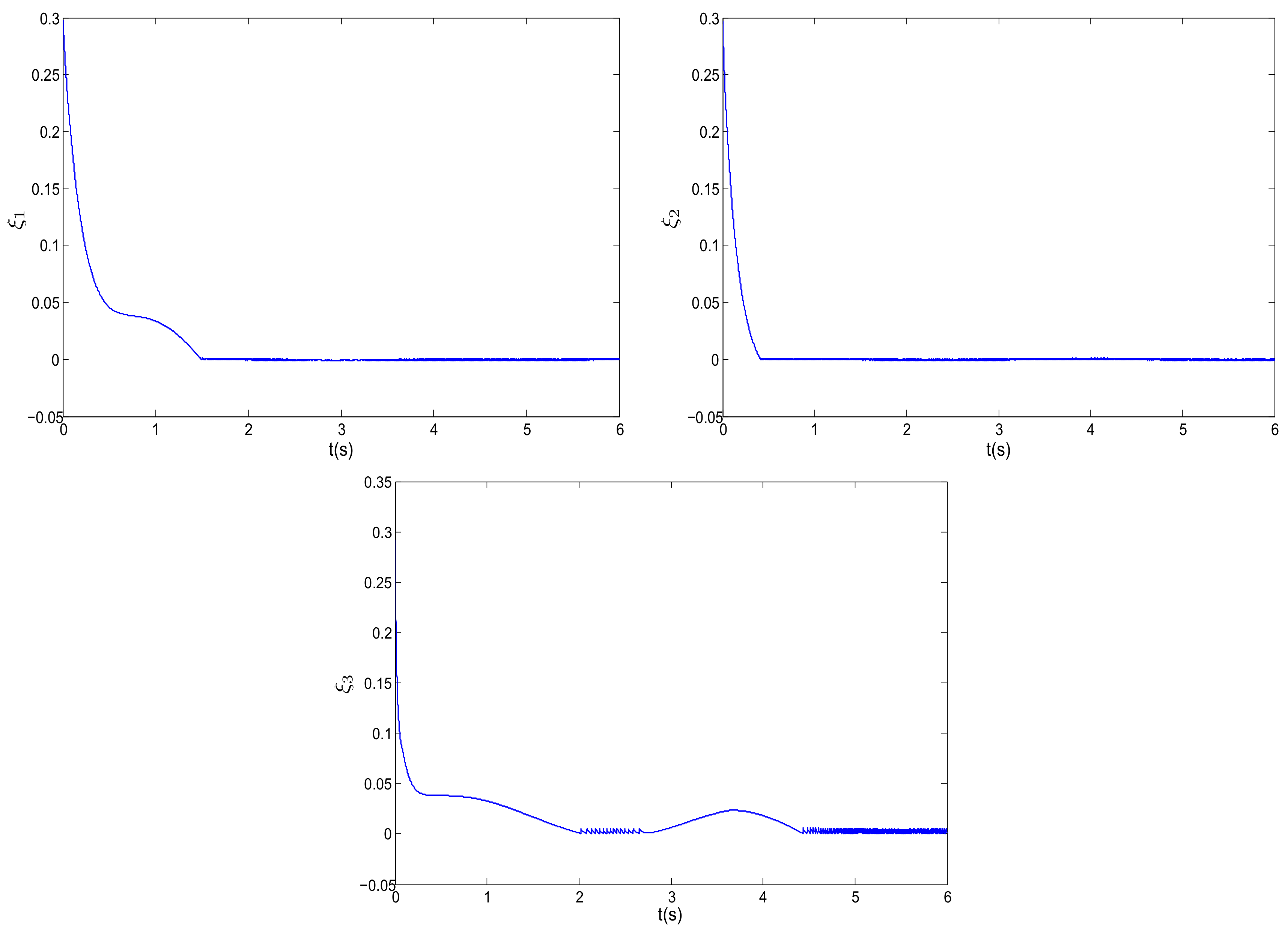
4.2. Adaptive Stabilization of Fractional-Order Rossler’s System with Dead-Zone Nonlinear Input
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bagley, R.L.; Calico, R.A. Fractional order state equations for the control of viscoelastically damped structure. J. Guid. Control Dyn. 1991, 14, 304–311. [Google Scholar] [CrossRef]
- Frederico, G.S.F.; Torres, D.F.M. A formulation of Noether’s theorem for fractional problems of the calculus of variations. J. Math. Anal. Appl. 2007, 334, 834–846. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhai, X.H. Noether symmetries and conserved quantities for fractional Birkhoffian systems. Nonlinear Dyn. 2015, 81, 469–480. [Google Scholar] [CrossRef]
- Zhai, X.H.; Zhang, Y. Noether symmetries and conserved quantities for fractional Birkhoffian systems with time delay. Commun. Nonlinear Sci. 2016, 36, 81–97. [Google Scholar] [CrossRef]
- Song, C.J. Noether symmetry for fractional Hamiltonian system. Phys. Lett. A 2019, 383, 12914. [Google Scholar] [CrossRef]
- Dumlu, A.; Erenturl, K. Trajectory tracking control for a 3-DOF parallel manipulator using fractional-order PIλDμ control. IEEE Trans. Ind. Electron. 2014, 61, 3417–3426. [Google Scholar] [CrossRef]
- Ni, J.; Liu, L.; Liu, C.; Hu, X. Fractional order fixed-time nonsingular terminal sliding mode synchronization and control of fractional order chaotic systems. Nonlinear Dyn. 2017, 89, 2065–2083. [Google Scholar] [CrossRef]
- Liu, H.; Pan, Y.; Chen, Y. Adaptive fuzzy backstepping control of fractional-order nonlinear systems. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 2209–2217. [Google Scholar] [CrossRef]
- Aghababa, M.P.; Khanmohammadi, S.; Alizadeh, G. Finite-time synchronization of two different chaotic systems with unknown parameters via sliding mode technique. Appl. Math. Model. 2011, 35, 3080–3091. [Google Scholar] [CrossRef]
- Bigdeli, N.; Ziazi, H.A. Finite-time fractional-order adaptive intelligent backsstepping sliding mode control of uncertain fractional-order chaotic systems. J. Frankl. Inst. 2017, 354, 160–183. [Google Scholar] [CrossRef]
- Luo, R.Z.; Huang, M.C.; Su, H.P. Robust control and synchronization of 3-D uncertain fractional-order chaotic systems with external disturbances cia adding one power integrator control. Complexity 2019, 2019, 8417536. [Google Scholar] [CrossRef]
- Shukla, M.K.; Sharma, B.B. Backstepping based stabilizaiton and synchronizaiton of a class of fractional order chaotic systems. Chaos Soliton Fract. 2017, 102, 274–284. [Google Scholar] [CrossRef]
- Shukla, M.K.; Sharma, B.B. Stabilizaiton of a class of fractional order chaotic systems via backstepping approach. Chaos Soliton Fract. 2017, 98, 56–62. [Google Scholar] [CrossRef]
- Wei, Y.H.; Sheng, D.; Chen, Y.Q.; Wang, Y. Fractional order chattering-free robust adaptive backstepping control technique. Nonlinear Dyn. 2019, 95, 2383–2394. [Google Scholar] [CrossRef]
- Wei, Y.H.; Chen, Y.Q.; Liang, S.; Wang, Y. A novel algorithm on adaptive backstepping control of fractional order systems. Neurocomputing 2015, 165, 395–402. [Google Scholar] [CrossRef]
- Sheng, D.; Wei, Y.H.; Cheng, S.S.; Shuai, J.M. Adaptive backstepping control for fractional order systems with input saturation. J. Frankl. Inst. 2017, 354, 2245–2268. [Google Scholar] [CrossRef]
- Ha, S.M.; Liu, H.; Li, S.G.; Liu, A.J. Backstepping-based adaptive fuzzy synchronization control for a class of fractional-order chaotic systems with input saturation. Int. J. Fuzzy Syst. 2019, 21, 1571–1584. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Trigeassou, J.C.; Maamri, N.; Sabatier, J.; Oustaloup, A. State variables and transients of fractional order differential systems. Comput. Math. Appl. 2012, 64, 3117–3140. [Google Scholar] [CrossRef]
- Trigeassou, J.C.; Maamri, N.; Sabatier, J.; Oustaloup, A. Transients of fractional-order integrator and derivatives. Signal Image Video Process. 2012, 6, 359–372. [Google Scholar] [CrossRef]
- Trigeassou, J.C.; Maamri, N. Initial conditions and initialization of linear fractional differential equations. Signal Process. 2011, 91, 427–436. [Google Scholar] [CrossRef]
- Shukla, M.K.; Sharma, B.B. Control and synchronizaiton of a class of uncertain fractional order chaotic systems via adaptive backstepping control. Asian J. Control 2018, 20, 707–720. [Google Scholar] [CrossRef]
- Chen, Y.Q.; Wei, Y.H.; Zhou, X.; Wang, Y. Stability for nonlinear fractional order systems: An indirect approach. Nonlinear Dyn. 2017, 89, 1011–1018. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, L.; Liu, C.X.; Zhu, Z.W.; Sun, Z.Q. Fractional-order adaptive backstepping control of a noncommensurate fractional-order ferroresonance system. Math. Probl. Eng. 2018, 8091757. [Google Scholar] [CrossRef]
- Luo, R.Z.; Wang, Y.L.; Deng, S.C. Combination synchronization of three classic chaotic systems using active backstepping design. Chaos 2011, 21, 043114. [Google Scholar]
- Liu, S.Y.; Liu, Y.C.; Wang, N. Nonlinear disturbance observer-based backstepping finite-time sliding mode tracking control of underwater vehicles with system uncertainties and external disturbances. Nonlinear Dyn. 2017, 88, 465–476. [Google Scholar] [CrossRef]
- Chen, C.P.; Wen, G.X.; Liu, Y.J.; Liu, Z. Observer-based adaptive backstepping consensus tracking control for high-order nonlinear semi-feedback multiagent systems. IEEE Trans. Cybern. 2016, 46, 1591–1601. [Google Scholar] [CrossRef]
- Ding, D.S.; Qi, D.L.; Peng, J.M.; Wang, Q. Asymptoic pseudo-state stabilization of commensurate fractional-order nonlinear systems with additive disturbance. Nonlinear Dyn. 2015, 81, 667–677. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N. A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn. 2002, 29, 3–22. [Google Scholar] [CrossRef]
- Li, C.; Chen, G. Chaos and hyperchaos in the fracitional-order Rossler equations. Physica A 2004, 341, 55–61. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, X.; Yang, Z. Adaptive Stabilization of a Fractional-Order System with Unknown Disturbance and Nonlinear Input via a Backstepping Control Technique. Symmetry 2020, 12, 55. https://doi.org/10.3390/sym12010055
Tian X, Yang Z. Adaptive Stabilization of a Fractional-Order System with Unknown Disturbance and Nonlinear Input via a Backstepping Control Technique. Symmetry. 2020; 12(1):55. https://doi.org/10.3390/sym12010055
Chicago/Turabian StyleTian, Xiaomin, and Zhong Yang. 2020. "Adaptive Stabilization of a Fractional-Order System with Unknown Disturbance and Nonlinear Input via a Backstepping Control Technique" Symmetry 12, no. 1: 55. https://doi.org/10.3390/sym12010055
APA StyleTian, X., & Yang, Z. (2020). Adaptive Stabilization of a Fractional-Order System with Unknown Disturbance and Nonlinear Input via a Backstepping Control Technique. Symmetry, 12(1), 55. https://doi.org/10.3390/sym12010055



